EN中文

地球信息科学学报 >

2025 , Vol. 27 >Issue 7: 1501 - 1519

DOI: https://doi.org/10.12082/dqxxkx.2025.250161

地球信息科学理论与方法

贝叶斯时空统计方法及应用进展与趋势

  • 李俊明 , 1, * ,
  • 胡雅璇 1 ,
  • 王楠楠 2 ,
  • 王斯雅琦 1 ,
  • 王若兰 1 ,
  • 吕琳 1 ,
  • 房紫晴 1
展开
  • 1.山西财经大学统计学院，太原 030006
  • 2.内蒙古包头市自然资源调查利用中心，包头 014010

作者贡献：Author Contributions

李俊明、胡雅璇和王楠楠参与了内容构思、文献收集与初稿写作；王斯雅琦和王若兰参与了初稿写作；李俊明、吕琳和房紫晴参与了论文修改。所有作者均阅读并同意最终稿件的提交。

LI Junming, HU Yaxuan, and WANG Nannan contributed to the conceptualization, literature collection, and initial draft writing; WANG Siyaqi and WANG Ruolan contributed to the initial draft writing; LI Junming, LÜ Lin and FANG Ziqing contributed to the manuscript revision. All authors read and approved the final manuscript for submission.

李俊明（1979— ），男，山西太原人，博士，教授，主要从事贝叶斯时空统计方面的研究。E-mail: ;

收稿日期: 2025-04-07

  修回日期: 2025-06-17

  网络出版日期: 2025-07-07

基金资助

国家社科基金重大项目(24&ZD183)

收起

Advances and Trends in Bayesian Spatio-Temporal Statistical Methods and Applications

  • LI Junming , 1, * ,
  • HU Yaxuan 1 ,
  • WANG Nannan 2 ,
  • WANG Siyaqi 1 ,
  • WANG Ruolan 1 ,
  • LYU Lin 1 ,
  • FANG Ziqing 1
Expand
  • 1. School of Statistics, Shanxi University of Finance and Economics, Taiyuan 030006, China
  • 2. Baotou Natural Resources Survey and Utilization Center, Inner Mongolia, Baotou 014010, China
*LI Junming, E-mail:

Received date: 2025-04-07

  Revised date: 2025-06-17

  Online published: 2025-07-07

Supported by

National Social Science Fund of China(Major Project)(24&ZD183)

Fold

摘要

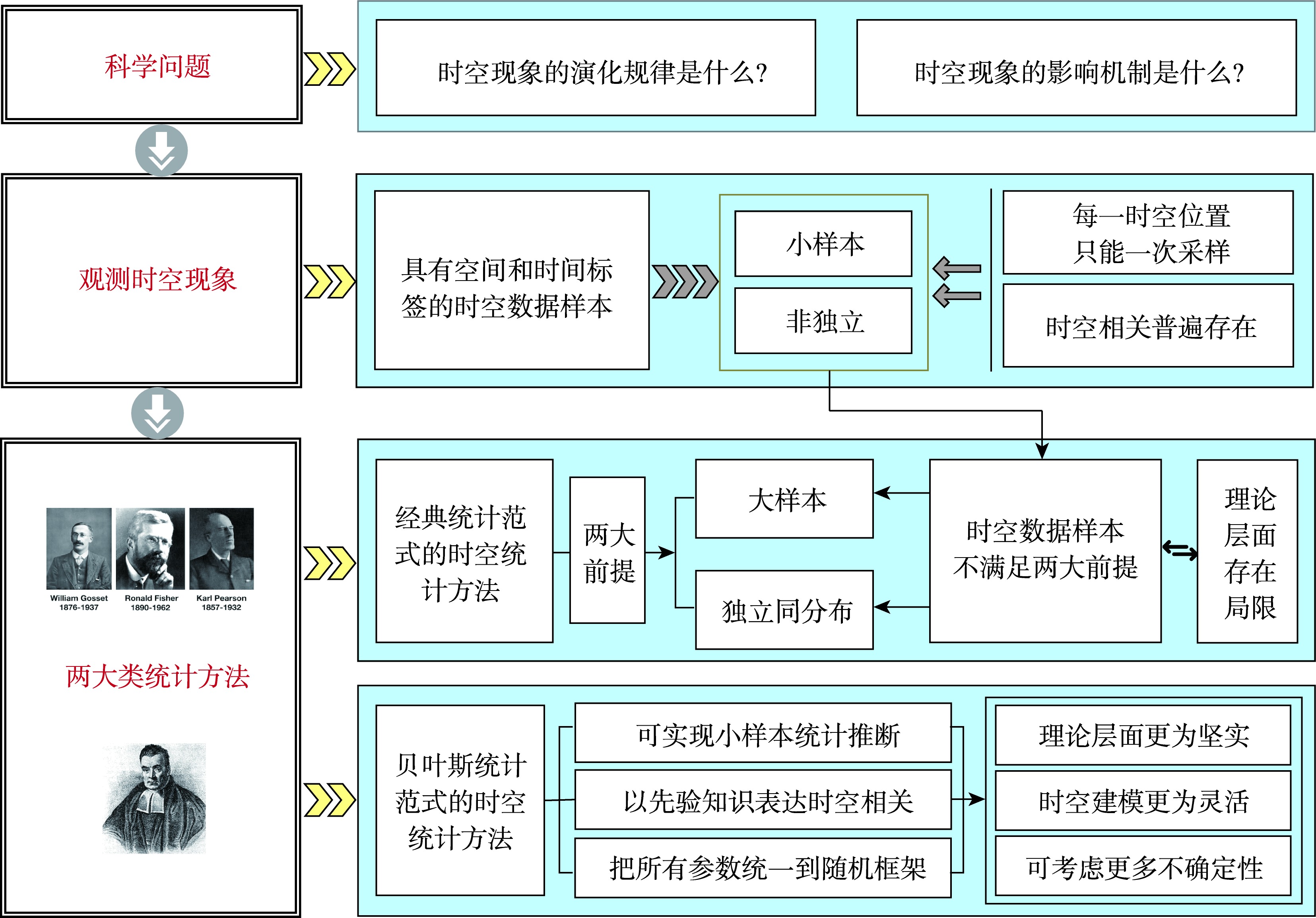
【意义】经典统计推断依赖大样本与独立同分布前提，但时空数据却往往不满足这两大前提，因此，经典统计框架下的时空统计方法具有一定理论局限；相较而言，贝叶斯统计范式下的时空统计方法通过融合先验信息、引入参数随机性，形成统一的概率推断框架，可考虑更多不确定性，并能有效克服时空数据中的小样本和非独立问题，在时空统计建模中体现出较强的自身优势，并受到广泛关注和快速发展。【进展】本文首先从方法论演进角度出发，从传统贝叶斯时空统计与贝叶斯时空机器学习两个视角系统梳理了主流的贝叶斯时空统计模型，前者包括贝叶斯时空演化层次模型、贝叶斯时空回归层次模型、贝叶斯空间面板数据模型、贝叶斯时空地理加权回归模型、贝叶斯时空变系数模型和贝叶斯网格化时空高斯过程模型，后者包括贝叶斯时空因果森林模型、贝叶斯时空神经网络模型和贝叶斯时空图卷积神经网络模型；后又从实际应用方面，重点回顾了贝叶斯时空统计模型在公共卫生、环境科学、经济社会与公共安全、能源与工程等领域的应用。【展望】贝叶斯时空统计方法需在多源异构数据建模、深度学习融合、因果推断机制引入及高性能计算优化等方面实现突破，以兼顾理论完备性与实践适应性，推动其发展为具备因果推断、自适应泛化及智能分析的下一代时空建模范式。

关键词： 贝叶斯统计; 时空统计; 时空依赖建模; 层次模型; 机器学习; 因果推断

本文引用格式

李俊明 , 胡雅璇 , 王楠楠 , 王斯雅琦 , 王若兰 , 吕琳 , 房紫晴 . 贝叶斯时空统计方法及应用进展与趋势[J]. 地球信息科学学报, 2025 , 27(7) : 1501 -1519 . DOI: 10.12082/dqxxkx.2025.250161

Abstract

[Objectives] Classical statistical inference typically relies on the assumptions of large sample sizes and independent, identically distributed (i.i.d.) observations, conditions that spatio-temporal data frequently violate, leading to inherent theoretical limitations in conventional approaches. In contrast, Bayesian spatio-temporal statistical methods integrate prior knowledge and treat all model parameters as random variables, thereby forming a unified probabilistic inference framework. This enables the incorporation of a broader range of uncertainties and offers robustness in modelling small samples and dependent structures, making Bayesian methods highly advantageous and increasingly influential in spatio-temporal analysis. [Progress] From the perspective of methodological evolution, this paper systematically reviews mainstream Bayesian spatio-temporal statistical models from two complementary perspectives: traditional Bayesian statistics and the Bayesian machine learning. The former includes Bayesian Spatio-temporal Evolutionary Hierarchical Models, Bayesian Spatio-temporal Regression Hierarchical Models, Bayesian Spatial Panel Data Models, Bayesian Geographically Weighted Spatio-temporal Regression Models, Bayesian Spatio-temporal Varying Coefficient Models, and Bayesian Spatio-temporal Meshed Gaussian Process Model. The latter includes Bayesian Causal Forest Models, Bayesian Spatio-temporal Neural Networks, and Bayesian Graph Convolutional Neural Networks. In terms of application, the review highlights representative studies across domains such as public health, environmental sciences, socio-economic and public safety, as well as energy and engineering. [Prospect] Bayesian spatio-temporal statistical methods need to achieve breakthroughs in multi-source heterogeneous data modeling, integration with deep learning, incorporation of causal inference mechanisms, and optimization of high-performance computing. These advances are essential to balance theoretical rigor with practical adaptability and to promote the development of a next-generation spatio-temporal modeling paradigm characterized by causal inference, adaptive generalization, and intelligent analysis.

Key words： Bayesian statistics; spatio-temporal statistics; spatio-temporal dependency modeling; hierarchical models; machine learning; causal inference

1 引言

在信息技术和数字经济的迅猛发展背景下，各领域数据呈爆炸式增长，数据已成为驱动经济社会发展的关键生产要素，而具有时空信息的多模态时空数据已成为数据要素中的重要组成部分，时空数据的深度挖掘也成为释放数据潜能的关键路径之一。时空统计方法主要存在2种范式：经典时空统计和贝叶斯时空统计。与经典时空统计方法相比而言，贝叶斯时空统计方法不仅可以克服时空数据中存在的小样本和非独立同分布问题，而且还具有强大的信息融合和不确定性处理能力。目前已在地球信息学、环境科学、公共卫生、经济学和社会学等众多领域中展现出独特的模型优势和广泛的应用前景，特别是近几年出现的贝叶斯机器学习模型，以此为基础可以构建出专门用于分析复杂时空过程的贝叶斯时空机器学习模型，这也是贝叶斯时空统计方法发展的新方向和新趋势，也会成为科学分析和深入理解时空动态过程的新途径和新视角。
贝叶斯时空统计方法不仅擅长于传统的时空数据分析场景，在时空大数据的深度挖掘方面，也表现出独特优势。贝叶斯时空统计方法继承了贝叶斯统计范式的底层思想，通过引入先验知识，实现了在总体、样本和先验等3个维度信息的综合基础上的时空统计推断，进而可以有效地解决经典统计方法在面对复杂时空数据结构时的局限性；另外，贝叶斯时空统计方法把所有变量（总体参数和样本统计量）都视为随机变量，都统一到了随机过程的同一框架下进行建模，确保了分析的一致性，同时提供了足够的灵活性来适应不同类型的数据结构和研究问题。其核心优势在于能够表达和量化参数的不确定性，同时允许先验信息整合到模型中，通过先验分布将先验知识与观测数据结合，利用贝叶斯定理更新后验分布，从而得到对参数更为准确的估计，为研究人员提供了一个强有力的分析工具。
然而，尽管贝叶斯时空统计方法已经取得了显著进展，但在应用过程中仍然面临着一系列挑战，如计算成本高、模型选择和评价的复杂性，以及如何更好地理解和解释模型结果等问题。近年来，随着机器学习和人工智能技术的迅速发展，也推动了贝叶斯时空统计方法的深入拓展。通过结合贝叶斯方法和深度学习技术，在提高预测精度和处理高维数据方面取得了重要进展。贝叶斯时空统计方法的最新发展，不仅推动了时空统计理论体系的丰富，也促进了时空分析应用领域的深化。 Bernardinelli等[1]在1995年把贝叶斯统计理念引入疾病风险时空数据分析领域， Li等[2]进一步完善了贝叶斯时空统计框架，并提出一种贝叶斯时空层次模型（Bayesian spatiotemporal hierarchy model, BSTHM），其将贝叶斯统计方法与时空交互模型有机融合，用于分析各类地理现象的时空演化趋势及其时空影响关系；随后，BSTHM在各个领域逐渐得到广泛应用，如环境保护[3-5]、公共卫生[6-9]、公共管理[10-11]、环境经济[12]、卫生经济[13-14]、宏观经济[15-16]等。
本综述旨在全面回顾贝叶斯时空统计的基本原理、研究进展以及在不同领域的应用，并提出当前面临的挑战和未来发展趋势。特别地，本文将探讨贝叶斯时空统计模型如何与机器学习相结合，以及这些技术如何帮助我们更好地理解和应对全球性挑战，如气候变化和公共卫生危机。通过对现有文献的深入分析和总结，希望能够为相关领域的研究人员提供一个系统的参考框架，促进贝叶斯时空统计方法的进一步发展和应用。

2 贝叶斯时空统计基础概述

贝叶斯统计作为一种将总体、样本和先验3类信息融合的概率推断范式，近年来在时空统计建模中得到广泛应用。其核心理念是将所有未知参数视为随机变量，并基于贝叶斯定理在观测数据基础上动态更新参数的先验认知，这一机制天然适用于小样本、高不确定性、非独立同分布等复杂问题场景。时空统计分析旨在解决2个基本问题：① 时空现象的演化规律是什么?即属性变量yit在空间和时间维度上的演化规律是什么? ② 时空现象的影响机制是什么?即属性变量yit变化的影响因素及其机制是什么?时空数据的典型特点是采样稀疏和非独立性，具体而言，对于每一个时空位置，只能一次采样，呈现出n = 1的小样本特征，同时，根据地理学第一定理，时空相邻位置间的样本又具有相关性，综上可知，时空数据打破了经典统计方法所依赖的大样本和独立同分布（i.i.d.）假设，基于经典统计范式的时空统计方法如空间面板模型、地理加权回归等，虽在实践中应用广泛，但往往依赖大样本与独立同分布假设，因此其具有一定理论局限性，而基于贝叶斯统计范式的时空统计方法可有效克服小样本问题，并且能够通过引入空间或时间滞后先验，把时空相关性以先验知识纳入模型，显式建模空间邻近与时间依赖关系，同时把所有参数统一到随机框架，具备了更强的不确定性捕捉能力与建模灵活性。相较于经典统计范式的时空统计方法，贝叶斯时空统计方法具有更为坚实的理论基础与自身优势，特别是通过层次模型结构，贝叶斯时空统计方法更易于刻画多层次、多尺度的时空异质性和时空过程，特别适用于处理时空结构复杂和数据多源异构的问题；此外，其灵活的建模框架使其易于扩展至非线性结构、动态过程建模及因果推理等任务中（图1）。尽管在计算效率方面仍存在一定挑战，但在不确定性考量、模型扩展与精确预测等实际问题中，贝叶斯时空统计方法表现出更强的适应性和实践优势。
图1 两大统计范式下的时空统计比较

Fig. 1 Spatiotemporal statistics compared under two major statistical paradigms

3 贝叶斯时空统计模型的现状及进展

近年来，围绕时空演化规律和时空影响机制两类问题，学界提出了多个贝叶斯时空统计模型。对于时空演化规律问题，贝叶斯时空演化层次模型（Bayesian Spatio-temporal Evolution Hierarchical Model, BSTEHM）是一种有效的建模框架，通过将空间和时间依赖关系整合纳入层次模型，在充分考虑时空相关性的基础上，科学地刻画复杂的时空演化过程，此外，BSTEHM还通过参数的后验分布来量化估计结果的不确定性，提供了更为精确和可信的估计结果；围绕时空影响机制问题，学界首先提出的是传统贝叶斯时空统计模型，可分为3类，即全局时空影响关系建模类，包括贝叶斯时空回归层次模型（Bayesian Spatiotemporal Regression Hierarchial Model, BSTRHM）和贝叶斯空间面板数据模型（Bayesian Spatial Panel Data Models, BSPDM），异质性时空局部建模类，包括贝叶斯时空变系数模型（Bayesian Spatiotemporal Variable Coefficient Model, BSTVCM）和贝叶斯时空地理加权回归模型（Bayesian spatiotemporal geographically weighted regression, BSTGWR），连续时空过程预测建模类——贝叶斯时空网格化高斯过程模型（Bayesian Spatiotemporal Meshed Gaussian Process, BSTMGP）；这些模型通过捕捉时空因素的相互作用，能够有效揭示时空属性变量yit变化的影响机制。随着机器学习技术的兴起和发展，贝叶斯时空统计与机器学习的结合产生了贝叶斯时空机器学习方法，主要有贝叶斯时空因果森林模型（Bayesian Spatiotemporal Causal Forest Model, BSTCFM）、贝叶斯时空神经网络模型（Bayesian spatiotemporal neutral network, BSTNN）和贝叶斯时空图卷积神经网络模型（Bayesian Spatiotemporal Graph Convolution Neutral Network, BSTGCNN）。这些前沿方法不仅能够揭示时空数据中的复杂非线性关系，还能有效处理大规模时空数据，特别是在交通流、气候变化、公共卫生和社交网络等领域的应用中具有广泛前景。图2展示了贝叶斯时空统计方法的体系框架。
图2 贝叶斯时空统计方法体系框架

Fig. 2  Conceptual framework of Bayesian spatiotemporal statistical methods

贝叶斯时空统计方法正在向更高维度、更复杂系统地建模与推断进化，不仅为时空数据的分析提供了新的视角，也推动了跨学科领域的融合与发展。表1列出了上述贝叶斯时空统计模型的优点与缺点。不管是传统贝叶斯时空统计模型还是贝叶斯时空机器学习模型，本质上都是贝叶斯统计范式下的时空依赖建模，即显式或隐式考虑空间邻近与时间连续对时空属性变量yit的影响关系。由于地理位置相近或时间相近的数据往往存在相似性（即“时空相关”），时空依赖建模通过引入如空间权重矩阵（如 CAR、 SAR）、时间结构项（如AR(1)、 RW1）或协方差函数（如高斯过程）等机制，捕捉这种时空交互作用与动态演化特征，从而提高模型对时空异质性和动态过程的刻画能力。接下来，将具体介绍贝叶斯时空统计方法的研究现状与进展。
表1 不同贝叶斯时空统计模型的优缺点对比

Table 1 Comparison of the advantages and disadvantages of different Bayesian spatiotemporal statistical models

方法类别 贝叶斯时空统计模型 模型优点 模型缺点
传统统计模型 时空演化规律分析类 贝叶斯时空演化层次模型 (BSTEHM) 可以捕捉总体和局部时空演化趋势 无法揭示时空影响机制
全局时空影响机制建模类 贝叶斯时空回归层次模型 (BSTRHM) 可估计总体时空影响关系，解释性强 假设影响关系时空同质，不能捕捉时空异质性
贝叶斯空间面板数据模型 (BSPDM) 同时考虑时空动态效应，适合面板数据 假设影响关系时空同质，无法刻画局部时空差异
异质性时空局部建模类 贝叶斯时空地理加权回归
模型 (BSTGWR)		 强调局部时空异质性，灵活捕捉局部
时空差异		 对空间权重敏感，存在边界效应，计算量较大
贝叶斯时空变系数模型 (BSTVCM) 时空动态参数变化灵活，体现局部
异质性		 参数多且复杂，易过拟合，计算量较大
连续时空过程分析类 贝叶斯网格化时空高斯过
程模型 (BSTMGP)		 连续时空分析能力强，擅长分析大规模
时空数据		 计算复杂度较高，实际应用受限
机器学习模型 时空因果
推断类		 贝叶斯时空因果森林模型 (BSTCFM) 能有效识别高维复杂数据中的因果机制 模型结构复杂，参数解释与计算负担较高
时空深度
学习类		 贝叶斯时空神经网络模型 (BSTNN) 对非线性、高维时空依赖结构建模优势
明显；泛化能力强		 参数规模大，计算负担重，解释性弱
时空图学习类 贝叶斯时空图卷积神经网
络模型 (BSTGCNN)		 可捕捉复杂网络结构中时空交互效应，
图结构数据适应性极强		 模型复杂度高，需较多计算资源，训练数据需求大

3.1 传统贝叶斯时空统计方法

传统贝叶斯时空统计方法主要基于分层建模理念，通过引入时空依赖项，形成系列贝叶斯时空建模框架。根据研究目的与模型结构，本文将传统贝叶斯时空统计方法归纳为以下4类（表1）：① 时空演化趋势分析类——贝叶斯时空演化层次模型，主要用于揭示时空响应变量Yit的时空动态演化规律； ② 全局时空影响关系建模类，包括贝叶斯时空回归层次模型与贝叶斯空间面板数据模型，强调全局变量关系分析与影响机制； ③ 异质性时空局部建模类，主要涵盖贝叶斯时空地理加权回归模型和贝叶斯时空变系数模型，侧重于探究影响关系的时空异质性特征； ④ 连续时空过程分析类——贝叶斯网格化时空高斯过程模型，适合于时空过程的连续拟合与高效预测场景。

3.1.1 时空演化趋势建模类：贝叶斯时空演化层次模型

时空演化过程是时空统计领域中的一个核心研究主题，旨在揭示属性变量随时间和空间变化的规律。目前，常见的研究方法主要包括简单描述统计、时空核密度分析和时空Dagum基尼系数法等，这些方法在一定程度上可以理解时空现象的基本模式和分布特征，但却无法充分考虑时空相关性和空间异质性，也缺乏对不确定性的量化分析。与之相比，贝叶斯时空演化层次模型（BSTEHM）通过引入空间和时间依赖关系的层次结构，能够在更为精细的框架下刻画复杂的时空演化过程，并通过参数的后验分布来量化不确定性。BSTEHM由Li和 Haining[2]在2014年提出，主要由贝叶斯统计层次模型与时空交互模型整合而成，其数学一般形式如下：
y i t ~ P ( μ i t ,   σ 2 )
μ i t = α + s i + v t + γ i t + ε i t
s i ~ C A R . N o r m a l ( W s i , τ i 2 )
v t ~ C A R . N o r m a l ( W v t , ω t 2 )
θ ~ Φ ( ϑ , ξ )
式中：yit是时空因变量； P(μit, σ2)为对应的似然分布，可根据具体问题具体确定，一般而言，对于计数数据，常用泊松分布或二项分布，对于连续数据，常用正态分布，式（1）是对应的时空演化方程； α是总体基底水平； Si和vt是稳态空间格局和总体变化趋势参数，其先验分别采用空间维和时间维的BYM模型先验[17]，把时空相关以先验知识纳入模型，表达时空结构效应； Wsi和Wvt分别表示i空间单元和t时间点的时空邻接； τ i 2和 ω t 2是对应的空间和时间非结构效应参数； γi(t)代表i空间单元上因变量的局部变化过程，一般是线性形式，代表线性变化过程，也可以根据研究采用非线性形式； θ代表所有的参数和超参数； Φ(ϑ，ξ）是θ的先验分布及其位置和尺度参数。
上述可知，BSTEHM可以把复杂的时空演化过程解耦为3个组分，稳态空间格局、总体变化趋势和局部变化趋势，其与通过简单平均获得的空间格局以及独立计算每个空间单元的变化趋势有本质区别；近年来，学者以BSTEHM为基础，提出了适用于遥感时空大数据的贝叶斯时空演化模型[18]，提高了BSTEHM的大数据分析能力，另外，围绕γi(t)的非线性改进，提出了贝叶斯自适应多阶段时空演化模型和贝叶斯时空样条模型[19]，大大增强了其非线性趋势估计的效能。BSTEHM充分体现了贝叶斯范式在不确定性建模与层次建模方面的优势，该模型将空间与时间依赖显式纳入层次结构，并结合后验分布推断机制，实现了对时空演化过程的精细刻画，其突出优点在于对稀疏观测、小样本情境具有良好鲁棒性，然而，BSTEHM主要聚焦于“趋势刻画”，不涉及驱动机制识别，同时，在面对大规模数据时，其计算成本仍需进一步优化。

3.1.2 全局时空影响关系建模类

（1）贝叶斯时空回归层次模型
贝叶斯时空回归层次模型（BSTRHM）综合了时空演化与时空影响过程，主要用于分析时空影响机制场景，其与常见的空间面板数据模型有一定区别，其为时空全局影响关系研究提供了坚实的贝叶斯范式支撑，可实现对回归系数的概率解释与不确定性度量，可扩展性也较强，支持多项式建模、分位数建模及高维稀疏结构建模，适应于多元复杂影响关系研究需求，但也应注意到，BSTRHM对时空结构建模仍较为有限，难以捕捉局部非平稳或异质性效应，其基础模型由Li和Haining在2018年提出[2]，BSTRHM的核心数学构成如下：
μ i t = α + s i + v t + ∑ k = 1 k β k X k i t + ε i t
在BSTRHM中，似然函数部分以及α、si、vt和εit的先验都与BSTEHM相同，不同的是增加了影响机制部分，即 ∑ k = 1 k β k X k i t， Xkit是影响因素，βk为对应的影响效应系数，其通过不同先验的确定，可以把OLS回归，岭回归和LASSO回归统一到一个框架，即，若βk的先验为无信息先验，则其均值点估计与OLS回归结果一致，若为正态先验，则与岭回归一致，若为拉普拉斯先验，则与LASSO回归一致，同时，由于贝叶斯统计可估计出βk的后验分布，因此明确估计出影响效应参数βk的不确定范围，而且也可以采用概率语言报告和解释影响关系的概率大小，比如，若估计出βk大于0的后验概率为0.85（P(βk>0|Data)=0.85），则可以解释为：因素xk有85%的概率对y具有正向影响作用。另外， BSTRHM中的时空固定效应参数si和vt是考虑了时空相关性的，因此其更能体现出多层次多水平的复杂效应，而空间计量模型中的时空固定效应是完全独立的，并未考虑实际存在的时空依赖关系。需要指出的是，贝叶斯时空分位数回归模型（Bayesian Spatio-temporal Quantile Regression Model, BSTQRM）[20]是BSTRHM 的一个重要变种，当关注响应变量在不同分位水平（如极端高值或低值）上的异质性影响机制时，可在BSTRHM框架下引入分位数损失函数与对应先验结构，构建BSTQRM，该模型不仅能估计响应变量在各分位点的影响效应，已被广泛用于气候变化、污染暴露和社会健康不平等等研究中。
BSTRHM自提出以来，学者在模型结构和计算方法方面进行了改进，以提高对复杂时空数据的处理能力，如针对高维数据，采用高斯过程先验和Pólya-Gamma分布的潜在变量，开发了高效的吉布斯采样器，提升了模型的计算效率和适用性[21]；此外，BSTRHM在流行病学领域中的应用也有所拓展。
（2）贝叶斯空间面板数据模型
贝叶斯空间面板数据模型（Bayesian Spatial Panel Data Model， BSPDM）[22]结合了空间计量模型与贝叶斯统计，通过引入空间滞后项与时空固定效应，以捕捉时空过程中的空间依赖和时间动态特征，具体而言， BSPDM通过引入空间权重矩阵衡量区域间的相互影响，通过引入空间滞后项WX，刻画自变量的空间溢出效应， BSPDM的数学表达式为：
μ i t = α + ∑ k = 1 k β k X k , i t + ∑ k = 1 k θ k W X k , i t + ψ i + λ t + ε i t
式中：因变量yit的似然函数同上，μit为似然分布的期望； α的意义同上； W是N×N的空间权重矩阵； Xk,it为第k个自变量； βk是自变量Xk,it的回归系数； θk为自变量空间滞后项WXk,it的回归系数，代表空间溢出效应； ψi和λt分别为空间和时间效应，其先验分布为无信息先验，这一点与BSTRHM存在区别； εit为随机误差项。
近年来BSPDM的研究进展主要是通过与分位数回归模型的结合，构建贝叶斯空间分位面板数据模型（Bayesian Spatial Quantile Panel Data Model，BSQPDM）[23-25]，以描述不同条件分位数下的变量关系。此外，为提高计算效率，学者提出了针对空间权重矩阵凸组合的重新参数化方法，简化了模型的贝叶斯估计过程[25-26]。改进的贝叶斯空间面板数据统计方法在区域经济分析、环境科学研究和公共健康领域应用广泛，揭示了时空依赖特征和空间溢出效应。
BSPDM的数学结构相对复杂，若参数维度较高，在高维协变量或非平稳场景中可能存在识别性问题，此外，空间权重矩阵的设定对BSPDM的估计结果影响较大，若未充分刻画真实邻接结构，可能导致有偏的空间效应估计，若能结合非线性影响、异质性动态响应与高维协变量选择等建模技术，或将拓展BSPDM的应用边界与适用能力。

3.1.3 异质性时空局部建模类

（1）贝叶斯时空地理加权回归模型
贝叶斯时空地理加权回归模型（Bayesian Spatiotemporal Geographically Weighted Regression, BSTGWR）是通过传统时空地理加权回归（STGWR）与贝叶斯统计框架融合实现，可同时捕捉空间和时间上的异质性及依赖性。模型的构成主要包括自变量的时空变化效应，并利用贝叶斯方法进行参数估计，其数学基本表达式为：
μ i t = α i t + ∑ k = 1 k X k , i t β k u i , v i , t + ε i t
同样，第i个位置在时间t上的因变量yit的似然函数同上； μit是对应似然分布的期望； Xk,it是第k个时空自变量； βk(ui,vi,t)是位置(ui, vi)和时间t的回归系数； εit为误差项。在贝叶斯框架下，回归系数βk(ui,vi,t)被视为随机变量，其一般被赋予无信息先验或正态先验，然后通过马尔可夫链-蒙特卡罗（MCMC）等方法获得后验分布及其点估计值。该模型能够有效描述影响关系在空间和时间上的不确定性及变异性。近年来，BSTGWR模型发展较为缓慢，主要集中在优化与扩展方面，有学者提出多尺度贝叶斯时空地理加权回归模型（MS-BSTGWR）[27]，通过引入集成嵌套拉普拉斯逼近（INLA）算法，实现了空间变化系数和带宽的高效估计，并成功应用于实际数据的分析。
BSTGWR模型结合了地理加权回归的局部建模思想与贝叶斯统计范式，能够有效刻画因变量与解释变量之间在不同地理位置和时间阶段的异质性影响关系，适合分析空间结构高度复杂或影响机制随时空变化的应用场景，其优势在于通过先验结构和后验推断，增强了模型对局部时空复杂变化的响应能力；然而，该模型在参数设定上存在较强的主观依赖性，同时对空间邻接结构和核函数选择较为敏感，可能会影响推断稳定性，当前BSTGWR主要挑战在于多尺度建模与高效推理方法的集成，未来可通过集成分层建模、空间多核方法及贝叶斯非参数扩展等手段提升其实用性与可解释性。
（2）贝叶斯时空变系数模型
贝叶斯时空变系数模型（Bayesian Spatiotemporal Varying Coefficients Model, BSTVCM）[28-29]是针对时空非平稳性而提出的贝叶斯时空统计模型，其核心思想是基于贝叶斯分层建模框架，通过同时处理空间与时间相关性，刻画自变量与因变量之间在不同空间和时间上的非平稳关系。相比传统的全局模型和局部模型，BSTVCM既继承了贝叶斯统计框架的灵活性，又提高了对复杂时空关系的适应能力。通过引入条件自回归先验和随机游走效应，BSTVCM能将空间和时间依赖性分开建模，进而有效降低计算复杂度，并增强模型对时空数据特征的解释能力。BSTVCM的基础公式为：
μ i t = α + ∑ k = 1 K β k ,   i X k ,   i t + ∑ k = 1 K β k ,   t X k ,   i t + ∑ h = 1 H μ h C h ,   i t + ε i t
式中：μit是时空因变量yit似然函数的期望； Xk,it是第k个核心解释变量； βk, i和βk, t分别代表第i个空间单元和第t时间点上Xk,it的回归参数，其随空间单元和时间点变化，通常分别赋予两者BYM空间条件自回归先验（CAR）与一阶随机游走（RW1）时间先验，从而体现相邻区域上和相邻时间内的相关性，体现和反映了时空依赖特征； ∑ h = 1 H μ h C h , i t代表其他协变量的影响； εit是误差项。需要指出的是，βk,i和βk,t的先验采用BYM先验模型，刻画了时刻依赖。
BSTVCM在最大优势在于综合了全局与局部分析能力，具备更强的解释能力，能够同时揭示不同空间位置和不同时间点上的影响关系，近年来，BSTVCM主要在应用层面得到了扩展，其被广泛用于公共健康、环境科学和社会经济研究等多个领域。然而， BSTVCM在实际应用中仍面临先验选择敏感性高、计算复杂度大等挑战，尤其在高维协变量与大尺度数据情境下，对计算效率与收敛性提出较高要求，未来可进一步通过因果正则、结构变系数建模等方式增强其稳健性与扩展性。

3.1.4 连续时空过程预测建模类：贝叶斯网格化时空高斯过程模型

贝叶斯时空网格化高斯过程模型（Bayesian Spatiotemporal Meshed Gaussian Process, BSTMGP）是一种专门为大规模时空地统计数据设计的可扩展贝叶斯建模方法[30]，其核心思想是将高维时空域划分为多个局部区域（即“网格化”），并通过具有重复结构的有向无环图（DAG）表达区域之间的条件依赖关系。BSTMGP通过时空立方划分，在空间与时间维度上同时实现结构对称性、并行性与条件独立性控制，并采用全局与局部统一建模策略，适用于遥感影像等具有时空栅格结构的数据场景。BSTMGP的基础数学结构为：
y l = X l T β + Z l T w l + ε l ,     l ∈ D ⊂ R d + 1
式中：l表示时空坐标； y(l)是时空响应变量； X(l)和Z(l)分别为具有固定系数与时空变系数的协变量矩阵； w(l)为潜在时空过程； ε(l)为测量误差项。BSTMGP中的空间与时间的划分通过如下方式构造：
D = ∏ r = 1 d + 1 D r
将每一维划分为Lr个子区间，即：
D r = ∪ j = 1 L r I r , j     ,   使 得 M = ∏ r = 1 d + 1 L r
由此获得M个网格立方时空子区域，每个子区域对应有个DAG节点，其时空效应参考点构成w(l)图结构近似。每个节点的时空效应wj条件于其“父节点”w[j]，满足如下局部回归结构：
w j | w j ~ N ( H j w j , R j )
式中：Hj表示条件均值系数矩阵； Rj为条件协方差矩阵； N(.)为正态分布。由上可见BSTMGP结构可在时空立方块上并行展开后验采样，其在保持贝叶斯计算精度的同时，显著缩短了迭代计算时间。随着遥感、气象、生态等领域时空大数据的积累，该模型有望成为新一代时空统计建模的重要方法。
BSTMGP针对大规模连续时空过程建模的挑战，提供了一种结构清晰、计算高效的解决方案。特别适合遥感、气象等大数据分析，另外， BSTMGP不依赖全域协方差结构假设，增强了模型在异质性区域下的适应性与泛化能力。然而，该方法在高维DAG构造与邻接图结构选择上仍存在一定主观性，且其网格划分策略在存在边界变化或异构区域时可能影响建模精度。未来可进一步探索自适应网格划分、可学习图结构等机制，以提升模型的灵活性与适应性。

3.2 贝叶斯时空机器学习方法

3.2.1 贝叶斯时空因果森林模型

贝叶斯时空因果森林模型（Bayesian Spatio-temporal Causal Forest Model, BSTCFM）是贝叶斯因果森林模型[31-32]基础上，引入空间邻接因变量WY、空间邻接核心解释变量WX和空间邻接协变量WZ等3类空间邻接变量，并同时考虑空间和时间2个维度的固定效应，同时融合BYM先验模型[17]。BSTCFM通过纳入了3类空间邻接变量，结合倾向性得分法实现了在充分考虑空间溢出效应下的时空因果推断。BSTCFM的另一优势是可估计每个空间单元的时空因果效应，其主要的数学构成如下：
μ i t = s i + v t + ψ i t W Y ,   W X ,   Z q , i t ,   W Z , P S i t ^ + β X i t ̿ Ω i t W Y ,   W X ,   Z q , i t ,   W Z ,   X ̿ + ε i t
Λ i t = β X i t ̿ = 1 Ω i t W Y ,   W X ,   Z q ,   i t ,   W Z ,   1 - β X i t ̿ = 0 Ω i t W Y ,   W X ,   Z q ,   i t ,   W Z ,   0
式中：μit含义同上； si和vt分别表示空间和时间固定效应，其采用BYM先验模型； X i t ̿为Xit的二分类划分变量； β X i t ̿为尺度参数，其先验为N(0, 0.5)[31-32]； ψ(·)和Ωit(·)分别代表混杂效应和因果效应拟合函数； Λit为排除混杂效应后的因果效应估计值； ψ(·)和Ωit(·)分别由多个决策树累加组成，其对应的数学构成和参数先验参见Hill等[33]的研究。 BSTCFM主要基于潜在因果框架，通过引入倾向性得分实现对混杂影响效应的分离和排除，当核心解释变量是本地变量时，其估计的是本地变量产生的因果效应，同理，当核心解释变量是周边变量时，估计的是周边变量产生的因果效应。 BSTCFM综合了贝叶斯统计、时空交互、因果推断、机器学习等思想，不仅实现了对本地空间单元和周边空间单元上因果效应的估计，通过连续分组的方式，还可识别非线性因果机制， BSTCFM的详细介绍和实际应用可参考李俊明等[34]的研究。
BSTCFM融合了时空因果推断思想与贝叶斯累加回归树模型，在高维数据场景下具备较强的时空因果识别与局部时空因果效应估计能力，通过引入倾向性评分分层建模，提升了对潜在混杂影响的控制能力，但该模型也存在计算复杂度高的问题，特别是在处理大规模多层次邻接结构时，对树模型集成与后验推断提出更高要求。未来可探索更高效的采样策略或结合深度森林结构以提升其扩展性。

3.2.2 贝叶斯时空神经网络模型

贝叶斯时空神经网络（Bayesian Spatiotemporal Neural Network, BSTNN）融合了贝叶斯统计的不确定性建模能力与深度神经网络（DNN）的强大表征能力，兼具模型拟合能力与不确定性量化能力，在处理非线性、非平稳与大规模异构时空数据方面展现出巨大潜力[35]。近年来，随着深度学习在时空预测中的广泛应用，其缺乏不确定性量化的局限日益凸显，贝叶斯统计提供一种可行的解决途径[36]。BSTNN通过对网络参数施加先验分布并在给定数据下推断后验分布来刻画模型不确定性，BSTNN的一般基础架构如图3所示，其每个神经元的权重参数W（即网络偏置参数）都是随机变量，W的先验常选用高斯分布，但近年来有学者提出采用稀疏先验（如Spike-and-Slab先验和Horseshoe先验）来提高BSTNN的可解释性和计算效率，采用混合激活函数提高其函数拟合能力[37-38]；确定先验后，需要求解后验分布，由于BSTNN的后验分布复杂高维，直接推断计算往往计算开销巨大，因此，学者提出了多种高效贝叶斯推断技术，如变分推断（VI）、Laplace近似、随机梯度MCMC（SG-MCMC）算法[39]等。BSTNN在数学上通过灵活的先验设定和深度网络结构，将时间序列模型与空间模型有机结合，在理论上为处理复杂时空依赖的数据提供了统一的概率框架，但在具体模型的开发方面还处于起步阶段， Saad等[40]在2024年提出了融合随机梯度下降和变分推断技术的贝叶斯神经网络场模型（Bayesian Neural Fields，BayesNF），有学者尝试将强化学习与BSTNN融合，提出一种估计时空场的贝叶斯强化学习框架[41]。尽管近年来BSTNN在环境科学、经济预测、流行病建模等领域得到一定应用，但还存在以下3个问题需要解决：① 多尺度时空数据的融合。如何在BSTNN中融合多尺度、多分辨率数据是重要挑战，需要设计高效的推断算法来估计跨尺度的大量参数，同时确保模型在不同空间和时间尺度上均能捕捉非平稳特征； ② 模型泛化能力与可靠性的提高。尽管BSTNN可以量化不确定性，但如何确保模型在未知场景下可靠仍是未来重点，一个方向是物理知识融合，即将领域先验（如物理定律或机理模型）融入贝叶斯神经网络结构中，另一个方向是样本高效学习，包括元学习和迁移学习。在许多场景下，一个地区的时空模式可能对另一地区有参考价值，贝叶斯框架下可以通过先验共享来实现知识迁移； ③ 计算效率仍需进一步提升。虽然现已提出一些高效采样算法，但对于时空大数据场景和时空AI大模型运行仍显力不从心，还需要进一步深入研究。
图3 贝叶斯时空神经网络基础架构

Fig. 3 Basic architecture of a Bayesian spatiotemporal neural network

3.2.3 贝叶斯时空图卷积神经网络模型

贝叶斯时空图卷积神经网络（Bayesian Spatio-Temporal Graph Convolutional Neural Network, BSTGCNN）是近年来提出的一种前沿的贝叶斯时空机器学习模型[42]。BSTGCN综合了贝叶斯统计与图卷积神经网络（GCN）的优势，能够同时建模复杂时空依赖关系并提供不确定性估计，尤其适用于节点空间位置复杂、动态关联频繁变动的情境。其核心优势在于通过图结构编码邻接依赖，从而实现对非欧几里得空间下的时空过程建模。与此同时， BSTGCNN也存在模型结构复杂、训练数据需求大、图结构构建易受噪声影响等挑战，未来可探索基于注意力机制的结构优化、动态图演化建模与多图异构融合等方法，以提升BSTGCNN的稳定性与可解释性。图4展示了BSTGCNN的基础构成。BSTGCNN可以很好地应对复杂时空数据中的不确定性和动态依赖关系，其核心在于通过贝叶斯框架增强传统图卷积神经网络的泛化能力。传统GCN模型通常依赖预定义的图结构（如道路网络的物理拓扑），但这种方式可能忽略时空数据中的潜在动态关系，但BSTGCNN通过引入参数生成模型，从数据中直接学习图结构，捕捉更真实的时空动态依赖关系。此外，贝叶斯方法的使用使得BSTGCNN可以考虑更多不确定性，使其面对噪声或缺失数据时表现出更强鲁棒性。目前， BSTGCNN应用主要集中在交通领域的短时交通流预测、拥堵分析和动态路径规划等方面，正逐步扩展到交通、医疗影像和地理数据分析等领域[43]。然而， BSTGCNN还有一些缺点需要克服，首先，端到端图结构学习需要较高的计算资源，可能影响其在超大规模网络上扩展性；其次，对多模态数据的整合能力尚未充分挖掘。一些学者通过注意力机制和多尺度建模引入来增强BSTGCNN对复杂时空依赖关系的捕捉能力[44]，随着更复杂架构和多模态数据融合技术的引入， BSTGCNN有望在未来时空数据分析中发挥更大潜力。
图4 贝叶斯时空图卷积神经网络模型基础结构图

Fig. 4 Basic architecture of a Bayesian spatiotemporal graph convolutional neural network model

综上所述，贝叶斯时空统计方法体系已形成了传统贝叶斯时空统计与贝叶斯时空机器学习两大框架，现有的方法模型不仅具有较强的空间依赖建模效能与时间动态过程表达能力，也在处理高维、多源、异构数据的泛化能力方面不断提升。然而，统计模型的价值主要体现在对实际问题的有效解决，为进一步展现贝叶斯时空统计方法在实际问题中的应用价值，接下来将系统梳理其在公共卫生、环境科学、经济社会与公共安全、能源与工程等关键领域中的应用成效，通过对具体问题背景下模型选择与建模策略等的归纳分析，可更全面了解贝叶斯时空统计方法在各类典型领域中的应用实践，展示其在复杂时空建模与科学决策中的关键作用。

4 贝叶斯时空统计的应用

贝叶斯时空统计模型能够同时兼顾空间依赖与时间动态2个方面，并在整合先验信息与量化不确定性方面具有显著优势，已成为多学科领域时空数据分析的重要工具，该模型在处理区域异质性、数据缺失以及极端值等复杂问题时表现出良好的稳定性与适应性。近年来，随着后验估计采样方法的发展，贝叶斯时空统计模型在公共卫生、环境科学、经济社会和其他等多个领域中的应用日益深入，成为时空大数据背景下的重要建模工具与决策支撑手段。相比传统统计方法，该模型更能揭示时空数据的深层结构，特别适用于分析具有时空异质性特征的现象。通过对疾病流行、环境污染、经济社会发展等复杂系统的时空动态建模，贝叶斯时空统计模型不仅加深了研究深度，也在政策制定、资源配置等方面提供了科学依据。以下从公共卫生、环境科学、经济社会发展和能源工程领域等几个主要领域应用方面进行详细阐述。

4.1 公共卫生领域

贝叶斯时空统计模型在公共卫生领域的应用尤为广泛，特别是在疾病传播监测、健康风险评估和卫生资源配置优化等方面展现出强大的建模与分析能力。根据研究主题与方法应用特点，本文将相关应用研究归纳为以下4个方面。

4.1.1 空气传播类传染病的时空建模分析

贝叶斯时空统计模型已广泛应用于流感、麻疹、肺结核等典型空气传播类传染病的研究中。相较传统时空统计方法，贝叶斯时空统计模型可同时捕捉空间异质性与时间动态变化，并通过后验不确定性量化增强风险表达的稳定性与解释力。在流感建模方面， Martin等[45]基于美国多年监测数据表明，贝叶斯时空条件自回归模型相较传统的SARIMA模型可将预测误差降低约18%，并可提前2~3 周识别高风险区域； Amorós等[46]进一步利用贝叶斯时空马尔科夫状态转换模型实现了早期暴发检测，敏感性提升至87%。在麻疹研究中，Jia等[47]基于带有时空交互项的贝叶斯层次模型，研究山东省136 个县2009—2017年的麻疹发病与气象因子的关联，显著提升了风险估计的精度与置信区间的可靠性。在慢性传染病肺结核分析方面，Chen等[48]基于贝叶斯时空层次模型系统评估了重庆市2014—2020年结核病的时空分布特征，识别出多个持续性高风险区域，并揭示了不同人群间的风险差异性。在 COVID-19疫情期间，贝叶斯时空统计模型也被广泛用于COVID-19动态传播的研究中，通过整合空间结构与时间趋势的贝叶斯时空层次模型，有效开展了COVID-19病例风险预测[49]、住院率分析[50]和超额死亡[51]等方面的研究，为COVID-19疫情防控提供了支撑。相较于传统固定效应方法，贝叶斯时空层次模型在空间风险识别与个体异质性解释方面更具优势。贝叶斯时空统计模型凭借优于传统方法的时空分析性能和可解释后验概率推断，已在传播风险估计、传播预警等方面展现出一定优势，正在成为应对空气传播类传染病的重要工具。

4.1.2 登革热与手足口病的传播与预警研究

登革热与手足口病等高发传染病均受到气象条件与社会经济因素的显著影响，近年来，贝叶斯时空统计模型被广泛用于相关疾病传播机制和传播风险预测研究中。虽然两类传染病在传播机理上存在本质差异（登革热为典型虫媒病，手足口病则主要通过飞沫、接触与粪口途径传播），但二者均具有明显的空间分异与时间动态特征，适合采用贝叶斯时空建模框架进行风险评估与预测预警，接下来，将从贝叶斯时空统计方法在两类疾病上的具体应用。在登革热方面，学者普遍将空间误差项或时间变化项纳入贝叶斯时空分析框架中，以增强预测稳定性与实践适应性。如敖琳珺等[52]通过引入空间误差项构建贝叶斯时空层次泊松模型，显著提升了对广东省登革热发病率的预测精度。Bukhari 等[53]则将登革热与其他蚊媒病毒（如寨卡、基孔肯雅热）纳入多响应变量联合建模，通过构建贝叶斯空间层次模型，捕捉多病原体之间的交互机制，探究气候与社会经济因子的复合影响。Rotejanaprasert等[54]提出的贝叶斯时空负二项预测模型融合了时间滞后项与空间依赖项，并结合移动平均平滑技术，实现了对泰国登革热病例的近实时预测与短期预警。在手足口病方面，学者则更关注城市环境与社会变量的影响。张辉国等[55]基于新疆地区监测数据，构建含时空随机效应的贝叶斯泊松模型，发现气温升高对疫情传播具有一定抑制效应。陈思秇等[56]通过引入空间误差结构项，并构建贝叶斯时空泊松回归模型，研究表明城中村比例、GDP水平等社会经济因素与手足口病发病率显著相关。He 等[57]则构建含条件自回归项（CAR）的贝叶斯负二项时空模型，揭示了大气污染、人口密度是手足口病的传播风险因素，而绿地覆盖率与公园密度是保护因素。

4.1.3 疟疾及其他热带病的防控干预研究

在疟疾及其他热带病的研究中，贝叶斯时空统计模型被广泛用于发病风险预测、影响因子发现和防控措施效应评估等方面，显著提升了疾病风险估计精度与政策评估科学性。在风险预测和影响因素发现方面， Semakula等[58]构建了两步贝叶斯时空建模框架，通过整合调查与常规数据，有效提高了对卢旺达小尺度疟疾风险的空间预测能力。 Takramah等[59]通过贝叶斯时空层次模型对加纳的儿童疟疾风险进行了建模分析，发现家庭规模、农村居住、降雨量及最高气温等是显著影响因子。Mougeni等[60]基于加蓬疟疾检测数据，利用贝叶斯时空层次模型估计制作了区县尺度的阳性率空间分布图，为精细化干预提供了定量依据。在防控措施时空效应评估方面， Rouamba等[61]在布基纳法索应用贝叶斯分层负二项模型评估疟疾干预措施效果，发现蚊帐发放和健康教育等干预在不同社区之间存在响应差异。 Semakula等[62]引入条件自回归（CAR）结构与时间趋势，对卢旺达室内残杀性喷洒（IRS）政策进行时空效能评估，揭示政策实施具有显著空间异质性。

4.1.4 健康空间不平等的风险建模与资源配置评估

在健康风险评估方面，研究者基于贝叶斯时空统计模型对慢性病的影响机制方面进行探讨。Liu 等[63]采用嵌套CAR结构的贝叶斯广义加性模型（GAM）分析了山东省数据，发现NO2和PM2.5短期暴露与心血管疾病住院率呈显著正相关。Zhang等[64]运用贝叶斯时间序列-空间滞后模型，分析了广州儿童流感的季节性波动，发现PM2.5浓度升高对10~14岁儿童群体的影响更为敏感。Li等[9]构建了零膨胀贝叶斯时空泊松回归模型，研究了中国县域孕产妇死亡率在不同亚国家区域的不同影响机制。Ren等[65]基于全球134个国家的空间面板数据，识别了空气污染、城市化程度与男女寿命差之间的协同作用机制，揭示了环境暴露在不同性别人群中的不均等健康影响。在医疗服务公平性评估方面，贝叶斯时空模型被用于识别健康资源配置与人口健康需求之间的动态匹配特征。陈胜亮等[66]采用包含空间滞后项的贝叶斯多层线性模型，系统评估了广东省住院率的空间集聚性及其驱动因素，提示医师学历和医院诊疗能力是县域医疗服务利用率的重要影响因素。Li[14]利用贝叶斯时空协同模型系统分析了2008—2017年间中国医疗资源与人口老龄化之间的时空匹配关系，发现经济发达地区资源适配性较好，而西部地区存在明显的匹配不足问题。

4.2 环境科学领域

在环境科学研究中，贝叶斯时空统计模型已广泛应用在空气质量监测、气候变化评估以及其他环境分析等多个方面。在空气质量监测方面，有的学者应用贝叶斯时空统计方法研究全球和中国的PM2.5污染的时空演化规律[3,5,67]，有些学者还关注大气污染影响因素的探究，Jin等[68]构建嵌入空间误差项的贝叶斯时空层次回归模型，系统分析了中国109个城市气温、湿度、风速、第二产业比重和人口密度等因素对PM2.5浓度的影响。Sarto等[69]则基于意大利佩鲁贾市高频一氧化氮（NO）与粒径分布数据，采用包含时间趋势项的贝叶斯动态层次模型，研究了大气污染物在城市尺度下的空间集聚与时间变化，拓展了该模型在高时间分辨率场景中的适用性。在气候变化评估方面，学者采用贝叶斯时空分位数回归模型研究极端气候事件的非对称变化趋势。Tan等[70]以加拿大冬季降水为研究对象，构建包含空间条件自回归（CAR）项的贝叶斯时空分位数回归模型，分析降水在低、中、高3个分位下的时空变化趋势，揭示了气候系统对不同降水水平的非线性响应机制。在水环境与土地系统建模方面，梁中耀等[71]针对滇池与异龙湖典型断面的水质监测数据，通过贝叶斯时空层次模型，识别水质指标变化的空间、时间与时空交互等不确定性来源，估计水质主要影响因子在流域不同区域的作用强度差异。于明雪等[72]在甘肃省土地利用分析中采用贝叶斯时空层次模型，系统评估了1995—2020年该地区土地利用强度的演变机制。吕建康等[73]结合MODIS遥感观测数据，构建带有时空趋势项的贝叶斯回归模型，分析了甘肃省气溶胶光学厚度（AOD）的年际波动与空间分布变化，揭示出典型气候区大气粒子浓度的长期演变路径。

4.3 经济社会与公共安全领域

近年来,贝叶斯时空统计模型在经济社会与公共安全领域也得到了广泛应用，通过引入空间结构与时间动态效应，能够有效刻画区域经济增长、结构变迁以及政策干预效应的异质性特征。在经济社会领域，早期有些学者采用贝叶斯时空层次模型对英国预测寿命[6]、全球和中国老龄化[7,74-75]等展开研究，近年来研究主题进一步拓展，李俊明等[3]通过构建贝叶斯自适应多阶段时空演化模型，研究黄河流域生态文明与共同富裕水平的协同演进轨迹，发现区域经济发展呈现非线性阶段性特征，并存在局部演化路径的显著分异。韩菲与闫书淇[16]则基于贝叶斯时空层次模型，评估了环境保护税政策对绿色全要素生产率的空间扩散效应，表明政策实施具有显著的区域溢出影响。韩秀兰等[15]基于贝叶斯时空层次模型研究了中国宏观税负的时空演化规律。此外，李俊明等[34]提出并应用贝叶斯时空因果森林模型，研究了中国市域数字经济对减污降碳协同的影响，结果表明数字经济对减污降碳协同具有显著促进作用，但其效应在不同地区存在空间异质性特征。在公共安全领域， Liu等[76]通过建立包含时空固定效应项的贝叶斯时空层次模型，识别出长春市的刑事安全的高风险区域及其时间变化的趋势。Li等[2]与Law等[77]进一步探索了贝叶斯时空统计模型在犯罪热点识别中的有效性，指出该模型在动态监测与空间聚集识别方面优于传统统计方法。在交通事故风险评估与机制识别方面， Zeng等[78]基于贝叶斯时空层次模型分析了城市道路交通事故的空间聚集与时间演变特征。 Liu等[79]则将气象、道路结构与驾驶行为等因素纳入贝叶斯时空层次回归模型，系统评估了高速公路交通事故风险的影响因素。

4.4 能源与工程领域

贝叶斯时空统计模型在能源和工程领域中也有广泛应用，尤其是在可再生能源预测、工程风险评估及环境承载力分析等方面。在可再生能源研究中，韩晓等[80]基于贝叶斯时空层次模型，重建了中国农村地区2000—2020年生物质能消费的时空动态轨迹，成功弥补了小尺度区域数据缺失问题，揭示了生物质能利用的空间异质性和时间变化规律。在分布式光伏系统性能监测方面，刘韵艺等[81]提出结合季节性趋势分解法（STL）与贝叶斯时空回归模型的异常检测方法，探测光伏出力数据中的异常点，显著提高了对光伏系统故障的检测灵敏度与准确率。在工程地质风险评估研究中， Yang等[82]基于贝叶斯时空回归模型，对高铁工程中的土壤参数变异性进行了建模分析，实现了地基承载特性的动态估计与工程风险可视化。此外，在生态系统服务价值分析中， Song等[83]结合贝叶斯空间自回归模型与空间误差模型，系统评估了中国省域生态系统服务价值的时空演化规律，并发现人类活动强度、土地利用变化与生态服务价值波动存在显著相关。
综观当前贝叶斯时空统计模型在公共卫生、环境科学、社会经济与工程能源等领域的应用实践，可以发现该类模型已逐步从方法探索向跨学科综合集成演化，展现出较强的普适性与延展性。其最大优势在于能够通过层次结构嵌套、多重时空项构建和先验知识融入，实现复杂系统中空间异质性与时间动态的联合建模，并通过后验不确定性的量化为风险评估、政策制定与资源调配等提供更具鲁棒性的科学依据。尤其在高风险传染病传播、环境污染暴露、健康不平等识别、区域政策响应评估等场景下，相较传统经典时空统计方法，贝叶斯时空统计模型在小样本场景、非独立观测、数据缺失及极端值处理等方面展现出显著优势。但也应注意到，目前多数应用仍以结构固定的分层模型为主，较少深入探讨复杂空间机制（如网络、非偶邻接）、参数先验的敏感性分析以及多模型集成等问题，部分研究在模型选择、推理效率与可解释性之间存在平衡瓶颈。未来有待在多源异构数据建模、因果机制嵌入、深度贝叶斯学习融合等方面进一步拓展方法边界，并推动从事后拟合向事前预测和在线更新过渡，使贝叶斯时空统计方法真正服务于智能决策与精准治理实践。

5 发展趋势

随着兼具高维、多源和异构特征的时空大数据的高速积累，贝叶斯时空统计模型在建模理论、计算方法与跨领域应用等方面均面临新的发展机遇与挑战。展望未来，其未来发展主要呈现以下5个趋势。
（1）多源异构时空结构的统一建模成为主流
传统贝叶斯时空统计模型多数以二维空间网格或规则区域划分为前提，难以同时刻画多尺度、跨层级的复杂时空过程。未来研究将更加注重对多层次区域（如国家—省域—市域—县域）和多类型空间关系（如邻接关系与经济联系）的耦合表达，以开发支持跨层级尺度嵌套建模与多维因果溯源的新型贝叶斯时空结构模型。例如，引入跨尺度空间权重矩阵、动态CAR结构、多分辨率随机效应等，将成为处理异构时空结构数据的关键技术路径。
（2）贝叶斯时空统计与深度学习融合将加速突破
面对高维复杂数据和非线性机制的现实需求，贝叶斯时空神经网络（BSTNN）、贝叶斯时空图卷积神经网络（BSTGCNN）等方法正成为前沿方向。未来贝叶斯时空建模将进一步与注意力机制（Attention）、Transformer技术、液态神经网络（LNN）等深度学习模型融合，强化模型对非平稳、多模态时空依赖关系的表达能力，推动“贝叶斯神经场”与“生成建模”的时空泛化应用。此外，深度先验学习、变分推断与贝叶斯估计的整合，将进一步提高贝叶斯时空统计模型的推理效率与刻画能力。
（3）因果推断与贝叶斯时空统计模型的深度融合
在政策评估、环境干预与健康效应研究中，传统的相关性分析已难以满足现实对于因果关系识别的需求。未来贝叶斯时空统计将更加重视与因果推断方法的融合发展，如结合倾向得分匹配、贝叶斯结构方程模型（BSEM）、贝叶斯因果森林（BCF）、贝叶斯网络（BN）等方法，发展具有“因果可识别性+时空依赖建模”双重优势的贝叶斯因果时空建模框架，以支持更精准的区域干预效应估计与政策仿真模拟。
（4）高性能计算与可解释性工具的协同推进
面对模型参数多、计算量大等挑战，未来贝叶斯时空统计建模需依赖高效推理机制（如INLA、SGMCMC、VI）和GPU并行化计算平台，构建支持大规模时空大数据实时更新与快速模拟的算法体系。同时，模型的可解释性也将成为研究重点，尤其是在公共卫生、环境政策等热点领域，对不确定性可视化、贝叶斯后验贡献分析、模型比较诊断指标（如WAIC、DIC）的开发将进一步增强模型对决策支持的服务能力。
（5）时空大模型与行业知识图谱驱动的智能建模
借助AI技术的发展，未来贝叶斯时空统计方法将与时空认知智能、知识图谱系统等深度融合，探索“数据-模型-知识”三元驱动下的智能建模路径。通过嵌入地理知识、气象知识、医学知识等领域先验，构建结构可约束、语义可解释的行业专属贝叶斯时空大模型，有望大幅提升模型的通用性、迁移性与智能决策能力。

6 结论与展望

6.1 结论

本文系统梳理了贝叶斯时空统计方法的发展脉络与核心构成，从传统模型和机器学习2个视角出发，先是归纳总结了时空演化趋势分析类、全局时空影响关系研究类、异质性时空局部建模类和连续时空过程分析类4类9个传统贝叶斯时空统计模型的核心数学构成和适用场景，随后又具体介绍了3个贝叶斯时空机器学习模型。总体而言，相较于经典时空统计方法，贝叶斯时空统计模型在不确定性考虑、小样本推断、先验知识融合与时空依赖表达等方面具有一定优势，目前已逐步形成时空演化建模、全局时空影响机制分析、局部时空异质性探究、连续过程预测与贝叶斯机器学习为代表的多元化模型体系。
在实际应用方面，贝叶斯时空统计方法已在公共卫生、环境科学、社会经济与公共安全、能源与工程等多个典型领域中展现出广泛的适用性与显著的应用价值，能够有效应对多尺度、多维度、多源异构的时空分析需求，特别是在时空演化过程分析、时空复杂影响机制探究、时空因果推断、复杂时空过程预测等任务中，贝叶斯时空统计模型表现出更强的建模灵活性、不确定性表达能力，其能够在信息稀疏、结构复杂或数据不完全的情境下稳健运行，这为复杂时空过程建模研究提供了强有力的方法工具，也为公共政策制定、风险管理与资源优化配置等实践方面提供了重要的支持作用。

6.2 展望

尽管贝叶斯时空统计方法在多个学科领域展现出高度适应性和广阔应用前景，但其发展仍面临诸多关键挑战，包括异构时空结构建模难度大、模型结构与解释能力的权衡、高维非线性关系下的推理效率瓶颈，以及因果识别与先验信息表达不足等。未来研究亟需在多源异构数据的一体化建模、贝叶斯方法与深度学习的融合创新、因果推断机制引入、高性能并行计算与可视化解释系统的协同优化等方向实现突破，从而推动贝叶斯时空统计模型在理论完备性与实践适应性兼具的基础上，进一步发展为具备因果推断、自适应泛化、智能辅助分析与高性能计算的下一代时空建模范式。总之，贝叶斯时空统计方法不仅是理解空间过程与时间演化耦合机制的重要工具，更将在未来应对复杂场景挑战中发挥不可替代的作用。其理论拓展与实践深化仍具有广阔的发展空间，值得持续关注与深入探索。
AI使用说明：本文在写作过程中使用了AI技术，主要用于语言通顺、英文初步翻译以及文字校对等方面。
■ 本文图文责任编辑：蒋树芳 黄光玉

利益冲突：Conflicts of Interest 所有作者声明不存在利益冲突。

All authors disclose no relevant conflicts of interest.

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
Bernardinelli L, Clayton D, Pascutto C, et al. Bayesian analysis of space-time variation in disease risk[J]. Statistics in Medicine, 1995, 14(21/22):2433-2443. DOI: 10.1002/sim.4780142112

[2]
Li G, Haining R, Richardson S, et al. Space-time variability in burglary risk: A Bayesian spatio-temporal modelling approach[J]. Spatial Statistics, 2014, 9:180-191. DOI:10.1016/j.spasta.2014.03.006

[3]
Li J, Han X, Jin M, et al. Globally analysing spatiotemporal trends of anthropogenic PM2.5 concentration and population's PM2.5 exposure from 1998 to 2016[J]. Environment International, 2019, 128:46-62. DOI:10.1016/j.envint.2019.04.026

[4]
Zhang X, Gu X, Cheng C, et al. Spatiotemporal heterogeneity of PM2.5 and its relationship with urbanization in North China from 2000 to 2017[J]. Science of the Total Environment, 2020, 744:140925. DOI:10.1016/j.scitotenv.2020.140925

[5]
Li J, Wang N, Wang J, et al. Spatiotemporal evolution of the remotely sensed global continental PM2.5 concentration from 2000-2014 based on Bayesian statistics[J]. Environmental Pollution, 2018, 238:471-481. DOI:10.1016/j.envpol.2018.03.050

[6]
Bennett J E, Li G Q, Foreman K, et al. The future of life expectancy and life expectancy inequalities in England and Wales: Bayesian spatiotemporal forecasting[J]. The Lancet, 2015, 386(9989):163-170. DOI:10.1016/S0140-6736(15)60296-3

[7]
Li J, Han X, Zhang X, et al. Spatiotemporal evolution of global population ageing from 1960 to 2017[J]. BMC Public Health, 2019, 19:127. DOI:10.1186/s12889-019-6465-2

PMID

[8]
Wang L, Xu C, Hu M, et al. Spatio-temporal variation in tuberculosis incidence and risk factors for the disease in a region of unbalanced socio-economic development[J]. BMC Public Health, 2021, 21(1):1817. DOI:10.1186/s12889-021-11833-2

PMID

[9]
Li J, Liang J, Wang J, et al. Spatiotemporal trends and ecological determinants in maternal mortality ratios in 2,205 Chinese counties, 20102013: A Bayesian modelling analysis[J]. PLoS Medicine, 2020, 17(5):e1003114. DOI:10.1371/journal.pmed.1003114

[10]
Ge Y, Yuan Y, Hu S, et al. Space-time variability analysis of poverty alleviation performance in China’s poverty-stricken areas[J]. Spatial Statistics, 2017, 21:460-474. DOI:10.1016/j.spasta.2017.02.010

[11]
刘大千, 宋伟, 修春亮. 贝叶斯方法在犯罪时空格局研究上的应用——以长春市为例[J]. 地理科学, 2022, 42(5): 820-830.

DOI

[Liu D, Song W, Xiu C, et al. Understanding the spatiotemporal pattern of crimes in Changchun, China: A Bayesian modeling approach[J]. Scientia Geographica Sinica, 2022, 42(5): 820-830.] DOI:110.13249/j.cnki.sgs.2022.05.008

[12]
Han F, Li J. Assessing impacts and determinants of China’s environmental protection tax on improving air quality at provincial level based on Bayesian statistics[J]. Journal of Environmental Management, 2020, 271:111017. DOI:10.1016/j.jenvman.2020.111017

[13]
Wang Z, Ye W, Chen X, et al. Spatio-temporal pattern, matching level and prediction of ageing and medical resources in China[J]. BMC Public Health, 2023, 23(1):1155. DOI:10.1186/s12889-023-15945-9

PMID

[14]
Li J, Chen X, Han X, et al. Spatiotemporal matching between medical resources and population ageing in China from 2008 to 2017[J]. BMC Public Health, 2020, 20(1):845. DOI:10.1186/s12889-020-08976-z

PMID

[15]
韩秀兰, 崔月彤, 李俊明. 基于贝叶斯时空层次模型的中国宏观税负时空演化特征研究[J]. 统计与信息论坛, 2022, 37(8):67-74.

[Han X L, Cui Y T, Li J M. Study on the spatio-temporal evolution of China's macro tax burden based on BSHM[J]. Journal of Statistics and Information, 2022, 37(8):67-74.] DOI:10.3969/j.issn.1007-3116.2022.08.006

[16]
韩菲, 闫书淇. 环境保护税能否促进区域绿色全要素生产率增长——基于贝叶斯时空统计的实证研究[J]. 经济问题, 2023(7):103-112.

[Han F, Yan S Q. Can environmental protection tax promote regional green total factor productivity Growth? An empirical study based on Bayesian space-time statistics[J]. On Economic Problems, 2023(7):103-112.] DOI:10.16011/j.cnki.jjwt.2023.07.014

[17]
Besag J, York J, Mollié A. Bayesian image restoration, with two applications in spatial statistics[J]. Annals of the Institute of Statistical Mathematics, 1991, 43(1):1-20. DOI:10.1007/BF00116466

[18]
Li J, Wang J, Wang N, et al. A Bayesian space-time hierarchical model for remotely sensed lattice data based on multiscale homogeneous statistical units[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2018, 11(7):2151-2161. DOI: 10.1109/JSTARS.2018.2818286

[19]
Vicente G, Goicoa T, Ugarte M D. Multivariate Bayesian spatio-temporal P-spline models to analyze crimes against women[J]. Biostatistics, 2023, 24(3):562-584. DOI:10.1093/biostatistics/kxab042

[20]
Das P, Ghosal S. Analyzing ozone concentration by Bayesian spatio-temporal quantile regression[J]. Environmetrics, 2017, 28(4):e2443. DOI:10.1002/env.2443

[21]
He Q, Huang H H. A framework of zero-inflated Bayesian negative binomial regression models for spatiotemporal data[J]. Journal of Statistical Planning and Inference, 2024, 229:106098. DOI:10.1016/j.jspi.2023.106098

[22]
LeSage J P. Spatial econometric panel data model specification: A Bayesian approach[J]. Spatial Statistics, 2014, 9:122-145. DOI:10.1016/j.spasta.2014.02.002

[23]
Reich B J, Fuentes M, Dunson D B. Bayesian spatial quantile regression[J]. Journal of the American Statistical Association, 2011, 106(493):6-20. DOI:10.1198/jasa.2010.ap09237

PMID

[24]
Fernandez R C, Gonçalves K C M, de Morais Pereira J B. A flexible Bayesian hierarchical quantile spatial model for areal data[J]. Statistical Modelling, 2025, 25(1): 35-54. DOI:10.1177/1471082x231204930

[25]
Cai Z, Zhu Y, Han X. Bayesian analysis of spatial dynamic panel data model with convex combinations of different spatial weight matrices: A reparameterized approach[J]. Economics Letters, 2022, 217:110695. DOI:10.1016/j.econlet.2022.110695

[26]
范真, 王西贝. 空间权重选择的模拟研究——基于贝叶斯方法[J]. 统计与决策, 2024, 40(10):52-57.

[Fan Z, Wang X B. Simulation study on spatial weight—Based on Bayesian method[J]. Statistics & Decision, 2024, 40(10):52-57.] DOI:10.13546/j.cnki.tjyjc.2024.10.009

[27]
Ma Z, Huang Z. A Bayesian implementation of the multiscale geographically weighted regression model with INLA[J]. Annals of the American Association of Geographers, 2023, 113(6):1501-1515. DOI:10.1080/24694452.2023.2187756

[28]
Song C, Shi X, Bo Y, et al. Exploring spatiotemporal nonstationary effects of climate factors on hand, foot, and mouth disease using Bayesian Spatiotemporally Varying Coefficients (STVC) model in Sichuan, China[J]. Science of the Total Environment, 2019, 648:550-560. DOI:10.1016/j.scitotenv.2018.08.114

[29]
Song C, Shi X, Wang J. Spatiotemporally Varying Coefficients (STVC) model: A Bayesian local regression to detect spatial and temporal nonstationarity in variables relationships[J]. Annals of GIS, 2020, 26(3):277-291. DOI:10.1080/19475683.2020.1782467

[30]
Peruzzi M, Banerjee S, Finley A O. Highly scalable Bayesian geostatistical modeling via meshed Gaussian processes on partitioned domains[J]. Journal of the American Statistical Association, 2022, 117(538):969-982. DOI:10.1080/01621459.2020.1833889

PMID

[31]
Hahn P R, Murray J S, Carvalho C M. Bayesian regression tree models for causal inference: Regularization, confounding, and heterogeneous effects (with discussion)[J]. Bayesian Analysis, 2020, 15(3):965-1056. DOI:10.1214/19-BA1195

[32]
Krantsevich N, He J, Hahn PR. Stochastic tree ensembles for estimating heterogeneous effects[C]. International Conference on Artificial Intelligence and Statistics, pp. 6120-6131. PMLR, 2023. DOI:10.48550/arXiv.2209.06998

[33]
Hill J, Linero A, Murray J. Bayesian additive regression trees: A review and look forward[J]. Annual Review of Statistics and Its Application, 2020, 7:251-278. DOI:10.1146/annurev-statistics-031219-041110

[34]
李俊明, 魏雯琪, 张鹏, 等. 中国市域数字经济发展对减污降碳协同的促进效应及其空间分异[J]. 经济地理, 2023, 43(12):169-180.

DOI

[Li J M, Wei W Q, Zhang P, et al. The promoting effect of China’s city-level digital economy development on pollution reduction and carbon emission synergy and its spatial heterogeneity[J]. Economic Geography, 2023, 43(12):169-180. ] DOI:10.15957/j.cnki.jjdl.2023.12.017

[35]
He, Wenchong and Zhe Jiang. "Uncertainty Quantification of Deep Learning for Spatiotemporal Data: Challenges and Opportunities." arxiv preprint arxiv:2311.02485, 2023. DOI:10.48550/arXiv.2311.02485

[36]
Chandra R, He Y. Bayesian neural networks for stock price forecasting before and during COVID-19 pandemic[J]. PLos one, 2021, 16(7):e0253217. DOI:10.1371/journal.pone.0253217

[37]
Hauzenberger N, Huber F, Klieber K, et al. Bayesian neural networks for macroeconomic analysis[J]. Journal of Econometrics, 2025, 249:105843. DOI:10.1016/j.jeconom.2024.105843

[38]
Hubin A, Storvik G. Sparse Bayesian neural networks: Bridging model and parameter uncertainty through scalable variational inference[J]. Mathematics, 2024, 12(6):788. DOI:10.3390/math12060788

[39]
Alexos A, Boyd AJ, Mandt S. Structured stochastic gradient MCMC[C]. Proceedings of the International Conference on Machine Learning, 2022:414-434. DOI:10.48550/arXiv.2107.09028

[40]
Saad F, Burnim J, Carroll C, et al. Scalable spatiotemporal prediction with Bayesian neural fields[J]. Nature Communications, 2024, 15:7942. DOI:10.1038/s41467-024-51477-5

PMID

[41]
Padrao P, Fuentes J, Bobadilla L, et al. Estimating spatio-temporal fields through reinforcement learning[J]. Frontiers in Robotics and AI, 2022, 9:878246. DOI:10.3389/frobt.2022.878246

[42]
Fu J, Zhou W, Chen Z. Bayesian spatio-temporal graph convolutional network for traffic forecasting[J]. arxiv preprint arxiv:2010.07498, 2020. DOI:10.48550/arXiv.2010.07498

[43]
Zeghina A, Leborgne A, Le Ber F, et al. Deep learning on spatiotemporal graphs: A systematic review, methodological landscape, and research opportunities[J]. Neurocomputing, 2024, 594:127861. DOI:10.1016/j.neucom.2024.127861

[44]
Li Y, Yu D, Liu Z, et al. Graph neural network for spatiotemporal data: Methods and applications[J]. arxiv preprint arxiv:2306.00012, 2023. DOI:10.48550/arXiv.2306.00012

[45]
Song Z, Jia X, Bao J, et al. Spatio-temporal analysis of influenza-like illness and prediction of incidence in high-risk regions in the United States from 2011 to 2020[J]. International Journal of Environmental Research and Public Health, 2021, 18(13):7120. DOI:10.3390/ijerph18137120

[46]
Amorós R, Conesa D, López-Quílez A, et al. A spatio-temporal hierarchical Markov switching model for the early detection of influenza outbreaks[J]. Stochastic Environmental Research and Risk Assessment, 2020, 34(2):275-292. DOI:10.1007/s00477-020-01773-5

[47]
Jia Y, Xu Q, Zhu Y, et al. Estimation of the relationship between meteorological factors and measles using spatiotemporal Bayesian model in Shandong Province, China[J]. BMC Public Health, 2023, 23(1):1422. DOI:10.1186/s12889-023-16350-y

PMID

[48]
Chen Z Y, Deng X Y, Zou Y, et al. A Spatio-temporal Bayesian model to estimate risk and influencing factors related to tuberculosis in Chongqing, China, 2014-2020[J]. Archives of Public Health, 2023, 81(1):42. DOI:10.1186/s13690-023-01044-z

[49]
Jaya I G N M, Folmer H. Bayesian spatiotemporal forecasting and mapping of COVID-19 risk with application to West Java Province, Indonesia[J]. Journal of Regional Science, 2021, 61(4):849-881. DOI:10.1111/jors.12533

PMID

[50]
Satorra P, Tebé C. Bayesian spatio-temporal analysis of the COVID-19 pandemic in Catalonia[J]. Scientific Reports, 2024, 14:4220. DOI:10.1038/s41598-024-53527-w

PMID

[51]
Saavedra P, Santana A, Bello L, et al. A Bayesian spatio-temporal analysis of mortality rates in Spain: Application to the COVID-19 2020 outbreak[J]. Population Health Metrics, 2021, 19(1):27. DOI:10.1186/s12963-021-00259-y

PMID

[52]
敖琳珺, 张昱勤, 许欢, 等. 评估气象对广东省登革热时空预测模型的贡献[J]. 现代预防医学, 2020, 47(16):2899-2903.

[ Ao L J, Zhang Y Q, Xu H, et al. Assessing the contribution of meteorology to the spatio-temporal prediction model of dengue in Guangdong Province[J]. Modern Preventive Medicine, 2020, 47(16):2899-2903.] DOI:10.20043/j.cnki.mpm.2020.16.005

[53]
Bukhari M H, Shad M Y, Nguyen U S, et al. A Bayesian spatiotemporal approach to modelling arboviral diseases in Mexico[J]. Transactions of The Royal Society of Tropical Medicine and Hygiene, 2023, 117(12):867-874. DOI:10.1093/trstmh/trad064

PMID

[54]
Rotejanaprasert C, Ekapirat N, Areechokchai D, et al. Bayesian spatiotemporal modeling with sliding windows to correct reporting delays for real-time dengue surveillance in Thailand[J]. International Journal of Health Geographics, 2020, 19: 1-13. DOI:10.1186/s12942-020-00199-0

[55]
张辉国, 岳铭, 胡锡健. 2018年新疆手足口病时空分布特征及气象因素相关性研究[J]. 病毒学报, 2022, 38(4):874-879.

[Zhang H G, Yue M, Hu X J. Study on the spatiotemporal distribution characteristics and correlation with meteorological factors of hand, foot, and mouth disease in Xinjiang in 2018[J]. Chinese Journal of Virology, 2022, 38(4): 874-879. ] DOI:10.13242/j.cnki.bingduxuebao.210286

[56]
陈思秇, 孙立梅, 马文军, 等. 基于贝叶斯时空模型广州市手足口病精细时空尺度下发病影响因素分析[J]. 中国公共卫生, 2020, 36(8):1171-1176.

[Chen S Y, Sun L M, Ma W J, et al. Analysis of influencing factors of hand, foot, and mouth disease incidence in Guangzhou at fine spatiotemporal scales based on Bayesian spatiotemporal model[J]. Chinese Journal of Public Health, 2020, 36(8):1171-1176. ] DOI:10.11847/zgggws1121488

[57]
He X, Dong S, Li L, et al. Using a Bayesian spatiotemporal model to identify the influencing factors and high-risk areas of hand, foot and mouth disease (HFMD) in Shenzhen[J]. PLOS Neglected Tropical Diseases, 2020, 14(3):e0008085. DOI:10.1371/journal.pntd.0008085

[58]
Semakula M, Niragire F, Faes C. Spatio-temporal Bayesian models for malaria risk using survey and health facility routine data in Rwanda[J]. International Journal of Environmental Research and Public Health, 2023, 20(5):4283. DOI:10.3390/ijerph20054283

[59]
Takramah W K, Afrane Y A, Aheto J M K. Bayesian spatiotemporal modelling and mapping of malaria risk among children under five years of age in Ghana[J]. BMC Infectious Diseases, 2025, 25(1):430. DOI:10.1186/s12879-025-10787-9

[60]
Mougeni F, Lell B, Kandala NB, et al. Bayesian spatio-temporal analysis of malaria prevalence in children between 2 and 10 years of age in Gabon[J]. Malaria Journal, 2024, 23:57. DOI:10.1186/s12936-024-04880-8

[61]
Rouamba T, Samadoulougou S, Tinto H, et al. Bayesian spatiotemporal modeling of routinely collected data to assess the effect of health programs in malaria incidence during pregnancy in Burkina Faso[J]. Scientific Reports, 2020, 10:2618. DOI:10.1038/s41598-020-58899-3

PMID

[62]
Semakula M, Niragire F, Faes C. Bayesian spatio-temporal modeling of malaria risk in Rwanda[J]. PLoS one, 2020, 15(9):e0238504. DOI:10.1371/journal.pone.0238504

[63]
Liu Y, Sun J, Gou Y, et al. Analysis of short-term effects of air pollution on cardiovascular disease using Bayesian spatio-temporal models[J]. International Journal of Environmental Research and Public Health, 2020, 17(3):879. DOI:10.3390/ijerph17030879

[64]
Zhang R, Lai K Y, Liu W, et al. Community-level ambient fine particulate matter and seasonal influenza among children in Guangzhou, China: A Bayesian spatiotemporal analysis[J]. Science of The Total Environment, 2022, 826:154135. DOI:10.1016/j.scitotenv.2022.154135

[65]
Ren Z, Wang S, Liu X, et al. Associations between gender gaps in life expectancy, air pollution, and urbanization: A global assessment with Bayesian spatiotemporal modeling[J]. International Journal of Public Health, 2023, 68:1605345. DOI:10.3389/ijph.2023.1605345

[66]
陈胜亮, 靳思慧, 赵冬宝. 广东省县域内住院率时空特征及其影响因素分析[J]. 中国医院管理, 2024, 44(1):23-27.

[Chen SL, Jin SH, Zhao DB. Analysis of spatiotemporal characteristics and influencing factors of hospitalization rates in counties of Guangdong Province[J]. Chinese Hospital Management, 2024, 44(1):23-27. ] DOI:CNKI:SUN:YYGL.0.2024-01-006

[67]
李俊明. 中国PM2.5污染时空趋势研究——基于贝叶斯时空统计视角[J]. 统计与信息论坛, 2019, 34(6):67-73.

[ Li JM. Study on the spatiotemporal trends of PM2.5 pollution in China — Based on the perspective of Bayesian spatiotemporal statistics[J]. Statistics & Information Forum, 2019, 34(6): 67-73. ] DOI:CNKI:SUN:TJLT.0.2019-06-011

[68]
Jin J-Q, Du Y, Xu L-J, et al. Using Bayesian spatio-temporal model to determine the socio-economic and meteorological factors influencing ambient PM2.5 levels in 109 Chinese cities[J]. Environmental Pollution, 2019, 254:113023. DOI:10.1016/j.envpol.2019.113023

[69]
Sarto SD, Ranalli MG, Bakar KS, et al. Bayesian spatiotemporal modeling of urban air pollution dynamics[C]. Topics on Methodological and Applied Statistical Inference, 2016:Springer. https://link.springer.com/chapter/10.1007/978-3-319-44093-4_10

[70]
Tan X, Gan T Y, Chen S, et al. Modeling distributional changes in winter precipitation of Canada using Bayesian spatiotemporal quantile regression subjected to different teleconnections[J]. Climate Dynamics, 2019, 52:2105-2124. DOI:10.1007/s00382-018-4241-0

[71]
梁中耀, 余艳红, 王丽婧, 等. 湖泊水质时空变化特征识别的贝叶斯方差分析方法[J]. 环境科学学报, 2017, 37(11):4170-4177.

[Liang Z Y, Yu Y H, Wang L J, et al. A Bayesian ANOVA method to identify the temporal and seasonal dynamics of lake water quality variables[J]. Acta Scientiae Circumstantiae, 2017, 37(11):4170-4177. ] DOI:10.13671/j.hjkxxb.2017.0276

[72]
于明雪, 孙建国, 杨维涛. 基于贝叶斯层次时空模型的甘肃省土地利用程度演变分析[J]. 地理科学, 2022, 42(5):918-925.

DOI

[Yu M X, Sun J G, Yang W T, et al. Evolution of land use degree in Gansu Province based on Bayesian hierarchical spatio-temporal model[J]. Scientia Geographica Sinica, 2022, 42(5):918-925.] DOI:10.13249/j.cnki.sgs.2022.05.017

[73]
吕建康, 孙建国, 谢甫. 贝叶斯层次时空模型在甘肃省AOD时空分布中的应用[J]. 无线电工程, 2023, 53(3):707-713.

[ Lyu J K, Sun J G, Xie F. Application of Bayesian hierarchical spatio-temporal model in spatio-temporal distribution of aerosol optical depth in Gansu Province[J]. Radio Engineering, 2023, 53(3):707-713. ]

[74]
李俊明. 基于Bayesian层次时空模型的我国老龄化分析与预测[J]. 统计研究, 2016, 33(8):89-94.

[ Li J M. Space-time variation of Chinese aging based on Bayesian hierarchy spatio-temporal model[J]. Statistical Research, 2016, 33(8):89-94. ] DOI:10.19343/j.cnki.11-1302/c.2016.08.011

[75]
Han X, Li J, Wang N. Spatiotemporal evolution of Chinese ageing from 1992 to 2015 based on an improved Bayesian space-time model[J]. BMC Public Health, 2018, 18:502. DOI:10.1186/s12889-018-5417-6

PMID

[76]
Liu D, Song W, Xiu C, et al. Understanding the spatiotemporal pattern of crimes in Changchun, China: A Bayesian modeling approach[J]. Sustainability, 2021, 13(19):10500. DOI:10.3390/su131910500

[77]
Law J., Quick M., Chan P.W. Analyzing hotspots of crime using a Bayesian spatiotemporal modeling approach: A case study of violent crime in the Greater Toronto Area[J]. Geographical Analysis, 2015, 47(1):1-19. DOI:10.1111/gean.12047

[78]
Zeng Q, Wen H, Huang H, et al. A Bayesian spatial random parameters Tobit model for analyzing crash rates on roadway segments[J]. Accident Analysis & Prevention, 2017, 100: 37-43. DOI:10.1016/j.aap.2016.12.023

[79]
Liu C, Sharma A. Using the multivariate spatio-temporal Bayesian model to analyze traffic crashes by severity[J]. Analytic Methods in Accident Research, 2018, 17:14-31. DOI:10.1016/j.amar.2018.02.001

[80]
韩晓, 魏楚, 吴施美. 中国农村居民生物质能消费估计[J]. 资源科学, 2023, 45(9):1817-1829.

DOI

[Han X, Wei C, Wu S M. Estimation of biomass energy consumption by rural residents in China[J]. Resources Science, 2023, 45(9):1817-1829. ] DOI:CNKI:SUN:ZRZY.0.2023-09-009

[81]
刘韵艺, 汤渊, 苏盛, 等. 基于STL-Bayesian时空模型的分布式光伏系统异常检测[J]. 中国电力, 2024, 57(5):222-231.

[Liu Y Y, Tang Y, Su S, et al. Anomaly detection in distributed photovoltaic systems based on STL-Bayesian spatiotemporal model[J]. China Electric Power, 2024, 57(5):222-231.] DOI:10.11930/j.issn.1004-9649.202305120

[82]
Yang HQ, Zhang L, Pan Q, et al. Bayesian estimation of spatially varying soil parameters with spatiotemporal monitoring data[J]. Acta Geotechnica, 2021, 16(1):263-278. DOI:10.1007/s11440-020-00991-z

[83]
Song J, Liu J, Zhang X, et al. Spatio-temporal fluctuation analysis of ecosystem service values in Northeast China over long time series: Based on Bayesian hierarchical modeling[J]. Land, 2024, 13(6):833. DOI:10.3390/land13060833

Options
文章导航

/

〈 〉