EN中文

Journal of Geo-information Science >

2015 , Vol. 17 >Issue 1: 22 - 30

DOI: https://doi.org/10.3724/SP.J.1047.2015.00022

Orginal Article

Vehicle Routing Problem: From a Perspective of Time Geography

  • QI Mingyao , 1, 2, * ,
  • WU Tao 1 ,
  • ZHANG Xin 3
Expand
  • 1. Division of Logistics and Transportation, Graduate School at Shenzhen, Tsinghua University, Shenzhen 518055, China
  • 2. Shenzhen Key Lab of Logistics Engineering and Simulation, Shenzhen 518055, China
  • 3. Institute of Remote Sensing and Digital Earth, Chinese Academy of Science, Beijing 100094, China
*Corresponding author: QI Mingyao, E-mail:

Received date: 2014-07-07

  Request revised date: 2014-09-06

  Online published: 2015-01-05

Copyright

《地球信息科学学报》编辑部 所有
Fold

Abstract

Vehicle routing problem (VRP) has typical characteristics of space-time distribution, thus it is influenced by constrains of space-time conditions. It is necessary to take the space and time factors comprehensively into the consideration of vehicle routing planning. In this paper, we proposed a new perspective to investigate vehicle routing problem and introduced a complete analytic framework from the aspects of time geography. Followed by the introduction of the fundamental theory of time geography, concepts including space-time constraints, space-time path, space-time prism, space-time accessibility, and space-time distance are illustrated in the context of VRP. Meanwhile, the diagrammatic and metric methods of these concepts are also provided. In addition, this paper developed a method to calculate space-time distance. This method considers the characteristics of both locations and time windows for different customers, thus it can be used to easily evaluate the proximity between customers. Finally, we illustrate the value and advantage of time geography by presenting an algorithm to solve a large-scale VRP with soft time windows, embedding the concept of spatio-temporal distance. Further efforts may be devoted to adopt time geography to solve real-time VRP and mobile facility routing problem, etc. The main contribution of this paper is that we find the potential and possibility of time geography in solving VRP problems. Using a series of conceptions and methods of time geography, we can integrate both spatial and temporal features of VRP in a unified frame, which could make solving the VRP problems to be more efficient and effective.

Key words： vehicle routing problem; time geography; space-time accessibility; logistics; GIS

Cite this article

QI Mingyao , WU Tao , ZHANG Xin . Vehicle Routing Problem: From a Perspective of Time Geography[J]. Journal of Geo-information Science, 2015 , 17(1) : 22 -30 . DOI: 10.3724/SP.J.1047.2015.00022

1 引言

车辆路径问题（Vehicle Routing Problem, VRP）的提出可以追溯到1959年[1]。经典车辆路径问题的定义为：有一组车辆为若干个顾客提供运输服务,车辆从场站出发,最终返回该场站,车辆的装载量有限,顾客的需求量已知,且一个顾客只能被服务一次,求通过所有顾客的最短运输路[1]。目前,该问题的目标函数、约束条件等已经被广泛扩展,出现了各种新的VRP模型,例如带时间窗的VRP（VRP with Time Windows, VRPTW）,需求可分离的VRP,随机需求VRP（VRP with Stochastic Demand, VRPSD）等。VRP的应用不仅仅局限在交通运输领域（如金融押运、城市物流配送、报纸邮件递送、外卖服务等的线路安排）,还被拓展应用到电路设计、电网布局等领域。
为了研究人的行为及其时空特征,瑞典地理学家Hägerstrand提出了时间地理学（Time-geography）理论框架[2]。该理论认为,人不是生活在一个没有约束的伊甸园中,而是处于各种约束之中的,这些约束限制了人的活动范围和行为模式。约束主要可分为3类,即能力约束、组合约束和权利约束。Hägerstrand创造性地提出了时空路径、时空棱柱、束（bundle）、交互（interaction）等概念,为研究约束条件下个体的时空行为建立了独特的理论框架。时间地理学的提出是基于社会科学研究背景的,因此被很自然地应用于社会问题的研究,例如Martensson[3]在研究社区如何影响儿童成长的问题时,应用时间地理学方法分析儿童一天的时间安排;Pred[4]应用时间地理学研究了技术和制度创新等对个人生活的影响;Miller[5]应用时间地理学研究了19世纪郊区家庭妇女的行为模式;Forer和Kivell[6]、Pred和Palm[7]和Kwan[8]同样研究了女性在日常生活中的制约以及其地域差异性。时间地理学本质上并不是一个学科方向,也不是一种狭义的理论[9],而是一种分析问题的理论框架,因而可以被应用到很多其它的领域,例如区域规划和交通规划。Lenntorp[10]最早将时间地理学用于区域规划领域,提出了著名的交通规划方案的PESASP（Program Evaluating the Set of Alternative Sample Paths）计算机模拟模型。然而,由于计算的复杂性,时间地理学的概念（例如时空棱柱、潜在路径区域）在很长一段时间内还是处于理论探讨阶段,并没有在真实环境下（如交通网络、大量个人层面（individual-level）的时空数据）得以实现。
20世纪90年代以来,随着GIS技术、ICT技术的普及,时间地理学的量测、分析和可视化方法得到了全面的提高[11-18]。Miller[11]首先将GIS方法引入时间地理学,提出了一种基于交通网络的潜在路径区域(PPA)计算方法。随后,Kwan和Hong[12]提出了一种在2个固定活动点之间插入非固定活动的可选集计算方法,并在ArcGIS软件上实现。时间地理学理论将三维的地理空间压缩到平面二维,用时间作为第三维,因此,借助三维GIS可以直观地展现时间地理学的很多概念,如时空路径、时空棱柱等,从而可以形象地表示活动的时空特征[19-22]。Yu和Shaw[23]扩展了Hagerstrand的时空棱柱模型,提出了一种基于交通网络的三维时空棱柱表示方法,具有一定的实用价值,戚铭尧等[24]在此基础上提出了基于交通网络的时空棱柱面。Neutens[25]则利用CAD实现了时间地理学基本概念的三维可视化。最近的研究中,刘钊等[26]提出了一种基于时空棱柱的人员搜寻范围优化。
车辆路径问题具有典型的时空分布特征,受到众多时空约束条件的制约。例如,随着准时制（JIT）、快速反应（QR）、“零库存”等先进制造和现代物流管理技术的普及,顾客对物流服务的时间要求越来越严格,通常都有一定的服务时间窗要求,即早于该时间窗上限到来的车辆必须等待,晚于该时间窗下限到来的车辆则不能被接受,这就是所谓的带时间窗的车辆路径问题（VRPTW）。此外,车辆调度还受到车辆当前位置、实时交通通行状况、新的顾客需求等各种时空限制条件的制约。由此可见,在车辆路径规划中,综合考虑时间和空间因素是非常必要的。若以车辆轨迹的横、纵坐标作为第一维和第二维,以时间为第三维,则可在一个三维坐标系中表示出车辆的“时空路径”,这就为时空一体化分析提供了便利。
本文借助时间地理学这一理论框架,从一个全新的视角来研究车辆路径问题,提出一套完整的时间地理学分析框架。论文首先阐述了时间地理学的基本概念,然后提出了车辆路径问题中的时空约束、时空路径、时空棱柱、时空可达性、时空距离等概念,并给出了图示和度量方法,最后,展望了时间地理学在VRP中的应用,包括顾客时空聚类、实时需求指派、车辆路径时空分析等。

2 车辆路径问题的基本概念

为了便于表述,我们提出了VRP的4个基本概念：模型（model）、实例（instance）、解决方案（solution）和路径（route）。
模型是指对VRP问题的定义,包括目标函数、约束条件以及各种假设等。VRP的优化目标可以是总行程最短、总时间最短、等待时间最短、费用最少等。约束条件包括：所有顾客需求都必须满足且一个顾客只能被访问一次、顾客只能在时间窗范围内被访问、车辆不能超载等。一些假设包括顾客需求是否确定、道路通行时间是否随时间变化等。
实例是指为顾客坐标、需求量、服务时间窗口,以及车辆容量等变量赋值后的一个具体的VRP问题。为了便于测试和比较,很多学者提出了VRP的实例集（benchmark problems）,比较经典的有Solomon[27]提出的含100个顾客的问题集,以及Gehring和Homberger[28]提出的从200到1000个顾客的大规模VRP问题集。
解决方案是指采用某种方法求得的VRP问题的一个可行解。解的表示方法可以采用自然数来编码,例如用0表示车场,从1开始的自然数表示各个顾客点,则“01203450”表示共2辆车完成任务,按顺序服务的顾客分别是第1辆车服务1、2顾客;第2辆车服务3、4、5顾客,如图1所示。这种解表示方法的好处是便于采用遗传算法等进行求解。
Fig. 1 A solution to a VRP instance

图1 一个VRP实例的解决方案

路径是指解决方案中一辆车从车场出发,服务若干顾客后返回车场的服务路线,或者说解决方案是一组路径的集合。

3 时间地理学的基本概念

时空路径和时空棱柱是时间地理学中的核心概念。Hägerstrand[2]提出,如果将三维空间压缩为平面二维表示,用时间来表示垂直的第三维,则人的活动可以表示为一条永远向上的时空线,即时空路径,图2表示了真实交通网络中2辆车的时空路径。如果将多条时空路径表示在一个立方体中,则形成一个可视化效果非常好的时空路径“水族馆”[19]。
Fig. 2 Two space-time routes based on the real transportation network

图2 真实交通网络的时空路径

时空路径表示个体的一系列具体的时空行为,而时空棱柱则表示人在一定的约束条件下活动的可能范围。一个典型的不考虑真实交通网络的时空棱柱在三维空间中表现为两个圆锥组成的交集（图3）。图中 L 1 和 L 2 分别为2个固定的活动地点,对应的时刻分别是 t 1 和 t 2 ; v 为最大平均速度,圆锥母线的斜率为 1 v 。个体活动的时空范围为时空棱柱的内部,任何超出时空范围的时空点都不可能被到达。如果将时空棱柱垂直投影到二维空间上,形成的范围称为潜在路径区域（Potential Path Area, PPA）。PPA的形状为一个椭圆,因为椭圆边线上任意一点到 L 1 和 L 2 的距离之和均等于 v ( t 2 - t 1 ) 。
Fig. 3 Space-time prism

图3 时空棱柱

时间地理学中存在3种约束[2]：（1）能力约束,指人的生理条件限制或者所采用工具的性能限制,例如人必须吃饭和睡觉,汽车在高速公路上限速120 km/h等;（2）组合约束,指人必须在规定的时间和地点与其他人进行一段时间交互的约束,在这种约束条件下,多个人的时空路径之间将会发生相交,称为路径束（bundle）;（3）权限约束,是指法律、习惯、社会规范等限制人在特定的时间和空间中出现的制约。

4 车辆路径问题中的时间地理学概念

4.1 时空约束

现有的时间地理学应用主要可以归结为在统一的时空框架下分析不同的约束条件对人的活动的影响。例如,不同性别、收入、地区、职业、肤色、宗教信仰的人有不同的社会活动特征和出行范围;不同的交通网络规划或者公共设施布局也会影响人的交通出行行为以及可达范围等。在物流配送这一商业活动中,我们认为各种活动的规划是“理性的”,即人们会按照特定的价值取向（目标函数）确定地选择自己的行为,而较少受到心理、社会、宗教等方面的影响。我们可以在VRP的背景下重新审视Hägerstrand的3种约束。
（1）能力约束。主要体现在：司机的工作时间约束、车辆的连续行驶里程（时间）约束、车辆的装载量约束。
（2）组合约束。在闭合的VRP中,要求车辆从停车场出发,完成任务后回到停车场,因此,多辆车的时空路径在停车场处形成路径束（bundle）。
（3）权限约束。在VRPTW中,顾客只有在规定的服务时间窗内才对配送车辆开放,这是一种权限约束。此外,对一些特殊物品的运输,例如危险品,车辆不能进入城市的中心区,这也是一种权限约束。

4.2 时空路径

VRP时空路径由多条时空路径组成,其中的每一条时空路径代表了一辆车的时空轨迹。这些时空路径不是孤立存在的,而是具有一定的相关性。以经典的VRP为例,每辆车的时空路径之和必须涵盖所有的顾客,同时每条时空路径通过的顾客集合之间没有交集。此外,所有车辆的时空路径都在停车场处形成路径束（bundle）。图4显示了由两辆车所组成的VRP时空路径。图中O为车场,ABCDE表示5个顾客点,O-A-B-O和O-C-D-E-O分别为两条空间路径,对应的时空路径分别为O-O1-A1-A2-B1-B2-O3-O5和O-O2-C1-C2-D1-E1-E2-O4-O5。每个顾客的时间窗用一个圆柱表示,圆柱的高度即为时间窗的长度。对于顾客A和E,车辆由于早于时间窗开始到达,因此,必须等到时间窗开始时才能被接受。对于顾客D,车辆由于到达时服务窗口已经关闭,故此不能服务该点,直接驶往下一点。
Fig. 4 Space-time routes of two vehicles in a VRP instance

图4 包含两辆车的VRP时空路径

4.3 时空棱柱

VRP中的时空棱柱是指在给定配送路径上的2个相邻点及其时间窗后,可以在这两点之间插入新的配送点的时空范围。
借助一个无向图 G 来描述一个VRP模型, G = V , A 。 V = 0,1 , 2 , ⋯ , n 为顶点集合,代表了VRP中的 n 个顾客,0代表车场。 A = 0,1 , 2 , ⋯ , m 代表 m 辆车。 E = ( i , j ) : i , j ∈ V , i < j ,代表图中的边。为简单起见,设边是无方向性的,边的距离为 d ij ,平均速度为 v 。顾客 i 的时间窗口为 e i , l i ,车辆在该处的服务时间为 s i 。待插入顾客为 k , i 和 j 为VRP路径上一对相邻的点,且 i 在 j 之前服务。设Instance（VRP）为该VRP模型的一个实例,而Solution（Instance（VRP））为该实例的一个可行解。按照该可行解,车辆到达 i 点的时刻为 t i - s i ,车辆离开 i 点的时刻为 t i 。由于 j 点的服务时间窗下限为 l j ,车辆可以最晚在 l j 时刻到达 j 点,因此顾客 i 和 j 之间的可用时间（time budget）为：
T = l j - t i   （1）
如果不考虑车辆在 k 点的服务时间,则VRP中顾客 i 和 j 之间的时空棱柱 Pri sm ( i , j ) 为类似于图3中的2个相向圆锥的交集。但事实上,车辆在顾客处往往需要一定的服务时间 s k （如装卸货）,因此需要将该时空棱柱中停留时间小于 s k 的部分去掉。最终的 Prism ( i , j ) 表示为为上下2个相向圆锥,以及一个椭圆柱所围成的一个封闭空间 φ ( x , y , t ) , x , y 为可到达的平面坐标, t 为到达时刻,如图5所示,其解析表达式为：
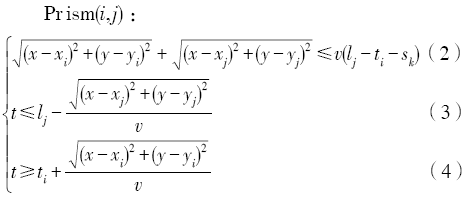
Fig. 5 A space-time prism in a VRP instance

图5 VRP实例中的时空棱柱

从图5可看出,考虑了顾客服务时间后,车辆的空间可达范围（即在水平坐标面上的投影椭圆）小于经典时间地理学定义下（即不考虑活动参与时间）的范围。根据式（2）-（4）,任意给定一个顾客点,由其坐标和时间窗就可判定其能否插入到 i 和 j 之间被服务。

4.4 时空可达性

可达性一词由于其含义的抽象性,具有多种不同的含义[25],只有在根据实际问题对其进行定义和计算时,人们才会使用诸多含义中的一个[29]。Morris等[30]对可达性的一般定义是：从一个地点出发,通过一定的交通系统到达活动地点的便利程度。Kwan等[29]将可达性分为地点可达性和个体可达性,其中前者是经典的可达性表述,反映了地点容易被接近的程度;后者是指个体在给定的日常活动的时空特性下可到达活动点的数量。与地点可达性不同,个体可达性更强调个体的活动特征,因为不同的个体由于自身的活动计划、能力及各种限制条件不同,其可达性是不同的。时间地理学由于提供了时空一体化的理论分析框架,因而被广泛应用于个体可达性的研究[8,13,25,31-36]。
车辆路径问题中的车辆可达性有其自身的特点,例如,活动点只需要考虑顾客点和车场,顾客有服务时间窗限制等,显然这是一种个体可达性。车辆可达性是指车辆在一定的限制条件下,可以服务的顾客点的范围;不同的车辆即使在同一个顾客点,也可能有不同的车辆可达性。例如,车辆如果已经安排了若干运输任务,则其活动范围就会大大受限。
应用时间地理学中的时空棱柱概念可以非常有效地计算车辆可达性。假设一个VRP模型的实例是Instance（VRP）,该实例的一个可行解是Solution（Instance（VRP））,某一辆车 v 从车场0出发,依次要服务的顾客点为 C 1 , C 2 , ⋯ , C k ,然后返回车场0。在任一时刻,车辆为以下4种状态中的一种：未出发、在途、在某个顾客点、任务完成。为不失一般性,考虑车辆在途的情况,假设在时刻 t 车辆 v 正在从 C i - 1 往 C i 的途中,其所在的地点为 P t ,则车辆 v 在 t 时刻的可达性可表示为多个时空棱柱的交集：
At = Prism P t , C i ⋃ Prism C i , C i + 1 ⋃ … ⋃ Prism ( C k , 0 ) （5）
式（5）规定了车辆 v 在时刻 t 的空间可达范围及其时间属性。空间可达范围是 A t 在平面上的投影,如图6所示,它是多个椭圆合并组成的集合。对于图6中的临时顾客点 C s ,由于不在车辆 v 的空间可达范围内,故不能被该车辆服务;对于顾客 C r ,虽然其在空间可达范围之内,但是还需要根据式（3）和式（4）判断其时间属性,以最终决定车辆 v 是否还能在不影响服务其它顾客的前提下服务顾客 C r 。
Fig. 6 The space-time accessibility of a vehicle in transit

图6 在途车辆的空间可达范围

4.5 时空距离

时间和空间是关于活动的两种不同的属性,有着不同的量纲,但是,借助于时间地理学的理论框架,它们得以在同一个坐标系中表达。时空距离就是用一个具体的数值衡量两点之间在时空上的邻近程度。在VRP问题中,两点之间的时空距离越小,说明车辆从一点到达另一点进行配送的代价（费用）越小。时空距离可通过时间距离和空间距离加权平均来求得,二者量纲不一致问题可通过归一化来解决。
D ij ST = α 1 ( D ij S - min m , n ∈ C m ≠ n ( D mn S ) ) / ( max m , n ∈ C m ≠ n ( D mn S ) - min m , n ∈ C ( D mn S ) ) + α 2 ( D ij T - min m , n ∈ C ( D mn T ) ) / ( max m , n ∈ C m ≠ n ( D mn T ) - min m , n ∈ C m ≠ n ( D mn T ) ) （6）
式（6）中, C 为顾客集合; D ij ST 为顾客 i 和顾客 j 的时空距离; D ij S 为空间距离; D ij T 为时间距离; α 1 、 α 2 为空间、时间距离权值,且 α 1 + α 2 = 1 。顾客之间的空间距离的度量非常直接,可以取两顾客点之间的最短交通路径长度。时间距离实际上是用来度量顾客相继被一辆车所服务的便利程度。在时间窗的影响下,时间距离表现出非对称性,即 D ij T ≠ D ji T 。假设顾客 i 和顾客 j 的时间窗分别是 a , b 和 c , d ,不妨设 a ≤ c 。如图7所示,若车辆依次服务顾客 i 和顾客 j ,开始为顾客 i 服务的时间为 t ∈ a , b ,顾客 i 的服务时间为 s i ,从顾客 i 到顾客 j 需要花费的时间为 t ij ,则到达顾客 j 的时间为 t ′ ∈ [ a + s i + t i j , b + s i + t ij ] , t ′ 的最小和最大值分别用 a ′ 和 b ′ 表示。则 t 时刻出发从 i 点到达 j 点的时间距离可以看作是早到时间、空余时间和晚到时间的函数,如式（7）所示。
D ij T ( t ′ ) = δ 1 max 0 , c - t ′ - δ 2 max 0 , d - t ′ + δ 3 max 0 , t ′ - d + d ′ - c ′ （7）
Fig. 7 The time windows of two customers

图7 2个顾客时间窗之间的关系

式（7）中, δ 1 ≥0, δ 2 ≥0, δ 3 ≥0,分别为早到时间、空余时间和晚到时间的系数。通常可将 δ 2 设为1, δ 1 和 δ 3 设为惩罚系数,分别代表车辆早到和车辆晚到的惩罚因子,而且一般 δ 3 > δ 1 。为保证 D ij T ( t ′ ) 非负,式中加入了一个固定的正数 ( d ′ - c ′ )   。
假设车辆到达顾客 j 的时间 t ′ 在 [ a ′ , b ′ ] 内服从均匀分布,则顾客 i 到顾客 j 之间的时间距离计算公式为：
D ij T = ∫ a ′ b ′ D ij T t ′ d t ′ ( b ′ - a ′ )           （8）

5 基于时间地理学的VRP算法

VRP问题具有典型的时空分布特征,因此,在求解VRP问题时,如果能在统一的框架下同时考虑VRP的时间和空间特征,将有利于更快或者更好地求解VRP问题。现已有一些VRP算法考虑了顾客的空间临近性[37]。本文在经典VRP问题基础上,考虑一种大规模、带软时间窗的VRP问题[38]。大规模VRP问题中顾客数量可达到几百、上千个,例如烟草配送求解这类问题往往采用“先聚类,再生成路径”（cluster-first and route-second）的方法。软时间窗是指如果车辆早于或晚于时间窗到达顾客也可服务,但会产生一个惩罚,单位时间的惩罚系数分别记为pe和pl。假设共有n个顾客,使用的车辆数为nv,单位车辆固定费用为cf,单位里程的运输费率为ct,总运输里程为D,总的早到等待时间te,总晚到时间tl,则本问题的目标是优化线路使得总费用C（式（7））最小。
C = n v c f + c t D + p e t e + p l t l （9）

5.1 算法基本流程

本算法采用了“cluster-first and route-second”的方法,基本流程如下：
（1）根据式（7）和式（8）,计算任意2个顾客之间的时空距离;
（2）以时空距离作为度量标准,采用k-medoid方法将n个顾客进行聚类,分为k组, k = n / Z , 为向上取整,Z为可快速求解的VRP问题的规模,此处设为100;
（3）对每一组中的顾客,采用某种启发式或元启发式算法求解,得到若干条线路;
（4）将上述各组所求解的线路进行汇总,得到最终结果。

5.2 算例分析

为了验证时空距离在VRP算法中的作用,在上述算法流程（2）中分别用时空距离和空间距离进行了聚类,然后基于Gehring和Homberger提出的大规模VRPTW标杆问题[28]中的R1类问题（9个算例）进行了测算。参数取值如下： n = 1000 , c f = 1000 , c t = 1 , p e = 1 , p l = 2 。为节约计算时间,流程（3）中采用了简单的Solomon I1插入算法,计算结果如表1所示。
Tab. 1 Computational comparison of the VRP algorithms between spatial distance and spatio-temporal distance

表1 采用空间距离和时空距离的VRP算法效果对比

算例 基于空间距离 基于时空距离
车辆数 费用 等待时间(s) 晚到时间(s) 车辆数 费用 减少比例(%) 等待时间(s) 减少比例(%) 晚到时间(s) 减少比例(%)
r110_1 96 1733292.0 55425.8 529240.6 97 906176.6 -47.7 18767.8 -66.1 318867.9 -39.7
r110_2 95 1447089.1 52428.1 387681.7 97 1001592.6 -30.8 40802.6 -22.2 225838.9 -41.7
r110_3 96 1156667.1 65600.8 201966.8 95 966187.8 -16.5 53328.4 -18.7 161426.5 -20.1
r110_4 97 657554.4 57327.6 58423.0 96 754247.5 14.7 60750.8 6.0 51716.1 -11.5
r110_5 96 1658948.7 44516.1 516980.2 96 831090.9 -49.9 18563.1 -58.3 297474.5 -42.5
r110_6 96 1498153.4 59679.4 339907.1 95 1090445.3 -27.2 45092.9 -24.4 241196.2 -29.0
r110_7 97 1128792.5 62913.7 170869.0 96 999666.0 -11.4 54165.1 -13.9 131242.6 -23.2
r110_8 96 544617.2 49471.3 58731.5 97 608456.5 11.7 50131.8 1.3 53238.3 -9.4
r110_9 97 1637284.8 55915.6 471687.5 95 816374.6 -50.1 18135.8 -67.6 283935.6 -39.8
从表1可看出,采用时空距离后,9个算例有了不同程度的提高：算例1、5、9中所有顾客都有时间窗限制,算法提高的比例最大;算例2、6中有75%的顾客有时间窗,提高比例次之;算例3、7及算例4、8拥有时间窗约束的顾客比例分别为50%和25%,算法提高的比例依次降低。这一结果说明,时间窗约束越严格,时空距离对于算法的提升作用就越明显,这证明了时间地理学对于求解这类VRP问题的价值。
需要指出的是,本算法得到的解未来还可以采用元启发式算法进行进一步改进。任丽[39]设计了一种可变邻域搜索算法来求解VRPTW,在邻域搜索算子relocate（将一个顾客尝试移到另一条线路上）中,借助时空聚类,只考虑将被移出的点插入到时空邻近点之前或之后,从而减少了搜索范围,取得了较好的计算结果。

6 结论与展望

时间地理学是研究约束条件下个体时空行为的一套独特的理论框架,在社会科学、交通规划等领域已经有一些成功的应用。车辆路径问题具有典型的时空分布特征,车辆路径的决策受到顾客空间分布及服务时间窗等的限制,是运筹学领域里公认的NP-hard问题,因此,将时间地理学应用于车辆路径问题的研究具有积极意义。本文首次系统地阐述了车辆路径问题中的时间地理学概念,即解释了车辆路径问题中的3种时空约束约束,描述了车辆的时空路径,特别是提出了车辆时空棱柱的几何图形和数学表达式,为判断车辆的可达范围提供了定量化的计算方法。其次,论文还提出了一种时空距离的度量方法,这一方法综合考虑了顾客之间在空间位置和时间窗口2个方面的因素,可以更科学地判定顾客之间的“邻近性”。
论文以求解大规模软件时间窗车辆路径为例,提出了时间地理学方法的VRP算法流程,并用算例验证了其有效性。在未来研究中,可以尝试借助时空棱柱和时空可达性模型求解动态车辆路径问题,也可以借助时空路径模型对车辆轨迹大数据进行时空分析。此外,车辆路径问题有很多扩展分支,比如移动服务设施的路径规划,预计时间地理学也会有应用的潜力。

The authors have declared that no competing interests exist.

References

Publishing order | Descend order by publishing year | Descend order by cited within
[1]
Dantzig G B, Ramser J H.The truck dispatching problem[J]. Management Science, 1959,6(1):80-91.

[2]
Hägerstrand T.What about people in regional science[J]. Papers and Proceedings of the Regional Science Association, 1970,24:7-21.

[3]
Martensson S.Childhood interaction and temporal organization[J]. Economic Geography, 1977,2:99-125.

[4]
Pred A.The impact of technological and institutional innovations on life content: Time geographic observations[J]. Geography Analysis, 1978,10:345-372.

[5]
Miller R.Household activity [atterns in nineteenth-century suburbs: A time-geographic exploration[J]. Annals of the Association of American Geographers, 1982,72:355-371.

[6]
Forer P C, Kivell H.Space time budgets, public transport, and spatial choice[J]. Environment and Planning A, 1981,13:497-509.

[7]
Pred A, Palm R.The status of american women: A time geographic view[M]//Lanegran D A, Palm R. Invitation to Geography. New York: Mcgraw2Hill, 1978:99-109.

[8]
Kwan M P.Gender, the home-work link, and space-time patterns of non-employment activities[J]. Economic Geography, 1999,75(4):370-394.

[9]
Lenntorp B.Time-geography——At the end of its beginning[J]. GeoJournal, 1999,48:155-158.

[10]
Lenntorp B.A time geographic simulation model of individual activity programs[M]//Carlstein T, et al. Timing Space and Spacing Time, Vol.2: Human Activity and Time Geography. London: Edward Arnold, 1978:162-180.

[11]
Miller H J.Modeling accessibility using space-time prism concepts within geographical information systems[J]. International Journal of Geographical Information Systems, 1991,5(3):287-301.

[12]
Kwan M P, Hong X D.Network-based constraints-oriented choice set formation using GIS[J]. Geographical Systems, 1998,5:139-162.

[13]
Kwan M P.Space-time and integral measures of individual accessibility: A comparative analysis using a point-based framework[J]. Geographical Analysis, 1998,30(3):191-216.

[14]
Miller H J, Wu Y H.GIS software for measuring space-time accessibility in transportation planning and analysis[J]. GeoInformatica, 2000,4(2):141-159.

[15]
Kwan M P, Weber J.Individual accessibility revisited: Implications for geographical analysis in the twenty-first century[J]. Geographical Analysis, 2003,35(4):341-353.

[16]
Miller H J.A measurement theory for time geography[J]. Geographical Analysis, 2005,37(1):17-45.

[17]
Shaw S L, Yu H, Bombom L. A space-time GIS approach to exploring large individual-based spatiotemporal datasets[J]. Transactions in GIS, 2008,12(4):425-441.

[18]
Shaw S L, Yu H.A GIS-based time-geographic approach of studying individual activities and interactions in a hybrid physical-virtual space[J]. Journal of Transport Geography, 2009,17(2):141-149.

[19]
Kwan M P, Lee J.Geovisualization of human activity patterns using 3D GIS: A time-geographic approach[M]// Goodchild M F, Janelle D G. Spatially Integrated Social Science. Oxford University Press: New York, 2004:48-66.

[20]
Kraak M J, Koussoulakou A.A visualization environment for the space-time cube[C]. SDH 2004: Proceedings of the 11th International Symposium on Spatial Data Handling: Advances in Spatial Data Handling II: 23-25 August 2004, University of Leichester, 2004:189-200.

[21]
Yu H.Spatial-temporal GIS design for exploring interactions of human activities[J]. Cartography and Geographic Information Science, 2006,33(1):3-19.

[22]
Yu H.Visualizing and analyzing activities in an integrated space-time environment: Temporal GIS design and implementation[J]. Transportation Research Record: Journal of the Transportation Research Board, 2007,2024:54-62.

[23]
Yu H, Shaw S L.Exploring potential human activities in physical and virtual spaces: A spatio-temporal GIS approach[J]. International Journal of Geographic Information Science, 2008,22(4):409-430.

[24]
戚铭尧,樊艳伟,彭昕,等.一种基于交通网络的时空棱柱表示[J].武汉大学学报(信息科学版),2010,12(35):1491-1495.

[25]
Neutens T, Witlox F, Demaeyer P.Individual accessibility and travel possibilities: A literature review on time geography[J]. European Journal of Transport and Infrastructure Research, 2007,7(4):335-352.

[26]
刘钊,罗智德,张耀方,等.基于时空棱柱的人员搜寻范围优化[J].地球信息科学学报,2014,16(4):531-536.

[27]
Solomon M.Algorithms for the vehicle routing and scheduling problems with time window constraints[J]. Operations Research, 1987,35(2):254-265.

[28]
Gehring H, Homberger J.Parallelization of a two-phase metaheuristic for routing problems with time windows[J]. Journal of Heuristics, 2002,8(3):251-276.

[29]
Pirie G H.Measuring accessibility: A review and proposal[J]. Environment and Planning A, 1979,11(3):299-312.

[30]
Morris J M, Dumble P, Wigan M.Accessibility indicators for transportation planning[J]. Transportation Research A, 1979,13:91-109.

[31]
Kim H M, Kwan M P.Space-time accessibility measures: A geocomputational algorithm with a focus on the feasible opportunity set and possible activity duration[J]. Journal of Geographical Systems, 2003,5(1):71-91.

[32]
Kwan M P, Alan T, Murray M E, et al.Recent advances in accessibility research: Representation, methodology and applications[J]. Journal of Geographical Systems, 2003,5(1):129-138.

[33]
Miller H J.Measuring space-time accessibility benefits within transportation networks: Basic theory and computational methods[J]. Geographical Analysis, 1999,31:187-212.

[34]
Weber J.Individual accessibility and distance from major employment centers: An examination using space-time measures[J]. Journal of Geographical Systems, 2003,5:51-70.

[35]
Weber J, Kwan M P.Bringing time back in: A study on the influence of travel time variations and facility opening hours on individual accessibility[J]. The Professional Geographer, 2002,54:226-240.

[36]
Weber J, Kwan M P.Evaluating the effects of geographic contexts on individual accessibility: A multilevel approach[J]. Urban Geography, 2003,24:647-671.

[37]
涂伟,方志祥,李清泉,等. 基于Voronoi邻近的物流车辆路径快速优化算法[J].地球信息科学学报,2012,14(6):781-787.

[38]
Qi M Y, Lin W H, Li N, et al.A spatiotemporal partitioning approach for large-scale vehicle routing problems with time windows[J]. Transportation Research: Part B, 2012,48:248-257.

[39]
任丽. 基于时空聚类的车辆路径分析与优化[D].北京:清华大学,2011.

Options
Outlines

/

〈 〉