EN中文

Journal of Geo-information Science >

2015 , Vol. 17 >Issue 2: 178 - 184

DOI: https://doi.org/10.3724/SP.J.1047.2015.00178

Orginal Article

A Quadratic Programming Model for Variable-Scale Representation of Graded Road Network Considering Spatial Conflict

  • HUANG Jianfeng , 1 ,
  • ZHANG Xinchang , 1, 2, * ,
  • GUO Taisheng 1
Expand
  • 1. School of Geography and Planning, Sun Yat-Sen University, Guangzhou 510275, China
  • 2. Guangdong Key Laboratory for Urbanization and Geo-simulation, Guangzhou 510275, China
*Corresponding author: ZHANG Xinchang, Email:

Received date: 2014-11-12

  Request revised date: 2014-12-02

  Online published: 2015-02-10

Copyright

《地球信息科学学报》编辑部 所有
Fold

Abstract

Variable-scale visualization technique has been widely applied in the representation of road network data. The main focus of this technology is to highlight the dense central area in a limited map layout with large-scale display method. On the other hand, the marginal and assistant map contents, which are relatively unimportant, will be displayed in small-scale. However, in previous studies, methods using coordinate transformation formula may cause excessive map deformation and spatial conflict among road elements. To solve these problems, a quadratic programming model is proposed to improve the visual effect of variable-scale transformation. In this paper, a line distortion rule based on road grade is constructed. In addition, a spatial conflict constraint rule based on support vector machine is applied to eliminate topological errors of road network. Finally, the road network data in Zengcheng District of Guangzhou city are used to testify the purposed model and the method in this paper. The result shows that this model can dynamically improve the visual effect of variable-scale. Conclusively, this paper provides a new idea to deformation controlling and spatial conflict elimination in the field of variable-scale visualization research.

Key words： Cartography; variable-scale; quadratic programming; support vector machine; road grade

Cite this article

HUANG Jianfeng , ZHANG Xinchang , GUO Taisheng . A Quadratic Programming Model for Variable-Scale Representation of Graded Road Network Considering Spatial Conflict[J]. Journal of Geo-information Science, 2015 , 17(2) : 178 -184 . DOI: 10.3724/SP.J.1047.2015.00178

1 引言

现代地图的表达往往需要突出某些重点关注区域和专题性内容,如城市旅游地图需要突出显示商业中心、景点设施,而城市交通地图则要求清晰显示密集区域的道路分布状况等。虽然大部分地图浏览设备均提供了地图漫游、缩放等工具,在一定程度上解决了用户浏览密集地图内容的难题,但其本质是在不同时刻切换显示地图在不同比例尺下的视图,这样往往只能显示局部信息,而无法表达全局内容,继而破坏了地图的完整性。变比例尺可视化技术可用于解决该问题,它使地图各部分可采用不同的比例尺显示,将局部密集区域夸大显示的同时,保持了中心区域向外围区域的连续过渡,从而增强了地图的可读性。因此,研究有效的变比例尺可视化技术具有重要的理论和现实意义。
国外的变比例尺可视化研究工作开展得较早,技术也较为成熟[1-4]。文献[5]实现了中心密集城区比例尺变大、周边区域比例尺线性变小的显示效果。文献[6]和文献[7]提出了Focus+Glue+Context模型,在满足Focus区域等比例放大的同时,将地图变形内容控制在Glue区域,而Context区域的内容保持不变。文献[8]利用变比例尺方法处理亚特兰大市复杂的地铁路线分布图,使线路清晰地显示于小屏幕上,且保证了线路之间正确的拓扑关系。近年来,变比例尺技术的研究在国内也逐渐得到重视[9-16],但不少是基于坐标转换或地图投影方面的研究,有可能导致地图变形过大或要素之间的空间冲突,且需要设计不同的变换公式或多次调整参数值以满足变换的需求。文献[17]将变比例尺技术应用于导航电子地图,实现了近大远小的“哈哈镜”显示效果。文献[18]以手机移动设备实现了道路网变比例尺效果,能在小屏幕中显示更详尽的道路信息。文献[19]则提出了一种能量优化的变比例尺模型,用于控制地图变形的范围,但计算较为复杂。
本文重点研究道路网变比例尺可视化技术,针对当前研究中难以控制道路变形和维持道路拓扑关系正确性等问题,构建了二次规划算法的等级道路网变比例尺模型,结合顾及道路等级的形变约束规则和支持向量机的线相交约束规则,动态优化道路网变比例尺的效果。

2 二次规划法的道路网变比例尺可视化模型

2.1 二次规划的数学含义

二次规划是最简单的约束非线性规划问题,在运筹学、经济数学和组合优化科学等领域得到广泛应用,其标准形式为：
min               q ( x ) = 1 2 x T Gx + g T x s . t .                           a i T x = b i ,                                       i ∈ E   a i T x ≥ b i ,                                   i ∈ I （1）
式（1）中,G是n×n的对称矩阵;T是有限指标集;E、I分别对应等式约束和不等式约束指标集合;g、x、{ai}、{bi}都是n维向量。二次规划问题的目标函数为二次函数,而约束条件为线性等式或不等式。当xTGx≥0时,该问题属于凸二次规划问题,如能求得凸规划下的局部极小点,即可得到整体的最小点。因此,构建二次规划法的道路网变比例尺模型就是要构造一个满足凸二次规划要求的二次目标函数和多个线性等式或不等式的约束条件。

2.2 道路网变比例尺建模原理

基于数学优化算法的道路网变比例尺模型最先由Haunert[20]提出,与Focus+Glue+Context模型[6-7]较为相似,均可对道路网中指定区域进行等比例放大,而且放大倍数可以人为定义。不同的是,前者采用最优化的思想将地图变形分散于放大区域以外的区域,使变换后的道路网与原始路网更为形似。
对于任意二维矢量道路网（图1）,可表示成G={V, E}。其中,V为道路网的结点集合,E表示道路网的线段集合,每一个道路网结点 u ∈ V ,均有2个坐标值xu和yu,相邻道路网结点 { u , v } 构成了道路网的一条线段,为E的一个子集。
Fig. 1 Representation of road network nodes and lines

图1 道路网结点及线段的表示方法

道路网任意线段 { u , v } ,经过变比例尺计算后,得到线段 { u ′ , v ′ } ,其角度没有发生变化,但长度可能发生改变。分别用 δ x uv 和 δ y uv 表示X方向和Y方向上长度的缩放偏差,满足式（2）：
δ x uv =   X v - X u - S u x v - x u δ y uv =   Y v - Y u - S u y v - y u   u , v ∈ V ，   v ∈ Adj u （2）
式中, S u ( S u > 0 ) 表示两结点距离的缩放倍数,其在X方向和Y方向上相同。 v ∈ Adj ( u ) 表示相邻于结点u的任意一个结点v。根据模型的特点,在变比例尺过程中,需要考虑以下3种情形：
（1）道路网中每一个结点 u ( x u , y u ) ,经过变比例尺计算后,将得到新的坐标值 u ′ ( X u , Y u ) 。若要求 u ′ 在原来的矩形视图范围下显示,则需满足约束条件（3）。函数min和max分别为求得视图范围内所有结点的横、纵坐标的最小值和最大值。
min v ∈ V x u ≤ X u   ≤ max v ∈ V x u min v ∈ V y u ≤   Y u ≤ max v ∈ V y u u ∈ V （3）
（2）当线段 { u , v } 的结点均在放大区域（Focus区域,用点集 F ∈ V 表示）内时,线段长度将依比例放大,则满足约束条件（4）：
X v - X u = S u ( x v - x u ) Y     v       - Y   u     = S u ( y   v     - y u ) S u = Z δ x uv = 0    δ y uv = 0 u , v ∈ F ， v ∈ Adj u （4）
式中,Z为Focus区域的放大倍数（可人为定义）, v ∈ Adj ( u ) 表示结点v为结点u的邻接结点, u , v ∈ F 表示结点u、v均在Focus区域内。约束条件（4）要求Focus区域中的线段等比例放大Z倍,其产生的缩放偏差不计入总偏差量中。
（3）当线段 { u , v } 存在一个或以上结点位于Focus区域以外时,其变化前后的长度不确定,但结点之间的缩放偏差仍可用式（5）表示。
δ x uv =   X v - X u - S u x v - x u δ y uv =   Y v - Y u - S u y v - y u   u ∉ F 或 v ∉ F ，   v ∈ Adj u （5）
在式（5）中,若道路网的线段存在一个或多个结点不在Focus区域内时,其坐标偏移所产生的缩放偏差是不确定,但必须计入总偏差量中,此时,可利用缩放倍数Su作为未知解加入二次规划模型中进行优化运算。假设道路网的结点数为n,则模型的目标解可定义为：
X 1 , Y 1 , S 1 , X 2 , Y 2 , S 2 ,   … , X i , Y i , S i , i = 1 , 2,3 , … , n （6）
为了达到整体道路网变形最小化,只需让所有结点之间的缩放偏差总和最小化。对于Focus区域内的线段而言,其缩放偏差总和为零,因此,模型的优化目标实质是使Focus区域以外区域的缩放偏差总和最小（式（7））。为使目标函数存在二次项,需求缩放偏差的平方和最小值。另外,为了保证Focus区域向外扩大时的自然过渡,目标函数中增加了距离倒数w作为缩放偏差的权重值,可使相距Focus区域较近的线段长度缩放偏差尽可能小,而较大的偏差量则分布于相距Focus区域较远的线段中。由于式（7）符合凸二次规划的一般形式,且约束条件（3）、（4）、（5）均为线性等式或不等式,因此,模型存在最优解。

2.3 顾及道路等级的形变约束规则

文献[20]构建的道路网变比例尺模型,仅采用距离的倒数作为权重因子,没有考虑不同道路等级对于整体路网布局的重要性。道路等级越高,其所受的关注程度越高,且等级高的道路一般分布在全局道路网中,因此,其缩放偏差也应尽可能小,以确保变化前后道路网的整体结构相似。文献[21]总结了不同比例尺下道路网要素类层次的演变规则,明确了道路网的基本分类与等级划分,将该成果运用到本模型中,构建顾及道路等级的道路形变约束规则。
首先,对路网中各线段按等级划分规则进行分级,得到总的级别数量N,然后,在式（7）中增加道路等级权重约束。修改后的目标函数为：
式（8）中,i表示道路的等级,最高级别的道路设为1,其他依次递增。由上述目标函数可知,道路的等级越高,其函数值越大,应在优化计算过程中尽量避免等级高的道路缩放过大,以保证道路网在变换前后的整体相似性。

2.4 道路要素空间冲突的预处理及约束规则

2.4.1 道路网空间冲突预处理
道路网数据经过矢量化工作之后,仍可能存在不易察觉的拓扑错误,如线段错交、重叠或不连通,这类错误均可通过构建拓扑关系消除。道路网连通性是本模型构建的内在要求,如果出现部分线段不连通的情况,将导致优化运算过程中忽略该部分数据,从而无法得到正确结果。因此,可在这些不连通的线段中引入一些假设的“道路”,以构建连通图,并在优化运算之后,删除这些“道路”。
针对道路网中存在形如公路桥横跨公路等情况,为了保证变比例尺过程中其拓扑关系不发生变化,需在线段之间增加假设的“结点”,并在运算之后删除。
2.4.2 基于支持向量机的线相交约束规则
坐标转换或地图投影的变比例尺方法有可能导致要素间空间冲突的产生（图2）,这类算法一般依照某种函数映射关系对坐标进行偏移,但难以避免线段相交或重叠。本模型若缺少一定的线相交约束条件,在优化过程中也可能会产生类似的问题。不少学者提出了避免线相交的方法,主要有以下2种：
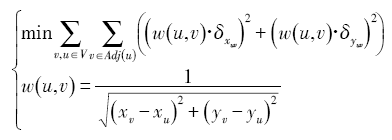
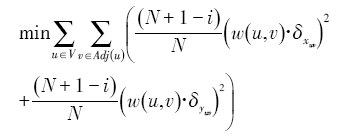
Fig. 2 Intersected lines during the process of variable-scale transformation

图2 变比例尺过程中产生线相交问题

（1）约束Delaunay三角化方法[19,22]
首先,对道路网构建Delaunay三角网,然后,在模型中增加限制所有三角形出现较大变形或者翻转等情况的约束条件。由于约束条件均为线性不等式,在模型求解过程中仍可得到全局最优解,但计算复杂,且密集的三角网局限了道路的形变范围。
（2）利用支持向量机的“分割”思想构建线相交约束规则[20]
对于道路网中的任意两条不相交的线段 l = { s , t } 和 r = { u , v } ,假设存在未知“分割线”c,将l和r分割于左右两侧（图3）,并在偏移过程中始终保持这种拓扑关系。则l、r和c需满足不等式组（9）,其中,线段c用 Δx , Δy 和点 ( x , y ) 表示。
Fig. 3 Construction of dividing line C with support vector machine

图3 利用支持向量机方法构建“分割线”C

y s - y ∙   Δx - x s - x ∙   Δy ≥   0 s 在 c 的左边或 c 上 y t - y ∙   Δx - x t - x ∙   Δy   ≥    0 t 在 c 的左边或 c 上 y u - y   ∙   Δx   - x u - x ∙   Δy ≤    0 u 在 c 的右边或 c 上 y v - y   ∙   Δx   - x v - x ∙   Δy   ≤    0 v 在 c 的右边或 c 上 （9）
由于 x ， y ， Δx ， Δy 均为未知解,因而式（9）是非线性不等式组,不能作为模型的约束条件,可利用支持向量机（Support Vector Machine,SVM）解决该问题。对于线性可分的直线l、r,将它们的端点坐标作为训练数据输入SVM模型中,设置其核函数为线性核函数,总是能够得到最大限度分割l、r的一条“分割线”C,且直线C的斜率唯一确定,由此不等式组（9）可转为线性的不等式组。同时,为避免出现l、r在优化运算过程中出现相距过近甚至重叠的情况,可将不等式组中的0值调整为 ε 2 和 - ε 2 ,从而得到不等式组（10）,其中, ε 根据地图单位而定。
y s - y ∙   Δx - x s - x ∙   Δy ≥ ε 2 s 在 c 的左边或 c 上 y t - y ∙   Δx - x t - x ∙   Δy   ≥   ε 2 t 在 c 的左边或 c 上 y u - y   ∙   Δx   - x u - x ∙   Δy ≤    - ε 2 u 在 c 的右边或 c 上 y v - y   ∙   Δx   - x v - x ∙   Δy   ≤    - ε 2 v 在 c 的右边或 c 上 （10）
利用式（10）可以避免任意两条不相交的线段相交。然而,若对每两条线段都建立该约束,必然增加模型的运算量。在模型初次运算时,可先不添加该约束,如果没有产生线相交的情况,则模型运算结束;如果出现部分线段相交的情况,则对该部分线段增加约束,重新运算。经过多次迭代,直至所有线段不相交时模型运算结束。

3 模型实验结果分析

增城区在规划建设广州市东部城市副中心进程中,提出“三大主体功能区”战略,规划“一核三区”的城市格局（图4）。本实验选取道路网密度较大的区域作为Focus区域,进行变比例尺可视化实验,并与现有的变比例尺算法进行比较,以验证模型的正确性和评价其优劣。
Fig. 4 Experimental data and the selection of focus region

图4 试验数据与Focus区域选取

实验数据是增城区的内控路网数据,格式为ShapeFile,可通过ArcGIS软件平台进行浏览、检查和编辑。模型利用Matlab R2010b平台运算,用其非线性最优化软件包和LIBSVM支持向量机函数库获得全局最优解。实验中对道路网划分等级数为6,即式（8）中N为6。
本文实现了局部的和全局的道路网变比例尺实验。在实验1中,提取增城区的荔城、增江及石滩镇区域道路网（图5（a））数据进行变比例尺实验,对其中的Focus区域（红框区域）放大1.4倍,并选择可调“放大镜”式地图投影[11]和基于Focus+Glue+Context模型[7]的方法作为对比。实验结果如图5（b）、（c）、（d）所示：
Fig. 5 Results of the first experiment

图5 实验1结果

在Focus+Glue+Context模型中,如果Focus区域变化过大或者Glue区域过小,将产生线相交甚至重叠的问题,运用可调“放大镜”式地图投影的方法,则容易造成道路网的变形过大,而使用本文的模型不仅没有产生明显的地图变形,而且道路要素间的空间冲突问题也得到了解决。
为探讨本模型如何控制地图变形,可分级显示变比例尺过程中产生的缩放偏差。由图6可知,除放大区域内道路的缩放偏差为零,其他区域的道路均发生了变形,且变形量逐渐向外扩展。因此,本模型能将地图变形量分散到整个区域,避免了局部区域产生较大的地图变形,且充分利用了地图空间。
Fig. 6 Distribution of scaling deviations regarding to the result of the first experiment

图6 实验1对应的缩放偏差分布图

在实验2中,对增城区整体道路网进行变比例尺实验（图7）。该实验同时对增城区多个道路密集区域进行了不同缩放比例的变比例尺实验。结果表明,同时对多处进行放大并没有造成整体路网的严重变形,说明本模型能满足多焦点、不同缩放比例的变比例尺需求。
Fig. 7 Results of the second experiment

图7 实验2结果

4 结论与展望

对于坐标公式转换或地图投影方式的地图变比例尺技术,尽管可实现各种满足用户需求的变比例尺效果,但其往往要求用户熟悉各类转换公式的特点,并且需要频繁调整公式参数,方可获得较为理想的实验结果。另外,仅仅依照指定的公式进行转换,难以避免地图要素空间冲突的产生。故此,本文运用数学优化的思想,以最小化道路网变形量之和为目标,建立了二次规划法的矢量道路网变比例尺模型,并在该模型基础上增加了顾及道路等级的形变约束规则和基于支持向量机的线相交约束规则。顾忌道路等级的形变约束规则可有效调整道路网的整体变形效果,而基于支持向量机的线相交约束规则可在变换过程中,有效避免线段间的空间冲突。模型实现过程中只需要用户自由选择需放大的圆形区域,指定放大倍数即可,无需过多了解模型的实现流程。通过局部和全局的道路网变比例尺实验结果可知,本模型具有良好的自适应性和实用性,是地图变比例尺研究领域中的重要研究方向之一。
然而,本文模型也存在一定的局限性,如果模型目标解数量庞大,其时间复杂度也相对较大,则难以满足实时的变比例尺可视化需求,须考虑使用其他优化算法快速解算模型的全局最优解。另外,本文仅实现了线要素的变比例尺建模,尚未完全解决矢量电子地图中点、线、面和注记全要素的建模,有待今后进一步研究。

The authors have declared that no competing interests exist.

References

Publishing order | Descend order by publishing year | Descend order by cited within
[1]
Kadmon N.Data bank derived hyperbolic-scale equitemporal town maps[J]. International Yearbook of Cartography, 1975,15:47-54.

[2]
Snyder J P.“Magnifying-Glass” azimuthal map projections[J]. The American Cartographer, 1987,14(1):61-68.

[3]
Guerra F, Boutoura C.An electronic lens on digital tourist city-maps[C]. Proceedings of 20th International Cartographic Conference, 2001:1151-1157.

[4]
Furnas G W.Generalized fisheye views[C]. Proceedings of the SIGCHI Conference on Human Factors in Computing Systems, ACM, 1986.

[5]
Fairbairn D, Taylor G.Developing a variable-scale map projection for urban areas[J]. Computers & Geosciences, 1995,21(9):1053-1064.

[6]
Takahashi N. An elastic map system with cognitive map-based operations[C]. In: International Perspectives on Maps and the Internet. Berlin: Springer Berlin Heidelberg, 2008:73-87.

[7]
Yamamoto D, Ozeki S, Takahashi N.Focus+Glue+Context: An improved fisheye approach for web map services[C]. Proceedings of the 17th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, ACM, 2009:101-110.

[8]
Wang Y S, Chi M T.Focus+ context metro maps[J]. IEEE Transactions on Visualization and Computer Graphics, 2011, 17(12):2528-2535.

[9]
黄国寿. 变比例尺城市平面地图的地图投影[J].测绘学报,1985,14(3):188-196.

[10]
胡毓钜. 变比例尺地图投影系统[J].武汉大学学报(信息科学版),1987,12(2):47-54.

[11]
王桥,胡毓钜.一类可调放大镜式地图投影[J].测绘学报,1993,22(4):270-279.

[12]
吴忠性. 多焦点地图投影[J].地理学报,1989,44(1):101-104.

[13]
杨晓梅,杨启和,赵琦.一类新的变比例尺地图投影——组合投影研究[J].武汉测绘科技大学学报,1998,24(2):162-165.

[14]
马俊海. 城市平面图变比例尺方法初探[J].地图,1990(2):14-18.

[15]
王桥,胡毓钜.保持矩形图廓的变比例尺地图投影[J].测绘信息与工程,1992(4):1-4.

[16]
王延亮. 变比例尺投影的一种通用方法[J].测绘通报,1988(5):34-41.

[17]
艾廷华,梁蕊.导航电子地图的变比例尺可视化[J].武汉大学学报(信息科学版),2007,32(2):127-131.

[18]
Li Q Q.Variable-scale representation of road networks on small mobile devices[J]. Computers & Geosciences, 2009, 35(11):2185-2190.

[19]
吴金亮,刘利刚.基于内容的Focus+Context可视化技术[J].计算机应用,2011,31(1):6-10.

[20]
Haunert J H, Sering L.Drawing road networks with focus regions[J]. IEEE Transactions on Visualization and Computer Graphics, 2011,17(12):2555-2562.

[21]
王艳慧,陈军,蒋捷,等.道路网多尺度数据建模的初步研究[J].地理信息世界,2004(3):42-48.

[22]
Jin Y, Liu L, Wu Q.Nonhomogeneous scaling optimization for realtime image resizing[J]. The Visual Computer, 2010,26(6-8):769-778.

Options
Outlines

/

〈 〉