EN中文

Journal of Geo-information Science >

2015 , Vol. 17 >Issue 3: 260 - 267

DOI: https://doi.org/10.3724/SP.J.1047.2015.00260

Orginal Article

A Hierarchical RBF Interpolation Method Based on Local Optimal Shape Parameters

  • LV Haiyang , 1 ,
  • SHENG Yehua , 1, * ,
  • DUAN Ping 1 ,
  • ZHANG Siyang 1 ,
  • LI Jia 2
Expand
  • 1. Key Laboratory of Virtual Geographical Environment, Ministry of Education, Nanjing Normal University, Nanjing 210023, China
  • 2. College of Tourism and Geographical Sciences, Yunnan Normal University, Kunming 650500, China
*Corresponding author: SHENG Yehua, E-mail:

Received date: 2014-04-22

  Request revised date: 2014-05-20

  Online published: 2015-03-10

Copyright

《地球信息科学学报》编辑部 所有
Fold

Abstract

As an accurate spatial interpolation method for data in arbitrary dimensions, Radial Basis Function (referred RBF), was particularly suitable for Digital Elevation Model (referred DEM) interpolation with respect to complex terrain that no assumption is needed for the experiment data. But the interpolation model would become difficult to solve when the number of points, whose elevation is already known, used to construct RBF interpolation model is too large. This is due to the reason that the inversed RBF interpolation matrix would become too huge or too slow to be solved. To address this issue, the hierarchical RBF interpolation method based on local optimal shape parameters, was proposed in this paper and the DEM was interpolated and reconstructed in the experiment. The interpolation procedure was described as follows: first, set the minimum point number in the tree node sub-regions of the study area and define the overlap rate between the adjacent child node sub-regions. Then, construct the regional binary tree recursively from top to bottom, that means the study area was firstly divided from a complete area into two small overlapped regions, and each region could be taken as the child nodes of the binary tree. Second, use the Leave One Out Cross Validation (referred LOOCV) method to calculate the optimal shape parameters in the leaf node regions of the binary tree. As the point distributions in each sub-region are different from each other, as well as the elevation properties, it would lead to different optimal shape parameters. Next, establish the optimal RBF interpolation model, i.e. calculate the linear combination coefficients for each RBF node in the interpolation model with the optimal shape parameter. Third, calculate the elevations of the unknown points in the leaf node regions and get the elevation values using the weighted average method according to the principle of Partition of Unity. The weight of the unknown point in the child node sub-region is calculated using the distance to the center point of the sub-region. Solve the interpolation problem from the bottom to the top recursively to get the final elevation values of the unknown points. Experiments was carried out by using the DEM in some area of Yunnan Province, and the results showed that RBF hierarchical interpolation method with local optimal shape parameters had good stability and high accuracy when DEM was reconstructed from random distributed spatial elevation points, thus it can be taken as an reliable interpolation method.

Key words： shape parameters; DEM; RBF; hierarchical interpolation

Cite this article

LV Haiyang , SHENG Yehua , DUAN Ping , ZHANG Siyang , LI Jia . A Hierarchical RBF Interpolation Method Based on Local Optimal Shape Parameters[J]. Journal of Geo-information Science, 2015 , 17(3) : 260 -267 . DOI: 10.3724/SP.J.1047.2015.00260

1 引言

目前,常见的DEM插值方法有线性内插、反距离权重（Inverse Distance Weighted,IDW）、二元样条、最小二乘配置、自然邻近、三角形插值、克里金插值、径向基函数等[1-2]。李新等人将这些插值方法归类为几何方法、统计方法、空间统计方法、函数方法、随机模拟方法、物理模型方法和综合方法,并对每种方法的适用范围和优缺点进行了分析和比较[3]。Li和Heap系统地总结和对比分析了在地学领域常用的42个确定性插值、空间统计学插值和综合插值方法的数学模型、插值性能及其影响因素和适用条件[4]。根据插值模型是否精确通过已知点,可以将这些方法分为2类：不确定性插值和确定性插值[5]。不确定性插值方法（如最小二乘配置、克里金插值及其扩展方法等）拟合得到的空间曲面不一定精确通过已知观测点,插值结果可以线性无偏地反映区域内研究对象的变化趋势;确定性插值方法（如IDW、RBF、全局多项式和局部多项式方法等）拟合得到的空间曲面可以精确通过已知观测点,具有局部保形、准确逼近等优势。Franke从插值参考点及权函数的选择、计算精度等方面进行实验分析,得出RBF插值方法具有更高的可靠性[6]。RBF作为一种维度无关的精确空间插值方法,分为全局RBF插值方法和局部RBF插值方法[7-9]。全局RBF插值方法精度较高,但插值模型中存在形态参数和基函数的选取问题,同时随着数据量增加插值模型求解困难,限制了RBF全局插值方法的广泛运用,而DEM插值重建一般需要大量已知高程点才能得到足够准确的插值结果。
为了解决大规模数据量RBF插值模型求解问题,Buhmann、Wu、Wendland等人提出并推导了一系列紧支撑径向基函数（Compact Supported Radial Basis Function,CSRBF）,通过设置合理紧支撑半径对空间曲面进行准确逼近[9-11]。但紧支撑基函数中没有形态参数,只能选择不同的紧支撑基函数,以提高插值结果的精度,并且紧支撑基函数受空间维度和光滑度的限制[8],导致插值结果的可靠性降低。根据单元分解原理,将大规模全局RBF求解问题分解为局部RBF插值问题[12-13],Pouderoux等人提出数据分块下的局部RBF插值方法（Pouderoux方法）,通过对研究区域内进行二叉树自适应分块,对每个子区域建立局部RBF插值模型,将RBF插值问题转换为局部求解[14],但由于所有子区域使用同一个形态参数,可能会导致部分局部区域插值模型求解产生奇异现象,使插值效果存在一定的不确定性[15-16]。通过逐点交叉验证（Leave Out One Cross Validation,LOOCV）方法,能有效获取RBF插值模型的最佳形态参数[17-19],进而提高插值结果的可靠性和精度。如果能将局部RBF分块插值方法与LOOCV方法有效融合,则既能对大量空间离散高程点进行RBF插值重建,又可提高插值方法的稳定性和插值结果的精度。
本文采用LOOCV方法将数据分块下的局部RBF插值模型的形态参数进行优化,对不同的局部区域选取不同的最优形态参数;对云南某地区DEM进行采样和插值重建,并进行实验和分析。

2 自适应分块插值与RBF最优形态参数

2.1 自适应分块插值

2.1.1 自适应分块
当研究区域数据量较大时,进行RBF全局插值,插值矩阵会过于庞大,导致插值模型求解失败。全局非重叠网格划分会导致子区域边界处不连续,破坏了地理现象的空间连续性,而单元分解方法将研究区域划分为相互重叠的子区域,并对插值结果进行加权求和,能够保证区块边界处的连续性。此外,二叉树形式简洁,操作方便,能很好地适应空间领域的分块操作,在众多领域有广泛的应用。因此,本文采用单元分解原理[12-13],首先,设定子区域最少已知点数nmin和区块间重叠率q∈[0,1]（即相邻叶子节点中包含的相同点的数目在叶子节点总数中所占的比率,表示相邻叶子节点的区域重叠程度）;然后,对研究区域进行二叉树递归分块,令第l层点集为Pl,点数为nl,研究区域为Ωl,则研究区域Ωl被划分为相互重叠的2个子区域 Ω 1 l + 1 和 Ω 2 l + 1 ,点集Pl被划分为 P 1 l + 1 和 P 2 l + 1 。
从l层至第l+1层点集分块规则如下：
（1）计算区域内点集外包矩形RecΩ信息,如果矩形沿着x轴方向的边长大于沿着y轴方向的边长,则将点集依x坐标进行排序,反之亦然;
（2）计算l+1层叶子节点的重叠点数为 n q l + 1 = q n 1 ,得到子区域 Ω 1 l + 1 中最后1个点序号为 n 1 l + 1 = n l + n q l + 1 2 ,子区域 Ω 2 l + 1 中第1个点序号为 n 2 l + 1 = n l - n q l + 1 2 ;
（3）将第1个点至第nl+1个点作为点集 P 1 l + 1 ,第nl+1+1个点至第nl个点作为点集 P 2 l + 1 。
根据该分块规则对研究区域递归分块,整个分块过程是自适应的,当达到最小点数阈值条件（区域点数nΩ<nmin）时,分块过程停止,递归返回。该分块过程通过在分块之前设定最小点数nmin,通过阈值条件自适应地完成分块过程。二叉树分块BinSegment伪代码表示如下：
输入：研究区域Ω内初始点集P
IF区域点数小于阈值nmin
求解最优形态参数;
计算该区域的RBF线性组合系数;
输出：NULL;
END
点集划分P1,P2;
左子树节点Rl=BinSegment（P1）;
右子树节点Rr=BinSegment（P2）;
输出：根节点Root
2.1.2 区域插值
区域分块完成后,需要对研究区域内的待插值点进行插值。本文根据单元分解的原理,通过加权平均递归得到待插值点的高程值。首先,根据距离区域中心的距离d定义权函数为从区域中心向区域边缘衰减函数V(d) [14]：
V ( d ) = 2 d 3 - 3 d 2 + 1 （1）
为能准确表示待插值点在矩形研究区域内的权重变化,将矩形子区域Ω左下角和右上角坐标分别表示为Sr和Tr,假定待插值点p在矩形子区域Ω中,定义待插值点与区域中心的距离函数Dp为：
将待插值点p距离Rec（即子节点区域的最小外包矩形）边界的距离Dp带入到权函数V(d)中,得到点p在该区域内的权重。权重公式 ν p 最终表达形式为：
ν p = VoD ( p ) （3）
该函数为一个复合函数,其中叶子节点区域内的权重变化如图1所示。
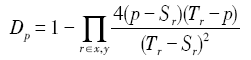
Fig. 1 Weight change in leaf area

图1 叶子节点区域权重变化

待插值点加权递归插值的过程（图2）：对于非重叠区域内的点P1,在子区域Ωl中的权重为vl,在另一个相邻区域内的权重vr（此时vr=0,即子区域之外的点的权重为0）,因此,P1在该层叶子节点中的插值结果为 f P l ;对于重叠区域内的点P2,在子区域Ωl中的权重为vl,在子区域Ωr中的权重为vr,则P2插值结果表示为：
f P 2 = λ l f P l + λ r f P r （4）
Fig. 2 Interpolation process for the unknown point

图2 待插值点插值过程

式（4）中, λ i = ν i ν l + ν r ,i=l,r,且λl+λr=1,加权递归,直至返回到根节点。区域加权递归插值求解插值结果Interpolation伪代码表示如下：
输入：待插值点坐标X0,节点区域Node
IF Node为叶子节点区域
根据线性组合系数和最优形态参数计算高程值 f P ;
根据权重函数计算待插值点在该区域内的权重 ν ;
ELSE
（插值结果 f P l ,相邻子节点权重 ν l ）= Interpolation（X0,相邻子节点Nodel）;
（插值结果 f P r ,相邻子节点权重 ν r ）= Interpolation（X0,相邻子节点Noder）;
输出：插值结果 f P = λ l f P l + λ r f P r ;X0在该区内的权重 ν ;
END

2.2 RBF最优形态参数求解

RBF插值模型十分简洁,设多维空间中包含n个已知点,使用向量xi表示第i个已知点,则径向基函数插值模型[9,20]可以表示为：
F ( x ) = ∑ i = 1 n c i φ ( x - x i 2 ) （5）
式（5）中,x为空间任意点; φ ( x - x i 2 ) 为基函数; x - x i 2 为任意点到第i个已知点的二阶范式;ci为第i个线性组合系数,由 ∑ i = 1 n c i φ ( x - x i 2 ) = y i 确定,i=1,2,…,n;yi为第i个已知点的高程值。几种常见的RBF基函数[8-9]如表1所示。
Tab. 1 Some RBF basis functions

表1 几种常见的RBF基函数

基函数 表达式
Gaussians φ(r)=e-r22α2
Multiquadric φ(r)=α2+r2
Inverse Multiquadric φ(r)=1α2+r2
Thin Plate Spline φ(r)=αr2lnαr

注：α为形态参数,控制基函数的平滑程度,r为待插值点与已知点之间的径向距（2-范数）

采用表1中任何一种基函数进行空间插值,插值模型都会随着α增大（到达某个临界值之前）,越来越光滑,若超过这个临界值,继续增加α,则插值模型连续性变差,误差随之变大,将该α的临界值称为最优形态参数。
为了有效获取最优形态参数,本文采用LOOCV方法,先从形态参数区间[p,q](其中, 0 ≤ p ≤ q )中按顺序选取一个值αi,再依次从n个插值点中选一个已知点作为验证点,使用剩余的n-1个点作为插值点,求解RBF插值模型,并对验证点进行插值。计算其插值误差作为交叉验证误差,循环n次;计算形态参数为αi时的交叉验证误差LOOCV（αi）,逐次选取α,建立形态参数与RBF交叉验证误差的函数映射关系LOOCV（α）,通过最小化LOOCV（α）获取最优形态参数α。其中,根据RBF求解过程的数学特性,可以根据式（6）将n次交叉验证过程进行优化,通过一次求解,即可获取形态参数αi对应的交叉验证误差,将交叉验证误差的计算复杂度从O(n4)降低为O(n3)。
f ˜ ( x i ( i ) ) - y i = c i Φ ii - 1 （6）
ci为使用全部已知点进行RBF插值模型求解,得到第i个已知点处的基函数线性组合系数; Φ ii - 1 为使用全部点集进行RBF模型求解,得到插值矩阵的逆矩阵第i个对角线元素值。因此,最优形态参数求解过程的伪代码表示如下：
输入：形态参数区间[p,q],插值点集X={x1, x2…, xn}
FOR α i ∈ p , q
使用插值点集X和形态参数αi求解RBF插值模型组合系数ci、插值矩阵 Φ ;
根据式（6）计算交叉验证误差 LOOCV ( α i ) = ∑ i = 1 n c i Φ ii - 1 2 ;
END
αoptimal=min(LOOCV(α));
输出：最优形态参数αoptimal

3 RBF插值实验分析

3.1 实验数据与插值

本文采用ASTER网站(http://asterweb.jbl.nasa.gov/gdem.asp)提供的DEM（30 m×30 m）,选取云南某地区DEM数据（区域范围约为10 km×10 km）进行实验,原始数据如图3所示。
Fig. 3 The study area

图3 研究区域DEM

对研究区域的坡度、高程信息进行统计,如表2所示。从图3和表2可知,该区域高程差为1340 m,平均坡度24.5°,沟谷特征信息明显,地形变化较大。
Tab.2 Topographic factors statistics in study area

表2 研究区域地形因子统计

最小高程(m) 最大高程(m) 平均高程(m) 标准差(m) 平均坡度(°)
1245 2585 2010 252 24.5
在原始DEM数据中随机采样10 000个高程点,空间分布如图4所示。从图4可知,采样点为空间随机分布,局部区域存在聚集,导致单位面积内采样点较多,而另一部分区域采样点分布较稀疏,单位面积内点数较少。
Fig. 4 10 000 random sample points

图4 10 000个随机高程采样点

RBF全局插值方法能够对研究区域内连续变化的地理现象准确重建,在形态参数最佳的情况下选用不同的基函数得到的插值结果差别不大,故适当地增加已知节点的数量可有效提高插值结果的精度,但会导致插值矩阵越来越大,矩阵求逆效率低下,插值运算速度越来越慢。为有效保留研究区域DEM局部细节特征并快速求解待插值点高程值,本实验选取叶子节点子区域内的最少采样点数阈值为100;为了减少相邻子区域之间的边界不连续现象,需要对相邻子区域之间设置一个合理的重叠率阈值,阈值设置过大,则会导致叶子节点过多,增加插值模型的运算量,阈值设置过小,则边界会出现不连续现象,本实验相邻叶子节点的重叠率设置为0.2,通过二叉树自适应分块和插值求解,基于LOOCV方法获取各个叶子区块的最优形态参数构建局部RBF插值模型,以表1中广泛使用的Multiquadric基函数[21]进行实验。
本文采用IDW插值方法、CSRBF插值方法、Pouderoux插值方法,使用本实验所提供的DEM采样数据进行实验。本文方法局部子区域点数最小阈值为100,因此,在保证局部区域点数大致相同的情况下,将IDW的搜索条件邻域最小搜索点数设为100,插值实验结果如图5（a）所示;CSRBF采用搜索半径为0.1倍的研究区域对角线长度,以Wendland提供[7]的C2光滑度的基函数 φ 3,1 = ( 1 - r ) + 4 4 r + 1 ) 进行实验,该基函数为紧支撑基函数,(1-r)+为紧支撑域的控制项,即在支撑域外函数值为0,插值实验结果如图5（b）所示;Pouderoux方法采用与本文方法相同的阈值条件和表1中的Multiquadric基函数,使用一个固定的形态参数进行实验,该形态参数为采用本文方法求取的各个叶子区块最优形态参数的平均值,插值实验结果如图5（c）所示。本文方法得到的DEM插值重建结果如图5（d）所示。
Fig. 5 Interpolation results comparison

图5 插值结果对比

从图3、5可知,4种方法获取的插值结果都能整体上反映研究区域内的地形变化。IDW插值结果细节保留较少,CSRBF、Pouderoux方法和本文方法对细节保留较完整,但仍然存在些差异。

3.2 实验结果与分析

对IDW插值方法、CSRBF插值方法、Pouderoux插值方法和本文方法的插值结果从可视化的角度进一步分析,选取图5中黑色矩形方框所示区域,进行局部放大（图6）。
Fig. 6 The local enlarged view of the original DEM and interpolation results

图6 原始数据与插值结果局部放大

从图6可见,IDW插值结果与实际地形相差较大,这是因IDW对研究区域内的最大值和最小值预测能力不足,故地形沟谷特征表达不是很明显,而RBF可有效地对区域内的最大值和最小值进行预测,能够更好地保留地形细节特征;Pouderoux方法、CSRBF和本文方法均属于RBF插值方法,获取的插值结果与原始数据差异较小。由于CSRBF的基函数中缺少控制基函数形态的参数,在部分区域插值结果与实际地貌不符,如图6（c）红色圆所包含区域,获得的插值结果并不能反映真实DEM区域,而Pouderoux方法与本文方法选取了相同的基函数,因此,在局部细节表现上要优于CSRBF,但是,Pouderoux方法在划分子区域后,会因全局使用同一个形态参数产生局部区域插值模型奇异,导致插值模型解算不正确,使局部区域插值结果产生了奇异,如图6（d）蓝色圆所包含区域,而本文方法的局部最优特性对局部细节特征保留较为完整。
为了分析插值结果的精度,本文以规则格网点的实际值与插值模型在相应格网点处的插值结果进行比较,获取各个插值模型的实验误差,计算研究区域内的插值模型的平均误差、均方根误差,并对误差取绝对值,计算最大误差和最小误差,结果如表3所示。
Tab. 3 Error statistic of different interpolation methods (m)

表3 不同方法插值结果分析（m）

插值方法 最大误差 最小误差 平均误差 均方根误差
IDW 137.4158 7.2966×10-4 19.0169 25.4318
CSRBF 302.3613 1.6825×10-4 9.7419 16.5656
Pouderoux方法 139.1777 3.9567×10-5 9.7295 13.6998
本文方法 74.8113 1.0037×10-5 7.2496 10.1841
从表3可知,依据均方根误差对插值结果误差从小到大进行排序,依次为：本文方法、Pouderoux方法、CSRBF和IDW。CSRBF与Pouderoux方法获取的插值结果平均误差基本相等,但CSRBF最大误差和均方根误差较大,本文方法均方根误差最小,并且各项误差指标优于其他几种插值方法。此外,基函数的选取对本文方法插值结果影响较小,子节点区域之间的重叠率和点数阈值的设置需根据区域内的高程的变化情况合理选取,对高程变化较大的区域,要适当增加重叠率和点数。

4 结论

RBF插值方法作为一种精确的插值方法,能适用于任意维度的空间插值,但随着已知点的增加,RBF全局插值方法插值矩阵求逆困难,限制了该方法的适用范围。本文基于单元分解原理,采用二叉树分块的方式对研究区域进行自适应分块,LOOCV方法求解子区域局部最优形态参数,构建RBF局部插值模型,对研究区域进行DEM递归插值重建。与IDW、CSRBF、Pouderoux方法进行比较和分析表明,本文方法精度高,插值结果可靠,是一种有效可行的空间插值方法。

The authors have declared that no competing interests exist.

References

Publishing order | Descend order by publishing year | Descend order by cited within
[1]
李志林,朱庆.数字高程模型[M].武汉:武汉大学出版社,2001:125-139.

[2]
汤国安,刘学军,闾国年.数字高程模型及地学分析的原理与方法[M].北京:科学出版社,2005:80-85.

[3]
李新,程国栋,卢玲.空间内插方法比较[J].地球科学进展,2000,15(3):260-265.

[4]
Li J, Heap A D.A Review of Spatial Interpolation Methods for Environmental Scientists[M]. Canberra: Geoscience Australia, 2008:10-13.

[5]
汤国安,杨昕. ArcGIS 地理信息系统空间分析实验教程[M]. 北京:科学出版社,2006:294-295.

[6]
Franke R.Scattered data interpolation: tests of some methods[J]. Mathematics of computation, 1982,38(157):181-200.

[7]
Wendland H.Scattered data approximation[M]. Cambridge: Cambridge University Press, 2005:119-120.

[8]
Fasshauer G E.Meshfree approximation methods with MATLAB[M]. Singapore: World Scientific, 2007:17-19.

[9]
Buhmann M D.Radial basis functions: theory and implementations[M]. Cambridge: Cambridge University press, 2003:11-29.

[10]
Wendland H.Piecewise polynomial, positive definite and compactly supported radial functions of minimal degree[J]. Advances in computational Mathematics, 1995,4(1):389-396.

[11]
Wu Z.Compactly supported positive definite radial functions[J]. Advances in Computational Mathematics, 1995,4(1):283-292.

[12]
Wendland H.Fast evaluation of radial basis functions: Methods based on partition of unity[C]. Approximation Theory X: Wavelets, Splines, and Applications, 2002:473-483.

[13]
Ohtake Y, Belyaev A, Alexa M, et al.Multi-level partition of unity implicits[C]. ACM SIGGRAPH 2005 Courses. ACM, 2005:173.

[14]
Pouderoux J, Gonzato J C, Tobor I, et al.Adaptive hierarchical RBF interpolation for creating smooth digital elevation models[C]. Proceedings of the 12th annual ACM international workshop on Geographic information systems. ACM, 2004:232-240.

[15]
Kansa E J, Carlson R E.Improved accuracy of multiquadric interpolation using variable shape parameters[J]. Computers & Mathematics with Applications,1992,24(12):99-120.

[16]
Fornberg B, Zuev J.The Runge phenomenon and spatially variable shape parameters in RBF interpolation[J]. Computers & Mathematics with Applications, 2007,54(3):379-398.

[17]
Rippa S.An algorithm for selecting a good value for the parameter c in radial basis function interpolation[J]. Advances in Computational Mathematics, 1999,11(2-3):193-210.

[18]
Fasshauer G E, Zhang J G.On choosing “optimal” shape parameters for RBF approximation[J]. Numerical Algorithms, 2007,45(1-4):345-368.

[19]
Scheuerer M.An alternative procedure for selecting a good value for the parameter c in RBF-interpolation[J]. Advances in Computational Mathematics,2011,34(1):105-126.

[20]
吴宗敏. 散乱数据拟合的模型、方法和理论[M].北京:科学出版社,2007:81-86.

[21]
Hardy R L.Theory and applications of the multiquadric-biharmonic method 20 years of discovery 1968-1988[J]. Computers & Mathematics with Applications, 1990,19(8):163-208.

Options
Outlines

/

〈 〉