EN中文

Journal of Geo-information Science >

2015 , Vol. 17 >Issue 7: 816 - 821

DOI: https://doi.org/10.3724/SP.J.1047.2015.00816

Orginal Article

Blind Watermarking Algorithm Based on Normalization for Vector Data

  • ZHANG Liming , 1, 2, * ,
  • YAN Haowen 1, 2 ,
  • QI Jianxun 3 ,
  • ZHANG Yongzhong 3
Expand
  • 1. Faculty of Geomatics, Lanzhou Jiaotong University, Lanzhou 730070, China
  • 2. Gansu Provincial Engineering Laboratory for National Geographic State Monitoring, Lanzhou 730070, China
  • 3. Lanzhou City Survey Mapping Institute, Lanzhou 750050, China
*Corresponding author: ZHANG Liming, E-mail:

Received date: 2014-10-29

  Request revised date: 2014-11-24

  Online published: 2015-07-08

Copyright

《地球信息科学学报》编辑部 所有
Fold

Abstract

In vector data watermarking technology, the geometric transform attack is commonly difficult to cope with. The existing algorithms that can resist the attacks of geometric transformation, however always cannot resist vertexes attacks. Therefore, a blind watermarking algorithm for vector data is proposed based on the idea of data normalization to solve this problem. In this algorithm, the coordinate values of spatial data were normalized before embedding the watermarks, in order to keep invariant with respect to translation and zooming. Watermarks were embedded in the normalized values of the vertex coordinate data for several times. There are no original data needed in the procedure of watermark detecting. The experiments show that the algorithm is robust against a series of different attacks, such as translation or scaling transformations, vertex insertion and removal, cropping, compression, reordering and data format conversion. In addition, it can control and limit the relevant errors of the watermarked spatial data that produced during the watermark embedding.

Key words： normalization; vector data; robustness; blind watermarking

Cite this article

ZHANG Liming , YAN Haowen , QI Jianxun , ZHANG Yongzhong . Blind Watermarking Algorithm Based on Normalization for Vector Data[J]. Journal of Geo-information Science, 2015 , 17(7) : 816 -821 . DOI: 10.3724/SP.J.1047.2015.00816

1 引言

随着计算机及网络技术的发展,数字产品版权保护引起人们广泛的关注和研究。水印技术在数字内容安全、版权保护和认证方面,被认为是目前最有前景的技术之一[1]。水印技术从最初的图像水印发展到视频水印、音频水印、文本水印、数据库水印、空间数据水印等。相较于其他水印技术,矢量空间数据水印技术的发展相对滞后。
一般来说,根据水印的嵌入方法不同,矢量空间数据水印算法可分为：空域水印算法[2-11]和频域水印算法[12-19]。
在空域算法方面,Cox等最早公开发表关于矢量数据水印算法的论文,该算法把水印信息直接嵌入矢量数据各顶点坐标,是一种空域算法,其不能抵抗一般的水印攻击[2]。贾培宏等提出采用最低有效位（Least Significant Bit, LSB）与矢量空间数据拓扑相结合的算法,并对水印信息加密,该算法在一定程度上提高了空域水印对剪切等攻击的抵抗能力[3]。Schulz等提出把地图数据分割成一定宽度的水平带或垂直带,根据水印信息调整各个带中数据点的坐标值,算法可以抵抗数据简化、裁剪和小幅度的随机噪声攻击[4]。王伟等将矢量地图按多边形特征进行分解,选择合适的多边形线段,水印嵌入到坐标顶点中,算法对图形的几何变换、增删操作具有较好的鲁棒性[5]。闵连权等根据矢量地图数据的数据量设计了2种数据映射规则,把水印信息嵌入在数据映射规则的数据分类上,具有很好的不可感知性和鲁棒性[6]。Ohbuchi等提出了经典的MQUAD算法,其应用四叉树划分矢量地图,把地图划分为矩形子块,并在不同子块中重复嵌入水印信息,提高了水印算法的鲁棒性[7]。YAN等根据矢量空间数据特点,分别选取点、线、面矢量图层,针对每一图层分别选取特征点,应用LSB空域算法加入水印[8]。王奇胜等利用脆弱水印技术,提出了数据点定位的水印算法,提高了水印检测的可靠性[9]。张弛等把数据分为特征点和非特征点,水印嵌入非特征点上。如果对数据进行压缩处理,首先被压缩掉的是非特征点,非特征点的失去意味着水印信息的丢失,因此,该算法对数据压缩鲁棒性不高[10]。吴柏燕等利用量化索引调制（Quantizafion Index Modulation, QIM）思想,基于变长量化步长,将水印信息隐藏于有效表征曲线形状的特征集合中,该算法在抵抗节点攻击、数据化简及地物删除等方面鲁棒性好[11]。
在频域水印算法方面,Kitamura[12]、李媛媛[13]、杨成松[14]等提出了离散小波变换的水印算法,水印嵌入多级小波变换后的系数中,这种水印算法不能抵抗旋转和平移等几何变换攻击。Voigt[15]提出将水印嵌入DCT变换系数中。Kitamura[17]、王奇胜[18]、许德合[19]利用了离散傅里叶变换的几何不变性,把水印嵌入傅里叶变换后的系数中,该类算法大多能抵抗几何变换攻击。
综上所述,空间域算法通常简单、易操作,水印嵌入量较大,能抵抗增加点、删除点、裁剪及噪声等攻击,但抵抗几何攻击方面效果较差;而部分频域算法（如DFT域算法）虽然能抵抗几何攻击,但是在顶点增加、删除方面鲁棒性差。因此,本文提出了归一化水印算法,能适应不同类型矢量空间数据,解决矢量空间数据水印算法同时遭受几何攻击和顶点攻击的问题,提高了水印算法的鲁棒性,且实现了盲检测。
Fig. 1 Watermarks embedding flowchart

图1 水印嵌入流程图

2 矢量空间数据归一化

矢量空间数据一般由空间数据和属性数据构成。空间数据包括几何数据和关系数据;属性数据是描述地理空间数据对象的属性,不能随便修改,因此,水印只能嵌入空间数据中[6]。数据归一化处理方法广泛应用于工程数据处理,能使数据具有统一性和可比性。由于不同的矢量空间数据单位不一致,为能在不同类型的矢量空间数据中嵌入水印,在水印嵌入之前,先对空间数据进行[0,1]归一化处理。同时,数据归一化可得到数据平移、缩放的不变性,这样在归一化后的数据中嵌入水印,可抵抗数据平移、缩放类型的几何攻击。

2.1 最小最大归一化

数据归一化常用的方法有线性映射的最小最大值归一化（Min-max normalization）。它是对原始数据进行线性变换[20]。设Valuemin和Valuemax分别为属性A的最小值和最大值,将A的一个原始值x通过式（1）,归一化映射成在区间[0,1]中的值 x ′ 。
x ′ = x - Valu e min Valu e max - Valu e min （1）

2.2 反归一化

在经过归一化后的空间数据嵌入水印信息后,用式（2）再进行反归一化,得到含水印空间数据 x ″ 。
x ″ = Valu e min + Valu e max - Valu e min × x ′ （2）

3 水印算法

本文选取矢量空间数据几何图形的顶点坐标嵌入水印。为了能使水印信息嵌入所有的矢量空间数据,以抵抗裁剪攻击,水印信息应尽可能均匀嵌入矢量空间数据所有顶点的X、Y坐标,以保证水印的抗攻击能力。在水印嵌入前,以图形要素为单位,对图形顶点的坐标值进行归一化处理,然后在归一化值中嵌入水印信息。这样,即使对含水印空间数据实施了几何变换,也不需对几何变换作校正,就可提取水印信息。与此同时,为了消除水印图像像元之间的相关性,增强水印的安全性,水印图像在嵌入之前,用Logistic混沌算法置乱。混沌变换的初始值可作为水印信息提取的密钥。

3.1 水印的嵌入过程

本算法以矢量图形对象为单位嵌入水印。图形对象的顶点用集合 V 0 表示为： V 0 = { v i } ; v i = ( x i , y i ) , i = 1,2 , … , N ; X 0 = { x i } ; Y 0 = { y i } , i = 1,2 , … , N , 其中,vi表示每一个顶点, ( x i , y i ) 表示顶点的2个坐标值,X0表示横坐标值的集合,Y0表示纵坐标值的集合,N为顶点的个数。
水印嵌入的具体流程如下：
（1）读取矢量空间数据,提取图形对象的所有坐标点,构造出 X 0 , Y 0 集合;
（2）对 X 0 , Y 0 分别进行数据归一化并放大10n倍,记为 X ′ 0 , Y ′ 0 ;
（3）在 X ′ 0 , Y ′ 0 中分别采用量化方法嵌入水印,具体嵌入方法如下：
① 计算Hash(x)函数的值wi,Hash(x)函数为x值与水印比特之间的哈希映射函数,Hash(x)=x%M+1,x为待嵌入水印数据;
②提取待嵌入水印位 w [ wi ] ( 1 ≤ wi ≤ M ) ,w为置乱后的水印,M为水印的长度;
③应用QIM方法,在x中嵌入水印,通过式（3）计算出嵌入水印后的数据 x ′ ,R为量化值;
x ′ = x - R 2 , 若 w wi = 0 且 Mod ( x , R ) > R 2 x , 若 w wi = 0 且 Mod ( x , R ) ≤ R 2 x + R 2 , 若 w wi = 1 且 Mod ( x , R ) ≤ R 2 x , 若 w wi = 1 且 Mod ( x , R ) > R 2 （3）
（4）对嵌入水印后的 X ′ 0 , Y ′ 0 缩小10n倍,并反归一化;
（5）将含水印空间数据输出保存。
在水印嵌入过程中,使用Hash函数建立归一化值的较高有效位部分（此部分不会嵌入水印）,与水印比特（1-M）之间的映射关系。通过对归一化数据放大10n倍后,就会使水印嵌入到数值的较低有效位部分,这样会大大减小水印嵌入引起的误差。嵌入水印后的数据还需使用极值反归一化,为尽可能减小数据误差,不影响水印的提取,在极值数据中不能嵌入水印。

3.2 水印的提取过程

水印的提取是嵌入流程的逆过程（图2）。水印提取具体过程如下：
（1）读取待测数据,对数据进行归一化并放大10n倍,n取与同水印嵌入时相同的n值;
（2）通过Hash()函数,计算出wi（wi是水印的位置）;
（3）通过QIM量化方法提取水印位 W ( wi ) 的值,R取水印嵌入时的量化值;
（4）对提取到的一维水印序列,进行升维处理并反置乱,得到最终水印图像。
Fig. 2 Watermarks detecting procedure

图2 水印提取过程

在水印嵌入中,水印可能被多次嵌入,因此采用投票原则来确定水印信息。计算的方法是：定义一个与水印序列等长的整数序列{B(i)=0, i=1,…,M},M为水印长度。单个水印位记为 b ′ i ={1,-1},相同水印位提取过程中,使用公式B(i)=B(i)+ b ′ i 来统计出水印信息值-1和1的多数,如“1”为多数,则 B i > 0 ;然后根据式（4）来重构出二值水印图像。
w ′ i = 1 , 若 B i > 0 0 , 若 B i ≤ 0 （4）

4 实验及分析

实验选用1:400万的中国地图,数据格式为ArcGIS的shp格式。该图有1785个要素,共80 965个坐标点。首先对嵌入水印后的数据进行了误差统计,并对水印的不可见性及鲁棒性进行了分析。实验中用的水印是32×64像元的二值水印图像（图3（a））。图3（b）是混沌置乱后的水印图像。
Fig. 3 Original watermark

图3 原始水印

本文采用均方根误差（RMSE）和最大误差等指标评价水印嵌入对矢量数据精度的影响大小。
RMSE= ∑ d i 2 N ,i=1,2,…,N。其中,N表示含水印坐标点的个数, d i 表示原始数据坐标点与含水印数据坐标点之间的绝对误差; d i = ∆ x 2 + ∆ y 2 , ∆ x , ∆ y 分别表示x方向、y方向的误差。
对提取到的水印图像与原始水印图像通常用相关系数来评价其相似性,计算公式如式（3）所示。
NC = ∑ i = 1 M ∑ j = 1 N XNOR ( W i , j , W ′ ( i , j ) ) M × N （5）
式中, M × N 表示水印图像的大小; w ( i , j ) 表示原始水印信息; W ′ ( i , j ) 表示提取的水印信息;XNOR表示异或非运算。

4.1 误差及不可见性分析

算法中,数据误差大小不仅与量化值R有关系,还与n（归一化数据后放大倍数10n）有关。如果量化值R太大,将会导致数据误差太大,如果R太小,水印的鲁棒性差,则难以提取到水印信息。通过实验分析,R取值20-100之间,可很好地提取到水印信息,实验中R取40。n值的大小不仅影响数据误差的大小,而且与水印的鲁棒性有一定的关系。n值与最大误差、RMSE关系见表1。
Tab. 1 Relationship between maximum error, RMSE and n

表1 n值与最大误差、RMSE关系

n MaxError RMSE NC
3 0.218261585 0.030237424 0.817871
4 0.021826158 0.003048796 0.821289
5 0.002182616 0.000304115 0.833008
6 0.000218262 3.04633E-05 0.843008
7 2.18262E-05 3.02807E-06 1
8 2.18262E-06 3.03757E-07 1
9 2.18262E-07 3.03369E-08 1
10 2.18262E-08 3.01902E-09 1
11 2.18262E-09 3.02866E-10 1
12 7.74349E-11 8.3593E-12 1
13 2.18304E-11 3.0356E-12 1
14 2.1892E-12 3.036E-13 1
15 2.174E-13 3.03E-14 0.999512
16 2.93E-14 3E-15 0.749023
从表1可看出,随着n的增大,最大误差、RMSE指数下降。但是,只有n值取[7-15]时,NC值大于0.999,可提取到水印信息。该实验中权衡误差大小及水印的鲁棒性,n取10。该算法对空间数据进行了归一化处理,对于不同的矢量数据,都会被变换到[0,1]空间,因而不同数据只需要根据数据精度的要求选取n的值,而R取20-100之间对水印的嵌入、提取几乎没有影响。从图4中可看出,嵌入水印后绝大部分数据误差很小,有少量误差较大的数据,但完全在数据精度要求之内,可见该算法不会影响数据的使用。
Fig. 4 Error distribution histograms

图4 误差分布直方图

通过对水印嵌入前后,对数据可视化叠加对比,并局部放大显示（图5）。从图5可看出,水印嵌入前后视觉上没有明显差别。从表1的误差分析数据来看,水印嵌入引起的最大误差及RMSE都很小,因此水印具有很好的不可见性。
Fig. 5 Visualization comparison

图5 可视化比较

4.2 水印的鲁棒性分析

4.2.1 几何攻击
由表2可看出,在经过平移、缩放攻击后,水印的提取基本不受影响。这是由于水印嵌入到空间数据坐标的归一化值中,对含水印空间数据实施平移和缩放攻击后,其归一化值仍然保持不变。因此,水印对几何变换中的平移和缩放攻击具有很好的鲁棒性。而对于旋转攻击,不能直接应用水印提取算法,需要得到旋转的参数,进行反向旋转后再提取水印。
Tab. 2 Robustness for geometric attacks

表2 几何攻击的鲁棒性

攻击类型 X,Y平移5 放大2倍 缩小0.5倍
水印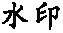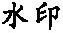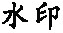
NC 1 1 1
4.2.2 增加点、删除点及修改点攻击
从表3可知,对含水印数据增加顶点2倍多后,依然能很好地提取水印。这是由于空域算法能很好地抵抗顶点攻击。增加顶点坐标时,可能会影响部分要素的极值,极值的变化意味着这部分数据的归一化值就会发生变化,水印信息无法提取。但是绝大部分要素的极值不变,因此在增加顶点后,并不影响原来数据的水印信息。通过对一定数量范围内删除顶点或修改顶点,对水印提取的影响并不大。如果删除或修改绝大部分的顶点数据,就会提取不到水印。当然删除掉大部分顶点后,空间数据也将失去其使用价值。如果删除或修改的顶点数据中包含少部分的极值坐标,水印的提取不会受到太大的影响,而如果删除或修改所有要素的极值坐标,就不能提取到水印信息。当然删除或修改太多的极值坐标,数据会产生较大的误差,会影响到数据的正常使用。
Tab. 3 Robustness for vertex insertion, removal and modification attacks

表3 増、删点及修改点攻击的鲁棒性

攻击类型 点增到24 4260个 删除10%点 修改10%点 修改50%点
水印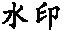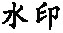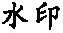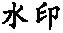
NC 1 1 1 1
4.2.3 压缩、要素删除及裁剪攻击
对含水印的数据进行D-P压缩试验,取阈值0.002,压缩至41 431个顶点后,提取水印不受影响,取阈值0.02压缩后,仍然可提取到NC值大于0.9的水印图像。而对于要素删除攻击,从表4可看出,即使删除50%要素后,依然能很好地提取水印。在该算法中,每一个水印都被多次嵌入各自的域空间,而且水印信息均匀地分布在每一个要素中,因此,部分要素的删除,不会对水印信息造成太大的破坏。
Tab. 4 Robustness for compression and removal attacks

表4 压缩、要素删除攻击的鲁棒性

攻击类型 阈值0.002坐标点压缩至
41 431个		 阈值0.02坐标点压缩至
12 903个		 删除20%要素 删除50%要素
水印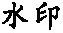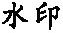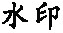
NC 1 0.907715 1 1
实验表明,对含水印的部分数据进行裁剪后,在剩余要素中仍然可提取到NC值很高的水印图像。如图6所示,在裁剪后剩余的要素（9084个坐标点）数据中提取到的水印图像NC值仍然为1。
Fig. 6 Visualization of data after cropping and the extracted watermark

图6 裁剪后数据及提取到的水印

4.2.4 重排序及格式转换攻击
本文对坐标排序、要素排序攻击进行了试验。在该算法中,水印的嵌入不依赖坐标点顺序及要素顺序,因此水印的提取不受影响。但是,当含水印的矢量空间数据,从一种格式转换成另一种矢量空间数据格式后,无法直接提取水印信息,需要转换到原来的矢量数据格式后,才可提取水印信息。2种不同数据格式的矢量空间数据进行格式转换时,由于二者数据结构、存储方式、单位、精度等的差异,转换前后的数据会产生微小的差异,这个差异对水印信息的提取影响很小。实验验证了含水印SHP数据转换到CAD、E00格式后,再转为SHP格式,可很好地提取水印信息。
此外,本文对含水印数据进行了多种组合攻击试验,结果表明,在上述多种类型的攻击中,具有鲁棒性的任意多种组合攻击,该算法均能提取水印 信息。

5 结语

本文对矢量空间数据实施归一化后,应用QIM嵌入水印,实现了水印的盲提取。仿真实验表明,本文提出的算法能很好地适应不同比例尺、不同单位的空间数据水印嵌入,很好地解决了平移、缩放攻击后水印提取需要重定位的问题,对平移、缩放、顶点攻击等具有较好的鲁棒性,并且计算简单、误差大小可控,具有一定的实用性。

The authors have declared that no competing interests exist.

References

Publishing order | Descend order by publishing year | Descend order by cited within
[1]
孙圣和,陆哲明,牛夏牧.数字水印技术及应用[M].北京:科学出版社,2004:10-14.

[2]
Cox G S, De Jager G.A survey of point pattern matching techniques and a new approach to point pattern recognition[C]. Proceedings of South African Symposium on Communications and Signal Processing, 1993:243-248.

[3]
贾培宏,马劲松,史照良,等.GIS空间数据水印信息隐藏与加密技术方法研究[J].武汉大学学报(信息科学版), 2004,29(8):747-750.

[4]
Schulz G, Voigt M.A high capacity watermarking system for digital maps[C]. Proceedings of the 2004 workshop on Multimedia and security, ACM, 2004:180-186.

[5]
王伟,李岩.一种鲁棒性的2D矢量图形水印算法[J].中国图象图形学报,2007,12(2):200-205.

[6]
闵连权. 一种鲁棒的矢量地图数据的数字水印[J].测绘学报,2008,37(2):262-267.

[7]
Ohbuchi R, Ueda H, Endoh S.Robust watermarking of vector digital maps[C]. 2002 IEEE International Conference on Multimedia and Expo, 2002:577-580.

[8]
Yan H, Li J, Wen H.A key points-based blind watermarking approach for vector geo-spatial data[J]. Computers, Environment and Urban Systems, 2011,35(6):485-492.

[9]
王奇胜,朱长青,符浩军.利用数据点定位的矢量地理数据数字水印算法[J].测绘学报,2013,42(2):310-316.

[10]
张驰,李安波,闾国年,等.以夹角调制的矢量地图可逆水印算法[J]. 地球信息科学学报,2013,15(2):180-186.

[11]
吴柏燕,李朝奎,伟王.顾及曲线形状的矢量地图数据水印模型[J].计算机工程与应用,2014,50(1):74-77

[12]
Kitamura I, Kanai S, Kishinami T.Digital watermarking method for vector map based on wavelet transform[C]. Geographic Information Systems Association, 2000,9:417-421.

[13]
李媛媛,许录平.矢量图形中基于小波变换的盲水印算法[J].光子学报,2004,33(1):97-100.

[14]
杨成松,朱长青.基于小波变换的矢量地理空间数据数字水印算法[J].测绘科学技术学报,2007(1):37-39.

[15]
Voigt M, Yang B, Busch C.Reversible watermarking of 2D-vector data[C]. Proceedings of the 2004 workshop on Multimedia and security, ACM, 2004:160-165.

[16]
Solachidis V, Nikolaidis N, Pitas I.Fourier descriptors watermarking of vector graphics images[C]. ICIP, 2000:9-12.

[17]
Kitamura I, Kanai S, Kishinami T.Copyright protection of vector map using digital watermarking method based on discrete Fourier transform [C]. Geoscience and Remote Sensing Symposium,IEEE 2001 International, 2001,3:1191-1193.

[18]
王奇胜,朱长青,许德合.利用DFT相位的矢量地理空间数据水印方法[J].武汉大学学报(信息科学版),2011,36(5):523-526.

[19]
许德合,朱长青,王奇胜.利用QIM的DFT矢量空间数据盲水印模型[J].武汉大学学报(信息科学版),2010,35(9):1100-1103.

[20]
Han J W, Kamber M.Data Mining: Concepts and Techniques, Second Edition[M]. San Francisco: Morgan Kaufmann Publishers, 2006.

Options
Outlines

/

〈 〉