EN中文

Journal of Geo-information Science >

2019 , Vol. 21 >Issue 10: 1502 - 1509

DOI: https://doi.org/10.12082/dqxxkx.2019.190214

An Algorithm for Simplifying Linear Elements of Vector Tile Maps

  • JIN Cheng 1, 2, 3 ,
  • AN Xiaoya , 2, 3, * ,
  • CUI Haifu 4 ,
  • ZHAO Yujun 5 ,
  • WANG Hui 5
Expand
  • 1. Faculty of Geospatial Information, University of Information Engineering, Zhengzhou 450052, China
  • 2. Xi'an Research Institute of Surveying and Mapping, Xi'an 710054, China
  • 3. State Key Laboratory of Geo-information Engineering, Xi'an 710054, China
  • 4. Faculty of Information Engineering, China University of Geosciences, Wuhan 430074, China
  • 5. Wuhan Zhongdi Research Institute, Wuhan 430074, China
*AN Xiaoya, E-mail:

Received date: 2019-05-07

  Request revised date: 2019-07-08

  Online published: 2019-10-29

Supported by

Defense “973” of China(613317)

Copyright

Copyright reserved © 2019
Fold

Abstract

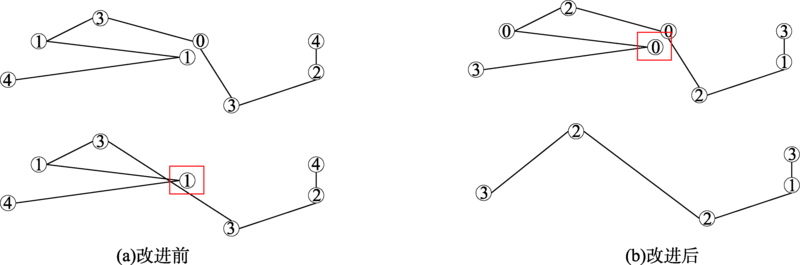
The simplification of linear elements is very important to improve the efficiency of data transmission and visual expression in vector tile map services. Most classical simplification algorithms do not consider the consistency of curves' spatial relations before and after the simplification, which leads to abnormal problems such as sharpening the results of simplification, missing local extremum points, generating line intersection. Considering consistency will affect the efficiency of simplification. In this context, an improved Visvalingam algorithm was proposed according to the application requirements of the vector tile map service.The algorithm applies the minimum heap technology to solve the problem of low efficiency of minimum weight value search, and uses the judgment strategy of self-intersecting topological relation of the line to consider the influence of other points on the current point from the global perspective. In so doing, we can solve the problem of consistency preservation of the topological relationship before and after the simplification of linear elements. The improved Visvalingam algorithm was compared with the original Visvalingam algorithm in terms of topological relationship, geometric features, position accuracy, and simplification efficiency. Results show that the improved Visvalingam algorithm accounted for the topological relations of linear elements and ensuredthe consistency of the overall morphology and topologicalrelationship before and after thesimplification.Our findings suggest that the prosposed Visvalingam algorithm can be applied to the online vector tile map service more efficiently.

Key words： vector tile maps; map service; map generalization; topological relationship; Visvalingam algorithm; linear simplification; minimum heap

Cite this article

JIN Cheng , AN Xiaoya , CUI Haifu , ZHAO Yujun , WANG Hui . An Algorithm for Simplifying Linear Elements of Vector Tile Maps[J]. Journal of Geo-information Science, 2019 , 21(10) : 1502 -1509 . DOI: 10.12082/dqxxkx.2019.190214

1 引言

地图综合是当前国际GIS和制图学领域的一个难题。地图化简是地图综合的基本操作,线要素化简在制图表达与综合领域一直是研究的热点[1,2]。矢量瓦片地图服务,是指在网络地图服务中,以多层次模型将矢量数据按照一定规则切分为矢量要素描述性文件存储于服务器端,在客户端根据指定的样式进行渲染绘图,与栅格瓦片地图相比,其优点是可以在客户端更改样式[3]。
将矢量数据按照全球地理空间金字塔索引模型划分为层次化和网格化瓦片数据,对每一层级的矢量数据进行不同粒度的化简操作,可有效解决当前有限的网络带宽和无限增长的空间数据之间的突出矛盾,也可实现矢量瓦片地图在客户端显示过程中从重要到次要、从高分辨率到低分辨率的逐级渐进式可视化,提高了数据传输效率与可视化表达效果[4]。矢量瓦片地图线要素化简算法的基本思想是在网络地图服务过程中,对不同层级的矢量数据进行不同粒度的化简操作。化简是有选择性地去掉曲线上的点,并对其他点进行合理位移,以尽可能地保持曲线的形状特征,最终实现矢量瓦片地图在客户端高效的多尺度渐进式可视化[5]。
线化简算法（如经典的Douglas-Peucker算法）在能够对整条曲线进行压缩的同时,更好地保留特征点,但易导致在特征点处出现尖角[6];Visvalingam算法是对最小面积的点进行重复式删除,便于网络地图服务过程中对线要素的渐进式化简,不足之处是每删除一个点,需要重新对三角形面积进行排序,导致化简效率降低[7];Li-Openshaw算法能很好地光滑线要素的特征点,可有效解决计算结果尖锐化的问题,但对所有弯曲点进行统一光滑处理会导致线要素发生变形[8];翟仁健等[9]提出基于地理特征约束的线化简算法,该方法主要通过约束Delaunay三角网模型对曲线形态的结构进行分析,其对线要素地理特征保持效果较好,但算法复杂度较高;弧比弦化简算法可以对曲线弯曲地方进行整体概括,但可能会出现连续节点被剔除的问题,导致局部曲线形状发生较大的变形[10];李成名等[11]提出了顾及空间关系的线化简算法,建立了线要素的全局化简方法,能够保持光滑美观的曲线形态,但对特征点的保持不够好。
上述方法大多数是对化简前后拓扑关系的保持考虑不充分,但在渐进式的网络地图线化简过程中保持拓扑关系的一致性更加重要[12,13,14]。鉴于此,本文对传统的Visvalingam算法进行了改进,引入最小堆技术提高网络地图服务过程渐进式化简的效率。在化简过程中,综合考虑化简前后线要素的拓扑关系,防止化简后拓扑关系发生改变,且实验结果验证了本文方法的有效性。

2 Visvalingam算法及其改进

2.1 Visvalingam算法

Visvalingam算法由Visualingam和Whyatt在1991年提出。其采用由下到上删除曲线上最不重要的点来化简曲线。如图1所示,以曲线上顶点 v i 与其前后相邻顶点 v i - 1 、 v i + 1 构成的三角形面积 E A i 作为衡量该顶点重要性权重 w i 。 E A i 越小,则权重 w i 越小,可以将顶点 v i 删除。具体步骤为：
图1 Visvalingam算法计算过程

Fig. 1 Calculation processes of the Visvalingam algorithm

（1）计算曲线上每个顶点权重值 w i （即 E A i ）;
（2）如果曲线上的顶点少于2个,则终止计算;
（3）选取当前曲线上权重最小的顶点 v i ;
（4）如果 w i 小于 ε （阈值）,则将此顶点 v i 从曲线上删除,然后重新计算此顶点 v i 在当前曲线上前后相邻顶点的权重,并返回步骤（2）;
（5）如果 w i 大于 ε ,则保留此顶点 v i ,退出判断。
Visvalingam算法主要存在以下问题：① 在删除顶点过程中只考虑了局部顶点之间的关系而没有考虑其他顶点,所以无法解决删除顶点后产生的自相交问题（图2）;② 在化简过程中要重复查找最小顶点权重值即每次迭代计算过程中要遍历所有权重数据进行排序,这将导致算法效率低下。
图2 Visvalingam算法处理后产生自相交现象

Fig. 2 The self-intersectionproblem of the the Visvalingam algorithm

2.2 Visvalingam算法改进

（1）基于最小堆技术的最小权重值查找
本文采用最小堆技术来解决最小权重值查找效率低下问题。最小堆是一棵完全二叉树,树中某节点值总是不大于其左右子节点值,保证堆顶元素最小。如果采用数组结构存储曲线上节点权重值,则查找最小权重值需要遍历整个数组,时间复杂度为O（N）,若采用最小堆,则时间复杂度为O（1）。本文采用最小堆技术存储曲线节点权重值,在利用Visvalingam算法化简矢量瓦片地图线要素过程中,需在最小堆中不断删除、插入顶点权重值,并进行最小堆的动态维护,此时无需遍历整棵树,只遍历当前树结构的某一条路径（这里不考虑删除点后相邻顶点面积更新）,而数组对应时间复杂度至少为O(N)。以图1所示线要素为例,其每个节点（首末节点除外,包括v2,v3,v4,v5）对应权重值集合为{6,5,4,2},初始化最小堆过程如图3所示。
图3 最小堆构造过程

Fig. 3 Processes of minimum heap construction

根据Visvalingam算法,图1线要素化简过程中首先删除v5,对应最小堆需要动态调整,调整过程如图4所示。
图4 最小堆删除调整过程

Fig. 4 Adjustment processes ofminimum heap deletion

（2）自相交问题处理
本文采用线自相交拓扑关系判断策略,并从全局考虑线上其他点对当前点的影响,解决化简后线自相交问题。具体策略为：首先判断待删除点是否会引起自相交,如果导致自相交,则记录该点,否则删除点,然后将所有前期被记录的点插入到最小堆中并更新最小堆（目的是判断这些被记录的点后期是否有可能被删除）。这样既能保证删除顶点后线要素不会产生自相交又能使线要素得到充分化简,充分考虑了当前化简效果对后续化简操作的影响。
如图5所示,左侧为原始算法计算过程,右侧为改进后算法计算过程。为便于理解,图中的面积权重值已经替换成了对应的数字权重值。
图5 改进前后的Visvalingam算法对比

Fig. 5 Comparison of the original and improved Visvalingam algorithms

图5中,原始Visvalingam算法在权重值为0的点被移除后导致线要素自相交,而改进后的算法已考虑到删除该点产生的影响,且当相同权重点一起移除时不会产生自相交。改进后算法实现步骤为：
（1）计算输入线顶点（起始点和终止点除外）权重值即三角形面积,利用权重值进行最小堆初始化;
（2）查找最小权重值并判断其是否小于阈值,如果小于则进行下一步处理,否则退出;
（3）判断移除当前待删除顶点后生成的新线要素是否产生自相交现象,如果产生则记录其顶点信息并执行步骤（2）,否则删除当前节点并更新相邻节点权重值;
（4）将步骤（3）中记录的所有删除后产生自相交的顶点重新插入到最小堆中,然后执行步骤（2）。
具体的算法伪代码如图6所示。
图6 改进后的Visvalingam算法伪代码

Fig. 6 Pseudo codefor the improved Visvalingam algorithm

3 实验及结果分析

3.1 实验数据及化简阈值

以中国南方某城市30 km2范围内的矢量瓦片地图水田边线和河流数据作为实验数据,初始比例尺数据为1:1万。本文采用原始Visvalingam算法与改进Visvalingam算法对其进行化简,并对其结果在拓扑关系、几何特征和位置精度方面[15]进行比较分析。
在实验过程中,本文以屏幕像素为参考,各尺度需要满足在屏幕上像素化简阈值保持一致的原则,不同比例尺下的化简阈值是由式（1）定义：
Distanc e n = P 1 × ( R / W ) × ( S 1 / S n )
式中： Distanc e n 是在n级别下的真实地理阈值; P 1 为第1级别（即化简前初始级别）下用户设置的像素阈值（第1级化简像素宽度的设置是由人眼可分辨的视域大小决定的,实际化简过程中用户也可自己设定） P 1 =2（参考商用网络地图服务平台）; R 为真实的地理范围;W为单张矢量瓦片的像素宽度; S 1 和 S n 为第1级和第n级下的比例尺。

3.2 拓扑关系评价

图7是将1:25万矢量瓦片地图化简成1:100万的结果,且用红线突出显示了拓扑关系的保持程度。其中图7（a）、（b）、（c）为整体化简示例图,图7（d）、（e）、（f）是局部放大显示的2种算法的化简结果。分析图7中2种化简算法的效果发现：
图7 2种算法对水田边线要素化简结果

Fig. 7 Comparison of the two algorithmsin simplifying paddy field boundaries

（1）图7中2种算法都能保留原始曲线上40%左右的点,在同等压缩率下,2种算法都具有较好的化简效果;
（2）原始Visvalingam算法虽然较好地保留了曲线整体形状（如图中极值点保持较好）,但由于删除了权重最小的点（相邻三角形面积较小的点）,且未能考虑曲线的拓扑特征,导致化简后曲线间发生相交。而改进的Visvalingam算法不仅对曲线的整体形态保持较好,同一压缩比率下,可保持较好的拓扑关系,避免发生相交,在不同化简粒度下,改进的Visvalingam算法对矢量瓦片地图线要素的化简效果更好。

3.3 几何特征评估分析

本文采用的几何特征评估主要包括线的长度比和线的曲折度2个指标。线的长度比值越小,说明对线的压缩量越大,如果不同线段之间的压缩比接近,表明该算法能较好地保持曲线的几何特征。而当线要素的长度变化较大、曲折度变化较小时,表明该算法维持了较好的曲线几何特征。具体如式（2）、式（3）所示。
∆ L = L ' / L
式中： L ' 、 L 分别为原始曲线和化简后曲线的长度。
Ang = ∑ i = 1 n - 2 1 + cos φ + 1 × 2 / ( n - 2 )
式中： Ang 是线的曲折度; φ 是每两条相邻直线段的夹角;n是曲线上的点数（首末节点除外）。
表1和表2为原始Visvalingam算法与改进Visvalingam算法在3种比例尺地图上的线要素化简结果,结果表明：
表1 2种算法化简河流要素的长度变化比

Tab. 1 Comparison of between the two algorithms in terms of river length, at different scales

比例尺
1:5万 1:10万 1:25万
Visvalingam算法 0.9978 0.9734 0.9513
改进Visvalingam算法 0.9986 0.9815 0.9722
表2 2种算法化简河流要素的曲折度变化比

Tab. 2 Comparison of between the two algorithms in terms of rivier sinuosity,at different scales

比例尺
1:5万 1:10万 1:25万
Visvalingam算法 0.9853 0.9703 0.9544
改进Visvalingam算法 0.9859 0.9795 0.9521
（1）改进的Visvalingam算法较原始Visvalingam算法稳定,但2种算法对河流化简后都随着比例尺的减小,长度和弯曲度也变小。
（2）改进的Visvalingam算法在比例尺1:25万的曲折度变化小于原始Visvalingam算法,主要是改进的Visvalingam算法保持了河流要素化简前后的拓扑关系,虽然比例尺变小,但仍可保持了原有的曲折度。
综上,与原始Visvalingam算法相比,改进的Visvalingam算法化简后线要素的长度变化较大、曲折度变化较小,能更好地保持矢量瓦片地图曲线的几何特征。

3.4 位置精度评估分析

本文主要采用位移标准差、位置误差、缓冲区限差3个指标来评价位置精度。对位移标准差与位置误差指标来说,值越小,说明算法化简结果更稳定,缓冲区限差指标值越大,说明算法较好地保持曲线的位置精度。
表3结果表明：改进的Visvalingam算法位移标准差与位置误差均小于原始Visvalingam算法,但位置误差值在小比例尺下较高,这是因为河流等自然要素,线弯曲多,且可能存在连续的小弯曲等现象。总体上看,改进的Visvalingam算法较原始Visvalingam算法更稳定。
表3 2种算法化简河流要素的位移标准差与位置误差比较

Tab. 3 Comparison of between the two algorithms in terms of river displacement standard deviation and location error at different scales

Visvalingam算法 改进Visvalingam算法
1:5万 1:25万 1:5万 1:25万
位移标准差/m 1.89 2.01 1.63 1.92
位置误差/m 1.71 7.27 1.54 6.86
根据图8所示,2种算法的缓冲区限差大体上接近,但缓冲区宽度相同时,利用改进的Visvalingam算法化简后的曲线落在缓冲区内的占比更大,因此改进的Visvalingam算法能更好地保持矢量瓦片地图曲线的位置精度。
图8 2种算法对1:5万河流要素化简的缓冲区限差比较

Fig. 8 Comparison of between the two algorithms in terms of limited measure of buffer, at the scale of 1:50 000

3.5 化简效率分析

采用改进的Visvalingam算法1（未处理自相交）、改进的Visvalingam算法2（处理自相交）和原始Visvalingam算法对上文实验数据中的河流数据进行化简,初始比例尺数据为1:1万,在硬件和基础软件平台相同情况下,算法的耗时对比如表4所示。分析表4实验结果发现：
表4 2种算法的化简效率对比

Tab. 4 Comparison of between the two algorithms in terms of simplification efficiency, at different scales (s)

比例尺
1:5万 1:10万 1:25万
Visvalingam算法 12 31 98
改进的Visvalingam算法1
改进的Visvalingam算法2		 10
28		 22
45		 79
110
（1）如果采用最小堆技术查找算法化简过程 中最小权重点,并且不检测自相交问题,则与原始Visvalingam算法相比,化简效率得到了极大提升,主要原因是采用最小堆技术,时间复杂度为O(1),而原始算法时间复杂度为O(N)。
（2）改进后的算法如果还要考虑化简前后自相交的问题,则耗时增加,主要原因是在化简过程还需要对数据进行拓扑检查操作,但随着比例尺缩小,曲线上总点数减小,化简耗时与原始算法逐渐趋同。
综上,改进后算法在化简结果的正确性和效率上整体优于原始Visvalingam算法。

4 结论

针对矢量瓦片地图服务过程中从重要到次要、从高分辨率到低分辨率的逐级渐进式可视化的需求,本文主要对当前线要素化简算法的效率问题和自相交问题进行了研究,主要结论包括：
（1）基于原始Visvalingam算法,针对效率问题,提出采用最小堆技术来解决最小权重值查找效率低下问题,可以将时间复杂度由O（N）减小到O（1）。
（2）针对自相交问题,采用线自相交拓扑关系判断策略,从全局考虑线上其他点对当前点的影响,本文方法不仅对曲线的整体形态保持较好,同一压缩比率下,可保持较好的拓扑关系,避免发生相交。
（3）采用真实数据试验验证了本文的算法,从拓扑关系、几何特征、位置精度和时间效率4个维度对算法进行了比较分析,试验结果表明,改进后算法在化简结果的正确性和效率上整体优于原始Visvalingam算法。

References

Publishing order | Descend order by publishing year | Descend order by cited within
[1]
Muller J C . Fractal and automated line generalization[J]. The Cartographic Journal, 1987,24(1):27-34.

[2]
Joao E M . Causes and consequences of map generalization[M]. Landon: Taylor and Francis, 1998.

[3]
Antonion V, Morley J, Haklay M . Tiled vectors: A method for vector transmission over the web[M]. Berlin: Springer Berlin Heidelberg, 2009.

[4]
孙路, 陈荦, 刘露 , 等. 一种面向服务器制图可视化的矢量数据多尺度组织方法口[J]. 计算机工程与科学, 2014,36(2):226-232.

[ Sun L, Chen L, Liu L , et al. A multi-scale management method for visualization of vector data on server cluster[J]. Computer Engineering & Science, 2014,36(2):226-232. ]

[5]
王家耀, 范亦爱, 韩同春 , 等. 普通地图制图综合原理[M]. 北京: 测绘出版社, 1993.

[ Wang J Y, Fan Y A, Han T C , et al. General cartographic generalization principle[M]. Beijing: Surveying and Mapping Press, 1993. ]

[6]
Douglas D H, Peucker T K . Algorithms for the reduction of the number of points required to represent a digitized line or caricature[J]. Canadian Cartographer, 1973,10(2):112-122.

[7]
Visvalingam M, Whyatt J D . Line generalisation by repeated elimination of points[J]. The Cartographic Journal, 1993,30(1):46-51.

[8]
Li Z L, Openshaw S. 基于客观综合自然规律的线状要素自动综合的算法[J].武测译文, 1994(1):49-58.

[ Li Z L, Openshaw S . An algorithm for automatic synjournal of linear elements based on objective synthetic natural law[J]. Translated by Wuhan University of Surveying and Mapping Science and Technology, 1994(1):49-58. ]

[9]
翟仁健, 武芳, 朱丽 , 等. 利用地理特征约束进行曲线化简[J]. 武汉大学学报·信息科学版, 2009,34(9):1021-1024.

[ Zhai R J, Wu F, Zhu L , et al. Line simplification method based on geographic feature constraint[J]. Geomatics and Information Science of Wuhan University, 2009,34(9):1021-1024. ]

[10]
Nako B , Mitropoulos V. Local length ratio as a measure of critical points detection for line simplification [EB/OL]. ( 2014-07-03).

[11]
李成名, 郭沛沛, 殷勇 , 等. 一种顾及空间关系约束的线化简方法[J]. 测绘学报, 2017,46(4):498-506.

[ Li C M, Guo P P, Yin Y , et al. A line simplification algorithm considering spatial relations between two lines[J]. Acta Geodaetica et Cartographica Sinica, 2017,46(4):498-506. ]

[12]
杜佳威, 武芳, 李靖涵 , 等. 采用多元弯曲组划分的线要素化简方法[J]. 计算机辅助设计与图形学学报, 2017,29(12):2189-2196.

[ Du J W, Wu F, Li J H , et al. Line simplification method based on multi-bends groups division[J]. Journal of Computer-Aided Design & Computer Graphics, 2017,29(12):2189-2196. ]

[13]
Samsonov T E, Yakimova O P . Shape-adaptive geometric simplification of heterogeneous line datasets[J]. International Journal of Geographical Information Science, 2017,32(8):1485-1520.

[14]
杜世宏, 秦其明, 王桥 . 空间关系及其应用[J]. 地学前缘, 2006,13(3):69-80.

[ Du S H, Qin Q M, Wang Q . The spatial relations in GIS and their applications[J]. Earth Science Frontiers, 2006,13(3):69-80. ]

[15]
武芳, 朱鲲鹏 . 线要素化简算法几何精度评估[J]. 武汉大学学报·信息科学版, 2008,33(6):600-603.

[ Wu F, Zhu K P . Geometric accuracy assessment of linear features' simplification algorithms[J]. Geomatics and Information Science of Wuhan University, 2008,33(6):600-603. ]

Options
Outlines

/

〈 〉