EN中文

Journal of Geo-information Science >

2020 , Vol. 22 >Issue 3: 505 - 515

DOI: https://doi.org/10.12082/dqxxkx.2020.190500

A Parallel Method of Surface Flow Dynamics Simulation based on CUDA

  • WU Qianjiao ,
  • CHEN Yumin , *
Expand
  • School of Resource and Environment Science, Wuhan University, Wuhan 430079, China
* CHEN Yumin, E-mail:

Received date: 2019-09-06

  Request revised date: 2019-12-11

  Online published: 2020-05-18

Supported by

National Natural Science Foundation of China(41671380)

Copyright

Copyright reserved © 2020
Fold

Abstract

Simulating the surface flow dynamics is of great importance in disaster prevention and mitigation, which could benefit the land remediation, regional planning, environmental protection and water resource management. Therefore, in this paper the Compute-Unified-Device-Architecture (CUDA) is embedded into the TIN-based surface flow dynamic simulation algorithm to get a parallel method for simulating the surface flow discharge. The aim of this study is to rapidly and accurately perform the surface flow dynamic simulation at any position and any time to meet the actual application requirements. First, the proposed algorithm extracts the critical points and drainage network from a high-precision Digital Elevation Model (DEM) to generate a drainage-constrained Triangulated Irregular Network (TIN). Second, the flow direction of each triangular facet over the TIN is calculated by the coordinate data of the triangular facets. Third, the flow path network is traced by the flow direction and rainfall source points. Fourth, the flow velocity of rain dropsover the flow paths is obtained by the flow velocity calculation kernel function based on the manning formula. Finally, by combing the flow velocity with the pre-set time, the algorithm can rapidly simulate the flow discharge at any location by usingthe flow discharge count kernel function. The specific paralle lization process consists of the transmission mode of data, partition model of thread and implement ation of the flow velocity calculation kernel function and flow discharge count kernel function. Data transmission in the paralle lization process includes the input and output of data. It inputs the data of the DEM, rainfall source points and flow path network from the CPU to GPU and outputs the data of the flow discharge calculated by the above two kernel functions from the GPU to CPU. The two kernel functions are parallelized by the flow paths. Each thread handles a single flow path. As a result, flow paths are divided by the partitioning method to obtain numerous thread blocks and the number of the thread in each thread block is allocated by the computing power of the GPU. The Black Brook Watershed (BBW) located in the north-eastern of New Brun swick was selected as the study area. To validate its accuracy and efficiency, the proposed method was compared with TIN-based surface flow dynamic simulation method. The experimental results demonstrate that the proposed algorithm can greatly improve the simulation efficiency while maintaining the accuracy simultaneously and its acceleration ratio can reach up to 11.2. In addition, the parallel algorithm was compared with the Soil and Water Assessment Tool (SWAT) model to verify its precision. The experimental results indicate that the Nash coefficient of the parallel method is increased by 88% and the correlation coefficient is increased by 5%.

Key words： Digital Elevation Model (DEM); Compute-Unified-Device-Architecture (CUDA); Triangulated Irregular Network (TIN); surface flow dynamic simulation; flow discharge; flow path; flow velocity; acceleration ratio

Cite this article

WU Qianjiao , CHEN Yumin . A Parallel Method of Surface Flow Dynamics Simulation based on CUDA[J]. Journal of Geo-information Science, 2020 , 22(3) : 505 -515 . DOI: 10.12082/dqxxkx.2020.190500

1 引言

随着自然环境与人类活动的变迁,洪涝、滑坡和泥石流等自然灾害发生的频次正在急剧增加,给人类的生产和生活带来了极大危害。如何高效地动态监测、模拟和预测地表水过程是防灾减灾中亟待解决的问题,也是科学化的国土整治、区域规划、环境保护和水资源管理的基础。目前地表水动态模拟方法可以分为基于格网数字高程模型（DEM）的地表水动态模拟和基于不规则三角网（TIN）的地表水动态模拟。基于格网DEM的地表水动态模拟常见模型有SHE（System Hydrologic European）模型[1,2,3,4],TOPMODEL（TOPgraphy based Hydrological MODEL）模型[5],SWAT（Soil and Water Assessment Tool）模型[6],LISFLOOD模型[7],DTVGM（Distributed Time Variant Gain Model）模型[8]和DR2-2013（Distributed Rainfall-Runoff）模型[9]。
SHE模型是由英国、法国、丹麦的科学家联合研制出的一种典型的三维分布式物理模型。该模型为了便于模型参数与降雨数据的结合[10],在平面上将流域划分为规则格网,在垂向上将每个格网划分为若干水平层,以完成产流和汇流等水文过程的模拟。该模型的物理过程描述明确,但模拟效率较低。TOPMODEL模型是1979年由Beven和Kirkby[11]提出的一种基于规则格网DEM获取地形因子,从而实现流域汇流动态模拟的水文模型。该模型的模拟精度较高,但因为未考虑到降雨和蒸发,只适用于非复杂过程的水文模拟,并且该模型的数据分析效率较低。SWAT模型是1994年由Arnold[12]提出的一种基于规则格网DEM提取水文响应单元（HRUs）的半分布式水文模型。该模型的模拟效率较高,但模拟精度却受到格网DEM分辨率的限制[13,14]。LISFLOOD模型是2000年由Bates等[15]提出的一种利用非线性分布函数来表达每个格网与汇流的对应关系的降雨—汇流模型。该模型比较适合大流域的地表水动态模拟。DTVGM模型是2002年由夏军等[16]提出的一种分布式水文模型,该模型从DEM上获取坡度、坡向、水流路径等地形因子,以水量平衡方程为核心来实现流域产流和汇流过程的模拟。该模型降低其模拟精度对模型参数的依赖性,适用于信息不全流域的模拟,但该模型的普遍性还未得到验证。DR2-2013模型是2014年由 Lopez等[9]提出的通过改进径流深度与流域水温之间的相关性,从而能够适用于不同季节的一种分布式水文模型。该模型能够完成不同空间模式的水文模拟,但模拟精度较低。
尽管具有较好的普遍性,但这些模型对格网DEM分辨率的依赖性较高,因此有学者利用TIN表达地形表面来实现高精度的地表水动态模拟。2001年,Tucker等[17]提出的CHILD模型（Channel-Hillslope Integrated Landscape Development）采用TIN作为地形单元模拟地形的演变以响应侵蚀和泥沙传输的地形流动过程。2005年,Vivoni等[18]研究的tRIBS模型（TIN-based Real-time Integrated Basin Simulator）是基于TIN的预测降雨后地表和地下的水文响应过程的一种分布式物理模型。2014年,Chen等[10,19-20]提出的一种基于FPN（Flow-Path Network）的地表水动态模拟模型,该模型通过TIN表面三角面的固定水流方向构建流水线网络,从而完成地表汇流的动态模拟,该模型具有较高的模拟精度,且能够满足多尺度的需求。在这些模型中,TIN结构能够较好地表达复杂多变的地形,提高模拟精度[21],但由于TIN结构的复杂性,以上模型的模拟效率还有待提高。因此,本文旨在对高精度的基于TIN的地表水模拟方法进行并行化改进,从而得到高精度、高效率的地表水动态模拟方法。
近年来,学者们提出了较多的并行计算方法,例如MPI、OpenMP、云计算、统一计算设备架构（CUDA）等。与多核CPU并行计算相比,基于GPU的CUDA[22,23,24,25]并行方法能够在PC环境下进行更简单的大数据并行计算,使得单机高性能处理成为可能。CUDA适用于数据量大、数据耦合度低、计算密度高的算法,这也是基于TIN的地表水动态模拟方法所具有的特点。随着GPU硬件的发展和CUDA的完善,并行计算的开发成本和难度大幅降低,并行化程度不断提高,使得CUDA被广泛应用于众多研究领域,例如环境建模[26,27,28]、遥感图像增强[29,30,31,32]、地形分析[33,34,35]等。同时,在水文模拟方面也有较为广泛的应用,如赵向辉等[36]2010年利用CUDA对基于DEM的流域等流时线绘制算法进行并行改进,实现了流域汇流曲线的快速绘制。Carlotto等[37]2018年采用CUDA对模拟二维地下水流动的有限差分模型进行并行处理,得到一种高效的地下水流动模拟并行算法,实验表明该并行算法的加速比高达56.0。
本文利用CUDA对基于TIN的地表水动态模拟方法进行并行化处理,得到一种高精度、高效率的基于CUDA的地表水动态模拟并行方法。该算法利用Parallel-Multi-Point算法[38]和Deterministic Eight-Node（D8）算法[39]从高精度的DEM上分别提取地形特征点和河网流域线,生成受流域线约束的TIN。在此基础上,根据TIN表面的三角面坐标数据获取水流方向,结合任意位置的降雨源点,追踪得到流水线网络,并基于曼宁公式,利用CUDA并行计算每条流水线的流速,再结合预设的时间,快速地进行地表水动态模拟,从而得到该时刻任意位置的地表汇流量。

2 基于TIN的地表水动态模拟方法与CUDA程序设计原理

2.1 基于TIN的地表水动态模拟方法

基于TIN的地表水动态模拟算法思路如下： ① 从高精度的DEM上分别提取地形特征点和河网流域线,生成受河流网约束的TIN;② 在TIN的基础上,结合降雨源点数据,生成流水线网络;③ 根据SWAT模型获得的产流数据计算得到每个降雨源点相对应的产流量;④ 利用曼宁公式（式（1））计算每条流水线上雨滴的流速;⑤ 结合预设的时间预测汇流移动距离,模拟该时刻的地表汇流量,从而实现任意时刻的地表水动态模拟[10]。
v = R 2 3 ∙ S 1 2 / n
式中：v是流速/（m/s）;R是水力半径/m;S是坡度 /（m/m）;n是曼宁系数。

2.2 CUDA程序设计原理

CUDA是2006年由NVIDIA公司研发的第一个类C语言的开发环境,一种全新的软硬件构架。它将GPU视为并行计算的设备,同时利用GPU的多核心提高运行效率。在CUDA框架中,硬件中的流处理器（Streaming Processor,SP）和流多处理器（Streaming Multiprocessor,SM）被映射为CUDA中的线程网格（Grid）、线程块（block）和线程（thread）。一个SP执行一个线程,同一个block中的所有线程在同一个SM中并行执行。
在CUDA编程模型中,CPU被视为主机（Host）,GPU被视为设备（Device）,一个系统可以包含一个Host和多个Device。一个完整的CUDA程序是由Host处理的串行部分（包括数据传输、初始化、复制、GPU启动和空间释放）和由Device处理的并行部分（若干kernel函数的并行实现）两部分组成。CUDA使用__global__或__device__类型限定符来定义kernel函数,使用<<<x, y>>>来定义kernel函数调用的线程数量,其中x表示Grid中block数量,y表示block中的thread数量（图1）,这种双层并行模式也是CUDA的优势。
图1 CUDA线程组织模型

Fig. 1 Model of the threads by the CUDA

3 基于CUDA的地表水动态模拟并行 方法

针对基于TIN的地表水动态模拟方法效率较低问题,本文利用CUDA对其进行并行化改进,提出一种基于CUDA的地表水动态模拟并行方法,希望在保证模拟精度的同时提高模拟效率。

3.1 基于TIN的地表水动态模拟并行化

在基于TIN的地表水动态模拟算法中,模拟任意时刻的地表汇流量耗时较多且可并行,因此利用CUDA中的核函数将该功能并行化,从而提高模拟效率。整个并行化过程主要包括3个部分：① 数据的传输;② CUDA中线程的划分;③ 流水线流速计算核函数和汇流量统计核函数的实现。
3.1.1 数据的传输
具体的传输过程如下：① 将DEM数据（在x和y方向上的坐标范围、分辨率、影像行数以及列数）、降雨源点数据（从DEM数据上随机采样获取）和流水线网络数据（流水线数量、流水线索引位置以及流水线上点的坐标值）由CPU传入GPU;② 循环计算得到地表任意位置的地表汇流量;③ 将上述步骤计算结果由GPU传到CPU,得到任意时刻的地表汇流量,如图2所示。
图2 基于CUDA的并行化过程中的数据传输方式

Fig. 2 Transmission mode of data during the parallelization process based on CUDA

步骤②的具体计算过程如下：
（1）根据降雨源点数据、DEM数据和流水线网络数据,基于曼宁公式,利用流水线流速计算核函数得到每条流水线上雨滴的流速;
（2）利用汇流量统计核函数得到该时刻的地表汇流量;
（3）循环计算,即可得到任意时刻的地表汇 流量。
3.1.2 CUDA中线程的划分
流水线流速计算核函数和汇流量统计核函数均以流水线的并行化方式实现,每个线程处理一条流水线,所有流水线按照分块方式进行划分,得到多个线程块。每个线程块中的线程数量按照GPU的计算能力进行分配。当核函数运行时,CUDA以线程块为执行单位进行并行计算,以分组方式对线程块中的线程进行依次计算。
例如,实验中的GPU计算能力是6.1,线程块中线程数量的最大值为1024,即一个线程块可分配32×32条流水线,线程块的数量为plineNum/1024+1个,如图3所示。其中,plineNum指流水线网络上流水线的数量。
图3 基于CUDA的并行化过程中的线程划分模型

Fig. 3 Partition model of thread during the parallelization process based on CUDA

3.1.3 核函数的实现
流水线流速计算核函数的具体计算过程如下：① 根据流水线网络数据获取流水线起始点的坐标值;② 由起始点的坐标值计算其所在栅格单元的行列号;③ 根据降雨源点数据获取该栅格内降雨源点的产流量;④ 基于曼宁公式计算流水线上每段折线上雨滴的流速;⑤ 结合预设的旅行时间,计算得到起始点流入的栅格单元的行列号,并将降雨源点的产流量赋给该栅格。流水线流速计算核函数的伪代码如算法 1所示。其中,blockIdx是线程块的索引,blockDim是线程块的维度,threadIdx是线程索引,gridDim是线程格网的维度。
汇流量统计核函数具体计算过程如下：①根据流水线网络数据计算得到流水线上所有雨滴的坐标值;②由雨滴的坐标值计算其所对应栅格单元的行列号;③将雨滴的产流量累加到该栅格单元,得到该时刻的地表汇流量。汇流量统计核函数的伪代码如算法2所示。其中,blockIdx,blockDim,threadIdx和gridDim的定义与算法1中的一样。
算法 1 流水线流速计算核函数
Input: number of the flow lines (e.g. flineNum), the location of the flow line (e.g. flineTrackSize[]), the break points of the flow line (e.g. flowTrack[]),range of the DEM (e.g. xMin, Ymax), the resolution of the DEM (e.g. dx, dy), the width of the DEM (e.g. imgWidth), the runoff of the rainfall source points (e.g. rVal)
1: idx = blockIdx.x * blockDim.x + threadIdx.x
2: idy = threadIdx.y
3: id= idy*(gridDim.x * blockDim.x) + idx
4: ifid>flineNum
5: terminate
6:ifid > 0
7: Calculate the index of the flow line over flow track network (e.g. flineStart = flineTrackSize[id-1])
8: Calculate the start point of the flow line over flow track network (e.g. sP = flowTrack[flineStart)
9: Calculate the column and row of the start point (e.g. col = (sP.x-xMin)/dx, row = (yMax-sP.y)/dy)
10: Calculate the runoff of the start point (e.g. pRVal = rVal[row*imgWidth+col])
11:ifpRVal> 0
12:Calculate the flow velocity by the Manning’s equation
13: Calculate the discharge of the start point’s location after time interval (e.g. fVal[]=pRVal)
Obtain: the discharge of all of the start points after everytime interval(e.g. fVal[])
算法 2 汇流量统计核函数
Input: number of the flow lines (e.g. flineNum), the location of the flow line (e.g. flineTrackSize[]),the width of height of the DEM (e.g. imgWidth, imgHeight),range of the DEM (e.g. xMin, Ymax), the resolution of the DEM (e.g. dx, dy), the width of the DEM (e.g. imgWidth), the discharge of all of the start pointsafter every time interval(e.g. fVal[])
1: idx = blockIdx.x * blockDim.x + threadIdx.x
2: idy = threadIdx.y
3: id = idy*(gridDim.x * blockDim.x) + idx
4: if id >flineNum
5: terminate
6: Calculate the index of the flow line over flow track network (e.g. flineStart = flineTrackSize[id-1])
7: Calculating the index of all of the raindrops (e.g. runP=flowTracks[flineStart+rainIdx[]])
8: Calculate the row and height of all the raindrops(e.g. col= (runP.x-xMin)/dx, row= (yMax-runP.y)/dy)
9: Calculate the discharge of all grid cells (e.g. pOutDis[]+=fVal[])
Output: the discharge of all grid cells (e.g. pOutDis[])

3.2 并行方法评价

采用Nash系数（N）、相关系数（R）和水量平衡系数（B）来评估该模型的模拟精度,采用运行时间加速比（S）来评估该模型的模拟效率。Nash系数（N）、相关系数（R）、水量平衡系数（B）和运行时间加速比（S）的计算公式如下：
N = 1 - ∑ t = 1 n ( Q o t - Q m t ) 2 / ∑ t = 1 n ( Q o t - Q o ¯ ) 2
R = ∑ t = 1 n ( Q m t - Q m ¯ ) ( Q o t - Q o ¯ ) / ∑ t = 1 n ( Q m t - Q m ¯ ) 2 ∑ t = 1 n ( Q o t - Q o ¯ ) 2
B = ∑ t = 1 n Q o t / ∑ t = 1 n Q m t
S = T c / T p
式中：t是时间; Q o t 是t时刻观测站的实测汇流量; Q m t 是t时刻模拟的汇流量; Q o ¯ 是实测汇流量的平均值; Q m ¯ 是模拟汇流量的平均值;Tc是串行算法的运行时间;Tp是并行算法的运行时间。对于N、R和B这3个参数,值越接近于1表示模型的模拟精度越高。对于参数S,值越大表示模型的模拟效率越高。

4 实验与结果分析

4.1 研究区域与实验环境

本文选取的实验区域是位于加拿大新布伦瑞克西北部的Black Brook Watershed （BBW）流域,采用的是从1:10 000比例尺的地形图上获取的5 m分辨率的DEM影像（图4,红色框内的子区域是图5-6的背景区域）。该影像由1284×942个栅格单元组成,高程在159.59 m和240.70 m之间。该流域位于47°05′N-47°09′N,67°43′W-67°48′W,占地面积约为14.5 km2,其中农用地占65%,森林占21%,土地占14%。该区域地形复杂,具有高密度的侵蚀特征,大量的降雨和降雪对土壤流失造成存在潜在威胁。实验采用2001年BBW流域日产流量来动态模拟该年日汇流量,日产流量数据是由SWAT模型根据日降雨数据模拟获得,该数据精度较高[10]。实验之前,利用ArcGIS Desktop 10.2对DEM影像进行填洼的预处理。
图4 实验中BBW流域的DEM影像

注：红色框区域是下文研究的子区域（图5-图6的分析区）。

Fig. 4 Test DEM of the BBW

图5 图4子区域内不同阈值下的TIN

Fig. 5 TINs on the sub-region under different thresholds

图6 图4子区域内不同降雨源点尺度下的流水线网络（阈值为0.5 m）

Fig. 6 Flow pathnetworks on the sub-region under different scales of the rainfall points （threshold is 0.5m）

为了评估并行算法的计算性能,实验在配置为i7-6800 CPU,64 GB RAM,500GB固态硬盘,1080 NVIDIA GeForce GTX显卡（20个SM）,64位Microsoft Windows 10操作系统的台式计算机上完成。通过改变特征点提取的阈值和降雨源点的尺度来统计运行时间以评估其模拟效率。另外,利用ArcGIS Desktop和Excel进行汇流结果的评价、分析以及可视化。

4.2 基于并行方法的地表水动态模拟实验

首先,采用parallel-multi-point算法[38]对填洼后的DEM数据进行特征点提取,该算法的提取过程包括：① 利用DEM的4个角点构建TIN,得到2个三角面;② 并行计算每个三角面所覆盖的所有离散点的高程差值,并找到每个三角面中具有最大高程差值的点;③ 将找到的点的高程差值与预设的阈值进行比较,如果高程差值大于阈值,将该点标记为特征点,并进行步骤④,否则,算法结束;④ 将提取的特征点添加到原来的特征点中,重新构建TIN; ⑤重复以上步骤,直到所有三角面中的最大高程差值均小于预设的阈值。
与常用的地形特征点提取算法（如Very Important Points（VIP）[40]算法和maximum z-tolerance[41]算法）相比,该算法能够快速高精度地提取地形特征点,且适用于较大的研究区域[38]。另外,由于该算法能够通过改变阈值的大小满足不同的精度需求,因此实验中采用parallel-multi-point算法提取地形特征点,并且选取不同阈值构建不同精度的TIN,验证基于CUDA的地表水动态模拟并行方法的一致性。根据State Bureau of Surveying and Mapping（2001）[42]标准,RMSE小于5 m均能满足该实验中DEM对高程精度的需求,因此实验选取的阈值分别为0.5,1.0,1.5,2.0和2.5 m。
常用的河流网提取算法是1984年由O'Callaghan and Mark提出的Deterministic Eight-Node（D8）算法[39],该算法的提取过程包括：① 计算所有栅格单元的水流方向;② 模拟所有栅格单元的汇流累积量;③ 将汇流累积量与给定的阈值进行比较,如果汇流累积量大于阈值,则将该点判定为河流点,连接河流点,得到河流网。D8算法简便易操作,执行效率快,且具有较强的适应能力,但受DEM精度误差的影响较大[43]。由于实验选取了BBW流域高精度的DEM数据,因此实验采用D8算法提取河流网。实验选取了不同的河流网提取阈值,分别为1000、2000、3000、4000和5000 m2,构建不同阈值、不同的河流网提取阈值下的TIN,生成DEM。将生成的DEM与原始的DEM进行对比,计算RMSE。结果表明,河流网提取的阈值大于2000 m2时,RMSE略微增大,因此河流网提取的阈值选取为2000 m2。
为了减少TIN中狭长形三角面的出现,本实验增加了特征点过滤的步骤,包括点点过滤和点线过滤。实验中选取不同的特征点过滤阈值,分别为6、7、8、9和10 m,构建不同特征点提取阈值下的受河流网约束的TIN,生成DEM。将生成的DEM与原始的DEM进行对比,计算RMSE。结果表明,特征点过滤阈值大于8 m时,RMSE基本不变,因此,点点过滤和点线过滤的阈值均选取为8 m,RMSE如表1所示。为了不同阈值下TIN上的三角面能够清晰可见,图5显示了图4中红色框内的TIN。
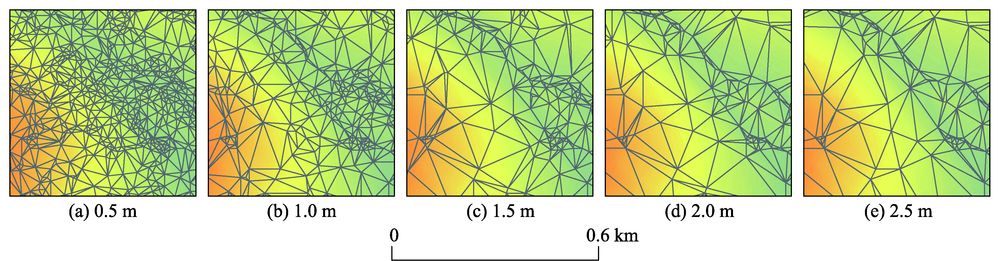
表1 BBW流域的不同阈值下TIN的精度结果

Tab.1 The accuracy of TIN under different thresholds on the BBW

阈值/m 0.5 1.0 1.5 2.0 2.5
特征点数量/个 10 859 4295 2149 1268 822
TIN表面三角面的数量/个 23 348 11 079 6854 5139 4285
RMSE/m 0.17 0.31 0.45 0.58 0.73
然后,对5 m的DEM数据进行重采样,分别得到10、15、20、25和30 m降雨源点数据,从而获得不同阈值、不同降雨源点尺度下的流水线网络。为了流水线能够清晰可见,图6显示了图4中红色框内阈值为0.5 m,不同降雨源点尺度下的流水线网络。
最后分别采用基于TIN的地表水动态模拟算法和基于CUDA的地表水动态模拟并行方法,结合2001年BBW流域的日产流量,模拟得到该年该流域不同阈值、不同降雨源点尺度下出口水处的日汇流量。

4.3 基于并行方法的地表水动态模拟结果

对基于TIN的地表水动态模拟算法和基于CUDA的地表水动态模拟并行方法得到的不同阈值、不同降雨源点尺度下的汇流量结果进行精度评估,如表2所示。
表2 BBW流域出口水汇流量模拟精度的评价对比结果

Tab. 2 Accuracy comparison of simulating the flow discharge at the outlet of the BBW

阈值/m 算法 模型 降雨源点尺度/m
10 15 20 25 30
0.5 基于TIN的地表
水动态模拟算法		 N 0.77 0.77 0.77 0.77 0.77
R 0.91 0.91 0.91 0.91 0.91
B 1.30 1.31 1.31 1.30 1.30
基于CUDA的地表水动态模拟并行方法 N 0.77 0.77 0.77 0.77 0.77
R 0.91 0.91 0.91 0.91 0.91
B 1.30 1.31 1.31 1.30 1.30
1.0 基于TIN的地表
水动态模拟算法		 N 0.77 0.77 0.77 0.77 0.77
R 0.91 0.91 0.91 0.91 0.91
B 1.31 1.31 1.31 1.31 1.31
基于CUDA的地表水动态模拟并行方法 N 0.77 0.77 0.77 0.77 0.77
R 0.91 0.91 0.91 0.91 0.91
B 1.31 1.31 1.31 1.31 1.31
1.5 基于TIN的地表
水动态模拟算法		 N 0.77 0.77 0.77 0.77 0.77
R 0.91 0.91 0.91 0.91 0.91
B 1.31 1.31 1.32 1.32 1.31
基于CUDA的地表水动态模拟并行方法 N 0.77 0.77 0.77 0.77 0.77
R 0.91 0.91 0.91 0.91 0.91
B 1.31 1.31 1.32 1.32 1.31
2.0 基于TIN的地表
水动态模拟算法		 N 0.77 0.77 0.77 0.77 0.77
R 0.91 0.91 0.91 0.91 0.91
B 1.31 1.32 1.31 1.32 1.31
基于CUDA的地表水动态模拟并行方法 N 0.77 0.77 0.77 0.77 0.77
R 0.91 0.91 0.91 0.91 0.91
B 1.31 1.32 1.31 1.32 1.31
2.5 基于TIN的地表
水动态模拟算法		 N 0.77 0.77 0.77 0.77 0.77
R 0.91 0.91 0.91 0.91 0.91
B 1.31 1.31 1.32 1.32 1.32
基于CUDA的地表水动态模拟并行方法 N 0.77 0.77 0.77 0.77 0.77
R 0.91 0.91 0.91 0.91 0.91
B 1.31 1.31 1.32 1.32 1.32
由表2可知,基于TIN的地表水动态模拟算法和基于CUDA的地表水动态模拟并行方法的模拟结果精度一致。选取Nash系数、相关系数和水量平衡系数最接近1的模拟情况（阈值为0.5 m,降雨源点尺度为30 m）下的汇流量,与SWAT模型和观测站获取的汇流量进行可视化表达,如图7所示。
图7 BBW流域出水口模拟汇流量的评价结果对比

注：阈值为0.5 m,降雨源点尺度为30 m。

Fig. 7 Comparison of the simulated results at the BBW's outlet

另外,为了验证其精度,利用SWAT模型进行降雨源点尺度为30 m的汇流量模拟,评价参数统计如表3。
表3 SWAT模型的精度评价结果（DEM为30 m）

Tab. 3 Statistical factors utilized to assess the precision of SWAT model （scale of DEM is 30 m）

评价参数
N R B
SWAT 0.41 0.87 0.96
上述2种算法在不同阈值、不同降雨源点尺度下模拟所需时间的统计结果如表4。
表4 BBW流域出口水汇流量模拟的运行时间统计结果

Tab. 4 Computation performance of simulating the flow discharge at the outlet of the BBW (s)

阈值/m 算法 降雨源点尺度/m
10 15 20 25 30
0.5 基于TIN的地表水动态模拟算法 953.82 425.37 278.18 213.77 169.77
基于CUDA的地表水动态模拟并行方法 93.16 43.49 28.34 22.72 19.00
1.0 基于TIN的地表水动态模拟算法 912.16 407.40 278.21 203.25 159.87
基于CUDA的地表水动态模拟并行方法 86.32 42.75 27.72 21.23 18.47
1.5 基于TIN的地表水动态模拟算法 899.07 395.99 267.96 196.33 159.60
基于CUDA的地表水动态模拟并行方法 80.51 41.88 27.23 20.74 17.88
2.0 基于TIN的地表水动态模拟算法 893.92 396.22 270.80 198.07 159.21
基于CUDA的地表水动态模拟并行方法 86.14 43.86 28.01 21.39 17.95
2.5 基于TIN的地表水动态模拟算法 892.59 400.38 260.40 199.60 164.56
基于CUDA的地表水动态模拟并行方法 85.61 43.60 27.77 20.80 17.29

4.4 模拟结果对比分析

（1）模拟效率的提高
由图8可知,随着降雨源点尺度的增大,特征点提取阈值为0.5 m时,加速比分别为10.2、9.8、9.8、9.4和8.9;特征点提取阈值1.0 m时,加速比分别为10.6、9.5、10.0、9.6和8.7;特征点提取阈值为1.5 m时,加速比分别为11.2、9.5、9.2、9.5和8.9;特征点提取阈值2.0 m时,加速比分别为10.4、9.0、9.7、9.3和8.9;特征点提取阈值2.5 m时,加速比分别为10.4、9.2、9.4、9.6和9.5。由此可知,基于CUDA的地表水动态模拟并行方法模拟效率大幅提高,加速比达到11.2。
图8 不同降雨源点尺度下的加速比

Fig. 8 Speed ratio under different scales of the rainfall points

（2）模拟精度的保持
结合图9-图11可知,该并行方法在完全保持基于TIN的地表水动态模拟方法的精度同时,Nash系数均为0.77,相关系数均为0.91,水量平衡系数均在1.31左右的小范围内波动。
图9 模拟结果的Nash系数分布

Fig. 9 Nash coefficient distribution map of simulation results

图10 模拟结果的相关系数分布

Fig. 10 Correlation coefficient distribution map of simulation results

图11 模拟结果的水量平衡系数分布

Fig. 11 Balance coefficient distribution map of simulation results

另外,由图7和表4相结合可知,该并行方法的模拟结果比SWAT模型的模拟结果更加接近观测站的实测数据,Nash系数增加88%,相关系数增加5%,水量平衡系数略有下降,但随着特征点提取阈值的减小,精度略有提高,因为模型具有较高的运行效率,可以通过减小特征点提取阈值来获得更高的模拟精度。SWAT模型将流域划分为水文响应单元（HRUs）,利用其独有的土地覆盖,坡度和土壤类型结合方法进行汇流演算[44]。该模型的参数较多,具有不确定性,且精度依赖于DEM分辨率[45]。基于CUDA的地表水动态模拟并行方法避免了参数和DEM的分辨率对精度的限制,保证了模拟精度的一致性。
由此表明,该并行方法在保持模拟精度的同时大幅提高了模拟效率。

5 结论与讨论

本文针对基于TIN的地表水动态模拟方法存在的效率较低问题,利用CUDA对其进行并行化优化,得到了一种基于CUDA的地表水动态模拟并行方法,从而快速高精度地完成地表水的动态模拟,为水土流失、国土规划和洪涝灾害等应用领域提供决策支持。
（1）通过对基于TIN的地表水动态模拟算法进行分析发现,该算法中模拟任意时刻的地表汇流量耗时较多且可并行,因此,利用CUDA将该汇流量模拟功能改进成核函数,得到地表水动态模拟并行方法;
（2）在加拿大新布伦瑞克西北部的BBW流域,通过改变特征点提取阈值和降雨源点尺度,对比分析该算法与基于TIN的地表水动态模拟方法的模拟精度和效率;
（3）在该实验区域,将该算法与经典的SWAT模型进行精度的对比分析。
结果表明,该并行方法与基于TIN的地表水动态模拟方法和的模拟结果一致,Nash系数均为0.77,相关系数均为0.91,水量平衡系数均在1.31左右较小范围内波动。同时,该并行方法模拟效率得到大幅提高,加速比达到11.2。相对于SWAT的模拟结果,该并行方法的Nash系数增加88%,相关系数增加5%。综上,基于CUDA的地表水动态模拟并行方法能够快速完成高精度的地表水动态模拟。

References

Publishing order | Descend order by publishing year | Descend order by cited within
[1]
Beven K J, Warren R, Zaoui J . SHE: Towards a methodology for physically-based distributed forecasting in hydrology[J]. Hydrological Forecasting (IAHS Publication), 1980,129:133-137.

[2]
Abbott M B, Bathurst J C, Cunge J A , et al. An introduction to the European hydrological system-systemehydrologiqueEuropeen, ‘SHE’, 1: History and philosophy of a physically-based, distributed modelling system[J]. Journal of Hydrology, 1986,87:45-59.

[3]
Bathurst J C, Wicks J M, Connell P E. The SHE/SHESED basin scale water flow and sediment transport modelling system. In: V.P. Singh, eds. Computer models of watershed hydrology[J]. Highlands Ranch, CO: Water Resources Publication , 1995: 563-594.

[4]
Refsgaard J C, Storm B, Mike S, Singh. Computer models of watershed hydrology[C]. Highlands Ranch, CO: Water Resources Publication, 1995: 809-846.

[5]
Beven K J, Kirkby M J . A physically based, variable contributing area model of basin hydrology[J]. Hydrological Sciences Bulletin, 1979,24:43-69.

DOI PMID

[6]
Arnold J G, Srinivasan R, Muttiah R R , et al. Large area hydrologic modeling and assessment part I: model development[J]. Journal of American Water Resources Association, 1998,34(1):73-89.

[7]
Bates P D, DE ROO A P J. A simple raster-based model for flood inundation simulation[J]. Journal of Hydrology, 2000,236(1-2):54-77.

[8]
王纲胜, 夏军, 谈戈 , 等. 潮河流域时变增益分布式水循环模型研究[J]. 地理科学进展, 2002,21(6):573-582.

[ Wang G S, Xia J, Tan G , et al. A research on distributed time variant gain model: A case study on Chaoheriver basin[J]. Progress in Geography, 2002,21(6):573-582. ]

[9]
Lopez-Vicente M, Perez-Bielsa C, Lopez-Montero T , et al. Runoff simulation with eight different flow accumulation algorithms Recommendations using a spatially distributed and open-source model[J]. Environmental Modelling & Software, 2014,62:11-21.

[10]
Chen Y, Zhou Q, Li S , et al. The simulation of surface flow dynamics using a flow-path network model[J]. International Journal of Geographical Information Science, 2014,28(11):2242-2260.

[11]
Romanowicz R, Beven K, Moore R . GIS and distributed hydrological models[J] //Mather P. Geographical information handling-research and applications Chichester[C]. UK: John Wiley & Sons, 1993: 197-205.

[12]
Shoemaker L, Dai T, Koenig J . TMDL Model Evaluation and Research Needs[M]. Newyork: The US Environmental Protection Agency, 2005.

[13]
Kumar N, Singh SK, Srivastava PK , et al. SWAT Model calibration and uncertainty analysis for streamflow prediction of the Tons River Basin, India, using Sequential Uncertainty Fitting (SUFI-2) algorithm[J]. Modeling Earth Systems and Environment, 2017,3(1):30.

[14]
Das B, Jain S, Singh S , et al. Evaluation of multisite performance of SWAT model in the Gomti River Basin, India[J]. Applied Water Science, 2019,9(5):134.

[15]
Van Der Knijff J M, Younis J, De Roo A P J. Lisflood: A GIS-based distributed model for river basin scale water balance and flood simulation[J]. International Journal of Geographical Information Science, 2010,24(2):189-212.

[16]
蔡明勇 . DTVGM模型参数的遥感驱动研究与应用[D]. 北京:北京师范大学, 2011: 14-16.

[ Cai M Y . Remote sensing based DTVGM and its application[D]. Beijing: Beijing Normal University, 2011: 14-16.]

[17]
Tucker G E, Lancaster S T, Gasparini N M , et al. The channel-hillslope integrated landscape development (CHILD) model[M]. In: Harmon R S, W Doe. Landscape erosion and evolution modelling. Dordrecht: Kluwer Academic/Plenum Publishers, 2001: 349-388.

[18]
Vivoni E R, Teles V, Ivanov V Y , et al. Embedding landscape processes into triangulated terrain models[J]. International Journal of Geographical Information Science, 2005,19(4):429-457.

[19]
Zhou Q, Pilesjö P, Chen Y . Estimating surface flow paths on a digital elevation model using a triangular facet network[J]. Water Resources Research, 2011,47(7):40.

[20]
Zhou Q, Chen Y . Generalization of DEM for terrain analysis using a compound method[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2011,66(1):38-45.

[21]
陈玉敏, 吴钱娇, 巴倩倩 , 等. 多尺度地表水动态模拟及应用[J]. 测绘学报, 2015,44(S0):36-41.

[ Chen Y M, Wu Q J, Ba Q Q , et al. Application research of multi-scale simulation of surface flowdynamics[J]. Acta Geodaetica et Cartographica Sinica, 2015,44(S0):36-41.]

[22]
Schenk O, Christen M, Burkhart H . Algorithmic performance studies on graphics processing units[J]. Journal of Parallel and Distributed Computing, 2008,68(10):1360-1369.

[23]
Mielikainen J, Huang B, Wang J , et al. Compute unified device architecture (CUDA)-based parallelization of WRF Kessler cloud microphysics scheme[J]. Computers and Geosciences, 2013,52:292-299.

[24]
NVIDIA Corporation. NVIDIA CUDA C Best Practice Guide[M]. Santa Clara, California: NVIDIA Corporation, 2010.

[25]
NVIDIA Corporation. NVIDIA CUDA C Programming Guide[M]. Santa Clara, California: NVIDIA Corporation, 2010.

[26]
Abouali M, Timmermans J, Castillo J E , et al. A high performance GPU implementation of Surface Energy Balance System (SEBS) based on CUDA-C[J]. Environmental Modelling and Software, 2013,41:134-138.

[27]
Xia X, Liang Q . A GPU-accelerated smoothed particle hydrodynamics (SPH) model for the shallow water equations[J]. Environmental Modelling and Software, 2016,75:28-43.

[28]
Zhu H, He L, Leeke M , et al. WolfGraph: The edge-centric graph processing on GPU[J]. Future Generation Computer Systems, 2019.

[29]
王浩, 王含宇, 杨名宇 , 等. Retinex图像增强在GPU平台上的实现[J]. 地球信息科学学报, 2019,21(4):623-629.

[ Wang H, Wang H Y, Yang M Y , et al. Implementation of Retineximage enhancement algorithm on GPU platform[J]. Journal of Geo-information science, 2019,21(4):623-629. ]

[30]
Pascal G, Pascal O, Camille D , et al. Ray-tracing of GNSS signal through the atmosphere powered by CUDA, HMPP and GPUs technologies[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014,7(5):1592-1602.

[31]
Chang F, Zhao Y, Liu S . CUDA parallel algorithm for CVA change detection of remote sensing imagery[J]. Journal of Remote Sensing, 2016,20(1):114-128.

[32]
刘扬, 付征叶, 郑逢斌 . 高分辨率遥感影像目标分类与识别研究进展[J]. 地球信息科学学报, 2015,17(9):1080-1091.

[ Liu Y, Fu Z Y, Zheng F B . Review on high resolution remote sensing image classification and recognition[J]. Journal of Geo-information science, 2015,17(9):1080-1091. ]

[33]
Qin C, Zhan L . Parallelizing flow-accumulation calculations on graphics processing units from iterative DEM preprocessing algorithm to recursive multiple-flow-direction algorithm[J]. Computers & Geosciences, 2012,43:7-16.

[34]
Ortega L, Rueda A J . Parallel drainage network computation on CUDA[J]. Computers & Geosciences, 2010,36:171-178.

[35]
Rueda A J, Jose M N, Adrian L . A comparison of native GPU computing versus OpenACC for implementing flow-routing algorithms in hydrological applications[J]. Computers & Geosciences, 2016,87:91-100.

[36]
赵向辉, 苗青, 付忠良 , 等. 基于CUDA的汇流分析并行算法的研究与方法[J]. 计算机应用研究, 2010,27(7):2445-2451.

[ Zhao X H, Miao Q, Fu Z L , et al. Research and realization in parallel algorithm of confluence analysis based on CUDA[J]. Application Research of Computers, 2016,87:91-100. ]

[37]
Carlotto T, da Silva R V, Grzybowski J M V . A GPGPU-accelerated implementation of groundwater flow model in unconfined aquifers for heterogeneous and anisotropic media[J]. Environmental Modelling and Software, 2018,101:64-72.

[38]
Wu Q, Chen Y, Wilson J P , et al. An effective parallelization algorithm for DEM generalization based on CUDA[J]. Environmental Modelling & Software, 2019,114:64-74.

[39]
O’Callaghan J F, Mark D M . The extraction of drainage networks from digital elevation data[J]. Computer Vision, Graphics and Image Processing, 1984,28:328-344.

DOI PMID

[40]
Chen Z, Guevara J. Systematic selection of very important points (VIP) fromdigital terrain model for constructing triangular irregular networks[C]. In: Proc.8th International Symposium on Computer-Assisted Cartography, AutoCarto 8, Baltimore, MD, 1987.

[41]
Chang K . Introduction to Geographic Information Systems, 4th ed[M]. New York: McGraw-Hill, 2007.

[42]
国家测绘局测绘标准化研究所. CH/T1008—2001基础地理信息数字产品1:10 000, 1:50 000数字高程模型[S]. 北京:国家测绘局, 2001.

[ State Bureau of Surveying and Mapping. 1:10000 and 1:50000 digital elevation model. The Basic Digital Geographical Information Product, Standard CH/T 1008-2001[S]. Beijing: The State Bureau of Surveying and Mapping of China, 2001. ]

[43]
刘学军, 卢华兴, 卞璐 , 等. 基于DEM的河网提取算法的比较[J]. 水利学报, 2006,37(9):1134-1141.

[ Liu X J, Lu H X, Bian L , et al. Comparison of algorithms for extracting drainage network from grid-based digital elevation model[J]. Journal of Hydraulic Engineering, 2006,37(9):1134-1141. ]

[44]
金鑫, 金彦香, 杨登兴 . SWAT模型在土地利用/覆被变化剧烈地区的改进与应用[J]. 地球信息科学学报, 2018,20(8):1064-1073.

[ Jin X, Jin Y X, Yang D X . Improved SWAT and its application to a region with severe land use/land cover changes[J]. Journal of Geo-information science, 2018,20(8):1064-1073. ]

[45]
Thavhana M P, Savage M J, Moeletsi M E . SWAT model uncertainty analysis, calibration and validation for runoff simulation in the Luvuvhu River catchment, South Africa[J]. Physics and Chemistry of the Earth, 2018,105:115-124.

Options
Outlines

/

〈 〉