EN中文

Journal of Geo-information Science >

2020 , Vol. 22 >Issue 4: 867 - 876

DOI: https://doi.org/10.12082/dqxxkx.2020.200060

Comparative Study of Different Temperature Interpolation Methods in the Belt and Road Regions based on GIS

  • YANG Yanzhao , 1, 2, 3, * ,
  • LANG Tingting 1, 2 ,
  • ZHANG Chao 1, 2 ,
  • JIA Kun 1, 2
Expand
  • 1. Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences, Beijing 100101, China
  • 2. University of Chinese Academy of Sciences, Beijing 100049, China
  • 3. Key Laboratory of Carrying Capacity Assessment for Resource and Environment, Ministry of Natural Resources, Beijing 101149, China
* YANG Yanzhao, E-mail:

Received date: 2020-02-08

  Request revised date: 2020-03-18

  Online published: 2020-06-10

Supported by

Strategic Priority Research Program of the Chinese Academy of Sciences(XDA20010201)

Copyright

Copyright reserved © 2016
Fold

Abstract

The Belt and Road initiative was a globalization cooperation initiative put forward by China to strengthen the opening-up in the new era. With the development of globalization, it is of great significance to optimize the allocation of resources and environment. As an important reference dataset and input factor, the result of temperature interpolation is the basis for optimal allocation of regional resources and environment in large scale study area. Here, taking the Belt and Road (BR) regions as the study area, the monthly and annual mean temperature data in 2679 meteorological stations from 1980 to 2017 were interpolated based on Geographic Information Technology (GIS), using Inverse Distance Squared (IDS), CoKriging (CK), Regression-IDS (RIDS) and Regression-CK (RCK) interpolation methods. The 10 km map of spatial interpolation were generated using aforementioned four methods. The results showed: (1) In the BR regions, the geographical distribution of temperature were better displayed by IDS, CK, RIDS and RCK. The Mean Square Root Error (RMSE) of monthly mean temperature were 1.93~2.43 ℃, 1.78~2.14 ℃, 1.31~2.23 ℃ and 1.23~1.92 ℃, IDS, CK, RIDS and RCK, respectively. And the RMSE of annual mean temperature were 1.94 ℃, 1.83 ℃, 1.37 ℃ and 1.27 ℃, IDS, CK, RIDS and RCK, respectively. (2) The accuracy of CK interpolation with covariates was better than that of IDS, and the peak values produced by IDS were corrected. (3) After considering the impact of terrain, the accuracy of interpolation in temperature based on Residual correction were improved by 29.4% and 30.6%, RIDS compared to IDS and RCK compared to CK, respectively. In summary, The Regression-CK performed better than other three methods in this study area and it can be considered as temperature and climate data interpolation methods in the BR regions.

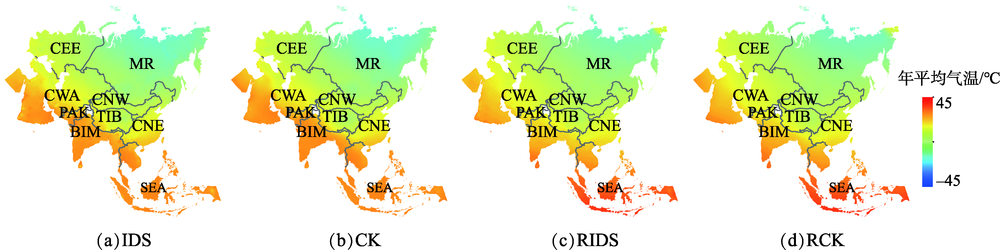
Key words： the Belt and Road; resources and environment; temperature interpolation; GIS; Inverse Distance Squared; CoKriging; regression; residual correction

Cite this article

YANG Yanzhao , LANG Tingting , ZHANG Chao , JIA Kun . Comparative Study of Different Temperature Interpolation Methods in the Belt and Road Regions based on GIS[J]. Journal of Geo-information Science, 2020 , 22(4) : 867 -876 . DOI: 10.12082/dqxxkx.2020.200060

1 引言

“一带一路”倡议是国家主席习近平于2013年9月和10月提出建设“新丝绸之路经济带”和“21世纪海上丝绸之路”的全球化合作倡议,是新时期国家统筹国内外形势变化而提出的一项具有国内外深远影响的重大战略[1]。“一带一路”合作倡议是沿线各国开放合作的共同愿景,也是中国经济转型的需要,但无论是当前世界格局和世界形势变化的需要,还是中国转变经济发展思路的需求,都要求我们从全球尺度去探索发展契机,谋划并实现全球资源的合理配置[2]。“一带一路”地区地域辽阔,资源禀赋各异,摸清不同地区资源环境现状,描绘主要自然资源的空间分布规律,是确立区域发展方向、合理布置自然要素、实现可持续发展目标的基础性工作[3]。随着合作倡议的提出,已有诸多学者开始关注“一带一路”沿线国家地理资源的空间规律性问题,充分发挥地理信息技术的优势,开展自然资源的空间计量与综合分析,成为重要的研究方向之一[4,5,6,7]。
气温是气象学、生态学、资源科学与环境科学等诸多研究中的基础性要素[8]。一方面,作为一项气候要素,气温能直接反映地表自然现象或揭示自然规律[9];另一方面,作为重要参数,气温参与地表过程模型的模拟,有助于分析区域资源环境状况及其变化规律,从而为区域资源环境与经济社会的协同发展提供依据[10]。目前,气温要素已成为“一带一路”地区事件决析的基础要素：王志芳[11]认为气候变化可能会给“一带一路”地区带来重大影响,如导致跨界资源冲突、恐怖袭击事件等;韩权等[12]将来自于文献的气温资料作为一项重要的基础地理要素,分析了“一带一路”沿线撒哈拉以南非洲地区能矿资源的投资活动情况,探讨了其投资风险;吴绍洪等[13]采用英国气象局哈德莱中心的气温数据,分析了“一带一路”地区环境要素的空间分布特征和时空差异,并预估了“一带一路”地区未来30年的灾害风险。由此可见,气温是“一带一路”地区气候变化、灾害评估、环境风险等研究领域的基础性数据,气温资料的获取在“一带一路”地区相关研究中显得尤为重要。
气温资料一般可以通过气象台站的实时观测直接获得,但为了研究其空间分布格局,如何获取空间上的连续数据一直是个难题。近年来,随着遥感技术的发展,遥感反演等方式成为重要的获取途径之一[14]。但是,随着研究尺度的扩大和研究目的的不同,综合考虑数据收集和处理等的时间成本和经济成本,遥感反演方法显现出一定的局限性。由此,借助气象站点数据来获取气温的空间数据成为大气科学、环境科学、生态学和地理学等诸多学科研究的热点方法[15,16,17]。随着计算机软硬件技术的进步,反距离加权法（Inverse Distance Weight,IDW）、距离平方反比法（Inverse Distance Squared,IDS）、普通克里格法（Ordinary Kriging,OK）、协同克里格法（Co-Kriging,CK）和样条插值法（Spline Methods,SP）等方法得到了迅速发展[18,19]。学者们基于站点数量和研究尺度,以及研究方法的改进,开展了区域插值最佳方法的研究[20,21,22,23,24,25]。一般来讲,IDW和IDS算法简单且操作便利,应用比较广泛,其缺点是没有考虑数据的空间异质性[26];OK能进行最佳线性无偏估计,但有一定的主观性,空间变异分析需要人工判断和分析[27],CK可以将其他相关要素作为协同变量考虑进去,用以提高插值精度[28];SP可以使拟合点更接近样本点,但不能估计结果的误差[29]。近年来,对插值方法优化的研究也越来越多,其中基于多元线性回归残差分析的回归距离平方反比法（Regression-IDS, RIDS）和回归协同克里格法（Regression-CK, RCK）不仅能考虑气象要素与地形之间的回归关系,又能考虑残差的自相关性,不断被应用于研究中[30,31,32]。实质上,在诸多气温插值方法中,并不固定存在一种最佳的插值方法,插值结果精度的高低与气象站点数量、空间分布情况等密切相关[11,33]。
由此,基于气温空间化资料在“一带一路”地区资源环境领域研究的基础性和重要性,结合气象要素空间插值方法的研究现状,本文采用GIS技术,以“一带一路”地区1980—2017年2679个气象站点观测资料为基础数据,选取距离平方反比法（IDS）、协同克里格法（CK）、回归距离平方反比法（RIDS）和回归协同克里格法（RCK）对气温进行插值,对比分析了4种插值方法的精度;在此基础上,生成了“一带一路”地区10 km×10 km分辨率的气温空间分布数据,以期为气象要素的区域空间化方法提供技术参考,为“一带一路”地区资源环境评价提供基础数据支撑。

2 研究区概况、数据来源及研究方法

2.1 研究区概况

“一带一路”是丝绸之路经济带和21世纪海上丝绸之路的简称,贯穿亚欧非大陆,东接亚太经济圈,西接欧洲经济圈。本研究“一带一路”地区范围主要包括中国、中亚5国、蒙俄、东南亚11国、中东欧19国、南亚8国、南西亚及中东19国,共计65个国家[34]。“一带一路”地区总人口约44亿,占世界总量的63%。“一带一路”地区地形复杂多样,涵盖山地、丘陵、盆地、高原和平原5大地形。“一带一路”地区跨越了赤道气候带、干燥气候带、暖温气候带、冷温气候带和极地气候带5大气候带,涵盖了季风气候、大陆性气候和沙漠气候等大多数气候类型。“一带一路”地区整体气温由南到北呈下降的趋势,多年平均气温最高为31.71℃,多年平均气温最低为 -20.94℃[35]。

2.2 数据来源

本研究气象站点原始数据来源于国家气象中心（http://data.cma.cn/）,共收集和整理1980年1月到2017年12月以来“一带一路”及其周边地区2780个站点的逐月数据。其中,“一带一路”地区内站点2463个,为提高边界地区插值精度,周边10 km以内地区站点317个（图1）。站台的原始数据项主要包括站点编号、经度、纬度、海拔等基础信息以及1980—2017年逐月的平均气温、最高气温和最低气温等指标项。研究首先剔除了各个站点的缺测数据,随后对观测异常的站点数据予以剔除,最终计入插值的站点共计2679个;对站点数据进行多年平均值的计算,获取了“一带一路”地区年平均气温和1—12个月的月平均气温数据。“一带一路”矢量数据来源于国家测绘地理信息局标准地图服务网站（http://bzdt.nasg.gov.cn/index.jsp）。“一带一路”陆域自然区域划分格局源自文献[14]及其数字化成果。
图1 “一带一路”及其周边气象站点分布

注：该图基于自然资源部标准地图服务网站下载的审图号为GS(2016)665号的标准地图制作,底图无修改。

Fig. 1 Distribution of meteorological stationson the Belt and Road (BR) regions

2.3 空间插值方法及精度验证方法

2.3.1 距离平方反比法（IDS）
距离反比插值法是一种确定性插值方法,它假定距离较近的事物之间有更相似的特征,随着距离的增加,事物之间的相似性减少,每个待估点的值根据周围已知点与待估点距离进行加权平均获得,距待估点距离相近的点位赋以较大的权重,距离远的点位则赋以较小的权重[6]。具体计算公式如下：
Z = ∑ i = 1 n Z i d i p ∑ i = 1 n 1 d i p
式中： Z 为待估点的气温预测值; n 为周围已知点的数量; Z i 为第 i 个已知点的值; d i 为预测点到已知点 i 的距离; p 是距离的幂。
当权重由距离反比给出时,即当幂值 p 为1时,称为距离反比法（IDW）;当权重由距离平方的反比给出时,即当幂值 p 为2时,称为距离平方反比法（IDS）[20]。鉴于距离平方反比法应该的广泛性[11],本研究选用距离平方反比法对“一带一路”地区的气温进行插值。
2.3.2 协同克里格法（CoKriging）
协同克里格插值法是一种最优线性无偏估计法,该方法中空间变异分析的主要指标是区域化随机变量的协方差和半变异值,当主变量与次变量距离较小时,二者是相似的,此时协方差较大,半变异值较小,反之,距离越大,协方差越小,半变异值越大[36]。具体计算公式如下：
Z ( x ) = ∑ i = 1 n a i Z ( x i ) + ∑ j = 1 m b j Y ( x j )
式中： Z ( x ) 为待估主变量气温; Z ( x i ) 为已知插值变量气温; Y ( x j ) 为次变量,分别为经度、纬度和海拔; a i 和 b j 分别是变量的权重值。
2.3.3 回归距离平方反比法（Regression-IDS）和回归协同克里格法（Regression-CK）
当目标变量与辅助变量具有相关关系时,可建立目标变量与辅助变量的多元回归关系,气温与其他地理要素具有相关性[30],通过多元线性回归方程可建立气温与经度、纬度和海拔高度的关系。多元线性回归方程计算的拟合值与观测值之间存在残差,利用IDS和CK两种插值方法对残差进行插值,并将残差插值面与拟合面加和作为插值结果,从而体现地理要素的空间相关性。多元线性回归方程表达式如下：
Z ( x i ) = m 0 + m 1 λ i + m 2 φ i + m 3 h i
Z ( x 0 ) 观测 = Z ( x 0 ) 拟合 + ε ( x 0 )
ε ( x i ) IDS = ∑ i = 1 n ε ( x 0 ) d i 2 ∑ i = 1 n 1 d i 2
ε ( x i ) CK = ∑ i = 1 n a i ε ( x 0 ) + ∑ j = 1 m b j Y ( x j )
Z ( x i ) IDS = Z ( x i ) + ε ( x i ) IDS
Z ( x i ) CK = Z ( x i ) + ε ( x i ) CK
式中： Z ( x i ) 为待估点多元回归拟合气温值; Z ( x 0 ) 观测 、 Z ( x 0 ) 拟合 和 ε ( x 0 ) 分别为已知点位的气温观测值、多元回归拟合气温值和残差值; m 0 、 m 1 、 m 2 和 m 3 分别为常数项和各项回归系数; λ 、 φ 和 h 分别代表经度、纬度和海拔高度; ε ( x i ) IDS 、 ε ( x i ) CK 、 Z ( x i ) IDS 和 Z ( x i ) CK 分别为IDS和CK插值后的待估点残差值和气温值。
2.3.4 精度验证方法
本研究采用交叉验证法对插值结果精度进行对比分析。交叉验证法是在插值过程中预留一个观测点为未知值,其余点全部参与插值,得到预留观测站的预测值,将预留观测站点的预测值与已知值进行对比,从而评价插值结果的精度[37]。研究过程中对2679个站点的插值结果全部进行了交叉验证。采用平均误差（Mean Error,ME）和均方根误差（Root Mean Square Error,RMSE）作为评价结果的指标,其中,ME是衡量模型预测偏移程度的指标,该值越接近于0,偏移程度越小,RMSE是衡量模型估算精度的指标,该值越小,模型精度越高[38],计算公式分别为：
ME = 1 n ∑ i = 1 n x p - x i
RMSE = 1 n ∑ i = 1 n x p - x i 2
式中： n 为气象站点数; x i 为第i个气象站点的观测值; x p 为第i个气象站点的预测值。

3 结果及分析

3.1 气温与地理要素相关分析

“一带一路”地区气象站点1980—2017年的平均气温与经度、纬度和海拔高度的相关分析结果（表1）表明：
表1 “一带一路”地区平均气温与经度、纬度和海拔高度之间的相关系数、复相关系数及回归方程

Tab. 1 Correlation coefficient, multiple correlation coefficient and linear regression equation of mean temperature with latitude, longitude and altitude in the BR regions

月份 相关系数（λ） 相关系数（φ） 相关系数（h） 复相关系数 回归方程 序号
1 -0.115** -0.877** -0.152** 0.951 Z1=46.648-0.127λ-0.913φ-0.005h （11）
2 -0.085** -0.896** -0.131** 0.957 Z2=45.946-0.112λ-0.886φ-0.004h （12）
3 -0.052** -0.910** -0.123** 0.959 Z3=44.328-0.088λ-0.777φ-0.004h （13）
4 -0.008** -0.904** -0.120** 0.941 Z4=42.320-0.060λ-0.635φ-0.003h （14）
5 0.007 -0.869** -0.140** 0.905 Z5=40.040-0.043λ-0.484φ-0.003h （15）
6 0.035 -0.803** -0.164** 0.837 Z6=37.136-0.026λ-0.349φ-0.002h （16）
7 0.020 -0.746** -0.180** 0.786 Z7=36.040-0.023λ-0.282φ-0.002h （17）
8 -0.009 -0.794** -0.171** 0.839 Z8=37.403-0.031λ-0.324φ-0.002h （18）
9 0.001 -0.872** -0.174** 0.915 Z9=38.679-0.040λ-0.434φ-0.003h （19）
10 -0.038** -0.899** -0.162** 0.950 Z10=41.693-0.064λ-0.594φ-0.004h （20）
11 -0.094** -0.888** -0.147** 0.954 Z11=45.833-0.102λ-0.785φ-0.004h （21）
12 -0.115** -0.875** -0.156** 0.949 Z12=46.378-0.122λ-0.874φ-0.005h （22）
年平均 -0.055** -0.901** -0.153** 0.956 Z年均=41.883-0.070λ-0.612φ-0.003h （23）

注：**表示在0.01级别（双尾）,相关性显著。

（1）从年平均气温来看,气温对经度、纬度和海拔高程的复相关系数为0.956,相关系数分别为-0.055、-0.901和-0.153,通过了置信度为0.01的显著性检验,各项相关系数表明“一带一路”地区年平均气温与纬度的相关性较强,与经度和海拔高度的相关性较弱。
（2）从月平均气温来看,气温对经度、纬度和海拔高程的复相关系数在0.786~0.959之间,相关系数分别在-0.115~0.035、-0.910~-0.746和-0.180~-0.120之间,通过了置信度为0.01的显著性检验（5—9月,与经度的相关性除外）,相关系数表明“一带一路”地区月平均气温与纬度的相关性较强,与经度和海拔高度的相关性较弱。

3.2 交叉验证结果分析

3.2.1 年平均气温插值验证结果
年平均气温插值交叉验证结果见表2。从平均误差ME的结果来看（ME绝对值大小表示误差顺序,正负号表示偏移观测值的方向）,CK（0.003）<RCK（-0.004）<IDS（0.013）<RIDS（-0.028）,CK法和IDS法的模拟值高于观测值,而RCK和RIDS的模拟值低于观测值。从均方根误差RMSE的结果来看,IDS、CK、RIDS和RCK的RMSE值分别为1.94、1.83、1.37和1.27 ℃,表明基于地学统计的CK法优于IDS;进一步对比发现,考虑地理要素的多元回归结果加入残差修正后插值精度有所提高,RIDS比IDS插值精度提高了29.4%,RCK比CK插值精度提高了30.6%。4种插值方法的均方根误差大小排序为RCK<RIDS<CK<IDS,可见,在“一带一路”地区,RCK插值法对年平均气温插值精度相对最高。
表2 “一带一路”地区IDS、RIDS、CK和RCK插值法的交叉验证结果

Tab. 2 The results of cross validation errors for IDS, RIDS, CK and RCK in the BR regions (℃)

月份 IDS RIDS CK RCK
ME RSME ME RMSE ME RMSE ME RMSE
1 0.026 2.30 -0.078 2.23 0.007 2.14 -0.009 1.92
2 0.038 2.30 -0.059 1.98 0.006 2.05 -0.007 1.70
3 0.030 2.30 -0.048 1.67 0.004 2.04 -0.004 1.52
4 0.003 2.19 -0.019 1.60 0.002 2.07 -0.001 1.51
5 -0.013 2.13 0.000 1.58 0.003 2.09 -0.002 1.51
6 -0.025 2.15 0.014 1.67 0.007 2.17 -0.004 1.62
7 -0.029 2.12 0.019 1.67 0.003 2.11 -0.006 1.66
8 -0.021 2.00 0.010 1.50 0.003 1.99 -0.017 1.59
9 -0.014 1.93 0.000 1.31 0.002 1.89 -0.003 1.28
10 0.019 1.97 -0.036 1.32 0.004 1.78 -0.003 1.23
11 -0.048 2.21 -0.068 1.73 0.007 1.85 -0.007 1.50
12 0.062 2.43 -0.086 2.14 0.016 2.04 -0.010 1.84
年均气温 0.013 1.94 -0.028 1.37 0.003 1.83 -0.004 1.27
3.2.2 月平均气温插值验证结果
从平均误差ME的结果来看（以ME绝对值表示误差区间范围）（表2）,IDS的平均误差在0.003~0.062 ℃之间,CK的平均误差在0.002~0.016 ℃之间,RIDS的平均误差在0~0.086℃之间,RCK的平均误差在0.001~0.010 ℃之间。IDS和RIDS插值法中,ME均有正负值存在,表明模拟值既有高于观测值的现象,也有低于观测值的现象;CK插值法中的ME均为正值,表明该方法模拟的气温值整体略高于观测值水平;RCK插值法的ME均为负值,表明RCK插值法模拟的气温整体略低于观测值水平。
从均方根误差RMSE的结果来看（表2）：IDS的均方根误差在1.93~2.43 ℃之间,RIDS的均方根误差在1.31~2.23 ℃,即RIDS较IDS的插值精度有所提高;CK的均方根误差在1.78~2.14 ℃之间,RCK的均方根误差在1.23~1.92 ℃之间,即RCK较CK的插值精度有所提高。通过插值精度区间大小可知,考虑地理要素的多元回归结果加入残差修正后插值精度有所提高。再对比RIDS和RCK的误差区间可知,RCK的插值精度高于RIDS,可见,在“一带一路”地区,RCK插值法对月平均气温插值精度相对最高。
图2为年平均气温及各月平均气温的4种插值方法均方根误差折线图,折线图反映的误差大小整体表现为RCK<RIDS<CK<IDS,基于以上误差对比分析,在“一带一路”地区,RCK插值法对平均气温插值精度相对最高。
图2 “一带一路”地区IDS、RIDS、CK和RCK插值平均气温的RMSE对比

注：横坐标中的数字1-12代表月份,13代表年。

Fig. 2 Comparison of RMSE based on IDS, RIDS, CK and RCK in the BR regions

3.3 气温空间分布格局

3.3.1 年平均气温空间分布格局
以10 km格网为单元,基于IDS、CK、RIDS和RCK法插值获取的“一带一路”地区年平均气温空间分布格局如图3所示。由图3可知,4种方法获得的“一带一路”地区年平均气温具有空间上的一致性,年平均气温的纬度地带性十分显著,整体均表现为由北向南逐渐升高的趋势。RIDS和RCK法高值区域更为显著,东南亚温暖湿润区气温较高的现象更为明显,蒙俄寒冷干旱区的低温范围略有减弱。此外,受青藏高原海拔较高的影响,青藏高原区年平均气温低于周围地区的气温。
图3 “一带一路”地区IDS、CK、RIDS和RCK法插值年平均气温栅格图

注：中东欧寒冷湿润区（CEE）;巴基斯坦干旱区（PAK）;青藏高原区（TIB）;蒙俄寒冷干旱区（MR）;孟印缅温暖湿润区（BIM）;中国西北干旱区（CNW）;中亚西亚干旱区（CWA）;东南亚温暖湿润区（SEA）;中国东部季风区（CNE）。

Fig. 3 Raster map of annul mean temperature based on IDS, CK, RIDS and RCK methods in the BR regions

3.3.2 月平均气温空间分布格局
以1月和7月为例,对“一带一路”地区1980—2017年多年月平均气温的空间分布格局（图4）进行分析：
图4 “一带一路”地区IDS、CK、RIDS和RCK法插值月平均气温栅格图

Fig. 4 Raster map of monthly mean temperature based on IDS, CK, RIDS and RCK methods in the BR regions

1月,“一带一路”地区多年平均气温在-45~45 ℃之间,区域差异十分显著。具体而言,4种插值方法的平均气温空间分布格局均呈现较强的纬度地带性,气温由北向南逐渐升高,蒙俄寒冷干旱区平均气温相对最低,东南亚温暖湿润区平均气温相对最高,此外,青藏高原区气温较周围地区的温度低。
7月,“一带一路”地区多年平均气温在0~40 ℃之间,4种插值方法的平均气温格局均呈现较强的纬度地带性,气温由北向南逐渐升高,但4种插值法的平均气温空间格局略有不同：虽低温区均出现在蒙俄寒冷干旱区,但IDS和CK插值法的低温范围较RIDS和RCK插值法范围广泛,且气温值相对较低;针对高温区而言,IDS和CK插值的高温区出现在中亚西亚干旱区和巴基斯坦干旱区,而经RIDS和RCK插值后,东南亚温暖湿润区成为高温区。此外,青藏高原作为地球的“第三极”,7月成为区域温度的低值中心,平均温度显著低于周边地区。
整体而言,从空间分布格局来看,4种方法的代表性月份的空间分布规律整体上具有较强的一致性。区别在于,IDS法在1月和7月都容易受极值的影响,“牛眼”现象较为突出;考虑地理相关性的RIDS和RCK法插值后,蒙俄寒冷干旱区的低温范围较IDS和CK法的低温范围有所缩减,高温区由中亚西亚干旱区和巴基斯坦干旱区转变到东南亚温暖湿润区,在青藏高原区,由于受海拔影响,低温现象较周围地区更为明显。

4 结论与讨论

4.1 结论

气温数据是开展“一带一路”地区自然资源空间计量的基础性数据,在实现全球资源优化配置方面具有重要地位。本研究采用距离平方反比法（IDS）、协同克里格法（CK）、回归距离平方反比法（RIDS）和回归协同克里格法（RCK）对“一带一路”地区的2679个气温站点数据进行插值,通过精度验证对比分析了4种方法在该区域的适宜性,生成了10 km“一带一路”地区1980—2017年的多年平均气温栅格资料。研究结果表明：
（1）“一带一路”地区气温要素的协同克里格法（CK）的插值精度高于距离平方反比法（IDS）,年平均气温插值精度提高了5.7%,月平均气温插值精度提高幅度在7.8%~26.7%之间;
（2）加入地理要素分析的回归残差插值,显著提高了“一带一路”地区气温插值精度。年平均气温RIDS的插值精度较IDS提高了29.4%,RCK的插值精度比CK提高了30.6%,月平均气温插值精度提高幅度分别在32.1%~46.9%和30.9%~42.5%之间;
（3）对比IDS、CK、RIDS和RCK4种插值方法在“一带一路”地区气温的插值精度,结果显示回归协同克里格法（RCK）插值精度最高。
（4）IDS、CK、RIDS和RCK4种插值方法整体上均较好地展示了“一带一路”地区气温空间分布的空间规律性,IDS受极值影响更大,出现了较多的同心圆现象,CK法加入协变量后,在一定程度上削减了同心圆现象,RIDS和RCK法考虑了地理要素,不仅削弱了同心圆现象,还修正了高温和低温区的分布位置。

4.2 讨论

本研究旨在开展“一带一路”地区气温资料的空间化方法研究,为“一带一路”地区的资源环境等研究提供基础数据支撑以及基本方法的探讨。研究采用多种方法对比分析了气温数据的插值精度,整体来看,回归协同克里格法插值气温数据能获得较好的精度,空间分布上削弱了极值,修正了气温空间分布格局,未来可以考虑将此方法作为“一带一路”地区逐日、逐月和逐年气温数据批量处理的方法之一。本文虽然采用经度、纬度与海拔高度与气温的相关分析提高了插值精度,相关系数也通过了显著性检验,但总体上,“一带一路”地区气温对经度和海拔高度相关性较弱,这一方面是由于高海拔地区气象站点分布较少,另一方面研究区域范围过大导致气温要素与地理要素相关性不显著,未来可以在进一步获取观测资料的基础上,开展相关研究工作,也可以对研究区进行分区研究,采用“自下而上”的方法提高精度。此外,从本文的研究结果来看,对于气象站分布密集的欧洲地区,采用4种插值方法的结果空间上无明显变化,即气象站点分布的密集程度影响了插值结果的精度,因此加强气温等要素数据的监测仍是开展气象要素空间化工作的基础。

References

Publishing order | Descend order by publishing year | Descend order by cited within
[1]
刘慧, 刘卫东 . “一带一路”建设与我国区域发展战略的关系研究[J]. 中国科学院院刊, 2017(4):18-25.

[ Liu H, Liu W D . Study on relationship between the Belt and Road initiative and regional development strategies of China[J]. Bulletin of Chinese Academy of Sciences, 2017(4):18-25. ]

[2]
刘卫东 . “一带一路”:引领包容性全球化[J]. 中国科学院院刊, 2017,32(4):331-339.

[ Liu W D . Inclusive globalization: New philosophy of China's Belt and Road Initiative[J]. Bulletin of Chinese Academy of Sciences, 2017,32(4):331-339. ]

[3]
刘清杰 . “一带一路”沿线国家资源分析[J]. 经济研究参考, 2017(15):70-104.

[ Liu Q J . The analysis of resource on the Belt and Road countries[J]. Review of Economic Research, 2017(15):70-104. ]

[4]
胡伟, 刘壮, 邓超 . “一带一路”空间信息走廊建设的思考[J]. 工业经济论坛, 2015(5):132-140.

[ Hu W, Liu Z, Deng C . A study on the 'One Belt and One Road' spatial information corridor[J]. Industrial Economy Review, 2015(5):132-140. ]

[5]
Mia M. Bennett . Is a pixel worth 1000 words? Critical remote sensing and China's Belt and Road Initiative[J]. Political Geography, 2020,78:102-127.

[6]
Zhao Y B, Liu X F, Wang S J , et al. Energy relations between China and the countries along the Belt and Road: An analysis of the distribution of energy resources and interdependence relationships[J]. Renewable and Sustainable Energy Reviews, 2019,107:133-144.

[7]
Yang Y, Fan M D . Analysis of the spatial-temporal differences and fairness of the regional energy ecological footprint of the Silk Road Economic Belt (China Section)[J]. Journal of Cleaner Production, 2019,215:1246-1261.

[8]
何鹏, 蹇东南, 李晓 , 等. 复杂地形影响下四川省逐月气温空间插值方法研究[J]. 生态与农村环境学报, 2019,35(6):801-808.

[ He P, Qian D N, Li X , et al. Study on Interpolation model of monthly temperature in Sichuan Province under the influence of complex topography[J]. Journal of Ecology and Rural Environment, 2019,35(6):801-808. ]

[9]
阎洪 . 气候时空数据的样条插值与应用[J]. 地理与地理信息科学, 2003,19(5):27-31.

[ Yan H . Spline interpolation of spatial-temporal climate data for China[J]. Geography and Geo-information Science, 2003,19(5):27-31. ]

[10]
唐焰, 封志明, 杨艳昭 . 基于栅格尺度的中国人居环境气候适宜性评价[J]. 资源科学, 2008,30(5):648-653.

[ Tang Y, Feng Z M, Yang Y Z . Evaluation of climate suitability for human settlement in China[J]. Resources Science, 2008,30(5):648-653. ]

[11]
王志芳 . 中国建设“一带一路”面临的气候安全风险[J]. 国际政治研究, 2015(4):56-74.

[ Wang Z F . Climate security risks associated with China's "the Belt and Road" Initiative[J]. The Journal of International Studies, 2015(4):56-74. ]

[12]
韩权, 江东, 付晶莹 , 等. “一带一路”沿线撒哈拉以南非洲地区能矿资源投资风险指数研究[J]. 科技导报, 2018,36(3):108-115.

[ Han Q, Jiang D, Fu J Y , et al. On the risk index of energy resources investment in sub-Saharan Africa along “the Belt and Road Initiative”[J]. Science Technology review, 2018,36(3):108-115. ]

[13]
吴绍洪, 刘路路, 刘燕华 , 等. “一带一路”陆域地理格局与环境变化风险[J]. 地理学报, 2018,73(7):1214-1225.

[ Wu S H, Liu L L, Liu Y H , et al. Geographical patterns and environmental change risks in terrestrial areas of the Belt and Road[J]. Acta Geographica Sinica, 2018,73(7):1214-1225. ]

[14]
王新鸿, 邱实, 姜小光 , 等. 高光谱热红外数据反演地表温度与比辐射率方法研究[J]. 干旱区地理, 2010(3):107-114.

[ Wang X H, Qiu S, Jiang X G , et al. Land surface temperature and emissivity retrieval from hyperspectral thermal infrared data[J]. Arid Land Geography, 2010(3):107-114. ]

[15]
封志明, 杨艳昭, 丁晓强 , 等. 气象要素空间插值方法优化[J]. 地理研究, 2004,23(3):357-364.

[ Feng Z M, Yang Y Z, Ding X Q , et al. Optimization of the spatial interpolation methods for climate resources[J]. Geographical Research, 2004,23(3):357-364. ]

[16]
修思玉, 吕泓辰, 康世伦 , 等. 地理信息系统中不同空间插值方法的比较研究[J]. 森林工程, 2014,30(5):110-113.

[ Xiu S Y, Lv H C, Kang S L , et al. Comparative study on different spatial interpolation methods in GIS[J]. Forest Engineering, 2014,30(5):110-113. ]

[17]
毛萍, 黄东晓, 王芋华 , 等. 全球变化领域研究现状与趋势的大数据分析[J]. 中国科学院大学学报, 2017,34(4):441-451.

[ Mao P, Huang D X, Wang Y H , et al. Big data analysis of status and trends of global change research[J]. Journal of University of Chinese Academy of Sciences, 2017,34(4):441-451. ]

[18]
Boer E P J, Beurs K M D, Hartkamp A D . Kriging and thin plate splines for mapping climate variables[J]. International Journal of Applied Earth Observation and Geoinformation, 2001,3(2):146-154.

[19]
Marquínez J, Lastra J, Garcia P . Estimation models for precipitation in mountainous regions: The use of GIS and multivariate analysis[J]. Journal of Hydrology, 2003,270:1-11.

DOI

[20]
林忠辉, 莫兴国, 李宏轩 , 等. 中国陆地区域气象要素的空间插值[J]. 地理学报, 2002,57(1):47-56.

DOI

[ Lin Z H, Mo X G, Li H X , et al. Comparison of three spatial interpolation methods for climate variables in China[J]. Acta Geographica Sinica, 2002,57(1):47-56. ]

[21]
彭彬, 周艳莲, 高苹 , 等. 气温插值中不同空间插值方法的适用性分析——以江苏省为例[J]. 地球信息科学学报, 2011,13(4):539-548.

DOI

[ Peng B, Zhou Y L, Gao P , et al. Suitability assessment of different interpolation methods in the gridding process of station collected air temperature: A case study in Jiangsu Province, China[J]. Journal of Geo-information Science, 2011,13(4):539-548. ]

[22]
段平, 盛业华, 李佳 , 等. 自适应的IDW插值方法及其在气温场中的应用[J]. 地理研究, 2014,33(8):1417-1426.

DOI

[ Duan P, Sheng Y H, Li J , et al. Adaptive IDW interpolation method and its application in the temperature field[J]. Geographical Research, 2014,33(8):1417-1426. ]

[23]
Hussain I, Spock G, Pilz J , et al. Spatial-temporal interpolation of precipitation during monsoon periods in Pakistan[J]. Advances in Water Resources, 2010,33(8):880-886.

DOI

[24]
Bhowmik A K, Cabral P . Statistical evaluation of spatial interpolation methods for small-sampled region: A case study of temperature change phenomenon in Bangladesh[J]. Lecture Notes in Computer Science, 2011,6782:44-59.

[25]
Brinckmann S, Krähenmann S, Bissolli P . High-resolution daily gridded datasets of air temperature and wind speed for Europe[J]. International Journal of Pharmaceutics, 2015,8(2):649-702.

[26]
李佳霖, 樊子德, 邓敏 . 基于空间异质分区的残差IDW插值方法[J]. 地理与地理信息科学, 2015,31(5):29-33.

[ Li J L, Fan Z D, Deng M . Residual inverse distance weighting spatial interpolation method based on spatial heterogeneity sub-region[J]. Geography and Geo-information Science, 2015,31(5):29-33. ]

[27]
李框宇, 周梅, 陈玖英 , 等. 一种适用于气温空间插值的改进梯度距离平方反比法[J]. 2019,36(4):491-497.

[ Li K Y, Zhou M, Chen J Y , et al. An approach of improved gradient plus inverse distance squared for spatial interpolation of temperature[J]. Journal of University of Chinese Academy of Sciences, 2019,36(4):491-497. ]

[28]
李巍 . 降雨量空间插值方法比较研究[J]. 安徽农业科学, 2014,42(12):3667-3669.

[ Li W . Study on interpolation methods of rainfall[J]. Journal of Anhui Agricultural Sciences, 2014,42(12):3667-3669. ]

[29]
彭思岭 . 气象要素时空插值方法研究[D]. 长沙:中南大学, 2011: 3-10.

[ Peng S L . Developments of Spatio-temporal interpolation methods for meteorological elements[D]. Changsha: Central South University, 2011: 3-10. ]

[30]
李波, 黄敬峰, 金志凤 , 等. 基于GIS的浙江省年降水量空间分布推算方法研究[J]. 浙江大学学报(理学版), 2010,37(2):121-126.

[ Li B. Huang J F. Jin Z F , et al. Methods for calculating precipitation spatial distribution of Zhejiang Province based on GIS[J]. Journal of Zhejiang University(Science Edition), 2010,37(2):121-126. ]

[31]
张国峰, 杨立荣, 瞿明凯 , 等. 基于地理加权回归克里格的日平均气温插值[J]. 应用生态学报, 2015,26(5):246-251.

[ Zhang G F, Yang L R, Qu M K , et al. Interpolation of daily mean temperature by using geographically weighted regression-Kriging[J]. Chinese Journal of Applied Ecology, 2015,26(5):246-251. ]

[32]
张国峰, 白蕤, 李伟光 , 等. 海南岛日最低、最高气温空间插值研究[J]. 中国农学通报, 2017,33(19):101-109.

[ Zhang G F, Bai R, Li W G , et al. Spatial interpolation of daily minimum temperature and daily maximum temperature in Hainan island[J]. Chinese Agricultural Science Bulletin, 2017,33(19):101-109. ]

[33]
李金洁, 王爱慧 . 基于西南地区台站降雨资料空间插值方法的比较[J]. 气候与环境研究, 2019,24(1):50-60.

[ Li J J, Wang A H . Comparison of spatial interpolation methods based on monthly precipitation observation data of station in southwest China[J]. Climatic and Environment Research, 2019,24(1):50-60. ]

[34]
邹嘉龄, 刘卫东 . 2001-2013年中国与“一带一路”沿线国家贸易网络分析[J]. 地理科学, 2016,36(11):1629-1636.

[ Zou J L, Liu W D . Trade Network of China and Countries Along "Belt and Road Initiative" Areas from 2001 to 2013[J]. Scientia Geographica Sinica, 2016,36(11):1629-1636. ]

[35]
郝林钢 . “一带一路”分区自然地理特征及水资源分析[D]. 2019: 20-25.

[ Hao L G . Physiographic Characteristics and Water Resources analysis of the regions among the Belt and Road[D], Henan: Zhengzhou University, 2019: 20-25. ]

[36]
杨凤海, 王帅, 刘晓庆 , 等. 基于ArcGIS的近10年黑龙江省旬平均气温插值与建库[J]. 黑龙江农业科学, 2009(5):126-130.

[ Yang F H, Wang S, Liu X Q , et al. The spatial interpolation and GeoDatabase foundation of average 10-day air temperature of Heilongjiang Province in recent 10 years based on ArcGIS[J]. Heilongjiang Agricultural Sciences, 2009(5):126-130. ]

[37]
马轩龙, 李春娥, 陈全功 . 基于GIS的气象要素空间插值方法研究[J]. 草业科学, 2008,25(11):13-19.

[ Ma X L, Li C E, Chen Q G . Study on the method of GIS based spatial interpolation of climate factors in China[J]. Pratacultural Science, 2008,25(11):13-19. ]

[38]
孙钰森, 王维芳, 李国春 . 基于地理加权回归克里格模型的帽儿山地区森林碳储量空间分布[J]. 应用生态学报, 2019,30(5):223-231.

[ Sun Y S, Wang W F, Li G C . Spatial distribution of forest carbon storage in Maoershan region,Northeast China based on geographically weighted regression kriging model[J]. Chinese Journal of Applied Ecology, 2019,30(5):223-231. ]

Options
Outlines

/

〈 〉