EN中文

Journal of Geo-information Science >

2020 , Vol. 22 >Issue 5: 1063 - 1072

DOI: https://doi.org/10.12082/dqxxkx.2020.190727

Computation of Carbon Emissions of Residential Buildings in Wuhan and Its Spatiotemporal Analysis

  • JIA Tao 1 ,
  • YANG Shihao 1 ,
  • LI Xin , 2, * ,
  • YAN Penggao 1 ,
  • YU Xuesong 1 ,
  • LUO Xi 1 ,
  • CHEN Kai 1
Expand
  • 1. School of Remote Sensing and Information Engineering, Wuhan University, Wuhan 430072, China
  • 2. School of architecture and civil engineering, Xiamen University, Xiamen 361005, China
* LI Xin, E-mail:

Received date: 2019-11-29

  Request revised date: 2020-03-19

  Online published: 2020-07-25

Supported by

National Natural Science Foundation of China(41971332)

Copyright

Copyright reserved © 2020
Fold

Abstract

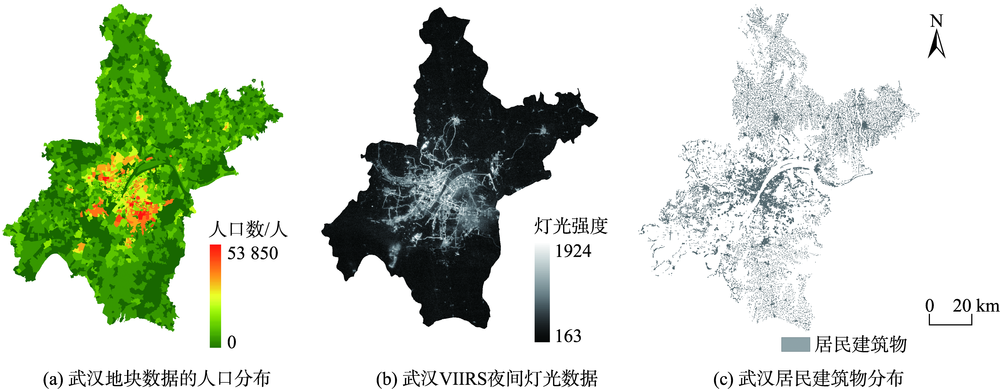
Carbon emissions of residential buildings have an important impact on energy conservation policies, emission reduction strategies, and sustainable urban development. However, current studies mainly focus on carbon emission estimation for an entire city or a large region. There is a lack of consistent methods of carbon emission estimation for residential buildings. Thus, this paper proposes a method to calculate carbon emissions of residential buildings by the fusion of multiple datasets. Our method firstly uses a top-down based strategy to assign the total carbon emission to each urban block. Then it adopts a bottom-up strategy to establish an emission calculation model for each residential building by taking into account urban block planning factors, socioeconomic factors, and residential building morphological factors. This paper applies the proposed method to estimate carbon emissions of all residential buildings in Wuhan city. Our results show that: (1) Carbon emissions of residential buildings decreases from the central city to the suburbs, which is closely related to population distribution; (2) Carbon emissions of residential buildings are heterogeneous and exhibit a heavy-tailed distribution. For instance, there are 89% of residential buildings with carbon emission lower than the average of 1.28 ton and 11% of residential buildings with carbon emission higher than the average; (3) Residential buildings within the same urban block have slight difference in carbon emission with an average standard deviation of 7.66 ton, while residential buildings located in different urban blocks tend to have significantly different carbon emissions with an average standard deviation of 51.30 ton; and (4) Carbon emissions of residential buildings are more likely to be affected by plot ratios in planning factors, population density in socioeconomic factors, and shapes of residential buildings. Our method and experimental results can provide decision support for sustainable planning of urban residential areas.

Key words： residential building; carbon emission; nighttime light; spatiotemporal analysis; urban block; planning factor; socioeconomic factor; Wuhan

Cite this article

JIA Tao , YANG Shihao , LI Xin , YAN Penggao , YU Xuesong , LUO Xi , CHEN Kai . Computation of Carbon Emissions of Residential Buildings in Wuhan and Its Spatiotemporal Analysis[J]. Journal of Geo-information Science, 2020 , 22(5) : 1063 -1072 . DOI: 10.12082/dqxxkx.2020.190727

1 引言

2015年我国承诺将于2030年使二氧化碳排放达到峰值且单位国内生产总值二氧化碳排放比2005年下降60%~65%[1]。在2017年,湖北省碳排放配额总量共计3.24亿吨,仅次于广东[2],在全国碳排放配额中占有较高比例。同时,城市中建筑物的碳排放量随城镇化率的提高而快速增长,且在城市碳排放总量中占较大比重。这为本文对武汉市居民建筑物碳排放量的反演计算和时空分析提供了契机。
目前,国内外关于碳排放的研究大部分基于宏观尺度上,研究对象多为国家[3]、省份[1]和城市[4],研究所采用的数据主要包括能源消耗统计数据和夜间灯光数据。例如,Li等[5]利用能源消耗数据,提出了省级碳排放估算和跨省碳排放分配方法,计算出省级碳排放因子;张仁杰等[6]选取省级能源消耗数据,基于OLS回归分析,研究我国碳排放影响因素的空间相关性;李德仁等[7]认为夜间灯光数据具备时空连续、独立客观等优势,可以广泛为碳排放研究提供重要依据;武娜等[4]使用夜间灯光数据模拟晋陕蒙地区碳排放空间分布并研究其碳排放空间分布特征和规律;Meng等[8]利用夜间灯光数据和能源统计数据来估算城市规模的碳排放量,发现夜间灯光数据适合城市规模碳排放量估算,但在人口稀少的地区使用时效果一般;Wang等[9]利用夜间灯光数据量化我国2000—2015年城市CO2排放的驱动因子[9]。但是,这些研究的碳排放量计算尺度多以省份和城市级别为主,缺乏尺度更小的研究模型与计算方法。
此外,目前文献中关于建筑碳排放（建筑物在建设、运行等全生命周期内消耗能源而产生的碳排放）和建筑物碳排放（单体建筑物或建筑群在完成建设之后因能源消耗而产生的碳排放）的研究方法较多。例如,张春霞等[10]提出了建筑全生命周期碳足迹和碳排放因子的概念,并给出其测定和选择方法;林波荣等[11]使用生命周期分析法对97个典型案例的计算模型和能耗、碳排放数据进行了分析总结;宋金昭等[12]基于系统动力学,分析能源对西安市居民建筑物碳排放的作用,得出其碳排放量将保持逐年攀升的趋势;张秀敏等[13]基于分类核算和生命周期的思路,构建了针对组织机构的建筑物分类碳核算方法;Zhang等[14]基于过程的方法和相同的建筑布局,比较了不同建筑物结构系统的排放量。然而,由于建筑物的复杂性[10,11,12,13,14,15]、碳排放影响因子的多样性[13,14,15,16]、现有计算方法的不一致性[10,11]、数据来源的苛刻性[12,13],使得目前的研究局限于城市建筑物碳排放总量的计算或者某一类别的单一建筑碳排放量的计算,很难针对大范围单体建筑物的碳排放量进行一致性计算。
因此,本文针对建筑物碳排放,提出以单体建筑物为最小单元来研究碳排放的计算反演方法,融合夜间灯光数据、能耗统计数据、地块数据和建筑物数据,构建地块碳排放量与地块规划因子、社会经济因子以及建筑物形态因子的非线性回归模型,并基于此模型,提出了单体居民建筑物的碳排放反演计算方法。本文通过计算武汉市所有单体居民建筑物的电能消耗碳排放量,分析了其空间分布特征与模式,研究成果可以为节能减排、土地规划、资源分配、城市管理、政策制定方面提供决策支持。

2 研究区概况和数据源

2.1 研究区概况

武汉市（113°41′E —113°41′E, 29°58′N —31°22′N）位于江汉平原东部、长江中游,是湖北省省会城市、全国重要的工业基地、科教基地和综合交通枢纽。总面积8494 km2,其中居民建筑物面积占比达到2.25%;2015年户籍人口数829万人,其中城市人口占比达到70.6%。武汉市作为我国中部核心城市,对其居民建筑物碳排放量反演计算具有重要的研究价值和科学意义。

2.2 数据来源

实验数据包括夜间灯光数据[17]、武汉市地块数据[18],以及居民建筑物数据[18]（本文研究的居民建筑物即为民用住宅建筑物）。地块数据包含3494条记录,如图1（a）所示,本文使用了每条记录的地块面积、地块人口总数和地块60周岁以上人口数。夜间灯光数据,如图1（b）所示,是美国地球观测委员会使用VIIRS（可见光红外成像辐射仪）卫星DNB（日/夜光数据）制作的平均辐射融合影像,空间分辨率约600 m。居民建筑物数据包含约187万条记录,如图1（c）所示,每条记录由基底面积、楼层数、建筑物周长等组成。然而,由于数据缺失,存在楼层数为0的记录,论文将其剔除,剩余186万条有效记录。此外,论文还使用了武汉统计年鉴记录的2015年居民用电量2.9E+08 TJ[19],以及IPCC提供的用电碳排放量转换系数28912 KG/TJ。
图1 2015年武汉市研究区数据

Fig. 1 Study area and data of Wuhan in 2015

3 研究方法

本文提出了一种综合考虑居民建筑物形态因子、地块规划因子以及地块社会经济因子,通过机器学习,构建非线性模型对单体居民建筑物的碳排放量进行反演计算的研究方法。该方法的技术路线如图2所示,主要由2个方法部分构成：地块居民建筑物碳排放分配方法和单体居民建筑物碳排放反演方法。
图2 研究方法技术路线

Fig. 2 The technical flow chart of our method

由于缺乏居民建筑物能耗的具体统计数据,且已有文献表明居民能耗中电能消耗占较大部分并会逐年增加[11,12],因此,论文采用居民建筑物用电量来代替能耗量,用于计算武汉市居民建筑物碳排放总量。需要说明的是,这种数据代替性并不影响论文研究方法的适用性。

3.1 地块居民建筑物碳排放分配方法

已有文献研究表明夜间灯光与人口具有较高的相关性[20],而灯光又与居民建筑物能耗具有直接关系。然而,一方面由于缺乏地块级别的真实能源消耗量,本文假设以通过地块人口改正后的地块灯光值占总灯光值的权重表示地块能源消耗量占总能源消耗量的权重,以此将城市居民总能耗量分配到每个地块;另一方面由于地块能耗存在多种结构,考虑数据易于获取,本文以电能消耗代替能源消耗,文中的碳排放即为电能消耗的碳排放（在此说明,文中不再具体区分）,这并不影响论文研究方法的适用性。① 叠置夜间灯光图像和地块数据,按照空间分布计算每个地块的夜间灯光值;② 对地块进行人工判读,剔除居民建筑物灯光异常的地块,包括商业活动密集的、以湖泊为主的、人口稀少的和含交通枢纽的地块;③ 通过分析地块灯光值和地块人口的关系,发现两者具有异速增长规律,采用拟合模型如式（1）所示。根据此模型,计算得到所有地块的纠正灯光值;最后,根据地块的纠正灯光值占所有地块灯光值总和的权重,将居民的电能消耗量分配到每个地块,进而根据电能碳排放转换系数求得各地块的碳排放量,如式（2）。
y j = c x j γ
f j = E × EF × y j ∑ y j
式中： x j 为地块j的人口数; c 为幂律模型系数; γ 为幂律模型指数; y j 为地块j的夜间灯光量; E 为城乡居民的总电能消耗量; EF 为电能消耗的碳排放量转换系数; f j 为地块j的碳排放量。

3.2 单体居民建筑物碳排放反演方法

已有研究文献表明社会经济因子对于碳排放量具有较大的影响[21],实际上,碳排放量还与空间规划与建筑物本身性质具有较高相关性。为此,论文提出一种顾及地块规划因子、地块社会经济因子和居民建筑物形态因子的单体居民建筑物碳排放反演计算方法,具体方法如式（3）所示。
f j = P F j × S F j × B F j
式中： P F j 为地块j的地块规划因子; S F j 为地块j的地块社会经济因子; B F j 为地块j的建筑物形态因子。从用地规划角度,地块规划因子一般可用地块容积率、地块空地率和地块平均楼层高度进行表示;从社会经济角度,由于地块GDP数据的不可获得性,这里的地块社会经济因子采用地块人口密度和地块老龄人口密度进行表示;从建筑物形态角度,居民建筑物形态因子可以表示为居民建筑物的基底面积和楼层高度。
3.2.1 居民建筑物分类方法
为了更准确地对单体居民建筑物的碳排放量建模,需要按照居民建筑物的形态特征对其分类。论文采用一种基于决策图的快速聚类方法[22],该算法根据任意两点之间的距离找到具有较高密度且相对孤立的聚类中心。具体而言,首先,计算任意一点的密度和距离,将该点的密度定义为与该点距离小于某一给定阈值的点的个数,将该点的距离值定义为到比该点密度值高且距离最远的点的距离,该距离值越大表明其越孤立（密度和距离计算公式详见文献[22],在此不再赘述）。其次,分别用密度、距离、密度、距离作为3个维度,做出决策图,并从决策图中选出那些具有较高密度、较大距离、较大密度×距离乘积的点集作为它们的聚类中心。
3.2.2 单体居民建筑物碳排放反演步骤
首先,论文采用多元非线性模型构建反演模型,具体如式（4）所示,其中,对式（3）中3个因子分别进行多元线性建模,这是由于任何复杂模型都可以用泰勒级数进行展开,考虑到计算可行性,每个因子采用一阶泰勒展开公式表示。
f j = ( k 1 m j + k 2 n j + k 3 p j + b 0 ) × ( c 1 α j + c 2 β j + b 1 ) × ∑ i = 1 n w i S i , j + b 2
式中： m j 为地块j的容积率; n j 为地块j的空地率; p j 为地块j的平均居民建筑物楼层数; α j 为地块j的人口密度; β j 为地块j的老龄人口密度; k 1 , k 2 , k 3 , c 1 , c 2 分别为相应自变量的模型系数; w i 为第i类居民建筑物的碳排模型系数; n 为研究区域内居民建筑物类型数目; S i , j 为地块j内第i类居民建筑物的总建筑面积; f j 为地块j的居民建筑物碳排放量, b 0 , b 1 , b 2 为常数。
其次,根据式（5）将式（4）所计算的地块碳排放量分配到该地块的每类建筑物中,再按每栋建筑物加权面积占该类建筑物总加权面积的比值,反演每栋建筑物的碳排放量,使得地块中所有单体居民建筑物碳排放量之和等于该地块的碳排放量。
g k , i , j = ( k 1 m j + k 2 n j + k 3 p j + b 0 ) × ( c 1 α j + c 2 β j + b 1 ) × w i s k , i , j + w i s k , i , j ∑ i = 1 n w i S i , j b 2
式中： g k , i , j 和 s k , i , j 分别为地块j内第i类居民建筑物中编号为k的居民建筑物的碳排放值和建筑面积。

4 结果与分析

4.1 地块居民建筑物碳排放分配结果

在地块尺度上,通过非线性拟合,可以发现地块人口与灯光量具有较好的幂律关系,如图3（a）所示,其中幂指数为0.75,拟合精度R2为0.35。然后,根据式（1）计算得到更正后的地块灯光值,并利用式（2）,将居民用电总碳排放量分配到每个地块,从而得到每个地块的居民建筑物碳排放量,如图3（b）所示。
图3 武汉市地块碳排放分布

Fig. 3 Carbon emission at the urban block level in Wuhan

从图3（b）中可以看出,武汉市地块居民建筑物碳排放量具有以下特征：① 总体呈现以城市中心向四周递减的趋势,和人口分布有着密切的关系; ② 居民建筑物稀疏的地块碳排放量极低,如东湖社区地块;③ 居民建筑物稠密的地块碳排放量较高,如南湖社区地块;④ 武汉市边缘碳排放量较低的地块往往是因为地块面积较大,所以含较多人口数,所以灯光值较高而碳排放量较大。

4.2 居民建筑物分类结果

基于决策图的快速聚类方法,采用基底面积和楼层高度计算建筑物之间的距离,得到武汉市居民建筑物分类决策图（图4（a））以及分类结果（图4（b））。
图4 居民建筑物分类

Fig. 4 Classification of residential buildings

首先,从决策图上选取具有较高密度,较远距离,以及二者之积较大的居民建筑点作为聚类中心点。如图4（a）所示,标为红色的5个居民建筑点为所选的聚类中心点,它们具有较大的密度且相对孤立。
其次,将每一个居民建筑物归类到距离它最近的聚类中心,得到居民建筑物的5种分类结果（图4（b））。不难看出,所有居民建筑物被一致整齐划分为5类,尽管第1类、第2类、第3类居民建筑物在基底面积较大时具有一定的混淆,但是楼层高度、基底面积相似的建筑物更容易被分到一类。
分类后的居民建筑物统计结果如表1所示,从中可以看出：① 第1类居民建筑物数量占绝大多数,平均楼层数目为2层,平均建筑面积为70 m2;② 第5类居民建筑物数据最少,平均楼层数目为45层,平均建筑面积为6430 m2;③ 第2、3、4类居民建筑物的平均基底面积差异不大,但是平均楼层数目差异较大,分别为11层、17层与29层。
表1 分类后居民建筑物统计结果

Tab. 1 Statistics of residential buildings in each class

建筑物类值 建筑面积和/km2 建筑物数量/个 平均楼层数目/层 平均基底面积/m2 平均建筑面积/m2
1 130.0 1 845 285 2 35.8 70.3
2 12.3 8006 11 149.6 1531.4
3 14.1 6385 17 139.6 2370.0
4 29.8 7481 29 136.1 3987.0
5 3.9 600 45 142.0 6430.0

4.3 单体居民建筑物碳排放反演模型拟合结果

通过多元非线性回归中最小二乘参数估计的Levenberg-Marquardt方法,计算得到式（4）中的13个参数（表2）,再通过式（4）计算出模型预测值（图4）。从图5中可知,模型预测值和观测值较为接近,具有较高的拟合精度,其R2达到0.77。基于表2,根据式（5）,从地块碳排放量中反演每种类别的每个居民建筑物,从而得到个体居民建筑物的碳排放量。此外,从表2中不难看出,居民建筑物碳排放量主要受到规划因子中的容积率影响,社会经济因子中的人口密度影响,以及居民建筑物第一类形态类型影响。
表2 居民建筑物碳排放反演模型参数

Tab. 2 Parameters of our model

参数 值 参数 值 参数 值 参数 值 参数 值
k1 -18.8 b1 -0.5 c1 69.5 w2 13.0 w5 4.3
k2 15.6 b2 1.5 c2 -19.6 w3 6.5
k3 11.2 b3 2.5 w1 53.0 w4 12.5
图5 地块观测碳排放与地块预测碳排放的相关性

Fig. 5 Correlation between observed carbon emissions and predicted carbon emissions

4.4 单体居民建筑物碳排放空间分布

武汉市居民建筑物碳排放量的空间分布图如图6所示,可以看出：① 区域差异性显著。从整个武汉市来看,居民建筑物碳排放量在空间分布上呈现从中心城区向四周递减的趋势,但中心城区仍存在碳排放量低的建筑物,而郊区也存在碳排放量高的建筑物;从地块为单元来看,同一地块中建筑物因处于同一小区或在相近时段建成,导致建筑物碳排放量在空间分布上具有一定的连续性,相对差异较小,而相邻地块建筑物碳排放量相对差异性较大,通过量化计算,发现地块之内居民建筑物碳排放平均标准差为7.66 t,而地块之间的平均标准差为50.30 t;② 呈现长尾分布特征,89%居民建筑物的碳排放量低于平均值1.28 t,而11%居民建筑物的碳排放量高于平均值;③ 中心城区（江岸区、江汉区等）的经济活动频繁,地块社会经济因子、地块规划因子,以及建筑物形态因子较高,故大多数居民建筑物具有中等或较高的碳排放量;而郊区（东西湖区、黄陂区等）大部分居民建筑物所处地块人口稀少,导致地块社会经济因子和地块规划因子较低,且建筑物本身形态因子也较低,所以具有较低的碳排放量。
图6 武汉市居民建筑物碳排放空间分布

Fig. 6 Spatial distribution map of carbon emissions from residential buildings in Wuhan

为了更好地探索居民建筑物的碳排放量分布,论文进一步选取了4个典型城市居民建筑物群进行分析：
（1） 光谷广场,位于洪山区,人口众多,是武汉市核心商圈之一。如图7（a）所示,其周围居民建筑物大多具有较高的碳排放量,比如光谷中心花园、华城新都等社区,由于该地区是武汉市交通枢纽,房价普遍较高且年轻人口占比高,使得这些社区具有较高的地块规划因子与社会经济因子。然而,也存在个别碳排放量较低的居民建筑物,比如南望社区,这个社区的居民建筑物具有较低的建筑物因子。
图7 典型城市建筑物群居民建筑物碳排放空间分布

Fig. 7 Spatial distribution of carbon emissions for selected residential buildings

（2） 八铺街社区,位于武昌区,是武汉市的一个老旧社区。如图7（b）所示,由于该社区修建年代已久,房屋老旧,房价偏低,老龄人口占比高,使得该社区社会经济因子较低,所以大多数居民建筑物具有较低的碳排放量,这些居民建筑物一般具有较低的建筑物因子,且建筑结构简单。然而,也存在个别建筑物具有中等程度的碳排放量,主要归因于这个社区具有较高的地块规划因子和较高的建筑物形态因子。
（3）四美苑社区和四十八栋社区,位于武昌区,前者是始建于20世纪初的一个敞开式混合型老社区,后者是始建于20世纪90年代末的一个新社区。如图7（c）所示,四十八栋社区中的大多数居民建筑物具有较低的碳排放量,基底面积较小,且楼层数目不超过3;四美苑社区中的大多数居民建筑物具有较高的碳排放量,基底面积较大,且楼层数目大多为7。这2个社区被一条道路隔开,碳排放量的区域差异性比较显著。
④ 华安里社区和发展社区,位于江汉区,这2个社区都属于城中村敞开型社区。如图7（d）所示,华安里社区中的大多数居民建筑物具有较低的碳排放量,分布密集,具有较小的基底面积,且楼层数目大多数为3;发展社区中的大多数居民建筑物具有较高的碳排放量,分布稀疏,但具有较大的基底面积,且楼层数目较高,最高的可达48层。这2个社区被一条铁路隔开,碳排放量的区域差异性也比较明显。

5 结论与讨论

基于自上而下分配地块碳排放与自下而上反演居民建筑物碳排放的策略,本文提出了一种多源数据融合的单体居民建筑物碳排放量反演计算模型。论文以武汉市为研究区域,结合夜间灯光影像,城市地块数据和居民建筑物数据,采用本方法计算了城市所有单体居民建筑物的碳排放量,分析了其空间分布特征和空间格局。研究结果表明：
（1）居民建筑物碳排放量在空间分布上具有明显的区域差异性,呈现由中心城区向郊区不断递减的模式,和人口分布有着密切的关系。
（2）居民建筑物碳排放量分布具有异质性,呈现出长尾分布的特性,89%居民建筑物的碳排放量低于平均值1.28 t,而只有11%居民建筑物的碳排放量高于平均值。
（3）同一地块上居民建筑物的碳排放量具有相对较小的差异性且平均标准偏差为7.66 t,而不同地块上居民建筑物的碳排放量具有较大的差异性且平均标准偏差高达51.30 t。
（4）居民建筑物的碳排放量更容易受到规划因子中的容积率影响,社会经济因子中的人口密度影响,以及居民建筑物不同形态类型（建筑物基底面积与楼层高度）的影响。
本文为城市单体居民建筑物碳排放量反演计算提供了一种可行的计算方法,研究成果可以对城市碳排放管控、土地规划、资源分配等城市管理决策提供依据。然而,本研究所采用的建筑物形态因子相对简单,不能完全反映建筑物的真实情况,例如建筑物不同材质与结构所带来的碳排放的差异性;另一方面,由于单体居民建筑物能耗数据的不可获得性,本研究采用城市所有居民能耗数据来进行碳排放量的反演计算,其中利用夜间灯光数据进行的地块级能耗分配模型精确度不高,需要进一步的改善。因此,下一步工作将进一步完善建筑物形态因子、社会经济因子及地块规划因子,利用土地利用类型等数据来研究建筑物碳排放的城乡差异,并通过抽样调查,获取单体居民建筑物的实际能耗数据以及居民的消费习惯等间接影响能耗的因素,从而对模型进行训练与优化,提高模型的计算精度与适用性。

References

Publishing order | Descend order by publishing year | Descend order by cited within
[1]
董昕灵, 张月友. 中国碳强度变化因素再分解的理论与实证[J]. 软科学, 2019,33(9):75-80.

[ Dong X L, Zhang Y Y. Theoretical and empirical study on the Re-decomposition of Chinese carbon intensity change factors[J]. Soft Science, 2019,33(9):75-80. ]

[2]
柯罡, 周瑶, 方雨, 等. 武汉某高校校园碳排放核算初探[J]. 绿色科技, 2015(6):220-223.

[ Ke G, Zhou Y, Fang Y, et al. A preliminary study on the carbon emission accounting of a university campus in Wuhan[J]. Journal of Green Science and Technology, 2015(6):220-223. ]

[3]
Jia T, Li Q, Shi W. Estimation and analysis of emissions from on-road vehicles in Mainland China for the period 2011-2015[J]. Atmospheric Environment, 2018,191:500-512.

[4]
武娜, 沈镭, 钟帅. 基于夜间灯光数据的晋陕蒙能源消费碳排放时空格局[J]. 地球信息科学学报, 2019,21(7):1040-1050.

[ Wu N, Shen L, Zhong S. Spatio-temporal pattern of carbon emissions based on nightlight data of Shanxi-Shaanxi-Inner Mongolia region of China[J]. Journal of Geo-information Science, 2019,21(7):1040-1050. ]

[5]
Li Y, Yang J. A new method of energy-related carbon dioxide emissions estimation at the provincial-level: A case study of Shandong Province, China[J]. Science of the Total Environment, 2020,700:134384.

DOI

[6]
张仁杰, 董会忠, 韩沅刚, 等. 能源消费碳排放的影响因素及空间相关性分析[J]. 山东理工大学学报(自然科学版), 2020(1):33-39.

[ Zhang R J, Dong H Z, Han Y G, et al. The spatial correlation analysis of influence factors on carbon emission from the energy consumption[J]. Journal of Shandong University of Technology (Natural Science Edition), 2020(1):33-39. ]

[7]
李德仁, 李熙. 论夜光遥感数据挖掘[J]. 测绘学报, 2015,44(6):591-601.

[ Li D R, Li X. An overview on data mining of Nighttime Light Remote Sensing[J]. Acta Geodaetica et Cartographica Sinica, 2015,44(6):591-601. ]

[8]
Meng L, Graus W, Worrell E, et al. Estimating CO2 (carbon dioxide) emissions at urban scales by DMSP/OLS (Defense Meteorological Satellite Program's Operational Linescan System) nighttime light imagery: Methodological challenges and a case study for China[J]. Energy, 2014,71:468-478.

[9]
Wang H, Liu G, Shi K. What are the driving forces of urban CO2 Emissions in China? A refined scale analysis between national and urban agglomeration levels[J]. International Journal of Environmental Research and Public health, 2019,16(19):3692.

[10]
张春霞, 章蓓蓓, 黄有亮, 等. 建筑物能源碳排放因子选择方法研究[J]. 建筑经济, 2010(10):106-109.

[ Zhang C X, Zhang B B, Huang Y L, et al. Study on the selection method of building energy carbon emission factors[J]. Construction Economy, 2010(10):106-109. ]

[11]
林波荣, 刘念雄, 彭渤, 等. 国际建筑生命周期能耗和CO2排放比较研究[J]. 建筑科学, 2013,29(8):22-27.

[ Lin B R, Liu N X, Peng B, et al. International comparative study on building Life-cycle energy consumption and CO2 emission[J]. Building Science, 2013,29(8):22-27. ]

[12]
宋金昭, 翟佳瑶, 王晓平, 等. 基于系统动力学的城市住宅碳减排潜力研究——以西安市为例[J]. 重庆理工大学学报(自然科学), 2019,33(8):213-221.

[ Song J Z, Zhai J Y, Wang X P, et al. Research on the potential of urban residential building carbon emission reduction based on a dynamic system model: Take Xi'an as an example[J]. Journal of Chongqing University of Technology( Natural Science), 2019,33(8):213-221. ]

[13]
张秀敏, 吴朝晖. 建筑物碳排放核算方法探析[J]. 工业技术经济, 2019,38(10):31-40.

[ Zhang X M, WU C H. Analysis on the accounting method of building carbon emission[J]. Journal of Industrial Technological Economics, 2019,38(10):31-40. ]

[14]
Zhang X C, Zheng R Y. Reducing building embodied emissions in the design phase: A comparative study on structural alternatives[J]. Journal of Cleaner Production, 2020,243:118656.

[15]
Visuvasam J, Chandrasekaran S S. Effect of soil-pile-structure interaction on seismic behaviour of RC building frames[J]. Innovative Infrastructure Solutions, 2019,4(1):45.

[16]
徐国泉, 刘则渊, 姜照华. 中国碳排放的因素分解模型及实证分析:1995-2004[J]. 中国人口·资源与环境, 2006(6):158-161.

[ Xu G Q, Liu Z Y, Jiang Z H. Decomposition model and empirical study of carbon emissions for China:1995-2004[J]. China Population, Resources and Environment, 2006(6):158-161. ]

[17]
Cao C, DeLuccia F, Xiong X, et al. Early on-orbit performance of the Visible Infrared Imaging Radiometer Suite (VIIRS) onboard the Suomi National Polar-orbiting Partnership (S-NPP) satellite[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014,52(2):1142-1156.

[18]
武汉市土地利用和城市空间规划研究中心. 武汉市土地利用数据库[DB]. 2015 -12-10.

[ Wuhan land use and spatial planning research center. Wuhan land use database[DB]. 2015 -12-10. ]

[19]
武汉市统计局, 国家统计局武汉调查队编. 武汉统计年鉴 2015[M]. 北京: 中国统计出版社. 2015.

[ Wuhan Municipal Bureau of statistics, compiled by Wuhan survey team of National Bureau of statistics. Wuhan statistical yearbook 2015[M]. Beijing: China Statistics Press, 2015. ]

[20]
张秋媛, 彭明春, 王崇云, 等. 基于DMSP/OLS夜间灯光数据的贵州省人口分布及影响因子分析[J]. 云南大学学报(自然科学版), 2019,41(5):992-1000.

[ Zhang Q Y, Peng M C, Wang C Y, et al. Population distribution of Guizhou province based on DMSP/OLS night lighting data[J]. Journal of Yunnan University: Natural Sciences Edition, 2019,41(5):992-1000. ]

[21]
Pei J, Niu Z, Wang L, et al. Spatial-temporal dynamics of carbon emissions and carbon sinks in economically developed areas of China: A case study of Guangdong province[J]. Scientific Reports, 2018,8(1):16683.

[22]
Rodriguez A, Laio A. Clustering by fast search and find of density peaks[J]. Science, 2014,344(6191):1492-1496.

Options
Outlines

/

〈 〉