EN中文

Journal of Geo-information Science >

2020 , Vol. 22 >Issue 8: 1642 - 1653

DOI: https://doi.org/10.12082/dqxxkx.2020.190383

A Hyperspectral Image Classification Algorithm based on the Weighted Exponential Function Model

  • LI Yu , 1 ,
  • LI Yiran , 1, * ,
  • WANG Guanghui 2 ,
  • SHI Xue 1
Expand
  • 1. The Institute for Remote Sensing, School of Geomatics, Liaoning Technology University, Fuxin 123000, China
  • 2. Land Satellite Remote Sensing Application Center, Ministry of Natural Resources, Beijing 100048, China
*LI Yiran, E-mail:

Received date: 2019-07-18

  Request revised date: 2019-11-27

  Online published: 2020-10-25

Supported by

National Natural Science Foundation of China(41301479)

Innovative Talents Support Program for Colleges and Universities in Liaoning Province(LR2016061)

Copyright

Copyright reserved © 2020
Fold

Abstract

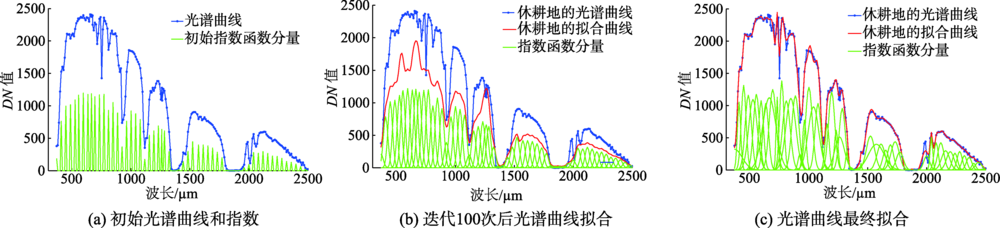
In recent years, the hyperspectral remote sensing technology has developed rapidly. Hyperspectral images obtained by hyperspectral sensors contain abundant spectral information of ground objects, such that they are good for fine spectral recognition. In hyperspectral image processing, its accurate classification is a solid foundation for the subsequent interpretation tasks. However, the numerous bands in hyperspectral imagery not only provide sufficient characteristics information for classification, but also bring the problem of how to use these characteristics effectively. In this paper, to make full use of the spectral information of hyperspectral images so to achieve accurate classification, a hyperspectral image classification method based on the Weighted Exponential Function (WEF) was proposed that considers the multi-peak characteristics of the spectral response curve of pixels. Firstly, the WEF model was used to build an ideal model of the spectral response curve of pixels, composed of several exponential functions with different weights. Because there are many parameters in the model (including weight, peak position and peak width), it is difficult to solve them. Therefore, the WEF model with fixed peak positions and number of exponential functions was used to model the spectral response curve of all pixels. Then, the parameters of the WEF model were determined according to the least square principle to fit the spectral response curve. Finally, the parameter set was used to replace the spectral measure vector, and the WEF model parameter vector of the pixel was used as its feature. Fuzzy C-means (FCM) algorithm was used for image classification. To validate the feasibility and effectiveness of the proposed method, the classification experiments of Salinas and PaviaU hyperspectral images were conducted by using respectively the proposed method, Principal Component Analysis (PCA) based classification method, Minimum Noise Fraction (MNF) based classification method, and FCM method with the spectral measure vector as the classification feature. The user accuracy, product accuracy, overall accuracy and Kappa coefficient of the results from these classification methods were calculated, and the experimental results were evaluated qualitatively and quantitatively. Compared with other methods, the classification accuracy of the proposed classification method for the Salinas image increased from 51% to 60%, and for the PaviaU image from 43% to 51%. In addition, the proposed classification method reduced the amount of hyperspectral image data while preserving the rich spectral information of hyperspectral images.

Key words： hyperspectral image classification; weighted exponential function model; least square method; Fuzzy C-means; spectral curve; curve fitting; principal component analysis; Minimum Noise Fraction

Cite this article

LI Yu , LI Yiran , WANG Guanghui , SHI Xue . A Hyperspectral Image Classification Algorithm based on the Weighted Exponential Function Model[J]. Journal of Geo-information Science, 2020 , 22(8) : 1642 -1653 . DOI: 10.12082/dqxxkx.2020.190383

1 引言

自20世纪80年代以来,因高光谱遥感能够同时提供地物的空间信息和光谱信息,致使其逐渐成为对地观测技术中的研究热点[1,2]。
高光谱遥感图像相比于其它遥感图像具有更高的光谱分辨率[3],因此高光谱图像的每个像素光谱测度对应精细的光谱曲线[4],从而更加有利于反演地物目标的物理、化学以及生物学特征[5]。近年来,高光谱图像在文物修复[6]、生态环境[7]、矿产资源勘查[8]、农林业资源分配[9]、油气勘探[10]、海洋监测[11]、以及军事领域[12]等均有广泛的应用。
高光谱图像分类是高光谱图像处理技术中关键的步骤[13]。高光谱图像可以获得地物更加精细的光谱信息,但其波段数的大幅度增加造成了高光谱图像高维性和信息冗余,这些都给高光谱图像分类带来了难题[14]。目前的高光谱图像分类算法大多以其数据降维为基础,而高光谱数据降维要求最大限度地保留高光谱图像的波段信息[15]。虽然已有很多高光谱数据降维策略,如线性判别分析（Linear Discriminant Analysis, LDA）、主成分分析（Principal Component Analysis, PCA）以及最小噪声分离（Minimum Noise Fraction, MNF）,但这些策略均通过线性变换投影到低维空间上,并只保留区别度较大的数据;局部线性嵌入（Locally Linear Embedding, LLE）是一种非线性变换,但只能保留降维后近邻之间的局部特性不变。上述降维方法均在不同程度上损失部分光谱信息,以至于影响后续的分类精度。因此,本文提出一种利用函数模型拟合光谱曲线的方法,在保留光谱信息的同时达到降维的目的。
目前,高光谱图像分类有2种思路[16]。一种是以所有波段光谱测度为特征的分类。例如,余铭等[17]利用条件随机场精细分类高光谱影像中的各种农作物。该方法利用支持向量机（Support Vector Machine, SVM）分类器计算各类地物的概率,以此定义条件随机场的一元势函数;进一步,将空间平滑项和局部类别标签成本项加入到二元势函数,并作为依据对高光谱图像进行分类。王秀和[18]结合K均值算法和改进蚁群优化算法（Ant Colony Optimization, ACO）实现高光谱图像地物目标分类。该方法首先利用K均值算法获取初步的图像聚类,然后将该结果看成是ACO的启发式信息以便调整信息素的初始状态,也便于蚁群在寻找路径过程中根据一定的概率将像素划分给信息素量最大的类别,最后通过迭代优化过程得到的最佳路径,即最优聚类结果,以此完成高光谱图像分类。因高光谱具有较高的维数,蚁群算法在处理较大规模优化问题时的运算量也随之增加,速率减慢。纪磊等[19]提出了一种空谱加权近邻（Spatial Spectral Weighted Nearest Neighbor, SSWNN）高光谱图像分类算法。该方法首先是通过构造待测样本点的近邻空间,过滤近邻空间中与测试样本标签不一致的空间近邻点,以达到改善图像椒盐现象的目的。再根据空间近邻点和测试像元之间的光谱相似性为空间近邻点赋予不同的权重,以增大同类像元间的相似性和异类像元间的差异性,并通过引入正则化系数,求训练样本和测试样本近邻空间的距离,选择距离最小的训练样本标签作为测试样本的标签,以此对高光谱图像进行分类。上述2种分类方法虽然充分利用以及较好地保留了高光谱图像丰富的空间信息和光谱信息,但由于高光谱图像中光谱信息的大量冗余,导致分类过程的计算过于复杂、效率低下。
有鉴于此,有学者提出了另一种分类方式,即先对高光谱图像进行降维处理,再设计分类算法对降维后的高光谱图像进行分类。例如,臧卓等[20]提出结合主成分分析（Principal Component Analysis, PCA）和BP （Back Propagation）神经网络实现高光谱图像的乔木树种分类。该方法首先利用PCA算法降维高光谱图像,并以BP （Back Propagation） 神经网络为分类器对降维后的高光谱图像进行分类测试。由于基于PCA的降维操作总是剔除贡献率相对较小的主成分,以达到降维的目的,这样不但损失了高光谱图像中所包含的部分信息,另一方面有些贡献率较小的主成分往往含有区分地物目标的重要信息。张磊等[21]提出结合改进最佳指数因子（Optimum Index Factor, OIF）和SVM的高光谱图像分类方法。该方法利用稳定系数和相关系数选择波段,再利用OIF得到最佳波段组合,并合成降维图像,然后利用SVM实现降维图像的分类。在最优波段组合过程中,OIF算法既要满足选取的波段间标准差最大,又要满足选取的波段间相关系数最小,对于高光谱数据而言这种计算量较大,此外OIF算法极易造成信息损失,如图像共包含242个波段最终仅选取了8个波段进行实验。张悦等[22]提出一种K-means聚类与ABS相结合的高光谱图像降维方法。该方法首先利用基于相关系数和欧氏距离2种相似性度的K-means算法对所有波段进行聚类,选取各聚类中利用自适应波段选择法（Adaptive Band Selection, ABS）计算出的指数最大波段,作为最优波段子集,最后使用SVM对得到的最优波段集合进行图像分类。利用ABS进行波段选择的方法、具有算法简单、操作方便等特点,有效缩短OIF算法的运行时间,降低了计算的复杂度。但同样地,该算法在包含185个波段的图像中仅选择了18个波段进行分类实验,损失了大部分光谱信息。虽然上述几种分类方式在一定程度上可以有效剔除图像中包含的冗余信息,减少了工作量,提升了分类算法的效率,但也损失了原数据中的大量信息。因此,本文利用函数模型对光谱曲线进行拟合,充分利用了图像中所有的光谱信息,最大程度地保存了图像光谱信息,并通过将光谱测度矢量转化为参数矢量达到降维的目的。
为了在充分利用高光谱图像丰富光谱信息的同时,又提升分类算法的工作效率,并实现高精度高光谱图像分类,本文提出一种基于加权指数函数（Weighted Exponential Function, WEF）模型拟合光谱曲线的高光谱图像分类方法。利用函数模型的降维不同于之前降维方法中尽量去除冗余信息的思路,而是将像素光谱曲线表达为函数,以期尽可能地利用所有波段光谱信息的相互关联性,并用函数参数的形式刻画像素特征。首先,根据高光谱图像中像素的光谱曲线呈现出的多高斯峰特点,采用WEF模型建立其理想光谱曲线模型。由于模型中参数较多（包括权重、峰值位置和峰宽）,导致求解参数较为困难。因此,为了更快地拟合光谱曲线,对所有像素光谱曲线理想模型中峰值位置采用同样的组合,并选取相同的指数函数个数。然后,根据最小二乘原理,调整加权指数函数模型中各个指数函数分量的权重和峰宽,得到理想光谱曲线模型的最优参数解集（包括权重和峰宽）,以实现对光谱曲线的拟合。最后,以像素理想光谱曲线模型的参数为特征,采用FCM（Fuzzy C-Means）算法[23]实现降维高光谱图像的分类。

2 模型与算法

2.1 理想光谱曲线模型

为了实现高光谱影像分类,首先建立其理想光谱曲线模型。给定高光谱图像,y = { yi ; i = 1, 2, …, n },式中,i为像素索引;n为总像素数;yi = { yij ; j = 1, 2, …, m } 为像素i的光谱测度集合,j为波段索引,m为总波段数,yij为像素i波段j的光谱反射强度。设x = { xj ; j = 1, 2, …, m }为高光谱影像中各波段中心波长集合,其中xj为波段j的中心波长。由于高光谱图像具有极高的光谱分辨率,每个像素的光谱测度yij随xj变化可近似看作该像素对应地物光谱曲线的高密度采样（在不致混淆情况下,后文统称为光谱曲线）,反映该像素对应地物区域的光谱反射或吸收特征[24]。
图1为Salinas高光谱图像中选取芹菜和生长期为六星期的莴苣对应像素的光谱曲线。其中,红色曲线和绿色曲线为同一类地物（芹菜）中的2个像素的光谱曲线,蓝色曲线为六星期莴苣的某1像素的光谱曲线。由图1所示光谱曲线可以看出,不同类型的植被对不同波长辐射能量的反射或吸收能力不同。虽然它们对应的光谱曲线均呈现多峰特性,但不同地物像素的光谱曲线无论在峰值大小还是在峰值位置上均存在很大的差异性,由此可根据各类地物像素光谱曲线的特点对其进行分类。
图1 高光谱图像像素光谱曲线

Fig. 1 Pixel spectral curves of hyperspectral imagery

为了充分利用像素光谱曲线实现地物目标的分类,需首先建立光谱曲线的理想模型。根据像素光谱曲线呈现的多峰特性,采用WEF建立其理想模型,即yij的理想值 y ˆ ij 定义为L个e指数函数的加权和,计算公式如下：
y ˆ ij = ∑ l = 1 L γ il exp - x j - α il 2 β il 2
式中：l为指数函数的索引;L为指数函数的个数;γil、αil和β2il分别为像素i中第l个指数函数所对应的权重、峰值位置及峰宽。
根据式（1）可知,其模型参数包括,θ = { θi ; i = 1, 2, …, n },其中θi = {{ γil, αil, β2il }; l = 1, 2, …, L}。对给定高光谱影像y,为了求解其理想模型的模型参数,根据最小二乘原理,使所有像素光谱测度值yij与其理想值 y ˆ ij 之间的误差平方和Qi之和 Q = ∑ i = 1 n Q i 达到最小,即：
θ ˆ = arg min θ Q = arg min θ ∑ i = 1 n ∑ j = 1 m y ˆ ij - y ij 2 = arg min θ ∑ i = 1 n ∑ j = 1 m ∑ l = 1 L γ il exp - x j - α il 2 β il 2 - y ij 2
由于模型参数较多,为了提高算法效率,对模型中的参数进行简化处理。由于参数γ、α和β2分别对应理想模型中的权重、峰值位置和宽度,函数形态变化可以通过调整这些参数而实现。图2所示为固定2个参数的情况下,函数形态随另一参数变化的示例。
图2 不同的峰值位置、权重和峰宽的指数函数曲线

Fig. 2 Exponential function curves with different peak positions, weights, and widths

由图2可知,在峰值位置α和权重γ不变的条件下,指数函数的宽度将随β2的不同有着明显变化,如图2中蓝色和红色曲线;当峰值位置α和峰宽β2固定时,指数函数的峰值高度随权重γ变化而改变,如图2中红色和绿色曲线;当权重γ和峰宽β2不变时,指数函数的位置将随峰值位置α变化,在横轴方向平移,如图2中蓝色和青绿色曲线。据此可以看出即使固定某些模型参数,也可得到可变的函数曲线,达到模拟不同理想模型的目的。由于光谱曲线反映地物目标光谱反射强度随电磁波波长的变化规律,即表现为波长和强度变化。从图2的分析可看出,只要简单地改变理想模型中γ和β2即可拟合实际的光谱曲线。因此,本文采用设定固定α、可变γ和β2的方式,构建式（1）的理想模型。
对给定高光谱图像,其波段中心波长集合为x = { xj ; j = 1, 2, …, m },在波段中心长度向量x中以等间隔步长ϕ选取L = ⌊ m / ϕ 」个波段中心作为峰值位置,其中 ⌊」 为取整操作。这些波段中心组合峰值位置集记为α = { αl , l = 1, 2,…, L },其中,
α l = x 1 + φ ( l - 1 )
式中：x为高光谱影像中各波段中心波长集合;ϕ为间隔步长;l为指数函数的索引。步长ϕ选取的越小,指数函数个数就越多,拟合的效果就越好,但耗费的时间就越多。由于所有像素的峰值位置集均相同,因此式（1）的光谱曲线理想模型变为：
y ˆ ij = ∑ l = 1 L γ il exp - x j - α l 2 β il 2
由式（4）可知,在光谱曲线的拟合过程中,由于各个像素的α相同,只需通过调整权重γil和峰宽β2il即可得到最优拟合的理想像素光谱曲线。
为了验证固定α时改变γ和β2的拟合方式的可行性,任意设置20个y值生成一条任意曲线,如图3中黑色曲线所示。将峰值位置α的选取步长间隔ϕ设置为4,任意初始峰宽β2和权重γ,得到拟合曲线的初始指数函数分量,如图3（a）中蓝色曲线所示,初始的曲线拟合结果示意图,如图3（a）中红色曲线所示;利用最小二乘原理,在区间（-1,1）中生成随机数调整峰宽和权重,在迭代200次后得到曲线的拟合结果,如图3（b）中的红色曲线所示;当随机给出的曲线和拟合曲线的误差平方和Q达到最小时,则迭代停止,得到最终拟合结果图,如图3（c）中的红色曲线所示。根据最终得到的拟合结果可以得出,通过固定峰值位置α,只调整峰宽和权重可以很好地得到任意曲线的拟合结果。
图3 任意曲线拟合结果

Fig. 3 Arbitrary curve fitting results

2.2 FCM分类算法

根据理想光谱曲线模型的数值拟合结果,可知由参数峰值位置、峰宽和权重组成的WEF模型可以很好地反映出原始光谱曲线的形态。由此,可将高光谱图像中每一像素的高维光谱测度矢量转化成低维的WEF模型参数集。在式（4）中,由于对所有像素设置了相同的峰值位置,因此该参数对确定像素的类属性不起作用。从分类的角度,将光谱测度矢量转化为WEF模型中的权重和峰宽参数即可。这2个参数既保留了波段信息也在更大程度上实现了高光谱图像的降维。对任意像素i ∈ { 1, 2, …, n },其低维参数集记为zi = { γi, β2i } = { zil' ; l' = 1, 2, …, 2L },其中,γi = { γil ; l = 1, 2, …, L },β2i = { β2il ; l = 1, 2, …, L }。
采用模糊C均值 （Fuzzy C-means, FCM） 算法利用降维数据z = { zi ; i = 1, 2, …, n } 对高光谱图像分类。则FCM目标函数为,
J = ∑ i = 1 n ∑ k = 1 K u ik q d ik
式中：q为模糊因子;k为类别索引;K表示类别数;uik为像素i隶属于第k类的隶属度,并满足式（6）所示的约束条件;dik为像素i与第k类的非相似度。设pk = { pkl' ; l' = 1, 2, …, 2L }是第k个类别的聚类中心,dik定义为zi和pk的欧式距离,如式（7）所示。
∑ k = 1 K u ik = 1                 ( i = 1,2 , … , n )
d ik = p k - z i 2 = ∑ l = 1 2 L ( p k l ' - z i l ' ) 2
为了获得最优分类解,需求式（5）中目标函数J的最小值,即对变量uik和pk求偏导,并解出偏导数为0时的uik和pk。由于uik需满足式（6）的约束条件,为了求其约束解,需目标函数中引入拉格朗日乘子λ,构建拉格朗日方程,如式（8）所示。
G = ∑ i = 1 n ∑ k = 1 K u ik q d ik + ∑ i = 1 n λ i ∑ k = 1 K u ik - 1
令G对uik求偏导为0,最终求得隶属度uik为：
u ik = ∑ k ' = 1 K d ik ' 2 q - 1 d ik 2 q - 1
将式（5）对聚类中心pk求偏导,并令其为0,可得：
p k = ∑ i = 1 n u ik q z i ∑ i = 1 n u ik q

3 实验与分析

3.1 实验数据集

为了验证本文算法的可行性和有效性,在Intel（R） Xeon（R） CPU E5-4650 @2.20GHz,内存为80GB,64位操作系统的PC机上,使用MATLAB R2018b对高光谱图像进行分类实验,实验采用如下2组数据。
（1）由航空可见近红外成像光谱仪（Airborne Visible Infrared Imaging Spectrometer, AVIRIS）获取的覆盖美国加利福尼亚州的萨利纳斯谷的高光谱图像Salinas。该影像尺度为512像素×217像素,空间分辨率为3.7 m,光谱分辨率为10 nm,波长范围为0.4~2.5 µm,共224个波段,去除水汽吸收带和低信噪比的20个波段,即108~112、154~167和224波段,用余下的204个波段用于分类实验。
为显示该图像,利用波段50、34、21分别做为红、绿、蓝3个波段形成假彩色图像,如图4（a）所示。Salinas图像所对应的标准分类图中仅将部分区域进行了类别属性的标注,即对Salinas图像中111 104个像素中的54 129个像素标记为16类地物,而其余像素在标准分类结果图中均标记为‘背景’,并显示为黑色,如图4（b）所示。
图4 Salinas和PaviaU高光谱图像及其地物标记模板

Fig. 4 Hyperspectral images of Salinas and PaviaU with template

（2）由反射光学成像光谱仪（Reflective Optics System Imaging Spectrometer, ROSIS）传感器在意大利北部帕维亚上空飞行时拍摄到的帕维亚大学的高光谱影像PaviaU。该影像尺度为610像素×340像素,空间分辨率是1.3 m,波长范围0.43~8.6 μm,含有9类地物,共包含115个波段,去除吸水严重的12个波段,用余下的103个波段用于分类实验。
为显示该图像,利用波段50、34、21分别做为红、绿、蓝3个波段形成假彩色图像,如图4（c）所示。PaviaU图像所对应的标准分类图中仅将部分区域进行了类别属性的标注,即对PaviaU图像中207 400个像素中的42 776个像素标记为9类地物,而其余像素在标准分类结果图中均标记为“背景”,并显示为黑色,如图4（d）所示。

3.2 实验分析

首先,选取间隔步长ϕ,以确定峰值位置集。为了尽可能地降低高光谱图像的维数,应选取较大的间隔步长ϕ,意味着仅需较少的指数函数;另外,为保证理想模型对光谱曲线的拟合精度,应选取较小的间隔步长ϕ,意味着需要较多的指数函数。以高光谱图像Salinas为例,为了平衡降维维度和拟合精度,实验研究了间隔步长ϕ与时间和拟合精度的关系。如图5（a）所示为间隔步长ϕ与时间的关系曲线,由此可知二者成指数关系增长。图5（b）为间隔步长ϕ与拟合精度的关系曲线,由此可知随着间隔步长ϕ的增长,拟合精度随之降低。在保证精度尽可能高,运行时间尽可能短,维数尽可能低的要求,本实验选取的间隔步长ϕ为4。
图5 选取步长与时间和拟合精度的关系

Fig. 5 Relationships between step size, time, and fitting accuracy

对所提出的算法中各部分的时间复杂度进行分析,首先利用最小二乘法对每一个像素进行拟合的时间复杂度为O（L3）;其次,整幅图像拟合的时间随着像素数量的不断增加而增加,复杂度成线性函数为O（n）;最后,在分类中利用的FCM算法的时间复杂度为O（n3log2n）。综上,提出算法的整体时间复杂度为多项式时间,因此从算法时间上说提出算法具有实用性。在实际使用中,通过设计优化的程序,即可提高算法效率。
确定了峰值位置的间隔步长ϕ为4,即是在得到拟合模型的峰值位置矢量α = { αl ; l = 1 ,2, …, L }的同时确定了指数函数的个数L为51。在休耕地中随机选择一个像素在设置好峰值位置后,设置峰宽和权重的初始值,得到拟合光谱曲线的初始形态,如 图6（a）;在随后的迭代过程中在区间（-1,1）中生成随机数调整权重γil和峰宽β2il,如图6（b）所示为迭代100次后的拟合情况;最后在原始光谱曲线与拟合曲线的误差平方和Q达到最小时,则迭代停止,继而得到这一个像素的最终拟合结果,如图6（c）所示。
图6 像素的光谱曲线拟合结果

Fig. 6 Pixel spectral curve fitting results

同理,通过固定峰值位置,调整权重γil和峰宽β2il得到了Salinas高光谱图像中所有像素的光谱曲线拟合后的曲线,其中Salinas高光谱图像包含16类地物,在每一类地物中任意选取其中一个像素显示光谱曲线的拟合结果,如图7（a）—图7（p）。为了表明拟合结果能够反映像素的原始光谱曲线,利用光谱角对拟合后的曲线进行精度评定,光谱角越小,说明原始曲线与拟合曲线相似度越大,如表1所示。
图7 Salinas高光谱图像16类地物光谱曲线拟合

Fig. 7 Fitting charts of spectral curves of 16 ground objects in Salinas hyperspectral images

表1 Salinas各类别光谱曲线拟合精度评价

Tab. 1 Evaluation of spectral curve fitting accuracy of Salinas by local matter category

地物 C1 C2 C3 C4 C5 C6 C7 C8 C9 C10 C11 C12 C13 C14 C15 C16
光谱角/° 1.01 1.00 2.64 1.03 1.00 -1.00 1.01 -1.23 1.50 -1.43 1.17 1.80 1.05 1.05 1.01 1.56

3.3 实验结果讨论

（1） Salinas高光谱图像中包括16类地物信息,即椰菜杂草1、椰菜杂草2、休耕地、粗糙的休耕地、光滑的休耕地、残株、芹菜、未结果的葡萄、正在开发的葡萄园土地、枯萎期玉米、四星期莴苣、五星期莴苣、六星期莴苣、七星期莴苣、未结果的葡萄园、葡萄园架。分别以提出的分类方法、基于主成分分析的分类方法、基于最小噪声分离的分类方法和以光谱测度矢量为分类特征的FCM方法进行对比,将FCM算法中的模糊度q设置为2,得出的Salinas高光谱图像分类结果如图8所示,其中,图8（a）为Salinas高光谱未降维的原始图像利用FCM算法得到的分类结果图,图8（b）为Salinas高光谱原始图像利用PCA算法降维后再根据FCM算法得到的分类结果图,图8（c）为Salinas高光谱原始图像利用MNF算法降维后再根据FCM算法得到的分类结果图,图8（d）为Salinas高光谱原始图像利用本文算法降维后再根据FCM算法得到的分类结果图。
图8 Salinas高光谱图像分类结果

Fig. 8 Classification results of the Salinas hyperspectral image

为了定量描述Salinas高光谱图像的分类结果,通过FCM分类算法对本文降维方法分类结果和未降维的分类结果、利用PCA降维算法的分类结果以及利用MNF降维算法的分类结果分别生成混淆矩阵,并且根据混淆矩阵计算用户精度、产品精度、总体精度和Kappa系数。表2是高光谱图像Salinas利用FCM分类算法对本文降维方法分类结果和未降维的分类结果、利用PCA降维算法的分类结果以及利用MNF降维算法的分类结果的用户精度、产品精度、总体精度、Kappa系数和运行时间。其中,用户精度表示正确分到该类的像素占被分到该类的所有像素的比例;产品精度表示正确分到该类的像素占应该分到该类的像素的比例;总精度表示正确分类的所有像素占总像素的比例;Kappa值表示算法分类较随机分类减少错误的比例。
表2 Salinas的用户精度、产品精度、总体精度、Kappa系数和运行时间

Tab. 2 User accuracy, product accuracy, overall accuracy, Kappa coefficient, and elapsed time of Salinas

分类图像 精度/% C1 C2 C3 C4 C5 C6 C7 C8 C9 C10 C11 C12 C13 C14 C15 C16
未降维 用户精度 48.50 99.65 40.01 94.66 90.49 100 91.08 68.85 59.00 0 16.26 5.90 43.29 90.86 49.15 0.11
产品精度 99.75 38.30 69.03 99.21 90.96 94.47 58.20 43.89 61.45 0 4.96 11.00 99.02 88.22 38.22 0.39
总体精度=51.91% Kappa值=0.4755 运行时间：21min
PCA降维 用户精度 48.50 99.65 40.01 94.66 90.46 100 91.08 68.87 58.81 0 16.26 5.71 43.29 90.86 49.14 0.11
产品精度 99.75 38.30 69.18 99.21 91.00 94.47 58.20 43.88 60.84 0 4.96 10.74 99.02 88.22 38.19 0.39
总体精度=51.83% Kappa值=0.4747 运行时间：17min
MNF降维 用户精度 58.73 99.28 0 93.39 87.27 100 89.89 61.85 67.33 2.38 17.07 47.39 40.25 68.75 61.91 18.54
产品精度 99.65 59.37 0 99.35 84.47 92.12 98.10 30.85 51.10 3.69 83.90 95.23 98.47 86.36 37.52 41.06
总体精度=55.08% Kappa值=0.5146 运行时间：18min
本文算法 用户精度 59.88 98.98 41.58 94.46 94.06 100 90.41 69.05 77.74 11.56 37.71 39.61 43.25 62.49 49.22 0.13
产品精度 99.40 60.06 60.88 99.07 83.35 94.14 97.15 40.11 88.59 0.70 74.25 38.76 99.02 86.26 41.48 0.50
总体精度=60.39% Kappa值=0.5682 运行时间：15min
根据图8,从视觉上可以得出,本文算法的分类结果优于基于PCA的分类方法和以光谱测度矢量为分类特征的FCM方法。从表2的定量分析结果可以看出,在少数区域这2个对比算法的产品和用户精度接近于本文算法,如C3休耕地、C4粗糙的休耕地、C6残株、C15未结果的葡萄园。但在大多数区域确远远低于本文算法,如在C2椰菜杂草2区域的产品精度从2个对比算法的38.3%左右提高到了本文算法的60.06%;C7芹菜区域的产品精度从2个对比算法的58.2%左右提高到了本文算法的97.15%、C9正在开发的葡萄园土地区域的产品精度从2个对比算法的61%左右提高到了88.59%、C11四星期莴苣区域的产品精度从2个对比算法的5%左右提高到了74.25%、C12五星期莴苣区域的产品精度从2个对比算法的11%左右提高到了38.76%。与基于最小噪声分离的分类方法相比,本文算法的分类精度,在C3休耕地区域的产品精度从0%提高到了60.88%、C9正在开发的葡萄园土地区域的产品精度从51.10%提高到了88.59%。即提出算法在分类结果上都有了明显的改进。
由表2可知,本文算法将总体分类精度从对比算法的最高值（MNF降维算法）55.08%提高到了60%,Kappa值从0.5146提高到了0.5682,运行时间缩短了3 min左右。因此,对于有较高维数的图像可以利用本文算法进行降维处理后再进行分类,既可以保留图像所有的光谱信息,又可以提高图像的分类精度。
（2）PaviaU高光谱图像包括9类地物信息,即柏油、草地、碎石、树、被喷漆的金属板材、裸地、沥青、有阻挡效应的砖、阴影。分别以提出的分类方法、基于主成分分析的分类方法、基于最小噪声分离的分类方法和以光谱测度矢量为分类特征的FCM方法进行对比。将FCM算法中的模糊度q设置为2,得出的PaviaU高光谱图像分类结果如图9所示,其中图9（a）为PaviaU高光谱未降维的原始图像利用FCM算法得到的分类结果图,图9（b）为PaviaU高光谱原始图像利用PCA算法降维后再根据FCM算法得到的分类结果图,图9（c）为PaviaU高光谱原始图像利用MNF算法降维后再根据FCM算法得到的分类结果图,图9（d）为PaviaU高光谱原始图像利用本文算法降维后再根据FCM算法得到的分类结果图。
图9 PaviaU高光谱图像分类结果

Fig. 9 Classification results of the PaviaU hyperspectral image

为了定量描述PaviaU高光谱图像的分类结果,通过FCM分类算法对本文降维方法分类结果和未降维的分类结果、利用PCA降维算法的分类结果以及利用MNF降维算法的分类结果分别生成混淆矩阵,并且根据混淆矩阵计算用户精度、产品精度、总体精度和Kappa系数。表3是高光谱图像PaviaU利用FCM分类算法对本文降维方法分类结果和未降维的分类结果、利用PCA降维算法的分类结果以及利用MNF降维算法的分类结果的用户精度、产品精度、总体精度、Kappa系数和运行时间。
表3 PaviaU的用户精度、产品精度、总体精度、Kappa系数和运行时间

Tab. 3 User accuracy,product accuracy,overall accuracy, Kappa coefficient, and elapsed time of PaviaU

分类图像 精度/% B1 B2 B3 B4 B5 B6 B7 B8 B9
未降维 用户精度 79.73 87.26 0.07 44.94 25.15 20.70 0 34.62 29.97
产品精度 83.26 28.75 0.04 90.70 99.48 24.70 0 42.02 99.05
总体精度=43.78% Kappa值=0.3515 运行时间：23 min
PCA降维 用户精度 79.65 87.81 0.06 45.06 25.36 21.95 0 35.45 29.88
产品精度 83.40 28.62 0.04 90.73 99.48 26.23 0 42.53 99.05
总体精度=43.97% Kappa值=0.3542 运行时间：19 min
MNF降维 用户精度 84.23 76.79 21.29 41.42 6.45 28.00 0 44.69 99.27
产品精度 73.52 40.93 41.07 38.35 16.88 37.28 0 81.88 100
总体精度=48.18% Kappa值=0.3769 运行时间：19 min
本文算法 用户精度 79.12 78.50 9.60 48.14 89.69 29.48 0 47.73 98.64
产品精度 84.42 38.52 7.96 70.82 75.02 37.78 0 86.39 99.89
总体精度=51.79% Kappa值=0.4229 运行时间：16 min
根据图9,从视觉上可以得出,本文算法的分类结果优于基于PCA的分类方法和以光谱测度矢量为分类特征的FCM方法。从表3的定量分析结果可以看出,在少数区域这2个对比算法的产品和用户精度接近于本文算法,如B1柏油。但在大多数区域确远远低于本文算法,如在B2草地区域的产品精度从 2个对比算法的28%左右提高到了本文算法的38.52%;B6裸地区域的产品精度从2个对比算法的25%左右提高到了本文算法的37.78%、B8有阻挡效应的砖区域的产品精度从2个对比算法的42%左右提高到了86.39%。与基于最小噪声分离的分类方法相比,本文算法的分类精度,在B4树区域的产品精度从38.35%提高到了70.82%、B5被喷漆的金属板材区域的产品精度从16.88%提高到了75.02%。即提出的算法在分类结果上都有了明显的改进。
由表3可知,本文算法将总体分类精度上从对比算法的最高值（MNF降维算法）48.18%提高到了51.79%,Kappa值从0.3769提高到了0.4229,运行时间缩短了3 min左右。因此,对于有较高维数的图像可以利用本文算法进行降维处理后再进行分类,既可以保留图像所有的光谱信息,又可以提高图像的分类精度。

4 结论

由于高光谱图像光谱信息较为丰富,但在实际图像处理工作中带来了较大困难。因此,本文提出了一种利用WEF模型拟合光谱曲线的高光谱图像分类方法。通过对提出算法的深入研究和广泛实验表明：
（1）最大限度地保留了高光谱影像中的光谱信息。根据光谱曲线所呈现的多高斯峰的特点,利用加权指数函数模型拟合曲线,将高光谱数据原有的光谱测度矢量转化成为带有权重和峰宽的参数矢量。拟合光谱曲线和原始光谱曲线的光谱角在±1°左右,说明拟合光谱曲线能够很好的表达原始光谱曲线的形态。即该方法能够很好地描述光谱信息,在利用所有波段信息的同时,又实现了图像的降维。
（2）与传统的和接近的算法相比,本文算法的分类精度均有所提高,如在Salinas中,未降维的总体分类精度为51.91%;利用PCA降维后的总体分类精度为51.83%;利用MNF降维后的总体分类精度为55.08%,而本文算法的总体分类精度为60.39%,比对比算法的最高值提高了5%左右。在PaviaU中,本文算法也比对比算法的最高值提高了3%左右。
高光谱图像中一些地物的光谱曲线的相似性比较大,如何更好地将各类的光谱曲线进行差异性的区分,使利用模型进行降维后的数据能进行更准确的分类,本文在拟合过程中对峰值位置进行了固定,而峰值位置的差异也是图像分类的一个特征;拟合的函数采用的是指数函数,是否其他的函数也可以更好地达到拟合的精度;是否可以开发出一种新的分类方法更加适用于降维后的图像,都将是今后主要研究的问题。

References

Publishing order | Descend order by publishing year | Descend order by cited within
[1]
张号逵, 李映, 姜晔楠. 深度学习在高光谱图像分类领域的研究现状与展望[J]. 自动化学报, 2018,44(6):961-977.

[ Zhang H K, Li Y, Jiang Y A. Deep learning for hyperspectral imagery classification: The state of the art and prospects[J]. Acta Automatica Sinica, 2018,44(6):961-977. ]

[2]
程希萌, 沈占锋, 邢廷炎, 等. 基mRMR特征优选算法的多光谱遥感影像分类效率精度分析[J]. 地球信息科学学报, 2016,18(6):815-823.

DOI

[ Cheng X M, Shen Z F, Xing T Y, et al. Efficiency and accuracy analysis of multispectral image classification based on mRMR feature selection method[J]. Journal of Geo-information Science, 2016,18(6):815-823. ]

[3]
童庆禧, 张兵, 张立福. 中国高光谱遥感的前沿进展[J]. 遥感学报, 2016,20(5):689-707.

[ Tong Q X, Zhang B, Zhang L F. Current progress of hyperspectral remote sensing in China[J]. Journal of Remote Sensing, 2016,20(5):689-707. ]

[4]
蔡悦, 苏红军, 李茜楠. 萤火虫算法优化的高光谱遥感影像极限学习机分类方法[J]. 地球信息科学学报, 2015,17(8):986-994.

DOI

[ Cai Y, Su H J, Li Q N. An extreme learning machine optimized by firefly algorithm for hyperspectral image classification[J]. Journal of Geo-information Science, 2015,17(8):986-994. ]

[5]
陈宏达, 普晗晔, 王斌, 等. 基于图像欧氏距离的高光谱图像流形降维算法[J]. 红外与毫米波学报, 2013,32(5):450-455.

DOI

[ Chen H D, Pu H Y, Wang B, et al. Image euclidean distance-based manifold dimensionality reduction algorithm for hyperspectral imagery[J]. Journal of Infrared and Millimeter Waves, 2013,32(5):450-455. ]

[6]
郭新蕾, 张立福, 吴太夏, 等. 成像光谱技术的古画隐藏信息提取[J]. 中国图象图形学报, 2017,22(10):1428-1435.

[ Guo X L, Zhang L F, Wu T X, et al. Hidden information extraction from the ancient painting using hyperspectral imaging technology[J]. Journal of Image and Graphics, 2017,22(10):1428-1435. ]

[7]
赵少华, 张峰, 王桥, 等. 高光谱遥感技术在国家环保领域中的应用[J]. 光谱学与光谱分析, 2013,33(12):3343-3348.

[ Zhao S H, Zhang F, Wang Q, et al. Application of hyperspectral remote sensing technology in environmental protection[J]. Spectroscopy and Spectral Analysis, 2013,33(12):3343-3348. ]

[8]
王晋年, 李志忠, 张立福, 等. “光谱地壳”计划——探索新一代矿产勘查技术[J]. 地球信息科学学报, 2012,14(3):344-351.

DOI

[ Wang J N, Li Z Z, Zhang L F, et al. "Spectral crust" project: Research on new mineral exploration technology[J]. Journal of Geo-information Science, 2012,14(3):344-351. ]

[9]
虞佳维, 程志庆, 张劲松, 等. 高光谱信息的农林植被种类区分[J]. 光谱学与光谱分析, 2018,38(12):3890-3896.

[ Yu J W, Cheng Z Q, Zhang J S, et al. An approach to distinguishing between species of trees and crops based on hyperspectral information[J]. Spectroscopy and Spectral Analysis, 2018,38(12):3890-3896. ]

[10]
汪大明, 肖晨超, 李志忠, 等. 高光谱遥感油气探测技术[J]. 地球科学(中国地质大学学报), 2015,40(8):1301-1309.

[ Wang D M, Xiao C C, Li Z Z, et al. Hyperspectral remote sensing technology in oil and gas exploration[J]. Earth Science (Journal of China University of Geosciences), 2015,40(8):1301-1309. ]

[11]
任广波, 过杰, 马毅, 等. 海面溢油无人机高光谱遥感检测与厚度估算方法[J]. 海洋学报, 2019,41(5):146-158.

[ Ren G B, Guo J, Ma Y, et al. Oil spill detection and slick thickness measurement via UAV hyperspectral imaging[J]. Acta Oceanologica Sinica, 2019,41(5):146-158. ]

[12]
罗素群, 郭宝峰, 沈宏海, 等. 一种定标缺失情况下的高光谱目标识别方法[J]. 火力与指挥控制, 2017,42(6):22-27.

[ Luo S Q, Guo B F, Shen H H, et al. A hyperspectral target recognition method without calibration information[J]. Fire Control and Command Control, 2017,42(6):22-27. ]

[13]
李竺强, 朱瑞飞, 高放, 等. 三维卷积神经网络模型联合条件随机场优化的高光谱遥感影像分类[J]. 光学学报, 2018,38(8):404-413.

[ Li Z Q, Zhu R F, Gao F, et al. Hyperspectral remote sensing image classification based on three dimensional convolution neural network combined with conditional random field optimization[J]. Acta Optica Sinica, 2018,38(8):404-413. ]

[14]
李雪轲, 王晋年, 张立福, 等. 面向对象的航空高光谱图像混合分类方法[J]. 地球信息科学学报, 2014,16(6):941-948.

DOI

[ Li X K, Wang J N, Zhang L F, et al. A hybrid of object-based and pixel-based classification method with airborne hyperspectral Imagery[J]. Journal of Geo-information Science, 2014,16(6):941-948. ]

[15]
黄鸿, 郑新磊. 高光谱影像空-谱协同嵌入的地物分类算法[J]. 测绘学报, 2016,45(8):964-972.

[ Huang H, Zheng X L. Hyperspectral image land cover classification algorithm based on spatial-spectral coordination embedding[J]. Acta Geodaetica et Cartographica Sinica, 2016,45(8):964-972. ]

[16]
杜培军, 夏俊士, 薛朝辉, 等. 高光谱遥感影像分类研究进展[J]. 遥感学报, 2016,20(2):236-256.

[ Du P J, Xia J S, Xue Z H, et al. Review of hyperspectral remote sensing image classification[J]. Journal of Remote Sensing, 2016,20(2):236-256. ]

[17]
余铭, 魏立飞, 尹峰, 等. 基于条件随机场的高光谱遥感影像农作物精细分类[J]. 中国农业信息, 2018,30(3):1-9.

[ Yu M, Wei L F, Yin F, et al. Hyperspectral remote sensing image crop fine classification based on conditional random field[J]. China Agriculture Information, 2018,30(3):1-9. ]

[18]
王秀和. 利用K均值算法改进后的蚁群优化算法对高光谱图像聚类研究[J]. 科技通报, 2015,31(3):202-206.

[ Wang X H. Ant colony optimization algorithm for hyperspectral image clustering based on k-means algorithm improved[J]. Bulletin of Science and Technology, 2015,31(3):202-206. ]

[19]
纪磊, 张欣, 张丽梅. 基于空谱加权近邻的高光谱图像分类方法[J]. 激光与光电子学进展, 2020,57(6):061013.

[ Ji L, Zhang X, Zhang L M. Hyperspectral image classification method based on space spectral weighted nearest neighbor[J]. Laser & Optoelectronics Progress, 2020,57(6):061013. ]

[20]
臧卓, 林辉, 杨敏华. 利用PCA算法进行乔木树种高光谱数据降维与分类[J]. 测绘科学, 2014,39(2):146-149.

[ Zang Z, Lin H, Yang M H. Dimensional reduction and classification of hyperspectral data for tree species using PCA algorithm[J]. Science of Surveying and Mapping, 2014,39(2):146-149. ]

[21]
张磊, 邵振峰. 改进的OIF和SVM结合的高光谱遥感影像分类[J]. 测绘科学, 2014,39(11):114-117,66.

[ Zhang L, Shao Z F. Hyperspectral remote sensing image classification based on improved OIF and SVM algorithm[J]. Science of Surveying and Mapping, 2014,39(11):114-117,66. ]

[22]
张悦, 官云兰. 聚类与自适应波段选择结合的高光谱图像降维[J]. 遥感信息, 2018,33(2):66-70.

[ Zhang Y, Guan Y L. Hyperspectral band reduction by combining clustering with adaptive band selection[J]. Remote Sensing Information, 2018,33(2):66-70. ]

[23]
Bezdek J C, Robert E, William F. FCM: The Fuzzy C-Means Clustering Algorithm[J]. Computers & Geosciences, 1984,10(2-3):191-203.

[24]
张莹彤, 肖青, 闻建光, 等. 地物波谱数据库建设进展及应用现状[J]. 遥感学报, 2017,21(1):12-26.

[ Zhang Y T, Xiao Q, Wen J G, et al. Review on spectral libraries: Progress and application[J]. Journal of Remote Sensing, 2017,21(1):12-26. ]

Options
Outlines

/

〈 〉