EN中文

Journal of Geo-information Science >

2021 , Vol. 23 >Issue 1: 134 - 142

DOI: https://doi.org/10.12082/dqxxkx.2021.200425

A Lossy Compression Method for AoT Sequence Data based on Tensor Decomposition

  • YANG Chen , 1, 2 ,
  • GAO Hong 1, 2 ,
  • ZHANG Liying 1, 2 ,
  • HU Xu 1, 2 ,
  • YU Zhaoyuan 1, 2, 3 ,
  • LI Dongshuang , 4, 5, *
Expand
  • 1. Key Laboratory of Virtual Geographic Environment of The Ministry of Education (Nanjing Normal University), Nanjing 210023, China
  • 2. Cultivation Base of State Key Laboratory of Geographical Environment Evolution, Jiangsu Province, Nanjing 210023, China
  • 3. Jiangsu Provincial Center for Collaborative Innovation in Geographical Information Resource Development and Application, Nanjing 210023, China
  • 4. Jiangsu Key Laboratory of Crop Genetics and Physiology/Jiangsu Key Laboratory of Crop Cultivation and Physiology, Agricultural College of Yangzhou University, Yangzhou 225009, China
  • 5. Jiangsu Co-Innovation Center for Modern Production Technology of Grain Crops, Yangzhou University, Yangzhou 225009, China
*LI Dongshuang, E-mail:

Received date: 2020-07-31

  Revised date: 2020-12-29

  Online published: 2021-03-25

Supported by

National Key Research and Development Program of China(2016YFB0502301)

National Natural Science Foundation of China(42001320)

National Natural Science Foundation of China(41976186)

Copyright

Copyright reserved © 2010.
Fold

Abstract

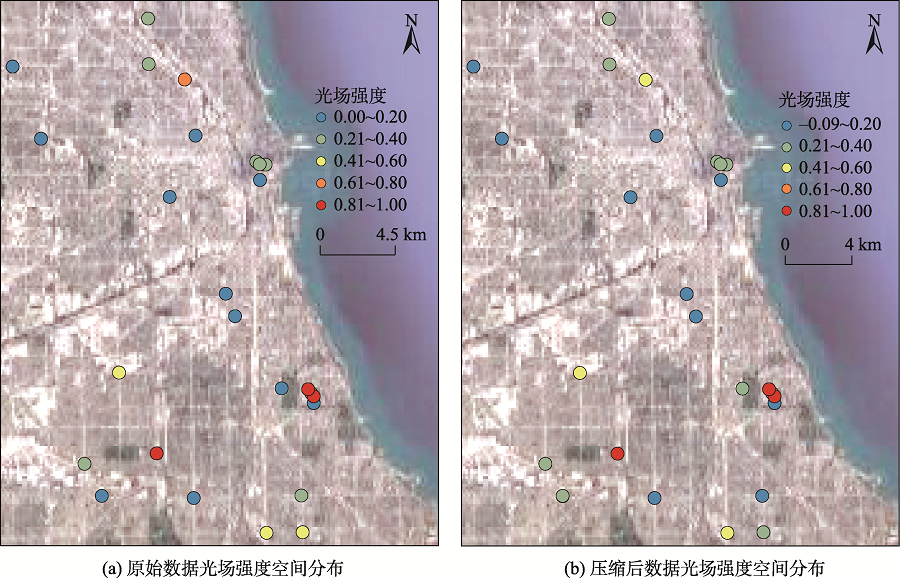
Array of Things (AoT) provides continuous and dynamic observations of urban systems through multiple sensors at a single location. How to utilize the limited computing resources to compress and transmit AoT sequence data becomes one of the key bottlenecks of the AoT application. Considering that most AoT sequence data are massive, high-dimensional and needed to be processed at the sensor side, a tensor decomposition method is introduced to the lossy compression for AoT sequence data in this work. This method first organizes the AoT sequence data as a high-dimensional tensor to preserve the multidimensional coupling relationship among the different dimensions. The CANDECOMP/PARAFAC (CP) decomposition, which has simple parameter, relatively simple principle and low algorithm complexity, is then utilized to decompose and extract the principal feature components in each dimension of AoT sequence data. Since these principal feature components are obtained by absorbing the multidimensional coupling relationship, they can be further combined with tensor reconstruction to approximate the original data accurately. Considering that the data approximation is obtained by removing the redundant information, it can achieve the data lossy compression with the feature preservation. The simulation experiment is conducted based on the acousto-optic electromagnetic data sensed within 24 hours in the downtown area of Chicago in the United States. The influences of different compression parameters on compression ratio, compression error, compression accuracy, compression time, memory usage under the conditions of different compression parameter are discussed. The experimental results show that, with the increase of compression parameter, the compression error obviously decreases and the memory occupation weakly increases, which demonstrates that tensor-based method can achieve lossy compression of AoT sequence data and both the memory occupation during the running process and the memory occupation of the final results can support the data compression of sensor segments. Compared with the original intensity of the light field, the compressed data maintain the spatio-temporal distribution characteristics of original data that would not affect the further data analysis. In addition, compared with the traditional vector quantization coding compression method, the compression ratio of this method is higher about 27%~76%, the compression time is less about 46%~73%, and the memory occupation of compression result is smaller about 17%~57%. Therefore, the tensor-based method has a higher compression ratio, less compression time and smaller memory occupation under the same compression accuracy. The tensor-based method can also be applied to the data with multidimensional features, such as spatial dimensions with different locations, time dimensions at different time nodes, and attribute dimensions of different variables (temperature, humidity, etc.), which could provide a feasible idea for large-scale lossy compression of massive multidimensional geographic sensor sequence data represented by AoT sequence data.

Key words： sensor; spatio-temporal sequence; Array of Things (AoT); lossy compression; multidimensional tensor; tensor decomposition; CANDECOMP/PARAFAC decomposition; tensor reconstruction

Cite this article

YANG Chen , GAO Hong , ZHANG Liying , HU Xu , YU Zhaoyuan , LI Dongshuang . A Lossy Compression Method for AoT Sequence Data based on Tensor Decomposition[J]. Journal of Geo-information Science, 2021 , 23(1) : 134 -142 . DOI: 10.12082/dqxxkx.2021.200425

1 引言

Array of Things (AoT)是由美国芝加哥大学、阿贡国家实验室及政府等多方面协作研发的基于边缘计算的多传感器集成的智慧城市传感器网络项目[1],其可在单一装置中放置湿度、温度、声音、光强、物体大小及运动速度等数十种传感器[2]。AoT成本低廉,可在城市内部大范围密集布设,实现空间全覆盖及冗余监测[2]。目前,AoT已在全球多个城市中部署了上千个多属性传感器节点,这些传感器节点以每30 s一次的数据采样频率更新,产生了海量、高维的地理时空序列数据[3]。如今,在城市内部布设多传感器监测城市内部信息逐渐成为智慧城市发展的趋势之一,因此对AoT序列数据进行高效压缩,降低数据传输过程中带宽和能源损耗有助于提升AoT传感网对城市的持续观测能力[4]。
有损压缩和无损压缩是数据压缩的两类主要方式[5]。有损压缩通常具有更高的压缩率,更适合AoT一类的海量数据压缩。传统的有损压缩通常分为3类：基于相似性压缩、基于时间序列压缩和基于时空序列压缩。例如,基于数据间相似性的常用压缩算法-矢量量化编码压缩,其算法实现简单,但压缩效率较低且未能充分运用数据自身的时空相关性[6]。Bakshi[7]提出了基于小波理论的数据压缩方法,该方法是基于时间序列压缩,其实现过程较容易,但不具有实时性且压缩率相对不高,不能兼顾数据的空间相关性。Ganesan针对时空冗余问题提出了基于时空序列的Dimensions算法,其利用小波变换和拓扑结构消除时间空间冗余,但多次小波分解的叠加,使得算法复杂度较高[8]。面向AoT序列数据多维耦合的结构特点,以及其以云端为基础的边缘计算能力和传输存储需求[9],需要一种简单、统一的有损压缩方法能够处理海量且不同种类的AoT序列数据。然而现有压缩方法大多仅适合一维向量和二维矩阵结构的数据,在面向高维数据压缩时,通常是将其拆分成二维矩阵或一维向量后再进行压缩,这不仅破坏了高维数据的多维嵌套结构,而且大量的数据转换操作也增加了算法复杂度,降低了其在高维数据的压缩性能以及在传感器端的数据传输效率。
张量分解是二维矩阵分解在高维空间的推广形式,可有效支撑多维数据的组织、存储与分析[10]。相较于传统的二维矩阵分解方法,张量分解直接作用于原始多维数据,可在综合考虑多维耦合嵌套结构的基础上提取多维数据在各个维度上的特征结构,有效避免了传统矩阵分析在处理多维数据时所带来的特征估计偏差和复杂计算等问题[11]。近年来,张量分解已被广泛应用于多维数据的压缩存储[12,13]。如袁林旺等[14]利用层次张量分解实现了气候模式数据的流式压缩。赵洪山等[15,16,17]利用Tucker分解实现高光谱数据压缩等。Ekta、Zhang等[18,19]利用CP分解实现了数据在线压缩。在这些张量分解方法中,CP分解原理简单、计算效率较高、内存占用较低。因此,面向新兴城市内部密集观测的AoT序列数据,针对其高维、海量数据特性及在传感器端的压缩需求,本文利用算法复杂度较低的张量CP分解实现AoT序列数据的有损压缩,探讨了不同压缩参数与压缩比、压缩误差、压缩精度、压缩时间、压缩运行过程的内存占用和压缩结果的内存占用之间的关系。

2 数据来源与研究方法

2.1 实验区AoT序列数据来源

AoT传感网络提供各种基于位置的环境数据、大气数据和人类活动数据等,包含温度、湿度、气压、空气中CO2、NO2和臭氧等气体浓度、声光电磁强度、人流、车流等18种不同属性信息（表1）。AoT序列数据包含所有节点的测量值文件、节点及其元数据表、传感器及其元数据表、数据集的元数据表。AoT采集数据后被存储在一个csv结构中,其中包括时间戳、节点ID、传感器参数、电子传感器读取原始值以及经转换后的可读值（HPF值）。HPF值表示从传感器测量值（电流电压水平）经过一系列特定转换成人类可读值（如温度、气压、浓度等）,传感器及其元数据表中包含评估从原始数据转换为HPF值的所需信息。每个AoT节点每30 s采集一次数据。截至2020年1月芝加哥市区内部署了130个节点,一天内芝加哥市区内的感测数据可以达到300 M以上。
表1 研究使用的数据集描述

Tab. 1 Datasets description used in the study

数据集名称 描述 数据集内容
data.csv 所有节点的感测值文件 数据采集时间戳、数据采集节点ID、传感器类型、传感器名称、感测类型、电子传感器原始测量值、经转换后的可读值（HRF值）
nodes.csv 数据集中的节点及其元数据 节点ID、项目ID、节点序列号（在物理机箱可见）、节点安装的街道地址、节点所在经度、节点所在纬度、节点构建和配置的更详细描述、节点安装开始时间戳、节点安装结束时间戳
sensors.csv 传感器及其元数据 数据采集内容、传感器类型、传感器名称、感测类型、转换值的物理单位、数据表的最小HPF值（用作范围过滤器的下限）、数据表的最大HPF值（用作范围过滤器的上限）、传感器数据表的参考网址
provenance.csv 整个数据集中的元数据 数据格式版本、项目ID、数据创建时间戳、数据结束时间戳、创建该摘要的时间戳、此摘要的URL地址

2.2 AoT序列数据有损压缩方法流程

基于张量分解的AoT序列数据有损压缩方法流程如图1所示。针对AoT传感网络所采集的地理时空序列数据进行数据选取、特征梳理和数据预处理。针对AoT序列数据的多维结构特性,对AoT序列数据进行张量组织。进而利用张量分解提取多维数据各个维度上的特征主分量,并通过选取主导分量进行张量重构去除数据冗余,从而实现特征保持的数据压缩,并通过多种压缩指标结果对比评价该方法压缩效果。
图1 基于张量分解的AoT序列数据有损压缩方法流程

Fig. 1 Workflow of lossy compression method for AoT sequence data based on tensor decomposition

2.2.1 AoT序列数据张量组织方法
AoT序列数据是一种多维地理时空序列离散点状数据,传统方法多是将这类数据按照特定时间或者空间维度组织成二维矩阵序列。然而,这种数据组织方式不仅破坏了数据的时空耦合特性,大量的矩阵结构也增加了数据分析的复杂性。张量作为矩阵在高维空间的推广,可有效支撑AoT序列数据的多维结构。一般来说,N阶张量结构可以表达N维数组结构,对于AoT序列数据 χ ∈ R 空间 × 属性 × 时间 ,其可以表达成三阶张量结构 χ ∈ R I × J × K ,如图2所示。
图2 基于张量的数据组织

注：图中I,J,K分别表达空间、属性、和时间维度上的数据个数。

Fig. 2 The tensor-based organization of data

在AoT序列数据中,声光电磁数据是更新频次最高,结构最复杂的一类观测数据。声光电磁数据可用于演化全球光环境、治理与防护光污染、声场模拟与噪声污染等,具有重要的应用价值[20]。感测磁场的传感器由X,Y,Z 3个方向的传感器组成,用于感测不同敏感轴方向的入射磁场强度,并转换为差分电压输出。感测光强、近红外光强和可见光光强的传感器主要对紫外线波段、近红外波段和可见光波段敏感,根据不同属性的光强将光电流转化为电压输出。感测声强的传感器是通过麦克风收集节点周围的声波将其转化为电压输出。
本文选取AoT传感网络所采集的2019年1月10日美国芝加哥地区所有数据（图3）。选取磁场强度、红外光强、可见光强、光强、声强5种类别数据,构建磁场-X向、磁场-Y向、磁场-Z向、红外、可见光、光、声7个属性维度。选取同时含有5类数据的节点,构建空间维度33维。AoT传感器节点每30 s感测一次数据,因秒、分钟尺度数据变化缓慢,因此简化所选数据的时间序列为1 h,构建时间维度24维。最终构建成空间维度33维,时间维度24维,属性维度7维的张量 χ ∈ R 7 × 24 × 33 。
图3 芝加哥城市内部传感器空间分布图与研究使用传感器类别

Fig. 3 Spatial distribution of sensors in Chicago city and category of sensors used in the study

2.2.2 AoT序列数据的张量分解与张量重构
张量分解是矩阵分解的高维推广,其直接作用于多维数据,能够在保持其多维结构的同时挖掘数据内部多维耦合特征[17]。目前的张量分解方法主要有Tucker分解、CP分解、层次张量分解等。其中,CP分解原理简单,计算复杂度较低,是最常用的张量分解形式之一[11]。
对于N阶张量 χ ∈ R I 1 × I 1 × … × I N ,CP分解可以表达为：
χ ≈ ∑ r = 1 R a r 1 ∘ a r 2 ∘ ⋯ a r N
而对于由空间维度、时间维度和属性维度构成的3阶张量 χ ∈ R I × J × K ,CP分解可以表达为如下形式[10]：
χ = ∑ r = 1 R a r ∘ b r ∘ c r + Res
式中： a r ∈ R I ; b r ∈ R J ; c r ∈ R K （r=1, 2, …, R）,分别表示了不同维度上的特征主分量,在本文中分别代表空间维度、时间维度和属性维度上的特征主分量,其主要通过将多维数据整体在高维时空中进行旋转变换,依次寻找协方差变异最大的变换方向作为主导特征方向,进而将数据整体沿着主导特征向量进行投影以获得特征主分量。具体求解则是将原始数据按照不同的维度组合拆分成对应模态上的矩阵,进而利用矩阵分解提取对应维度上的特征主分量。 ∘ 表示向量外积,意为张量中的每个元素都是对应向量的乘积。 Res 为残差,表示未被特征分量捕捉的数据特征即数据冗余。具体分解流程图如图4所示。
图4 三维张量的CP分解过程

Fig. 4 CP decomposition process diagram of 3D tensor

从式（2）可以看出,张量CP分解将多维数据作为整体考虑,可有效利用多维数据在各个维度上的嵌套结构,提取出多维数据在各个维度上的主导特征。在CP分解的过程中,决定特征提取与重构的重要模型参数是R。R代表特征分量的个数也是CP分解的唯一参数[10]。对于三阶张量 χ ∈ R I × J × K ,R的取值范围如下式[10]：
R ≤ min I × J , I × K , J × K
一般而言,较小的R值对应的是张量的主导特征分量（此时的累计方差贡献率>90%）,捕捉的是多维数据的大尺度结构特征,随着R值的增加,所提取出的特征分量结构更加精细。对于分解得到的特征分量序列 a r ∈ R I , b r ∈ R J , c r ∈ R K （r=1,2, …, R）,利用张量重构可以得到逼近后的张量 χ ˆ ≈ ∑ r = 1 R a r ∘ b r ∘ c r 。相较于原始张量数据 χ ∈ R I × J × K ,该张量逼近可以认为是保留了主导特征,去除了数据冗余,从而实现了数据压缩。
相比Tucker分解等其他的张量分解方法,其需要在多维数据的各个维度上分别设置特征分量数,CP分解具有唯一参数（R）——数据整体的特征主分量个数,因此其原理更加简单,计算复杂度更低。并且已有研究证明了CP分解的经验计算复杂度为 O ( n 3 ) [21],因此CP分解更适用于实现传感器端的数据压缩。并且该压缩后的张量维度与原始张量数据保持一致,保持了原始张量的特征结构,因此该数据并不影响后续的数据分析。

2.3 压缩效果评价方法

根据上述张量CP分解与张量重构理论可知,张量分解与张量重构的关键在于R的选择。R值的选取决定着压缩性能如压缩比、压缩精度、压缩误差的大小。因此构建压缩比、压缩误差和压缩精度与R之间的关系（表2）。数据压缩比通常定义为原始数据大小与压缩后数据大小之比。压缩误差与压缩精度是描述还原后数据与原始数据之间的一致性,一般通过RMSE（均方根误差）、 R-Squared（决定系数）来计算压缩误差与压缩精度。
表2 压缩方法评价指标

Tab. 2 Evaluation metrics of compression method

结果评价 评价指标 指标计算公式 编号 参数描述
压缩效果 压缩比 Compressionratio=A.dataSizeAˆ.dataSize（4） A.dataSize 表示原始数据内存大小
Aˆ.dataSize 为压缩结果数据内存大小
压缩误差 均方根误差 RMSE=1IJK∑i=1I∑j=1J∑k=1K(χijk-χˆijk)2（5） χˆijk为重构张量的对应位置上的元素
χijk为原始张量值对应位置上的元素
χ̅ 为原始张量的平均值
I、J、K分别为空间、属性、和时间维度上的数据个数
压缩精度 决定系数 R-Squared=∑i=1I∑j=1J∑k=1K(χijk-χ̅)2-∑i=1I∑j=1J∑k=1K(χijk-χˆijk)2∑i=1I∑j=1J∑k=1K(χijk-χ̅)2（6）

3 结果及分析

3.1 实验结果与分析

原始声光电磁数据通过张量组织为 χ ∈ R 7 × 24 × 33 ,通过CP分解和重构得到压缩结果,并被存储为csv格式的特征向量数据。根据式（3）可知,R是CP分解与张量重构的唯一参数,且其取值范围为1~168。本文随机选取间隔为5的R值下的压缩结果,分别为1,5,10,15,20,25,30,35,40,45,50,55,60,65,70,75,80共17个不同R值显示不同的压缩效果。根据目前的实验结果图（图5）可知,当R>80时,各类压缩效果指标变化均趋于平缓,因此将R值选取至80。这里R值的选取与数据本身特征密切相关。一般而言,异质性较弱的数据,较小的R值就能够实现给定精度条件下的数据压缩。异质性较强的数据,则需要更大的R值来实现给定精度条件下的数据压缩。不同的R值与压缩误差、压缩精度、压缩比、压缩时间、压缩过程运行所占内存和压缩结果所占内存之间关系如图5所示。实验结果表明,随着R值的逐渐增加,压缩误差整体呈现逐渐减小的趋势;压缩精度越来越高且增长速度由快变慢,最后逐渐趋于1;压缩比代表原始数据大小（87.4 K）与压缩结果数据大小之比,压缩比整体呈现逐渐减小趋势;且在R≤10,压缩比指数级减少,而后压缩比减小速度逐渐减缓,最终压缩比趋于1;压缩最短耗时为0.0028 s,最长耗时为0.10 s;压缩结果所占内存线性增加,其内存占用范围在0.86 K~61.09 K。结果显示张量分解能够实现AoT序列数据有损压缩,且其内存占用可以支撑传感器段的数据压缩。
由张量压缩结果图5可知,当R值逐渐增加到10时,压缩误差、压缩精度、压缩比变化速率明显减小;当R值再逐渐增加时,其变化速率逐渐趋于平缓。因此将R取为10时的压缩结果和原始数据在初始时刻的空间分布图进行绘制,结果如图6所示。结果表明,压缩后的数据的光场强度值未发生较大改变,且与原始数据的光场强度空间分布在高低趋势间基本保持一致,表明了该张量压缩方法具有较好的特征保持特性,因此对后续数据分析的影响较小。
图5 张量压缩结果

Fig. 5 The result of tensor compression

图6 芝加哥初始时刻原始数据光场强度与压缩后数据光场强度空间分布

Fig. 6 Spatial distribution of the original light intensity and compressed one at the initial moment in Chicago

3.2 结果与分析

矢量量化压缩是一种成熟的数据有损压缩方法,其原理是将输入矢量与码书中的码字相匹配,存储与传输矢量编码索引以实现数据压缩。本文将高维数据按不同属性类别拼接成 A ∈ R 24 × 231 的二维矩阵,采用分类矢量量化的方法[22],基于聚类算法根据不同的相似性特征将训练矢量分为1-24类,其压缩精度、压缩比、压缩误差、压缩时间、压缩过程运行内存和压缩结果所占内存随分类个数变化[23]。在同一压缩精度下将本文方法与矢量量化编码压缩方法对比,结果如图7所示。在同一压缩精度下,张量压缩比整体优于矢量量化压缩方法（优于约27%~76%）。压缩精度相同时本文方法压缩时间和内存占用整体明显小于矢量量化压缩;压缩精度在[0.8, 0.99]之间时,张量压缩方法的结果内存占用（11.64 ~42.23 MB）明显小于矢量量化编码压缩（18.20 ~64.95 MB）,其余则略小于矢量量化编码。这可能由于矢量量化压缩多将多维数据拆成二维矩阵处理,虽然算法实现简单,解码速度快,但其破坏了高维数据本身时空维度和属性维度之间的耦合关系。从而降低了压缩比和压缩精度,增加了压缩时间和结果内存占用。本文方法另一个优势在于,随着对于压缩精度需求的降低,张量压缩的压缩比的提升速度指数级增加,压缩时间和压缩结果内存占用的减小速度指数级降低。且在精度小于0.8后,压缩时间和压缩结果所占内存都趋于稳定,说明当压缩精度要求不高时,张量压缩的效果较矢量量化压缩方法更稳定、更好。根据图7（c）可知,张量压缩运行时内存占用高于矢量量化编码压缩,可能由于张量分解计算采用的是SVD分解,其复杂度略高于矢量量化编码算法,因此导致其结果内存占用高于矢量量化编码结果内存占用。
图7 张量压缩与矢量量化压缩结果对比

Fig. 7 Comparison results between tensor compression and vector quantization

4 结论

本文提出了一种基于张量分解的AoT序列数据的有损压缩方法,通过引入参数简洁、原理相对简单且计算复杂度较低的张量CP分解模型,在保持多维数据的耦合嵌套结构的基础上,提取各个维度上的特征主分量,进而利用张量重构实现了去掉数据冗余后的数据有损压缩。本文方法综合考虑了多维数据的维度耦合关系,避免了矩阵转换带来的特征提取的估计偏差和复杂运算,使得其可以支撑在AoT传感器端部署应用。本文以美国芝加哥城市内部密集布设的AoT传感器网络所产生的声光电磁数据作为研究案例,与传统矢量量化编码压缩方法对比,在相同压缩精度条件下,整体压缩比、压缩时间和内存占用均占有优势。该方法的压缩比约高27%~76%,压缩时间约节省46%~73%,压缩结果所占内存约节省17%~57%,且当对于压缩精度要求不高于0.99时,张量压缩的压缩比、压缩时间和结果内存占用均呈指数衰减,压缩效果明显优于矢量量化编码。
AoT作为一种新兴的多维时间序列数据,因其丰富的感测数据类型,因此大多研究基于其数据本身进行一系列的数据预测、高维信息可视化以及增强现实应用等,鲜有针对海量高维的AoT序列数据进行有损压缩研究,因此本文方法可为以AoT序列数据为代表的海量多维地理时空数据的有损压缩提供了一种可行思路,该方法适用于具有多维结构的数据压缩,如具有不同位置的空间维度、不同时间节点的时间维度以及不同变量的属性维度（温度、湿度等）,并且对于体量较大的多维数据具有更明显优势。未来可尝试实现多种时空数据的有损压缩,如多维密集点云、高维时空场数据等。本文方法的瓶颈在于张量分解过程中使用了SVD分解,导致运行内存占用略高,未来可通过构造迭代式优化算法构造更适用于AoT在线处理的数据有损压缩方法。

References

Publishing order | Descend order by publishing year | Descend order by cited within
[1]
Wang S, Hou Y, Gao F , et al. A reconfigurable smart interface based on IEEE 1451 and field programmable gate array for multiple internet of things devices[J]. International Journal of Distributed Sensor Networks, 2017,13(2):1-20.

[2]
Catlett C E, Beckman P H, Sankaran R , et al. Array of things: A scientific research instrument in the public way [C]// International Workshop. ACM, 2017: 26-33.

[3]
胡永利, 孙艳丰, 尹宝才 . 物联网信息感知与交互技术[J]. 计算机学报, 2012,35(6):75-91.

[ Hu Y L, Sun Y F, Yin B C . Information sensing and interaction technology in internet of things[J]. Journal of Software, 2012,35(6):75-91.]

[4]
Kolo J G, Shanmugam S A, Lim D W G , et al. An adaptive lossless data compression scheme for wireless sensor networks[J]. Journal of Sensors, 2012,2012(1):1-20.

[5]
Shannon C E . A Mathematical Theory of Communication[J]. The Bell System Technical Journal, 1948,27(4):623-656.

DOI

[6]
Kasban H, Hashima S . Adaptive radiographic image compression technique using hierarchical vector quantization and huffman encoding[J]. Journal of Ambient Intelligence and Humanized Computing, 2018,10(7):2855-2867.

DOI

[7]
Hale J C, Sellars H L . Historical data recording for process computers[J]. Chemical Engineering Progress, 1981,77(11):38-43.

DOI

[8]
Ganesan D, Estrin D, Heildemann J . Dimensions: Why do we need a new data handling architecture for Sensor Networks?[J]. Acm Sigcomm Computer Communication Review, 2002,33(1):143-148.

DOI

[9]
Beckman P, Sankaran R, Catlett C , et al. Waggle: An open sensor platform for edge computing [C]// 2016 IEEE SENSORS. IEEE, 2017: 1-3.

[10]
Kolda T G, Bader B W . Tensor decompositions and applications[J]. SIAM Review, 2009,51(3):455-500.

DOI

[11]
Li D S, Yang L, Yu Z Y , et al. A tensor-based interpolation method for sparse spatio-temporal field data[J]. Journal of Spatial Science, 2018,65(2):307-325.

DOI

[12]
Phan A H, Cichocki A . Tensor decompositions for feature extraction and classification of high dimensional datasets[J]. Nonlinear Theory and Its Applications, 2011,1(1):37-68.

[13]
Bengua J A, Ho P N, Tuan H D , et al. Matrix product state for higher-order tensor compression and classification[J]. IEEE Transactions on Signal Processing, 2017,65(15):4019-4030.

DOI

[14]
Yuan L, Yu Z, Luo W , et al. A hierarchical tensor-based approach to compressing, updating and querying geospatial data[J]. IEEE Transactions on Knowledge and Data Engineering, 2015,27(2):312-325.

DOI

[15]
王东方, 周激流, 何坤 , 等. 基于张量Tucker分解的彩色图像压缩[J]. 四川大学学报:自然科学版, 2010,47(2):287-92.

[ Wang D F, Zhou J L, He K , et al. Compression of color images based on tucker-tensor[J]. Journal of Sichuan University (Natural Science Edition), 2010,47(2):287-292.]

[16]
张乐飞, 何发智 . 基于张量分解的超光谱图像降秩与压缩[J]. 武汉大学学报·信息科学版, 2017,42(2):193-197.

[ Zhang L F, He F Z . Hyper-spectal image rank-reducing and compression based on tensor decomposition[J]. Geomatics and Information Science of Wuhan University, 2017,42(2):193-197.]

[17]
赵洪山, 马利波 . 基于张量Tucker分解的智能配电网大数据压缩[J]. 中国电机工程学报, 2019,39(16):4744-4752.

[ Zhao H S, Ma L B . Big data compression of smart distribution systems based on tensor tucker decomposition[J]. Proceedings of the CSEE, 2019,39(16):4744-4752.]

[18]
Gujral E, Pasricha R, Yang T , et al. OCTEN: Online compression-based tensor decomposition [C]// 8th IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP), 2019: 455-459.

[19]
Zhang Q, Yang L T, Chen Z , et al. High-order possibilistic c-means algorithms based on tensor decompositions for big data in IoT[J]. Information Fusion, 2018,39:72-80.

DOI

[20]
Koyama S, Furuya K I, Uematsu H , et al. Real-time sound field transmission system by using wave field reconstruction filter and its evaluation[J]. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, 2014, E97.A(9):1840-1848.

DOI

[21]
Xiong H, Pan Z, Ye X , et al. Sparse spatio-temporal representation with adaptive regularized dictionary learning for low bit-rate video coding[J]. IEEE Transactions on Circuits Systems for Video Technology, 2013,23(4):710-728.

DOI

[22]
Nowakova J, Prilepok M, Snasel V . Medical image retrieval using vector quantization and fuzzy s-tree[J]. J Med Syst, 2017,41(2):18.

DOI PMID

[23]
Zang M, Liu T, Lang L , et al. Dictionary learning for VQ feature extraction in ECG beats classification[J]. Expert Systems with Application, 2016,53:129-137.

DOI

Options
Outlines

/

〈 〉