EN中文

Journal of Geo-information Science >

2021 , Vol. 23 >Issue 2: 274 - 283

DOI: https://doi.org/10.12082/dqxxkx.2021.200415

Modeling and Application of Epidemic Risk Assessment Considering Spatial Interaction of Spatial-temporal Objects

  • WEI Yuanyuan , 1, 2 ,
  • JIANG Nan , 1, * ,
  • CHEN Yunhai 1 ,
  • LI Xiang 1 ,
  • YANG Zhenkai 1
Expand
  • 1. Institute of Geospatial Information, Information Engineering University, Zhengzhou 450052, China
  • 2. School of Geography and Tourism,Zhengzhou Normal University, Zhengzhou 450001, China
* JIANG Nan, E-mail:

Received date: 2020-07-30

  Revised date: 2020-10-19

  Online published: 2021-04-25

Supported by

National Key Research and Development Program of China(2016YFB0502300)

Copyright

Copyright reserved © 2021.
Fold

Abstract

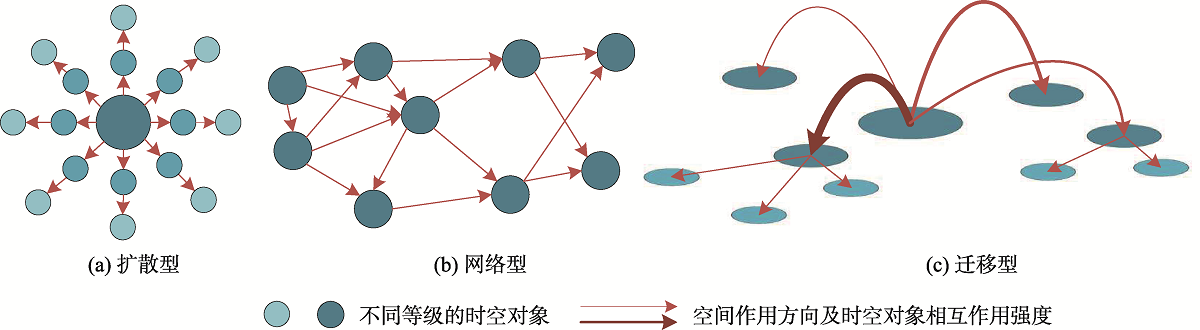
Coronavirus Disease 2019 (COVID-19) is still spreading all over the world. According to the early diffusion characteristics of covid-19 in China, From the perspective of geography, an epidemic risk assessment model considering spatial interaction of spatial-temporal objects was constructed. which realizes the correlation and dynamic analysis of the inter city transmission of epidemic risk on the basis of referring to the transfer mode of spatial interaction of spatial-temporal objects, and took into account the spatial-temporal process, spatial dependence and spatial heterogeneity. In the stage of empirical research, the epidemic risk and its dynamic evolution in Wuhan and its surrounding cities from early January 2020 to early April 2020 were evaluated based on this model. Compared with the real-time epidemic risk index and its spatial distribution calculated based on the urban object's own attributes, the effectiveness of the spatial interaction model based on spatial-temporal objects in epidemic risk assessment was verified. The results show that: on the one hand, The model took into account the spatial dependence and heterogeneity of epidemic transmission, and reflected the transmission process between cities of epidemic risk. It provides a new perspective and method for the study of epidemic risk assessment and related spatial problems. On the other hand, there is a significant positive correlation between the input epidemic risk from source objects and the spatial interaction intensity between objects. Therefore, comprehensive decision-making should be made in combination with the main influencing factors of spatial interaction in epidemic prevention and control.

Key words： COVID-19; spatio-temporal object; spatial interaction; migration model; spatial heterogeneity; epidemic model; risk analysis

Cite this article

WEI Yuanyuan , JIANG Nan , CHEN Yunhai , LI Xiang , YANG Zhenkai . Modeling and Application of Epidemic Risk Assessment Considering Spatial Interaction of Spatial-temporal Objects[J]. Journal of Geo-information Science, 2021 , 23(2) : 274 -283 . DOI: 10.12082/dqxxkx.2021.200415

1 引言

新型冠状病毒肺炎（Coronavirus Disease 2019,COVID-19）爆发以来,关于疫情风险扩散及动态演变的研究越来越受到关注。目前,在疫病传播领域,已存在比较成熟的传播动力学模型,能从定量角度对疫情的传播过程进行建模,也是流行病学、地理学等领域研究相关问题的常用方法。例如,Kermack[1]在1927年最早提出的SIR模型,此外,还有SI、SIS、SEIR及LSEIR等动力学模型也被广泛应用于传染病的时空扩散过程研究[2,3]。其中,基于SIR模型的研究具有明显的统计学意义,但该模型假设人口是均匀分布且传播过程是瞬时完成的,并未充分考虑人与人、城市与城市之间的空间距离差异及空间异质性问题[4,5],这与真实情况并非完全吻合。王丽[6]在对2003年的SARS传播空间格局及人口流动驱动因子研究中,已证实SARS传播和人口迁移同时具有明显的地理空间依赖性及异质性。因此,对疫情风险传播的研究,如果不考虑空间依赖及异质性因素,在应对客观条件的空间差异性方面将面临困难。
从地理学视角看,疫情风险的扩散及动态演变属于地理空间信息范畴的问题,可以把它看作是一种典型的城市尺度之间时空对象相互影响及动态演变的地理过程[7]。其中,“时空对象”作为全空间信息系统的基本数据模型[8],从时空参照、位置、属性、形态、关系、行为、组成结构及认知8个方面对现实世界进行描述[9],克服了传统数据模型的片段式描述与地理对象之间孤立存在的缺陷[10],从数据结构层面将空间信息世界作为相互联系的整体看待[11],能够对地理实体或对象之间相互影响、相互作用的关系进行模型构建和动态表达,因此在兼顾空间依赖性及空间异质性问题方面具备更好的适用性。在现代便利的交通条件下,疫情风险的城际传播,类似于要素在时空对象之间的迁移和传导。因此可以考虑基于时空对象的空间相互作用模式,构建一种城际的疫情风险评估模型,并对其动态演变进行分析。
有学者从对象化的角度在疫情数据建模、分析、可视化等方面进行了探索,如蒋秉川等[12]从对象化的时空视角出发,利用地理知识图谱对COVID-19的疫情态势进行了交互式可视分析,潘理虎等[13]运用多智能体建模仿真技术构建COVID-19病毒防控模型,模拟了不同防控措施下的疫情动态发展趋势。这些研究从不同角度采用对象化思想,取得了良好的研究效果,但是并未从对象的相互作用角度对疫情传播进行建模。本文将在构建时空对象空间相互作用理论的基础上,充分考虑时空对象之间的关联强度及影响传播机制两方面因素,构建出城际尺度的疫情扩散风险预测模型,以期能够在顾及空间依赖性及异质性的前提下,为城市之间疫情风险传播的关联性、动态性分析提供支持。

2 时空对象空间相互作用理论基础及传导模式

2.1 时空对象空间相互作用的理论基础

空间相互作用理论主要用于研究城市或区域之间物质、人员、信息等要素的交换,将地理空间中分布的各个城市作为相互联系的整体进行研究[14,15,16]。这种顾及时空对象之间相互联系、相互影响的研究方法,能够为关联性、动态性的时空过程演化分析提供理论参考。从时空对象模型角度,可以对时空对象的空间相互作用进行理论界定,即相互关联的时空对象在位置、属性、形态等方面的变化或行为结果,对其所在的时空环境或其它时空对象能够产生的影响和作用机制。
时空对象空间相互作用模型能够根据时空对象自身的属性特征、行为能力和时空对象之间的关联关系,构建一个空间上相互联系,时间上动态演化的抽象世界。这一研究范式强化了时空对象之间的内在联系[17],相互作用且不断演化的时空对象本身又具备丰富的属性特征,有助于实现复杂的时空语义描述和动态过程分析。如果将城市作为时空对象,则城市之间的空间相互作用强度则可作为对象的关联强度。在此基础上构建COVID-19风险在城市间传播的动态过程模型,符合时空对象空间相互作用理论的基本意涵。

2.2 时空对象空间相互作用的传导模式

海格特（P.Haggett）[18]将经典的地理空间相互作用形式分为对流、传导和辐射。表明传导性也是时空对象空间相互作用的一个基本特征和主要的作用形式,传导的前提是对象之间存在联系,这种联系可以是空间上的接近关系,也可以是属性、行为、组成等其它方面的联系。时空对象自身描述的丰富性,必然决定了基于各类关联关系形成的空间相互作用的传导性也存在多种模式。
实现时空对象空间相互作用不同传导模式的描述,构建相应的空间相互作用传导模型,并借助相关的理论和方法对这种传导模型进行分析、实现和验证,是基于时空对象的空间相互作用分析中重要的研究内容。从理论层面考虑,时空对象空间相互作用的传导,应涉及扩散型传导、网络型传导、迁移型传导等多种传导模式（图1）。
图1 时空对象空间作用的传导模式

Fig. 1 The conduction mode of spatial impact of spatio-temporal objects

时空对象空间作用的不同传导模式各有其特点和适用场景。扩散型传导主要依托于时空对象的空间邻近关系,如污染、火灾的扩散等。网络型传导主要依托于时空对象的关系网络,通过关系边实现对象节点到节点之间的影响传递,如网络舆情的扩散、路网中拥堵的传导和扩散等。而迁移型传导主要指时空对象之间的影响和相互作用不依托于对象之间的空间邻接关系,而是具备一定的空间跳跃性特征,这一模式在人类活动相关问题的研究中存在较多适用场景,如文化的迁移扩散、人口的迁徙等,而疫情风险在城际的的传播,符合时空对象空间相互作用的传导模式。通过时空对象空间相互作用模型对客观世界的描述,特征丰富,模式多样,能够以统一的时空数据结构和分析模式,满足不同条件下的空间相互作用分析需求。

3 迁移型传导模式的疫情风险扩散建模

3.1 建模思路

基于迁移型传导模式的疫情风险扩散,是将各个城市作为相互联系的时空对象,将风险指数作为对象之间的传导内容。模型构建的主要内容涉及对象相互作用强度的计算、作用机制的确定以及空间影响因子随时间变化的动态计算。
考虑到COVID-19在国内的传播的特点,早期主要以武汉单一点源为主[19],因此这里构建单源迁移模型（图2）。但同时考虑到空间依赖性和空间异质性,对象之间的距离以广义距离表征,则时空对象之间的空间相互作用强度在理论上与广义距离成反比,并同时参照其它因素进行相互作用强度计算。对象之间空间作用机制的表达,在这里主要指源对象的疫情风险向不同对象的传染函数。实际上无论采用怎样的表达机制,首先可以明确的是,每个对象的疫情风险应主要取决于该对象与源对象的空间相互作用强度,即某地的疫情输入风险 c i 是 φ i 的函数,可记为 c i = g ( φ i ) 。此外,时空对象相互作用的动态性,首先体现在不同时刻的疫情风险扩散强度不同,另外,由于受到交通管制等各方面因素影响,不同时刻对象间的空间相互作用强度也不相同。而每个对象从 t 0 到 t i 不同时刻受到源对象疫情风险的影响程度,可根据图2表达的逻辑进行计算。
图2 基于迁移模型的疫情风险评估计算过程

注：图中箭头的方向和粗细分别表示疫情的传播方向及对象之间的相互作用强度,记为 φ ; c 0 表示源对象的疫情风险指数; c 1 到 c i 为受影响对象的疫情风险指数。

Fig. 2 Calculation process of epidemic risk assessment based on migration model

3.2 时空对象相互作用强度计算

重力模型作为经典空间相互作用理论中的代表性方法,能够有效表征区域之间的关联强度[20],因此,对象之间的关联强度可采用重力模型评价。
φ ( i , j , t ) = K m i m j D ( x i , y i , x j , y j ) 2 · f ( i , j , t )
式中 : φ ( i , j , t ) 表示 t 时刻时空对象 i , j 之间的关联强度; m i 、 m j 分别为 i , j 的广义质量,该因子可以在不同情境下采用合适的指标来进行衡量,本研究以常住人口、2019年GDP及研究时期内的确诊病例数3个因子计算的广义质量代替; f ( i , j , t ) 为 t 时刻 i 到 j 的人口流动指数,研究中以每天 i 向 j 的迁出人口占 i 迁出总人口的比例计算。 D ( x i , y i , x j , y j ) 为 i , j 之间的广义距离。如果单纯以欧式距离对D进行计算,在实际应用中并不适用,由于地理环境的异质性,时空对象之间的相互作用往往受到地形地势、道路交通、河流水面等综合因素的影响。因此,为更好地拟合当地的实际情况,以成本距离来测度两地之间距离更为合理[21],成本距离基于两地间最快交通方式的时间成本和对应交通线路的距离综合计算得到,2个因子分别占60%和40%的权重。即：
G = K m i m j D ( x i , y i , x j , y j ) 2
K = 1 G max - G min
式中： K 为标准化系数; G 为城市对象间的引力强度。

3.3 疫情风险评估建模

人员的真实流动情况并非各方向的匀速扩散,而是沿着道路的定向迁移扩散。根据早期疫情传播的单一点源模式,本文考虑对用于点源污染扩散模拟的一维稳态水质迁移模型进行改进。首先,在水质模型中,某一点的水体污染浓度,随着该点与污染源的距离增加而衰减。而在基于时空对象广义距离构建的迁移模型中,疫情风险在城际的传播,同样遵循距离衰减规律。另外,源对象在t时刻迁出到各城市的人口比例,与水质模型中在不同距离上的污染物滞留比例存在相似性。再结合式（1）的重力模型,能够构建一个基于时空对象相互作用的迁移型疫情风险扩散模型,对疫情传染风险的迁移与扩散进行模拟。构造疫情风险迁移模型如下：
c ( i , t ) = s i - 1 c o ( t - ∆ t ) exp - k d i φ ( o , i , t - ∆ t )
式中： c ( i , t ) 为对象 i 在 t 时刻的疫情风险; c o 为起源对象的风险指数, ∆ t 为对象相互作用传导的耗时,在疫情风险传导情境下,可以综合考虑对象之间的时空距离及疫情传染的时空过程进行确定,本研究将 ∆ t 的初始值设为1 d,另外每个对象计算时的取值为初始值加上其与源对象的通勤时间; k 为传染系数,取1/R0,其中,R0数值参照文献[19]的计算结果, d i 为对象 i 至源头广义距离的标准化取值; φ ( o , i , t - ∆ t ) 为对象 i 与源对象在距离当前时间为 ∆ t 的上一时刻的相互作用强度, s 为阻力参数,在疫情传播情境下,用各城市的管控强度代替,计算方式为该城市有出行的人数与该城市居住人口比值指数化结果的倒数。参照实时疫情风险指数的计算方法[22],源对象的风险指数 c o 可根据如下指标进行评估：
c o = r die + ρ n N r cure + s o
式中： r die 为死亡率; ρ 为人口密度;n为确认人数;N常住人口数量; r cure 为治愈率; s o 为管控强度。

4 实证研究

实证研究主要选定在COVID-19疫情在国内的早期传播阶段,目前关于这一阶段的疫情传播已有较多研究。例如Zhou等[23]基于SEIR模型,估算得到了COVID-19的再生数,并对疫情发展进行了预测。喻孜等[24]基于时变参数-SIR模型对疫情传播进行了评估,得到了疫情会在2020年2月9日左右发展到高峰期的预测结果。Rinaldo等[25]和余锦芬等[26]也分别利用SIR模型与元胞自动机模型对疫情风险进行了评估,并在不同防控情境下进行了疫情风险预测。类似研究很多,其中多数研究模型是对SIR、SEIR等经典传播动力学模型的应用或改进,对城际的空间距离差异及空间异质性问题问题考虑不足。
与上述研究相比,本文的疫情风险评估模型,更多顾及了空间异质性因素,重点研究城际的疫情风险扩散及其动态演变。每个城市的疫情风险评价不再是孤立和静态的,而是考虑了与传染源头的相互作用强度以及随时间推移的变化。

4.1 数据获取

根据百度出行大数据,获取一月份武汉市向全国各主要城市的人口迁出比例,分析发现,2020年1月10日春运启动到1月23日武汉“封城”前,除神农架林区之外的湖北省其它15个地市,占据了武汉市迁出人口比例的71.65%,能够代表疫情前武汉市人口的主要流向。因此,本文将这15个城市作为研究对象,分别获取这些城市的常住人口规模、2019年GDP、到武汉的城际通勤时间和距离等常规数据（表1）。此外还收集了这些城市在研究时期内的疫情数据（包括确诊数、治愈数、死亡人数等）和市内逐日出行强度数据。其中,常住人口与GDP数据从统计年鉴获取[27],通勤时间通过查询铁路网站获得[28],出行相关数据在百度迁徙大数据网站爬取[29],病例相关数据根据卫健委官方通报整理获得[30]。
表1 2020年1月23日前武汉市主要人口流向及相关城市基本情况

Tab.1 Main outflow cities of Wuhan population and their basic situation before January 23, 2020

城市 人口/万人 2019年GDP/亿元 通勤方式 用时/h 铁路线距离/km 占武汉迁出人口比例/%
孝感市 481.45 2301.40 高铁 0.50 126 13.87
黄冈市 750.00 2322.73 动车 0.42 50 13.50
荆州市 569.17 2516.48 动车 1.63 240 7.17
咸宁市 246.26 1594.98 高铁 0.40 85 4.77
襄阳市 550.03 4812.84 高铁 1.51 281 4.44
荆门市 287.37 2033.77 特快 3.37 256 3.76
黄石市 242.93 1767.19 动车 1.13 105 3.74
随州市 216.22 1162.23 高铁 1.00 162 3.54
鄂州市 104.87 1140.07 动车 0.37 56 3.28
仙桃市 154.30 868.47 动车 1.00 77 3.23
宜昌市 405.97 4460.82 动车 2.33 323 3.05
天门市 127.23 650.82 动车 0.95 114 2.28
十堰市 334.08 2012.72 高铁 2.00 460 2.00
恩施州 329.03 1159.37 动车 4.02 526 1.83
潜江市 96.20 812.63 高铁 0.80 134 1.19

4.2 结果及分析

4.2.1 城市对象空间相互作用强度计算
将各城市常住人口、2019年GDP、研究时期内确诊病例、武汉到各城市的通勤时间、距离及人口迁出比例作为参数,根据式（1）进行时空对象的相互作用强度计算,结果见图3。
图3 湖北省各市与武汉的空间相互作用强度及COVID-19累计确诊病例的空间分布

Fig. 3 Spatial interaction intensity of cities in Hubei Province and Wuhan and spatial distribution of covid-19 cases

根据计算结果,各城市与武汉市的相互作用强度分布,与“封城”前武汉市的主要人口流向基本一致。分析发现,城市间的空间相互作用强度并非完全取决于其空间距离,交通便捷程度、人口、经济均是重要影响因素。例如,天门、潜江、仙桃3个城市,虽然与武汉市的空间欧氏距离较近（分别为105、135和83 km）,但是由于交通便捷性、人口、GDP等 （表1）各方面因素与荆门、襄阳甚至宜昌（与武汉欧式距离分别为208、260、288 km）相比,都存在较大差距,因此与武汉的空间相互作用强度反而更低,其中天门、潜江、仙桃与武汉间的空间相互作用强度归一化数值分别为0.10、0.04和0.17,而荆门、襄阳和宜昌的数值分别为0.36、0.41和0.81。上述结果主要基于对象的时空距离及各自的广义质量计算得到,也能初步验证式（1）和式（3）计算的合理性。
4.2.2 源头城市疫情风险指数评估
在对每个城市进行疫情风险评估之前,首先需要计算传染“源头”的每日疫情风险指数。考虑到1月10日后春运开始,人口流动大幅增加,因此本研究选择从1月11日起算,分析时间截止4月11日。根据官方统计数据,通过式（5）计算源对象的每日风险指数,计算中涉及的具体参数随时间变化见（图4）。
图4 武汉市疫情风险及主要参数变化趋势

Fig. 4 Trend of epidemic risk and main parameters in Wuhan

分析发现,武汉市作为国内其他地区COVID-19疫情的主要传染来源,其疫情风险的主要影响因子在早期存在明显的波动特征。死亡率在1月26日左右达到峰值,其后逐渐下降并渐趋平稳,治愈率同样在早期波动较大,至2月下旬,疫情得到有效控制,新增病例逐渐减少,且出院人数逐渐增多,治愈率才逐渐攀升,最终达到90%以上。市内管控强度主要参照市内出行强度大数据计算得到,从1月23日武汉“封城”开始显著增强,于1月26日达到最高,并在此后较长一段时间保持了高强度的管控,至3月下旬疫情得到基本控制之后,管控强度才缓慢下降,直至4月11日,管控强度仍未恢复至疫情前状态。
4.2.3 基于时空对象迁移模型的各地疫情风险评估
在已知源头每日风险指数的情况下,根据式（4）的迁移型疫情扩散模型,即可计算每个城市对象不同日期来自源头的输入型疫情风险,结果见图5。
图5 湖北省主要城市疫情风险指数的动态变化

Fig. 5 Dynamic changes of epidemic risk index in major cities of Hubei Province

基于时空对象迁移模型完成的疫情风险评估,能够直观地表现出各地输入型疫情风险随时间的动态变化趋势。① 整体上,疫情风险在1月19日之后急剧增高,且其他城市的疫情风险变化相对于 武汉市 存在时间上的滞后性,此后分别在1月28日和2月15日前后出现峰值,2月16日之后逐渐平稳下降。这一趋势与武汉及周边地区的疫情发展过程基本一致。其中,1月11日出现的小峰值,原因是前期累计病例均归入该日所致。② 1月23日“封城”之后,至2月16日疫情风险稳定下降之前,其他城市的疫情风险相对于武汉市的差值,相较于1月23日之前显著增加。主要原因在于1月23日之后,各城市的管控强度均显著增强,且武汉市的迁出人口急剧下降,进而导致城市对象之间的空间相互作用强度骤减,来自武汉市的输入型风险降低,因此与武汉的疫情风险差值扩大。③ 各城市与武汉之间的空间相互作用强度,决定了其受到武汉市疫情风险波动的影响程度。对比图3与图5可发现,与武汉市空间相互作用强度越高的城市,其疫情风险走势及波动情况与武汉市越接近。
通过以上分析,能够对湖北省内主要城市COVID-19疫情风险及其动态演变实现整体上的认识。另外,对各城市研究时期内的每日疫情风险进行累计,可以探索疫情风险的空间分布规律。（图6）。
图6 湖北省各城市输入型风险累计值

Fig. 6 Cumulative value of importation risk of cities in Hubei Province

根据图6,在整个研究周期内,湖北省各城市的疫情输入型风险分布整体上符合Tobler第一定律,即距离武汉市越近,输入型风险越高。风险累计最高的孝感、黄冈、鄂州三地,都是距武汉的广义距离较近且空间相互作用强度较高。另外,在时空对象的空间相互作用计算时,也考虑了通勤时间、人口、经济等因素,因此风险指数的评估结果并不完全取决于空间距离,如天门、潜江、仙桃等地,这一结果符合空间异质性规律。与图3中各地COVID-19最终确诊病例数量的空间分布对比可发现,基于时空对象空间相互作用迁移型影响模型计算得到的疫情输入型风险,其空间分布与前者基本吻合,这一结果也初步验证了本文模型在空间模拟上的可靠性。

4.3 对比验证

根据各城市对象的空间相互作用强度等级及疫情风险分析结果,在高疫情风险区和中、低疫情风险区分布选取4个城市,将计算得到的每日输入型疫情风险与其实时疫情风险指数进行对比分析（图7）,其中各城市的实时疫情风险指数根据式（4）计算。
图7 基于迁移模型的疫情风险评价与实时疫情风险指数的相关性

Fig. 7 Correlation between epidemic risk index based on migration model and real-time epidemic risk index

对比发现,在所有选取的城市中,基于时空对象迁移模型计算得到的疫情风险指数,与各城市的实时疫情风险指数均存在较高的正相关性,即城市自身疫情风险,会随着武汉的输入型风险增加显著提高,这一结果初步验证了式（4）构建的迁移模型具备一定合理性和科学性。
但是不同风险等级、不同城市,2种风险指数存在不同的拟合形式。主要原因在于不同城市对象的自身属性、以及与源对象（武汉）的空间相互作用强度均有所不同。但这些差异中依然存在某些共性,例如几个高风险城市的拟合曲线主要呈现出指数型模式,虽然在实验中黄冈市以三次多项式拟合得到的相关系数最高,但与其他3个城市相比,2种疫情风险指数的相关性依然表现出一个共同点,即实时疫情风险在高值区会随着迁移型疫情风险的增长而快速递增。这一现象的实际意义是：这些高风险城市在自身实时风险评估较低时,来自武汉的输入型风险是其主要的风险来源,即受到武汉的影响更为显著。
在中、低疫情风险城市,2种风险指数呈现出线性相关或二次多项式相关,整体的规律不再如高风险城市那样具有一致性,且个别城市（如荆门市和宜昌市）在实时疫情风险的低值区,来自武汉的输入型风险占比较低,主要原因在于：相对于其他城市,这些城市与武汉的空间相互作用强度更弱,观察图3可以得到验证。分析结果初步表明,基于时空对象空间相互作用模式的疫情风险分析方法具备合理性。

5 结论与展望

5.1 结论

本文在分析疫情传播动力学模型相关研究的基础上,认为在构建疫情风险传播模型时,应更多顾及空间异质性因素及疫情传播的时空过程性。构建了一种基于时空对象空间相互作用机制的迁移型疫情扩散模型,在城市尺度上,基于该模型对COVID-19在武汉及其周边城市的疫情风险进行了评估,并分析了各城市疫情风险的动态演变过程。主要结论如下：
（1）通过与基于城市自身属性计算得到的实时疫情风险指数进行相关性分析,验证了时空对象空间相互作用模型在时空过程模拟方面的有效性。这一方法为城际疫情风险扩散研究提供了一种新的思考,也是对时空对象模型在空间分析方面应用的一次尝试。
（2）相对于经典疫情传播模型,本文模型同时兼顾了空间依赖性及空间异质性因素,在分析城际疫情风险的扩散及动态演变方面具有更好的适用性。
（3）基于本文模型的研究发现,此次武汉疫情对湖北省其他城市的空间影响是显著的,且这种影响的空间依赖性和空间异质性同时存在,基于时空对象迁移模型的风险指数评价结果及其空间分布规律,均得到现有方法和数据的验证。
（4）来自源对象的输入性疫情风险,与对象间的空间相互作用强度存在显著正相关性。而空间相互作用强度的大小取决于对象之间的时空距离、关系强弱以及对象的自身属性。各城市自身属性不同、城市之间的交通条件、联系强度不同,导致相互作用强度的计算结果必然呈现一定的空间异质性规律,部分城市的疫情风险,并非取决于同武汉的空间距离。但是在整体上,空间相似性规律依然存在,在空间上距离源对象越远的城市,空间相互作用强度和疫情风险等级整体呈下降趋势。

5.2 展望

对于疫情防控来说,公共卫生事件发生后,进行科学有效的城际、城内交通管控,降低人员出行强度是必要且有效的举措。如果顾及疫情风险在城际传播中的空间异质性因素,城际疫情防控的布局可考虑以下3个方面：
（1）每个城市要根据自身属性和城际空间相互作用强度,对疫情风险进行动态研判,制定科学的防控举措,既要足够重视,又要避免盲目恐慌。例如疫情爆发初期,各地在做好全民防控的同时,也要避免出现一刀切的封村堵路,阻塞交通等恐慌现象。
（2）疫情中心城市的防控是关键,直接决定了疫情风险的输出总量。从本文的计算结果看,对武汉进行果断的“封城”,属于科学、及时的防控举措,对今后可能发生的突发公共卫生事件防控及目前国际上的COVID-19疫情防控都具有重要启示意义。
（3）关于支援性防疫物资和医疗力量的调配,不能只根据行政隶属或“离武汉远近”等单一因素进行衡量,而是要基于城际空间相互作用强度对疫情风险进行综合研判,分类分级,制定科学的资源调配方案,并根据各地疫情风险的动态变化情况及时调整。
本研究提供了一种新的研究角度,但方法及模型并不完全成熟,例如对于时空对象之间相互作用的多级传导模式在模型设计时尚未加入。另外,此次建模重点考虑了单源影响模式,即武汉市对其他城市疫情风险的影响,而对于其他城市对象自身的风险累积及其对后期的持续性影响,在模型中参与度不足,还有其他对象之间的相互影响和作用,在本次模型中也未考虑,计划在后续研究中进一步探索。

References

Publishing order | Descend order by publishing year | Descend order by cited within
[1]
Kermack W O, Mckendrick A G. A contribution to the mathematical theory of epidemics[J]. Proceedings of the Royal Society of London, 1927,115(772):700-721.

[2]
Saito M M, Imoto S, Yamaguchi A R, et al. Extension and verification of the seir model on the 2009 influenza a(H1N1) pandemic in Japan[J]. Mathematical Biosciences, 2013,246(1):47-54.

DOI

[3]
Chang C Y, Cao C X, Wang Q, et al. The movel H1N1 influenza a global airline transmission and early warning without trave containments[J]. Chinese Science Bulletin, 2010,55(26):3030-3036.

DOI PMID

[4]
邹霞. 具有时空时滞的非局部扩散SIR模型的行波解[J]. 应用数学和力学, 2018,39(5):611-630.

[ Zou X. Traveling wave solutions for nonlocoal dispersal SIR models with spatio-temporal delays[J]. Applied Mathematics and Mechanics, 2018,39(5):611-630. ]

[5]
俞建康, 何芳, 陈袁芳, 等. 顾及空间异质性的温州市COVID-19疫情预测[J]. 地理空间信息, 2020,18(8):1-6,141.

[ Yu J K, He F, Chen Y F, et al. Prediction of covid-19 epidemic situation in Wenzhou considering spatial heterogeneity[J]. Geospatial information, 2020,18(8):1-6,141. ]

[6]
王丽. 2003年中国SARS传播空间格局及人口流动驱动因子研究[D]. 北京:中国科学院大学, 2016.

[ Wang L. Modeling on SARS transmission in 2003 and population migration based on flow data[D]. Beijing: University of Chinese Academy of Sciences, 2016. ]

[7]
刘张, 千家乐, 杜云艳, 等. 基于多源时空大数据的区际迁徙人群多层次空间分布估算模型——以COVID-19疫情期间自武汉迁出人群为例[J]. 地球信息科学学报, 2020,22(2):147-160.

[ Liu Z, Qian J L, Du Y Y, et al. Multi-level spatial distribution estimation model of the inter- regional migrant population using multi- source spatio- temporal big data: A case study of migrants from Wuhan during the spread of COVID-19[J]. Journal of Geo-information Science, 2020,22(2):147-160. ]

[8]
周成虎. 全空间地理信息系统展望[J]. 地理科学进展, 2015,34(2):129-131.

DOI

[ Zhou C H. Prospects on pan-spatial information system[J]. Progress in Geography, 2015,34(2):129-131. ]

[9]
华一新, 周成虎. 面向全空间信息系统的多粒度时空对象数据模型描述框架[J]. 地球信息科学学报, 2017,19(9):1142-1149.

DOI

[ Hua Y X, Zhou C H. Description frame of data model of multi-granularity spatio-temporal object for Pan-spatial Information System[J]. Journal of Geo-information Science, 2017,19(9):1142-1149. ]

[10]
张政, 华一新, 张晓楠, 等. 多粒度时空对象关联关系基本问题初探[J]. 地球信息科学学报, 2017,19(9):1158-1163.

DOI

[ Zhang Z, Hua Y X, Zhang X N, et al. The basic issues of associative relationship of spatial-temporal objects of multi-granularity[J]. Journal of Geo-information Science, 2017,19(9):1158-1163. ]

[11]
张江水, 华一新, 李翔. 多粒度时空对象建模的基本内容与方法[J]. 地理信息世界, 2018,25(2):12-16.

[ Zhang J S, Hua Y X, Li X. The basic content and methods of multi-granularity spatio-temporal object modeling[J]. Geomatics world, 2018,25(2):12-16. ]

[12]
蒋秉川, 游雄, 李科, 等. 利用地理知识图谱的COVID-19疫情态势交互式可视分析[J]. 武汉大学学报·信息科学版, 2020,45(6):836-845.

[ Jiang B C, You X, Li K, et al. Interactive visual analysis of COVID-19 epidemic situation using geographic knowledge graph[J]. Geomatics and Information Science of Wuhan University, 2020,45(6):836-845. ]

[13]
潘理虎, 秦世鹏, 李晓文, 等. COVID-19病毒防控多智能体仿真模型[J/OL]. 系统仿真学报, 1-15. https://doi.org/10.16182/j.issn1004731x.joss.20-0312. 2020-08-25.

[ Pan L H, Qin S P, Li X W, et al. The multi-agent simulation model for COVID-19 virus prevention and control[J/OL]. Journal of System Simulation, 1-15. https://doi.org/10.16182/j.issn1004731x.joss.20-0312. 2020-08-25.]

[14]
薛景丽. 基于GIS和SEM的城市空间相互作用测度方法研究[D]. 北京:中国地质大学(北京), 2012.

[ Xue J L. Research on measurement method of urban spatial interaction based on GIS and SEM[D]. Beijing: China University of Geosciences(Beijing), 2012. ]

[15]
Manuel G R, Farok V. Population, convenience and distance de-cay in a short-haul model of United States' air transportation[J]. Journal of Transport Geography, 1995,3(3):179-185.

DOI

[16]
Waldo R. Tobler. A computer movie simulating urban growth in the detroit region[J]. Economic Geography, 1970,46(2):234-240.

DOI

[17]
徐爱功, 车莉娜. 一种新的时空过程模型建模方法[J]. 测绘科学, 2013,38(6):60-63.

[ Xu A G, Che L N. Discussion on a new spatio-temporal process model[J]. Science of Surveying and Mapping, 2013,38(6):60-63. ]

[18]
Peter H. Geography: A modern synbook[M]. Geography: A modern synbook. Harper & Row, 1991.

[19]
中国—世界卫生组织新型冠状病毒肺炎(COVID-19)联合考察组. 中国-世界卫生组织新型冠状病毒肺炎(COVID-19)联合考察报告[R]. 北京:中华人民共和国国家卫生健康委员会, 2020.

[ China - WHO novel coronavirus pneumonia (COVID-19) joint investigation group. China - WHO novel coronavirus pneumonia (COVID-19) joint investigation report[R]. Beijing: National Health Commission of the people's Republic of China, 2020. ]

[20]
Grosche T, Rothlauf F, Heinzl A. Gravity models for airline pas-senger volume estimation[J]. Journal of Air Transport Manage-ment, 2007,13(4):175-183.

[21]
Liu J, Zhan J, Deng X. Spatio-temporal patterns and driving forces of urban land expansion in China during the economic reform era[J]. AMBIO: a journal of the human environment, 2005,34(6):450-456.

DOI

[22]
李辉智, 易大莉, 李高明. 重庆市新型冠状病毒肺炎疫情风险分区分级评估方法比较研究[J/OL]. 重庆医科大学学报, 1-7. https://doi.org/10.13406/j.cnki.cyxb.002564. 2020-08-23.

[ Li H Z, Yi D L, Li G M. Comparative study on assessment methods of epidemic risk of COVID-19 in Chongqing[J/OL]. Journal of Chongqing Medical University, 1-7. https://doi.org/10.13406/j.cnki.cyxb.002564. 2020-08-23. ]

[23]
Zhou T, Liu Q H, Yang Z, et al. Preliminary prediction of the basic reproduction number of the Wuhan novel coronavirus 2019-nCoV[J/OL]. Journal of Evidence Based Medicine, 2020,13:3-7. http://arxiv.org/abs/2001.10530. 2020-01-23.

[24]
喻孜, 张贵清, 刘庆珍, 等. 基于时变参数-SIR模型的COVID-19疫情评估和预测[J]. 电子科技大学学报, 2020,49(03):357-361.

[ Yu Z, Zhang G Q, Liu Q Z, et al. The outbreak assessment and prediction of COVID-19 based on time-varying SIR model[J]. Journal of University of Electronic Science and Technology of China, 2020,49(03):357-361. ]

[25]
Rinaldo M C, Mauro G, Francesca M, et al. An age and space structured SIR model describing the Covid-19 pandemic[J/OL]. Medical Letter on the CDC & FDA, 1-16. https://doi.org/10.1101/2020.05.15.20103317. 2020-05-15.

[26]
余锦芬, 宋玉凯, 费菲, 等. 基于机器学习和动力学模型的湖北省新型冠状病毒肺炎疫情分析[J/OL]. 生物医学工程研究, 1-5. http://kns.cnki.net/kcms/detail/37.1413.R.20200422.1303.002.html. 2020-09-14.

[ Yu J F, Song Y K, Fei F, et al. Analysis of COVID-19 in Hubei province based on machine learning and dynamics model[J/OL]. Journal of Biomedical Engineering Research, 1-5. http://kns.cnki.net/kcms/detail/37.1413.R.20200422.1303002.html. 2020-09-14.

[27]
湖北省统计局. 湖北统计年鉴2019[M]. 北京: 中国统计出版社, 2019.

[ Hubei Provincial Bureau of Statistics. Hubei statistical yearbook-2019[M]. Beijing: China Statistics Press, 2019. ]

[28]
http://search.huochepiao.com/chaxun/resultc.asp?txtCheci=D2&cc.x=0&cc.y=0.

[29]
百度迁徙-百度地图慧眼.[DB/OL]. https://qianxi.baidu.com/2020. 2020-05-08.

[ Baidu migration - Baidu map insight.[DB/OL]. https://qianxi.baidu.com/2020. 2020-05-08. ]

[30]
澎湃新闻“美数课”. 新增确诊新型冠状病毒肺炎数据.[DB/OL]. https://github.com/839-Studio/Novel-Coronavirus-Updates. 2020-04-19.

[ MEISHUKE column of surging news. New diagnostic data of covid-19.[DB/OL]. https://github.com/839-Studio/Novel-Coronavirus-Updates. 2020-04-19. ]

Options
Outlines

/

〈 〉