EN中文

Journal of Geo-information Science >

2022 , Vol. 24 >Issue 3: 437 - 447

DOI: https://doi.org/10.12082/dqxxkx.2022.210409

VCS Optimization Method of Vatti Algorithm for Polygon Overlay and Parallelization Using GPU

  • ZHANG Zhikun , 1 ,
  • FAN Junfu , 1, * ,
  • XU Shaobo 2 ,
  • CHEN Zheng 1
Expand
  • 1. School of Civil and Architectural Engineering, Shandong University of Technology, Zibo 255000, China
  • 2. School of Architecture & Urban Planning, Shenzhen University, Shenzhen 518060, China
*FAN Junfu, E-mail:

Received date: 2021-07-18

  Request revised date: 2021-08-19

  Online published: 2022-05-25

Supported by

National Natural Science Foundation of China(42171413)

National Key R&D Program of China(2017YFB0503500)

Natural Science Foundation of Shandong Province(ZR2020MD015)

Natural Science Foundation of Shandong Province(ZR2020MD018)

Major Scientific And Technological Innovation Projects of Shandong Province(2019JZZY020103)

Young Teacher Development Support Program of Shandong University of Technology(4072-115016)

Copyright

Copyright reserved © 2022
Fold

Abstract

Vatti algorithm is one of the widely used vector polygon clipping algorithms. In the process of intersection calculation based on the construction of scanning beams, the data structure of binary tree and recursive calculation method lead to an obvious increase in time consumption when dealing with polygons with plenty of vertices. The calculation efficiency of the algorithm is significantly affected by the boundary vertex number of the overlapping polygons. Aiming at the efficiency improvement of the time-consuming scanning beam construction process of Vatti algorithm, this paper proposes an optimization approach based on polygon boundary vertex pre-sorting method, which is named VCS (Vertex Coordinate Pre-Sorting) method, and realizes a fine-grained level parallel Vatti algorithm on GPU device based on CUDA. The VCS method replaces the original binary tree data structure of Vatti algorithm with a double linked list, and obtains an obvious efficiency improvement on polygon boundary vertex information searching process with a smaller additional storage space. In GPU environment, the bitonic sorting method is used to sort the elements of polygon boundary vertex array in parallel and filter out the valid values, which overcomes the defect of low efficiency caused by the original algorithm using binary tree data structure. Experimental results show that the improved algorithm presents higher efficiency with the same calculation accuracy as the original algorithm. When the number of polygon vertices is 920 000 and the number of threads in each thread block is 32, compared with the serial algorithm which builds scan beams using CPU, the VCS optimization method with GPU-based parallel polygon clipping algorithm obtains a relative acceleration ratio of 39.6 times, and the efficiency of vector polygon superposition analysis algorithm is improved by 4.9 times overall.

Key words： overlay analysis; polygon clipping; CUDA parallel; bitonic sort; VCS; Vatti algorithm; data structure; high performance computing; GIS

Cite this article

ZHANG Zhikun , FAN Junfu , XU Shaobo , CHEN Zheng . VCS Optimization Method of Vatti Algorithm for Polygon Overlay and Parallelization Using GPU[J]. Journal of Geo-information Science, 2022 , 24(3) : 437 -447 . DOI: 10.12082/dqxxkx.2022.210409

1 引言

随着传感器及相关技术的发展,空间数据的获取方式不断丰富,空间数据集的规模也急剧增长。越来越多的空间大数据应用场景下,传统的串行空间分析算法已逐渐不能满足各类应用对计算性能的需求,高性能计算技术是解决上述问题的有效方法[1]。其中多核并行、集群并行、GPU并行等是实现高性能计算的常用方法,这几种实现并行化的方法各有特点[2,3,4]。多核并行内存访问友好,算法改造成本低,但处理规模较小,系统扩展困难;集群并行系统扩展能力较强,不需要维持内存一致性,但并行化改造成本较高;GPU并行能以较低的成本获得相对明显的效率提升且扩展较为方便,但付出的学习成本较高[5]。近年来,基于CUDA的通用GPU计算技术的应用不断向各个领域延伸[6],已成为并行空间分析算法研究的主流方向之一。
叠加分析（Overlay Analysis）是地理信息系统中重要且基础的空间分析功能之一[7]。在面向矢量数据的叠加分析算法中,其核心是多边形的裁剪算法。常见的多边形裁剪算法有Sutherland-Hodgeman算法[8]、Weiler-Atherton算法[9]、Vatti算法[10]、Greiner-Hormann算法[11]等,这些算法各具优缺点。Sutherland-Hodgeman算法仅可以处理凸多边形的叠加分析操作,且会产生重复的结果多边形[12]。Weiler-Atherton算法可以处理凹多边形、凸多边形的叠加分析,但是在处理存在重合边的叠加情形时存在失效的可能[13]。Greiner-Hormann算法和Vatti算法是普遍认可的能在有限的时间内处理任意多边形裁剪问题并且可以获得正确结果的有效算法,然而Greiner-Hormann算法在某些情况下其计算效率却可能低于Vatti算法[14,15]。刘氏算法与 Greiner-Hormann 算法相比并无实质改进[16],Martinez等[15,17]所提出的算法并未得到广泛应用。
在当前空间大数据的应用背景下,包含矢量多边形叠加分析在内的大量复杂的地理数据的空间分析问题,已呈现出典型的计算密集型任务特征[18]。研究面向新型计算架构的矢量多边形并行叠加分析算法对完善高性能GIS理论和方法,提升传统地学分析算法的计算效率具有重要价值和意义[5]。一些学者重新设计了叠加算法以充分利用并行计算框架的计算性能[19,20,21,22],Zhou等[23]提出了一种高效的多边形叠加分析并行算法,在多边形几何对象粒度上实现了矢量多边形叠加分析的并行化求解。范俊甫等提出了一种基于栅格化思想的多边形裁剪算法,使用CUDA处理顶点数量较多的多边形时,获得了将近5倍的加速比[24,25]。邱强等[4]指出在GIS的并行化领域中的3个主要研究方向,即空间数据的并行处理、并行空间数据库研究以及并行空间分析。其中空间数据并行是空间分析算法并行化采用的主要方式[1],张鹏等[26]基于CUDA对串行D8算法采用规则格网划分的方式进行了并行化设计及算法优化。吴旭桥等[27]提出了基于条带划分的面向大规模DEM数据的并行填挖算法,并大幅提高了填挖分析效率。为获得最大的加速比,负载均衡是需要解决的关键问题之一[28]。Zhou 等[29]使用边界代数填充的方法对输入多边形进行栅格化处理时,针对不同的工作负载分解和任务调度过程开发了适用的并行策略以平衡工作负载。此外,陈达伦等[30]实现了基于MPP架构的并行空间数据库。在并行空间分析方面,范俊甫等使用MPI实现了多边形合并及缓冲区算法的粗粒度任务并行[31,32]。而传统的多边形裁剪算法计算过程与数据结构紧密耦合,难以实现细粒度并行化[24]。
针对上述问题,本文采用CUDA框架对Vatti多边形裁剪算法进行了GPU细粒度并行化改造和优化,并对并行化之后的算法开展了多方面比较。具体来说,测试并统计了Vatti算法执行过程各环节的时间开销,根据各环节耗时以及算法之间的依赖性寻找出最适合并行化的部分,对该部分的数据结构重新设计,降低了原始算法各环节之间的依赖性,使其能够在GPU上实现并行化。最后在所采用的实验平台上确定出最适合的并行线程数量,尽可能地提高算法的计算效率。

2 Vatti算法优化过程

2.1 Vatti算法计算流程及效率分析

Vatti算法的步骤主要包括预处理、扫描束的构建、裁剪以及结果写入、数据清理等其他部分,其流程如图1（a）所示。在Vatti算法的预处理阶段,读取矢量多边形后需要利用最小外包矩形（MBR）过滤掉不存在相交可能性的多边形。在扫描束构建过程中,通过如图1（b）所示的扫面线M与扫描线N构成的有序扫描线集合自下而上来遍历多边形的所有顶点,提取多边形的每个节点的位置信息存放到边表（Edge Table）中,同时将所有不相同的y值存放到二叉树中。找到所有的局部最小点,将局部最小点存储到局部最小点表（LMT）中,所有的局部最小点以单向链表的形式连接在一起。同时,从LMT的最低点处递归,根据每条边界线的第一条边的x值和斜率信息确定当前边界线在边界线列表中插入的位置,其结构如图1（c）所示。
图1 Vatti算法流程

Fig. 1 Flow chart of Vatti algorithm

在Vatti算法的裁剪过程中进行如下处理：当一对边界中局部最小点处各自第一条边处于活动状态时,根据活动边表中的其余边的奇偶校验值来判断这两条边分别属于左侧边还是右侧边。根据边的位置来判断局部最小点是否为输出多边形的贡献点。当扫描束到达一组边界的y值最大处时,把左右侧边的标志传递给y值最大边的后继边。每条边以双向链表的形式存储在边表中。当扫描束到达一条贡献边的上顶点时,需要确定输出顶点的类型（局部最小点、局部最大点或左右中间节点）。自下而上对每一个扫描束内的活动边进行以上操作后,得到输出多边形的一组组的有序顶点坐标。最后通过结果的写入和数据清理完成对多边形数据集的裁剪操作。
本文测试代码使用Alan Murta基于Vatti算法的多边形裁剪库[33]——GPC（General Polygon Clipper）,通过地理数据抽象库（Geospatial Data Abstraction Library,GDAL）读取多边形的Shapefile文件[34],实验数据为宁夏部分地区2009年和2010年的土地利用数据,详细信息如表1所示。该数据中存在凹多边形、凸多边形以及含有洞的多边形和水平边等,符合一般数据的情况。
表1 实验数据详细信息

Tab. 1 Details of experimental data

年份 多边形数/个 顶点数/个 单个多边形最大顶点数/个
2009 9129 856 238 9475
2010 9383 832 827 9472
使用Vatti算法的DIFF算子对该数据进行求异计算,各部分耗时占比如图2所示,其中二进制文件读取操作耗时1.47 s,扫描束的构建过程耗时20.01 s,扫描束逐行扫描裁剪耗时7.46 s,其他部分耗时0.19 s。扫描束的构建过程和裁剪过程占据了该算法所消耗时间的绝大部分,其中扫描束的构建过程耗时占总耗时的2/3。因此,有必要对扫描束的构建过程与裁剪过程进行优化,以提高整个算法的运行效率。而在进行裁剪的过程中数据结构较复杂,难以进行高效的算法优化,因此本文仅对扫描束的构建过程进行了优化。
图2 Vatti算法各部分耗时

Fig. 2 Time consumption of each part of Vatti algorithm

2.2 VCS优化方法

在Vatti算法构建扫描束的过程中,每个顶点的y值插入到二叉树特定位置上的过程以及寻找每条边界线相连的局部最小点的过程,需要一次次的递归操作,而为每条扫描线赋值时又需要从二叉树中逐一取出,原始方法的递归操作花费了较多时间。针对该问题,本文提出了一种预先提取多边形顶点坐标信息后使用排序算法进行排序的优化方法—VCS（Vertex Coordinate Pre-Sorting）优化方法。其优化思路及与原始算法的对比如图3所示： ① 利用一个用于存放y坐标的数组,接收每个多边形的顶点信息,替换掉原始算法中使用二叉树存放顶点信息的方式,如图4所示分别将局部最小点H、E、A和所有顶点存储到数组Array[H,E,A]和Array[E,F,G,I,J,H,A,B,C,D,]中。② 使用排序算法对每个数组中的每个顶点按照其y值由小到大进行排序得到有序数列Array[A,H,E]和Array[A,H,D,E,I,J,G,B,F,C],该排序过程的并行优化在图5中有详细叙述。③ 对排序后的数组中的重复数据做清洗工作,坐标数组中的某一项数值大小与下一个数值相同,则跳过当前数值;若2个数值不相同,则使用一个新的数组接收所有的有效值,将新的数组中的有效值一一对应赋给扫描线。
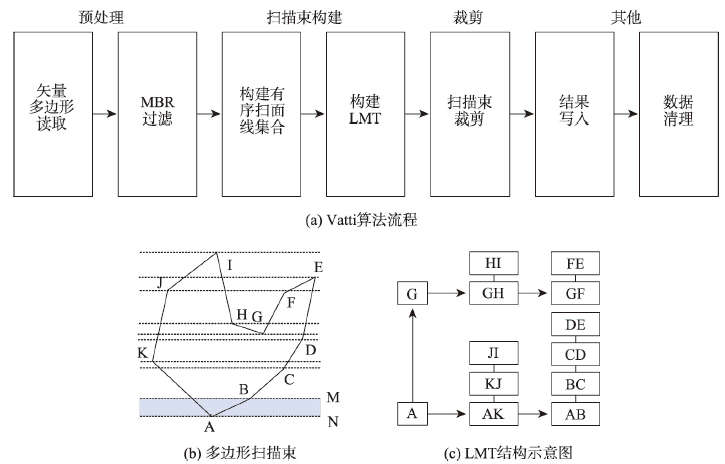
图3 原始算法与VCS优化方法的扫描线赋值、边界线位置查询过程

Fig. 3 The process of scan line assignment and boundary line position query between the original algorithm and VCS optimization method

图4 VCS优化方法的并行化流程

Fig. 4 Flow chart of algorithm parallelization

图5 使用VCS方法优化前后耗时对比

Fig. 5 Comparison of time consumption before and after optimization using VCS method

在VCS优化方法中,提取出所有的局部最小点,利用数组存储,通过排序算法进行排序,把有序数组中的元素以双向链表的方式连接起来,在边界线寻找局部最小点时,便可以仅仅通过指针的移动,在有序的双向链表中查找到每条边界线所需要连接的局部最小点的位置。如图3所示在查询HI与IJ的连接位置时,可以通过移动局部最小点序列中双向链表的指针来实现。因此,与原始算法中插入和查询时需要多次的递归操作相比,该优化方法以较小的存储空间换取了效率上的提升。

2.3 VCS优化方法的并行化

双调排序算法是一种特别适合并行化的排序算法[35,36],在构建扫描束时引入该算法对多边形顶点坐标和局部最小点进行排序,将有效提高扫描束的构建效率。双调序列是指一个序列中的值先增大再减小（或者先减小后增大）,该序列中仅有一个局部最大值或一个局部最小值。其思路为将一个单调递增序列和其相邻的单调递减序列看作一个双调序列,小的元素放到左侧序列中,大的元素放到右侧序列中。以相同的方法进行递归合并,直到最后得到一个前半段序列单调递增、后半段序列单调递减的双调序列。在构造排序时,各个值与其对应位置处的值进行大小比较以及位置交换是互相不受影响的,因此可以对该过程进行并行化改造。通过对整个无序数列的不断调整来实现2个相邻双调序列片段一次次归并,进而得到最终的双调序列。
根据双调排序的原理,将无序序列转化为有序序列,需要找出每个元素与之对应的位置做数值大小的比较与数值交换,通过一轮一轮的异或操作找到对应位置。为了实现核函数线程同步的特点,必须对核函数多次调用,但是该方式占用了大量资源来分配线程。本文将该过程转移到核函数内部进行,使用每一个线程执行整步操作。将无序序列转化为步长为线程块大小的双调序列的过程内置到核函数中,因此会在核函数中对不同位置处的数据进行多次交换。由于同一个线程块中的线程使用共享内存,因此可以先将数据预先取出存储到共享内存中,在共享内存中对每一轮对应位置处的要素进行比较、交换等操作,从而减少对全局内存的访问次数,提升数据交换的效率。
CUDA框架下的程序流程一般为：主机端首先准备数据,将信息复制到设备端的内存中,在设备端完成并行计算后将结果拷贝回主机端。将图3中元素排序的过程转移到设备端实现并行化,其具体流程如图4所示,在主机端将多边形的顶点坐标信息提取出来,存放到数组中,利用极值将数组扩充从而得到一个无序数组。当启动CUDA内核时,利用CUDA的内存拷贝函数将该数组的信息从主机端拷贝到设备端。此时,流多处理器中将被分配足够多的线程块,同时对线程块再次划分成为更加细致的结构——由32个线程组成的线程束。在设备端实现数据大小的比较、交换等操作之后将数据拷贝回主机端,此时数组中的要素已是有序的。对有序数组中的要素过滤,去除无效值和重复值,便可以为每条扫描线赋值。

3 实验及算法优化效率分析

3.1 实验及VCS优化方法效率分析

本文实验环境如表2所示,测试数据来源于OpenStreetMap的中国土地利用斑块矢量数据,共包含925 872个顶点,该面状数据中存在简单多边形、凹多边形、带洞多边形甚至是自相交多边形等,具有叠加分析中面状地理数据一般特征和应用价值。使用VCS方法对原始Vatti算法进行优化,得到了优化前与优化后所花费的时间对比如图5所示。图5中横坐标表示使用的测试数据中包含的多边形顶点数量,纵轴表示使用Vatti算法进行多边形求交计算所花费的时间。由图5可得,当多边形顶点数量达到40万以上时,使用VCS优化方法后在效率上可以提高10 s以上。通过对原始数据计算得到的拟合函数可以看出,原始算法的耗时与多边形的顶点数量呈二次多项式的增长关系。数据结构优化之后的Vatti算法耗时虽然下降了一部分,但是总体趋势还是和原算法保持一致,当面临大量数据时,串行下的排序算法依然耗时严重。原因是一次次的递归操作容易造成滚雪球效应,这也与Leonov所研究的结果相吻合[37]。
表2 实验环境配置

Tab. 2 Experimental environment configuration

设备型号 CPU GPU CUDA处理器核心数/个 显存位宽
/位		 显存频率
/ MHz		 内存
/GB		 外部存储
/ GB SSD		 操作系统 编译器
HP Pavilion 15-ak004TX Intel Core i7-6700HQ四核2.6 GHz NVIDIA GTX 950 M 640 128 1000 8 128 Windows 10 Visual Studio 2017

3.2 VCS优化方法并行化效率分析

为了定量地研究并行化之后算法的运行速度相对于串行算法提高了多少,本文从以下2个方面探究不同情况下加速效率的差异。① 探究针对同一副数据不同数量的并行线程对加速效率的差异;② 探究在相同数量的并行线程条件下,处理不同规模数据时加速效率的差异。
分别在CPU串行和不同数量的并行线程条件下进行测试,实验结果如图6所示。其中横轴表示在每个线程块中使用不同数量的并行线程和仅使用CPU的情况,纵轴表示扫描束构建所花费的时间。从图6可以得知,当每个线程块中并行线程的数量不断增加时,扫描束的构建所花费的时间不断降低,当线程数量达到32时,耗时达到最低,花费的时间为1255 ms。在这一阶段,线程数量的增加能够充分发挥出并行化的效果。之后随着线程数量继续增加,耗时反而略有增加,原因是当线程块中的线程数量太多时,存储器增大,从而使得流处理器效率下降。因此对于该方法每个线程块中线程数量为32时可以满足最优的加速效果。
图6 不同数量的并行线程扫描束构建耗时情况

Fig. 6 Time consumption of scanning bundle construction with different number of parallel threads

为了定量探究使用GPU加速后的Vatti算法面对不同数据时加速效率的差异,对上述测试数据进行了实验,得出了如图7所示的实验结果。横坐标表示的是测试数据不同的顶点数量,左侧纵轴表示的是不同数据量各自所花费的时间,右侧纵轴表示的是加速比。由图7可以看出,随着多边形顶点数量的增长,串行下的Vatti算法所花费的时间与多边形顶点数量呈二次多项式的增长关系,而并行化之后的Vatti算法可以基本维持线性增长关系。加速比随顶点数量的增加不断升高,在多边形顶点数量达到92万时,加速比达到了4.9倍。
图7 不同数据量耗时情况及加速比

Fig. 7 Time consumption and speedup ratio for different data volumes

图8展示了原始的Vatti算法、数据结构优化之后的Vatti算法、使用GPU加速后的Vatti算法处理不同数据量的耗时情况。随着多边形顶点数量的增长,原始Vatti算法和数据结构优化后的Vatti算法计算所花费的时间迅速增加,而并行化之后的算法耗时不会明显增加。在多边形顶点数量维持在7万以下时,数据结构优化后的串行Vatti算法可以取得相对较好的效果。随着多边形顶点数量增加到7万以上时,并行化之后的Vatti算法其加速效果逐渐显现出来,且顶点数量越多加速效果越明显。
图8 并行化前后的Vatti算法耗时对比

Fig. 8 Time consumption comparison of Vatti algorithm before and after parallelization

4 结论与讨论

叠加分析是地理信息系统空间分析中基础且重要的空间分析功能之一,面向矢量数据的叠加分析算法具有数据结构复杂、计算难度大的双重特点。在面对大量数据时,传统算法耗时较多,使用GPU对传统的多边形叠加分析算法进行并行化能够有效地提升计算效率。本文针对原始Vatti算法中耗时最多的扫描束构建过程提出了预先提取多边形顶点坐标信息后使用排序算法进行排序的VCS优化方法,优化了顶点信息读取及存储方式,降低了原始算法之间的部分依赖性,使用较小的空间存储代价换取了串行算法计算效率的提升。最后通过双调排序算法对使用VCS优化方法后的Vatti算法进行了并行化改造,对比了不同情况下串行与并行Vatti算法的计算效率,发现加速比随顶点数量的增加不断升高,当多边形顶点数量为92万,CUDA每个线程块中的线程数量为32时,效率总体提升了4.9倍,由此验证了本文提出方法对Vatti算法优化及并行化改造的有效性。本文通过对Vatti算法的并行化改造,以及对高性能细粒度并行叠加分析问题关键技术的探讨与研究,提升了基于Vatti算法的矢量多边形叠加分析过程的计算效率,在廉价消费级硬件平台上获得较为理想的加速比,对于解决面向海量地理数据的空间分析问题具有一定的参考价值。
本文在对Vatti算法的扫描束构建过程的优化过程中,没有涉及算法依赖性更为紧密的裁剪过程,但是其时间开销在Vatti算法的整体计算过程中也占据较高比例,因此有必要对该过程开展深入的优化方法研究,以提升算法整体的计算效率,是我们下一步工作的重点方向。

References

Publishing order | Descend order by publishing year | Descend order by cited within
[1]
王结臣, 王豹, 胡玮, 等. 并行空间分析算法研究进展及评述[J]. 地理与地理信息科学, 2011, 27(6):1-5.

[ Wang J C, Wang B, Hu W, et al. Review on parallel spatial analysis algorithms[J]. Geography and Geo-information Science, 2011, 27(6):1-5. ] DOI: CNKI:SUN:DLGT.0.2011-06-002

[2]
左尧, 王少华, 钟耳顺, 等. 高性能GIS研究进展及评述[J]. 地球信息科学学报, 2017, 19(4):437-446.

DOI

[ Zuo Y, Wang S H, Zhong E S, et al. Research progress and review of high-performance GIS[J]. Journal of Geo-Information Science, 2017, 19(4):437-446. ] DOI: 10.3969/j.issn.1560-8999.2017.04.001

[3]
赵银利, 范俊甫, 王崇倡. GIS典型几何计算算法的并行化及优化研究[J]. 测绘与空间地理信息, 2017, 40(7):163-166.

[ Zhao Y L, Fan J F, Wang C C. Parallelization and optimization for several typical geometic-analysis algorithms in GIS[J]. Geomatics & Spatial Information Technology, 2017, 40(7):163-166. ] DOI: 10.3969/j.issn.1672-5867.2017.07.052

[4]
邱强, 秦承志, 朱效民, 等. 全空间下并行矢量空间分析研究综述与展望[J]. 地球信息科学学报, 2017, 19(9):1217-1227.

[ Qiu Q A, Qin C Z, Zhu X M, et al. Overview and prospect on spatial analysis of parallel vectors in pan-spatial concept[J]. Journal of Geo-information Science, 2017, 19(9):1217-1227. ] DOI: 10.3724/SP.J.1047.2017.01217

[5]
范俊甫. 并行化矢量多边形叠加算法研究[J]. 测绘学报, 2016, 45(4):502.

[ Fan J F. Parallel algorithms for polygon overlapping[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(4):502. ] DOI: 10.11947/j.AGCS.2016.20150495

[6]
彭志云, 王惜民, 赖美森, 等. 并行计算时代:基于CUDA的通用GPU计算的发展[J]. 科技与企业, 2016, 11:80.

[ Peng Z Y, Wang X M, Lai M S, et al. The era of parallel computing: the development of general GPU computing based on CUDA[J]. Technology And Enterprise, 2016, 11:80. ] DOI: 10.3969/j.issn.1004-9207.2016.11.074

[7]
姚晓, 邱强, 肖茁建, 等. Spark框架下矢量多边形求交算法研究[J]. 高技术通讯, 2018, 28(6):500-507.

[ Yao X A, Qiu Q A, Xiao Z J, et al. Research on vector polygon intersection algorithm in Spark framework[J]. Chinese High Technology Letters, 2018, 28(6):500-507. ] DOI: 10.3772/j.issn.1002-0470.2018.06.003

[8]
Sutherland I E, Hodgman G W. Reentrant polygon clipping[J]. Communications of the ACM, 1974, 17(1):32-42. DOI: 10.1145/360767.360802

DOI

[9]
Weiler K, Atherton P. Hidden surface removal using polygon area sorting[J]. ACM SIGGRAPH Computer Graphics, 1977, 11(2):214-222. DOI: 10.1145/965141.563896

DOI

[10]
Vatti B R. A generic solution to polygon clipping[J]. Communications of the ACM, 1992, 35(7):56-63. DOI: 10.114 5/129902.129906

DOI

[11]
Greiner G, Hormann K. Efficient clipping of arbitrary polygons[J]. ACM Transactions on Graphics, 1998, 17(2):71-83. DOI: 10.1145/274363.274364

DOI

[12]
苏诚, 韩俊刚. Sutherland-Hodgman裁剪算法的改进[J]. 西安邮电大学学报, 2013, 18(3):80-82.

[ Su C, Han J G. An advanced Sutherland-Hodgman algorithm[J]. Journal of Xi'an University of Posts and Telecommunications, 2013, 18(3):80-82. ] DOI: 10.3969/j.issn.1007-3264.2013.03.020

[13]
白晨. 一种任意多边形的裁剪算法[D]. 电子科技大学, 2012.

[ Bai C. A clipping algorithm for arbitrary polygon[D]. University Of Electronic Science And Technology Of China, 2012. ] DOI: CNKI:CDMD:2.1011.054140

[14]
刘勇奎, 高云, 黄有群. 一个有效的多边形裁剪算法[J]. 软件学报, 2003, 14(4):845-856.

[ Liu Y K, Gao Y, Huang Y Q. An efficient algorithm for polygon clipping[J]. Journal of Software, 2003, 14(4):845-856. ] DOI: CNKI:SUN:RJXB.0.2003-04-018

[15]
范俊甫. 并行化矢量多边形叠加算法研究[D]. 北京:中国科学院大学, 2014.

[ Fan J F. Parallel algorithms for polygon overlapping[D]. Beijing: University of Chinese Academy of Sciences, 2014. ]

[16]
彭杰, 刘南, 唐远彬, 等. 一种基于交点排序的高效多边形裁剪算法[J]. 浙江大学学报(理学版), 2012, 39(1):107-111,122.

[ Peng J E, Liu N, Tang Y B, et al. An efficient algorithm for polygon clipping based on intersection points sorting[J]. Journal of Zhejiang University (Science Edition), 2012, 39(1):107-111,122. ] DOI: 10.3785/j.issn.1008-9497.2012.01.022

[17]
Martínez F, Rueda A J, Feito F R. A new algorithm for computing Boolean operations on polygons[J]. Computers & Geosciences, 2009, 35(6):1177-1185. DOI: 10.1016/j.cageo.2008.08.009

DOI

[18]
Zhao K, Jin B, Fan H, et al. High-performance overlay analysis of massive geographic polygons that considers shape complexity in a cloud environment[J]. ISPRS International Journal of Geo-Information, 2019, 8(7):290. DOI: 10.3390/ijgi8070290

DOI

[19]
Zhou C, Chen Z J, Li M C. A parallel method to accelerate spatial operations involving polygon intersections[J]. International Journal of Geographical Information Science, 2018, 32(12):2402-2426. DOI: 10.1007/s10586-019-02944-y

DOI

[20]
Zhou C, Li M C. A systematic parallel strategy for generating contours from large-scale DEM data using collaborative CPUs and GPUs[J]. Cartography and Geographic Information Science, 2021, 48(3):187-209. DOI: 10.1080/15230406.2020.1854862

DOI

[21]
Zhou C, Li M C. Performance evaluation of spatial indexing to identify polygon intersection[J]. Geocarto International, 2020, 35(16):1850-1872. DOI: 10.1080/10106049.2019.1624987

DOI

[22]
Zhao K, Jin B X, Fan H, et al. A data allocation strategy for geocomputation based on shape complexity in A cloud environment using parallel overlay analysis of polygons as an example[J]. IEEE Access, 2020, 8:185981-185991. DOI: 10.1109/ACCESS.2020.3030700

DOI

[23]
Zhou Y K, Wang S H, Guan Y. An efficient parallel algorithm for polygons overlay analysis[J]. Applied Sciences, 2019, 9(22):4857. DOI: 10.3390/app9224857

DOI

[24]
范俊甫, 孔维华, 马廷, 等. RaPC:一种基于栅格化思想的多边形裁剪算法及其误差分析[J]. 测绘学报, 2015, 44(3):338-345.

[ Fan J F, Kong W H, Ma T, et al. RaPC: A rasterization-based polygon clipping algorithm and its error analysis[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(3):338-345. ] DOI: 10.11947/j.AGCS.2015.20140017.

[25]
Fan J F, He H X, Hu T Y, et al. Rasterization computing-based parallel vector polygon overlay analysis algorithms using OpenMP and MPI[J]. IEEE Access, 2018, 6:21427-21441. DOI: 10.1109/ACCESS.2018.2825452

DOI

[26]
张鹏, 俞宵, 马子云, 等. 统一计算设备架构的D8算法并行化研究[J]. 测绘科学, 2020, 45(3):163-169.

[ Zhang P, Yu X A, Ma Z Y, et al. Research on parallelization of D8 algorithm based on CUDA[J]. Science of Surveying and Mapping, 2020, 45(3):163-169. ] DOI: 10.16251/j.cnki.1009-2307.2020.03.025

[27]
吴旭桥, 吴烨, 陈荦, 等. 面向大规模DEM数据的并行填挖算法[J]. 地理信息世界, 2019, 26(6):21-25.

[ Wu X Q, Wu Y, Chen L, et al. A parallel cut-fill algorithm for large-scale DEM data[J]. Geomatics World, 2019, 26(6):21-25. ] DOI: 10.3969/j.issn.1672-1586.2019.06.004

[28]
Guo M Q, Han C D, Guan Q F, et al. A universal parallel scheduling approach to polyline and polygon vector data buffer analysis on conventional GIS platforms[J]. Transactions in GIS, 2020, 24(6):1630-1654. DOI: 10.1111/tgis.12670

DOI

[29]
Zhou C, Chen Z J, Li M C. A parallel method to accelerate spatial operations involving polygon intersections[J]. International Journal of Geographical Information Science, 2018, 32(12):2402-2426. DOI: 0.1080/13658816.2018.1508689

DOI

[30]
陈达伦, 陈荣国, 谢炯. 基于MPP架构的并行空间数据库原型系统的设计与实现[J]. 地球信息科学学报, 2016, 18(2):151-159.

DOI

[ Chen D L, Chen R G, Xie J. Research of the parallel spatial database proto system based on MPP architecture[J]. Journal of Geo-Information Science, 2016, 18(2):151-159. ] DOI: 10.3724/SP.J.1047.2016.00151

[31]
范俊甫, 马廷, 周成虎, 等. 几何部件缓冲区域合并的Buffer算法及其并行优化方法[J]. 测绘学报, 2014, 43(9):969-975.

[ Fan J F, Ma T, Zhou C H, et al. Research on a buffer algorithm based on region-merging of buffered geometry components and its parallel optimization[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(9):969-975. ] DOI: 10.13485/j.cnki.11-2089.2014.0122

[32]
范俊甫, 马廷, 周成虎, 等. 基于集群MPI的图层级多边形并行合并算法[J]. 地球信息科学学报, 2014, 16(4):517-523.

DOI

[ Fan J F, Ma T, Zhou C H, et al. Implementation of cluster MPI-based parallel polygon union algorithm at the feature layer level[J]. Journal of Geo-Information Science, 2014, 16(4):517-523. ] DOI: 10.3724/SP.J.1047.2014.00517

[33]
Alan Murta. A general polygon clipping library[EO/OL]. http://www.cs.man.ac.uk/~toby/alan/software/gpc.html 2020-05-30.

[34]
Angus Johnson. Clipper-an open source freeware library for clipping and offsetting lines and polygons[EO/OL].

[35]
张林波. 并行计算导论[M]. 北京: 清华大学出版社, 2006.

[ Zhang L B. An introduction to parallel computing[M]. Beijing: Tsinghua University Press Co., Ltd., 2006. ]

[36]
Velusamy K, Rolinger T B, McMahon J. Performance strategies for parallel bitonic sort on a migratory thread architecture[C]// 2020 IEEE High Performance Extreme Computing Conference (HPEC). IEEE, 2020:1-7. DOI: 10.1109/HPEC43674.2020.9286172

[37]
Leonov M. Comparison of the different algorithms for polygon boolean operations[EO/OL]. http://www.complex-a5.ru/polyboolean/comp.html 2020-05-30.

Options
Outlines

/

〈 〉