EN中文

Journal of Geo-information Science >

2022 , Vol. 24 >Issue 4: 631 - 642

DOI: https://doi.org/10.12082/dqxxkx.2022.210582

A Synergistic Simplification Method of Contours of Natural Continuous Polygons

  • ZHANG Fubing , 1 ,
  • SUN Qun , 1, * ,
  • ZHU Xinming 1, 2, 3 ,
  • MA Jingzhen 1, 2, 3
Expand
  • 1. Institute of Geospatial Information, University of Information Engineering, Zhengzhou 450052, China
  • 2. Collaborative Innovation Center of Geo-information Technology for Smart Central Plains, Zhengzhou 450052, China
  • 3. Key Laboratory of Spatiotemporal Perception and Intelligent processing, Ministry of Natural Resources, Zhengzhou 450052, China
*SUN Qun, E-mail:

Received date: 2021-09-26

  Revised date: 2021-10-25

  Online published: 2022-06-25

Supported by

National Natural Science Foundation of China(41801313)

National Natural Science Foundation of China(41901397)

The Fund Project of ZhongYuan Scholar of Henan Province(202101510001)

Copyright

Copyright reserved © 2022
Fold

Abstract

The simplification of contours of natural continuous polygons is an important step of automatic cartographic generalization of natural polygons in topographic map and natural patches in general survey of geographical conditions. Most of the existing simplification algorithms of polygonal contours are based on the line simplification algorithms, which cannot effectively simplify bending features, maintain the area balance, and meet the requirements of graphic visual clarity. Moreover, there are topological problems in the simplification result, such as inconsistent shared contour, self-intersection of contour and intersection between contours. Therefore, combined with the expression characteristics and simplification requirements of natural continuous polygons, a synergistic simplification method is proposed for the contours of natural continuous polygons. First, the natural continuous polygons are transformed into topological data structure, and the constrained Delaunay triangulation is constructed based on the arc segment to be simplified and its adjacent arc segments to identify the simplified region. Second, the arc segment bilateral hierarchical multiple tree model is used to gradually remove or partially remove narrow bends and simplify small bends. Third, the narrow regions are adaptively exaggerated to avoid unclear details on the map. The simplification experiment of Vegetation and Soil polygons in 1:50000 scale topographic map of a region in Henan, China was carried out. Compared with the reference methods, our proposed method can effectively maintain the topological consistency and area balance among natural continuous polygons before and after the simplification and fully simplify the invisible details under the target map scale, and the position accuracy of our simplification results meet the requirement. Therefore, the proposed method has better superiority in terms of topological consistency, visual clarity, and area balance.

Key words： cartographic generalization; natural continuous polygons; arc segment synergistic simplification; topological consistency; visual clarity; area balance; structured model

Cite this article

ZHANG Fubing , SUN Qun , ZHU Xinming , MA Jingzhen . A Synergistic Simplification Method of Contours of Natural Continuous Polygons[J]. Journal of Geo-information Science, 2022 , 24(4) : 631 -642 . DOI: 10.12082/dqxxkx.2022.210582

1 引言

面要素边线化简是自动制图综合重要的研究内容之一[1,2],旨在化简面要素外部轮廓,消除当前地图比例尺无法清晰表示的边线局部细节[2,3]。面群是制图区域中呈连续空间分布结构特征的面要素群组,其中自然连续面群区别于城市街区等人工连续面群和湖泊等自然离散面群,与地理国情普查图全覆盖、无重叠、无缝隙的分布特征具有相似性。因此,自然连续面群边线化简在消除人眼无法清晰分辨局部细节的同时,还需保持化简前后的拓扑一致性、面积平衡、几何和地理特征等。
目前,面要素边线化简研究工作多数以大比例尺居民地作为研究对象[1],而针对自然面要素边线的化简多是以曲线化简算法为基础。线要素化简作为制图综合中重要的研究内容和经典的研究问题之一[1,4],已经产生了大量的研究成果,包括针对曲线顶点处理的化简算法[5,6,7,8,9]以及基于弯曲识别的化简算法[4,10-17]。现有的自然面要素边线化简策略多按照闭合曲线[10,11,12]或者特征点约束分段[15,18-23]采取曲线化简算法,也有文献尝试从图像处理的角度对边线进行化简[24,25]。针对化简产生的图形冲突问题,现有研究主要通过模型来进行控制,如李成名等[9]建立全局化简判断模型标记间距较小部位进行选择性处理以保证拓扑关系正确,但标记不作处理部分在目标比例尺易产生图面视觉冲突;胡凤敏等[23]通过转换图斑数据表达模型进行弧段化简以避免共享边界不一致,但对自然弧段的统一光滑处理会发生变形[6];张立华等[26]依据约束Delaunay三角网（Constrained Delaunay Triangulation,CDT）结构化模型实现海岸线的单侧协同化简,并进行了相应的夸大处理,化简结果符合海图制图应用要求。
CDT在探测弧段邻近关系、标识化简区域、识别弯曲特征点[10,15]和条带状弯曲[27]等方面具有明显优势,针对CDT的树结构化模型已产生较多的研究成果,其中弯曲深度二叉树[10,15]、弯曲多叉树[13,14]、骨架线二叉树[27]均是针对单个线要素的结构化表达模型,未标识线要素之间的化简区域,线要素之间易产生拓扑问题和视觉冲突。虽然层次二叉树[26]考虑了海岸线之间的空间邻近关系,但是“扩陆缩海”的海图综合原则,只能实现海岸线单侧化简。
整体而言,目前化简方法多关注线/面边线本身的图形特征或拓扑关系,未同时顾及面群内要素之间的拓扑一致性、视觉清晰性和面积平衡,化简结果存在边线相接或相交的拓扑问题。鉴于以上分析,结合面群表达特点和化简要求,本文以面群中的拓扑弧段为化简单元,综合考虑待化简弧段与其相邻弧段之间的空间关系,构建CDT支持下的弧段双侧层次多叉树模型,基于此模型,通过条带状弯曲识别与渐进式退化、细小弯曲化简、狭窄“瓶颈”识别与夸大步骤实现边线协同化简。

2 自然连续面群边线结构化表达

2.1 表达特点

自然连续面群作为反映要素类型、分布范围与结构、形状特征、数目种类以及与其他要素关系的矢量空间要素,受到不同区域气候、地形、地质、人类活动、空间认知水平等条件的影响,其形态、结构具有诸多特点,体现在以下3个方面。① 分布态势的复杂性。基础地理信息中的自然连续面群具有部分覆盖、无重叠、相邻分布和相离分布同时存在的空间分布特点,面群内部邻近要素之间相接情形复杂多变。② 弯曲特征的多样性。条带状弯曲与非条带状弯曲无序分布,在条带状弯曲密集分布面群边线上,边线两侧面要素呈“犬牙交错”分布态势,随着比例尺缩小,边线易产生视觉上的粘连和冲突,需进行化简处理。③ 拓扑关系的严格一致性。连续面群内部邻近面要素之间的共享边线在数据存储和表达上均保持着严格的一致性,应用化简措施时应保持其化简前后的拓扑一致性。如图1显示了河南省某区域1:5万地形图植被与土质面要素局部分布特征。
图1 自然连续面群边线分布特征

Fig. 1 Distribution characteristics of contours of natural continuous polygons

2.2 化简要求

结合自然连续面群表达特点,边线化简结果应满足以下要求：
（1）保持化简前后的拓扑一致性。自然连续面群化简的过程中,需要保证边线两侧面要素拓扑关系正确,保持化简前后的拓扑一致性。
（2）满足视觉清晰性要求。综合考虑自然连续面群边线的地理特征和几何形态,消除目标比例尺下无法清晰表达的边线细节。
（3）顾及不同面要素之间的面积平衡。自然连续面群作为面状分布要素,其化简应保持化简前后不同面要素间的面积平衡。

2.3 CDT构建

以自然连续面群拓扑弧段为化简单元可以有效避免共享边界不一致的问题[23],但是单纯进行弧段化简难以避免弧段之间的图形冲突。本文以待化简弧段及其左右多边形所包含的邻近弧段（记为约束弧段）构建CDT,标识弧段内部和弧段之间的化简区域,避免图形冲突。参照文献[28]进行面群简单数据结构与拓扑数据结构的相互转换,以线段平均长度对弧段进行加密,CDT构建完成后,提取与待化简弧段除首末结点之外至少共用一个顶点的三角形作为化简处理区域,提升化简效率。本文将CDT中不与其他三角形相邻且不与弧段重合的边定义为开口边,依据三角形约束边和开口边数量以及三角形位置将三角形分为4类：① Ⅰ类三角形,包含两条约束边的三角形;② Ⅱ类三角形,只有一条约束边或者位于面群内只有一个开口边的三角形;③ Ⅲ类三角形,不包含开口边和约束边的三角形;④ Ⅳ类三角形,位于面群外且包含一个开口边的三角形。图2显示了由2个自然面要素组成的简单面群不同类型弧段构建CDT的结果,Ⅰ类、Ⅱ类、Ⅲ类、Ⅳ类三角形分别被填充为绿色、灰色、粉色、橙色,其中Ⅰ类三角形分布于弯曲底部,Ⅲ类三角形分布于分叉处,Ⅳ类三角形位于面群外侧弯曲开口处,Ⅱ类三角形实现对以上三角形的连接;图2中 n i ( i > 0 )表示Ⅲ类三角形或者Ⅳ类三角形, e j ( j > 0 )表示Ⅰ类三角形。
图2 待化简弧段CDT构建结果

Fig. 2 CDT construction results of arc segment to be simplified

2.4 弧段双侧层次多叉树模型建立

本文采用多叉树结构对弧段两侧CDT进行结构化组织,构建弧段双侧层次多叉树模型,建模待化简弧段内部及其与约束弧段之间的化简区域。针对共享弧段左右两侧CDT连续（图2(a)）,而非共享弧段内侧CDT连续但外侧CDT离散（图2(b)）的特点,模型构建步骤如下：
（1）初始化CDT中所有三角形为“False”,利用待化简弧段将CDT划分为多个子CDT,依次对这些子CDT构建树结构化模型,若该子CDT位于面群内,选择面积最大的Ⅲ类三角形作为起点,沿Ⅲ类三角形3条边方向分别构造二叉树,转步骤（2）;否则,选择子CDT中开口边最长的Ⅳ类三角形作为起点,沿Ⅳ类三角形非约束边方向构造二叉树,转步骤（2）。
（2）将当前三角形作为二叉树的根三角形放入根节点存储,并将其标记为“True”,转步骤（3）;当所有Ⅰ类三角形均作为叶子节点加入树模型,转步骤（6）。
（3）由当前三角形所在节点开始,寻找未标记为“True”的非约束边邻近三角形,若该三角形为Ⅱ类三角形,则将其放入当前节点进行存储,并将其标记为“True”,寻找其另一个未被标记为“True”的邻近三角形,直到邻近三角形为Ⅰ类三角形、Ⅲ类三角形、Ⅳ类三角形或者已标记为“True”的三角形时停止,若该邻近三角形为Ⅰ类三角形或者已标记为“True”的三角形,转步骤（4）;否则,转步骤（5）。
（4）将当前节点设置为叶子节点,Ⅰ类三角形或者已标记为“True”的三角形放入叶子节点进行存储,并将Ⅰ类三角形标记为“True”。
（5）为当前节点设置子节点,Ⅲ类三角形或Ⅳ类三角形放入当前节点和子节点进行存储,并标记为“True”,由子节点出发重新执行步骤（3）。
（6）新建根节点,关联待化简弧段两侧所有树结构的根节点,实现弧段双侧层次多叉树模型构建。
按照上述步骤对图2中2种类型弧段构建弧段双侧层次多叉树模型,模型构建结果如图3所示。需要说明是,虽然2种弧段双侧层次多叉树构建步骤和建模的CDT区域存在差异,但构建的树结构具有相似性,应用于化简不作区分;模型中根节点n0不存贮任何信息,只起到关联作用,模型构建方法对组成“岛”的弧段同样有效,构建步骤同共享弧段。
图3 弧段双侧层次多叉树模型构建结果

注：n0为根节点;ni(i>0)为Ⅲ类或Ⅳ类三角形;ej(j>0)为Ⅰ类三角形。

Fig. 3 Construction results of arc segment bilateral hierarchical multiple tree model

基于上述模型实现了弧段两侧CDT结构化表达,除根节点之外,每一个节点均代表一处独立的待处理区域。值得注意的是,分别提取弧段双侧层次多叉树模型中每个待处理区域的骨架线,将骨架线放入对应的节点进行存储,即可获取弧段双侧的骨架线多叉树模型,如图4所示。骨架线作为待处理区域的降维表达,能够表达其结构特点,是重要的化简参量。本文综合考虑一维骨架线和二维待处理区域应用于化简处理的优势,在弧段双侧层次多叉树模型中并行存储节点对应的待处理区域及其骨架线,生成所需结构化表达模型。
图4 弧段双侧层次骨架线多叉树模型

注：m0为根节点mi(i>0)为骨架线端点。

Fig. 4 Multiple tree model of arc segment bilateral hierarchical skeletons

3 自然连续面群边线协同化简

3.1 化简流程

以弧段双侧层次多叉树模型为基础实现待化简弧段的协同化简,化简流程如图5所示。实现步骤包括：① 基于本文结构化模型识别叶子节点中的条带状弯曲,渐进式退化条带状弯曲中从Ⅰ类三角形开始目标尺度下不清晰的部分;②对细小弯曲构建包络带[15],实现顾及面积平衡的化简曲线选择;③对完成条带状弯曲退化和细小弯曲化简的弧段重新构建结构化模型,遍历模型中的节点,识别狭窄“瓶颈”并进行自适应夸大处理。
图5 弧段协同化简流程

Fig. 5 The process of arc segment synergistic simplification

为便于化简过程叙述,将三角形 tri可视宽度阈值记为 L thd,弯曲化简深度阈值记为 D thd,特征弯曲识别参数记为 γ,包络带路径连接控制参数记为 μ thd; node为模型中除根节点以外的节点, Area node表示当前节点 node包含待处理区域的面积, Len ( node )表示当前节点 node包含骨架线的长度, Tris node表示节点 node包含待处理区域中三角形的集合; Len tri表示待处理区域中单个三角形 tri的宽度,依据三角形类型的不同,计算方式定义如下：Ⅰ类三角形宽度为非约束边的长度,Ⅱ类三角形宽度为约束边（开口边）相对的顶点到约束边（开口边）的最短距离,Ⅲ类和Ⅳ类三角形不计算其宽度; minLen p k , L Arc表示点 p k与弧段 L Arc之间最短距离,Ori p k , L Arc表示点 p k与弧段 L Arc之间最短距离的方向。

3.2 条带状弯曲识别与渐进式退化

条带状弯曲作为对一种弯曲特征空间认知的结果,缺乏明确的度量标准,故按照专家经验,将满足深度为平均宽度2倍以上的弯曲视为条带状[27],并利用骨架线长度衡量弯曲深度。同时,为了保持面积平衡,减少退化面积,对细小条带状弯曲（弯曲骨架线长度小于 D thd）不作退化处理,将在3.3节同细小弯曲一起进行化简。识别和退化具体步骤如下：
（1）遍历模型中的叶子节点,若 Area node < 0.5 Len node 2,且 Len node > D thd,则叶子节点 node所包含的化简区域为条带状弯曲,转入步骤（2）;否则,继续判断下一个叶子节点;
（2）从Ⅰ类三角形开始遍历 Tris node,依次获取三角形宽度 Len tri,判断 Len tri < L thd,若是,则将该三角形标记为“待退化”（如图6(a)中的灰色三角形）;否者,标记结束,转步骤（3）;
图6 条带状弯曲退化

Fig. 6 The simplification results of narrow bend

（3）获取“待退化”三角形集合,删除待化简弧段上标记为“待退化”三角形顶点所在子弧段顶点序列,并保留子弧段首尾点,实现单个条带状弯曲的退化操作（图6(b)）;重新构建待化简弧段的弧段双侧层次多叉树模型,转步骤（1）,直到构建的模型中不存在满足退化操作条件的条带状弯曲,退化操作结束。

3.3 顾及面积平衡约束的细小弯曲化简

针对细小弯曲化简,引入顾及面积平衡约束的包络带化简算法[15],基于弧段双侧层次多叉树模型,由根节点向子节点依次遍历,获取弯曲深度小于 D thd的细小弯曲,并排除弯曲深度大于 γ ∙ D thd的特征弯曲顶点所在弯曲,构建包络带结构（图7(a)）,基于CDT提取包络带中连接前后2个端点 P m与 P n之间的骨架线作为中心线（图7(b)）。
图7 包络带构建与中心线提取

Fig. 7 Envelope construction and centerline extraction

除中心线外,将包络带左右两侧的边界线也作为细小弯曲的化简结果,形成左边界、中心线、右边界3种化简结果,依据包络带内两侧细小弯曲的面积差异 μ选择合适的路径连接,面积差异 μ计算方式如下：
μ = Are a BL - Are a BR Are a BL + Are a BR
式中： Are a BL和 Are a BR分别是包络带内左右两侧细小弯曲的总面积。路径连接规则[15]如下：
（1）如果 μ ≤ μ thd,选择中心线作为路径连接;
（2）如果 μ < - μ thd,说明右侧细小弯曲面积明显大于左侧,选择左边界线作为路径连接;
（3）如果 μ > μ thd,说明左侧细小弯曲面积明显大于右侧,选择右边界线作为路径连接。
基于连接规则,通过控制参数 μ thd的大小,选择有利于保持面群中要素间面积平衡的包络带路径连接作为化简结果。

3.4 狭窄“瓶颈”识别与自适应夸大

狭窄“瓶颈”识别方式与条带状弯曲“待退化”区域识别相似,遍历模型中的 node,比较 Tris node中三角形宽度 Len tri,提取满足 Len tri < L thd三角形集合（图8(a)中灰色三角形及其之间的三角形）进行夸大处理,比较时自动排除叶子节点中的Ⅰ类三角形,三角形集合为空时,退出当前 node的夸大操作。狭窄“瓶颈”夸大处理操作如下：
图8 狭窄“瓶颈”识别与自适应夸大

Fig. 8 Schematic diagram of local narrow details identification and adaptive exaggeration process

（1）遍历满足 Len tri < L thd条件的三角形集合,按照三角形邻近关系提取待化简弧段和约束弧段上与三角形顶点重合的子弧段,转步骤（2）;
（2）遍历子弧段上的顶点 p k,计算其与相对弧段 L Arc之间的最短距离 minL en p k , L Arc,将点 p k沿Ori p k , L Arc方向偏移 L thd - min Len p k , L Arc / 2距离（图8（b））,完成所有子弧段顶点的偏移。
上述偏移方式,偏移距离和方向计算不局限于单个三角形,综合考虑狭窄“瓶颈”顶点与相对弧段之间的距离和方向关系,且不受加密步长影响。偏移完成后,以偏移后的结果替换待化简弧段和约束弧段上对应的子弧段（图8(c)）,实现夸大操作。
依次遍历拓扑结构组织的自然连续面群所有弧段,执行上述操作实现边线化简处理。通过CDT标识弧段之间和弧段内部的化简区域,基于弧段双侧层次多叉树模型的协同化简处理方式,可有效保持拓扑一致性;条带状弯曲退化和细小弯曲化简操作可以在充分化简不清晰弯曲区域的同时,保证化简前后的面积平衡;狭窄“瓶颈”自适应夸大可以消除边线内部和边线之间的视觉冲突,避免边线产生相接和相交的拓扑问题。

4 实验与分析

4.1 实验数据与参数设置

选取河南省某区域1:5万地形图中33 km2范围内的植被与土质面要素层作为实验数据（图9）,分别将其化简至1:10万和1:25万。需要说明的是,连续面群综合涉及合并、边线化简、降维等诸多操作,为便于实验分析和评价,本文进行实验时仅采取化简操作。为评价本文方法有效性和优越性,将本文方法与Douglas-Peucker算法[5]、顾及空间关系约束的全局线化简算法[9],包络带化简算法[15]进行比较,化简对象均为面群拓扑弧段,以避免共享边界不一致问题。按照人眼最小可分辨距离设置 L thd=0.2 mm;参照文献[15]设置弯曲深度 D thd=0.5 mm, γ=3, μ thd=0.7,包络带化简算法参数与本文方法相同; D-P算法化简阈值同 L thd;参照文献[9],全局线 化简算法中设置L-O算法最小可视目标参数 D=0.4 mm,D-P算法化简阈值为 4 L thd,不同比例尺图上间距阈值均同 D。
图9 河南省某区域植被与土质实验数据

Fig. 9 The test data of polygonal vegetation and soil of a region in Henan, China

4.2 定性分析

D-P算法、全局线化简算法、包络带化简算法和本文方法2种化简尺度的化简结果如图10所示,对部分细节进行了叠加放大显示,红色线为化简结果,黑色线为原始边线。化简前后拓扑一致性保持结果如表1所示,定性评价从化简效果、拓扑一致性和视觉清晰性展开。
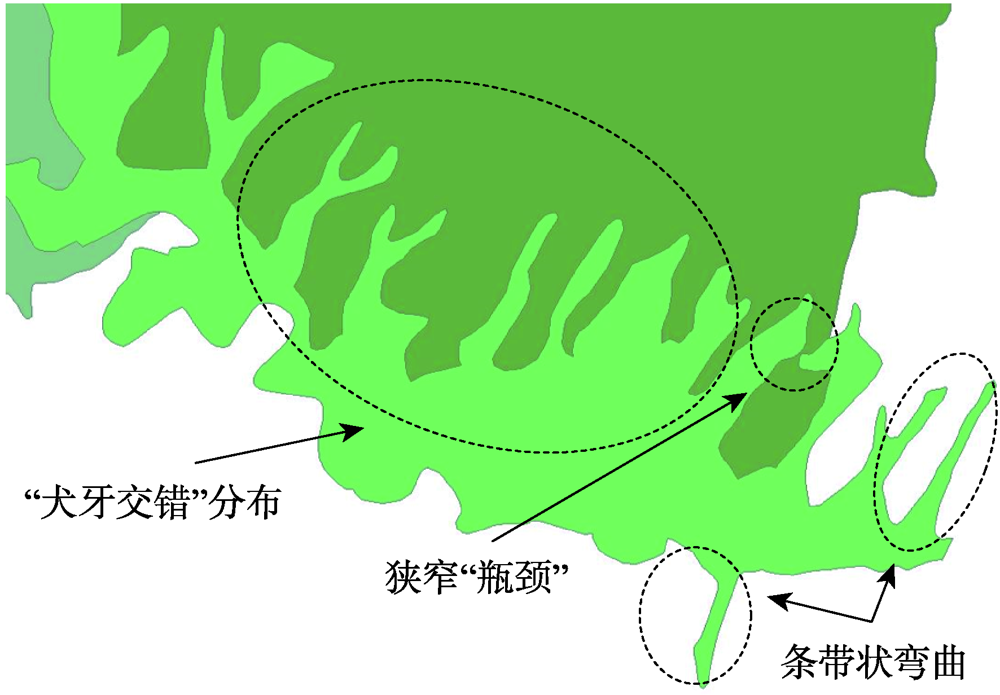
图10 不同算法化简结果

注：子图左下角的2个蓝色虚线圈为相应图上区域1和区域2的放大显示,其中红色线为化简结果,黑色线为原始边线。

Fig. 10 The simplification results of different algorithms

表1 实验区域拓扑一致性保持结果

Tab. 1 The results of topological consistency maintaining

方法 1:10万 1:25万
存在边线自交 存在边线之间相交或相接 存在边线自交 存在边线之间相交或相接
DP算法 是 否 是 是
全局线化简算法 否 否 否 否
包络带化简算法 否 否 否 是
本文方法 否 否 否 否
D-P算法化简结果（图10(a)和图10(b)）较为生硬、尖锐,条带状弯曲被削尖,增加了条带状弯曲的不清晰范围;对狭窄“瓶颈”未起到夸大效果,部分“瓶颈”狭窄程度加剧,且2种化简尺度均产生边线相接和相交的拓扑问题。全局线化简算法化简结果（图10(c)和图10(d)）未产生拓扑问题,化简结果光滑,显示其作为顾及空间关系约束线化简算法的优势,但是对间距较小边线的选择性处理使得狭窄“瓶颈”保持原状,产生了视觉上的不清晰性,随着化简尺度增加,不清晰性加剧;条带状弯曲易被识别为特征弯曲而未施加化简措施。包络带化简算法化简结果（图10(e)和图10(f)）自然平滑,细小弯曲化简满足应用需求,但是算法受制于保留局部弯曲特征点的约束,对条带状弯曲化简效果有限,如图10(e)和图10(f)中1处的条带状弯曲在两种化简尺度下均未受到化简处理;与前2种算法相同,包络带化简算法对狭窄“瓶颈”未起到夸大效果,虽然该算法在2种化简尺度未产生边线自相交的问题,但是在化简至1:25万时产生了与其他边线相交或者相接的拓扑问题。如图10(g)、图10(h)和表1所示,本文方法在2种化简尺度均未产生自相交和与其他边线相交的拓扑问题,有效保持了化简前后的拓扑一致性,同时分别对条带状弯曲和狭窄“瓶颈”进行退化和夸大处理,化简细小弯曲的同时保留了局部弯曲特征点,消除了目标比例尺下边线的不清晰细节,化简结果自然平滑符合认知。
通过定性对比分析,本文方法在化简结果视觉清晰性上优于3种对比算法,与全局线化简算法具有同样的拓扑一致性保持结果,化简效果较好,符合制图应用要求。

4.3 定量分析

采用位置误差[29]、面积变化率[15]和平均面积变化率[15] 3类评价指标定量评价不同算法对实验区域自然连续面群边线的化简效果。位置误差计算结果与化简效果对比如表2所示,分析可知：DP算法化简结果的位置误差较大,化简结果不符合视觉要求,全局线化简算法、包络带化简算法与本文算法化简结果的位置误差相对较小,表明3种方法均维持了化简前后边线的整体形状特征,化简结果精度较高。其中全局线化简算法位置误差明显较低,造成此结果的原因如下：① 为避免化简结果出现拓扑关系变化,算法依据全局化简判断模型对间距较小部分进行标记和选择性处理,2种目标比例尺分别有351个（1:10万）和1142个（1:25万）顶点未受到化简处理,其中也包含了组成细小弯曲的顶点;② 算法实施特点导致,且对极值点稀疏曲线段处理方式进一步减少化简处理的顶点。相较于全局线化简算法和包络带化简算法,本文方法在2种化简尺度下的化简结果位置误差值均稍大,主要原因是为保持化简前后的拓扑一致性和视觉清晰性,对条带状弯曲退化和狭窄“瓶颈”的夸大处理均增加了边线上顶点的位移值,导致位置误差变大,这是难以避免的。
表2 位置误差计算结果与化简效果对比

Tab. 2 Location errors of simplification results and comparison of simplification effect

方法 位置误差/m 条带状弯曲 细小弯曲 狭窄“瓶颈”
1:10万 1:25万
DP算法 69.7 258.9 未退化 已化简 未夸大
全局线化简算法 14.5 42.0 部分退化 部分化简 未夸大
包络带化简算法 26.1 106.6 部分退化 已化简 未夸大
本文方法 26.4 216.6 退化 已化简 夸大
保持不同面要素的面积平衡是面要素边线化简的重要约束条件,因此本文采用面积变化率比较化简前后面群中面要素面积变化,2种化简尺度面积变化率计算结果分别如图11和图12所示,平均面积变化率比较如表3所示。分析可知：本文方法与全局线化简算法和包络带化简算法在化简尺度为1:10万时,面积变化率均控制在1 %左右,平均面积变化率绝对值小于0.07 %,较好维持了化简前后的面积平衡,而DP算法的面积变化率起伏波动较大。化简尺度为1:25万时,除全局线化简算法外,3种算法在面要素4处均产生超过10 %的面积变化率,进一步分析可知,面要素4为面积较小、同时包含条带状弯曲和狭窄“瓶颈”的复杂面目标,应用不同化简算法后均产生了较大的面积变化;比较其他面要素化简前后的面积变化率,本文方法与全局线化简算法和包络带化简算法化简结果均表现良好,面积变化率控制在了4 %以内,平均面积变化率小于1 %,符合面积平衡要求。
图11 面积变化率对比（1:10万）

Fig. 11 Comparison of area change of simplification results at scale 1:100 000

图12 面积变化率对比（1:25万）

Fig. 12 Comparison of area change of simplification results at scale 1:250 000

表3 平均面积变化率统计

Tab. 3 Statistics of average area change rate

方法 平均面积变化率/%
1:10万 1:25万
D-P算法 -0.19 -1.37
全局线化简算法 -0.07 -0.24
包络带化简算法 0.01 0.99
本文算法 0.02 -0.96
通过定量对比分析,本文方法能够较好平衡自然连续面群弧段两侧条带状弯曲退化区域、细小弯曲化简区域以及狭窄“瓶颈”夸大区域,较好顾及了不同面要素之间的面积平衡,化简精度较高。

5 结论

针对现有的线/面边线化简方法难以同时兼顾自然连续面群内要素之间的拓扑一致性、视觉清晰性和面积平衡的问题,提出了一种面向自然连续面群边线的协同化简方法,对待化简弧段及其邻近弧段构建CDT支持下的弧段双侧层次多叉树模型,通过条带状弯曲识别与渐进式退化、细小弯曲化简、狭窄“瓶颈”识别与夸大步骤实现边线协同化简。选取河南某区域1:5万地形图中的植被与土质面要素进行实验,结论如下：
（1）针对拓扑一致性保持,利用CDT标识弧段内部及弧段之间的待化简区域、识别弯曲特征和应用化简措施,无拓扑问题产生,优于包络带化简算法和D-P算法。
（2）基于提出的弧段双侧层次多叉树模型,渐进式识别条带状弯曲并进行退化、化简细小弯曲以及自适应夸大狭窄“瓶颈”,可较好保证图面视觉清晰性,优于3种对比方法。
（3）依据局部弯曲特征点约束,对相邻细小弯曲建立包络带,并应用路径连接规则,较好顾及面积平衡保持,化简结果自然平滑、精度高,符合制图应用要求。
本文方法可以应用于地形图自然连续面群和地理国情普查图自然图斑的边线化简。未来,如何与面群分布区域内的其他类型要素进行协同综合需要深入研究,算法执行过程优化、效率提升有待进一步研究。

References

Publishing order | Descend order by publishing year | Descend order by cited within
[1]
武芳, 巩现勇, 杜佳威. 地图制图综合回顾与前望[J]. 测绘学报, 2017,46(10):1645-1664.

[ Wu F, Gong X Y, Du J W. Overview of the research progress in automated map generalization[J]. Acta Geodaetica et Cartographica Sinica, 2017,46(10):1645-1664. ] DOI: 10.11947/j.AGCS.2017.20170287

DOI

[2]
程绵绵, 孙群, 徐立, 等. 面轮廓线相似性和复杂性度量及在化简中的应用[J]. 测绘学报, 2019,48(4):489-501.

[ Cheng M M, Sun Q, Xu L, et al. Polygon contour similarity and complexity measurement and application in simplification[J]. Acta Geodaetica et Cartographica Sinica, 2019,48(4):489-501. ] DOI: 10.11947/j.AGCS.2019.20180124

DOI

[3]
王光霞, 游雄, 於建峰. 地图设计与编绘[M]. 北京: 测绘出版社, 2011.

[ Wang G X, You X, Yu J F. Map design and compilation[M]. Beijing: Sino Maps Press, 2011. ]

[4]
杜佳威, 武芳, 李靖涵, 等. 采用多元弯曲组划分的线要素化简方法[J]. 计算机辅助设计与图形学学报, 2017,29(12):2189-2196.

[ Du J W, Wu F, Li J H, et al. Line simplification method based on multi-bends groups division[J]. Journal of Computer-Aided Design & Computer Graphics, 2017,29(12):2189-2196. ] DOI: 10.3724/SP.J.1089.2017.16609

DOI

[5]
Douglas D H, Peucker T K. Algorithms for the reduction of the number of points required to represent a digitized line or its caricature[J]. Cartographica: the International Journal for Geographic Information and Geovisualization, 1973,10(2):112-122. DOI: 10.3138/FM57-6770-U75U-7727

DOI

[6]
Li Z L, Openshaw S. Algorithms for automated line generalization based on a natural principle of objective generalization[J]. International Journal of Geographical Information Systems, 1992,6(5):373-389. DOI: 10.1080/02693799208901921

DOI

[7]
朱鲲鹏, 武芳, 王辉连, 等. Li-Openshaw算法的改进与评价[J]. 测绘学报, 2007,36(4):450-456.

[ Zhu K P, Wu F, Wang H L, et al. Improvement and assessment of Li-openshaw algorithm[J]. Acta Geodaetica et Cartographica Sinica, 2007,36(4):450-456. ] DOI: 10.3321/j.issn:1001-1595.2007.04.015

DOI

[8]
金澄, 安晓亚, 崔海福, 等. 矢量瓦片地图线化简算法研究[J]. 地球信息科学学报, 2019,21(10):1502-1509.

DOI

[ Jin C, An X Y, Cui H F, et al. An algorithm for simplifying linear elements of vector tile maps[J]. Journal of Geo-information Science, 2019,21(10):1502-1509. ] DOI: 10.12082/dqxxkx.2019.190214

DOI

[9]
李成名, 郭沛沛, 殷勇, 等. 一种顾及空间关系约束的线化简算法[J]. 测绘学报, 2017,46(4):498-506.

[ Li C M, Guo P P, Yin Y, et al. A line simplification algorithm considering spatial relations between two lines[J]. Acta Geodaetica et Cartographica Sinica, 2017,46(4):498-506. ] DOI: 10.11947/j.AGCS.2017.20160546

DOI

[10]
艾廷华, 郭仁忠, 刘耀林. 曲线弯曲深度层次结构的二叉树表达[J]. 测绘学报, 2001,30(4):343-348.

[ Ai T H, Guo R Z, Liu Y L. A binary tree representation of curve hierarchical structure in depth[J]. Acta Geodaetica et Cartographic Sinica, 2001,30(4):343-348. ] DOI: 10.3321/j.issn:1001-1595.2001.04.013

DOI

[11]
李靖涵, 武芳, 杜佳威, 等. Delaunay三角网支持下的海图等深线化简[J]. 武汉大学学报·信息科学版, 2019,44(5):778-783.

[ Li J H, Wu F, Du J W, et al. Chart depth contour simplification based on delaunay triangulation[J]. Geomatics and Information Science of Wuhan University, 2019,44(5):778-783. ] DOI: 10.13203/j.whugis20170223

DOI

[12]
杜维, 艾廷华, 徐峥. 一种组合优化的多边形化简方法[J]. 武汉大学学报·信息科学版, 2004,29(6):548-550.

[ Du W, Ai T H, Xu Z. A polygon simplification method based on combinatorial optimization[J]. Geomatics and Information Science of Wuhan University, 2004,29(6):548-550. ] DOI: 10.3321/j.issn:1671-8860.2004.06.020

DOI

[13]
翟仁健, 武芳, 朱丽, 等. 曲线形态的结构化表达[J]. 测绘学报, 2009,38(2):175-182.

[ Zhai R J, Wu F, Zhu L, et al. Structured representation of curve shape[J]. Acta Geodaetica et Cartographica Sinica, 2009,38(2):175-182. ] DOI: 10.3321/j.issn:1001-1595.2009.02.014

DOI

[14]
操震洲, 李满春, 程亮. 曲线弯曲的多叉树表达[J]. 测绘学报, 2013,42(4):602-607.

[ Cao Z Z, Li M C, Cheng L A. Multi-way trees representation for curve bends[J]. Acta Geodaetica et Cartographica Sinica, 2013,42(4):602-607. ]

[15]
Ai T H, Ke S, Yang M, et al. Envelope generation and simplification of polylines using Delaunay triangulation[J]. International Journal of Geographical Information Science, 2017,31(2):297-319. DOI: 10.1080/13658816.2016.1197399

DOI

[16]
钱海忠, 何海威, 王骁, 等. 采用三元弯曲组划分的线要素化简方法[J]. 武汉大学学报·信息科学版, 2017,42(8):1096-1103.

[ Qian H Z, He H W, Wang X A, et al. Line feature simplification method based on bend group division[J]. Geomatics and Information Science of Wuhan University, 2017,42(8):1096-1103. ] DOI: 10.13203/j.whuis20150239

DOI

[17]
Qian H Z, Zhang M, Wu F. A new simplification approach based on the oblique-dividing-curve method for contour lines[J]. ISPRS International Journal of Geo-Information, 2016,5(9):153. DOI: 10.3390/ijgi5090153

DOI

[18]
Bose P, Cabello S, Cheong O, et al. Area-preserving approximations of polygonal paths[J]. Journal of Discrete Algorithms, 2006,4(4):554-566. DOI: 10.1016/j.jda.2005.06.008

DOI

[19]
Kronenfeld B J, Stanislawski L V, Buttenfield B P, et al. Simplification of polylines by segment collapse: Minimizing areal displacement while preserving area[J]. International Journal of Cartography, 2020,6(1):22-46. DOI: 10.1080/23729333.2019.1631535

DOI

[20]
Gökgöz T, Sen A, Memduhoglu A, et al. A new algorithm for cartographic simplification of streams and lakes using deviation angles and error bands[J]. ISPRS International Journal of Geo-Information, 2015,4(4):2185-2204. DOI: 10.3390/ijgi4042185

DOI

[21]
Tong X H, Jin Y M, Li L Y, et al. Area-preservation simplification of polygonal boundaries by the use of the structured total least squares method with constraints[J]. Transactions in GIS, 2015,19(5):780-799. DOI: 10.1111/tgis.12130

DOI

[22]
Buchin K, Meulemans W, Renssen A V, et al. Area-preserving simplification and schematization of polygonal subdivisions[J]. ACM Transactions on Spatial Algorithms and Systems, 2016,2(1):1-36. DOI: 10.1145/2818373

DOI

[23]
胡凤敏, 卢小平, 李成名, 等. 一种顾及图斑拓扑关系的化简方法[J]. 测绘通报, 2017(6):49-52.

[ Hu F M, Lu X P, Li C M, et al. A method of line simplification considering patches outline considering topological relations[J]. Bulletin of Surveying and Mapping, 2017(6):49-52. ] DOI: 10.13474/j.cnki.11-2246.2017.0188

DOI

[24]
Shen Y L, Ai T H, He Y K. A new approach to line simplification based on image processing: A case study of water area boundaries[J]. ISPRS International Journal of Geo-Information, 2018,7(2):41. DOI: 10.3390/ijgi7020041

DOI

[25]
Du J W, Wu F, Xing R X, et al. Segmentation and sampling method for complex polyline generalization based on a generative adversarial network[J]. Geocarto International, 2021:1-23. DOI: 10.1080/10106049.2021.1878288

DOI

[26]
张立华, 唐露露, 贾帅东, 等. 多条海岸线协同化简的层次化三角网分区法[J]. 测绘学报, 2019,48(4):520-531.

[ Zhang L H, Tang L L, Jia S D, et al. A collaborative simplification method for multiple coastlines based on the hierarchical triangulation network partition[J]. Acta Geodaetica et Cartographica Sinica, 2019,48(4):520-531. ] DOI: 10.11947/j.AGCS.2019.20180382

DOI

[27]
杜佳威, 武芳, 李靖涵, 等. 一种河口湾海岸线渐进化简方法[J]. 测绘学报, 2018,47(4):547-556.

[ Du J W, Wu F, Li J H, et al. A progressive simplification method for the estuary coastline[J]. Acta Geodaetica et Cartographica Sinica, 2018,47(4):547-556. ] DOI: 10.11947/j.AGCS.2018.20170440

DOI

[28]
华一新, 赵军喜, 张毅. 地理信息系统原理[M]. 北京: 科学出版社, 2012.

[ Hua Y X, Zhao J X, Zhang Y. Principles of geographic information system[M]. Beijing: Science Press, 2012. ]

[29]
武芳, 朱鲲鹏. 线要素化简算法几何精度评估[J]. 武汉大学学报∙信息科学版, 2008,33(6):600-603.

[ Wu F, Zhu K P. Geometric accuracy assessment of linear features' simplification algorithms[J]. Geomatics and Information Science of Wuhan University, 2008,33(6):600-603. ]

Options
Outlines

/

〈 〉