EN中文

Journal of Geo-information Science >

2022 , Vol. 24 >Issue 4: 643 - 656

DOI: https://doi.org/10.12082/dqxxkx.2022.210405

Contour Generation Algorithm and Quality Evaluation of Regular Hexagon Grid DEM

  • XIAO Kun ,
  • AI Tinghua , * ,
  • WANG Lu
Expand
  • College of Resources and Environmental Sciences, Wuhan University, Wuhan 430072, China
*AI Tinghua, E-mail:

Received date: 2021-07-17

  Revised date: 2021-08-13

  Online published: 2022-06-25

Supported by

Key Projects of National Natural Science Foundation of China National Natural Science Foundation of China(41531180)

Copyright

Copyright reserved © 2022
Fold

Abstract

Due to the advantages of isotropy, adjacency equivalence, and high fitting accuracy, regular hexagonal grid is used as the grid unit of regular grid DEM data structure and has been applied to digital terrain analysis such as flow direction analysis and valley line extraction. However, its quality detection and evaluation has not been well studied, and the quality of DEM directly affects the correctness and reliability of subsequent data analysis results and related decisions. Conventional methods such as checkpoint method and profile method can only evaluate the error of DEM locally, and cannot comprehensively evaluate the quality of DEM. Contour lines can reflect the overall situation of topography. Therefore, contour playback method is a relatively comprehensive and accurate method to evaluate the quality of DEM by analyzing the quality of playback contour lines and then detecting and evaluating the quality of DEM. Therefore, this paper applies the vertex height difference marking method to the grid structure of hexagonal DEM, proposes a contour generation algorithm for regular hexagonal grid DEM, and evaluates and analyzes the data quality of regular hexagonal grid DEM. Firstly, this paper uses three indexes: the topological correctness of the generated contour, the fit with the original contour, and the maintenance of bending features to evaluate the contour tracked by the vertex height difference marking method under the hexagonal grid structure. It has no topological errors such as self-intersection, fits well with the original contour, and maintains the bending features well, which proves the feasibility of the algorithm. In addition, this generation method is applied to the quality comparison of DEM with different regular grids, that is, the contour lines of quadrilateral DEM and hexagonal DEM are generated respectively based on the vertex height difference marking method, and the quality of contour lines generated by hexagonal DEM and quadrilateral DEM is compared based on the above three indexes, so as to compare the quality difference between hexagonal DEM and quadrilateral DEM. The experimental comparison shows that under the same resolution, the contour played back by hexagonal DEM has a higher fit with the original contour, and the bending feature is maintained better, and with the decrease of resolution, the decrease of fit is smaller, the loss of bending feature is less, there is no sharp angle, excessive shape deformation, etc. Therefore, the quality of hexagonal DEM is better than that of quadrilateral DEM, and with the decrease of resolution, the accuracy loss of hexagonal DEM is smaller.

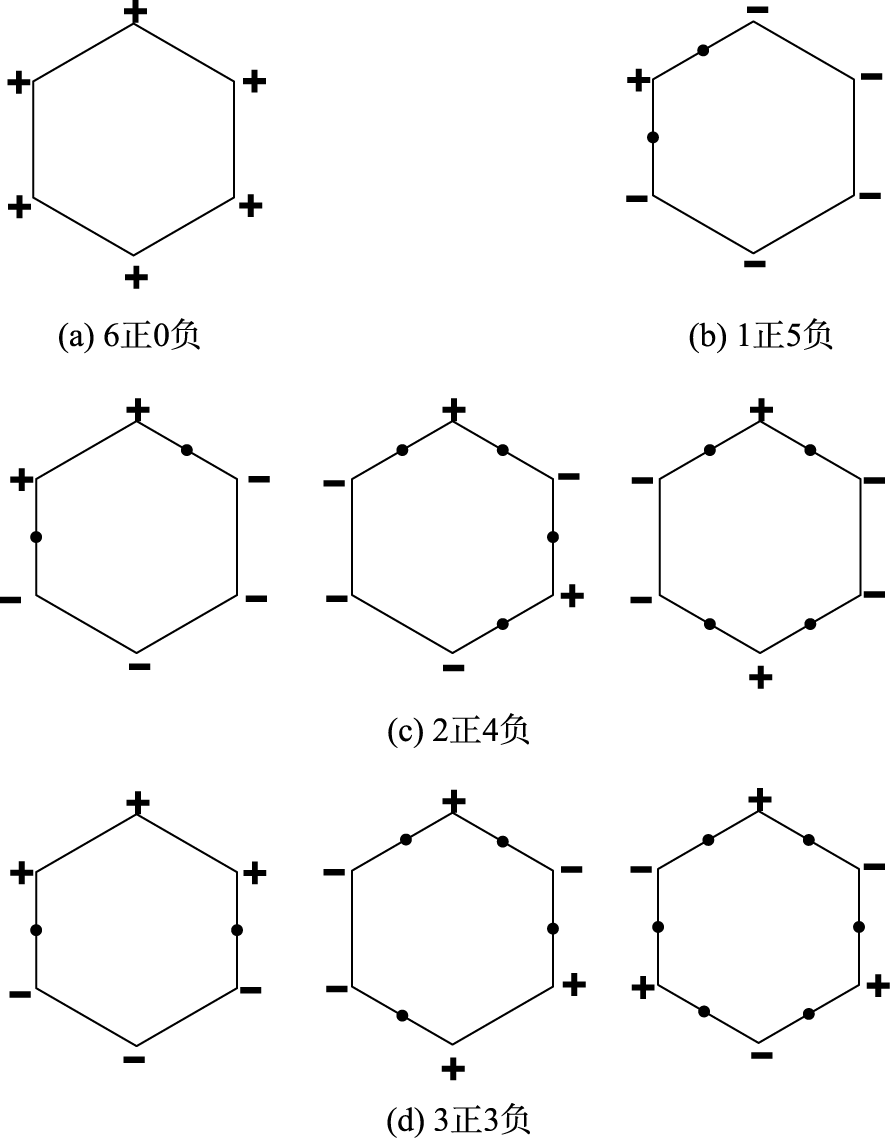
Key words： hexagonal grid structure; hexagonal DEM; vertex height difference mark; contour playback method; contour generation algorithm; DEM quality evaluation; contour quality evaluation; grid DEM

Cite this article

XIAO Kun , AI Tinghua , WANG Lu . Contour Generation Algorithm and Quality Evaluation of Regular Hexagon Grid DEM[J]. Journal of Geo-information Science, 2022 , 24(4) : 643 -656 . DOI: 10.12082/dqxxkx.2022.210405

1 引言

规则格网数字高程模型（Grid Digital Elevation Model,Grid DEM）,是通过有限的、连续的、带有高程属性的规则格网单元对地表进行全覆盖,从而实现的对地表形态的数字化模拟。其蕴含了大量地学应用分析所需要的地形地貌信息,目前已成为遥感与GIS中进行地理空间数据处理与地形分析所不可或缺的数据源[1],被广泛应用于国家地理信息基础数据建设、地形地貌分析、军事模拟、地表三维显示等各个方面[2]。现有的DEM数据结构大多以正四边形作为格网单元,它的结构编码简单,存储方便,但存在不足,正四边形有两种不同的最近邻关系,即共享一条边的正交近邻和共享一个角的对角近邻[3],对角近邻单元到质心的距离大于正交近邻单元到质心的距离,其比值为 2 /1,因此DEM在使用正四边形作为规则格网单元时,必须区别对待两种近邻关系在地形表示中的差异性以及两种近邻单元的可达性[4]。考虑到规则格网单元需无间隙且无重叠地覆盖整个地面的要求,除了正四边形之外,等边三角形和正六边形也可作为DEM规则格网单元。其中三角形作为规则格网单元时也不具有一致的邻接性,每个单元格都有3条边和9个顶点相邻。另外,基于三角形的DEM方向具有不一致性,增加了后续分析的难度与复杂性[5]。
顾及到格网的各向同性、邻接等效特性,最符合条件的几何单元应当是圆,但邻近的圆无法无缝拼接到一起,折中的方案便是寻找能够逼近圆的正多边形单元。通过比较,正六边形具有逼近圆的特性而且可以无缝拼接,正六边形具有一致的邻接性,其6个相邻单元全部与其共享一条边,不存在共享一个顶点的情况,并且6个相邻单元到中心单元的距离相同,这种特性使得六边形在处理最近邻域、移动路径、连通性等问题时具有一定的优势[3]。正六边形在形状上更接近圆形,能够更紧凑的覆盖地面,因此在量化平面时产生的平均误差最小[6],并且提供了更高的角分辨率[7]。另外,相同面积下,周长越小的正多边形格网单元产生的误差越小[8],在相同面积下,正四边形、等边三角形以及正六边形 3种形状中正六边形的周长最小,因此正六边形作为DEM规则格网单元有更高的精度。正六边形的对称性更高,因此比正四边形更具各向同性[9]。此外,在六边形组成的DEM规则格网中,其格网单元群的轮廓不再是单调的直线,更具多样性[3],而且正六边形在拓扑上更类似现实世界的不规则分区[10]。考虑到上述优势,基于正六边形单元的规则格网DEM数据组织,在谷地线提取[11]、地形结构线流径分析[12,13]等方面比正四边形格纹模型有明显优势。
虽然六边形DEM已经得到了一些应用,但是其质量检测还没有得到很好的研究。DEM质量的好与坏直接影响到后续数据的分析处理、影响到相关决策结果的正确性和可靠性等[14]。检查点法、剖面法、等高线回放法常常被用来检测DEM的质量,其中检查点法即事先按照格网或任意形式分布检查点,通过对比DEM在这些点处的高程值和原始高程值进行DEM质量的检查[15,16]。剖面法是按照一定的剖面量测DEM计算高程点与实际高程点之间误差的质量检查方法。上述两种方法都只在局部评价DEM的误差情况,难以在整体上反映DEM的质量,因而无法判定所建立的DEM与实际地形的吻合情况[17]。而等高线回放法则能够有效地避免这些缺点,能够从整体上评价DEM的质量,等高线能够很好地反映地形地貌的整体情况,地形地貌的变化必将引起等高线的变化,因此这种方法通过从生成的DEM上提取等高线,并与原始等高线进行对比,能够全面、准确地检测DEM的质量[18]。
在使用等高线回放法来进行六边形DEM的质量检测时,由DEM生成对应等高线是整个流程中最为关键的一环。目前由DEM生成等高线的基本算法是：经过线性内插获得格网边上的等值点,再按一定的追踪法则追踪出一条等值线的全部等值点[19]。王涛[20]在基本算法的基础上设计了一种新的遍历策略,保证了提取的等高线结果具有统一的方向,并提出区间树索引加快了等高线起点的查找。Fei[21]将扩展到三维的Douglas-Peucker算法应用到等高线的提取当中,既保持了宏观地形的起伏,又抑制了微观地质形态振动。但是这些方法在沟道、山脊等地形变化的位置并不能保证生成的等高线不出现拓扑相交。针对这个问题,通过对各个格网顶点与给定高程值进行比较,进行高差标记,可以确定等高线与格网中各条边的交点,并且根据交点的数目以及格网中心点高差标记能够对等高线进行追踪,这个方法用于四边形DEM生成等高线时能够很好的避免同一等高线的自相交拓扑问题[22]。
因此本文将上述顶点高差标记方法应用到六边形DEM中,进行等高线的生成。首先由文献[11]中的六边形DEM构建方法构建出了多分辨率六边形DEM数据,并基于六边形结构的顶点高差标记方法提取出了等高线。然后,经过拓扑检测,以及从贴合度和弯曲特征保持情况两方面进行评价,以证明此方法在六边形DEM中进行等高线回放的可行性。最后,将该方法应用到四六边形DEM的质量对比检测中,评价六边形DEM的质量。

2 研究方法

2.1 基于顶点高差标记法寻找等高线行进方向

在DEM生成等高线过程中,除了需要确定等值点之外,还需要对其进行正确的追踪,因此当一个格网单元出现多于两个等值点时,需要确定等值点在等高线上的相互位置关系,即需要确定沿等高线距离较近的点,本文将其称为邻近等值点。若判断邻近等值点错误时,则会造成同一等高线自相交的情况。在四边形DEM中,顶点高差标记方法则能够对格网单元顶点及其中心点进行高差标记,正确判断邻近等值点的位置,从而正确追踪等高线,避免了同一等高线产生自相交的情况。本文受四边形DEM中顶点高差标记方法启发,将此方法应用到了六边形DEM中,基于格网顶点高程变化值进行顶点高差标记,确定等值点,寻找等高线的行进方向。
首先对六边形DEM各个格网单元的顶点进行高差标记,假设给定的高程为H,假设存在某顶点A,其高程为 Z A,若 Z A > H,则将顶点A标记为 +,若 Z A < H,则顶点A标记为 -,若 Z A = H,则令 Z A = H + ∆ H,再进行顶点状态值的计算, ∆ H为一个极小的高程值,通过加上这样 ∆ H这样一个极小的值,虽然计算出来的等值点与原始等值点有所偏差,但这种偏差是极小的,形成的等高线距离原始等值点是十分接近的,因此形状上与原始等高线也是极为接近的,不会影响到生成等高线的精确性,并且避免了后续等高线追踪出现混乱[23]。在一个格网单元中,当一条边的2个顶点同时被标记为同号时,这条边上不存在等值点,反之,当2个顶点被标记为异号时,这条边有且仅有一个等值点[22]。此时设边的2个顶点分别为 A x A , y A、 B x B , y B,其对应的高程值分别为 Z A、 Z B,该边上存在等值点 C x C , y C,假定高程在格网单元边上呈线性分布,则可利用线性插值方法计算出该等值点的坐标,经推导,等值点坐标如式（1）所示。
x C = x A + H - Z A Z B - Z A ( x B - x A ) y C = y A + H - Z A Z B - Z A ( y B - y A )
同时通过列举所有顶点高差标记情况可以证明出六边形DEM一个格网单元中只可能存在0、2、4或6个等值点。顶点高差标记情况不同时等值点可能存在的个数如表1所示。
表1 六边形DEM等值点存在情况

Tab. 1 The existence of hexagon DEM equivalent points

顶点高差标记情况 等值点可能存在个数/个
情况① 6正0负/6负0正 0
情况② 1正5负/1负5正 2
情况③ 2正4负/2负4正 2/4
情况④ 3正3负 2/4/6
各种情况下等值点存在个数可由图1得出,图中位于格网边中心的黑点表示该边上存在等值点,当顶点高差标记情况为表中情况①时,以6正0负为例,如图1（a）,此时不存在等值点;当为情况②时,以1正5负为例,如图1（b）,此时只存在2个等值点;当为情况③时,以2正4负为例,按照2个正号间夹杂0个负号、1个负号、2个负号又可以将其再分为3种情况,如图1（c）可以看出分别存在2、4、4个等值点;当为情况④时,按照3个正号间夹杂0个负号、1个负号、2个负号又可以将其再分为3种情况,如图1（d）可以看出分别存在2、4、6个等值点;因此在六边形DEM一个格网单元只可能存在0、2、4或6个等值点。
图1 六边形DEM等值点存在情况

Fig. 1 The existence of hexagon DEM equivalent points

当格网单元有0个等值点时,说明等高线与此格网单元不相交;当格网单元有2个等值点时,则追踪到其中一个等值点时,可以直接确定其邻近等值点。当格网单元有4个或6个等值点时,如果没有正确地追踪到邻近等值点,则会出现同一等高线的自相交问题,如图2（a）,为表示方便,假设等值点全部位于格网边上的中心位置。为了避免同一等高线出现自相交,需要插值计算出格网单元中心点的高程并进行高差标记,利用中心点的高差标记可以正确追踪出邻近等值点。其邻近等值点追踪过程如下：
图2 六边形DEM等值点错误、正确追踪情况示例

Fig. 2 Examples of error and correct tracking of hexagon DEM equivalent points

首先对格网单元中心点进行高差标记,假设将其标记为+,如图2（b）,从AF边上的等值点P1开始追踪,由于A点与O点同号,所以AO上不存在等值点,因而等高线不穿过AO,而F点与O点异号,FO上存在等值点,等高线穿过FO,因此按照端点连接的方式进行逆时针搜索各条边,直至找到其邻近等值点。即查找以F为顶点的另一条边FE,FE上不存在等值点,继续查找ED,仍然不存在等值点,继续查找DC,最终找到等值点P4,即P1的邻近等值点为P4。同理,若从AB上的等值点P2开始追踪,由于O与B异号,则按照端点连接的方式进行顺时针搜索,BC上存在等值点P3,因此P2的邻近等值点为P3。
通过六边形DEM顶点高差标记的方法,可以确定等值点的存在情况,并且可以判断出邻近等值点的位置从而正确地进行等高线的追踪,很好地避免了同一等高线出现自相交的情况。

2.2 六边形DEM等高线生成

2.2.1 六边形格网结构
在六边形DEM生成等高线过程中,当确定等值点位置以及邻近等值点之后,需要判断当前格网单元的邻近格网单元,来确定所要追踪的下一个格网单元,因此需要进行邻域关系的构建,从而在多个格网单元中进行等高线的追踪。
正六边形格网坐标系统主要包括正交行列坐标系、二斜轴坐标系以及三斜轴坐标系（对称六边形坐标系）[3,23]。其中正交行列坐标系是描述六边形格网最简单的方式,其通过行列号来记录格网单元的位置,并且由于坐标轴是正交的,与笛卡尔坐标系兼容,所以很容易将格网坐标转换为地理坐标。但是正交行列坐标系也存在间距沿2个轴不同、隔行偏移的情况。本文基于“奇数行左偏移”的正交行列坐标系来进行六边形格网结构的构建（图3）。
图3 六边形格网结构

Fig. 3 Hexagonal grid structure

如图4所示,按照行号和列号对格网单元进行编码,x轴代表格网单元的列号,y轴代表格网单元的行号,设某个格网单元的行号为j,列号为i,则该格网单元的的格网坐标为 ( i , j ),其中(0, 0)格网中心点为坐标系的原点。六边形DEM具有一致的六邻域关系,即每个格网单元与其他6个格网单元邻近,并且具有一致的邻接性,中心格网单元到6个相邻格网单元的距离相同。但是由于在正交行列坐标系中六边形格网单元存在隔行偏移的情况,奇数行与偶数行的格网单元的6邻域关系并不一致。如 图5所示,奇数行格网单元除左右邻近格网单元外,其他的邻近格网单元均比偶数行格网单元对应的邻近格网单元列数小1。因此针对奇数行、偶数行不同的邻域关系规律,并通过正六边形格网单元的6条边来记录6个对应的邻域单元,从而构建六边形格网间整体的邻域关系。
图4 六边形DEM邻近格网单元追踪示意图

Fig. 4 Schematic diagram of hexagonal DEM adjacent grid unit tracking

图5 六边形DEM生成等高线的两种情况

Fig. 5 Two cases of generating contour lines from hexagon DEM

2.2.2 六边形DEM等高线生成算法
在六边形DEM等高线生成过程中,通过顶点高差标记的方法能够解决同一格网单元内邻近等值点的追踪问题,保证同一等高线不会出现自相交的情况。在一个格网单元内确定邻近等值点后,还需要确定等高线所要经过的下一个格网单元,才能够追踪出整条等高线,此时需要根据六边形格网的邻域关系来确定要追踪的下一个格网单元,具体追踪方法为通过等值点所在边来确定对应的邻近格网单元。如图4所示,假设P1为起始追踪等值点,在3号格网单元内追踪到邻近等值点P2,与3号格网单元共享等值点P2所在边的邻近格网单元为4号格网单元,因此下一个要追踪的下一个格网单元为4号格网单元,同理,在4号格网单元中找到P2的邻近等值点P3,再从邻近的2号格网单元中找到P3的邻近等值点P4。
在格网范围足够大的情况下,等高线应该是由等值点连成的闭合曲线,但是由于格网范围的限制,部分生成的等高线可能不是闭合的,因此六边形DEM生成的等高线可能存在两种情况,如图5所示,第一种情况为红线的情况,等高线不闭合,等高线与DEM的格网边界存在两个交点。第二种情况则是蓝线的情况,等高线闭合,等高线与DEM的格网边界不存在交点。因此在获得等值点时,进行边界标记,以判断等值点是否处于格网的边界上,从而根据以上两种情况进行等高线的回放。
对于给定高程值进行等高线的生成,建立两个表,一个为等值点表,记录等值点的序号、坐标、所在格网单元、所在边、边界标记以及已使用标记。另一个表为等高线表,用来记录每一条等高线的序号、高程以及该等高线上的系列等值点坐标。在等高线追踪过程中,首先将边界上的等值点作为起始追踪等值点,当追踪的下一等值点也处于边界上时,追踪结束,此时为不闭合的等高线。重复进行以上步骤直至追踪完全部不闭合的等高线。然后将不在边界上的任意等值点作为起始追踪等值点,当追踪的下一等值点与起始等值点重合时,追踪结束,此时为闭合的等高线。同样需要重复步骤以追踪出所有闭合的等高线。等高线生成的具体算法如下：
在此算法中,用 G n n = 1 , 2 , 3 , …表示第 n个网格,其邻域为 N ni n = 1 , 2 , 3 , … ; i = 1 , 2 , … , 6,其格网中心点高差标记为 C n n = 1 , 2 , 3 , …,其格网边为 E ni n = 1 , 2 , 3 , … ; i = 1 , 2 , … , 6,其顶点高差标记为 H ni n = 1 , 2 , 3 , … ; i = 1 , 2 , … , 6, B ni n = 1 , 2 , 3 , … ; i = 1 , 2 , … , 6代表该格网中存在的第 i个等值点。其中由于各个格网紧密连接,存在共享边以及共享顶点,因此 E ni以及 H ni中会存在重复的高差标记点以及边。
（1）根据给定高程,对各个顶点进行高差标记,第 n个网格的第 i个顶点的高差标记记录为 H ni。
（2）根据顶点的高差标记 H ni ( n = 1 , 2 , 3 , … ; i = 1 , 2 , … , 6 )确定所有等值点 B ni ( n = 1 , 2 , 3 , … ; i = 1 , 2 , … , 6 ),并根据其是否在任意一条格网边界上,将其进行边界标记,插入到等值点表中。
（3）在等值点表中选取第一个有边界标记并且为未使用状态的等值点作为起始追踪点,若不存在有边界标记的等值点,选取第一个为未使用状态的等值点作为起始追踪点。假设选取的起始追踪点为 B ni n = 1 , 2 , 3 , … ; i = 1 , 2 , … , 6,在等高线表中,按照序号、高程插入新记录,并将起始追踪点插入到等高线表的等值点中。
（4）根据当前格网中心点的高差标记 C n n = 1 , 2 , 3 , …,追踪格网内的邻近等值点。找到邻近等值点后,将邻近等值点插入到等高线表的等值点中,并将上一个等值点标记为已使用状态。若起始追踪点 B ni n = 1 , 2 , 3 , … ; i = 1 , 2 , … , 6为有边界标记的等值点,则当该邻近等值点同样有边 界标记时,转至步骤（6）,若起始追踪点 B ni n = 1 , 2 , 3 , … ; i = 1 , 2 , … , 6为没有边界的等值点,则当该邻近等值点不在等值点表中时,转至步骤（6）,此时起始追踪点与最终追踪点重合。
（5）根据邻域关系,在邻域单元中确定与当前格网单元共享等值点所在边的格网单元,假设其邻域格网单元为 N ni n = 1 , 2 , 3 , … ; i = 1 , 2 , … , 6,将其作为当前格网单元,进行步骤（4）。
（6）重复步骤（3）—步骤（5）,直至等值点表中所有点都被标记为已使用状态。
（7）对等高线表中每条记录按照等值点坐标顺序用样条曲线依次连接输出。
此六边形DEM等高线算法与四边形DEM等高线算法在本质上为同一个算法,因此二者的复杂度是相同的,计算效率与计算数量成负相关,即与等值点个数成负相关,而等值点的个数是与边数成正比的。因此相同分辨率（面积）下,六边形格网与四边形格网个数相同,边数比为3：2,因此计算效率也大致在2:3左右,六边形DEM等高线算法的计算效率低于四边形DEM等高线算法。

3 实验与分析

3.1 实验区域

本文实验区为龙门山脉中段地区,位于四川省德阳市西北部,地势起伏明显,西北高东南低,其海拔高度均在1000 m及以上。实验数据为国家测绘部门标准化采集生产的1:5万等高线数据[11],等高线数据高程范围为1000~4400 m,等高距为100 m。
本文实验区域原始等高线数据如图6所示,由于原始等高线数据以及后续回放出的等高线数据过于密集,影响对其进行视觉分析,因此后续对所有数据进行处理,但只对红色方框区域内的数据进行可视化及其分析。
图6 实验区域等高线数据

Fig. 6 Contour data of test area

以此数据作为原始等高线数据,由文献[14]中的六边形DEM构建方法,通过建立格网结构、获取格网中心地理坐标以及TIN线性插值进行六 边形DEM数据以及四边形DEM数据的构建。在构建过程中,分别构建了6种分辨率的数据。分辨率表示最小可分辨范围,因此本文中以面积来定义分辨率。由于原等高线间隔为100 m,为了使 六边形DEM能够较好的回放出等高线、防止后续由于分辨率过大或者过小时使得四六边形DEM回放的等高线差距不明显以及能够反映出随着分辨率的变化四六边形DEM回放等高线质量的变化,因此设置了6个分辨率,每个分辨率下六边形的边长分别为50、100、150、200、250、300 m,并得出了对应分辨率下四边形DEM格网的边长。表2为各个分辨率下四六边形格网单元的边长对比情况。后续等高线回放均在此DEM数据基础上进行。
表2 6种分辨率下2种DEM格网边长对比

Tab. 2 Comparison of grid side length of two kinds of DEM under six resolutions

分辨率编号 格网单元边长/m
六边形 四边形
1 50.0 46.5
2 100.0 93.0
3 150.0 139.5
4 200.0 186.0
5 250.0 232.5
6 300.0 279.0

3.2 六边形DEM等高线回放结果

基于3.1节生成的六边形DEM数据,根据六边形DEM等高线生成算法,分别进行6种分辨率下的等高线回放。由于原始等高线与回放等高线均以100 m作为间隔,因此本文将 ∆ H取为足够小的0.01 m,这保证了生成等高线的精确性。
对生成的等高线在ArcGIS下进行拓扑检测,来检查同一高程等高线的自相交数量。具体检测过程为：通过工具箱-数据管理工具-要素-检查几何,填入需要检测的等高线图层,即可进行检测,通过生成的表可以检查等高线的自相交记录。经检测,6种分辨率下六边形DEM生成的等高线自相交数量均为0,即不存在自相交的情况,满足等高线同一高程不自相交的特点,因此由基于六边形DEM的顶点高差标记方法回放出的等高线具有正确的拓扑特征。
将回放出的等高线与原始等高线进行对比,如图7所示,各个分辨率下生成的等高线均与原始等高线基本吻合,在分辨率1下,回放的等高线与原始等高线吻合程度最高,随着分辨率的降低,两等高线的吻合程度逐渐降低。回放等高线与原始的等高线的吻合程度具体可由贴合度以及弯曲特征保持情况来描述,其中贴合度用来描述回放等高线与原始等高线在位置上的差异,弯曲特征保持情况用来描述回放等高线与原始等高线在形状上的差异。为了更直观的观察回放的等高线与原始等高线的贴合度、弯曲特征保持情况以及二者随着分辨率变化而发生的变化,将图7中蓝色方框区域内的等高线数据进行放大显示,由图8可知,分辨率1时,回放的等高线与原始等高线的贴合度最高,更接近原始等高线的位置,并且其弯曲特征保持情况良好,在形状上能够更加逼近原始等高线。随着分辨率的降低,回放等高线逐渐偏离原始等高线的位置,贴合度降低,另外某些弯曲特征逐渐丧失,形状逐渐被简化、尖锐化,但仍保持了基本的轮廓特征。当分辨率6时,回放等高线与原始等高线贴合度最低,弯曲特征保持情况最差。
图7 六边形DEM等高线回放结果

Fig. 7 Playback results of hexagon DEM contour

图8 六边形DEM等高线回放局部结果

Fig. 8 Playback of local results of hexagon DEM contour

为了定量化回放等高线与原始等高线的贴合度,本文以平均偏移量来表示各个分辨率下回放的等高线偏离原始等高线的程度。当分辨率为r时,其平均偏移量为：
D r = ∑ i = 1 n d i n
式中：回放等高线有 n个折点; d i为第 i个折点到对应高程原始等高线的最近距离;将 n个折点的 d i进行求和后计算平均值,便可得到平均偏移量 D r。
如图9所示,将回放等高线中各个等值点到原始等高线的最短距离 d i,进行平均,得出平均偏移量,用此平均偏移量便可模拟出一条各个等值点与原始等高线最短距离都相同的等距等高线,这时各个等值点到原始等高线的最短距离就是平均偏移量 D r,由于等距等高线的各个等值点到原始等高线的最短距离之和与回放等高线的各个等值点到原始等高线的最短距离之和是相等的,因此模拟的等距等高线与原始等高线越贴合,即平均偏移量 D r越小,则回放等高线与原始等高线的贴合度越高。
图9 平均偏移量示意图

Fig. 9 Diagram of average offset

由表3各个分辨率下平均偏移量可知,随着分辨率的降低,平均偏移量逐渐增大,因此回放等高线与原始等高线的贴合度逐渐降低。
表3 6种分辨率下六边形DEM生成的等高线平均偏移量

Tab. 3 Average offset of contour lines generated by hexagon DEM at six resolutions

分辨率编号 1 2 3 4 5 6
平均偏移量/m 6.68 8.84 11.02 12.84 14.45 16.44
各个分辨率下回放等高线都没有出现拓扑自相交的情况,因此满足等高线的拓扑特征,并且虽然随着分辨率的降低,回放等高线的贴合度降低,弯曲特征保持情况变差,但是这些变化是规律性的,在最低分辨率下回放等高线仍然保持着较高的贴合度以及大致的形状轮廓,因此使用顶点高差标记方法来进行六边形DEM等高线的回放是可行的,回放出的等高线满足等高线不自相交等拓扑特征,并且在形状、位置方面能够很好地与原始等高线保持一致。因此可以通过顶点高差标记方法来进行四六边形DEM等高线回放,从而进行四六边形DEM质量的对比。

3.3 四六边形DEM质量对比

通过等高线回放法进行四六边形DEM质量的对比,可以通过回放的等高线的质量来评价对应DEM的质量。为了保证对实验进行控制变量,防止其他因素的影响,因此本实验中通过面积来控制六边形DEM与四边形DEM的分辨率,分辨率相同的情况下面积也相同,由此来控制分辨率对实验的影响,并且同样通过顶点高差标记方法,将 ∆ H设置为0.01 m,进行四边形DEM等高线的回放。
由顶点高差标记方法分别对6种分辨率下的四边形DEM进行等高线的回放,将各个分辨率下四六边形DEM回放的等高线以及原始等高线进行叠加对比,如图10所示,在各分辨率下两回放等高线与原始等高线大致吻合,随着分辨率降低,吻合程度也逐渐降低。
图10 四六边形DEM等高线回放结果对比

Fig. 10 Comparison of contour playback results of quadrilateral and hexagon DEM

对四六边形DEM回放的等高线进行质量评价对比,同样由等高线的拓扑正确性、贴合度以及弯曲特征保持情况对比来完成。经拓扑检测,通过四边形DEM回放的等高线拓扑自相交数量同样为0,也保持了正确的拓扑特征,因此只通过贴合度和弯曲特征保持情况2个指标进行对比评价等高线质量。
将图10中蓝框区域进行放大以观察两等高线的弯曲特征保持情况,如图11所示,在分辨率1、2的情况下,两等高线均保持了大多数的弯曲特征,但由于六边形格网单元采样点较多,因此六边形DEM回放出的等高线在形状上更加逼近原始等高线,从分辨率3开始,四边形DEM回放的部分等高线开始丧失某些重要的弯曲特征,出现狭长尖角情况,随着分辨率降低,形状也出现了过度化简的情况,如图11（c）—图11（f）黑框区域中的尖角以及过度化简的形状,到分辨率6时,等高线尖角化,形状化简最为严重。而6种分辨率下六边形DEM回放出的对应等高线则都良好地保持了大多数的弯曲特征,没有出现尖角化、形状过度化简等情况。
图11 四六边形DEM等高线回放局部结果对比

Fig. 11 Comparison of local contour playback results of quadrilateral and hexagon DEM

由式（2）计算各个分辨率下四六边形DEM回放的等高线与原始等高线的平均偏移量,并通过折线图分析,从而定量对比两回放等高线与原始等高线的贴合度,由图12可知,随着分辨率降低,两回放等高线的平均偏移量均以类线性的方式增加,但在各个分辨率下,六边形DEM回放等高线的平均偏移量均小于四边形DEM回放等高线的平均偏移量,因此前者与原始等高线的贴合度更高。并且随着分辨率的减小,六边形DEM回放等高线的平均偏移量增长速度小于四边形DEM。
图12 四六边形DEM回放等高线平均偏移量对比

Fig. 12 Comparison line graph of average offset of quadrilateral DEM playback contour

在各个分辨率下六边形DEM回放的等高线在弯曲特征保持上均优于四边形DEM回放的等高线,并且前者与原始等高线的贴合度更高,说明六边形DEM回放的等高线质量更好,因此可以证明六边形DEM的质量优于四边形DEM,并且随着分辨率的降低,与四边形DEM回放的等高线出现尖角化、过度化简等情况不同,六边形DEM回放的等高线仍能保持大致的轮廓形状,而且其平均偏移量增长速度小于四边形,因此随着分辨率的降低,六边形DEM的精度折损程度更小。

4 结论

六边形DEM在流向分析、谷地线提取等方面已经得到了一些应用,但是对于六边形DEM的质量检测研究却少之又少,检查点法、剖面法等都只能在局部评价DEM的质量,而等高线回放法则能克服这些缺点,从整体上评价DEM的质量,因此本文将顶点高差标记方法应用到六边形DEM中,提出了一种六边形DEM中的等高线生成算法,对该算法进行可行性验证,并由该算法生成的等高线进行了六边形DEM的质量评价。
本文首先由上述算法生成了多分辨率下六边形DEM的等高线,并从拓扑正确性、与原始等高线贴合度以及弯曲特征保持情况3个指标方面证明了该算法的可行性。并且同样通过顶点高差标记方法生成多分辨率四边形DEM的等高线,并通过上述3个指标进行六边形DEM与四边形DEM的质量对比评价,首先拓扑正确性方面,四六边形DEM回放出的等高线自相交数量均为0,二者相同;然后在贴合度方面,根据得出的数据,四边形DEM6种分辨率下回放出的等高线与原始等高线的平均偏移量分别为8.10、11.49、14.31 、16.81、19.70、22.30 m,六边形DEM6种分辨率下回放出的等高线与原始等高线的平均偏移量分别为6.68、8.84、11.02、12.84、14.45、16.44 m,每种分辨率下六边形DEM回放的等高线与原始等高线的平均偏移量更小,因此贴合度更高,并且根据折线图可以看出随着分辨率的增大,六边形DEM回放的等高线与原始等高线贴合度的下降速度更慢;最后在弯曲特征保持情况方面,根据视觉分析得出了六边形DEM回放的等高线比四边形DEM回放的等高线弯曲特征保持得更好,并且随着分辨率增大,也未出现较大的变形及尖角化等;因此得出了在各个分辨率下六边形DEM质量均优于四边形DEM,并且随着分辨率降低,六边形DEM的精度折损程度更小的结论。
但是在本研究中,拓扑正确性和贴合度分别通过自相交数量、平均偏移量进行定量评价,而等高线的弯曲特征保持情况只通过视觉分析进行了定性评价,没有提出定量指标,需要在后续研究中完善。

References

Publishing order | Descend order by publishing year | Descend order by cited within
[1]
汤国安, 龚健雅, 陈正江, 等. 数字高程模型地形描述精度量化模拟研究[J]. 测绘学报, 2001,30(4):361-365.

[ Tang G A, Gong J Y, Chen Z J, et al. A simulation on the accuracy of DEM terrain representation[J]. Acta Geodaetica et Cartographic Sinica, 2001,30(4):361-365. ] DOI: 10.3321/j.issn:1001-1595.2001.04.016

DOI

[2]
胡鹏, 黄杏元, 华一新. 地理信息系统教程[M]. 武汉: 武汉大学出版社, 2002.

[ Hu P, Huang X Y, Hua Y X. Geographic information system tutorial [M]. Wuhan: Wuhan University Press, 2002. ]

[3]
Birch C P D, Oom S P, Beecham J A. Rectangular and hexagonal grids used for observation, experiment and simulation in ecology[J]. Ecological Modelling, 2007,206(3/4):347-359. DOI: 10.1016/j.ecolmodel.2007.03.041

DOI

[4]
Wang J, Kwan M P. Hexagon-based adaptive crystal growth voronoi diagrams based on weighted planes for service area delimitation[J]. ISPRS International Journal of Geo-Information, 2018,7(7):257. DOI: 10.3390/ijgi7070257

DOI

[5]
Sahr K, White D, Kimerling A J. Geodesic discrete global grid systems[J]. Cartography and Geographic Information Science, 2003,30(2):121-134. DOI: 10.1559/152304003100011090

DOI

[6]
Conway J H, Sloane N J A. Sphere Packings, Lattices and Groups[J]. Zeitschrift Für Kristallographie, 1990,191(3-4):286-286.

[7]
Golay M J E. Hexagonal parallel pattern transformations[J]. IEEE Transactions on Computers, 1969,C-18(8):733-740. DOI: 10.1109/T-C.1969.222756

DOI

[8]
林辉, 彭长辉. 地理信息系统中栅格单元大小和形状的选择[J]. 遥感信息, 2001(1):21-23.

[ Lin H, Peng C H. Selection of grid cell size and shape in GIS[J]. Remote Sensing Information, 2001(1):21-23.] DOI: 10.3969/j.issn.1000-3177.2001.01.005

DOI

[9]
Sahr K. Location coding on icosahedral aperture 3 hexagon discrete global grids[J]. Computers, Environment and Urban Systems, 2008,32(3):174-187. DOI: 10.1016/j.compenvurbsys.2007.11.005

DOI

[10]
Feick R, Robertson C. A multi-scale approach to exploring urban places in geotagged photographs[J]. Computers, Environment and Urban Systems, 2015,53:96-109. DOI: 10.1016/j.compenvurbsys.2013.11.006

DOI

[11]
王璐, 艾廷华. 正六边形规则格网表达的DEM谷地线提取[J]. 测绘学报, 2019,48(6):780-790.

[ Wang L, Ai T H. The valley extraction based on the hexagonal grid-based DEM[J]. Acta Geodaetica et Cartographica Sinica, 2019,48(6):780-790. ] DOI: CNKI:SUN:CHXB.0.2019-06-013

DOI

[12]
Hyväluoma J. Reducing the grid orientation dependence of flow routing on square-grid digital elevation models[J]. International Journal of Geographical Information Science, 2017,31(11):2272-2285. DOI: 10.1080/13658816.2017.1358365

DOI

[13]
Sousa L D, Nery F, Sousa R, et al. Assessing the accuracy of hexagonal versus square tilled grids in preserving DEM surface flow directions[EB/OL]. 2006

[14]
Bolstad P V, Stowe T. Evaluation of DEM accuracy. Elevation, slope, and aspect[J]. Photogrammetric Engineering and Remote Sensing, 1994,60(11):1327-1332.

[15]
汤国安, 刘学军, 闾国年. 数字高程模型及地学分析的原理与方法[M]. 北京: 科学出版社, 2005.

[ Tang G A, Liu X J, Lv G N. Geographic information system tutorial[M]. Beijing: Science Press, 2005. ]

[16]
Höhle J, Höhle M. Accuracy assessment of digital elevation models by means of robust statistical methods[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2009,64(4):398-406. DOI: 10.1016/j.isprsjprs.2009.02.003

DOI

[17]
肖雁峰. DEM质量检查与精度评定研究[D]. 成都:西南交通大学, 2008.

[ Xiao Y F. Quality inspection and accuracy evaluation for DEM[D]. Chengdu: Southwest Jiaotong University, 2008. ] DOI: 10.7666/d.y1345655

DOI

[18]
Sharma A, Tiwari K N, Bhadoria P B S. Measuring the accuracy of contour interpolated digital elevation models[J]. Journal of the Indian Society of Remote Sensing, 2009,37(1):139-146. DOI: 10.1007/s12524-009-0005-y

DOI

[19]
Wang T. An algorithm for extracting contour lines based on interval tree from grid DEM[J]. Geo-Spatial Information Science, 2008,11(2):103-106. DOI: 10.1007/s11806-008-0029-4

DOI

[20]
王涛, 毋河海, 刘纪平. 基于区间树索引的等高线提取算法[J]. 武汉大学学报·信息科学版, 2007,32(2):131-134.

[ Wang T, Wu H H, Liu J P. An algorithm for extracting contour lines based on interval tree from grid DEM[J]. Geomatics and Information Science of Wuhan University, 2007,32(2):131-134. ] DOI: 10.3321/j.issn:1671-8860.2007.02.010

DOI

[21]
Fei L, HUANG L, HE J. An indirect generalization of contour lines based on DEM generalization using the 3D Douglas-Peucker algorithm[J]. School of Resource and Environment Science, Wuhan University, 2008,129:751-756.

[22]
张显全, 刘忠平. 基于格网模型的等高线算法[J]. 计算机科学, 2005,32(9):199-201.

[ Zhang X Q, Liu Z P. An algorithm of contour lines based on regular grid[J]. Computer Science, 2005,32(9):199-201. ] DOI: 10.3969/j.issn.1002-137X.2005.09.052

DOI

[23]
王欢, 王峰. 基于格网DEM生成等高线算法的一种改进[C]. 创新与发展高校gis论坛.中国地理信息系统协会, 2006:349-352.

[ Wang H, Wang F. An improvement of contour generation algorithm based on Grid DEM[C]. Innovation and Development of University GIS Forum, China Association for Geographic Information Society, 2006:349-352. ]

[24]
Her I. A symmetrical coordinate frame on the hexagonal grid for computer graphics and vision[J]. Trans.of the Asme Jour.of Mechanical Design, 1993,155(3):447-449. DOI: 10.1115/1.2919210

DOI

Options
Outlines

/

〈 〉