EN中文

Journal of Geo-information Science >

2022 , Vol. 24 >Issue 4: 738 - 749

DOI: https://doi.org/10.12082/dqxxkx.2022.210181

A New Method to Reconstruct MODIS EVI Time Series Data Set based on Graph Theory

  • CHEN Wen , 1, 2 ,
  • SUN Liqun , 1, * ,
  • LI Qinglan 1 ,
  • CHEN Chen 3 ,
  • LI Jiaye 3
Expand
  • 1. Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences, Shenzhen 518055, China
  • 2. Xiangtan University, Xiangtan 411100, China
  • 3. Dongguan University of Technology, Dongguan 523808, China
*SUN Liqun, E-mail:

Received date: 2021-04-06

  Revised date: 2021-07-06

  Online published: 2022-06-25

Supported by

National Natural Science Foundation of China(51679233)

13thFive-Year National Key Research and Development Program of China(2017YFC0403600)

Special Fund for Science and Technology Development of Guangdong Province(2017A030310057)

Copyright

Copyright reserved © 2022
Fold

Abstract

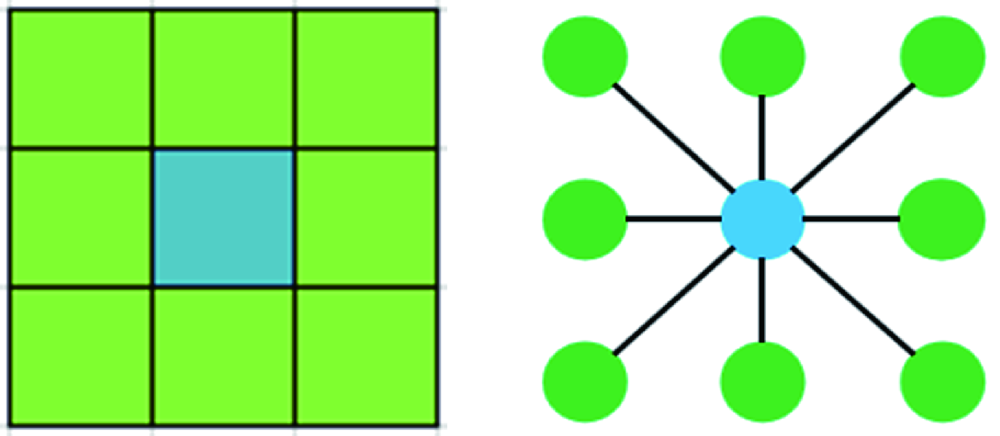
The MODIS Enhanced Vegetation Index (EVI) time-series data has been widely used in many research fields such as vegetation observation, ecological environment, and global meteorological changes. However, even though the EVI time series data has undergone strict preprocessing, there are still some noises in it. Therefore, this paper develops a simple and effective method to reconstruct EVI time-series data and eliminate the noise in EVI time-series data, especially some noise caused by atmospheric clouds and snow cover. The theory of the new method is derived from graph theory, using the relationship of the Laplacian matrix to assign the weight of the pixel of the selected neighborhood window in EVI to get the fitting of the center pixel. The new method has been applied to MODIS MOD13A1 products from 2016 to 2018 and compared with the S-G filtering method, Harmonic Analysis of Time Series method, Double Logistic function method, and Asymmetric Gaussian model function method. The results show that in the desert, grassland, and woodland, the absolute difference of the leave-one verification test of the new method is the smallest, which is better than other methods; when fitting EVI time-series data of different vegetation types, the graph theory neighbor method presents a better detailed fitting curve; the RMSE values of the new method in the five vegetation types are 200.59, 46.58, 63.48, 165.47, and 40.95 respectively, which are the smallest values among the five methods and are more effective in obtaining high-fidelity and high-quality EVI time-series data. The method research in this article can provide a useful reference for the denoising of vegetation remote sensing time-series data and the study of the ecological environment.

Key words： graph theory neighbor point method; EVI; time-series data; vegetation remote sensing; MODIS; curve fitting; denoising; reconstruction method

Cite this article

CHEN Wen , SUN Liqun , LI Qinglan , CHEN Chen , LI Jiaye . A New Method to Reconstruct MODIS EVI Time Series Data Set based on Graph Theory[J]. Journal of Geo-information Science, 2022 , 24(4) : 738 -749 . DOI: 10.12082/dqxxkx.2022.210181

1 引言

植被的动态变化,对地球的生态系统和气象变化有着重大影响。为了监测植被波动变化,科学家使用了归一化植被指数（Normalized Difference Vegetation Index,NDVI）来描述全球植被的绿化程度,但遗憾的是NDVI观测数据中有来自大气云层或地表环境所造成的误差[1]。1999年12月,NASA发射了Terra卫星,搭载了中分辨率成像光谱仪[2]（Moderate Resolution Imaging Spectroradiometer,MODIS）。MODIS的团队开发了一种新的数据——增强型植被指数（Enhanced Vegetation Index,EVI）,用来改进NDVI数据[3]。EVI数据相较于NDVI数据,有较好的大气矫正,减少了气溶胶的影响;削弱了植被指数中土壤背景的影响;在测量植被高覆盖区域（如雨林）时不会像NDVI一样产生过饱和的情况[2]。尽管EVI数据改善了NDVI数据中部分大气噪声、易受土地背景影响和在高植被覆盖区过饱和的缺点,但还是不能完全克服来自大气云层、地形、数据传输和观测角度等造成的影响,带有不可避免的噪声[4]。因此,研究MODIS EVI时间序列数据的重构方法,尽可能地还原植被生长的真实情况,是植被生态遥感研究的重点[5]。
目前EVI时间序列重构的主要方法还是与NDVI时间序列重构方法一致,并没有太大的区别[6],主要包括：阈值法、滤波法、函数拟合法、时空融合方法和其他方法。阈值法[7]出现较早,经历了最大值合成法[8]（Maximum Value Composite,MVC）、最佳指数斜率提取法[9]（The Best Index Slope Extraction,BISE）和修正的最佳斜率提取法[10]（Modified BISE,M-BISE）。阈值法易与其他方法相结合使用,因此被广泛应用。滤波法主要是Savitzky-Golay（S-G）滤波法[11]和均值迭代滤波法[12]（Mean Value Iteration Filter,MVI）,其他滤波重建方法应用较少,比如Whittaker滤波[13]和扩展卡尔曼滤波法[14]（Extended Kalman Filtering,EKF）,EKF法可以对时间序列数据的线性系统进行最优估计从而达到去噪的效果。函数拟合法是应用范围最广数目最多的方法,它利用平滑模型函数来对时间序列数据进行拟合,从而达到去噪的效果。主要包括谐波函数法[15]（Harmonic Analysis of Time Series,HANTS）、双逻辑斯蒂拟合法[16]（Double Logistic Function,D-L）、非对称高斯函数法[17]（Asymmetric Gaussian Model Function,A-G）、Sellers算法[18]及其优化方法[19]、多项式拟合[20]和其他函数拟合方法[21]等。时空融合方法是近几年发展起来的,与一般时间序列方法不同的是,该类别的方法摆脱了其他类别方法仅在时间序列分析方向的限制,结合了空间分析的方向,出现了多种时空融合方法,从而得到高分辨率高质量的EVI数据[22]。主要方法有UBDF[23]（Unmixing Based Data Fusion）、线性混合增长法[24]（Linear Mixing Growth Model,LMGM）、时空自适应反射率融合法[25]（Spatial and Temporal Adaptive Reflectance Fusion Model,STARFM）、空间滤波补偿法[26]（Spatial Filtering and Residual Compensation,SFRC）、OPDL法[27]（One Pair Dictionary Learning Method）和灵活时空数据融合法[28]（Flexible Spatiotemporal Data Fusion,FSDF）。其他时间序列数据重构方法应用较少,主要有小波变换[29]（Wavelet Transform,WT）和数据迭代插值重建法[30]（Iterative Interpolation for Data Reconstruction,IDR）。
上述方法已成功处理了某些植被指数的时间序列数据的重构,但是还存在一定的局限性。即使目前最常用的方法：S-G滤波法、HANTS法、A-G法和D-L法,也有一些不足[31,32]。例如,A-G法的优点在于方便获取高质量的EVI时间序列,但会忽略真实合理的最大值和最小值,尤其是对于季节性不明显或有多个生长季的地区。D-L法与A-G法类似,但在最大值和最小值上处理略优于A-G,且能够有效地处理离群值。此外,D-L法与A-G法一样不适用于有多个生长季地区的时序数据重构。HANTS法具有较强的曲线平滑能力,能够快速将时间序列进行简化和压缩,并剔除其中的噪点,但保真能力较差。S-G法能将时间序列中绝大多数的噪点快速识别并纠正,重构时间序列。然而,S-G滤波对某些峰值点存在低估现象,且与HANTS方法一样会改变几乎所有像元的值,于是这两个算法的保真性较弱。
鉴于上述方法的缺点,本文提出了一种基于图论的简单但有效的方法,用来减少EVI时间序列中由大气云层和冰雪覆盖产生的噪声,使数据更接近EVI的真实值,并通过迭代过程描绘EVI变化的趋势。该方法已在MODIS EVI时间序列数据上进行测试应用。

2 研究方法

与其他减少噪声和构建高质量EVI时间序列的策略相似,新方法基于2个假设：① EVI时间序列数据主要与植被有关,其变化过程与植被生长发育的变化相一致;② MODIS的MOD13A1产品中,PR数据可以精准无误地指示对应EVI在各点的各个时刻数据是否良好。云层和恶劣的环境通常会突然地降低EVI值,从而产生噪点,这些噪点会被PR数据详细记录下来。根据这2个假设,开发了一种基于图论的新方法,以使EVI数据值更接近真实值,并通过迭代来拟合植被的EVI值的最佳变化过程。接下来,简要介绍下图论邻点去噪方法。
MODIS EVI数据本身就是一种栅格图像数据,其像元点规则排列在点阵之上,可以把所有像元点都看成图的顶点。对于每个顶点（图1中蓝点）,只与离它最近的k个邻居（图1中绿点）顶点相连,同时对边赋予权重值。边的权重赋值成两顶点间距离的倒数,并把单个栅格的边长定义为1,那么顶点间的权重就可以简单地计算出来。从数学的角度出发,在现实地理环境中可以认为,当2个顶点在空间上越接近时它们就越相似,由于边的权重就等于距离的倒数,所以边的权重也能够表示两个顶点的相似性（图1）。
图1 顶点与其周围邻点

Fig. 1 Vertex and its surrounding adjacent points

图的数学形式为 G ( V , E ),一般用点的集合 V和边的集合 E来描述, L为图的拉普拉斯矩阵,其定义为 L = D - W,式中 D为图的度矩阵, W为图的邻接矩阵（权重）。度矩阵与邻接矩阵的关系： d i = ∑ i = 1 n w ij, d i为 D的对角线元素, w ij为 W中i行j列的元素。对于顶点组成的任意向量 f,有
f T L f = 1 2 ∑ i , j = 1 n w ij f ( v i ) - f ( v j ) 2
式中： f T为向量 f的转置向量,拉普拉斯矩阵 L表示像元点之间距离的测度;顶点 v i与顶点 v j之间边的权重是 w ij,当 w ij = 1时,其对应的意义就是多像元数据点之间的距离和; f ( v i )表示点 v i的函数,对应实际应用它可以是一个概率值、一个像元值等。
令矩阵 X = x 1 , x 2 , ⋯ , x l , ⋯ , x n , 1 ≤ l ≤ n,其中 X为MODIS中EVI的像元矩阵; x l为矩阵 X的第l列向量, x l T为向量 x l的转置向量,于是有：
x l T L x l = 1 2 ∑ i , j = 1 n x l ( v i ) - x l ( v j ) 2
X T LX = x 1 T ⋮ x l T ⋮ x n T L x 1 ⋯ x l ⋯ x n = x 1 T L x 1 x 1 T L x 2 ⋯ x 1 T L x n x 2 T L x 1 x 2 T L x 2 ⋯ x 2 T L x n ⋮ ⋮ ⋱ ⋮ x n T L x 1 x n T L x 2 ⋯ x n T L x n
式中： x l ( v i )和 x l ( v j )表示顶点 v i与顶点 v j的EVI像元值; L是像元矩阵 X对应的拉普拉斯关系矩阵。
令 σ ( x ) = x l T L x l 1 ≤ l ≤ n ,由式(2)可知, σ ( x )正定二次型函数,它满足二次型的对称双线性形式,于是存在正定二次型 Q ( x )使得
2 Q ( x ) = x l T L x l .
数据间的空间光滑性在一定程度上指示了数据的质量,从式(2)—式(4)可以得出式（5）,来表示数据的空间光滑性。
S ( X ) = 1 2 tr ( X T LX )
式中： S ( X )为像元矩阵 X的光滑函数; X T为矩阵 X的转置矩阵; L为图的拉普拉斯矩阵; tr表示求矩阵的迹,即矩阵对角线元素之和。于是,函数 S越小,代表数据的空间光滑性越好。
为了描述EVI时间序列数据变化的规律性,引入时间差分的概念,数据的时间差分是指用后一个时刻的数据减去前一个时刻的数据得到的值。数据的时间差分在空间上具备很好的光滑性,也就是说,顶点数据的变化趋势与它附近顶点的趋势一致。代入时间差分：
Δ X i = X i + 1 - X i = [ x 1 i + 1 - x 1 i , ⋯ , x l i + 1 - x l i , ⋯ , x n i + 1 - x n i ]
式中： X i为EVI第 i个时间段的像元矩阵; x i为对应 X i的列向量; Δ X i为第 i个时间段的像元时间差分矩阵。用 S ( ΔX )表示所有时段组成的像元时间差分矩阵 ΔX的光滑函数,用矩阵 ΔX代替式(5)中的像元矩阵 X,则数据时间差分的空间光滑性可由下式计算：
S ( ΔX ) = 1 2 tr ( ΔX ) T L ( ΔX )
用MODIS MCD12Q1提供的PR图层来划分可用信号和噪声,详细代号见表1。在所有数据中,只有质量代号为“0”的良好数据才被视为直接可用数据,而其他质量等级的数据均为噪点或未知数据。使用采样算子 J来区分信号与噪声, J是一个与植被指数EVI像元矩阵 X尺寸相同的矩阵。若数据为可用数据,那么 J中相应位置的像元值等于1,若像元点是噪声或未知数据则等于0。这样,可用的信号就可以表示成 Y = J * X,其中*表示Hardamard积（矩阵对应元素相乘）。那么,植被指数EVI数据重建的问题就可以表示为：在给定 Y和 J的条件下,改变 X中噪声部分的值,使数据质量提升。
表1 MCD12Q1 PR图层质量评估分类

Tab. 1 MCD12Q1 PR layer quality assessment classification

代号 质量情况（PR） 描述
255 无数据 未处理
0 良好数据 可直接使用
1 边缘数据 部分可用,具体参考质量数据
2 雪/冰 不可用,雪/冰覆盖
3 云 不可用,云层覆盖
这样,EVI数据重建问题就等价于一个最优化问题：保持 X中的可用数据（代号为“0”的数据）不变,改变其他值,使得 S ( ΔX )的值最小,即
min X F ( Y ) = S ( ΔX ) s . t . Y = J × X
式中： F ( Y )为非线性的目标函数;矩阵 Y为 F ( Y )的决策变量矩阵。这个最优化问题可以使用优化方法中线搜索方法进行求解,得出最优解即可生成最佳方案的EVI时间序列数据。

3 实验区概况与数据来源

3.1 实验区概况

选定MODIS全球区域中的h25v05和h26v05为实验范围,实验区在北纬30° N—40° N、80° E—120° E范围内,与中国地区重合的部分有着复杂的地形和气候条件,包括了国际地圈—生态圈计划（IGBP）制定的所有植被分类类型,如图2所示。
图2 IGBP土地覆盖类型分布

注：h25v5和h26v5表示MODIS的区域块。

Fig. 2 IGBP land cover type distribution

3.2 数据来源及处理

EVI时间序列数据用的是MODIS（https://ladsweb.modaps.eosdis.nasa.gov/search/）的MOD13A1产品,其空间分辨率为500 m,时间分辨率为16 d。此外,还需要将EVI数据对应的像元质量可信度（Pixel Reliability,PR）数据提取出来,PR数据将作为判断EVI数据是否可信的依据。土地覆盖类型选用的是2018年MODIS的MCD12Q1产品,它采用的是IGBP分类标准,将土地覆盖类型分为17种（具体的类型可见图2,它显示了全部的分类类型）。研究中根据需要将IGBP的分类进行了合并：将阔叶林、针叶林和混合林合并为林地,封闭灌木丛和开放灌木丛合并为灌木,木本稀树草原、稀树草原和草地合并为草原,耕地与农田合并为农作物,荒漠占地面积较大且植被的覆盖面积不超过10%,将其单独作一类。其他的类型比如城市和建筑用地、永久的冰雪、永久湿地和水体不在研究的范围之内。因此,本文研究的土地覆盖类型就可分为5类：林地、灌木、草原、农作物和荒漠。

4 新方法的实现

根据流程图（图3）来对新方法的主要步骤进行详细说明。步骤中的数据选择了以16 d为一期的一年数据（一年23期,在第1期前和最后1期后分别多选1期,一共25期）进行新方法的实现。
图3 新方法的流程

Fig. 3 Flowchart of the new method

（1）噪点数据的线性插值
MODIS的EVI时间序列数据集将每个数据点的质量或受什么因素影响作为辅助数据包含在PR数据集内（表1）。尽管PR数据不能完全准确地标注出EVI时间序列数据的所有情况,但却可用来标注出不确定的EVI值,当一个EVI数据没有被PR标注为“Good Data”时,就将其视为不确定值。通过对不确定的EVI值进行线性插值,可改善EVI的时间序列。在这一步中,将使用线性插值对PR中标注代号为2（雪/冰）、3（云）和255（空）的数据进行替换。例如,假设存在一个数据点 ( t i , E i , P i ) , i = 1,2 , ⋯ , n的EVI时间序列,其中 t i是时间序列, E i是EVI值, P i是PR值。如果第 j个点的 P j被标注的代号为噪点,则 E j为噪点数据,于是将噪点 E j替换为该点EVI时间序列线性插值的数据,之后可获得新EVI时间序列。由图4可看出,3个噪点的EVI值突然下降,线性插值的结果弥补了这部分地下降。
图4 线性插值效果

Fig. 4 Linear interpolation effect graph

（2）选择邻点个数k
对EVI时间序列数据中云、雪/冰和空数据的噪点完成线性插值替换后,接下来需要用图论方法对除了标记代号为“0”之外的数据类型进行处理（主要是表1中代号为“1”的“边缘数据”）。首先,需要确定的是噪点周围邻点的个数。一般情况下,每个噪点只选择周围距离最近的4个点作为邻点 （图5（a））,这样在图论中噪点与每个邻点之间边的权重即为 w = 1。经过测试,如果选择八个邻点来影响噪点,那么空间复杂度会变得非常巨大,且对噪点质量的提升也十分有限。此外,对于区域边界数据,只考虑在区域范围之内的数据,虽然会出现边界点仅有2个或3个邻点（图5（b））,但对于整体效果的影响可以忽略不记。
图5 选择邻点的分布和数目

注：蓝色框为噪点,绿色框为邻点。

Fig. 5 Selects the distribution and number of adjacent points

（3）确定噪点的动态变化
给每个噪点选择周围4个邻点之后,需要确定每个邻点对噪点的权重。在时间序列中,4个邻点与噪点的变化趋势是一致的。于是,可以用 V 1 , V 2 , V 3 , V 4来表示4个邻点此刻的值,用 V 1 ' , V 2 ' , V 3 ' , V 4 '表示4个邻点前一刻的数据,并将4个邻点的时间差分用 Δ V表示（例如,第一个邻点的时间差分为 Δ V 1 = V 1 - V 1 '）。噪点处值的时间差分为 Δ N = N 1 - N ',其中 N '指的是噪点前一时间点的值, N为噪点此时的值（这时的 N是经过第一步线性插值预处理后的值）。那么噪点值的动态变化将由以下公式给出：
Δ N = α n ∑ i = 1 n w i ( Δ N - Δ V i ) 2
式中： Δ N是噪点的时间差分; n表示邻点为良好数据的数目; w i为邻点与噪点之间边的权重; α为动态变化的步长; Δ V i = V i - V i '是第 i个是好数据邻点的时间差分。
有2点事项需要注意：① 噪点的前后时间点的EVI值是必须存在的;② 周围的邻点可以不需要全部为良好的EVI数据。当邻点是一个不良数据点时,初始迭代时邻点与所求噪点之间边的权重 w = 0。但是还有一种特殊的情况,即周围邻点全部为不良数据的噪点时,噪点周围的数据就无法对噪点起到良好地改善作用了。为了解决这个问题,可以将进行了改善的噪点暂时当成一个良好的数据点,从而进行下一个噪点的迭代优化,再根据式(8)的最优化方案：判断光滑性函数 S是否为最小值,若不是,则回到最初的噪点继续进行迭代优化。
（4）生成新的EVI数据
对EVI时间序列数据中的每个噪点进行了改变后,根据空间光滑性式(7),判断光滑性函数 S的值是否为最小值就显得至关重要了。本文新方法使用了线搜索算法中的随机梯度下降（Stochastic Gradient Descent,SGD）方法,采用以指数衰减的学习率去进行训练。从而在不断改善噪点值的同时,让空间光滑性函数 S的值达到最小。在解决这个最优化问题之后,便可以得到高质量的EVI时间序列数据集。图6显示了对噪点进行图论的邻点插值后的效果图,显而易见,在经过步骤（1）处理后的线性插值折线的基础上,图论邻点方法保留了时间序列中被PR数据标记为“0”的准确真实值（折线中黑色方块与红色圆点完全重合的位置）,同时根据邻点的变化趋势对不准确的值进行了优化。
图6 图论邻点方法效果

Fig. 6 The effect of graph theory neighbor point method

5 结果及分析

从MODIS的MOD13A1产品中选取2016—2018年的时间序列数据作为评估新方法的数据,考虑到时间差分需要前后数据,所以需要多提取2个以16 d为时间刻度的EVI数据（2015年12月19日至2019年1月1日共计71个时期）。利用新方法生成了3年的高质量EVI时间序列数据。根据之前的IGBP土地覆盖分类,已经将17类植被类型规划为 5类：林地、灌木、草原、农作物和荒漠。为了检验新方法效果,先从这5类植被类型中每类随机抽出100个测试点,通过PR数据的标注来识别测试点在时间序列中是否为噪声,检查每个测试点的最终优化效果。之后进行更加细致准确的对比检验,从500个测试点中随机抽出5个点（每类抽出一个测试点）进行验证实验,具体坐标见图2。

5.1 留一验证

为了检验周围邻点对噪点数据的影响是否能够优化噪点数据,将对测试点进行留一验证的方法测试。将每个测试点在某一个时刻的真值当作验证数据,其余数据作为训练数据。当去掉这个时刻的真实值时,会用线性插值将这个缺值补上,然后参与图论邻点方法去噪的插值中。这样,就获得了5类植被类型的对比测试数据（表2）,选择真实值和插值之间的绝对值作为衡量指标,可以看出邻点插值的值距离真实值有多大的变化。每一个点都测试3次,第一次是随机去掉一个不是最大值或最小值的普通真实值进行测试,之后2次再分别测试去掉一个是最大值或最小值的真实值。结果表明,在普通值的测试中,除农作物外,其余类型测试点的效果均十分良好;对于最大值的测试,农作物测试点效果依旧较差;而在最小值测试中,5种类型的测试点效果比较相近,林地的略差。从农作物周围邻点对目标农作物点位的插值测试中可以看出,由于邻点与目标点之间可能存在不同的农作物种类,而不同植被种类农作物的生长季也不尽相同,这样会对农作物测试点的邻点插值产生影响;同时,人为因素也是产生影响的原因之一,如人们对农作物进行收割、施肥、保护和控制生长环境,都会对农作物的生长产生影响,导致预计的插值数据与实际不符,造成二者的绝对差值变大。在普通值和最大值的测试中,农作物测试点误差大就是很有可能的。而在最小值的测试中,一般在冬季,其余植被类型因为不属于生长季的原因,测试效果相差不大,但林地存在部分树木有落叶的情况,所以绝对差值会最大。
表2 5类测试点留一验证的对比数据

Tab. 2 Leave one to verify the comparative data for the 5 types of test points

类型 普通值 最大值 最小值
真实值 邻点插值 绝对差值 真实值 邻点插值 绝对差值 真实值 邻点插值 绝对差值
林地 5619 5579.871 39.129 7124 7049.797 74.203 1058 941.051 116.949
灌木 1116 1166.937 50.937 1888 1745.814 142.186 657 704.244 47.244
草原 857 895.397 38.397 1826 1655.251 170.749 430 526.679 96.679
农作物 3128 3474.913 346.913 5715 5487.952 227.048 897 944.294 47.294
荒漠 886 882.815 3.185 982 958.190 23.810 548 605.805 57.805
将新方法的留一验证与S-G滤波法、HANTS法、A-G法和D-L法的留一验证进行对比,选定表2中普通值的真实值作为下一阶段不同方法的留一测试数据,得到表3。结果表明,在5种方法的留一验证中,林地、草原和荒漠3个测试点拟合值与真实值之间绝对值最小的是图论邻点方法,灌木和农作物 2个测试点拟合效果最好的方法分别是S-G方法和A-G方法。可以看出,在测试点属于大范围植被类型的情况下,新方法的效果明显优于其他方法;而在测试点属于有人工干预和较小范围的农作物与灌木时,邻点方法就没有其他方法的精准度高,会产生一些误差。
表3 5类测试点在不同方法的留一验证

Tab. 3 Five types of test points in different methods leave one to verify

类型 真实值 线性插值数据 邻点插值 S-G方法 HANTS方法 A-G方法 D-L方法 最小绝对差
林地 5619 5488.500 5579.871 5481.347 5211.238 5476.249 5684.763 邻点插值
灌木 1116 1132.000 1166.937 1127.458 996.877 1137.098 1149.358 S-G方法
草原 857 867.500 895.397 801.331 743.219 799.136 786.916 邻点插值
农作物 3128 3291.000 3474.913 3318.579 2879.664 3218.487 3279.521 A-G方法
荒漠 886 875.000 882.815 863.136 923.531 844.394 837.469 邻点插值

5.2 整体效果

将2016年第225 d的EVI数据图选出,这个时期的16 d的EVI数据图刚好是7月中旬,此时日照长、温度高和降水充足,植被生长较好。将2016年该时间点的h25v05区域和h26v05区域的EVI数据图线性插值预处理后合成一张EVI初始分布图,再将经过图论邻点处理后的数据图用同样的方法合成一张去噪后的EVI数据图进行整体效果的对比,如图7。图7(a)和图7(b)中,图论邻点方法处理前后2张图的EVI大致上没有发生太大变化,说明经过线性插值预处理的原始分布图,即使没有用图论方法,也有能去除大部分的云、冰雪和未知噪点的效果,而在此基础上使用了图论邻点方法之后,会使得细微处的边缘噪点继续被优化。为了更便捷体现出新方法的效果,将处理后的实验区域EVI数据图减去处理前的EVI图,得到图8的差值面积比例柱状图和图9的差值空间分布图,可以看出EVI减少500以内的面积比例最大,占到了71.6%。图9中还可以发现,左侧h25v05区域中大部分的湖泊数据在经过图论邻点方法处理后,EVI指数会变高,这是因为MODIS中将湖泊水体的EVI设定为-3000,而湖泊周围又有植被,所以根据图论邻点的算法,就会把这部分区域当成噪点进行插值,得出的值会比 -3000大,所以当测试地区水体面积较大时,可选择在去噪处理后用合成的5种植被类型分布（图10）进行筛选。除此之外,去噪效果最好的地区在h26v05的右下角,大致在四川盆地处,其他地区起到的去噪效果一般;EVI变高的值保持在2000以内（EVI值在0~10 000）,分布在实验区的广大区域。通过图9与图10的对比还可发现,草原大部分地区的EVI值发生了减少,中部部分地区的EVI值减少超过了500,农作物和林地的EVI值在优化后略有上升,灌木EVI处理前后变化不明显,实验区西北角的荒漠EVI有所增长,增长幅度小于500。
图7 2016年7月中旬实验区域图论邻点方法处理前后的EVI数据分布

Fig. 7 EVI data distribution before and after processing with graph theory neighbor method in the experimental area in mid-July 2016

图8 EVI处理前后差值的面积占比

Fig. 8 The area ratio of the difference before and after EVI processing

图9 2016年7月中旬实验区域EVI处理前后的差值分布

Fig. 9 Distribution of differences before and after EVI treatment in the study area in mid-July 2016

图10 实验区5种植被类型的分布

Fig. 10 Distribution of five types of quilts in the experimental area

5.3 与其他方法的讨论

图论邻点方法属于时空融合方法类别,相较于其他同类方法,新方法是得到一个区域的最优估计,并没有针对每一种植被类型进行单独取函数去噪。其他同类方法都有在条件上进行了一些限制或在结果上有一些不同。例如,UBDF法假设了土地覆盖类型的不变,使用了固定的植被类型与区域面积的比例;LMGM法在UBDF法的假设条件下,又对同类植被类型下每个像元点的时间差分值进行了固定;STARFM法是基于权函数的融合方法,本文方法与其类似,STARFM法通过选择大小不同的空间移动窗口来确定不同点对中心像元点的权重来改变中心像元,这样做会改变所有的中心像元值,降低EVI值的真实性;SFRC法通过每次选择 2个不同的窗口用于回归模型预测,再采用空间距离加权相似邻域像元的空间滤波来进行去噪,得到的结果与STARFM法一样会降低某些点位的真实性;OPDL法通过字典学习,固定一对图像的系数来拟合图像,存在一定的误差,但效率非常高;FSDF法结合了区域分解、空间插值和相邻像元平滑,得到的结果同样对所有像元值进行了拟合改变。
本文将把图论邻点方法与常用的4种方法进行EVI时间序列数据的重构效果比较,4种方法分别是S-G滤波法、HANTS法、A-G法和D-L法。为方便快捷底使用这4种方法,测试过程中使用了HANTS插件和TIMESAT软件[33]。HANTS插件使用了IDL语言进行编译,可以在ENVI软件中便捷的使用HANTS法对时间序列数据进行重构;TIMESAT软件基于MATLAB的软件包,集成了S-G滤波法、 A-G法和D-L法,能实现对时间序列数据同时进行多种不同方法的重构效果。接下来,首先对EVI时间序列数据采用了线性插值的预处理,排除明显的云或雪造成的影响,并将预处理后的数据视为初始数据,然后分别使用图论邻点方法、HANTS法、S-G滤波法、A-G法和D-L法对初始数据进行重构,时间序列曲线的不同方法重构结果见图11。
图11 不同植被类型的EVI时间序列数据重构曲线对比

Fig. 11 Comparison of reconstruction curves of EVI time series data of different vegetation types

图11的曲线图表明,5种方法对于预处理后的初始数据的优化都是有效的,均能去掉一些时间序列数据上的噪声。不同植被类型的测试点经过线性插值去掉了显著的云或雪造成的噪声后,得出了图11(a)中初始数据的曲线图：林地、灌木、草原和农作物均随着时刻的推移,有着显而易见的季节性变化,符合植被的生长季特征;荒漠由于植被较少,特征不明显。之后,选取其中一年23期数据来观测各种不同植被类型的不同方法去噪效果。林地的拟合曲线中,HANTS法的拟合在前期出现极其显眼的低估;在第13个时期时,相较于其他方法,图论邻点方法的拟合更贴近实际变化（图11(b)）。对于灌木的拟合曲线,HANTS法在峰值出现了高估;邻点插值方法的拟合效果十分好,其他3种函数拟合方法效果相似（图11(c)）。在草原的拟合曲线图中,5条拟合曲线的变化大致相同,但在峰值处的拟合值略有不同（图11(d)）。5种方法在农作物测试点的拟合处理上与在草原上一样,均表现出相似的效果,EVI曲线峰值和陡峭变化程度也有很大的相似性,但邻点插值由于真实值的影响,保真度较高（图11(e)）。在草原和农作物的测试点中表明,当曲线陡峭变化程度较大时,HANTS法会在峰值出现明显的数据低估。荒漠的植被绿化程度低,EVI范围仅在500~1000波动,5种方法的拟合基本上都能保持EVI的真实性（图11(f)）。

5.4 不同方法的保真度比较

保真度就是保持测试后数据为真实值的程度,不同方法得出的数据相较于初始数据会发生改变,保真度能在一定程度上说明方法的稳定性和真实性。在这里,衡量保真度使用的指标是均方根误差RMSE（Root Mean Square Error）：
RMSE = 1 N ∑ i = 1 n ( x i - y i ) 2
式中： N为每组的样本数; x i代表不同方法测试得出的第i个值; y i为对应的第i个初始数据（本文还是将线性插值预处理后的数据视为初始数据）。通过这个指标来衡量各个方法的保真性,均方根误差RMSE越小,就说明保真度越强。
对5种植被类型的测试点进行了不同方法的2016—2018年MODIS EVI时间序列数据保真度实验,结果如图12所示。可以看出,在不同植被类型的EVI时间序列数据重构的RMSE对比中,图论邻点方法的RMSE值分别为200.59、46.58、63.48、165.47和40.95,在5种方法中其RMSE值均为最小。说明相较于HANTS法、S-G法、A-G法和D-L法,图论邻点方法在一定程度上,保真能力效果最好。
图12 不同植被类型的EVI时间序列数据重构的RMSE对比

Fig. 12 RMSE comparison of EVI time series data reconstruction of different vegetation types

6 结论与讨论

6.1 结论

EVI数据噪声的存在是不可避免的,造成噪声的主要来源为地理环境、气象变化和数据处理的方式。因此,为了研究植被生态遥感和环境急剧变化,EVI的时间序列数据重构方法就成为了解决问题的重点之一。
设定了2个符合现实的假设：① EVI数据主要与植被有关,其变化过程与植被生长发育的变化相一致;② MODIS的MOD13A1产品中,PR数据可以精准无误地指示对应EVI在各点的各个时刻数据是否良好。于是,给出了一种基于图论的邻点插值方法,具体实现采用优化方法中的线搜索算法,用来消除EVI数据中由大气云层和冰雪覆盖产生的噪声。同时将新方法应用于2016—2018年MODIS-MOD13A1产品上,得到了经过去噪的良好EVI时间序列数据,并与HANTS法、S-G法、A-G法和D-L法在不同植被类型的测试点上进行了对比。结果显示,新方法的去噪效果较好,且保真程度比其他4种方法要更优。

6.2 讨论

本文提出的新方法存在着一些问题尚未解决,会对EVI数据集的优化起到一定影响。
（1）图论邻点方法使用在不同植被边界时,通过周围邻点来对噪点进行插值可能会产生与现实不符合的错误,原因是未考虑到部分植被与相邻植被的EVI并不是渐变的,若出现突变,则噪声的插值点数据会出现一定误差。
（2）由于邻点插值是分辨率越高越精准,而分辨率高则意味着计算量的复杂,导致计算时间略长,但相对的精准度也越高。
尽管新方法有一些瑕疵,但在绝大范围内仍然是十分有效和良好的,可以给植被遥感数据的处理和生态环境的研究提供有益借鉴。

衷心感谢中国科学院深圳先进技术研究院高性能计算研究中心提供技术帮助以及NASA提供了本文的原始EVI数据。

References

Publishing order | Descend order by publishing year | Descend order by cited within
[1]
Marcos B, Gonçalves J, Alcaraz-Segura D, et al. Improving the detection of wildfire disturbances in space and time based on indicators extracted from MODIS data: A case study in northern Portugal[J]. International Journal of Applied Earth Observation and Geoinformation, 2019,78:77-85.

DOI

[2]
王正兴, 刘闯, Huete Alfredo. 植被指数研究进展:从AVHRR-NDVI到MODIS-EVI[J]. 生态学报, 2003,23(5):979-987.

[ Wang Z X, Liu C, Huete Alfredo. Research progress of vegetation Index: from AVHRR-NDVI to MODIS-EVI[J]. Acta Ecologica Sinica, 2003,23(5):979-987. ]

[3]
孙立双, 马运涛, 毕天平, 等. 辽宁地区不同地表覆盖类型EVI和NDVI特征[J]. 沈阳建筑大学学报(自然科学版), 2013,29(6):1024-1029.

[ Sun L S, Ma Y T, Bi T P, et al. EVI and NDVI characteristics of different surface cover types in Liaoning area[J]. Journal of Shenyang Construction University (Natural Science Edition), 2013,29(6):1024-1029. ]

[4]
周惠慧, 王楠, 黄瑶, 等. 不同时间间隔下的遥感时间序列重构模型比较分析[J]. 地球信息科学学报, 2016,18(10):1410-1417.

DOI

[ Zhou H H, Wang N, Huang Y, et al. Comparison and analysis of remote sensing time series reconstruction models under different time intervals[J]. Journal of Geo-information Science, 2016,18(10):1410-1417. ]

[5]
刘建文, 周玉科. 站点尺度的青藏高原时序NDVI重构方法比较与应用[J]. 地理科学进展, 2018,37(3):427-437.

DOI

[ Liu J W, Zhou Y K. Comparison and application of site-scale NDVI reconstruction methods for Qinghai-Tibet Plateau time series[J]. Progress in Geography, 2018,37(3):427-437. ]

[6]
贾若楠, 杜鑫, 李强子, 等. 近15年锡林郭勒盟植被变化时空特征及其对气候的响应[J]. 中国水土保持科学, 2016,14(5):47-56.

[ Jia R N, Du X, Li Q Z, et al. Spatio-temporal characteristics of vegetation change and its response to climate in Xilingol League in recent 15 years[J]. Science of Soil and Water Conservation, 2016,14(5):47-56. ]

[7]
刘倩楠, 岳彩荣, 欧阳志云, 等. 基于MODIS—NDVI时序数据的重庆市植被变化研究[J]. 测绘与空间地理信息, 2012,35(3):99-102.

[ Liu Q N, Yue C R, Ouyang Z Y, et al. Study on vegetation change in Chongqing based on MODIS-NDVI time series data[J]. Geomatics & Spatial Information Technology, 2012,35(3):99-102. ]

[8]
Holben B N. Characteristics of maximum-value composite images from temporal AVHRR data[J]. International journal of remote sensing, 1986,7(11):1417-1434.

DOI

[9]
Viovy N, Arino O, Belward A S. The Best Index Slope Extraction (BISE): A method for reducing noise in NDVI time-series[J]. International Journal of remote sensing, 1992,13(8):1585-1590.

DOI

[10]
Lovell J L, Graetz R D. Filtering pathfinder AVHRR land NDVI data for Australia[J]. International Journal of Remote Sensing, 2001,22(13):2649-2654.

DOI

[11]
Chen Jin, Jönsson P, Tamura M, et al. A simple method for reconstructing a high-quality NDVI time-series data set based on the Savitzky-Golay filter[J]. Remote sensing of Environment, 2004,91(3-4):332-344.

DOI

[12]
Ma MingGuo, Veroustraete F. Reconstructing pathfinder AVHRR land NDVI time-series data for the Northwest of China[J]. Advances in Space Research, 2006,37(4):835-840.

DOI

[13]
Ryo Michishita, Zhenyu Jin, Jin Chen, et al. Empirical comparison of noise reduction techniques for NDVI time-series based on a new measure[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2014,91(5):17-28.

DOI

[14]
蒋雪冰, 胡月明, 刘振华, 等. 基于线性内插的扩展卡尔曼滤波法NDVI时间序列重构研究[J]. 科技通报, 2017,33(2):137-142.

[ Jiang X B, Hu M H, Liu Z H, et al. Research on NDVI time series reconstruction based on Extended Kalman Filter based on linear interpolation[J]. Bulletin of Science and Technology, 2017,33(2):137-142. ]

[15]
Roerink G J, Menenti M, Verhoef W. Reconstructing cloudfree NDVI composites using Fourier analysis of time series[J]. International Journal of Remote Sensing, 2000,21(9):1911-1917.

DOI

[16]
Beck P S A, Atzberger C, Høgda K A, et al. Improved monitoring of vegetation dynamics at very high latitudes: A new method using MODIS NDVI[J]. Remote sensing of Environment, 2006,100(3):321-334.

DOI

[17]
Jonsson P, Eklundh L. Seasonality extraction by function fitting to time-series of satellite sensor data[J]. IEEE transactions on Geoscience and Remote Sensing, 2002,40(8):1824-1832.

DOI

[18]
Sellers P J, Randall D A, Collatz G J, et al. A revised land surface parameterization (SiB2) for atmospheric GCMs.1. Model formulation[J]. Journal of Climate, 1996,9(4):676-705.

DOI

[19]
Zhang X, Li R, Yue Y M, et al. Improved algorithm for reconstructing vegetation index image time series based on Fourier Harmonic Analysis[J]. Journal of Remote Sensing, 2010,14(3):437-447.

[20]
何月, 樊高峰, 张小伟, 等. 浙江省植被物候变化及其对气候变化的响应[J]. 自然资源学报, 2013,28(2):220-233.

[ He Y, Pan G F, Zhang X W, et al. Phenological change of vegetation in Zhejiang province and its response to climate change[J]. Journal of Natural Resources, 2013,28(2):220-233. ]

[21]
张晗, 任志远. 多种时序NDVI重建方法比较与应用分析[J]. 中国农业科学, 2014,47(15):2998-3008.

[ Zhang H, Ren Z Y. Comparison and application analysis of several temporal NDVI reconstruction methods[J]. Scientia Agricultura Sinica, 2014,47(15):2998-3008. ]

[22]
Zhou J X, Chen J, Chen X H, et al. Sensitivity of six typical spatiotemporal fusion methods to different influential factors: A comparative study for a normalized difference vegetation index time series reconstruction[J]. Remote Sensing of Environment, 2021,252:112-130.

[23]
Zurita M R, Clevers J G, Schaepman M E. Unmixing-based Landsat TM and MERIS FR data fusion[J]. IEEE geoscience and remote sensing letters, 2008,5(3):453-457.

DOI

[24]
Rao Y, Zhu X, Chen J, et al. An improved method for producing high spatial-resolution NDVI time series datasets with multi-temporal MODIS NDVI data and Landsat TM/ETM+images[J]. Remote Sensing, 2015,7(6):7865-7891.

DOI

[25]
Gao F, Hilker T, Zhu X, et al. Fusing Landsat and MODIS data for vegetation monitoring[J]. IEEE Geoscience and Remote Sensing Magazine, 2015,3(3):47-60.

[26]
Wang Q, Peter M A. Spatio-temporal fusion for daily Sentinel-2 images[J]. Remote Sensing of Environment, 2018,204:31-42.

DOI

[27]
Huang B, Song H. Spatiotemporal reflectance fusion via sparse representation[J]. IEEE Trans. Geoscience and Remote Sensing, 2012,50(10):3707-3716.

DOI

[28]
Zhu X, Helmer E H, Gao F, et al. A flexible spatiotemporal method for fusing satellite images with different resolutions[J]. Remote Sensing of Environment, 2016,172:165-177.

DOI

[29]
Atzberger C, Eilers P H C. A time series for monitoring vegetation activity and phenology at 10-daily time steps covering large parts of South America[J]. International Journal of Digital Earth, 2011,4(5):365-386.

DOI

[30]
Julien Y, Sobrino J A. Comparison of cloud-reconstruction methods for time series of composite NDVI data[J]. Remote Sensing of Environment, 2010,114(3):618-625.

DOI

[31]
耿丽英, 马明国. 长时间序列 NDVI 数据重建方法比较研究进展[J]. 遥感技术与应用, 2014,29(2):362-368.

[ Geng L Y, Ma M G. Progress in comparative study of NDVI data reconstruction methods for long time series[J]. Remote Sensing Technology and Application, 2014,29(2):362-368. ]

[32]
王乾坤, 于信芳, 舒清态, 等. MODIS EVI时序数据重建方法及拟合分析[J]. 地球信息科学学报, 2015,17(6):732-741.

DOI

[ Wang Q K, Yu X F, Shu Q T, et al. Analysis of time-series data reconstruction method and fitting based on EVI of MODIS[J]. Journal of Geo-information Science, 2015,17(6):732-741. ]

[33]
Jönsson P, Eklundh L. TIMESAT: A program for analyzing time-series of satellite sensor data[J]. Computers and Geosciences, 2004,30(8):33-845.

DOI

Options
Outlines

/

〈 〉