EN中文

Journal of Geo-information Science >

2022 , Vol. 24 >Issue 5: 864 - 874

DOI: https://doi.org/10.12082/dqxxkx.2022.210628

Research on Route of Mountain Flood Disaster Avoidance based on Equivalent Distance Algorithm

  • ZHANG Chaoqin , 1, 4, 5 ,
  • XUE Fengchang , 1, 3, 4, 5, * ,
  • CHEN Xiaojuan 2 ,
  • LI Ting 2 ,
  • HAN Yu 1, 4, 5 ,
  • JIANG Jian 1, 4, 5 ,
  • TANG Weigan 1, 4, 5
Expand
  • 1. School of Remote Sensing & Geomatics Engineering, Nanjing University of Information Science & Technology, Nanjing 210044, China
  • 2. Hebei Meteorological Disaster Prevention Center, Shijiazhuang 050000
  • 3. Digital Fujian Institute of Meteorological Big Data (Minnan Normal University), Zhangzhou 363000
  • 4. Key Laboratory of Meteorological Disaster, Ministry of Education, Nanjing University of Information Science &Technology, Nanjing 210044, China
  • 5. Meteorological disaster Geographic Information Engineering Laboratory, Nanjing University of Information Science & Technology, Nanjing 210044, China;
* XUE Fengchang, E-mail:

Received date: 2021-10-13

  Request revised date: 2021-11-20

  Online published: 2022-07-25

Supported by

Meteorological Disaster Monitoring and Early Warning Project of Hebei Meteorological Disaster Prevention Center-Project of Compiling Meteorological Disaster Risk Map of Mountain Villages(2211042001101)

Digital Fujian Institute of Meteorological Big Data (Minnan Normal University) Open Fund(202010701)

Copyright

Copyright reserved © 2022.
Fold

Abstract

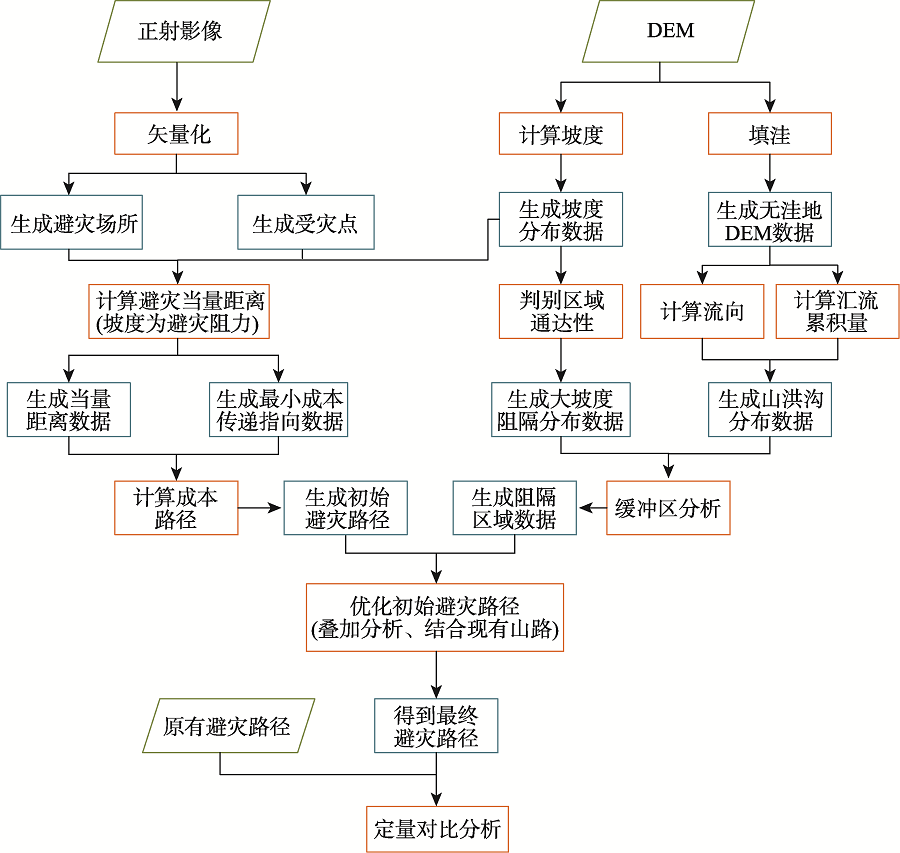
The ability of disaster prevention and mitigation in mountainous and rural areas is weak. Mountain flood disasters have strong suddenness, and the response time of disaster avoidance is short, which are likely to cause casualties. Reasonable design of avoidance routes can help reduce losses caused by disasters. Based on GIS, this paper designs disaster avoidance routes in Tianbaizhi Village, Xingtai City, in the Hebei Province. The Digital Elevation Model (DEM) and orthophoto of the research area are obtained through Unmanned Aerial Vehicle (UAV) photogrammetry. Factors that influence disaster avoidance route planning including slope, cost distance, and function of cost path are used to calculate the initial avoidance route in the mountainous areas. The area where the mountain flood ditch is located and the area with a large slope are used as the interrupted area of the disaster avoidance route. The existing mountain roads are fully considered and rationally used to optimize the final disaster avoidance route. Based on the distance and average slope of the disaster avoidance route, the disaster avoidance route obtained by this method is quantitatively compared with the original disaster avoidance route. The result shows that (1) Among the 20 long-distance disaster avoidance routes designed, this method shortens the length of 18 routes, reduces the average slope of 10 routes, and controls the increase of the average slope of the other 8 routes within 2°; (2) Compared with the original route, the maximum length of each route can be shortened by 329.74 m, and the average slope only increases by 0.68°. The disaster avoidance distance is shortened by adding a small amount of average slope, which improves the disaster avoidance efficiency; (3) The length of remaining two routes increases by 15.21 m and 9.57 m, respectively, resulting in an average slope reduction of 8.43° and 1.43°. The average slope of the routes is reduced by adding a small amount of distance, which improves the safety of disaster avoidance routes; (4) The southern part of Tianbaizhi Village is close to the disaster avoidance point, and the avoidance of disasters is relatively difficult. In contrast, the northern part of Tianbaizhi Village has a longer route to the disaster avoidance point. The longest distance is 1210.02 m, and the difficulty of disaster avoidance is greater. The optimized disaster avoidance path has been separated from the barrier area with large slope, and the degree of overlap between disaster avoidance path and the mountain flood ditch is greatly reduced. The method proposed in this study provides a sufficient scientific basis for relevant decision-makers.

Key words： mountain torrent disaster; mountainous country; disaster avoidance resistance; accessible path; disaster avoidance route; cost distance; average slope; disaster avoidance distance

Cite this article

ZHANG Chaoqin , XUE Fengchang , CHEN Xiaojuan , LI Ting , HAN Yu , JIANG Jian , TANG Weigan . Research on Route of Mountain Flood Disaster Avoidance based on Equivalent Distance Algorithm[J]. Journal of Geo-information Science, 2022 , 24(5) : 864 -874 . DOI: 10.12082/dqxxkx.2022.210628

1 引言

我国的山地面积约6.2239×106 km2,占陆地国土总面积（小于100 km2岛屿除外）的64.89%[1]。由于地形崎岖,基础设施建设难度大,经济基础比较落后,山区乡村防灾减灾能力薄弱,山洪灾害突发性强,避灾响应时间短,容易造成人员伤亡,合理设计避灾路线,有助于降低灾害损失。
避灾路线的可达性通常被认为是个体从灾害隐患点到达避灾点的难易程度,而避灾难易程度的高低又与个体到达避灾点所克服的多种空间阻力大小有关,其衡量指标包括时间、距离等[2]。当前对于避灾路线的研究主要集中于矿井、楼宇等领域。Hou等[3]通过设计数值模型模拟不同坡度条件来定量评估洪水侵入地下空间时通过不同坡度楼梯的行人疏散风险,并采用安全指数来评估行人在不同坡度下通过楼梯疏散的风险,从而得到更安全的逃生路线。Marfai等[4]以高分辨率正射影像和由结构从运动过程生成的数字高程模型为主要数据,基于海啸淹没模型和邻近运算,得到海啸发生时的疏散路线。Herschelman等[5]基于给定的一个交通网络、一个人口和一组目的地,提出一种新的CF-ERP方法来最小化疏散时交通事故、拥堵和延误的运动冲突,同时最小化人口疏散时间。Lee等[6]利用具有外源输入神经网络的非线性自回归和地理信息系统,设计并测试了一种考虑到空间和时间淹没情况的疏散路线指定方法,并通过将其应用于韩国首尔的洪水易发地区。Sun等[7]采用Voronoi图分区方法确定安置点的最优布局和合理配置,以聚落可能的人口容量作为聚落规划选择的权重,建立了具有最短路径的聚落非线性全复盖解模型,基于人员安置布局优化模型,提出了重大突发事件下人员快速转移逃生路径的求解方法。童兴等[8]基于Dijkstra算法分类求取了矿井最佳避灾路线,将巷道当量长度作为可行路线各边的权值,并将其代入拓扑图中,进一步求解得到各拓扑图对应的最佳避灾路线;Tamakloe等[9]基于链路的中心性度量开发了一种车辆疏散算法,根据拓扑特征和网络内链路上不断变化的时空交通集中度,动态识别敏捷疏散路径;秦艮娟等[10]通过兴趣点（POI）量化评估山地城市绿地避灾能力和服务水平,对山地城市绿地避灾可达性进行研究;Sun等[11]利用人群密度图确定拥挤区域的位置,并采用改进的蚁群算法对该位置到出口的疏散路线进行优化,该方法能够以最短的距离和最少的转折点实现最优疏散路径;陈帼鸾[12]则基于TOP-N算法,依据影响巷道当量长度的多种因素,提出一套用于计算巷道当量长度的方法,该方法可实现短时间内从事故发生点到安全地面最优路径的计算,同时分析多条辅助避灾路径以确保所选避灾路线的正确性及合理性。王金华等[13]将巷道类型、高度等因素纳入指标体系,并根据井下的有害气体、温度、烟雾和风向等监测数据,研究形成了动态的井下避灾路线规划方法,并运用多种技术手段将实时信息发布给井下人员,确保遇险人员能够安全快速地逃生。
当前对于避灾路线的研究主要集中于矿井、楼宇等领域,研究区具有明确的路网,形成的技术方法不适合于山区开放性自然地貌,现阶段有关山区山洪灾害避灾路线的设计存在很大的主观性。本文结合河北省示范应用项目,在河北省太行山区选择典型代表性山区,基于山洪避灾原则,综合考虑山区复杂地形地貌,从距离和坡度两个角度出发,利用GIS距离算法结合自然坡度对人的体力消耗影响进行当量距离分析,根据山洪沟分布以及山区现有道路对基于当量距离生成的避灾路线进行优化,探索基于GIS技术进行山洪灾害避灾路线规划设计的技术方法。

2 研究方法、研究区概况及数据来源

2.1 研究方法

本研究基于GIS技术,首先明确避灾过程的阻力值,并结合距离,联合计算研究区所有栅格点到避灾场所的最小当量距离,将避灾点取到最小当量距离的栅格连线作为初始避灾路线。通过叠加分析将阻隔区域与初始避灾路线重叠区域分割,初始避灾路线缺失部分结合可通达的现有道路补全,实现对初始避灾路线的安全性和通达性优化。
以河北省邢台市田白芷村所在山区避灾路线规划为例,图1为技术流程,通过正射影像确定避灾场所和受灾点,以坡度作为避灾阻力值,通过当量距离计算和最小成本传递指向计算生成初始避灾路线。对DEM进行填洼并计算山洪沟流向以及汇流累积量,从而确定山洪沟分布;同时提取坡度 ≥35°区域,从而确定大坡度危险区。将山洪沟与大坡度危险区分布进行缓冲区分析得到避灾的阻隔区域。通过叠加分析,结合山区现有道路对初始避灾路线优化,得到最终避灾路线。为验证GIS方法的有效性,将不依赖本文方法,仅通过山区现有道路进行避灾的原有避灾路径与本文最终避灾路线进行定量对比分析。
图1 技术流程

Fig. 1 Technical flow chart

2.2 研究区概况

田白芷村位于河北省邢台市内丘县獐獏乡东南部,历史文化名山鹊山腹地,处于太子岩、龙驹岭之阴和古关隘苓塞之下。田白芷村向东距离内丘县城30 km,向西距离乡政府獐獏4 km,东偏南 7 km为太行高速鹊山路口,东南3 km为邢台内丘县扁鹊庙名胜区,海拔300~850 m。年均气温11.8℃,年降水量684 mm。
田白芷村位于泜河源头,山脉呈现凹槽结构,造成了暴雨漏斗形式,形成了降雨集中地带,水文特征极为明显,2018年被中国气象学会认定为“中国大陆持续暴雨极值中心”[14]。强降水发生时,田白芷村会遭受到山洪灾害的威胁。

2.3 数据来源

（1）研究区DEM数字高程模型和正射影像是委托河北省测绘院通过高分辨率无人机摄影测量获得,分辨率为0.5 m×0.5 m,具有较高的精度。DEM专题图和正射影像图如图2、图3所示。
图2 DEM专题图

Fig. 2 DEM thematic map

图3 研究区正射影像

Fig. 3 Orthophoto image map of the study area

（2）通过现场调研和咨询村民,现有部分建筑较为安全可靠,能够满足山洪灾害发生时的避灾需求,因此将适宜避灾的指定房屋建筑矢量化,将其作为灾害发生时的避灾场所。由于风险是随机的,整个研究区都存在受灾风险,所以建立避灾路线从风险点的随机分布来考虑,采用均匀分布的形式,相邻风险点间距50 m。

3 实验验证

3.1 研究区三维场景构建

利用无人机倾斜摄影得到田白芷村山区小流域正射影像以及DEM数字高程模型,为了使研究分析过程中生成的各种数据结果能直观、立体的表达,需要构建研究区三维场景。研究区三维场景通过ArcScene构建。基于DEM数据将正射影像数据设置在DEM表面上浮动,即通过DEM为原始平面数据中的每个像元对应赋予一个高程值,实现像元地表特征和高程值结合的三维可视化表达,构建的三维场景如图4。
图4 田白芷村山区小流域三维场景

Fig. 4 3D scene of small watershed in mountainous area of Tianbaizhi Village

3.2 山区山洪灾害避灾分析

山区地形较为复杂,山洪灾害频发,避灾影响因素与避灾行为二者存在显著的相关性,山区复杂地形和开放性自然地貌使得避灾过程也存在一定的危险性。避灾过程中较大的坡度容易对山区村民造成伤害,主观规划的避灾路线难以确保村民避灾的安全性,人为想定的避灾路线也很难定量的评价避灾路线规划的合理性。避灾路线并不是越短越合理,“远离山洪沟、远离陡峭地带、避灾行程尽可能短的同时满足避灾过程尽可能安全”是乡村山洪避灾的主要原则,易达性和安全性是避灾路线规划设计的基本要求。

3.3 确定村民避灾阻力值

避灾阻力是指在不同地物类型的影响下人们从出发点到达目的地的干扰因子[15]。山区沿避灾路线到达避灾点最直接的阻力影响为地形坡度,因此本文选用坡度作为确定山区山洪灾害避灾阻力值计算依据,利用GIS中坡度计算工具进行计算,坡度计算结果如图5所示。图中坡度值的大小决定了地形地势的陡峭程度,坡度值较小区域地势较为平坦,坡度值较大区域地势较为陡峭。图5中红色区域为地势陡峭区域,而绿色区域则为地势平坦区域。
图5 田白芷村所在区域坡度值

Fig. 5 The slope value of the Tianbaizhi Village

3.4 避灾当量距离计算

避灾当量距离是指以避灾阻力值作为通行成本沿避灾路线到达避灾点的避灾成本距离。避灾当量距离可以利用GIS中成本距离计算工具进行计算,可得到每个计算单元到避灾点的最小累积成本距离[16]。GIS中成本距离与欧氏距离的不同点在于欧氏距离计算的是灾害隐患点到避灾点的实际距离,仅仅考虑距离这一因素,而成本距离是用于确定各灾害隐患点距离最近避灾点所在位置的最短加权距离。
成本距离函数可在栅格数据中为每个栅格分配到最近避灾点栅格的累积当量距离。将研究区现有房屋作为避灾场所,计算得到的研究区当量距离栅格如图6所示,每个像元的取值是该点到避灾场所的最小累计成本,最小成本传递指向数据如 图7,记录了计算中最小成本的传递方向。
图6 研究区栅格当量距离分布

注：图中当量距离值是由避灾阻力值和距离共同计算决定的,故无常规物理单位。

Fig. 6 Equivalent distance distribution of grid in the study area

图7 研究区栅格最小成本传递指向

注: 最小成本传递指向指的是某栅格点到避灾场所当量距离最小的情况下, 该栅格点到达下一个栅格的指向。

Fig. 7 Minimum cost transfer direction of grid in study area

3.5 生成避灾路径

基于最小成本传递指向数据和当量距离数据,通过最短路径工具可以得到最短避灾路径。最短路径即为从出发点到达避灾点的理论最低成本路径。
在进行最短避灾路径的求算过程中,可以将点要素或者区域要素作为起始点。所以,最短路径计算方法[17]有3种:
（1）Each Cell：为风险点中每一个单元点寻找一条成本最小的避灾路线;
（2）Each Zone：为每个风险区域寻找一条成本最小避灾路线,风险区域中所有单元共享同一条避灾路线;
（3）Best Single：为所有风险点找寻一条成本最小避灾路线,此时,只有一个风险点与一个相应的避灾点或避灾点组相连。
本文选用Each Cell作为避灾路径选取计算方法,计算原理如图8所示。图中每个像元都存在一个cost值,即上文所计算得到的阻力值,将图中的起始点视为避灾出发点,其到达相邻像元的成本可通过图8(a)中的公式计算,到达对角像元的成本可通过图8(b)中的公式计算,成本值为两临近像元的平均阻力值乘以两像元的距离。当避灾出发点到避难场所的连线所经过的像元成本累加量最小,即图8(c)中accum_cost最小时,可将该条线路视为理论最佳避灾路径,得到避灾路径如图9。
图8 避灾路径计算原理

Fig. 8 Calculation principle of disaster avoidance path

图9 初始避灾路线

Fig. 9 Initial route for disaster avoidance

3.6 避灾路径优化

基于当量距离计算生成的路径虽然在理论上达到了成本算法的最小值,但由于较大的坡度和现实障碍物会造成路径的阻隔,并考虑到山区山洪灾害整体呈现出发生频繁高、影响范围广和危害大的特征,在面临暴雨时山洪沟也会对避灾路径产生阻碍影响,因此仅由该最小值确定的路径无法直接用于现实场景中,需要对其进行优化处理,使其具有现实的通达性和安全性。
3.6.1 山洪沟提取及其对避灾路径影响分析
（1）山洪沟提取
利用GIS中的水文分析工具确定山洪沟分布[18]。首先将田白芷村所在区域DEM数据进行填洼,得到无洼地DEM,再计算水流的流向和汇流累积量,并为汇流累积量设定阈值从而得到栅格河网,其原理是利用所设定的阈值对整个区域分析并生成一个新的栅格图层,其中将汇流累积量大于所设阈值的栅格设定为1,将汇流累积量小于或等于阈值的栅格设定为0。最后对栅格河网矢量化,得到山洪沟分布如图10所示,从图中可以看出山洪沟在研究区分布比较密集,因此在进行避灾路线设计时应充分考虑这一因素。
图10 山洪沟分布

Fig. 10 Distribution of mountain torrents

（2）避灾路径影响分析
为了更直观的表现山洪沟对避灾路径的影响,现将山洪沟和初始避灾路径放入同一图层中,得到结果如图11所示,从图中可以看出初始避灾路径中存在部分路径与山洪沟的贴合度较高,因此需要将此类路径进行优化,使得优化后的路径能够尽可能的避开山洪沟,提高避灾路径的安全性。
图11 山洪沟及初始避灾路径

Fig. 11 mountain torrents and initial disaster avoidance path

3.6.2 避灾路径通达性判别
避灾路径的通达性主要通过判断避灾路线上是否存在路径阻隔来确定。本研究中以较大坡度的危险区域作为路径阻隔。当坡度大到一定程度时会影响人们避灾,将坡度≥35°的区域定义为大坡度危险区域,得到大坡度危险区域如图12所示,将该结果用于优化基于坡度值而确定的初始避灾路线,避灾路线需避开该危险区域。
图12 大坡度危险区域

Fig. 12 Dangerous area with steep slope

3.6.3 优化后的避灾路径
充分考虑前文中的山洪沟及大坡度的阻断,将山洪沟及其周围5 m视为避灾阻隔区域,对山洪沟进行缓冲区分析,缓冲距离为5 m,得到山洪沟的避灾阻隔区域。考虑到避灾奔跑时人具有惯性,将大坡度区域及其周围5 m视为避灾阻隔区域,对大坡度区域进行缓冲区分析,缓冲距离为5 m,得到大坡度区域的避灾阻隔区域。通过叠加分析中的擦除工具除去初始避灾路径中对避灾有阻隔作用的区域。并结合现有山路补全擦除的路径,适当取舍初始避灾路径的主路与岔路,将初始避灾路径进行优化,最终得到优化后的避灾路径如图13所示。
图13 优化后避灾路径

Fig. 13 Optimized disaster avoidance path

3.6.4 避灾路径距离计算
将优化后的避灾路线和研究区DEM作为输入数据,通过ArcGIS中3D分析工具添加表面信息,选择输出属性为surface_length,求得避灾路线在三维场景下的实际距离如图14。
图14 避灾路线实际距离

注: 图中数值代表该受灾点到避灾场所的实际三维距离。

Fig. 14 The actual distance of the avoidance route

4 结果与分析

图13中呈现了优化后避灾路线的空间分布,由于避灾场所主要集中在研究区南部,因此研究区南部的避灾难度较低,保留的避灾路径数量较少且长度较短;研究区北部及东北部设置的避灾点较少,避灾难度较高,村民活动范围大,避灾路线也较多,户外活动的村民可以依据所在位置选择一条最优避灾路线。最终共确定了42条避灾路线,在图14中标记了每条避灾路线到就近避灾场所的实际距离,平均距离为457.27 m,最短的一条避灾路线长为63.04 m,位于研究区南部,周围存在大面积的避难场所。最长的一条避灾路线长为1210.02 m,位于研究区最北部,周围没有避难场所,因此需要较长的避灾行程。研究区南部的避灾路线长度普遍在200 m以下,研究区北部的避灾路线长度则普遍在850 m以上,避灾难度较大,因此村民可以考虑在村庄北部增添避灾场所。
图15为不依赖本文方法,仅通过山区现有道路进行避灾的路径分布图。由于距离避灾点较远的受灾人群避灾难度较大,危险性较高,选取20条路程较长的避灾路线与原始避灾路线进行定量比较和分析。表1、表2统计了图15（原始避灾路线）和图14（本文规划的避灾路线）2种避灾路线规划方案的线路实际距离和线路平均坡度以及两者的差值;图16和图17是其可视化结果。从图16、图17中可以看出在20条路线中,距离和平均坡度总体得到降低。其中有18条路线的实际距离低于原始避灾路线,且其中的10条路线平均坡度同时也得到了降低,而另外8条路线的平均坡度较原始路线增幅较小,均低于2°;1号线路虽然提升了15.21 m的避灾路程,但却降低了8.43°的平均坡度,20号线路提升了9.57 m路程,降低了1.43°的平均坡度,实现增加少量的距离来降低线路的平均坡度,提高了避灾的安全性;而8号线路为避灾缩短了329.74 m,且平均坡度仅提高了0.68°,实现增加少量的平均坡度来缩短避灾距离,从而提高避灾效率。
表1 避灾路线距离统计

Tab. 1 Statistics of the distance of route to avoid disaster (m)

路径编号 原始距离 优化后距离 距离差 路径编号 原始距离 优化后距离 距离差
1 894.76 909.97 15.21 11 712.42 706.39 -6.03
2 1022.30 876.60 -145.70 12 473.05 411.88 -61.17
3 1076.39 1038.04 -38.35 13 434.78 295.93 -138.85
4 1148.99 1111.46 -37.53 14 490.02 416.61 -73.41
5 1258.20 1210.02 -48.18 15 745.37 644.38 -100.99
6 1396.12 1206.16 -189.96 16 399.14 376.63 -22.51
7 1152.66 1094.90 -57.76 17 351.64 329.77 -21.87
8 1029.31 699.57 -329.74 18 420.65 339.46 -81.19
9 912.53 504.01 -208.52 19 304.96 215.82 -89.14
10 1289.55 874.96 -314.59 20 241.88 251.45 9.57
表2 避灾路线平均坡度统计

Tab. 2 Statistics of the average slope of disaster avoidance route (°)

路径编号 原始平均坡度 优化后平均坡度 坡度差 路径编号 原始平均坡度 优化后平均坡度 坡度差
1 23.38 14.95 -8.43 11 20.68 16.93 -3.75
2 19.93 21.89 1.96 12 27.44 22.44 -5.00
3 25.07 23.27 -1.80 13 25.08 27.05 1.97
4 23.43 20.62 -2.81 14 29.31 28.28 -1.03
5 26.21 19.07 -7.14 15 21.70 21.57 -0.13
6 26.69 27.06 0.37 16 11.83 8.57 -3.26
7 20.30 21.13 0.83 17 21.27 20.06 -1.21
8 17.37 18.05 0.68 18 19.82 20.01 0.19
9 23.56 19.73 -3.83 19 18.04 19.11 1.07
10 16.93 18.06 1.13 20 21.47 20.04 -1.43
图15 原始避灾路线

注: 图中数值代表该受灾点到避灾场所的实际三维距离。

Fig. 15 Original disaster avoidance path

图16 避灾路线距离

Fig. 16 Statistics of the distance of route to avoid disaster

图17 避灾路线平均坡度

Fig. 17 Statistics of the average slope of disaster avoidance route

5 讨论

由于山区数据资料的局限性,本文在避灾路线规划中考虑了坡度、距离、山洪沟等阻隔因素,对于暴雨山洪灾害具有一定适用性。然而仍存在一些不足,进一步研究中还需考虑山区避灾过程中其他方面干扰因素,如在避灾时山区不均匀的土质等因素对避灾的影响;也可以采用基于GPU加速技术的高分辨率数值模型对灾害过程进行数值模拟,利用灾害数值模拟成果精确确定避灾危险性阻隔,为避灾路线设置提供有力依据。

6 结论

本文以田白芷村避灾路线规划为例,通过高分辨率无人机摄影测量获得研究区DEM数字高程模型和正射影像,以坡度作为避灾阻力值,利用成本距离和成本路径函数计算山区初始避灾路线,以山洪沟所在区域、坡度较大区域作为避灾路线阻隔,同时充分考虑现有山路,优化形成最终避灾路线。在应用本研究技术方法的42条路线中,选取20条路程较长的避灾路线与原始避灾路线进行定量比较和分析,得到以下4点结论：
（1）在选取的20条路程较长的避灾路线中,大部分避灾路线的长度得到了缩短,并同时降低了线路的平均坡度。其中有18条路线的实际距离低于原始避灾路线,且其中的10条路线平均坡度同时也得到了降低,而另外8条路线的平均坡度较原始路线增幅均低于2°,该方法对于躲避暴雨山洪灾害具有一定适用性。
（2）对于平均坡度较原始路线增幅低于2°的8条路线,实际距离均低于原始避灾路线,其中一条线路为避灾缩短了329.74 m,而平均坡度仅提高了0.68°,实现增加较小坡度来缩短较长的避灾行程,提高了避灾效率。
（3）对于实际距离高于原始避灾路线的2条路线,其中一条线路虽然提升了15.21 m的避灾路程,却降低了8.43°的平均坡度,另一条线路提升了9.57 m路程,降低了1.43°的平均坡度,实现增加较短的避灾行程来降低线路的平均坡度,提高了避灾的安全性。
（4）利用上述方法计算得到研究区42条避灾路线,避灾路线平均距离为457.27 m。其中田白芷村南部区域离避灾点较近,避灾行程在100 m左右,山洪灾害发生时村民能够快速有效的避灾。而田白芷村北部山区避灾点较少,到达避灾点的行程接近1 km,最远长达1210.02 m,避灾难度较大,山洪灾害发生时对户外活动村民的生命安全存在较大的威胁,应加强避灾场所建设。

References

Publishing order | Descend order by publishing year | Descend order by cited within
[1]
南希, 李爱农, 陈昱, 等. 竖版中国数字山地图(1:670万)的设计与编制[J]. 遥感技术与应用, 2016, 31(3):451-458.

[ Nan X, Li A N, Chen Y, et al. Design and compilation of digital mountain map of China(1:6700 000) in Vertical Layout[J]. Remote Sensing Technology and Application, 2016, 31(3):451-458. ]

[2]
王兰. 山地城市公园可达性研究[D]. 重庆:西南大学, 2008.

[ Yu L. Research on accessibility of park in the mountalnous urban areas[D]. Chongqing: Southwest University, 2008. ]

[3]
Hou J M, Chen G Z, Zhang Y W, et al. A simulation study on risks of pedestrian evacuation from flooded staircases of different slopes in the underground space[J]. Natural Hazards, 2021(8):1-25. DOI: 10.1007/S11069-021-04956-7.

DOI

[4]
Marfai M A, Khakim N, Fatchurohman H, et al. Planning tsunami vertical evacuation routes using high-resolution UAV digital elevation model: Case study in Drini Coastal Area, Java, Indonesia[J]. Arabian Journal of Geosciences, 2021, 14(19):1-13. DOI: 10.1007/S12517-021-08357-9.

DOI

[5]
Herschelman R, Qutbuddin A, Yang K. Conflict-Free evacuation route planning[J]. GeoInformatica, 2021(10):1-24. DOI: 10.1007/S10707-021-00435-0.

DOI

[6]
Lee Y H, Kim H I, Han K Y, et al. Flood evacuation routes based on spatiotemporal inundation risk assessment[J]. Water, 2020, 12(8):2271. DOI: 10.3390/w12082271.

DOI

[7]
Sun X, Chen Y Z, Zhan Z N. Research on the personnel shelter location and evacuation route model planning under emergent events[J]. IOP Conference Series:Earth and Environmental Science, 2020, 510(6):062015. DOI: 10.1088/1755-1315/510/6/062015.

DOI

[8]
童兴, 原帅琪, 方伟鹏, 等. 基于Dijkstra算法的矿井最佳避灾路线分类求取[J]. 工矿自动化, 2018, 44(4):94-99.

[ Tong X, Yuan S Q, Fang W P, et al. Classification and calculation of the best escape route of coal mine based on Dijkstra algorithm[J]. Industry and Mine Automation, 2018, 44(4):94-99. ] DOI: 10.13272/j.issn.1671-251x.17314

DOI

[9]
Tamakloe R, Hong J, Tak J, et al. Finding evacuation routes using traffic and network structure information[J]. Transportation Research Part D, 2021, 95:102853. DOI: 10.1016/J.TRD.2021.102853.

DOI

[10]
秦艮娟, 马长乐. 基于POI数据的山地城市绿地避灾可达性研究—以贵阳市中心城区为例[J]. 美术大观, 2020(12):133-137.

[ Qin G J, Ma C L. Research on the accessibility of green space in mountainous cities based on POI data for disaster avoidance: A case study of the central urban area of Guiyang City[J]. Art Panorama, 2020(12):133-137. ]

[11]
Sun S L, Zhao Q, Xie W Z. Study on safe evacuation routes based on crowd density map of shopping mall[J]. IEEE ACCESS, 2020, 8:153981-153992 DOI: 10.1109/ACCESS.2020.3015956.

DOI

[12]
陈帼鸾. 基于TOP-N算法的井下紧急避灾路径寻优研究[J]. 煤炭技术, 2017, 36(7):206-208.

[ Chen G L. Optimization of underground emergency avoidance path based on TOP-N algorithm[J]. Coal Technology, 2017, 36(7):206-208. ] DOI: 10.13301/j.cnki.ct.2017.07.083

DOI

[13]
王金华, 汪有刚, 张雷, 等. 基于实时数据的井下避灾路线动态规划与发布方法研究[J]. 中国煤炭, 2015, 41(2):67-71.

[ Wang J H, Wang Y G, Zhang L, et al. Dynamic programming and release system of underground emergency escape route based on real-time data[J]. China Coal, 2015, 41(2):67-71. ] DOI: 10.19880/j.cnki.ccm.2015.02.015

DOI

[14]
中国气象局. 内丘:獐么乡被认定为中国大陆持续暴雨极值中[EB/OL]. http://www.cma.gov.cn/2011xwzx/2011xqxxw/2011xjctz/201811/t20181128_484431.html,2018-10-28.

[ China Meteorological Administration. Neiqiu: Zhang Mo Township was identified as the extreme center of continuous heavy rain in mainland China [EB/OL]. http://www.cma.gov.cn/2011xwzx/2011xqxxw/2011xjctz/201811/t20181128_484431.html,2018-10-28.]

[15]
陈玲蒙. 基于GIS的安陆市河滨公园可达性研究[J]. 湖北大学学报(自然科学版), 2017, 39(1):60-64.

[ Chen L M. A study on the accessibility of Hebin Park in Anlu based on GIS[J]. Journal of Hubei University(Natural Science), 2017, 39(1):60-64. ]

[16]
高青. 基于GIS的绿道规划分析方法与应用研究[D]. 长沙:湖南大学, 2012.

[ Gao Q. The study of analysis method and application in GIS-based greenway planning[D]. Hunan University, 2012. ]

[17]
汤国安, 杨昕. ArcGIS地理信息系统空间分析实验教程[M]. 北京: 科学出版社, 2006.

[ Tang G A, Yang X. ArcGIS geographic information system spatial analysis experiment tutorial[M]. Beijing: Science Press, 2006. ]

[18]
徐靖宇, 邱丽静. 基于GIS的湖南省山洪沟提取技术及其应用[J]. 地理科学研究, 2016, 5(2):5.

[ Xu J Y, Qiu L J. Extraction and Application of Flash Flood Ditch in Hunan Province Based on GIS[J]. Geographical Science Research, 2016, 5(2):5 ] DOI: 10.12677/GSER.2016.52009

DOI

Options
Outlines

/

〈 〉