EN中文

Journal of Geo-information Science >

2022 , Vol. 24 >Issue 8: 1445 - 1458

DOI: https://doi.org/10.12082/dqxxkx.2022.210729

Bayesian Geostatistical Modelling for Precipitation Data with Nested Anisotropy Measured at Sparse Reference Stations

  • GAO Xin , * ,
  • YUAN Shengyuan ,
  • LI Jingzhong ,
  • ZHAO Huibing ,
  • XU Shuna
Expand
  • College of Urban and Environmental Sciences, Xuchang University, Xuchang 461000, China
*GAO Xin, E-mail:

Received date: 2021-11-15

  Revised date: 2022-02-18

  Online published: 2022-10-25

Supported by

National Natural Science Foundation of China(42001265)

Fold

Abstract

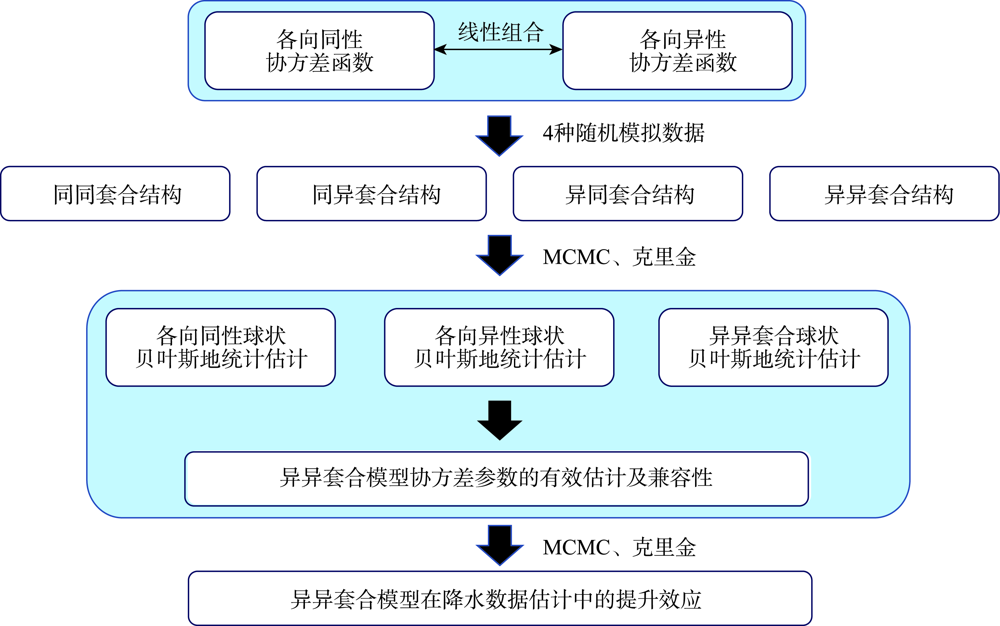
Spatially continuous precipitation data are important data input in hydrological simulation in a watershed, hydrological modeling of land surface, eco-environmental sensitivity evaluation, comprehensive investigation and zoning of geographical environment, and so on. These data are often interpolated from the discrete observations of monitoring points. However, due to the operations and interactions of the underlying physical processes on different scales, the spatial variations of precipitation are generally viewed as a result of the superposition of different geographical processes on multiple scales and directions. The multi-scale, multi-direction natures of geographical processes determine the weights between spatial points, which have an important impact on spatial interpolation. Therefore, it is necessary to establish a multi-scale and multi-direction spatial model to better reflect the dynamic process for regional precipitation estimation and spatial analysis, especially in sparse monitoring areas. Bayesian geostatistical models have the ability of multi-scale and multi-direction modeling and provide a scalable statistical inference framework by integrating observations (external implementation with errors), unknown variables, prior information, and complex dynamical models (real processes). In view of the superposition phenomena of precipitation on scales and directions, this study explored the possibility of decomposition estimates for the sparse data with nested anisotropy based on Bayesian and geostatistical methods to accurately determine the contribution of each independent component. We also further demonstrated the application potential of this model in precipitation interpolation. The results showed that, firstly, the nested anisotropy and multi-scale properties hidden in the sparse data could be well estimated by the Bayesian and geostatistical methods applied in the four random simulations with nested structures using a Fourier integration method. The more complex the model was, the more difficult the estimation was and the stronger the uncertainty was, and the convergence and estimation accuracy could be improved by introducing some prior information. The interpolation accuracy of the heterogeneous models was better than that of the models with simple isotropy or anisotropy. And also the more complex the covariance structure of the data was, the more obvious the improvement effect was. Secondly, complex structures had the ability of downward compatibility with simple structures, but simple structures did not have the ability of upward compatibility with complex structures. Finally, based on the interpolation results, the nested model played an obvious role in improving the accuracy of regional precipitation interpolation, which was about 10% higher than the estimation accuracy of the two basic models. Compared with the two basic structures, the method in this study not only identified two kinds of superposition information but also obtained the contributions of the two components, with a contribution ratio close to 1:1.

Key words： Bayesian statistics; precipitation; nested structures; anisotropy; Kriging interpolation; sparse stations; covariance function; spatial heterogeneity

Cite this article

GAO Xin , YUAN Shengyuan , LI Jingzhong , ZHAO Huibing , XU Shuna . Bayesian Geostatistical Modelling for Precipitation Data with Nested Anisotropy Measured at Sparse Reference Stations[J]. Journal of Geo-information Science, 2022 , 24(8) : 1445 -1458 . DOI: 10.12082/dqxxkx.2022.210729

1 引言

空间上连续分布的降水数据是流域水文模拟、陆面模式研究、生态环境敏感性评价和地理环境综合调查与区划等研究工作中一个重要的输入变量[1⇓-3]。除了使用各种遥感降水数据以外,通过插值或者数值模型的方法将离散监测数据转化为连续数据也是一种常见的处理方法。然而,遥感数据在使用之前需要进行校核,尤其在山区误差较大,此时采用插值的方法便成为一个不错的选择。常见的插值方法有泰森多边形[4]、反距离权重[5]、角距离权重[6]、样条函数[7]和克里金[8]等方法,其中克里金插值法因提供了一种可伸缩统计推断的随机框架而被广泛应用于各种环境中,尤其是在站点稀疏不确定性高的复杂地形地区。
区域降水的空间分布受到地理变量、大气环流和天气系统等因素的综合影响,因此呈现出明显的随机性、近邻相关性、空间异质性和多尺度性等一般地学过程共有的特征。若想获得较为理想的插值结果,就需要了解和分析某区域降水的空间分布形态及与影响因素如地形、气象因子等在不同尺度上的相互作用机制。早在20世纪70年代,Zawadzki[9]就采用自相关函数和雷达数据研究了强对流暴雨的时空分布特征,对存在的尺度和各向异性进行了定量表征;随后,Smith[10]对地形雨形成过程的复杂性进行了全面评述,并提出了一个气流沿坡抬升降水强度的计算模型。自2000年至今,在多源降水数据和新方法、新技术的支撑下,越来越多的基于大气运动路径、海陆距离以及地形阻隔等影响因素的区域降水形态研究工作开始涌现。因此,为了提升插值精度,一系列融入降水和地理、气象等因子关系的随机和确定性插值模型得到建立,如Pardo-Igúzquiza[11]、Goovaerts[12]将高程分别作为协变量和自变量采用协同克里金和泛克里金方法实施降雨插值;Hofierka等[13]将嵌入风向和地形变化的规则张力样条函数应用于降水插值中,通过仿射变换实现了降水空间分布上的各向异性; Hutchinson[14]提出了顾及地形效应的薄板光滑样条函数插值算法。当然,也有不通过引入影响因子实现各向异性插值的,例如Tomczak[15]构造了一种考虑局部形态参数的反距离权重插值算法;Zhang等[16]探讨了各向异性相关距离对角距离权重插值方法的精度影响效应。Hofierka[13]、Tomczak[15]等通过研究证实了引入各向异性可以有效提升降水插值的精度。上述插值模型更多的是将影响因子看作自变量来建立线性或者非线性模型,类似于地统计方法中的趋势项或者均值项。在地统计框架中,除了趋势性携有刻画空间分布形态的能力以外,也可以通过构造依赖方向的协方差函数,即各向异性协方差函数来描述其形态特征,例如,Atkinson等[17]采用简单和指示克里金,Saveliev等[18]使用带状克里金,Kastelec等[19]采用泛克里金,Agou等[20]采用回归克里金,进行各向异性插值或者对多种插值结果进行对比研究。近年来,一种适宜于自动化插值的非参数协方差矩阵计算方法也受到了关注,该方法利用频率域的正定化处理来获取有效协方差矩阵,但要求参与计算的样本量不能太少,因此,一些研究工作常常采用遥感数据来代替稀疏样本计算协方差矩阵[21],另外,时空各向异性的克里金插值方法也得到了发展[22]。然而,Zawadzki[9]分析得到,降水的空间分布形态呈现出了多尺度各向异性的特点,即变形信息随着尺度的变化而变化,例如Zawadzki[9]的研究揭示了某地区强降雨协方差函数呈现出10 km以下为各向同性,而10 km以上为各向异性的特点,Lovejoy等[23]甚至认为降水是由运行在无穷多个各向异性尺度上的过程综合作用后的结果。
上述工作中的各向异性考虑常常限制在某一个固定尺度上,而没有考虑或者明确提出各向异性在空间分布上的多尺度性[24]。显然,这样做的后果会使地理事物发展的真实过程得到简化,模型的建模能力和系统参数不确定性的挖掘潜力大打折扣,从而监测点位之间的相互位置关系得不到正确估计,插值精度势必受到影响。针对这种多尺度各向异性的情况,地统计学提供了一种协方差函数结构套合的解决方案,就是将协方差函数表示成一组简单协方差函数的和。本研究正是立足于此方案,试图通过套合各向异性协方差函数模型来刻画空间变异的多尺度和多方向性,并以此进行降水的空间插值。当协方差函数采用了套合结构以后,参数的数量有了成倍的增长,如何得到精确的估计便成了一个难题。传统的矩估计方法依赖于观测值数量、对实验协方差函数的目视观察和手动调整,严重依赖于经验判断,尤其是面对稀疏的采样数据,其弊端愈发明显。例如,Webster等[25]在对土壤空间变异的研究中提出,若想使用矩方法获得各向同性半变异函数的可靠估计大约需要100~150个样本,225个样本最为理想,那么如果面对各向异性尤其是套合各向异性的数据,这些样本数量是远远不够的。Pardo-Igúzquiza[26]指出,当面对小样本时,没有一种方法可以给出可靠的估计,但是总有一些方法比其他方法更有估计优势,例如最大似然估计法。既然面对小样本和复杂地理环境,没有哪一种方法可以给出可靠的估计,那么在这种环境下,对参数不确定性的估计更值得关注。贝叶斯方法在地统计建模中的应用及发展,有效地解决了这一难题。作为一种最大似然估计方法,它不需要计算实验协方差函数,因此就避免了主观意义上距离和方向的划分,更重要的是,它还可以兼容尽可能多的先验信息（主观的或者客观的）以消除小样本或者复杂环境带来的不确定性[27]。鉴于以上分析,本研究将采用贝叶斯地统计方法探讨稀疏采样环境下套合模型分解估计的可能,以及复杂模型的引入对于稀疏站点降水插值精度的提升究竟有无效果。

2 研究方法

2.1 研究路线

本研究的技术流程如图1所示：① 根据各向同性协方差函数和各向异性协方差函数的线性组合分别构造4个矩阵,即同同套合、同异套合、异同套合和异异套合矩阵,然后根据傅里叶积分法生成这4种矩阵的模拟数据;② 在对上述数据抽样的基础上使用贝叶斯地统计方法对系统参数进行估计,包括验证参数的估计精度、挖掘参数的不确定性以及探索系统的结构化分析提升能力和复杂模型对简单模型的兼容能力;③ 探索和研究异异套合模型在真实数据中的应用效果。
图1 套合各向异性贝叶斯地统计估计及降水插值应用研究流程

Fig. 1 The research process of Bayesian geostatistical estimation with nested anisotropy and its application on precipitation interpolation

2.2 4种套合协方差矩阵

对于1个地统计框架下的二维随机过程,如果不考虑均值过程在空间分布上的变异,那么该随机过程空间上的所有变异信息便集中在了协方差函数上,协方差函数理论模型抽象和概括的能力直接决定了系统结构认识的深度和参数推断的精度。在地统计学中,用基本协方差函数的线性组合可以表达复杂的协方差结构,它们之间存在如下关系：
C ( h ) = ∑ i = 1 n C i ( h )
式中：C(h)为套合结构;Ci(h)为基本结构;i为基本结构的数量。由于二级结构已经能够满足大多数情况,因此本研究主要围绕二级套合进行验证,即 C(h)=C1(h)+C2(h),C1和C2可以代表不同尺度上的各向同性或者各向异性协方差函数。由于球状模型在地学领域应用的普遍性,本文仅以球状模型为例,不去考虑其他模型之间的套合,在引入套合结构之前,首先看一下2种基本结构。
第1种结构为各向同性协方差矩阵。如果某协方差函数仅仅是距离h的函数,则视它为各向同性的,对于一各向同性过程,根据球状协方差函数理论模型,其协方差矩阵 Σ ( θ ) i i '有形式：
Σ ( θ ) i i ' = σ 2 + τ 2 h i i ' = 0 σ 2 1 - 3 2 h i i ' a + 1 2 h i i ' a 3 0 < h i i ' ≤ a 0 h i i ' > a
式中：Σ为协方差矩阵; θ表示参数空间;ii' 代表两点之间的意思; σ 2>0为系统方差, τ 2≥0为块金常数或者仪器误差; h i i '为任意两点si,si'之间的距离; a为变程。
第2种结构为各向异性协方差矩阵。如图2所示,假设某随机过程的变程等值线为一椭圆,其长短半径分别为amax和amin,对于任意两点si,si'之间的增量 Δ x i i '和 Δ y i i ',经旋转后在新坐标轴中的坐标为：
Δ u i i ' Δ v i i ' = c o s ( β ) s i n ( β ) - s i n ( β ) c o s ( β ) Δ x i i ' Δ y i i '
式中：新坐标轴u、v以椭圆等值线长短半径方向设置; Δ u i i '、 Δ v i i '为转换后的坐标值;β为椭圆变程等值线长轴与x轴之间的夹角。另外,这两点之间的距离为 h i i ' = Δ u i i ' 2 + Δ v i i ' 2 = Δ x i i ' 2 + Δ y i i ' 2。sisi'与椭圆变程等值线交点sφ,sisφ即为两点所成向量方向的变程,其形式为：
a φ i i ' = h i i ' a m a x a m i n / a m i n 2 Δ u i i ' 2 + a m a x 2 Δ v i i ' 2
式中： a φ i i '为φii'方向的变程。
因此,对于球状各向异性模型,其协方差矩阵可以表示为：
Σ ( θ ) i i ' = σ 2 + τ 2 h i i ' = 0 σ 2 1 - 3 2 h i i ' a φ i i ' + 1 2 h i i ' a φ i i ' 3 0 < h i i ' ≤ a φ i i ' 0 h i i ' > a φ i i '
从式（5）中可看出,两点之间的协方差既是两点方向,也是两点距离的函数。
图2 各向异性变程计算[28]

Fig. 2 The calculation of an anisotropic range for one direction φ

为了能够基本覆盖已有成果中出现的复合结构,根据不同结构在尺度和方向上的变化特征,本研究构造了4种套合结构,分别是同同、同异、异同和异异套合结构,其计算公式见表1。同同结构是由2个各向同性结构构成的套合结构,2种结构没有方向上的变化,只有尺度上的变化,目前绝大多数的成果都是基于该结构;同异结构是由1个小尺度的各向同性结构和1个大尺度的各向异性结构构成,可以用来表征在小尺度上是各向同性而在大尺度上是各向异性的地理现象,例如Zawadzki[9]、Gyasi-Agyei[21]和Wei[29]的研究中出现的某些地理现象。异同结构是由1个小尺度的各向异性结构和1个大尺度的各向同性结构构成,可以用来表征在小尺度上是各向异性而在大尺度上是各向同性的地理现象,例如Zawadzki[9]和高歆[30]的研究中出现的某些地理现象。异异结构是由2个各向异性结构构成的套合结构,2种结构既有方向上的变化,又有尺度上的变化,显然,这种结构对应着自然界中广泛存在的具有二级套合结构的分层异质性地理现象[31-32]。纵观这4种结构,参数越多,结构越复杂,概括和建模能力就越强,不确定性挖潜空间也就越大,尤其是异异套合结构,它将协方差函数模型提升到一个更为一般的水平,不仅前面3种结构成为它的特殊形式,连上述2种基本结构也成为了其特殊形式。面对上述不断复杂化的模型,不禁要问,复杂模型适用于简单模型对应数据集的结构化分析吗?复杂模型有概括简单模型的能力吗?
表1 4种球状套合协方差矩阵的计算公式和参数空间

Tab. 1 The formulas and parameter spaces of covariance matrices for the four spherical models with nested structures

结构 公式 参数空间 参数说明 公式编号
同同套合 Σ ( θ ) i i ' = σ 1 2 + σ 2 2 + τ 2 h i i ' = 0 σ 1 2 1 - 3 2 h i i ' a 1 + 1 2 h i i ' a 1 3 + σ 2 2 1 - 3 2 h i i ' a 2 + 1 2 h i i ' a 2 3 0 < h i i ' ≤ a 1 σ 2 2 1 - 3 2 h i i ' a 2 + 1 2 h i i ' a 2 3 a 1 < h i i ' ≤ a 2 0 h i i ' > a 2 θ{μ,τ2, σ 1 2, σ 2 2,a1,a2},
a1 ≤ a2		 μ：均值;τ2：块金值; σ 1 2：结构1方差; σ 2 2：结构2方差;a1：结构1变程;a2：结构2变程 （6）
同异套合 Σ ( θ ) i i ' = σ 1 2 + σ 2 2 + τ 2 h i i ' = 0 σ 1 2 1 - 3 2 h i i ' a 1 + 1 2 h i i ' a 1 3 + σ 2 2 1 - 3 2 h i i ' a 2 , φ i i ' + 1 2 h i i ' a 2 , φ i i ' 3 0 < h i i ' ≤ a 1 σ 2 2 1 - 3 2 h i i ' a 2 , φ i i ' + 1 2 h i i ' a 2 , φ i i ' 3 a 1 < h i i ' ≤ a 2 , φ i i ' 0 h i i ' > a 2 , φ i i ' θ{μ,τ2, σ 1 2, σ 2 2,a1,a2,min,a2,max,β2},
a1 ≤ a2,min≤a2,max		 μ：均值;τ2：块金值; σ 1 2：结构1方差; σ 2 2：结构2方差;a1：结构1变程;a2,min,：结构2变程短半径;a2,max：结构2变程长半径;β2：结构2倾角 （7）
异同套合 Σ ( θ ) i i ' = σ 1 2 + σ 2 2 + τ 2 h i i ' = 0 σ 1 2 1 - 3 2 h i i ' a 1 , φ i i ' + 1 2 h i i ' a 1 , φ i i ' 3 + σ 2 2 1 - 3 2 h i i ' a 2 + 1 2 h i i ' a 2 3 0 < h i i ' ≤ a 1 , φ i i ' σ 2 2 1 - 3 2 h i i ' a 2 + 1 2 h i i ' a 2 3 a 1 , φ i i ' < h i i ' ≤ a 2 0 h i i ' > a 2 θ{μ,τ2, σ 1 2, σ 2 2,a1,min,a1,max,a2,β1},
a1,min≤ a1,max≤ a2		 μ：均值;τ2：块金值; σ 1 2：结构1方差; σ 2 2：结构2方差;a1,min：结构1变程短半径,a1,max：结构1变程长半径;a2：结构2变程;β1：结构1倾角 （8）
异异套合 Σ ( θ ) i i ' = σ 1 2 + σ 2 2 + τ 2 h i i ' = 0 σ 1 2 1 - 3 2 h i i ' a 1 , φ i i ' + 1 2 h i i ' a 1 , φ i i ' 3 + σ 2 2 1 - 3 2 h i i ' a 2 , φ i i ' + 1 2 h i i ' a 2 , φ i i ' 3 0 < h i i ' ≤ a 1 , φ i i ' σ 2 2 1 - 3 2 h i i ' a 2 , φ i i ' + 1 2 h i i ' a 2 , φ i i ' 3 a 1 , φ i i ' < h i i ' ≤ a 2 , φ i i ' 0 h i i ' > a 2 , φ i i ' θ{μ,τ2, σ 1 2, σ 2 2,a1,min,a1,max,a2,min, a2,max,β1,β2},
a1,min≤ a1,max≤ a2,min≤ a2,max		 μ：均值;τ2：块金值; σ 1 2：结构1方差; σ 2 2：结构2方差;a1,min：结构1变程短半径,a1,max：结构1变程长半径;结构2变程短半径;a2,max：结构2变程长半径; β1：结构1倾角;β2：结构2倾角 （9）

2.3 贝叶斯模型和计算

假设{Y(s: s∈D),D∈R2}为1个二维空间的平稳随机过程,Y(s)在层次贝叶斯框架下的标准模型为[33]：
Y(s)=μ(s)+ω(s)+ε(s)
式中：μ(s)为均值过程或者趋势项,可以表达成一组解释变量的线性关系和,例如降水量和高程、坡度、坡向之间的关系;ω(s)为一具有空间相关性的随机过程,其方差为 σ 2,均值为0,相关性可以由任意有效协方差函数C(h)来表示;ε(s)则是均值为0,方差为τ2的白噪声。假设有一组来自某高斯过程下的观测值Y={Y(s1), …, Y(sn)},由于套合协方差函数的参数估计是本次研究的重点,因此,本文μ(s)被视为不依赖位置变化的全局均值,根据上述模型,可以得出Y为服从多元正态分布的向量,有Y~Nn(μ1, Σ(θ)),其中μ为该随机向量的全局均值;1为n×1的单位向量;Σ为Y中样点的协方差矩阵;由C(h)派生,θ为C(h)中的参数。从上述模型可以看出,对某一随机过程的统计推断本质上就是对均值向量μ(s)和协方差函数C(h)的估计,也可以理解为这二者携带了该随机过程几乎所有的信息。
贝叶斯估计在于贝叶斯后验概率的计算,然而很多情况下面对的是维度很高的数据或者没有 解析关系式的后验密度函数,这时候可以直接采用贝叶斯数值计算方法,例如马尔科夫链蒙特卡洛（Markov Chain Monte Carlo,MCMC）抽样方法。根据采样方式的不同,MCMC方法可以分为Gibbs采样和Metropolis采样,前者需要所有参数全条件概率密度函数的解析形式,后者是一种拒绝-接受算法,对此没有限制。本文采用Metropolis方法,实现步骤如下[33]：
（1）假设参数抽样已进行了s轮,已抽样集合记为{θ (1), …, θ(s)},现在进行第s+1次抽样,首先从建议分布J(θ*|θ(s))中采样一未接受的新值θ*,建议分布J通常选择的是对称分布,因此有,J(θ*|θ(s))= J(θ(s)|θ*),J(θ*|θ(s))表示θ(s)为条件的密度函数。
（2）计算接受率,如式（11）所示。
r s = p ( θ * Y ) p ( θ ( s ) Y ) = p ( Y θ * ) p ( θ * ) p ( Y θ ( s ) ) p ( θ ( s ) )
（3）按照均匀分布us~U(0,1)采样,如果rs>us,则接受θ*为θ(s+1)。
根据采样方式的不同,Metropolis方法又可以分为逐参数采样法和整体采样法,前者是按照顺序依次对每一个参数进行采样和判断,后者则是同时对所有的参数进行采样并做出判断,前者接受率高,后者接受率低,但是前者对相关性强的参数估计误差较大。考虑到上述影响因素,采取2种方法的结合来进行估计,相互影响小的参数采用逐步法,而影响大的参数采用整体法。实施过程中,除了μ和β的建议分布使用正态分布以外,其余参数的建议分布均采用截尾正态分布,所有参数的先验分布采取均匀分布。 σ 2/( σ 1 2, σ 2 2),a/(a1,a2)/(a1,min,a1,max,a2,min,a2,max), β/( β 1, β 2)之间存在相关性,采样的时候将其合并在一个采样步骤中。在建议分布中,关于各参数的初始取值范围,μ分布的均值设为样本均值,方差设置成一个较大的数;β/( β 1, β 2)采样设置在一个较大的区间内并进行取模运算,得到位于[0, π]之间的采样值;a/(a1,a2)/(a1,min,a1,max,a2,min,a2,max)以样本边界长度的10倍作为上界,采样时,要对(a1,a2)/(a1,min,a1,max,a2,min,a2,max)大小关系做出限制,例如,在一次采样过程中,要保证a1,min≤a1,max≤a2,min≤a2,max; τ2、 σ 2/( σ 1 2, σ 2 2)分布的均值取样本方差,以样本方差的10倍作为上界进行采样。为确保采样的充分性和收敛的稳定性,在马氏链训练过程中按照25%的样本接受率动态调整建议分布参数。

2.4 克里金估计

假设有一组观测值Y=(Y(s1),…,Y(sn)),待估计点为Y(s0),其后验分布可以通过对θ积分获得,计算Y(s0)的边缘分布,有[33]：
p ( Y ( s 0 ) Y ) = ∫ p ( Y ( s 0 ) , θ Y ) d θ = ∫ p ( Y ( s 0 ) Y , θ ) p ( θ Y ) d θ
式中： p ( Y ( s 0 ) Y , θ ) ~ N ( μ + r T ( B + τ 2 I ) - 1 ( Y - μ 1 ), σ 2 + τ 2 - r T ( B + τ 2 I ) - 1 );r为s0和其他采样点大小为n×1的协方差向量;I为单位矩阵;B是所有已知点大小为n×n的协方差矩阵。因此,对Y(s0)的估计,可以按照上述公式通过组合采样来完成,即,先从p(θ|y)中抽样得到θ0,然后,将θ0代入p(Y(s0)|Y, θ0),得到的抽 样就是满足上述边缘分布的估计值。

2.5 一个完整的贝叶斯地统计过程

下面给出一个完整的贝叶斯地统计估计过程,以异异套合协方差结构为例：
（1）确定理论协方差函数模型,确定异异套合协方差参数的初始值、先验分布和建议分布。
（2）从建议分布中为每个参数采样,将参数空间分成两组,分组方案见2.3节。
（3）对第1组采样,其余的参数保持上一轮的采样值（如果是第一轮,则为初始值）,计算异异套合协方差矩阵,计算样本观测值以本次参数采样值为条件的似然函数和本次参数采样值的先验分布,根据公式p(Y|θ*)p(θ*)计算该次采样参数的后验分布,根据2.3节的判断条件（3）,确定该次采样是接受还是拒绝。
（4）对第2组参数重复步骤（3）的过程。
（5）将步骤（3）—步骤（4）循环10 000次,取后5000次作为最终的参数估计值。
（6）从步骤（5）获得的样本估计中每隔20个样本采样,然后根据式（12）采样以获取未知点的克里金估计。

3 模拟数据验证

3.1 随机模拟数据生成

本节要解决的2个问题是：① 在贝叶斯框架下,套合模型参数是否能够得到准确估计;② 复杂模型是否有向下兼容的能力,即复杂模型能否识别出简单模型数据的协方差结构。为此,首先要生成参数值已知的模拟数据,要生成满足参数预先设置如已知均值和协方差矩阵的各向同性、各向异性或者套合结构的模拟数据集,可以使用地统计中的随机模拟方法如矩阵分解、序贯模拟、谱模拟等方法,也可以直接使用生成的随机数。本文采用谱模拟方法中的傅里叶积分法,它是一种频域中的计算方法,可以用来生成多维的、各向异性的或者复杂套合协方差结构的模拟数据,具有理论简单、计算容易和速度快等优点[34]。按照谱模拟流程分别生成同同套合、同异套合、异同套合和异异套合球状协方差结构的模拟数据,大小为128×128,假设模拟数据不存在块金效应,所有参数取值汇总于表2中,生成的模拟数据及协方差函数结构见图3。
表2 4种套合模拟数据的协方差参数值

Tab. 2 The values of covariance parameters for the four nested simulation data

同同套合 取值 同异套合 取值 异同套合 取值 异异套合 取值
μ 0 μ 0 μ 0 μ 0
σ 1 2 5 σ 1 2 3 σ 1 2 3 σ 1 2 5
σ 2 2 5 σ 2 2 7 σ 2 2 7 σ 2 2 5
a1 15 a1 15 a1,min 15 a1,min 8
a2 40 a2,min 20 a1,max 30 a1,max 16
a2,max 40 a2 40 a2,min 20
β2 π/6 β1 π/6 a2,max 40
β1 π/6
β2 π/2
图3 4种协方差函数等值线和对应模拟数据

注：图中红色数值表示协方差函数值。

Fig. 3 The four kinds of covariance with nested structures different each other and the corresponding simulations

3.2 结果及分析

本次验证将分别采用一级结构包括各向同性和各向异性2种传统常用地统计模型,以及异异套合模型对上述4种套合模拟数据进行估计,估计流程见2.5节,目的是探讨简单模型如前者在估计套合结构时存在的不足,以及后者向下兼容其4种特殊结构形式的估计能力。在验证之前,首先进行正态分布检验,利用χ2(0.05)作为判断标准,如不满足正态分布,对其进行对数转换。本次实验趋势项取全局均值,协方差函数为球状模型,将4种数据处理成样本容量为100的数据分别进行验证。每次估计,采样次数均设为10 000次,预烧期为5000次,采样间隔为20次。由各向同性模型对多参数的套合模拟数据建模结果可以看出（表3）,模型无法对角度做出估计（图4(a)—图4(d)）。由各向异性模型建模结果来看（表4）,同样,μ和 σ 2的估计较为准确,还能看出,它向下兼容同同套合数据,同同估计的长短半径比较接近,且角度分布在一个较大的区间内,没有出现特别明显的峰值（图4(e)）;对同异和异同套合数据变程估计也较为准确（图4(f)和图4(g)）,随着各向异性强度的增加,角度的估计也趋于真值,然而各向异性模型对于异异套合数据的估计误差较大,体现在变程和角度的估计中,原因是经过2个各向异性结构的叠加,其主方向被模糊了（图4(h)）。根据异异模型估计结果（表5）,纵观4种数据,μ和 σ 1 2+ σ 2 2估计较为准确,从角度和变程的估计可以看出,该模型能够向下兼容同同、同异、异同3种模型 （图4(i)—图4(l)）,另外,对异异数据的估计效果也较好,能够还原叠加的角度信息。然而,在球状模型中,变程a和 σ 2之间存在比例关系,估计过程中,双方容易彼此影响,表现出一定的不稳定性。计算估计值和模拟数据之间的预测均方根误差（Root Mean Square Error, RMSE）,可以得出,异异套合的估计精度最高,结构越复杂,精度提升的越明显。从3种模型的估计可以看出,μ、β估计比较稳定,收敛性较好,对插值精度有着决定性的影响,而变程估计较为敏感,对插值结果影响相对较小。
表3 各向同性模型用于4种套合数据的分位数估计（2.5%, 50%, 97.5%）

Tab. 3 The quantile estimates (2.5%, 50%, 97.5%) for the four simulations using an isotropic model

参数 同同套合 同异套合 异同套合 异异套合
2.5% 50% 97.5% 2.5% 50% 97.5% 2.5% 50% 97.5% 2.5% 50% 97.5%
μ 0.02 0.36 0.73 -0.14 0.18 0.49 -0.47 -0.07 0.39 -0.01 0.26 0.53
σ2 8.39 9.49 11.05 7.82 9.07 10.50 8.03 9.15 9.97 7.02 7.87 8.86
a 21.45 23.75 27.17 17.24 20.39 23.69 25.39 29.28 37.21 15.30 16.77 18.73
RMSE 2.3262 3.6353 2.1857 2.6992
表4 各向异性模型用于4种套合数据的分位数估计（2.5%, 50%, 97.5%）

Tab. 4 The quantile estimates (2.5%, 50%, 97.5%) for the four simulations using an anisotropic model

参数 同同套合 同异套合 异同套合 异异套合
2.5% 50% 97.5% 2.5% 50% 97.5% 2.5% 50% 97.5% 2.5% 50% 97.5%
μ 0.02 0.38 0.73 -0.06 0.30 0.65 -0.64 -0.13 0.34 -0.02 0.25 0.55
σ2 8.54 9.70 11.09 8.27 9.47 11.03 8.36 9.59 9.92 7.14 8.02 9.33
amin 20.25 23.19 26.90 12.07 15.92 18.01 17.99 28.89 31.21 13.23 15.59 18.64
amax 22.77 25.81 29.85 30.89 38.15 44.00 38.99 44.18 52.66 16.07 19.23 25.11
β 0.05 2.06 3.10 0.27 0.39 0.57 0.06 0.27 3.13 0.21 1.18 2.90
RMSE 2.3343 3.6691 2.2126 2.6905
表5 异异套合模型用于4种套合数据的分位数估计（2.5%, 50%, 97.5%）

Tab. 5 The quantile estimates (2.5%, 50%, 97.5%) for the four simulations using a nested model with anisotropy and anisotropy

参数 同同套合 同异套合 异同套合 异异套合
2.5% 50% 97.5% 2.5% 50% 97.5% 2.5% 50% 97.5% 2.5% 50% 97.5%
μ -0.04 0.33 0.73 -0.04 0.32 0.65 -0.50 -0.07 0.33 -0.16 0.16 0.50
σ 1 2 0.03 4.08 8.23 0.73 1.27 1.95 1.69 2.75 3.72 1.62 2.67 3.92
σ 2 2 1.30 5.33 9.93 5.50 6.77 8.17 4.17 5.02 6.51 3.65 5.27 6.96
a1,min 1.33 12.84 21.93 0.23 2.24 4.57 4.78 9.66 11.14 2.03 3.91 6.58
a1,max 2.60 20.87 25.38 2.11 5.90 13.90 25.20 30.13 32.53 13.75 21.54 29.21
a2,min 21.19 26.69 44.99 15.20 17.58 19.84 35.13 38.57 43.62 22.98 26.79 30.75
a2,max 23.29 48.00 62.23 36.14 42.16 48.55 39.85 43.76 51.10 27.02 31.50 48.21
β1 0.03 0.80 3.11 0.05 2.26 3.11 0.10 0.24 3.13 0.27 0.49 0.61
β2 0.16 2.07 3.01 0.30 0.41 0.52 0.01 2.60 2.74 0.26 1.73 2.82
RMSE 2.2998 3.5819 2.1831 2.6225
图4 贝叶斯地统计框架下4种模拟数据中位数估计的二维协方差等值线图

注：图中红色数值表示协方差函数值。

Fig. 4 Two dimensional covariance contour maps of the four simulated data based on the median estimation using Bayesian geostatistical modeling

4 降水数据验证

4.1 实验区概况及数据来源

本文以山西省降水数据为例,验证异异套合模型对真实数据插值精度的提升效应。山西省位处我国华北地区,地形较为复杂,全域70%以上的面积被三大地形单元所控制,分别是东部以太行山为主脉形成的块状山地,西边以吕梁山脉为主体的黄土丘陵沟壑区,以及夹在中间的由汾河、滹沱河、桑干河等河流冲积成的呈串珠状相连的盆地,除了这几大单元以外,在南部、东南部还分布有太岳山脉、中条山脉以及长治、晋城盆地等次一级地形单元。直观上看,这些地形单元相互交错、互相影响,大多呈现出南北展布的趋势,具有明显的方向性和空间异质性等特征。气候上全省都位于中纬度大陆性季风气侯带内,一年中除夏季几个月受海洋性暖湿气流影响雨量比较集中且时间持续较短以外,大部分时间处于干燥大陆性气团的控制之下,雨雪稀少且持续时间长。数据为中国气象监测信息网上下载的累计年均值数据[35],全省共计108个站点,几乎覆盖到了全部的县市,站点设置典型,数据较为完整,能够很好地反映过去30年山西省降水的平均分布,站点具体位置信息见图5。
图5 山西省地形和降水站点分布

Fig. 5 The topography and precipitation stations in Shanxi province

4.2 结果及分析

将108个监测数据分为2组,一组78个,一组30个,前一组用于估计和插值,后一组用于精度验证,重复实验100次,协方差函数采用球状模型,循环次数与预烧期与上述相同。在实验之前,对样本数据进行正态分布检验,经检验,本实验数据不满足正态分布,因此,使用自然对数对其进行转换。为了节省时间,本文每次实验均采用其参数的中位数进行估计,而不再在每个估计点上随机抽样,因此不设采样间隔,另外本验证中采用的也是全局均值作为趋势项,估计结果见表6。从RMSE的表现来看,异异套合模型比另外2种模型有了更高的精度,比各向同性模型估计提升了将近10%左右。从参数估计结果来看,异异模型不仅捕捉到系统存在的角度（84°左右）,各向异性比（2.53）,另外还考虑到了近乎相等的各向同性方差的贡献,若不考虑变程的影响,其权重占比接近 1/2。显然,后者综合了前2种方法的特点,体现了方法上的优势。从插值结果图6也可以看出,相较于各向同性方法（图6(a)）,各向异性（图6(b)）和异异套合（图6(c)）插值结果在全省范围内具有明显的方向性,与地形单元保持了较好的一致性,例如在大同、太原、临汾和运城盆地,以及吕梁和太岳山脉等区域。但是,后2种方法却在某些局部没有明显方向性的地形单元中表现出一定的劣势,例如五台县周围区域,通过分析不难得出,后二者明显受到了全局方向特征的影响。图7为3种插值模型之间的互相比较结果,通过两两求差再取绝对值得到,能够直观感受到3种插值结果在空间分布上的异同。如果说各向同性和各向异性、异异套合插值结果（图7(a)和图7(b)）主要表现为纵向差异的话,那么后两者则主要表现为横向的差异（图7(c)）,这是由其基本原理决定的。这些差异主要体现在一些地形过渡区域,例如位于山西中北部的宁武、忻州、古交和静乐站点围成的三角地带,霍州东部,交口东南部,五台县南部,闻喜东部,以及山西东南部的阳城、晋城站点周边等区域,显然,导致二者之间差异的直接原因是参与插值样点分布和权重的不同,也即各向异性模型仅受到变形特征的约束,而异异套合模型则受到变形特征和值的双重约束。
表6 3种模型应用于降水数据中的分位数估计（2.5%, 50%, 97.5%）

Tab. 6 The quantile estimates(2.5%, 50%, 97.5%) for precipitation data using the three models including an isotropic, an anisotropic and a nested model with anisotropy and anisotropy

参数 各向同性模型 各向异性模型 异异套合模型
2.5% 50% 97.5% 2.5% 50% 97.5% 2.5% 50% 97.5%
μ/mm 6.12 6.16 6.18 6.12 6.14 6.16 6.13 6.15 6.19
τ2/mm2 1.45E-03 2.31E-03 3.04E-03 3.06E-05 7.06E-04 1.61E-03 2.24E-05 5.07E-04 1.53E-03
σ2/mm2 σ 1 2 1.48E-02 1.62E-02 1.68E-02 1.34E-02 1.52E-02 1.68E-02 5.19E-03 8.34E-03 9.23E-03
σ 2 2 - - - - - - 5.92E-03 8.60E-03 1.51E-02
a/km amin a1,min 181.70 253.30 270.96 86.37 97.74 119.64 67.28 83.08 86.29
a1,max - - - - - - 176.06 210.49 250.03
amax a2,min - - - 178.67 237.96 272.50 196.82 237.39 292.93
a2,max
- - - - - - 267.80 290.50 304.16
β β1 - - - 1.15 1.39 1.60 1.33 1.48 1.54
β2 - - - - - - 0.06 0.43 3.07
RMSE/mm 22.14 22.21 20.07
图6 各向同性、各向异性和异异套合模型的插值结果

Fig. 6 The interpolation results using an isotropic, an anisotropic and a nested model with anisotropy and anisotropy for the precipitation data measured in Shanxi province

图7 3种模型插值结果的互相比较

Fig. 7 The intercomparisons among the interpolation results using an isotropic, an anisotropic and a nested model with anisotropy and anisotropy

5 结论与讨论

5.1 结论

本研究采用4种模拟数据验证了异异套合参数估计的可行性,分析和比较了基本结构和套合结构的建模能力和插值精度,并通过对各组分贡献的分解和定量计算,在充分挖掘和优化未知点周围潜在邻域信息的基础上,分析和总结了克里金插值在降水数据中的精度提升效应。主要结论如下：
（1）通过对同同、同异、异同和异异4种随机模拟数据的验证,发现叠加的各向异性可以被分解,相关参数也能得到较准确的估计。复杂结构具有向下兼容简单结构的能力,但是简单结构没有向上兼容复杂结构的能力。模型越复杂,估计的难度越大,不确定性也越强,但可以通过引入先验信息来提升收敛性和估计精度。异异模型的插值精度要优于各向同性和各向异性模型,数据协方差结构越复杂,其提升效果越明显。
（2）从对山西省的降水插值来看,异异套合模型对于提升区域降水插值精度具有明显作用,比2种基本结构模型的估计精度提升了约10%。相较于2种基本结构,其不仅识别到了2种叠加信息,一种是各向异性比为2.53,倾角为84°各向异性结构,另外一种是接近各向同性的结构,拥有较小的异向比和较大的倾角分布区间,同时也得到了2种组分的贡献,贡献比接近1:1。从插值结果上也能明显看出3种模型之间的差异,尤其是在地形过渡区域,可以明显地看到异异套合模型既利用了周围的各向同性信息,同时也利用了整体的方向性信息,提供了一种介于各向同性和各向异性两者之间的估计结果。

5.2 讨论

在本研究中,虽然发现贝叶斯方法极大地提升了复杂环境下稀疏数据的统计推断能力,但是像其他优化方法一样,它也无法保障在一次优化过程中得到的是全局最优值。尤其是在估计具有相关关系参数的时候,例如球状模型中, σ 2和a存在比例效应,很容易使双方走向极端。为了避免这种问题,Zhang[36]使用参数乘积替代单个参数来估计,Sigurdarson等[37]则使用数值计算的方法独立于MCMC来估计。如果有较准确的参数先验信息,也可以使用缩小参数的取值上界和区间或者改变先验分布函数来消除,例如可以使用观测样本的方差和均值作为先验信息,或者采用一级非套合模型的参数估计作为先验信息,因为后者估计受到的影响较小。总之,本研究不仅在理论上是对当前贝叶斯地统计建模的一次扩展和延伸,同时,在实践上也是对稀疏环境下地理变量多尺度各向异性结构化分析及估计的一次积极探索和尝试。

References

Publishing order | Descend order by publishing year | Descend order by cited within
[1]
郑度, 欧阳, 周成虎. 对自然地理区划方法的认识与思考[J]. 地理学报, 2008, 63(6):563-573.

[ Zheng D, Ou Y, Zhou C H. Understanding of and thinking over geographical regionalization methodology[J]. Acta Geographica Sinica, 2008, 63(6):563-573. ] DOI: 10.3321/j.issn:0375-5444.2008.06.001

DOI

[2]
陈广宇, 韦志刚, 董文杰, 等. 中国西部陆面过程次网格地形参数化的改进对区域气温和降水模拟的影响研究[J]. 大气科学, 2019, 43(4):846-860.

[ Chen G Y, WEI Z G, DONG W J, et al. Effects of improvement of land surface subgrid topographic parameterization on regional temperature and precipitation simulation in western China[J]. Chinese Journal of Atmospheric Sciences, 2019, 43(4):846-860. ] DOI: 10.3878/j.issn.1006-9895.1807.18156

DOI

[3]
范泽孟. 中国生态过渡带分布的空间识别及情景模拟[J]. 地理学报, 2021, 76(3):626-644.

DOI

[ Fan Z M. Spatial identification and scenario simulation of ecotone distribution in China[J]. Acta Geographica Sinica, 2021, 76(3):626-644. ] DOI: 10.11821/dlxb202103010

DOI

[4]
Thiessen A H. Precipitation averages for large areas[J]. Monthly Weather Review, 1911, 39(7):1082-1089. DOI: 10.1175/1520-0493(1911)39<1082b:PAFLA>2.0.CO;2

DOI

[5]
Shepard D. A two-dimensional interpolation function for irregularly-spaced data[C]. Proceedings of the 1968 23rd ACM National Conference, 1968:517-524. DOI: 10.1145/800186.810616

DOI

[6]
Willmott C J, Matsuura K. Smart interpolation of annually averaged air temperature in the United States[J]. Journal of Applied Meteorology and Climatology, 1995, 34(12):2577-2586. DOI: 10.1175/1520-0450(1995)034<2577:SIOAAA>2.0.CO;2

DOI

[7]
Franke R. Smooth interpolation of scattered data by local thin plate splines[J]. Computers & Mathematics with Applications, 1982, 8(4):273-281. DOI: 10.1016/0898-1221(82)90009-8

DOI

[8]
Phillips D L, Dolph J, Marks D. A comparison of geostatistical procedures for spatial analysis of precipitation in mountainous terrain[J]. Agricultural and Forest Meteorology, 1992, 58(1-2):119-141. DOI: 10.1016/0168-1923(92)90114-J

DOI

[9]
Zawadzki I I. Statistical properties of precipitation patterns[J]. Journal of Applied Meteorology and Climatology, 1973, 12(3):459-472. DOI: 10.1175/1520-0450(1973)012<0459:SPOPP>2.0.CO;2

DOI

[10]
Smith R B. The influence of mountains on the atmosphere[M]. Advances in Geophysics. Elsevier, 1979, 21:87-230. DOI: 10.1016/S0065-2687(08)60262-9

DOI

[11]
Pardo-Igúzquiza E. Comparison of geostatistical methods for estimating the areal average climatological rainfall mean using data on precipitation and topography[J]. International Journal of Climatology: A Journal of the Royal Meteorological Society, 1998, 18(9):1031-1047. DOI: 10.1002/(SICI)1097-0088(199807)18:93.0.CO;2-U

DOI

[12]
Goovaerts P. Geostatistical approaches for incorporating elevation into the spatial interpolation of rainfall[J]. Journal of Hydrology, 2000, 228(1-2):113-129. DOI: 10.1016/s0022-1694(00)00144-x

DOI

[13]
Hofierka J, Parajka J, Mitasova H, et al. Multivariate interpolation of precipitation using regularized spline with tension[J]. Transactions in GIS, 2002, 6(2):135-150. DOI: 10.1111/1467-9671.00101

DOI

[14]
Hutchinson M F. Interpolating mean rainfall using thin plate smoothing splines[J]. International Journal of Geographical Information Systems, 1995, 9(4):385-403. DOI: 10.1080/02693799508902045

DOI

[15]
Tomczak M. Spatial interpolation and its uncertainty using automated anisotropic inverse distance weighting (IDW)-cross-validation/jackknife approach[J]. Journal of Geographic Information and Decision Analysis, 1998, 2(2): 18-30.

[16]
Zhang Y, Hidalgo J, Parker D. Impact of variability and anisotropy in the correlation decay distance for precipitation spatial interpolation in China[J]. Climate Research, 2017, 74(1):81-93. DOI: 10.3354/cr01486

DOI

[17]
Atkinson P M, Lloyd C D. Mapping precipitation in Switzerland with ordinary and indicator kriging. Special issue: Spatial Interpolation Comparison 97[J]. Journal of Geographic Information and Decision Analysis, 1998, 2(1-2):72-86.

[18]
Saveliev A A, Mucharamova S S, Piliugin G A. Modeling of the daily rainfall values using surface under tension and kriging[J]. Journal of Geographic Information and Decision Analysis, 1998, 2(2):52-64.

[19]
Kastelec D, Košmelj K. Spatial interpolation of mean yearly precipitation using universal kriging[J]. Developments In Statistics, 2002, 17:149-162.

[20]
Agou V D, Varouchakis E A, Hristopulos D T. Geostatistical analysis of precipitation in the island of Crete (Greece) based on a sparse monitoring network[J]. Environmental Monitoring and Assessment, 2019, 191(6):1-24. DOI: 10.1007/s10661-019-7462-8

DOI

[21]
Gyasi-Agyei Y. Assessment of radar-based locally varying anisotropy on daily rainfall interpolation[J]. Hydrological Sciences Journal, 2016, 61(10):1890-1902. DOI: 10.1080/02626667.2015.1083652

DOI

[22]
Cassiraga E, Gómez-Hernández J J, Berenguer M, et al. Spatiotemporal precipitation estimation from rain gauges and meteorological radar using geostatistics[J]. Mathematical Geosciences, 2021, 53(4):499-516. DOI: 10.1007/s11004-020-09882-1

DOI

[23]
Lovejoy S, Schertzer D, Allaire V C. The remarkable wide range spatial scaling of TRMM precipitation[J]. Atmospheric Research, 2008, 90(1):10-32. DOI: 10.1016/j.atmosres.2008.02.016

DOI

[24]
Davis A. Nested anisotropic geostatistical gridding of airborne geophysical data[J]. Geophysics, 2021, 87(1):E1-E12. DOI: 10.1190/geo2021-0169.1

DOI

[25]
Webster R, Oliver M A. Sample adequately to estimate variograms of soil properties[J]. Journal of soil science, 1992, 43(1):177-192. DOI: 10.1111/j.1365-2389.1992.tb00128.x

DOI

[26]
Pardo-Igúzquiza E. Bayesian inference of spatial covariance parameters[J]. Mathematical Geology, 1999, 31(1):47-65. DOI: 10.1023/A:1007541330206

DOI

[27]
He J, Kolovos A. Bayesian maximum entropy approach and its applications: a review[J]. Stochastic Environmental Research and Risk Assessment, 2018, 32(4):859-877. DOI: 10.1007/s00477-017-1419-7

DOI

[28]
Eriksson M, Siska P P. Understanding anisotropy computations[J]. Mathematical Geology, 2000, 32(6):683-700. DOI: 10.1023/A:1007590322263

DOI

[29]
Wei J, Li Z, Hu J, et al. Anisotropy of atmospheric delay in InSAR and its effect on InSAR atmospheric correction[J]. Journal of Geodesy, 2019, 93(2):241-265. DOI: 10.1007/s00190-018-1155-x

DOI

[30]
高歆. 基于线性GSI二维半变异函数各向异性结构建模及估计研究——以DEM数据为例[J]. 地理研究, 2020, 39(11):2607-2625.

DOI

[ Gao X. Anisotropic modeling and estimation for a two-dimensional semi-variogram based on the linear GSI Model: Taking DEM data as an example[J]. Geographical Research, 2020, 39(11):2607-2625. ] DOI: 10.11821/dlyj020190794

DOI

[31]
王劲峰, 徐成东. 地理探测器:原理与展望[J]. 地理学报, 2017, 72(1):116-134.

DOI

[ Wang J F, Xu C D. Geodetector: Principle and prospective[J]. Acta Geographica Sinica, 2017, 72(1):116-134. ] DOI: 10.11821/dlxb201701010

DOI

[32]
葛咏, 刘梦晓, 胡姗, 等. 时空统计学在贫困研究中的应用及展望[J]. 地球信息科学学报, 2021, 23(1):58-74.

DOI

[ Ge Y, Liu M X, Hu S, et al. The application and prospect of spatiotemporal statistics in poverty research[J]. Journal of Geo-information Science, 2021, 23(1):58-74. ] DOI: 10.12082/dqxxkx.2021.200628

DOI

[33]
Banerjee S, Carlin B P, Gelfand A E. Hierarchical modeling and analysis for spatial data[M]. New York: Chapman and Hall/CRC, 2014. DOI: 10.1201/9780203487808

DOI

[34]
Pardo-Iguzquiza E, Chica-Olmo M. The fourier integral method: An efficient spectral method for simulation of random fields[J]. Mathematical Geology, 1993, 25(2):177-217. DOI: 10.1007/BF00893272

DOI

[35]
中国地面气候标准值年值数据集(1981-2010)[DB/OL]. 国家气象科学数据中心

[The annual normalized dataset of surface climate in China 1981-2010)[DB/OL]. China Meteorological Data Service Center ]

[36]
Zhang H. Inconsistent estimation and asymptotically equal interpolations in model-based geostatistics[J]. Journal of the American Statistical Association, 2004, 99(465):250-261. DOI: 10.1198/016214504000000241

DOI

[37]
Sigurdarson A N, Hrafnkelsson B. Bayesian prediction of monthly precipitation on a fine grid using covariates based on a regional meteorological model[J]. Environmetrics, 2016, 27(1):27-41. DOI: 10.1002/env.2372

DOI

Options
Outlines

/

〈 〉