EN中文

Journal of Geo-information Science >

2022 , Vol. 24 >Issue 8: 1631 - 1644

DOI: https://doi.org/10.12082/dqxxkx.2022.210766

Enhanced Remote Sensing Image SRGAN Algorithm and Its Application in Improving the Accuracy of 3D Reconstruction

  • MIN Jie ,
  • ZHANG Yongsheng ,
  • YU Ying , * ,
  • LV Kefeng ,
  • WANG Ziquan ,
  • ZHANG Lei
Expand
  • Information Engineering University, Zhengzhou 450001, China
*YU Ying, E-mail:

Received date: 2021-11-30

  Revised date: 2022-03-07

  Online published: 2022-10-25

Supported by

National Natural Science Foundation of China(42071340)

Fold

Abstract

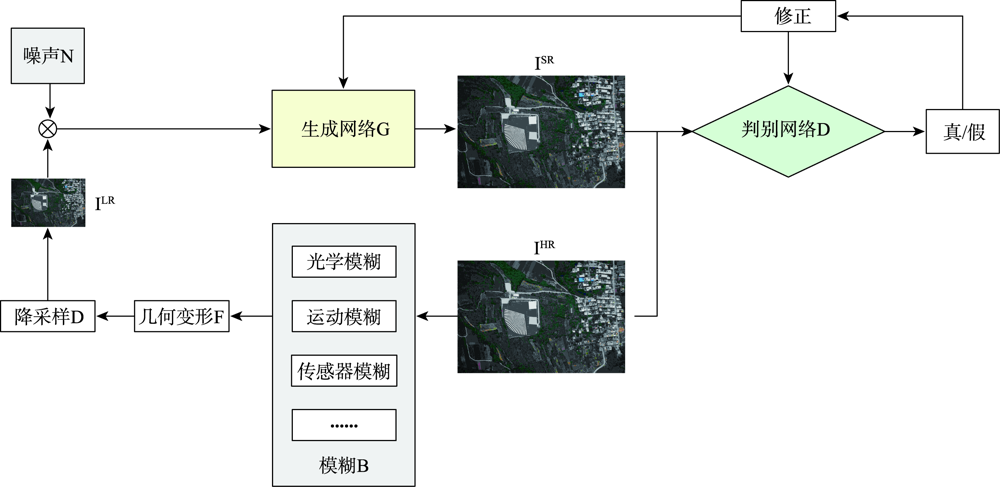
Remote sensing images are important data sources for terrain mapping, 3D reconstruction, and other tasks. The spatial resolution of remote sensing images determines the representation ability of the measured object on the image and plays an important role in the positioning accuracy and reconstruction effect of 3D model in the later stage. In view of the characteristics of high resolution remote sensing images including large scale, complex target features, and rich details, an enhanced SRGAN algorithm for remote sensing image reconstruction is proposed to meet the needs of 3D model reconstruction. The proposed algorithm overcomes the problems of edge effect and fuzzy reconstruction using traditional methods for super-resolution reconstruction. In traditional methods, there is limitation that simple convolutional networks can only extract the shallow feature information of the image and cannot retain the rich details of the image with the increasing resolution. The proposed algorithm is based on the generative adversarial networks using deep learning, in which dense residual blocks are used to extract deep features, and multi-scale discrimination is introduced into the discriminant model. In the training, the generation model and the discrimination model learn features together and are optimized to finally obtain a super-resolution reconstruction model suitable for remote sensing image application. This model can improve the resolution and image quality of remote sensing images, and ensure the integrity and accuracy of feature texture, detail information, and high-frequency target. In our study, the proposed algorithm is compared with the Bicubic, SRGAN, and ESRGAN algorithms. Our results show that the PSNR of the proposed algorithm is improved by about three units, the Penetration Index (PI) is stable and closer to one, and the SSIM and clarity index Q are also improved. In 3D reconstruction, the number of image dense matching points is increased, and the error is reduced. The measured point values of the model are closer to the measured point values from the field. The visual perception of the model is also more real and delicate, which indicates that the precision and positioning accuracy of the 3D model can be significantly improved using the remote sensing images constructed by the proposed algorithm. The results demonstrate the proposed algorithm that considers the characteristics of remote sensing images performs better than other algorithms for the super-resolution reconstruction, and the geometric accuracy and visual accuracy of the real 3D models based on the constructed images are also significantly improved.

Key words： super-resolution reconstruction; 3D reconstruction; deep learning; SRGAN; multi-scale relative discrimination; high-resolution remote sensing; image processing; positioning accuracy

Cite this article

MIN Jie , ZHANG Yongsheng , YU Ying , LV Kefeng , WANG Ziquan , ZHANG Lei . Enhanced Remote Sensing Image SRGAN Algorithm and Its Application in Improving the Accuracy of 3D Reconstruction[J]. Journal of Geo-information Science, 2022 , 24(8) : 1631 -1644 . DOI: 10.12082/dqxxkx.2022.210766

1 引言

当“智慧测绘”与“数字孪生”的概念逐步推进,通过获取无人机遥感影像,从二维平面信息中重建地形地貌、城市建筑等特定目标的实景三维模型[1]受到各行业的广泛关注。三维模型重建效果受限于原始数据的质量与重建算法的性能,如目前在遥感影像的分辨率与解析力、侧立面影像信息的获取、影像间特征的提取与匹配等方面仍存在难点与不足[2],因此如何有效提高三维模型重建的精度又是研究的关键问题。
提升三维模型重建精度的直接方法,主要分为通过在外业阶段提高原始数据的质量和在内业阶段对三维模型进行后期修补两大类[2]。前者对于三维模型精度的提升依赖于硬件设备的改进,通常需要改进无人机平台、遥感传感器或成像硬件设备,以更为先进的硬件条件弥补影像存在的不足,改进模型纹理的精细程度,但所需成本较高。后者依赖于手动处理的精细程度,需要大量人工操作进行修补与细化,耗时耗力[3]。此外,国内外学者在三维模型重建中遥感影像的后期处理算法上也进行了大量研究。文献[4⇓-6]表明,在遥感影像匹配与密集匹配方面,各算法重点加强影像间的匹配能力,通过剔除误匹配,使匹配点分布更加均匀且提高匹配的正确率;在空中三角测量平差与密集点云构建三角网方面,算法旨在使空间点三维坐标信息更为精确,实现优化三角网格构建与精细模型纹理的效果,从而改进三维模型视觉观感与定位测量精度[7]。但后期处理算法已研究多年,目前处于瓶颈阶段,仍然通过影像匹配、平差优化的方法想要较大程度改进三维模型重建精度的可能性较小且难度极大。
超分辨率重建（Super-resolution Reconstruction, SR）[8]技术当前广泛应用在机器视觉、遥感分析等领域,起初由Harris[9]和Goodman[10]于20世纪60年代提出,是一种采用图像处理的方式,利用单张或多张（序列或无序）低分辨率（Low Resolution, LR）影像构建相应场景高分辨率（High Resolution, HR）影像的技术。遥感影像的空间分辨率作为目标细节在影像中可分辨的最小尺寸,是表现影像质量的关键指标之一[11]。通过SR算法提升影像分辨率,能够使目标特征边缘清晰、细节纹理信息更加丰富,为遥感影像三维模型重建精度的改进提供了一种全新的解决思路。
早期SR插值法操作简单,复杂程度较低,重建后影像在一定程度上会产生边缘效应、马赛克效应,影像中细节内容恢复较差。重构法操作复杂,计算量大且对于不同影像的普适性较差。传统学习法过分依赖样例学习库,并需要序列影像组进行处理,无法针对单一影像进行超分重建。2014年Dong[12]首次将深度学习技术应用于SR问题,提出了仅包含3个卷积层的网络结构SRCNN（Super-Resolution CNN）,此后基于深度学习的SR重建网络模型在不同方向积极探索并不断改进,在各类标准数据集上的性能表现优秀[13]。
由于SRCNN算法主要针对标准数据集中影像进行超分重建,网络简单且层数较少,较小的感受域使得提取出的特征非常局限,对影像全局特征的捕捉不足,并考虑到遥感影像具有丰富的细节纹理、自相关性较强,适合使用深度学习领域中生成对抗网络（Generative Adversarial Networks, GAN）[14]模型进行特征提取,通过提取更为细致的影像特征,建立好的学习模型,从而实现从遥感影像LR到HR的转变以及较大放大因子下纹理细节和目标特征的恢复。
基于以上分析,本文提出一种增强型遥感影像SRGAN算法（以下简称增强型SRGAN）：以原始SRGAN算法思想作为基础,结合遥感影像的特点,以及在高精度实景三维模型重建问题中的需求,对生成模型的网络结构进行调整,在判别模型中引入多尺度判别思想,使得遥感影像超分辨率重建效果更优。在实验验证阶段引入渗透指数和清晰度指标,更加准确客观地体现本文算法在遥感影像SR重建问题上的优势;对验证数据集进行超分重建和三维模型重建,通过分析3种算法在影像密集匹配中的误差和三维模型的直观视觉判断,证明了本文算法在遥感影像三维模型重建应用中对于精度提升的有效性。

2 改进残差网络与多尺度判别模型的增强型SRGAN

由于生成对抗网络具有极强的图像生成能力,模型能够恢复重建边缘结构突出、真实细致的图像,因此针对遥感影像应用的增强型SRGAN以传统SRGAN为框架基础并进行调整：算法由主动生成模拟真实影像的生成网络G（Generator）和判别生成影像是否为真的判别网络D（Discriminator）主要组成,生成网络改进原始残差网络思想,利用密集剩余残差网络模块提取遥感影像中目标的高频特征信息,判别网络采用多尺度判别模型,G与D通过相互对抗、不断学习的方式来进行模型训练,同步提升网络的性能,最终获得细节纹理更为丰富、更为清晰且边缘特征准确真实的遥感超分辨率影像。算法整体结构如图1所示。
图1 增强型SRGAN算法结构

Fig. 1 Enhanced SRGAN algorithm structure

首先对原始HR遥感影像IHR进行预处理,通过模糊、变形、降采样等方式构建相应的LR遥感影像ILR,将ILR及遥感成像过程中可能存在的随机噪声N（算法常设为高斯白噪声）共同输入生成网络G,通过模型输出超分辨率重建后的影像ISR。判别网络D对参考影像IHR与ISR进行鉴别,计算损失并作为反馈回传至生成网络G中,二者相互对抗博弈,不断修正优化,最终使生成网络模型尽可能生成近似于真实高分辨率的影像,鉴别网络提高鉴别真假的能力,实现对LR遥感影像的高分辨率重建。

2.1 生成模型

增强型SRGAN在生成模型中借鉴ESRGAN[15]算法思想,使用密集剩余残差块（Residual-in-Residual Dense Block, RRDB）取代残差模块（Residual Block, RB）。模型中首先通过卷积层提取遥感影像的浅层特征信息,继而由16个RRDB组成的特征提取模块进行深层特征提取,最后经非线性映射后与浅层信息同时进行上采样操作,对影像进行超分重建。
RB通过特征求和将上层提取到的信息传递至下层,随着网络层数的加深,信息得到有效传递,但各层中有自己独立的权重,网络模型学习重复冗余的特征图,导致参数量过大的情况出现。密集模块（Dense Block, DB）通过各层之间的跳跃建立更多连接,特征图可传至后面所有层中,浅层信息也可直连向后进行传递,每层均能从损失函数和原始信号中获取梯度信息,无需学习重复冗余的特征图,因此所需参数更少。在深层网络中直接提取SR空间中每个卷积层的输出较为困难,因此增强型SRGAN将RB与DB进行融合,充分结合原始SR影像中的浅层和深层特征,利用RRDB残差加性结构加深网络深度的同时,使用密集连接传递浅层与深层的特征信息重建出细节更加丰富纹理更加清晰的遥感影像。
在图像SR网络结构中使用批量归一化（Batch Normal）层会由于训练数据和测试数据的统计量相差较大,导致重建后影像生成不好的伪影,限制模型的稳定性、一致性与泛化性,因此本算法去除原始SRGAN残差网络中的BN层,在RRDB中将卷积层与激活函数LeakyReLU直接相连[16]。减少了训练过程中可能出现重复复杂的计算过程,节省了内存占用和时间消耗,同时杜绝了超分重建前后BN层对成像色彩的归一拉伸,保证了遥感影像色相、明度及对比度的一致性。生成网络模型结构如图2所示。
图2 生成网络模型结构图

Fig. 2 Generate network model structure

2.2 判别模型

增强型SRGAN采用多尺度判别模型,以Radford等[17]所提相对判别思想为基础,在生成模型G生成影像为真的概率提高的同时降低真实影像为真的概率,克服原始GAN训练过程中的弊端,起到相对判别的作用。此外将尺度不同的三个相同判别器进行组合,得到多尺度相对判别模型网络结构。每个判别器均由卷积层和全连接层组成,其中11个卷积层对影像进行特征提取,批归一化操作使得模型加速收敛,且使用LeakyReLU作为激活函数（α=0.2）,避免使用Max Pooling操作,简化计算过程。原始GAN网络中判别器仅判断输入数据为真或假,将结果通过Sigmoid层映射至0或1,而增强型SRGAN中最后使用全连接层对所有卷积层提取到的影像特征进行分类与组合,且去除Sigmoid层使得输出结果由二分问题转换为回归问题,实现相对判别。
判别器尺度的粗糙程度与感受野成正比,更粗尺度的判别器获取影像更多的全局信息,反之更加关注影像的细节特征信息。最小尺度判别器D1侧重于影像细节重建,关系影像中微小的细节信息;中间尺度判别器D2承接上下两个判别器,在重建过程中起到过渡作用,以减缓不同尺度影像间重建时可能存在的突变;标准尺度判别器D3通过获取全局影像指导生成模型,使重建影像具有较强的全局一致性。
多尺度判别模型结构如图3所示,将生成模型G生成的SR影像进行2倍、4倍下采样操作,构建分层金字塔影像,分别结合原始HR影像输入3个不同大小尺度的判别器,各判别器学习空间距离不同的影像中的像素间关系特征,得到各自的判定结果O1,O2和O3,取其平均值作为最终输出结果。增强型SRGAN综合了不同尺度判别器的优势,同时关注重建后影像的细节与全局,在加强判别模型鉴别准确性的同时,指导生成模型生成细节丰富、具有全局一致性的SR遥感影像。
图3 多尺度判别模型结构

Fig. 3 Multi-scale discriminant model structure

2.3 SR质量评价指标

本文旨在探究增强型SRGAN在遥感影像三维重建中的应用,影像SR的质量评价通过全参考客观评价和无参考客观评价2种方式进行。
全参考客观评价以原始高分辨率遥感影像作为参考基准,定量对重建后的影像进行评价。目前基于深度学习的SR算法均采用峰值信噪比（Peak Signal to Noise Ratio, PSNR）和结构相似性（Structural Similarity, SSIM）对超分重建后的图像进行客观质量评价[18]。实际应用于遥感影像的SR问题时,存在评价指标数值表现优秀,但重建影像会部分区域过于平滑,提升分辨率的同时损失细节纹理信息,视觉判读与影像分析受限,影像真实性下降等情况的出现。因此本文增加渗透指数（Permeability Index, PI）对重建后遥感影像进行质量评价。
PSNR（式（2））基于均方根误差（RMSE）（式（1））计算2幅影像的相似度,单位为分贝（dB）。PSNR值越大,说明重建后影像的失真越少,离散程度越小,重建效果越好,一般认为当其超过40 dB时,重建效果极好。
R M S E = 1 m n ∑ i = 0 m - 1 ∑ j = 0 n - 1 I H R i , j - I S R i , j 2
P S N R = 20 × l o g 10 M A X R M S E
式中： R M S E为均方根误差; P S N R为超分重建峰值信噪比指标; I H R与 I S R分别表示用于参考的原始高分辨率影像与超分辨率重建后的影像; i , j为其相应像素点坐标; m与 n为影像的长宽像素数; M A X为最大灰度级。
遥感影像具有极强的结构特征,SSIM（式（3））从影像结构、亮度、对比度3个角度综合估计SR重建质量,衡量SR影像与HR影像之间的结构相似程度。
S S I M I H R , I S R = 2 μ I H R μ I S R + K 1 L 2 2 σ I H R I S R + K 2 L 2 μ I H R 2 + μ I S R 2 + K 1 L 2 σ I H R 2 + σ I S R 2 + K 2 L 2
μ I H R = ∑ i = 1 N w i I H R i
σ I H R = ∑ i = 1 N w i I H R i - μ I H R 2 1 2
σ I H R I S R = ∑ i = 1 N w i I H R i - μ I H R I S R i - μ I S R
式中： S S I M为超分重建结构相似性指标; I H R与 I S R分别表示原始高分辨率影像与重建后的影像; μ I H R和 μ I S R为影像整体灰度均值; σ I H R和 σ I S R为方差; σ I H R I S R为协方差; L = 255表示动态范围; K 1和 K 2为常数,通常取值为0.01和0.02; w为高斯窗口,通常大小取为11×11; N为当前影像高斯窗口的总数。当影像 I H R与 I S R非常接近时,SSIM约等于1,此时表示重建影像的失真越小。
渗透指数（式（7））即原始影像和超分辨率重建后影像间的Laplace算子（式（8））方差之比。渗透指数越大,表示重建后影像越清晰,细节保留越完好,渗透指数越小,表示重建后影像越模糊越平滑,也即虚假超分重建。当渗透指数的数值过于大时,需要考虑重建影响是否存在过多的伪细节,伪细节对后期遥感影像特征提取与匹配时会产生一定误差。
P I = ∑ i = 1 N S R G x i , y i - G - S R 2 ∑ j = 1 N H R G x j , y j - G - H R 2
G x , y = f x , y + c f x + 1 , y + f x - 1 , y + f x , y + 1 + f x , y - 1 - 4 f x , y
式中： P I为超分重建渗透指数; x , y为像素点坐标; f为对应像素点灰度; c为动态参数,其值在0至1之间; G为影像原始灰度数值与Laplace算子数值的加权和;; G -为整幅影像加权和的均值; N S R和 N H R分别为SR影像与HR影像的总像素数;。
无参考评价选用清晰度指标Q[19]（式（9））,清晰度指标是影像的平均梯度值,反映重建后影像的细节反差。Q值越大,表明重建后影像细节反差越明显,特征信息表现更为突出。
Q = 1 m - 1 n - 1 × ∑ i = 0 m - 1 ∑ j = 0 n - 1 I S R i , j - I S R i + 1 , j 2 + I S R i , j - I S R i , j + 1 2 2
式中： Q为超分重建清晰度指标; i , j为像素点坐标; I H R与 I S R分别表示原始高分辨率影像与重建影像, m与 n为影像的长宽像素数。

3 实验与分析

本文使用内部自行构建的无人机遥感影像数据集进行增强型SRGAN模型训练,在用于测试的遥感影像数据上进行超分辨率重建,对重建后影像进行质量评价。除此之外,分别使用原始HR影像、对应LR影像和超分辨率重建后的SR影像进行实景三维模型重建,通过横向对比实验,验证增强型SRGAN在遥感影像三维重建应用中的有效性。实验流程如图4所示。
图4 实验流程

Fig. 4 Experiment process

3.1 实验数据与实验环境

增强型SRGAN在Ubuntu系统下基于PyTorch深度学习框架,使用Python编程语言实现;三维模型在Windows系统下利用Pix4D和Context Capture软件进行重建,具体参数如表1所示。
表1 实验环境配置

Tab. 1 Experimental environment configuration

软硬件名称 参数及信息
CPU Intel® Core™i9 1100K @3.70GHz
GPU Intel(R) UHD Graphics (Driver: 27.20.100.9168)NVIDIA GeForce RTX 3080 (Driver: 27.21.14.6192)
RAM 32 GB
系统配置 Ubuntu 18.04 LTS Windows 10
程序语言 Python 3.7.0
底层框架 PyTorch 1.4.0
模型重建软件 Pix4D, Context Capture
当前超分辨率重建算法的训练与测试主要在DIV2K、Set5和Set14、BSD100等标准数据集上进行,此类数据集多为模拟图像、自然图像或是特殊场景下特定目标的影像,并非摄影测量与遥感领域中使用的真实影像数据,其本质与遥感影像有极大区别。遥感影像场景广阔且复杂、细节丰富、特征信息多、目标特殊,以及影像上高频信息更多,局部信息变化较快、整体连续性较小,因此本文选取内部自行构建的无人机遥感影像数据集对增强型SRGAN进行验证。数据集主要包括3组河南省郑州市登封地区（丘陵地形）不同年份、不同季节、不同遥感设备、不同飞行航高获取的无人机遥感影像数据、2组城市院校内部低空无人机遥感影像数据以及一组独立建筑倾斜摄影无人机遥感影像数据,具体数据参数如表2所示。实验中对所有影像进行数据增广,通过旋转、平移、镜像、光照调整、伽马变换等手段处理后,再加以随机扰动,将每幅遥感影像增广4倍。并进行步长为100,分辨率128×128的随机裁切,实现影像分辨率大小的统一。
表2 SR重建训练与验证实验数据集

Tab. 2 SR reconstruction training and validation experimental datasets

数据集 指标 内容 展示图
数据集1 时间 2014年夏季5月
覆盖区域 登封嵩山遥感卫星定标场
影像数量/幅 176
飞行航高/m 200
镜头焦距/mm 15
传感器大小/mm 23.52×15.68
影像分辨率（尺寸）/像素 6000×4000
影像像素大小/um 3.92
数据集2 时间 2017年夏季9月
覆盖区域 登封雪沟及其周边地区
影像数量/幅 191
飞行航高/m 1220
镜头焦距/mm 35
传感器大小/mm 35.00×23.35
影像分辨率（尺寸）/像素 7952×5304
影像像素大小/um 4.40
数据集3 时间 2017年冬季12月
覆盖区域 登封雪沟及其周边地区
影像数量/幅 206
飞行航高/m 1255
镜头焦距/mm 35
传感器大小/mm 35.00×23.35
影像分辨率（尺寸）/像素 7952×5304
影像像素大小/um 4.40
数据集4 时间 2018年夏季5月
覆盖区域 郑州市某校区
影像数量/幅 55
飞行航高/m 90
镜头焦距/mm 35
传感器大小/mm 36×24
影像分辨率（尺寸）/像素 6000×4000
影像像素大小/um 6.00
数据集5 时间 2016年夏季9月
覆盖区域 郑州市某独立建筑
影像数量/幅 496
飞行航高/m 90
镜头焦距/mm 3.5
传感器大小/mm 6.32×4.74
影像分辨率（尺寸）/像素 4000×3000
影像像素大小/um 1.58
数据集6 时间 2021年秋季10月
覆盖区域 沈阳市某校区
影像数量/幅 390×5
飞行航高/m 153
镜头焦距/mm 下视25,前后左右侧视35
传感器大小/mm 下视30.78×20.52,前后左右侧视42.81×28.54
影像分辨率（尺寸）/像素 6000×4000
影像像素大小/um 下视5.13,前后左右侧视7.14

3.2 遥感影像SR重建与分析

将数据集1、3、4、5以及数据集6中左、右、后视遥感影像经过增广后的2520幅影像用于训练,对数据集二和数据集六中部分影像（下视、前视）进行测试。观察训练进程中LR遥感影像块重建的效果（图5）,随着训练迭代次数的不断增加,超分辨率重建效果逐渐趋好,遥感影像的视觉直观感受更好,解析力更强,细节纹理更加显著,目标更为清晰。
图5 训练进程中影像SR重建效果

Fig. 5 Image SR reconstruction effect during training

为证明增强型SRGAN在遥感影像三维重建中应用的有效性,本文对增强型SRGAN算法以及Bicubic双三次插值法、原始SRGAN算法和ESRGAN算法分别在测试数据上以2倍、4倍放大因子进行超分辨率重建,重建后影像质量评价指标的各项数值（均值）如表3所示。
表3 4种SR算法评价指标数值（均值）对比

Tab. 3 Comparison of evaluation index values (mean value) of each of the four SR algorithm

算法 Bicubic[20] SRGAN[14] ESRGAN[15] 增强型SRGAN
评价指标 放大因子 DF1000 DB_x DB_q DF1000 DB_x DB_q DF1000 DB_x DB_q DF1000 DB_x DB_q
PSNR ×2 20.32 21.07 20.97 25.47 29.17 26.64 25.39 28.01 28.13 25.43 28.14 29.43
×4 23.14 26.21 24.32 31.02 29.95 28.46 30.34 34.96 34.11 30.78 35.07 34.11
SSIM ×2 0.53 0.48 0.43 0.51 0.63 0.52 0.62 0.69 0.70 0.69 0.72 0.71
×4 0.56 0.66 0.70 0.90 0.78 0.78 0.86 0.87 0.84 0.89 0.90 0.89
PI ×2 23.87 22.67 23.71 1.48 0.67 0.55 1.36 1.14 1.09 1.31 1.07 1.11
×4 25.56 23.47 27.32 1.66 0.48 0.61 1.23 1.27 1.10 1.19 1.21 1.09
Q ×2 4.13 4.07 4.00 5.44 5.37 5.80 5.89 6.12 5.88 5.91 6.18 5.92
×4 4.34 3.98 4.03 5.69 5.72 5.75 6.00 6.03 6.11 6.12 6.29 6.22
以2倍放大因子进行遥感影像超分辨率重建时,增强型SRGAN在4项评价指标上均取得了较好的结果,以4倍放大因子进行重建时,对比更为显著。平均PSNR数值在4组数据上远高于Bicubic,较原始SRGAN与ESRGAN也有一定程度的提高。在平均SSIM数值上,增强型SRGAN算法稳定且趋近于1,重建后影像更接近于真实HR影像。Bicubic的平均PI值过高,证明影像重建后产生了过多虚假信息,而增强型SRGAN比SRGAN数值波动程度更小,较ESRGAN算法也更加稳定,反映了算法重建的可靠性。对于无参考评价指标清晰度Q,增强型SRGAN算法与ESRGAN接近,并高于双三次插值与原始SRGAN。综合证明了该算法重建后影像的特征细节会保留更完整、更清晰,遥感影像重建效果更佳。
图6分别选取测试数据中具有代表性的5幅遥感影像进行细节展示（缩放至同一尺度大小）,放大区域均为遥感应用中着重关注的兴趣目标,分别是村落、道路、定标场靶标、汽车、建筑。4倍放大因子下,各算法重建结果如下：
在视觉观感上,ESRGAN与增强型SRGAN 重建效果要优于双三次插值法和原始SRGAN。Bicubic重建后影像依旧存在拉伸模糊现象,靶标边缘有明显的锯齿现象,插值法的局限导致目标与背景间的层次性有所降低。原始SRGAN重建后影像的纹理感极强,甚至部分区域超过参考HR影像,但同时出现了较为明显的棋盘效应与过度锐化,后期特征匹配时可能存在错误。通过观察与分析,增强型SRGAN在各类型遥感影像上的重建均未出现明显棋盘、锯齿与拉伸模糊等效应,色度、明度、对比等效果接近参考HR影像,特征边缘清晰、细节纹理恢复较好,在遥感影像超分辨率重建中质量最高。
图6 4倍放大因子各算法SR重建效果对比

注：示意图下的4个数字分别为PSNR、SSIM、PI、Q 评价指标数值,其中HR_Orig、HR_Cropped与LR_Cropped不计算。

Fig. 6 Comparison of SR reconstruction effects of various algorithms with 4 times magnification factor

3.3 SR影像在三维重建中的应用

遥感影像三维模型重建时,影像经密集匹配后确定目标点的位置信息。匹配连接点即为重叠影像间提取出特征明确的关键点,它们共存于多幅遥感影像上,在密集匹配与模型重建时起到连接和传递几何结构信息的作用,重投影误差是指目标点在影像平面上的投影（像点坐标）与重投影（计算得到的虚拟坐标）之间的差值。实验选择数据集6的下视与前视遥感影像进行三维模型重建,表4分别展示了重建过程中,重叠影像密集匹配平差处理时各算法连接点的数量、每个连接点影像覆盖中位数、每幅影像上匹配连接点中位数、重投影误差中值、重投影均方误差以及投影射线的均方误差。
表4 各SR算法密集匹配对比

Tab. 4 Comparison of dense matching of various SR algorithms

指标 LR Bicubic SRGAN ESRGAN 增强型SRGAN
连接点的数量/个 183 348 198 627 313 914 353 418 340 024
每个连接点影像覆盖中位数 3 3 3 3 3
每幅影像上匹配连接点中位数 396 429 678 791 734
重投影误差中值 1.68 1.44 0.72 0.891 0.41
重投影均方误差 1.60 1.53 1.03 1.00 0.62
投影射线的均方误差 0.01380 0.00921 0.00748 0.00803 0.00247
由表4可知,低分辨率遥感影像进行密集匹配时,每幅影像上用于匹配的连接点数量最少,区域内连接点总数最少,插值法较原始LR影像有所提升但提升并不明显,SRGAN与增强型SRGAN算法在匹配连接点数量上的提升更为优秀。ESRGAN算法虽然在影像总体连接点与单幅影像连接点的数量上表现更好,但重投影误差中值与均方根误差较大,对于遥感影像复杂细节特征存在的错误重建使得其在重投影误差和射线均方根误差上表现不佳,增强型SRGAN投影射线均方根误差的减小也表明了恢复遥感影像空间位姿的能力最强。
图7为原始LR影像和增强型SRGAN算法处理后影像重建区域内密集匹配每个连接点的重投影误差,分别为所有连接点的俯视图（XY平面）、侧视图（ZY平面）和前视图（XZ平面）。其中增强型SRGAN算法处理后影像最小重投影误差为0.01像素,最大为1.88像素,平均重投影误差为0.55像素。观察分布图中橙色、红色范围内连接点的分布,增强型SRGAN明显少于原始LR影像,证明本文算法在三维模型重建密集匹配中能较好地提高其计算准确度。
图7 LR与增强型SRGAN连接点重投影误差分布

Fig. 7 Reprojection error distribution of the connection point between LR and enhanced SRGAN

重叠遥感影像密集匹配平差处理后,生成实景三维模型,分割选取沈阳市某校区遥感影像三维模型中一处高大建筑物（图8）进行分析,观察各算法Mesh网格模型,经过增强型SRGAN算法得到的影像重建模型更为细腻,建模网格更为密集、细致,建筑物与地形地貌表面更为平滑自然,汽车、植被等目标特征更为真实突出。对比各算法纹理模型,Bicubic由于匹配错误与失败导致模型存在空洞和模糊,虽实现了三维模型分辨率的提升,但同时造成了模型变形、拉伸与扭曲,模型细节丢失的情况;SRGAN模型重建纹理较为细致,但算法追求高峰值信噪比与结构相似性,导致生成的三维模型色彩明度失真,特征结构存在异常重建;ESRGAN算法三维模型重建结果虽优于传统双三次插值与原始SRGAN,但存在的更多错误匹配与虚假超分重建使得模型存在异常结构,尤其在侧立面上的细节纹理匹配存在一定错误。综合对比,增强型SRGAN算法处理后遥感影像三维重建模型Mesh网格密集,能准确覆盖模型表面,三维模型色彩、结构更能还原真实场景,遥感应用中的兴趣目标、兴趣特征表现准确,细节纹理更为丰富,重建效果最好。
图8 4倍放大因子各算法SR影像三维模型重建效果对比

Fig. 8 Comparison of 3D model reconstruction effects of SR images of various algorithms with 4 times magnification factor

另选取重建模型中左上、左下、右上、右下及中间5个特殊角点进行各SR算法在三维重建后模型的精度对比,表5为各点位空间三维坐标及误差情况。以原始HR影像重建模型作为参考值,通过分析可知ESRGAN与本文增强型SRGAN在模型定位精度的提升上更为有效,而在空间Z方向上的定位精度,本文针对遥感影像增强型SRGAN算法超分重建后影像的定位精度优于ESRGAN,证明其超分重建时更好的恢复了遥感影像的视差信息与边缘细节特征,从而提高了在三维模型重建时的定位精度。
表5 各SR算法三维模型重建点位精度对比

Tab. 5 Comparison table of 3D model reconstruction point accuracy of each SR algorithm

HR Bicubic SRGAN ESRGAN 增强型SRGAN
P1 (391.44, 437.50, 54.74) (387.41, 429.37, 51.09) (388.37, 435.42, 50.97) (392.49, 435.55, 51.92) (390.47, 436.01, 55.91)
P2 (414.69, 681.50, 61.82) (416.78, 688.79, 58.79) (419.03, 678.69, 57.64) (413.04, 683.93, 63.87) (415.81, 682.47, 60.01)
P3 (267.69, 381.00, 57.34) (263.14, 377.35, 60.19) (264.83, 385.01, 60.03) (265.97, 383.71, 55.46) (266.03, 382.64, 59.43)
P4 (293.63, 541.52, 54.28) (296.19, 537.99, 47.39) (297.97, 543.979, 50.97) (291.68, 539.98, 51.49) (294.84, 543.87, 51.86)
P5 (352.19, 466.13, 118.53) (353.46, 469.37, 108.42) (350.29, 462.18, 112.49) (354.40, 464.71, 115.51) (350.97, 467.71, 120.03)
△X △Y △Z △X △Y △Z △X △Y △Z △X △Y △Z
平均误差 2.90 5.17 5.31 3.30 3.06 4.00 1.72 2.01 2.51 1.24 1.61 1.80
最大误差 4.03 8.13 10.11 4.34 4.01 6.04 2.21 2.71 3.02 1.67 2.35 2.42

注：△X,△Y,△Z为当前算法在该方向上的误差。

4 结论与讨论

（1）本文通过改进原始SRGAN算法的网络结构,设计了一种更加适用于遥感影像超分辨率重建的增强型SRGAN算法。在生成模型中使用由16个RRDB组成的特征提取模块对遥感影像的深层特征进行提取,同时去除网络中的BN层保证泛化性与超分前后的色彩一致性。在判别模型中采用相对判别思想,并引入多尺度判别器使生成的SR影像保证全局一致性的前提下尽可能提高和保留影像细节。
（2）增强型SRGAN稳定地学习高分辨率遥感影像与低分辨率遥感影像之间的映射关系,针对遥感影像的特点,该算法能够在保留影像特征信息和目标细节信息的前提下提升遥感影像的分辨率和整体质量,改善三维重建任务中密集匹配环节特征点提取的数量与准确性,从而提升模型的精细程度和定位精度。通过与现有三种算法进行对比实验,结果表明本文算法在SR重建的各项质量评价指标和三维模型空间点位的精度上表现优秀,证明了算法在遥感影像超分重建效果和三维模型重建精度提升中的有效改进。
（3）但目前生成对抗网络难于训练的问题仍有待解决,深度学习方法依靠数据集进行模型训练与验证,当遥感影像样本数量较少或种类较为单一时,经特定训练集训练后的深度学习网络模型在更多场景更多种类与目标的遥感测试验证集上的普适性还有待提升。
（4）本文除使用常规超分辨率重建中采用的PSNR, SSIM与Q作为质量评价指标,另引入渗透参数PI对重建后是否存在伪细节进行评估,防止影像密集匹配中产生大量错误匹配。另外由于主观质量评分法（MOS）是由人工进行判定打分,本文并未采用此类主观方法对重建后遥感影像进行比对,因此如何制定一套统一的、直接的、客观并适用于遥感影像超分重建的评价指标体系值得深入讨论与研究。
（5）平衡超分辨率重建与保持遥感影像细节特征、改善生成对抗网络的计算量与效率、提高不同类型数据普适性的同时保证模型重建效果,以及如何更加准确有效的构建高低分辨率的遥感影像训练数据集,是未来需要研究的方向和考量的重点。

References

Publishing order | Descend order by publishing year | Descend order by cited within
[1]
张春森, 张卫龙, 郭丙轩, 等. 倾斜影像的三维纹理快速重建[J]. 测绘学报, 2015, 44(7):782-790.

[ Zhang C S, Zhang W L, Guo B X, et al. Rapidly 3D texture reconstruction based on oblique photography[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(7):782-790. ] DOI: 10.11947/j.AGCS.2015.20140341

DOI

[2]
王冬, 丁奥, 施银迪, 等. 基于倾斜摄影测量的油库精细三维建模方法研究[J]. 测绘与空间地理信息, 2021, 44(5):8-11,16.

[ Wang D, Ding A, Shi Y D, et al. Research on precise three-dimensional modeling method of oil depot based on tilt photogrammetry[J]. Geomatics & Spatial Information Technology, 2021, 44(5):8-11,16. ] DOI: 10.3969/j.issn.1672-5867.2021.05.003

DOI

[3]
Leonardo G, Olga R P B and Luciano S. 3D reconstruction methods for digital preservation of cultural heritage: A survey[J]. Pattern Recognition Letters, 2014, 50:3-14. DOI: 10.1016/j.patrec.2014.03.023

DOI

[4]
李德仁, 肖雄武, 郭丙轩, 等. 倾斜影像自动空三及其在城市真三维模型重建中的应用[J]. 武汉大学学报·信息科学版, 2016, 41(6):711-721.

[ Li D R, Xiao X W, Guo B X, et al. Oblique image based automatic aerotriangulation and its application in 3D city model reconstruction[J]. Geomatics and Information Science of Wuhan University, 2016, 41(6):711-721. ] DOI: 10.13203/j.whugis20160099

DOI

[5]
Hu H, Zhu Q, Du Z, et al. Reliable Spatial Relationship Constrained Feature Point Matching of Oblique Aerial Images[J]. Photogrammetric Engineering&Remote Sensing, 2015, 81(1):49-58. DOI: 10.14358/PERS.81.1.49

DOI

[6]
Hartley R, Zisserman A. Multiple view geometry in computer vision: Two-view geometry[J]. 2004,(PART II):237-238. DOI: 10.1017/CBO9780511811685.013

DOI

[7]
肖雄武, 李德仁, 郭丙轩, 等. 一种具有视点不变性的倾斜影像快速匹配方法[J]. 武汉大学学报·信息科学版, 2016, 41(9):1151-1159.

[ Xiao X W, Li D R, Guo B X, et al. A robust and rapid viewpoint-invariant matching method for oblique images[J]. Geomatics and Information Science of Wuhan University, 2016, 41(9):1151-1159. ] DOI: 10.13203/j.whugis20140405

DOI

[8]
李德仁, 袁修孝. 误差处理与可靠性理论:第2版[M]武汉大学出版社, 2012:44-62.

[ Li D R, Yuan X X. Error Processing and Reliability Theory: Second Edition[M]. Wuhan University Press, 2012:44-62. ]

[9]
Tsai R Y, Huang T S. Multi-frame image restoration and registration[J]. Advances in Computer Vision and Image Processing, 1984, 1:317-339.

[10]
Harris J L. Diffraction and resolving Powerp[J]. Journal of the Optical Society of America, 1964, 54(7):931-933. DOI: 10.1364/josa.54.000931

DOI

[11]
Goodman J W, Gustafson S C, Reviewer. Introduction to fourier optics, second edition[J]. Optical Engineering, 1996, 35(5):1513-1515. DOI: 10.1117/1.601121

DOI

[12]
李欣, 韦宏卫, 张洪群. 结合深度学习的单幅遥感图像超分辨率重建[J]. 中国图象图形学报, 2018, 23(2):209-218.

[ Li X, Wei H W, Zhang H Q. Super-resolution reconstruction of single remote sensing image combined with deep learning[J]. Journal of Image and Graphics, 2018, 23(2):209-218. ] DOI: 10.11834/jig.170194

DOI

[13]
Dong C, Loy C C, He K, et al. Learning a deep convolutional network for image super-resolution[A].European Conference on Computer Vision[C]. Springer, Cham, 2014:184-199. DOI: 10.1007/978-3-319-10593-2_13

DOI

[14]
唐艳秋, 潘泓, 朱亚平, 等. 图像超分辨率重建研究综述[J]. 电子学报, 2020, 48(7):1407-1420.

DOI

[ Tang Y Q, Pan H, Zhu Y P, et al. A survey of image super-resolution reconstruction[J]. Acta Electronica Sinica, 2020, 48(7):1407-1420. ] DOI: 10.3969/j.issn.0372-2112.2020.07.022

DOI

[15]
Ledig C, Theis L, F Huszar, et al. Photo- realistic single image super-resolution using a generative adversarial Network[C]. 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). New York:IEEE, 2017:105-114. DOI: 10.1109/CVPR.2017.19

DOI

[16]
Wang X, Yu K, Wu S, et al. ESRGAN: Enhanced super-resolution generative adversarial networks[C]. Computer Vision -- ECCV 2018 Workshops. Cham: Springer International Publishing, 2018:63-79. DOI: 10.1007/978-3-030-11021-5_5

DOI

[17]
毕晓君, 潘梦迪. 基于生成对抗网络的机载遥感图像超分辨率重建[J]. 智能系统学报, 2020, 15(1):74-83.

[ Bi X J, Pan M D. Super-resolution reconstruction of airborne remote sensing images based on the generative adversarial networks[J]. CAAI Transactions on Intelligent Systems, 2020, 15(1):74-83. ] DOI: CNKI:SUN:ZNXT.0.2020-01-014

DOI

[18]
Radford A, Metz L, Chintala S. Unsupervised representation learning with deep convolutional generative adversarial networks[J]. Computer ence, 2015. DOI: 10.48550/arXiv.1511.06434

DOI

[19]
Wang Z, Bovik A C, Sheikh H R, et al. Image quality assessment: from error visibility to structural similarity[J]. IEEE Transactions on Image Processing, 2004, 13(4):600-612. DOI: 10.1016/j.jvcir.2019.102655

DOI

[20]
范冲, 龚健雅, 朱建军, 等. ALOS-PRISM遥感影像超分辨率重建[J]. 遥感学报, 2009, 13(1):75-82.

[ Fan C, Gong J Y, Zhu J J, et al. Super-resolution reconstruction of ALOS-PRISM remote sensing images[J]. National Remote Sensing Bulletin, 2009, 13(1):75-82. ] DOI: 10.3321/j.issn:1007-4619.2009.01.010

DOI

[21]
Keys R G. Cubic convolution interpolation for digital image processing[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 2003, 29(6):1153-1160. DOI: 10.1109/TASSP.1981.1163711

DOI

Options
Outlines

/

〈 〉