EN中文

Journal of Geo-information Science >

2022 , Vol. 24 >Issue 10: 1982 - 1992

DOI: https://doi.org/10.12082/dqxxkx.2022.210601

Delineating Urban Subdistricts with Comprehensive Functions from Taxi Trajectory Data in Multiple Years

  • ZHEN Zhuo , 1 ,
  • KANG Chaogui , 1, 2, *
Expand
  • 1. School of Remote Sensing and Information Engineering, Wuhan University, Wuhan 430079, China
  • 2. National Engineering Research Center of Geographic Information System, China University of Geosciences (Wuhan), Wuhan 430078, China
*KANG Chaogui, E-mail:

Received date: 2021-10-03

  Revised date: 2021-12-01

  Online published: 2022-12-25

Supported by

National Key Research and Development Program of China(2017YFB0503600)

National Key Research and Development Program of China(2019YFE0106500)

National Natural Science Foundation of China(41601484)

National Natural Science Foundation of China(41830845)

Fold

Abstract

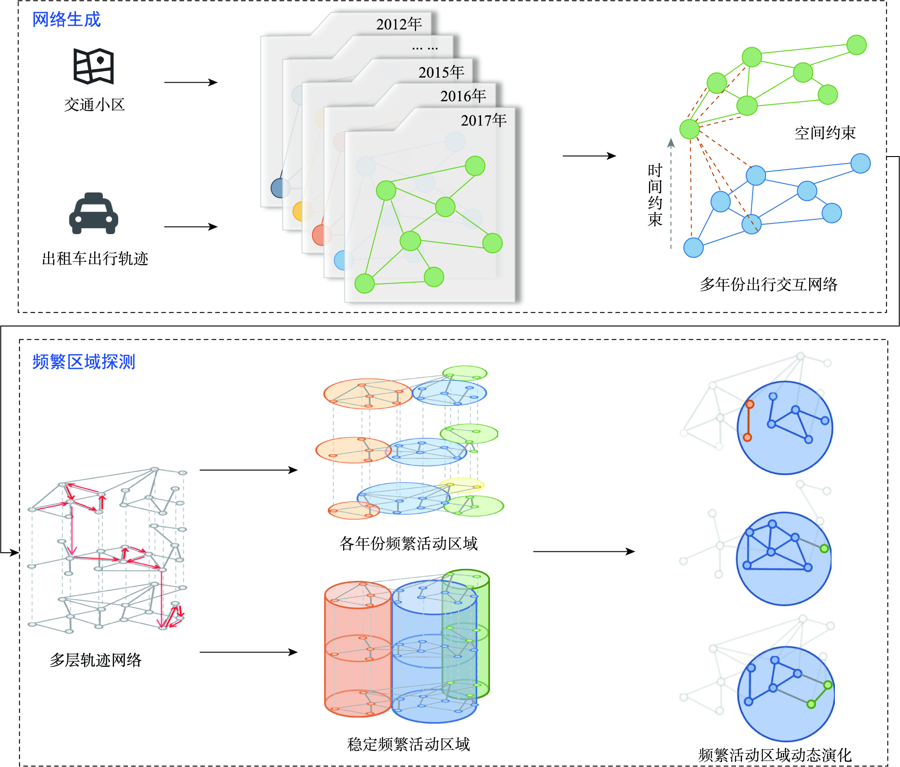
With the penetration of portable devices such as mobile phones and navigators that carry GPS sensors, the trajectory data generated by people's daily life have rapidly increased. Such kind of large-scale trajectory data have been gradually applied to traffic planning, urban management, behavioral analysis, recommendation system, and other fields. In urban studies, urban sub-center detection has always been one of the important topics in the exploration of urbanization. In this paper, we define urban subdistricts with comprehensive functions as a collection of sub-regions within which the internal traffic is significantly higher than their external connected traffic. To detect these subdistricts, a spatiotemporal coupling network model for time series trajectory data is proposed. Based on this model, a multi-layer network community discovery algorithm is proposed to detect dynamic activity sub-area. Taking the taxi trajectory data of Beijing from 2012 to 2017 as an example, this method is used to realize the dynamic detection and analysis of subdistricts with comprehensive urban functions in Beijing.

Key words： trajectory analysis; urban functional area; community discovery; spatio-temporal network model; taxi trajectory; Beijing

Cite this article

ZHEN Zhuo , KANG Chaogui . Delineating Urban Subdistricts with Comprehensive Functions from Taxi Trajectory Data in Multiple Years[J]. Journal of Geo-information Science, 2022 , 24(10) : 1982 -1992 . DOI: 10.12082/dqxxkx.2022.210601

1 引言

随着城市化进程的迅猛发展,大型城市的城市化区域不断扩大,交通基础设施建设日趋完善,城市功能区域划分也更为显著,城市化逐渐向着郊区化方向发展[1],从而引导城市空间结构从单核的封闭模式逐渐向着多核的均衡模式发展。城市功能分布的扁平化使得一些具有完备功能的子区域出现,这些子区域相比于城市的其他区域具有显著的区域内交通和人口流动。因此,通常可以将这些频繁交互的子区域定义为城市内部的完备功能子区。完备功能子区是当下多核心城市结构的重要组成部分,对这些子区域进行探测和结构分析可以帮助人们更好地理解影响城市多核心形成的因素以及城市的演化规律,并且在交通和基础设施建设规划、医疗卫生资源分配和城市发展导向等方面都具有指导作用,有助于发现城市功能结构的不合理之处,促进城市资源的高效利用与分配。与此同时,大数据环境的到来使得城市研究在时间尺度上经历了由静态截面到动态连续的变革[2]。随着城市的发展,功能子区在城市中的结构与规模也存在着动态的变化,对完备功能子区动态变化进行研究一方面可以发现城市子区域的核心部分,另一方面可以通过对子区边缘区域时序变化的分析得到城市子核心区域发展的规律与趋势。
依据完备功能子区的定义,探测完备功能子区的目标是寻找城市居民日常活动空间中内部流量较高的区域。利用社会感知数据,汇总个人或车辆轨迹可以获得地点之间的交通流量,进而构建空间交互网络,将一系列网络分析方法应用到城市研究之中[3]。从网络分析的角度出发,探测完备功能子区可理解为寻找城市居民出行网络中具有更高概率互相连接的节点的集合,即社团。网络分析中的社团发现算法主要分为非重叠社团发现算法[4⇓-6]和重叠社团发现算法[8⇓⇓-11]。在这些方法的基础上,为了在多层网络中发现稳定社团,研究者们又改良和提出了多层网络社团发现算法[12⇓⇓⇓-16]。这些社团发现算法近年来也被广泛应用于出行模式分析[17-18]、城市区域功能识别[19-20]和城市边界描绘[21]等城市研究领域,并取得了丰富的成果。
近年来,一些学者利用出租车轨迹数据[23-24]、手机记录数据[25]等社会感知数据,通过社团探测算法对城市中心和子区域的静态空间结构进行了研究。在城市结构动态变化的研究方面,Zhou等[26]将图论中的指标应用于社团探测发现的城市空间结构,对一天之内的城市结构变化进行了评估;Zhong等[27]利用公共交通智能卡数据构建加权移动网络,通过网络分析方法对3年内城市的中心枢纽和子区域边界变化进行了对比分析。然而,由于社团探测结果很大程度上与数据质量相关,不同数据源上的探测结果在尺度和分布上都可能存在较大差异。因此,在数据来源不同、时间跨度长的多年份空间网络中探测稳定的功能区域,并通过量化指标评估其演变过程仍然是一个挑战。除此之外,出行交互网络中的节点还存在着地理意义上的空间关联,为了在复杂网络分析中考虑空间相关性带来的影响,还需要对地理上的空间约束进行建模并加入网络中,例如,Koylu等[28]在族谱迁徙网络的研究中提出了在空间关联网络中通过空间权重矩阵引入地理约束的方法。
结合本研究的背景和目标,我们提出了对多层时序轨迹网络内部存在的时间耦合和空间关联进行量化建模的策略,从而基于时空轨迹数据得到多层时空网络的一般模型,克服了多时间片段出行数据中存在的潜在时空随机性（如时间/空间上的突变）;进而,利用信息流思想,在构建的时空网络模型上实现一种城市完备功能子区的动态探测分析方法;最后,本文以2012—2017年北京市出租车轨迹数据为例,应用本研究提出的方法,对轨迹数据进行时空网络建模并在得到的时空网络中进行社团探测,对得到的完备功能子区通过量化指标进行了动态演变分析,实现对北京市城区完备功能子区的动态探测。

2 研究方法

本研究的研究方法如图1所示,主要包括： ① 使用图分析的方式将轨迹数据抽象为网络模型,并对多层时序轨迹网络内部存在的时间耦合和空间关联进行量化,得到针对各种时空网络的一般模型;② 在构建的时空网络模型的基础上,研究基于信息流的社团探测算法在该模型上的使用,并提出一种城市完备功能子区的动态探测分析方法;③ 以2012—2017年北京市出租车轨迹数据为例,应用提出的方法,对轨迹数据进行时空网络建模并在得到的时空网络中进行社团探测,对得到的完备功能子区进行动态演变分析。
图1 研究方法流程

Fig. 1 Framework of the proposed methodology

2.1 多年份出行交互网络构建

本研究使用的轨迹数据为北京市2012—2017年的出租车GPS轨迹数据,由某匿名出租车运营公司提供,并且从每一年的数据中选取了11月第一周的数据作为样本进行实验。预处理时,从采样点数据中选取出租车上车-下车的过程来作为一条轨迹,得到了6年来的北京市出租车出行轨迹数据,并对得到的轨迹数据进行了清洗,选取了持续时间在60~18 000 s之间,轨迹长度大于500 m的轨迹数据,数据概况如表1所示。
表1 2012—2017年出租车出行轨迹数据概况

Tab. 1 Descriptive information of the taxi trajectory data from 2012 to 2017

年份 原始轨迹数/条 出租车数/辆 筛选后轨迹数/条 平均出行时间/s 平均出行距离/m
2012 2 059 066 9 030 1 716 325 861.5 7259.3
2013 1 990 625 28 272 1 684 826 1160.4 6197.4
2014 1 506 303 - 1 234 329 1256.8 6756.6
2015 2 811 254 33 043 2 155 565 1081.3 6239.4
2016 2 166 601 29 966 1 945 297 1186.1 6270.6
2017 1 845 424 29 627 1 660 466 1190.9 6665.7
为了从原始轨迹数据获得出行交互网络,首先将原始轨迹转化为OD轨迹,之后对研究区域进行划分（可根据实际情况进行规则或非规则划分,为表述方便,暂时将划分后的单元统称为格网）,根据OD轨迹的起始点坐标将每一条轨迹转化为2个格网区域之间的一条连接,最后将每个格网区域作为一个节点,根据格网区域之间的连接构建带权有向网络,将格网区域之间连接的数量作为网络边上的权重并进行归一化,从而得到轨迹网络。本研究中,根据北京市区的交通特征将城市划分为了1971个交通小区,相比于规则格网划分,交通小区的划分在城市中心等交通流量集中的地区划分较为密集,而在郊区等交通流量较低的区域划分较为稀疏,这样的分割方式更容易保证网络的连通性,也更能反映城市的多尺度的结构特征。根据数据的分布情况和研究目的,从全市的交通小区中选取了北京市城区六环以内的1371个交通小区作为最终的研究区域。
在多层时空网络模型中,位于不同层的观测网络反映了不同的时间段中网络节点与节点之间的关系;而与此同时,同一物理节点在不同时间段中对应的网络节点之间也存在着关联,将这种关联定义为网络层之间的时间耦合。为了使多层网络在时间维度上相互约束以保持其在时间上的连续性,需要对时间耦合进行建模。在本研究中,通过如下的方法量化多层网络节点之间在时间维度上的约束 τ α β：
τ α β = e - | t α - t β | 2 ( α , β 层 间 存 在 时 间 耦 合 ) 0 ( α , β 层 间 不 存 在 时 间 耦 合 )
式中：时间维度衰减的计算依据来自于牛顿冷却定律[29], t α和 t β表示网络层所对应的时间点。为了反映时序多层网络的层间关系,常见的时间关联模型包括：时序耦合（当前时刻只与前一时刻相关）、记忆性耦合（当前时刻只与之前的时刻相关）以及全连接耦合（当前时刻与所有时刻相关）。本研究中将使用记忆性耦合进行建模,即对于每一个网络层 l i,只有 l j , j < i会与其产生关联,关联的强度由 式（1）计算得到。这种方式旨在更真实地反映多年份交互网络的特征,使单层网络结构仅受过去时刻节点的影响,而不受未来时刻节点的影响。
与通常的多路复用网络相比,多层出行交互网络中在存在对应节点间的时间耦合的同时,地理意义使得邻近节点之间还存在空间相关性,研究中将这些关系定义为节点间的空间耦合。在建模分析中,空间权重矩阵[30]通常被用于反映区域之间的空间相关性,常见的构建方法有K最邻近法、邻接矩阵法、核函数法等。为了更灵活地通过参数调节网络的空间约束,本研究中使用高斯核函数构建空间矩阵 W,如式（2）所示。
W i j = 2 π - 1 2 · e - ( d i j / h ) 2 2 ( d i j ≤ h ) 0 ( d i j > h )
式中： d i j表示节点（ i , j）所对应的区域之间的距离; h表示核函数带宽,研究中取值为出行轨迹的平均长度。在实际应用中,权重矩阵十分稀疏,将空间权重矩阵非零化处理后再与网络邻接矩阵相乘可以避免造成网络连接信息损失。除此之外,研究中可通过引入地理约束系数 μ来调节模型中地理约束的强度,引入地理约束后的单层轨迹网络 N g α表示为：
N g α = N α × ( 1 + μ W )
式中： N α表示单层轨迹网络; W表示空间权重矩阵。在后续研究中,在使用高斯核函数构建空间权重矩阵时,将核函数带宽设置为出租车轨迹的平均轨迹长度。对于网络层间的空间约束,也采用相似的方法计算,使用 α 、 β网络层的度矩阵 A α 、 A β和空间权重矩阵 W来计算层间约束 G α β。
G α β = A α W A β - 1
综合以上方法,最终可以构建出北京市的多 年份出行交互网络。由于存在层内和层间2种连接关系,该多层网络可以表示为四维张量模型 M ∈ R n × n × m × m,张量的前2个维度代表网络中边的起始节点和到达节点,后2个维度则分别代表起始节点和到达节点所在的网络层,可将其展开为 m × m个 n × n的矩阵形式,对于 α 、 β ∈ [ 0 , m ),张量 M为：
M = D - 1 N g α ( α = β ) D - 1 τ α β × G α β ( α ≠ β )
式中： N g α表示引入了地理约束的 α层层内节点关系网络的邻接矩阵; τ α β和 G α β分别表示 α和 β层之间的时间耦合和空间耦合的关系矩阵; D则表示计算得到的网络的度矩阵,通过其将邻接矩阵归一化（从而可以作为进一步研究中随机游走的转移矩阵）。该模型在最大程度上反映了多层时空网络中的层间和层内关系,并且具有一定的灵活性,因此可以在其基础上使用各种图分析方法来探索网络结构。

2.2 基于信息流的频繁交互子区探测

为了达到在大规模时序轨迹数据中发现频繁交互子区的目的,本研究使用Infomap社团探测算法[6],并在其原理的基础上扩展进行多层网络的频繁交互子区探测。
Infomap社团探测算法是一种基于随机游走和信息流编码的有向带权网络社团探测方法,逻辑上的流程包括：① 从网络中构建随机游走的转移矩阵;② 模拟漫步点根据转移矩阵在给定网络上进行随机游走得到随机游走的节点序列;③ 计算序列中各节点的到访频率,并根据它来对网络节点进行霍夫曼编码得到原网络中随机游走的平均码长（信息量）;④ 进行社团分割,由于社团内移动频率远高于社团间移动,进行社团分割后,网络的编码长度会小于原始网络码长;⑤ 利用贪婪算法对分割结果进行优化,寻找平均码长最短的分割策略。
实际计算中无需真正对网络进行编码,而只需计算给定社团分割对应的理论上的最短编码码长,即信息熵作为优化的目标。对于社团分割 M,它将网络中的 n个节点分割为 m个社团,则最短编码长度 L ( M )表示为式（6）。其中, q ↷ H Q表示随机游走在社团间的转移所需要的码长; ∑ i = 1 m p ↻ i H ( P i ),表示社团内部编码的所需码长。
L M = q ↷ H Q + ∑ i = 1 m p ↻ i H ( P i )
式中： q ↷表示发生社团转移的概率,即游走过程中离开社团的概率 q i ↷之和; H Q表示社团编码的最低码长,以随机游走离开社团的概率 q i ↷ q ↷作为随机变量计算熵值得到：
q ↷ = - ∑ i = 1 m q i ↷
H Q = ∑ i = 1 m q i ↷ q ↷ l o g q i ↷ q ↷
式中： p ↻ i表示社团 i内部所有节点 α ∈ i的访问频率 p α之和加上进入该社团的概率 q i ↶,以此作为社团的整体访问频率,而 H P i表示社团 i内部节点编码的最低码长,通过根据内部节点访问频率的信息熵进行计算：
p ↻ i = q i ↶ + ∑ p α
H P i = q i ↶ p ↻ i l o g q i ↶ p ↻ i + ∑ p β p ↻ i l o g p β p ↻ i
为了将Infomap社团探测算法推广到多层网络,首先需要将矩阵中的单层随机游走推广到张量模型中的多层随机游走（图1展示了一条多层网络中随机游走的路径示例）,从而获得多层网络节点的访问频率。为此,可以将跨层的移动分解为两步,即从 α层 i节点到 β层 j节点的转移概率可以表示为经由不同的中间节点 p,从 α层 i节点到 β层 p节点再从 β层 p节点到 β层 j节点的概率之和, M表示式（5）中的多层时空网络,则转移概率 p表示为：
p i j α β = ∑ p = 0 n M i p α β ∑ q = 0 n M i q α β M i j β β ∑ q = 0 n M p q β β
在此基础上,多层网络中社团间的转移概率可以按下式进行定义：
q θ ↶ = ∑ p i j α β
q θ ↷ = ∑ p i j α β
式中： i , α ∈ θ表示属于社团 θ的 α层节点 i, j , β ∉ θ表示不属于社团 θ的 β层节点 j。之后,结合转移概率 p, q θ ↶和 q θ ↷,利用式（6）计算多层网络社团发现的优化目标函数,即可发现多层网络中存在的稳定子区。因此,基于信息流的多层网络社团探测方法利用随机游走和信息论编码理论可以解决多层耦合网络中节点的层间转移和社团的跨层关联等问题,实现多年份轨迹数据网络中的频繁交互子区探测。

2.3 动态演变特征分析

为了分析功能子区的动态演变过程,本研究将功能子区在多年份中的稳定变化范围定义为稳定功能子区窗口,通过分析稳定功能子区窗口内功能分布的特征变化来反应功能子区的动态演变特征。为此,本研究定义了以下的评价指标用于进行分析。
混合指数 M：在稳定功能子区窗口内部按照属于各个社团的区域节点的分布占比,计算窗口区域分布的熵值,对于包含 n个社团的窗口区域 ω,其混合指数 M ω可由式（14）计算。
M ω = ∑ i = 0 n - N i ∑ j = 0 n N j l o g N i ∑ j = 0 n N j
稳定指数 S：对于稳定功能子区窗口内部存在的每一个社团,用窗口将社团划分为2部分（ N i i n 、 N i o u t分别表示社团 i中位于窗口内部的区域节点数量和位于窗口外部的节点数量）,计算社团被分割的熵值作为窗口与该社团的吻合程度的度量,将所有社团得到的计算结果累加作为窗口的稳定指数 S ω。
S ω = ∑ i = 0 n - N i i n N i l o g N i i n N i + N i o u t N i l o g N i o u t N i
混合指数用于衡量窗口内部子区域分布的混合程度,混合指数越大则表示窗口内部的社团混合程度越高,虽然存在社团尺度的影响,但能够一定程度上反映窗口内频繁交互子区的分离和合并特征;稳定指数反映了忽略单层网络探测导致的社团尺度变化后,窗口内频繁交互子区与窗口的吻合程度,稳定指数越小则反映出社团与稳定功能子区窗口的重合率越高,其方差的大小反映了则随时间变化,窗口内完备功能子区演变的稳定性,通过对稳定指数变化进行分析能够评估完备功能子区的动态演变过程。

3 结果与分析

3.1 单层网络功能子区探测结果

为了分析完备功能子区随时间推移的演变规律,本研究先使用单层网络Infomap社团探测算法分别探测单一年份下的出行交互网络中的社团,得到不考虑层间耦合时各年份轨迹数据所反映的完备功能子区,结果如图2（a）所示。其中,社团之间通过不同的颜色进行区分。为了更好地显示轨迹网络流量在社团中的分布和在社团间的关联,将随机游走的稳定态访问频率定义为区域节点的节点信息流量,以每个社团内节点的信息流量作为权重计算社团重心,以每个社团的重心作为圆心,以社团内部所有节点的总信息流量为半径在地图上绘制圆形符号;将归一化后的随机游走过程中社团之间的转移频率定义为社团间信息流量,以宽度与社团间信息流量成正比的连线连接每个社团,得到如图2（b）的单层网络社团连接图,从这些结果中可发现：
图2 各年份出行交互网络完备功能子区探测结果

Fig. 2 Subdistricts detected from the single-layer spatial interaction network

（1）出行网络的信息流量主要集中在北京市三环内的几个主要社团中,包括海淀区、北京南站附近以及西城区一带,这些区域的流量分布随着时间不断发生变化。在2014年以后的出行网络中,通州区一带也拥有较高的信息流量。
（2）城市郊区部分社团的空间分布随时间变化较为稳定,如大兴区、房山区、通州区等区域的社团范围的变化始终不明显。
（3）社团间的转移信息流量主要集中在中心城区的几个社团内部以及城市郊区社团向中心城区的转移中,城市郊区之间很少存在社团间的流量转移。

3.2 多层网络功能子区探测结果

单层网络功能子区探测结果得出的规律基本符合人们对于研究区城市结构的认知,然而其无法提供分析完备功能子区动态性的手段。由于不能在多层之间得到完整的社团的映射关系,除较明显社团外,不易观察这些社团所代表的完备功能子区的演变情况,并且单层网络的社团发现算法在分类时每次只考虑一个网络,得到的网络结构很大程度上取决于各年份的数据情况,这样得到的社团在尺度,结构等方面都存在差异,难以进行横向比较。
因此,本研究在多层耦合网络中进行社团探测来进一步探索时间序列上城市完备功能子区的动态性。使用2.2节中提出的多层网络社团探测方法得到的结果如图3所示,相比于单层网络中得到的结果,多层网络的探测方法考虑了时序网络层间存在的时间耦合与空间耦合,得到的结果是跨越整个多层网络的社团分布,每一层上社团分布结果都是这一多层社团分布在该层网络上的映射,不同层中社团的尺度相同,且存在着确定的对应关系。观察结果发现：算法得到的多层网络社团映射在每一层网络上的社团分布的动态变化很小,只有社团内部一些节点区域的访问频率存在微弱的变化,整体上随时间变化呈现出较强的稳定性。从算法原理出发考虑,多层网络的探测方法在时空网络模型中探测到的是给定的时间序列上城市完备功能子区分布的稳定区域,即一定时间内完备功能子区随时间变化的稳定变化范围。
图3 多年份出行交互网络完备功能子区探测结果

Fig. 3 Subdistricts detected from the multi-layer spatial interaction network

3.3 功能子区动态演变分析

为了分析城市中完备功能子区的动态变化特征,本研究结合单层网络社团探测与多层网络社团结果,通过2.3节中介绍的方法进行了窗口化分析。将多层网络上进行社团探测得到的完备功能子区随时间的稳定变化范围定义为稳定功能子区窗口,将其作为在单层网络中分析完备功能子区变化特征的分析窗口,对每个窗口所代表的完备功能子区计算混合指数和稳定指数。
为了结合实际验证分析结果,本研究针对如图4中标注出的8个稳定功能子区窗口进行了分析,所选择的八个区域在地理位置上分别对应着：海淀区、北京南站、房山区、大兴区、朝阳区、通州区、望京以及奥运村。通过统计这些窗口内单层网络社团划分结果的混合指数与稳定指数（图5）可发现一些显而易见的规律：城市中心区域的完备功能子区的混合指数和稳定指数显著高于城市边缘区域的子区;一些发展成熟的区域的混合指数和稳定指数随时间的变化十分微弱而一些发展中的区域的指数变化十分明显等。进一步,基于混合指数和稳定指数的分布,可根据完备功能子区的动态特征将其分为以下4类。
图4 稳定功能子区窗口

Fig. 4 Spatial windows for dynamic analysis

图5 功能子区动态演变窗口分析统计结果

Fig. 5 Dynamic characteristics of subdistricts in each spatial window

（1）城市中心的核心子区：如海淀区、朝阳区等城市中心的发展较为成熟的完备功能子区无论在混合指数还是稳定指数方面都远高于其他区域,并且相对而言这些指数的变动较小,这可能源自于城市中心相比于郊区承担了更多的功能和来自周围城区甚至城市边缘地区的需求,因此区域内部的结构处于不稳定的状态,在外部环境发生变化（其他区域的发展过程）的过程中,容易受到其影响而导致区域内部结构的变化。
（2）城市边缘单一功能子区：如大兴区、房山区、通州区等位于城市边缘的完备功能子区无论是通过观察社团发现的结果还是通过分析其混合指数和稳定指数的分布,都可以得出同样的结论,这些区域的结构非常稳定,且内部社团分布较为单一,出现这种现象的原因是城市边缘区域的城市功能相对单一,它们主要提供住宅和起居相关的功能,并且由于距离限制,邻近区域的发展对其造成的影响也较为有限,因此这些区域的完备功能子区在时间的推移过程中呈现出一种稳定的态势。
（3）功能特殊的频繁交互子区：观察可以发现奥运村这一区域虽然位于城市中心,但是其周围海淀区、朝阳区完备功能子区频繁的结构变化并没有对其造成影响,始终保持着区域内社团分布的稳定性,将其作为一种独特的动态特征单独划分出来,其区域内奥体中心、国家体育馆、奥林匹克公园等设施的存在使该区域具有不可代替的城市功能,因此在整个城市发展的过程中始终保持着相对稳定的结构。观察社团分布的情况可以发现首都国际机场附近的完备功能子区也呈现出类似的趋势。
（4）城市次中心核心子区：如望京、北京南站等区域,它们经过初步发展的过程形成了完备功能子区。望京一带完备功能子区的变化尤其具有代表性,通过观察表格中数据可以发现：该区域的混合指数随着时间推移逐年降低,在所有窗口中具有最大的方差,完备功能子区内部的社团分布逐渐聚集,在2017年时降低到了0.70,与城市边缘的子区内社团单一化程度相当;另一方面,该区域的窗口稳定指数也逐年降低,区域内的社团边缘从与窗口的大量相交逐渐发展到与完备功能子区重合,在北京南站区域的稳定指数分布中也能发现相同的趋势。这种趋势反映了稳定的完备功能子区逐步发展和形成的过程。望京区域从2009年底启动旧村改造工程,并于2011年成为“十二五”重点建设基地,逐步发展为朝阳区自成一体的独立性新城区,具备了丰富的居住、商业、教育、医疗和娱乐功能;北京南站自2009年竣工以及2011年京沪高铁通车逐步成为北京市铁路交通枢纽区域,这很好地解释了本研究中通过观测和统计得到的结果。

4 讨论

本研究使用多年份的出租车轨迹数据,从城市区域间的人口流动层面构建了城市居民出行网络,并引入时间和空间耦合构建了多年份时空交互网络,进而利用社团发现算法对城市中完备功能子区域的分布及动态变化进行了分析。相比于先前的研究,本研究提出的方法能够适用于时间跨度更长、数据源存在差异的更复杂的情境,并通过空间权重矩阵在出行交互网络中引入了对于区域在地理上相关性的考量。此外,研究中还提出了窗口分析的量化指标,为城市中完备功能子区的演化进程提供了定量的评价方法。
本研究存在的不足和改进方向主要包括3个方面：① 单一类型的社会感知数据（出租车数据）难以覆盖城市中所有的活动功能,因此不能代表真实的活动模式,仅通过出租车轨迹数据得到的研究结果存在一定的片面性。因此,整合多源数据（如,公共交通、手机定位数据等）更能够反映真实的城市人群活动,考虑多种出行方式和换乘行为的多源出行网络模型及针对其的社团探测方法是未来研究中的一个挑战;② 缺少对于完备功能子区探测结果的量化评价指标,难以对模型中的模型参数进行学习和优化,只能依靠先验知识衡量结果的优劣,因此需要探索标准化的指标来对划分结果进行评价;③ 未来可以使用更符合城市完备功能区域定义的重叠社团（网络分析中的重叠社团使网络中被频繁访问的部分更容易被划分至多个社团,更能反映城市区域的功能性和辐射范围等特征）来进一步探索出行交互网络中完备功能子区的分布和演变规律。

5 结论

在漫长的城市化进程中,城市的发展总是伴随着一个个热点的出现与衰败,从城市化到逆城市化再到再城市化,城市的生命力也在一次次的兴衰更迭中不断成长,能够从浩如烟海的坐标点中一步步的探索,直到发现城市的演变中所蕴含的奥秘,这是一个充满挑战与想象力的过程。在尝试实现这一目标的过程中,本研究的主要贡献包括3个方面：① 提出了一种将时间约束和空间约束纳入考虑的针对多年份轨迹数据的多层耦合网络建模方法; ② 通过改进Infomap社团探测算法在多年份出行交互网络中实现了完备功能活动区域的探测;③ 根据探测得到的完备功能子区并结合实际,对北京市6年间城市完备功能子区的动态演化进行了分析与讨论,帮助人们理解北京市的城市发展规律和进行城市规划。

References

Publishing order | Descend order by publishing year | Descend order by cited within
[1]
Stanback T M. The new suburbanization: Challenge to the central city[M]. Routledge, 2019. DOI: 10.4324/9780429 313172

DOI

[2]
龙瀛, 刘伦伦. 新数据环境下定量城市研究的四个变革[J]. 国际城市规划, 2017, 32(1):64-73.

[ Long Y, Liu L. Four transformations of Chinese quantitative urban research in the new data environment[J]. Urban Planning International, 2017, 32(1):64-73. ] DOI: 10.22217/upi.201 5.299

DOI

[3]
Liu Y, Liu X, Gao S, et al. Social sensing: A new approach to understanding our socioeconomic environments[J]. Annals of the Association of American Geographers, 2015, 105(3):512-530. DOI: 10.1080/00045608.2015.1018773

DOI

[4]
Fodor J A. The modularity of mind[M]. MIT press, 1983. DOI: 10.2307/2184717

DOI

[5]
Rosvall M, Bergstrom C T. Maps of random walks on complex networks reveal community structure[J]. Proceedings of the National Academy of Sciences, 2008, 105(4):1118-1123. DOI: 10.1073/pnas.0706851105

DOI

[6]
Rosvall M, Bergstrom C T. Maps of information flow reveal community structure in complex networks[J]. arXiv preprint, 2007,arXiv:0707.0609. DOI: 10.1007/978-3-642-31821-4

DOI

[7]
Gao C, Ma Z, Zhang A Y, et al. Achieving optimal misclassification proportion in stochastic block models[J]. The Journal of Machine Learning Research, 2017, 18(1):1980-2024. DOI: 10.5555/3122009.3153016

DOI

[8]
Xie J, Kelley S, Szymanski B K. Overlapping community detection in networks: The state-of-the-art and comparative study[J]. ACM Computing Surveys, 2013, 45(4):1-35. DOI: 10.1145/2501654.2501657

DOI

[9]
Lancichinetti A, Fortunato S, Kertész J. Detecting the overlapping and hierarchical community structure in complex networks[J]. New Journal of Physics, 2009, 11(3):033015. DOI: 10.1088/1367-2630/11/3/033015

DOI

[10]
Evans T S, Lambiotte R. Line graphs, link partitions, and overlapping communities[J]. Physical Review E, 2009, 80(1):016105. DOI: 10.1103/PhysRevE.80.016105

DOI

[11]
Yang J, Leskovec J. Overlapping community detection at scale: a nonnegative matrix factorization approach[C]// Proceedings of the Sixth ACM International conference on Web Search and Data Mining. ACM, 2013:587-596. DOI: 10.1145/2433396.2433471

DOI

[12]
Lambiotte R, Delvenne J C, Barahona M. Laplacian dynamics and multiscale modular structure in networks[J]. arXiv preprint, 2008,arXiv:0812.1770. DOI: 10.1109/TNS E.2015.2391998

DOI

[13]
De Bacco C, Power E A, Larremore D B, et al. Community detection, link prediction, and layer interdependence in multilayer networks[J]. Physical Review E, 2017, 95(4):042317. DOI: 10.1103/PhysRevE.95.042317

DOI

[14]
De Domenico M, Lancichinetti A, Arenas A, et al. Identifying modular flows on multilayer networks reveals highly overlapping organization in interconnected systems[J]. Physical Review X, 2015, 5(1):011027. DOI: 10.1103/phy srevx.5.011027

DOI

[15]
Hmimida M, Kanawati R. Community detection in multiplex networks: A seed-centric approach[J]. Networks & Heterogeneous Media, 2015, 10(1):71-85. DOI: 10.3934/n hm.2015.10.71

DOI

[16]
Kuncheva Z, Montana G. Community detection in multiplex networks using locally adaptive random walks[C]// Proceedings of the 2015 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining 2015. ACM, 2015:1308-1315. DOI:10.1145/280879 7.2808852

[17]
Long Y, Shen Z. Finding public transportation community structure based on large-scale smart card records in Beijing[M]//Geospatial Analysis to Support Urban Planning in Beijing. Springer, Cham, 2015:155-167. DOI: 10.1007/978-3-319-19342-7_8

DOI

[18]
Li J, Zheng P, Zhang W. Identifying the spatial distribution of public transportation trips by node and community characteristics[J]. Transportation Planning and Technology, 2020, 43(3):325-340. DOI: 10.1080/03081060.2020.1 735776

DOI

[19]
王波, 甄峰, 张浩. 基于签到数据的城市活动时空间动态变化及区划研究[J]. 地理科学, 2015, 35(2):151-160.

DOI

[ Wang B, Zhen F, Zhang H. The dynamic changes of urban space-time activity and activity zoning based on check-in data in Sina web[J]. Scientia Geographica Sinica, 2015, 35(2):151-160. DOI: 10.13249/j.cnki.sgs.2015.02.151

DOI

[20]
钮心毅, 丁亮, 宋小冬. 基于手机数据识别上海中心城的城市空间结构[J]. 城市规划学刊, 2014(6):61-67.

[ Niu X, Ding L, Song X. Understanding urban spatial structure of Shanghai central city based on mobile phone data[J]. Urban Planning Forum, 2014(6):61-67. DOI: 10.3969/j.is sn.1000-3363.2014.06.009

DOI

[21]
Tu W, Cao J, Yue Y, et al. Coupling mobile phone and social media data: A new approach to understanding urban functions and diurnal patterns[J]. International Journal of Geographical Information Science, 2017, 31(12):2331-2358. DOI: 10.1080/13658816.2017.1356464

DOI

[22]
Yin J, Soliman A, Yin D, et al. Depicting urban boundaries from a mobility network of spatial interactions: A case study of Great Britain with geo-located Twitter data[J]. International Journal of Geographical Information Science, 2017, 31(7):1293-1313. DOI: 10.1080/13658816.2017.12 82615

DOI

[23]
宋辞, 裴韬. 北京市多尺度中心特征识别与群聚模式发现[J]. 地球信息科学学报, 2019, 21(3):384-397.

DOI

[ Song C, Pei T. Exploring polycentric characteristic and residential cluster patterns of urban city from big data[J]. Journal of Geo-information Science, 2019, 21(3):384-397. DOI: 10.1 2082/dqxxkx.2019.180608

DOI

[24]
Liu X, Gong L, Gong Y, et al. Revealing travel patterns and city structure with taxi trip data[J]. Journal of Transport Geography, 2015, 43:78-90. DOI: 10.1016/j.jtrangeo. 2015.01.016

DOI

[25]
Guo D, Jin H, Gao P, et al. Detecting spatial community structure in movements[J]. International Journal of Geographical Information Science, 2018, 32(7):1326-1347. DOI: 10.1080/13658816.2018.1434889

DOI

[26]
Zhou M, Yue Y, Li Q, et al. Portraying temporal dynamics of urban spatial divisions with mobile phone positioning data: A complex network approach[J]. ISPRS International Journal of Geo-Information, 2016, 5(12):240. DOI: 10.3390/ijgi5120240

DOI

[27]
Zhong C, Arisona S M, Huang X, et al. Detecting the dynamics of urban structure through spatial network analysis[J]. International Journal of Geographical Information Science, 2014, 28(11):2178-2199. DOI:10.1080/136588 16.2014.914521

DOI

[28]
Koylu C, Guo D, Kasakoff A, et al. Mapping family connectedness across space and time[J]. Cartography and Geographic Information Science, 2014, 41(1):14-26. DOI: 10.1080/15230406.2013.865303

DOI

[29]
Winterton R H S. Newton's law of cooling[J]. Contemporary Physics, 1999, 40(3):205-212. DOI: doi.org/10.1080/001075199181549

DOI

[30]
Bavaud F. Models for spatial weights: A systematic look[J]. Geographical Analysis, 1998, 30(2):153-171. DOI: 1 0.1111/j.1538-4632.1998.tb00394.x

DOI

Options
Outlines

/

〈 〉