EN中文

Journal of Geo-information Science >

2022 , Vol. 24 >Issue 11: 2186 - 2197

DOI: https://doi.org/10.12082/dqxxkx.2022.220041

Close-Range Image Line Matching based on Mesh Descriptor and Homography Constraint

  • ZHANG Shan , 1, 3 ,
  • ZHANG Ka , 1, 2, 3, 4 ,
  • ZHAO Like 5, 6 ,
  • WANG Yujun 5, 6 ,
  • ZHANG Lunning 7 ,
  • ZHOU Yaqin 1, 3
Expand
  • 1. Key Laboratory of Virtual Geographic Environment (Nanjing Normal University), Ministry of Education, Nanjing 210023, China
  • 2. Jiangsu Center for Collaborative Innovation in Geographical Information Resource Development and Application, Nanjing, 210023, China
  • 3. School of Geography, Nanjing Normal University, Nanjing 210023, China
  • 4. Key Laboratory of Urban Land Resources Monitoring and Simulation, Ministry of Natural Resources, Shenzhen 518034, China
  • 5. Geological Survey of Jiangsu Province, Nanjing 210018, China
  • 6. Natural Resources Satellite Application Technology Center of Jiangsu Province, Nanjing 210018, China
  • 7. Shanghai Huace Navigation Technology Co., Ltd., Shanghai 201702, China
*ZHANG Ka, E-mail:

Received date: 2022-01-22

  Revised date: 2022-02-25

  Online published: 2023-01-25

Supported by

Natural Science Foundation of Jiangsu Province(BK20201372)

Open Fund of Key Laboratory of Urban Land and Resources Monitoring and Simulation,Ministry of Natural Resources(KF-2019-04-003)

National Natural Science Foundation of China(41631175)

National Natural Science Foundation of China(42071301)

A Project Funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions(164320H116)

Fold

Abstract

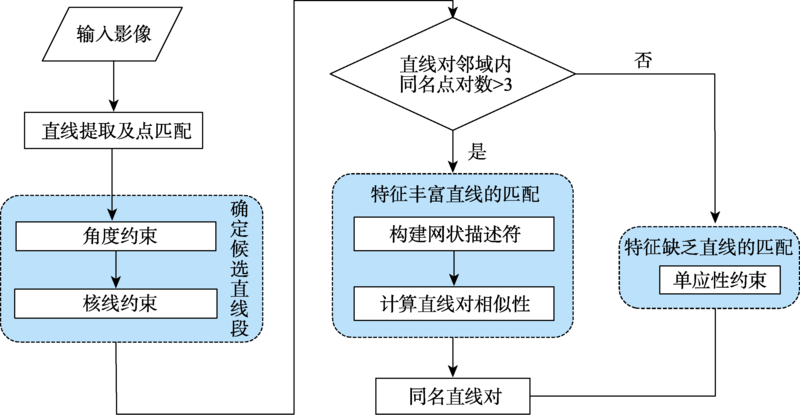
Aiming at the problem that the line descriptor in the existing stereo image line matching methods only depends on local gray features, resulting in weak reliability, a line matching method based on mesh descriptor and homography constraint is proposed in this study. Firstly, we extract line segments and the corresponding point pairs in reference image and search image using the Line Segment Detector (LSD) and Scale-Invariant Feature Transform ( SIFT) algorithms. And line segments that do not satisfy the length requirements to eliminate the noise caused by shadows or other ground objects are deleted. Secondly, after roughly estimating the rotation angle and homography matrix between the two images according to the obtained corresponding point pairs, the candidate lines are determined through the angle constraint and epipolar constraint, which can reduce the line search range in search image and exclude a large number of mismatches. In addition, the overlap between the reference line and the candidate line is calculated to ensure the consistency of the endpoints. Thirdly, a circular neighborhood using the midpoint of the line segment as the center and the length as the radius is constructed. The corresponding point pairs are searched in the neighborhood of the reference line and the candidate line to calculate the mesh descriptor. In order to improve the accuracy of line matching, for the line pairs whose number of corresponding point pairs is greater than three, we arbitrarily select three groups of different corresponding point pairs to calculate the line similarity value and take the maximum value as the final similarity of the line segment, so as to determine the corresponding line pair. Finally, the line segments that are not searched for the corresponding point pairs are mapped into the search image using the homography matrix. Three criteria are established according to the angle difference between the two lines and the vertical distance between the endpoints and the radiation information. Based on this, the final matching result is obtained, which can improve the number of corresponding line pairs. To verify the effectiveness and robustness of our algorithm, this paper selects five groups of close-range images in the international open standard test data set, and compares with three existing representative algorithms. The results show that the accuracy and effectiveness of our algorithm are higher than the other three algorithms. The matching accuracy and operation efficiency are improved by 16.1% and 49 times, respectively, and satisfactory line matching results can be obtained for close-range images under different conditions.

Key words： close-range image; line matching; angle constraint; epipolar constraint; line neighbor-hood; mesh descriptor; line similarity; homography constraint

Cite this article

ZHANG Shan , ZHANG Ka , ZHAO Like , WANG Yujun , ZHANG Lunning , ZHOU Yaqin . Close-Range Image Line Matching based on Mesh Descriptor and Homography Constraint[J]. Journal of Geo-information Science, 2022 , 24(11) : 2186 -2197 . DOI: 10.12082/dqxxkx.2022.220041

1 引言

直线是数码相机拍摄的照片、航空影像及遥感图像上的重要稳定特征，它包含了丰富的几何和语义信息，能够很好的表达出类似建筑物等地物的几何轮廓。直线特征的匹配是计算机视觉[1]、特征识别[2]、图像配准[3]等领域的关键技术和经典问题，也是三维重建[4]的首要解决问题。
目前的线特征匹配按照流程可分为确定候选直线段与利用相似性度量匹配直线两个步骤。为了减少直线段搜索范围、提高算法效率，在对直线进行匹配前一般先用约束条件确定候选直线段。常有的约束条件有基于直线几何属性的约束[5]、同名点约束[6-7]、核线约束[8]、单应性约束[9-10]、三角网约束[11⇓-13]5类。其中，因直线端点不一致问题，基于直线自身几何属性的约束会出现明显误差；同名点约束通常根据线特征与邻域内同名点对的距离关系、分布情况或是两幅影像间的旋转角筛选直线段；单应性约束是基于图像深度不大为前提的，具有一定的适用性限制。
利用相似性度量匹配直线的方法主要分为直线邻域描述子构建与点线不变量构建2种。前者一般利用直线或直线组邻域内的灰度信息、纹理信息建立等大小向量，通过判定向量间的欧式距离来确定直线对。最为经典的有均值-标准差直线描述符（Mean-Standard Deviation Line Descriptor, MSLD）[14]、直线条带描述符（Line Band Descriptor, LBD）[10]，该类描述符统计了像素支撑域中4个方向的梯度向量，一定程度上可以克服线段碎片化、大尺度等问题。此外，利用直线组蕴含更多的几何信息这个优点，有学者提出构建直线组描述符的方法[15-16]，该方法鲁棒性较强，但计算量大、处理较为耗时；后者是在定义直线段邻域后，利用直线和若干个同名点对的局部几何信息构建不变量计算相似度从而进行匹配。常见的不变量有仿射不变量[17]、投影不变量[17]及交叉比不变量[18]等。此类方法不严格依赖端点，能够解决端点不一致问题，但线匹配结果受点匹配数量及精度影响。
现有大多数直线描述符只是基于局部灰度特征构建，忽略了拓扑分布等信息，导致算法适用范围较小；根据点线不变量评估直线相似性的方法过度依赖同名点匹配结果，未对其他特征属性加以利用。针对上述直线匹配存在的问题，本文在借鉴文献[19]思路的基础上提出了一种结合网状描述子和单应约束的匹配算法，算法除了利用灰度特征之外还充分考虑了影像中地物之间的拓扑分布，对影像的几何、尺度与辐射等变化具有较强鲁棒性。

2 研究方法

本文算法流程如图1所示，其主要分为直线提取及点匹配、确定候选直线段、特征丰富直线的匹配、特征缺乏直线的匹配4个步骤：① 对图像进行直线提取及特征点匹配；② 用角度约束和核线约束对右影像中的直线段进行过滤，再根据核线计算参考直线与候选直线的重叠部分；③ 在参考直线与候选直线一定大小邻域内搜索同名点对，点对数量大于3的直线（文中命名为特征丰富直线）构建网状描述符并计算相似性，将满足要求的直线对视为同名直线对；④ 对符合上述条件但却未搜索到足够数量同名点对的直线（特征缺乏直线）单独进行单应性约束，从而得到两影像的最终同名直线对。
图1 本文方法的整体流程

Fig. 1 The overall flow diagram of the proposed method in this paper

2.1 直线提取及点匹配

采用LSD算法[20]、尺度不变特征变换（Scale-Invariant Feature Transform, SIFT）算法[21]对影像进行直线提取及特征点匹配。LSD算法是一种利用梯度方向取代梯度幅值进行边缘提取的方法，具体流程为：
（1）高斯降采样。采用高斯滤波对图像进行去噪和平滑，减少数字离散图像的阶梯效应；
（2）计算像素梯度。计算图像各像素的梯度幅值及方向，规定直线方向从暗的一侧指向亮的一侧，并按照大小对其进行排序。小于给定阈值的像素标记为USED，反之标记为UNUSED；
（3）区域增长。一般情况下具有较高梯度幅值的像素点所在区域通常有较强的边缘，将最大梯度的像素作为种子点。种子点对应的方向作为矩形区域初始方向，对周围满足方向阈值的UNUSED像素用区域生长算法生成直线支撑区域（Line Support Regions），遍历区域中所有像素并更新直线角度，直到没有任何像素添加至区域中；
（4）直线验证。计算NFA（Number of False Alarms）来确定是否接受或拒绝提取的直线。
由于该算法所提取的直线未设置最小长度，因此所得到的直线比较断裂，而较短直线段通常是由噪声产生的，为确保后续匹配的准确度，本文在直线检测后将长度小于20像素的直线段剔除。特征点容易提取且描述方式简单，使用率最高的还是SIFT算法，该算法具有较好的稳定性和不变性，能够适应旋转、尺度缩放、亮度的变化，一定程度上不受视角变化、仿射变化、噪声的干扰。因此本文选择了此方法进行特征点匹配。经过以上处理可以得到近景影像对直线集合以及同名点对。

2.2 确定候选直线段

（1）角度约束。获得同名点对之间的对应关系后，通过统计同名点对角度差直方图能够得到两幅影像的旋转角度θ2。若两条直线是正确匹配对，那么不论拍摄前后影像如何变换，两者之间的方向差与影像的旋转角度始终是在一给定阈值中，如不满足这个条件即可视为其不匹配，该方法能够剔除大量非匹配直线段，从而加快匹配速度。但角度阈值的设定对最终匹配结果起决定性作用，具体取值将会在后续章节中进行讨论。角度约束的判别方法如式（1）所示：
$\left| {{\theta }_{1}}-{{\theta }_{2}} \right|\le \theta $
式中：θ1为参考直线与候选直线的角度差值；θ为角度阈值，若角度差小于阈值，则将该直线加入到候选集中，否则弃用。
（2）核线约束。因影像视角改变、局部变形等问题，仅仅利用角度约束确定候选直线段是不稳定的。而且同名直线段端点的不对应会破坏其邻域信息的一致性，导致利用直线邻域进行匹配的方法受限。为了解决所述问题，在角度约束确定候选直线后考虑加入核线约束进一步检核。如图2所示，左影像中直线l1为参考直线，右影像中r1、r2、r3、r4为候选同名直线段，线段r1的两端点为C（x1, y1）、D（x2, y2），与参考直线l1端点核线的交点为P（x3, y3）、Q（x4, y4）。核线约束具体步骤为：首先，通过计算4点之间的欧式距离，确定最远距离的两点称为远点对，剩下的两点则视为近点对；其次，根据两点对的距离计算重叠部分所占远点对长度的比例，即重叠度s（其计算方法见式（2））；最后，若重叠度大于给定阈值，则保留该候选直线且将直线端点更新为两交点，否则剔除。
图2 直线匹配中的核线约束示意

Fig. 2 The sketch of epipolar constraint in line matching

$s=\frac{sqrt({{({{x}_{4}}-{{x}_{3}})}^{2}}+\left( {{y}_{4}}-{{y}_{3}}{{)}^{2}} \right)}{sqrt({{({{x}_{2}}-{{x}_{1}})}^{2}}+\left( {{y}_{2}}-{{y}_{1}}{{)}^{2}} \right)}$

2.3 特征丰富直线的匹配

2.3.1 直线的网状描述符构建

如图3所示，描述符由直线的两端点（A, B）及邻域内3个特征点（P1, P2, P3）组成，连接这5个点构成一个网状结构，每个点之间的连线称为网络边，通过采样每条网络边上的像素灰度值来构建描述符。该描述符很好的兼顾了灰度特征及拓扑特征，考虑到了大尺度变化、光照变化等影响，并给予了解决办法，具有较强的适用性。具体构建过程如下：
图3 网状描述符示意 （仅显示2条采样点）

Fig. 3 The sketch of mesh descriptor (only sample points in two sides are displayed)

（1）网络边定义规则。描述符由5个点（A, B, P1, P2, P3）构成，从5个点中任选2个点进行连线，共得到10条网络边，由于直线段是有方向的，在对网络边进行灰度采样时需要确保边的起点与终点一致，现对网络边的方向定义如下：① 优先索引值小的特征点，优先特征点与直线段端点连接；② 特征点与直线段端点连接时，规定由特征点指向端点；③ 特征点互相连接时，规定由索引值小的一方指向索引值大的一方；④ 由直线段起点指向终点。上图中，特征点已按照索引值进行排序，按照以上规则得到的10条网络边为：（P1, A），（P1, B），（P1, P2），（P1, P3），（P2, A），（P2, B），（P2, P3），（P3, A），（P3, B），（A, B）。
（2）灰度采样。为了提高大尺度变化的性能及降低长网络边的计算复杂度，在灰度采样之前使用影像金字塔构建影像内容的多尺度表达。本文金字塔共构建8层，若在每一层金字塔影像中都进行描述子构建，则会耗费大量计算时间，因此本文仅仅是按照直线长度确定金字塔索引后，将原始影像中的直线段映射到该金字塔层中并计算描述符。确定好层级索引且将网络边映射到该层影像中后，便对其进行灰度采样。以一条网络边（A, B）举例，假设A点坐标为（x1, y1），B点坐标为（x2, y2）。为了降低网络边起点和终点位置的敏感性，本文对网络边10%-90%部分，即从点（x1+0.1（x2-x1）, y1+0.1（y2-y1））->（x1+0.9（x2-x1）, y1+0.9（y2-y1））进行等间隔采样，将获取到的像素灰度值存储至向量中。
（3）向量分块。由于各网络边的长度不等，灰度采样之后的向量大小不一，且影像中会有噪声点存在。为了统一描述符大小、减少噪声影像，对获取到的灰度向量等分为N（本文N = 6）块,对每块计算灰度平均值作为新值存储至向量D（式（3））中，表示为：
$D={(g_{1}^{1},g_{2}^{1},...,g_{5}^{10},g_{6}^{10})}^{T} \in R^{6 \times 10}$
式中： g j i表示第i条网络边中第j行灰度值。
（4）向量归一化。将所有网络边的向量合并后进行L2范数归一化得到最终的直线描述符向量ND（式（4））：
$ND=\left( \frac{g_{1}^{1}}{{{D}_{2}}},\frac{g_{2}^{1}}{{{D}_{2}}},...,\frac{g_{6}^{10}}{{{D}_{2}}} \right)\in {{R}^{6\times 10}}$
式中： · 2表示欧几里得范数。

2.3.2 基于几何距离的直线对相似度计算

（1）邻域内同名点搜索。在保证直线邻近范围的基础上，尽可能扩大邻域的范围和方位，使其充分利用周围像素点。直线段在经过核线约束后，参考直线与候选直线的端点一致，此时直线段中点可用，因此将直线邻域定义为以中点为中心，r为半径（文中用L表示）的圆形区域（图4）。
图4 直线段邻域示意图

Fig. 4 The sketch of line segment's neighborhood

（2）距离计算。当同名点对有误时会影响直线匹配的结果，为了避免这个问题，我们随机选取特征丰富直线和其候选直线圆形邻域内3组不同的同名点对，计算相似性后取最大的相似值作为最终统计值。假设特征丰富直线lm的描述子为： N D l e f t = ( x 1 , x 2 , . . . , x 60 ) Τ，第i组同名点对应的候选直线ln描述子为: N D r i g h t = ( y 1 , y 2 , . . . , y 60 ) Τ ,   i = 1,2 , 3，两向量的欧式距离（式（5））表示为：
$\begin{array}{*{35}{l}} {{D}_{i}}\left( {{l}_{m}},{{l}_{n}} \right)=\sqrt{{{({{y}_{1}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{x}_{2}})}^{2}}+...+{{({{y}_{60}}-{{x}_{60}})}^{2}}} \\ ==\sqrt{\underset{k=1}{\overset{60}{\mathop \sum }}\,{{({{y}_{k}}-{{x}_{k}})}^{2}}} \\ \end{array}$
经过L2范数归一化后，一组向量的欧式距离与余弦相似度等价，因此将特征丰富直线与候选直线的相似性（式（6））表示为：
${{S}_{i}}\left( {{l}_{m}},{{l}_{n}} \right)=1-{{D}_{i}}\left( {{l}_{m}},{{l}_{n}} \right)$
式中：i表示候选直线邻域内第i组同名点对，i =1,2,3。对于不同组的同名点对与直线段端点所计算的相似值是不同的，选择3组中最大相似值为特征丰富直线与候选直线的最终相似度。
（3）确定初始同名直线对。匹配过程中可能会出现“一对多”、“多对一”、“多对多”情况，无法保证匹配结果一对一。基于此，本文初始化一个大小为m×n（m、n分别两幅影像直线数量）的全零矩阵，将满足角度约束和核线约束后计算出的直线对相似性存储至对应的位置中，矩阵全部更新完成后对某一行搜索所有列中的相似值，并将最大值那列对应的直线作为匹配直线段。

2.4 特征缺乏直线的匹配

现实情况中在弱纹理、纹理重复区域中很少能提取到特征点，这将导致一部分直线段因为缺少同名点对而漏选。因此在上述步骤后追加第二阶段对特征缺乏直线进行匹配，该阶段利用单应性矩阵将左直线映射至右影像中，并建立3个准则判断特征缺乏直线与候选直线是否匹配：① 投影直线与候选直线间的角度差在阈值β内；② 投影直线与候选直线四端点的垂直距离小于阈值d；③ 特征缺乏直线与候选直线两侧的灰度大小是正相关的。假设单应矩阵已知，则可以利用式（7）将特征缺乏直线两端点映射到右影像中：
$\left[ \begin{array}{*{35}{l}} {{x}^{1}} \\ {{y}^{1}} \\ 1 \\\end{array} \right]=H\left[ \begin{array}{*{35}{l}} x \\ y \\ 1 \\\end{array} \right]=\left[ \begin{matrix} {{h}_{11}} & {{h}_{12}} & {{h}_{13}} \\ {{h}_{21}} & {{h}_{22}} & {{h}_{23}} \\ {{h}_{31}} & {{h}_{32}} & {{h}_{33}} \\\end{matrix} \right]\left[ \begin{array}{*{35}{l}} x \\ y \\ 1 \\ \end{array} \right]$
式中：（x1, x1,1）与（x, y, 1）分别表示左右影像中某一对应点对的齐次坐标，H表示单应矩阵。
若两直线相匹配，经单应矩阵映射后的直线必定与候选直线在距离和方位上相近。因此通过计算两直线间4个端点到另一直线的平均距离及的角度（同式（1））判定直线段是否相匹配。图5中，AB表示特征缺乏的直线映射到右影像上后的直线，CD表示候选直线，两直线间距离值（式（8））表示为：
${{d}_{v}}=\frac{{{d}_{1}}+{{d}_{2}}+{{d}_{3}}+{{d}_{4}}}{4}$
图5 两直线段端点距离示意

Fig. 5 The sketch of end point distance of two line segments

如果提取的直线比较密集，直线段在空间上是紧邻在一起的，这会导致众多误匹配，需要更多的信息来辅助匹配。直线左右两侧内的像素灰度值是呈正相关的，如果特征缺乏直线左侧灰度值大于右侧灰度值，那么与其匹配的候选直线段两侧必然符合此情况。同时满足以上3个判断准则的视为正确匹配对，将结果与初始同名直线对合并后即为两幅影像的最终匹配直线对。

3 实验及分析

3.1 实验数据来源

为了验证算法的可靠性及有效性，在Windows10环境下，使用C++语言结合OpenCV函数库对本文算法进行编程实现。实验共采用5组近景影像对作为匹配数据（图6），均来源于网站http://www.robots.ox.ac.uk/~vgg/data[17]。其中包含两对具有旋转变化的近景影像（640像素×480像素）、一对具有尺度变化的近景影像（644像素×428像素）、一对具有光照变化的近景影像（900像素×600像素）及一对具有视点变化的近景影像（800像素×600像素）。
图6 本文所用的实验影像

Fig. 6 The experimental images used in the paper

3.2 参数对匹配准确率的影响分析

方法中涉及到的参数有直线间角度差阈值θ、核线约束中的重叠度阈值ɑ、圆形邻域半径r、向量分块数N、单应约束中的角度阈值β以及垂直距离阈值d共6个。分析假如阈值发生变动，是否会影响到本文的算法性能是十分重要的。在确定角度差阈值和核线约束重叠度约束阈值时，除了达到剔除错误匹配效果的同时还需要保证同名直线的数量。因此本文采取经验化阈值θ=20°，ɑ=0.25，以上2个阈值取值适用于任何影像对。下面对剩余参数以图6(a)中的近景影像为例进行详细分析：

3.2.1 特征丰富直线匹配中的阈值选择

该过程中涉及到的参数有圆形邻域半径r及向量分块数N。直线段邻域的大小决定了最终的匹配结果，若邻域半径过小，参考直线段与候选直线段搜索不到同名点从而使得算法适用性大大降低；但若半径过大，搜索到的同名点对远离直线段，那么后续构建的直线描述子则不能反映局部信息，尤其是当图像纹理重复时会存在大量误匹配。向量分块数大小则会影响网状描述子的准确性及鲁棒性。在保持其他参数一致条件下，对两参数进行研究，其中r取值为3/4×L、L、3/2×L， N ∈ [ 5,9 ]，步长为1。实验结果如图7所示。
图7 参数r、N不同取值的匹配结果

Fig. 7 Line matching results for different values of parameter r and N

从图7可以看出，当N值固定时，r=L对应的匹配准确率最高，而当取值较大或较小时准确率均有所下降。虽然匹配对数随着半径增大而增加，但考虑到准确度等因素，最终选择L为圆形半径邻域。当r值确定，N=5,9时，匹配准确率明显低于N取值为6、7、8，这是由于分块数较小，向量过平均化导致采样信息损失严重，不能够有效的描述网络边的局部信息。当N=6、7、8时对应的匹配准确率接近， 为防止向量维数过高增加算法处理时间，本文选择N=6。

3.2.2 特征缺乏直线匹配中的阈值选择

该过程需要讨论的参数有单应约束中的角度阈值β及垂直距离阈值d。将直线段映射至同一坐标系中，如果两直线是同名直线对，那么其在几何上是相近的。若两阈值设置过大，那么约束条件起不到作用，会出现大量误匹配；若阈值过小，一定程度上会减少同名直线对数量甚至无匹配对。在其余参数确定的情况下，我们将2个阈值取值范围分别设置为10~30°、2.5~4.0，对应步长为5、0.5进行实验。
如图8所示，参数β的大小对匹配准确率和同名直线对数量影像微弱，因此选取阈值范围中间值20°。此外，在其他参数确定的情况下，随着d取值不断增大，匹配准确率呈现先增后减的趋势，且d=3.5时达到峰值。d<3.5时，阈值过小导致匹配结果不理想；当d>3.5时，同名直线对数量增至282后便开始保持稳定，这是因为阈值设置过大，一些直线段仅是因为几何距离相近就被保留下来，从而导致误匹配率上升。综合来看，本文将d设置为3.5像素。由上述分析可知：本文参数对匹配结果影响均较小，表现出较强的鲁棒性，建议读者可根据本文取值经验适当调整完成所需实验。
图8 参数β、d不同取值的匹配结果

Fig. 8 Line matching results for different values of parameter β and d

3.3 匹配结果分析

为验证本文算法的优越性，在直线提取及点匹配结果相同的基础上，分别实现了基于MSLD描述子[14]、基于线结线（Line-Junction-Line, LJL）描述子[15]及基于线点不变量（Line-Point, LP）的线匹配方法[17]与本文方法进行对比。现在绝大多数学者提出的线匹配方法都是使用自己选择的图像和线段检测器进行评估，同时采取目视检查来得到匹配结论，这一做法难以有效地对不同方法进行公平的对比分析。针对这个问题，Li等[22]提供了一个直线匹配的基准数据，该基准包含了利用两种线段检测器从15对具有代表性图像中提取的30对已匹配线段集。本文实验对比过程中所采用的5幅影像均来自该基准，匹配结果的正确与否均参照该基准中提供的真值。图9(a)—9(e)展示了用本文算法得到的5幅影像匹配结果，图中匹配颜色随机选择，相同颜色的直线对视为同名直线对，左右两线段上显示的数字为同名直线对的索引顺序号。从图9的匹配结果和表1的结果对比表可以看出，在影像发生旋转、尺度变化、光照变化及视点变化等情况下，本文算法得到的直线匹配结果一定程度上均优于其他3种算法，现从匹配准确率及运行时间两方面进行分析。
图9 本文算法直线匹配结果

Fig. 9 The line matching results of the proposed algorithm

表1 不同算法匹配结果对比

Tab. 1 Comparison of line matching results of different algorithms

影像 提取直线数量（左，右）/条 算法名称 同名直线数/对 正确同名直线数/对 准确率/% 运行时间/s
6(a) （538,556） MSLD 109 90 82.6 11.97
LJL 305 281 92.1 946.13
LP 285 275 96.5 42.77
本文算法 287 282 98.3 32.25
6(b) (526,398) MSLD 158 139 88.0 8.76
LJL 159 145 91.2 450.30
LP 149 141 94.6 9.10
本文算法 164 157 95.7 29.13
6(c) (374,681) MSLD 39 28 71.8 3.58
LJL 47 35 74.5 1193.85
LP 52 37 71.2 19.84
本文算法 51 43 84.3 23.58
6(d) (971,504) MSLD 126 104 82.5 4.88
LJL 297 289 97.0 803.13
LP 219 212 96.8 30.47
本文算法 222 219 98.6 42.45
6(e) (1071,1016) MSLD 165 149 90.3 31.75
LJL 533 499 93.6 1423.01
LP 550 518 94.2 20.16
本文算法 541 524 96.9 79.23
与MSLD算法相比，本文算法得到的准确率均高于MSLD算法。后者构建描述符时仅仅利用直线一定相邻区域的梯度信息，未能顾及到线段端点及尺度变化等因素，导致提取的直线两侧信息较弱，从而降低了匹配数量。同时，该方法定义的直线支撑区域是固定大小，当图像出现尺度变化时同名支撑区域不一致，导致匹配结果效果不理想。而本文构建的网状描述符除了邻域内灰度信息外，还很好的利用了直线拓扑分布，而且均是在网络边一维方向上进行，具有旋转不变性，能够比MSLD更好的适用在旋转变换情况下。与LP算法相比，本文算法得到的同名直线数和准确率都高于LP算法。原因在于：① LP算法在搜索同名点前未对直线段端点进行处理；② LP算法忽略了某些直线段邻域内未能搜索到给定数量的同名点情况，而本文在最后阶段利用单应性约束对其进行了扩展。LJL算法所获得的匹配结果与前两者相比，同名直线的数量均有一定程度的上升，尤其是图6(d)得到了289对同名直线。但是该方法在影像发生尺度变化时（如影像6(c)）效果不佳，所适用的范围不广。而本文方法在确保数量的前提下，对于不同场景的近景影像仍具有较强的鲁棒性。
为了清晰展示不同算法的匹配结果，本文在影像6(a)上选取了2个局部区域，并对结果进行放大显示。图10(a)从左至右依次为本文算法、MSLD算法、LJL算法及LP算法在影像1处的结果图，图中黄色直线为正确匹配直线，红色为错误匹配直线。从各图椭圆形圈出来的匹配结果可以看出，在光照较暗且纹理弱的情况下，MSLD算法不能准确获取到同名直线，LJL算法出错了明显的误匹配。而在图10(b)中,索引值为58的直线段，本文算法匹配正确，但其他3种方法均出现了误匹配、未匹配现象，准确度较低。
图10 局部影像各算法匹配对比

Fig. 10 Line matching comparison of algorithms in local image

在算法运行时间方面，除影像6(a)外，MSLD算法耗时最少，LP算法次之，本文算法居第三，LJL算法耗费的时间最长。基于MSLD描述子的线匹配方法计算过程中仅仅构建了直线描述符，也未进行多尺度分析，计算过程量较小。LP算法在搜索直线邻域内同名点对时较为耗时，为了保证直线匹配结果对每一条直线计算了多个仿射不变量，并且在前者的基础上还增加了全局角度约束，这都会降低算法运行速率。而本文在使用角度约束及核线约束后，还计算了候选直线与参考直线的重叠部分，以及后续增加的对于特征缺乏直线的匹配过程，一定程度上均导致了运行时间的增加。LJL算法在高斯金字塔各级别中分别构建描述子，通过基本矩阵逐渐增加接受点实现LJL匹配传播，过程计算量极大，不具有普适性。综合匹配准确率和运行时间来看，本文提出的算法原理清晰、处理较快、准确性较高，且能适用图像旋转、尺度变换、光照变化等情况，具有较高的鲁棒性。

4 结论

本文提出一种结合网状描述符和单应约束的立体影像直线匹配方法，算法利用核线约束计算候选直线段的重叠部分，解决了直线端点不一致问题；构建的网状描述符充分利用了直线段邻域的拓扑分布，大大提高了匹配准确率，描述子构建过程均在一维边上进行，同时进行了平均分块及归一化处理，增加了近景影像中光照变化、旋转变化的适用场景；在最后阶段对未满足网状描述子构建条件的直线利用单应性矩阵进行了扩展，保证了同名直线的数量。
实验结果表明，本文方法相较于所对比的3种方法在直线匹配准确率、运行效率上最高有16.1%、49倍的提升，算法对近景影像中存在的不同场景变化具有较大优势及较强鲁棒性。值得指出的是，本文算法需要借助同名点进行匹配，在同名点稀疏情况下匹配结果会有所影响，这需要在未来的研究中进一步优化改进。

References

Publishing order | Descend order by publishing year | Descend order by cited within
[1]
刘婉君. 一种基于几何约束和直线特征的目标跟踪算法[J]. 现代计算机, 2021(7):107-110.

[ Liu W J. A target tracking algorithm based on geometric constraints and line features[J]. Modern Computer, 2021(7):107-110.] DOI:10.3969/j.issn.1007-1423.2021.07.023

DOI

[2]
行瑞星, 武芳, 巩现勇, 等. 建筑群组合直线模式识别的模板匹配方法[J]. 测绘学报, 2021, 50(6):800-811.

[ Xing R X, Wu F, Gong X Y, et al. The template matching approach to combined collinear pattern recognition in building groups[J]. Acta Geodaetica et Cartography Sinica, 2021, 50(6):800-811. ] DOI:10.11947/j.AGCS.2021.20200298

DOI

[3]
卢朝梁, 马丽华, 于敏, 等. 基于平行直线组的可见光与红外图像配准算法[J]. 解放军理工大学学报(自然科学版), 2015, 16(5):439-446.

[ Lu C L, Ma L H, Yu M, et al. Fast aglorithm of visible and infrared image registrat- ion using parallel lines[J]. Journal of PLA University of Science and Technology(Natural Science Edition), 2015, 16(5):439-446. ] DOI:10.7666/j.issn.1009-3443.201411003

DOI

[4]
曹林. 基于倾斜影像线特征的建筑物三维模型重建与优化方法研究[D]. 郑州: 战略支援部队信息工程大学, 2020.

[ Cao L. Research on building 3D model reconstruction and optimization method based on inclined image line features[D]. Zhengzhou: Information Engineering University, 2020. ] DOI:10.27188/d.cnki.gzjxu.2020.000147

DOI

[5]
何腕营, 王竞雪. 基于直线间几何属性特征相似性约束的组直线匹配算法[J]. 地球信息科学学报, 2020, 22(9):1766-1778.

DOI

[ He W Y, Wang J X. Pair-wise line matching algorithm based on feature similarity constraints of geometric attributes between the lines[J]. Journal of Geo-information Science, 2020, 22(9):1766-1778. ] DOI:10.12082/dqxxkx.2020.190334

DOI

[6]
梁艳, 盛业华, 张卡, 等. 利用局部仿射不变及核线约束的近景影像直线特征匹配[J]. 武汉大学学报(信息科学版), 2014, 39(2):229-233.

[ Liang Y, Sheng Y H, Zhang K, et al. Line feature matching of close range images using local affine invariance and kernel constraint[J]. Geomatics and Information Science of Wuhan Universi-ty, 2014, 39(2):229-233. ] DOI:10.13203/j.whugis20120611

DOI

[7]
欧阳欢, 范大昭, 纪松, 等. 结合离散化描述与同名点约束的线特征匹配[J]. 测绘学报, 2018, 47(10):1361-1371.

[ OuYang H, Fan D Z, Ji S, et al. Line matching based on discrete description and conjugate point constraint[J]. Acta Geodaetica et Cartography Sinica, 2018, 47(10):1361-1371. ] DOI:10.11947/j.AGCS.2018.20170231

DOI

[8]
刘肃艳, 王竞雪, 沈昭宇, 等. 结合线对几何特征及单线描述符约束的直线匹配算法[J]. 武汉大学学报·信息科学版, 2021, DOI:10.13203/J.whugis20210147.

DOI

[ Liu S Y, Wang J X, Shen Z Y, et al. Line matching algorith-m based on pair-wise geometric features and individual line descriptor constraints[J]. Geomatics and Informa-tion Science of Wuhan University, 2021, DOI:10.13203/j.whugis20210147. ]

DOI

[9]
余美. 倾斜立体影像匹配若干问题研究[J]. 测绘学报, 2021, 50(9):1278.

[ Yu M. Research on several issues of oblique stereo image matching[J]. Acta Geodaetica et Cartographica Sinica, 2021, 50(9):1278. ] DOI:10.11947/j.AGCS.2021.20200401

DOI

[10]
Zhang L L, Koch R. An efficient and robust Line segment matching approach based on LBD descriptor and pairwise geometric consistency[J]. Journal of Visual Communicanication and Image Representation, 2013, 24(7):794-805. DOI:10.1016/j.jvcir.2013.05.006

DOI

[11]
王竞雪, 何腕营. 多重约束条件下的LBD描述子与直线段匹配[J]. 中国图象图形学报, 2019, 24(2):237-247.

[ Wang J X, He W Y. Line band descriptors based on multiple constraints and straight-line matching[J]. Journ-al of Image and Graphics, 2019, 24(2):237-247. ] DOI:10.11834/jig.180379

DOI

[12]
王竞雪, 崔昊. 局部点、线仿射不变性约束的近景影像直线段匹配[J]. 地球信息科学学报, 2019, 21(2):137-146.

DOI

[ Wang J X, Cui H. Line segment matching based on local point-line affine invariance constraints for closerange image[J]. Journal of Geo-information Science, 2019, 21(2):137-146. ] DOI:10.12082/dqxxkx.2019.180339

DOI

[13]
张云生, 朱庆, 吴波, 等. 一种基于三角网约束的立体影像线特征多级匹配方法[J]. 武汉大学学报·信息科学版, 2013, 38(5):522-527.

[ Zhang Y S, Zhu Q, Wu B, et al. A hierarchical stereo line matching method based on a triangle constraint[J]. Geomatics and Information Science of Wuhan University, 2013, 38(5):522-527. ] DOI:10.13203/j.whugis2013.05.002

DOI

[14]
Wang Z H, Wu F C, Hu Z Y. MSLD: A robust descriptor for line matching[J]. Pattern Recognition, 2009, 42(5):941-953. DOI:10.1016/j.patcog.2008.08.035

DOI

[15]
Li K, Yao J, Lu X, et al. Hierarchical line matching based on Line-Junction-Line structure descriptor and local homography estimation[J]. Neuro Computing, 2016, 184:207-220. DOI:10.1016/j.neucom.2015.07.137

DOI

[16]
Li K, Yao J, Lu X. Robust line matching based on Ray-Point-Ray structure descriptor[C]. Proceedings of the 12th Asian Conference on Computer Vision, 2014:54-569. DOI:10.1007/978-3-319-16628-5_40

DOI

[17]
Fan B, Wu F C, Hu Z Y. Robust line matching through line-point invariants[J]. Pattern Recognition, 2012, 45(2):794-805. DOI:10.1016/j.patcog.2011.08.004

DOI

[18]
Jia Q, Gao X K, Fan X, et al. Novel coplanar line-points invariants for robust line matching across views[C]. Pr-oceedings of the 14th European Conference on Computer Vision, 2016:599-611. DOI:10.1007/978-3-319-46484-8_36

DOI

[19]
Hundelshausen F V. D-Nets: Beyond patch-based image descriptors[C]. Proceedings of IEEE Conference on Computer Vision and Pattern Recognition, 2012:2941-2948. DOI:10.1109/cvpr.2012.6248022

DOI

[20]
Von G R, Jakubowicz J, Morel J M, et al. LSD: A fast line segment detector[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(4):722-732. DOI:10.1109/iscas51556.2021.9401660

DOI

[21]
Lowe D G. Distinctive image features from scale-invariant keypoints[J]. International Journal of Computer Vison, 2004, 60(2):91-110. DOI:10.1023/b:visi.0000029664.99615.94

DOI

[22]
Li K, Yao J, Lu X, et al. Line segment matching:A benchmark[C]. Proceedings of IEEE Winter Conference on Applications of Computer Vision, 2016:1-9. DOI:10.1109/WACV.2016.7477726

DOI

Options
Outlines

/

〈 〉