EN中文

Journal of Geo-information Science >

2022 , Vol. 24 >Issue 12: 2265 - 2281

DOI: https://doi.org/10.12082/dqxxkx.2022.220163

Review and Prospect: Management, Multi-Scale Transformation and Representation of Geospatial Data

  • WANG Di ,
  • QIAN Haizhong , * ,
  • ZHAO Yuzhe
Expand
  • Institute of Geospatial Information, Information Engineering University, Zhengzhou 450000, China
*QIAN Haizhong, E-mail:

Received date: 2022-04-08

  Revised date: 2022-09-21

  Online published: 2023-02-25

Supported by

National Natural Science Foundation of China(42271463)

Natural Science Foundation for Distinguished Young Scholars of Henan Province(212300410014)

Fold

Abstract

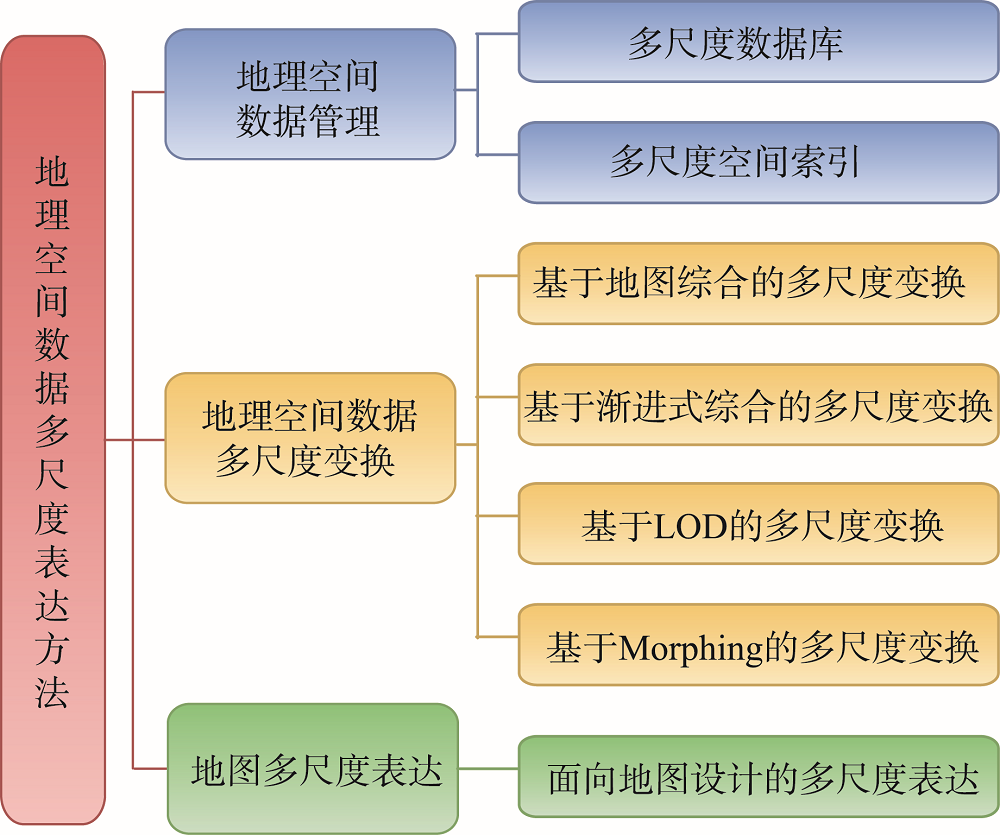
Multi-scale representation is one of the important research contents of geospatial data. This paper summarizes the research status of multi-scale representation of geospatial data from three aspects: geospatial data management, geospatial data scale transformation, and multi-scale representation of the map, and makes a systematic analysis and prospect of current research results. The main conclusions are as follows: ① In terms of multi-scale database and multi-scale spatial index of geospatial data management, three kinds of multi-scale database can provide better data support for multi-scale representation methods, and the hierarchical multi-scale index is the mainstream construction structure for the multi-scale database. However, at present, multi-scale database and multi-scale spatial index still have limited integration and matching ability of data at different levels, and the real-time consistency adjustment ability of data at different scales is also insufficient; ② In terms of the multi-scale transformation of geospatial data, automatic map generalization can be well combined with artificial intelligence technology. But due to the limitation of knowledge acquisition, there is still a long way to achieve automatic map generalization. The relevant achievements of intelligent automatic generalization research are mainly used to assist decision-making now, and the autonomous learning of comprehensive knowledge needs further research. Currently, most of the research is based on a discrete scale transformation model, which is incapable of continuous scale transformation. And due to the lack of a strong quality control mechanism, the results of automatic scaling have great uncertainty; ③ In terms of multi-scale representation of the map, map data types are multi-source, diverse, and flexible to use, and the multi-scale display is highly complex. Currently, the phenomena of hidden geographic information in map visualization need to be further explored. Finally, the future prospect of research on geospatial data presentation is proposed from the aspects of intelligent automatic generalization method, continuous multi-scale representation model, deep learning and cartographic synthesis, and multi-scale representation in the "new" era.

Key words： multi-scale representation; automatic generalization; geospatial data; scale transformation; artificial intelligence; map visualization

Cite this article

WANG Di , QIAN Haizhong , ZHAO Yuzhe . Review and Prospect: Management, Multi-Scale Transformation and Representation of Geospatial Data[J]. Journal of Geo-information Science, 2022 , 24(12) : 2265 -2281 . DOI: 10.12082/dqxxkx.2022.220163

1 引言

地理空间数据的多尺度表达是当今地理信息科学研究的基础前沿核心课题之一[1]。多尺度表达是指在数据库中存储、维护、组织不同尺度下的地理要素，根据用户需求，在其中选取相同地理要素不同详细程度的时间、空间及属性信息，用于多比例尺、多分辨率的空间推理和分析应用。从地理信息科学领域的相关研究技术来看，地图作为地理空间数据多尺度表达的最重要方法之一，自动综合就是多尺度表达的主要手段。自20世纪60年代以来，自动综合的多尺度表达发展一直与计算机技术的发展紧密结合。早期的研究成果聚集在地图目标地几何量测与定量约束，包括符号之间的定量与约束关系、单独要素目标地选取与化简等等；20世纪80年代以来，随着专家系统地提出与发展，学者更多地关注自动综合的规则和知识的获取与应用，研究出了更多复杂算法；90年代以后，进一步发展了地图综合质量评价规则与多种算法的集成模型，出现了商业化的制图综合软件；21世纪以来，随着计算机技术与人工智能技术得飞速发展，自动综合不断汲取着新方法，在当前智能化与大数据时代下，制图综合的智能化是研究的必然趋势。Robinson等[2]认为地图的尺度问题仍然需要得到进一步重视，如何适应与跟上地理空间数据大爆发节奏是目前要解决的难题。
地理空间数据作为地理信息的载体，是客观地理世界的抽象表达。其内容丰富，信息量大而且结构复杂，处理与应用难度大，只有经过合理尺度抽象才能产生利用价值。从数据源角度看，传统地理空间数据类型主要包括地图数据、遥感影像数据、实测数据、地形数据、文本数据、统计数据及多媒体数据等，新型数据源包括点云数据、环境感知数据及网络关联数据等，新型数据的出现，促使传统地理空间数据迈入时空大数据时代。多源海量地理空间数据呈现爆发式增长，数据来源各异、类型不一、尺度不同，通过对其进行相应的尺度变换与表达，可以使人们准确客观地去认识真实的世界；从表达需求方面来看，地理空间数据表达要根据用户需求展现其自身特性及空间关系。其中新型表达需求的相关研究主要包括对全空间中不同尺度多粒度时空对象的模型描述[3]、组织与管理[4]及可视化[5]，以及利用在线自助制图的快速、自助、众源等特点对数据信息进行选取并利用变尺度平衡机制开发相应泛在制图系统[6]等，以进一步满足不同服务对象的个性化需求；从视觉认知角度看，人的视觉信息获取机制要求将多余细节去掉的同时保留主要的相关内容[7]。数字孪生作为新显示环境，其中最具代表性的就是构建知识图谱，即借助知识图谱的概念及相关理论，抽象表达实现多源异构的大规模地理实体的图谱构建[8⇓-10]，由于地理实体具有时空多尺度性，高纬度的复杂性提升了地理实体构建难度[8]，因此现在多数都是针对于网络文本等地理数据或知识进行系统化构建。新型数据结合传统数据构建的时空大数据环境，因其数据来源不同、尺度各异、格式多样，相关尺度变换研究较少，研究主要聚焦在对数据的存储与索引[11]、分类[12]、网络分析[13]、数据挖掘、知识发现等方面。而地图数据作为GIS主要数据源，是一种多尺度图形数据，矢量数据进行多尺度表达时不会随着尺度变化而失真，可以简洁、形象地表达地理信息，长期以来是地图学的研究焦点，研究成果也十分丰富，因此本文主要归纳与总结矢量地理空间数据的多尺度表达方法，文末也对新兴时空大数据的多尺度表达研究进行了展望。
地理空间数据的多尺度表达模型与方法很多，依据GIS中对地理空间数据从获取到呈现的步骤，即数据存储与管理、计算与分析及可视化显示与描述等功能序列，分别按地理空间数据管理、地理空间数据多尺度变换以及地图多尺度表达3个方面的多尺度表达方法进行系统性梳理和归纳（图1）。总结地理空间数据多尺度表达的研究成果，并展望其发展前景。
图1 地理空间数据多尺度表达

Fig. 1 Multi-scale representation of geospatial data

2 地理空间数据管理

面对多源、海量、多尺度的各类传统与新类型数据源，地理空间数据管理主要解决存储与索引问题，多尺度数据库地建立可满足对地理空间数据的多尺度存储与集成管理；多尺度空间索引方法可满足对不同尺度地理空间数据地查询与获取。因此，从多尺度数据库建立和多尺度空间索引方法2个方面进行阐述。

2.1 多尺度数据库

多尺度数据库MSDB(Multiple Scale Database)是一种维护和管理同一地理客体在几何、拓扑结构和属性方面的不同比例尺表达形式的数据库。
艾廷华等[14]提出，构建多尺度数据库需要解决的问题有：比例尺变化粒度适宜、数据容量最小化、兼容考虑语义特征、操作响应速度实时、横向数据表达一致。Alessandro Cecconi等[15]认为制图综合的需求能够为多尺度数据库设计提供参考，包括细节层次模型（LOD）的生成、多尺度数据库中LOD的应用限定以及不同LOD变换的综合算子等因素[16]。而在逻辑上，李霖等[17]提出3种方法来建立多尺度数据库，总结为多库多版本数据库、一库多版本数据库和一库一版本数据库。
多尺度数据库的建立对数据传输方式、自适应的空间可视化以及横向一致性匹配等操作有重要的作用，能够增强不同数据的集成匹配能力，实时地对不同尺度的数据进行一致性调整[18]；同时能够辅助空间认知中从粗到细的信息认知，尽量减少大的跳跃，较好地满足了思维连续性的需求。

2.2 多尺度空间索引

多尺度数据库中一库多版本的模式是目前实现的比较实际的策略，层次树数据结构是其实现的先决条件。国内外许多学者依据用户不同需求提出了相应多尺度空间索引相关技术，总结如表1所示。
表1 多尺度空间索引方法

Tab. 1 Multi-Scale Spatial index method

索引方法 优点 缺点
DAG[19] 不同层次结构表示同一对象的特征可以被链接起来 各尺度空间对象不能自动地彼此相连;生成层次并建立链接的过程复杂
R-Tree[20] 平均查找性能高
 插入和删除节点效率低
Reactive Tree[21-22] 优先保留重要性高的实体，舍去另一部分 是一个非平衡树，查询性能不高；只进行选取操作
GAP Tree[22⇓-24] 可实现多比例尺地图的无缝动态显示；扩展到支持聚合、合并等操作；转换为全拓扑结构 构建过程中拓扑关系维护难度大；是不平衡树，检索耗时较长
Multiple R-Tree[22,25] 可对空间数据进行选取、化简、合并等多种操作；可检索不同尺度需求的数据 除选取操作外的其他综合操作结果中，数据冗余量较大；对制图综合的要求高，需较多人为干预
Z-Value[22,26] 冗余量小；维护量少；算法效率高
 对于复杂的地理数据，索引效果不理想
多尺度金字塔数据结构[27] 基于线性链金字塔和线性四叉树实现，可针对不同应用合并新的算法 不同层次特征间语义信息不一致，降低多尺度特征表示的能力
树状层次结构侧重建立多级尺度目标间、上下尺度之间的关联关系，以及目标层次的尺度划分。除层次化数据结构，还有一些从其他角度建立的多尺度数据模型分类，如面向对象的数据结构、基于尺度依赖的空间数据模型等。针对多数据结构仅面对单一地理要素的缺点，基于关系描述的面向实体-面向对象的整体数据模型更注重整体的特征变化等。

3 地理空间数据多尺度变换

在地理空间数据多尺度变换中，分别就基于地图自动综合、基于渐进式综合、基于LOD以及基于Morphing的多尺度表达方法进行总结。地理空间数据多尺度变换主要应用到综合技术和计算机图像学技术。其中综合技术主要包括地图综合和渐进式综合，计算机图像学技术主要包括LOD方法和Morphing方法。地图综合是地理空间数据多尺度表达的核心与关键，是实现地理空间数据多尺度表达的主要途径，系列比例尺地图的多尺度表达主要依托地图综合的方法进行。渐进式综合作为地理空间数据的多尺度表达方法之一，侧重表达近似连续的综合方法。由于地图综合受到地图用途、地图比例尺、制图区域地理特点及地图符号设计等诸多因素影响，因此为满足数据分析与显示的需求，使用LOD方法，采用不同详细程度的表达模型来表示同一对象，同时可为多尺度数据库设计提供参考。区别于传统地图综合技术只受一端控制的尺度变换，Morphing方法则是针对2个相邻的表达，通过关键尺度内插导出中间状态的数据，为地理空间数据的多尺度表达提供了多角度的变换效果。因此，主要从基于地图综合、基于渐进式综合、基于LOD与基于Morphing的多尺度变换4个方面进行阐述。

3.1 基于地图综合的多尺度变换

王家耀院士[28]在2001年提出了空间数据多尺度表达的研究框架（图2），包括3个层次：基本比例尺空间数据库，空间数据图层的定义工具，空间数据的自动综合。
图2 空间数据多尺度表达的基本框架[28]

Fig. 2 A basic framework for multi-scale representation of spatial data

Grünreich[29]提出将自动综合分为模型综合与制图综合。其中模型综合是根据目标模型进行综合变换的过程，要解决的基本问题包括：数据内容的取舍、属性的改变及空间位置的改变[30]。制图综合是采用选取、化简、概括等多种综合算法，在图层基础上，对地图内容随比例尺变化过程中的增减进行综合变换，实际上是为了可视化图形的输出而进行的综合工作，要解决的基本问题包括：要素选取、图形化简及对要素空间冲突的控制[30]。Schuurman[31]等从多个方面分析并总结了模型综合与制图综合的差别，如表2所示。
表2 模型综合与制图综合特点[31]

Tab. 2 Characteristics of model and cartographic generalization

模型综合 制图综合
可视化 不需要 核心内容
知识形式化 可以显式描述 只可隐含描述
聚合 分级 符号化
可读性 不考虑 核心内容
过程 基于规则算法 半规则/基于经验
滤波 统计学 艺术性/取决于尺度
二者并不是相互独立的，相反，在综合时，利用模型综合从数据中提取所需尺度地理空间数据的核心内容，再根据需求进行地图内容可视化，使地图综合的应用范围更广，针对性更强。
地图综合历经了由客观向定量化、模型化、算法化、系统化、智能化等发展历程，智能化综合之前可称为传统综合。智能化综合与传统综合的主要区别在于，智能化综合能够让计算机自主学习并模拟制图专家地图综合抽象、概括思维的理论、方法和技术，具有创造性，可解决单纯数学方法难以直接解决的问题。在传统综合方法不断被推进的同时，智能化综合方法也不断涌现。下文分别对传统和智能化地图自动综合方法研究现状进行梳理。

3.1.1 传统地图自动综合方法

（1）面向信息的综合方法
面向信息的自动综合基本思路是在原始地图上先找出信息密度太大并且难以保证地图缩小后的视觉易读性的位置，通过在该处改变制图目标，使制图目标概率增加，从而使信息量减少[18]。典型的算法有Douglas-Peucker算法[32]和开方根模型[33]，其中DP算法针对要素细节进行综合，在保留特征点的同时进行整体压缩，但化简结果过于生硬，容易产生尖角；开方根模型针对要素数量进行综合，主要用于要素选取，但没有考虑地理要素密度分布变换。
（2）分形综合方法
分形理论的核心是自相似性，也就是局部与局部、局部与整体之间在形态、时间和空间等多个维度具有统计意义上的自相似性[34]。通过分形综合方法，使不同比例尺间同一地理要素相似性最高，将曲线长度与空间尺度变换模型定量化。
（3）小波分析综合方法
小波分析在数学中应用广泛，同时，小波分析可以随着不同频率信号在时域、频域取样的疏密情况进行自动调节，能够在任意尺度下观察信号或图像的细节，这些都为地图自动综合提供了思路[35]。小波分析方法能够有效分析和处理多尺度、多层次、多分辨率的问题[36]。小波分析作为一种尺度变换方法，在DEM等数据的尺度上推及线状目标的综合中应用较广泛。
（4）数学形态学综合方法
数学形态学主要在几何代数的基础上分析要素几何形状，利用集合论定量描述几何结构的数学方法。数学形态学综合主要应用于二值图像处理问题中，包括根据栅格综合算法对面要素多边形进行合并与化简等，被广泛应用于模式识别领域。
（5）Delaunay三角网模型
Delaunay三角网模型中，所有生成的三角网中任意一个三角形的顶点与其他三角形不存在包含关系。在地图自动综合中主要应用于对矢量模式下多边形的化简、选取、图形等级变换、合并、夸大、位移等操作。
传统地图自动综合方法（表3）中，对建立精确模型的单个制图目标选取效果较好，适用性较强。但对于周围环境复杂、考虑因素较多的综合中，适用性较弱。
表3 传统自动综合方法

Tab. 3 Traditional automatic generalization method

方法 优点 缺点 应用
面向信息的自动综合方法[18] 综合结果直观，综合目标明确 偏重于整体的研究，对单一目标设计较少 基于DP算法的线要素全自动化简[38]、基于三元弯曲组的线化简[39]、建立方根规律扩展模型[40]等
分形综合方法 适合描述线状特征，在尺度变换过程中能够帮助实现统一要素连续的自适应变换 分形自相似性仅存在于一定尺度阈值之内，应用限制较大 在地形模拟中的具体应用[41]、基于分形尺度依赖性的信息空间尺度模型[42]、运用分形理论建立地理信息分维扩展模型[43]、提出基于分形理论的地理空间要素多尺度表达模型[44-45]等
小波分析综合方法 将多尺度的分解信号融合在一起，保留原数据信号的结构特征 处理二维图像时有较大的局限性 小波分析在线要素自动综合中的应用[46]、利用小波分析对DEM数据进行自动综合[47]等
数学形态学综合方法 计算方便，设计灵活，快捷，容易控制 对图像边界噪声较敏感 在居民地街区合并中的应用[48]、对外围轮廓的化简[49]等
Delaunay三角网模型 数据结构简单，冗余度小，存储效率高，易于更新 算法实现较复杂和困难 对面状要素进行综合[50-51]、提出同名道路要素匹配方法[52]、对海岸线协同化简综合[37]等

3.1.2 智能化地图自动综合方法

（1）基于知识的综合方法
由于地图综合受人工干预较强，所以不同学者将制图专家的经验知识进行总结并转化为计算机可识别形式的知识，进而实现自动综合技术。翟仁建等[53]在分析河系自身特点并提取河流规则性知识的基础上，提出了河流自动选取模型；刘春等[54]基于知识库制定了水系要素制图的知识规则；还有学者根据居民地的面积、重要性、标志性等对其进行形式化表示，对居民地进行综合[55]。
专家系统自动综合就是将人类制图经验知识存储在专家系统中，来解决不能单纯用数学模型解决的自动综合问题。张文星等[56]早期就人工智能及专家系统与制图综合的关系进行了探讨，孙群[57]则就专家系统在制图综合领域的应用进行了分析，王家耀等[58]研究设计了制图综合的专家系统工具CGES，运用制图专家与制图规范的知识与经验，将各类知识、模型与算法整合到系统中并进行应用。专家系统的基础是符号推理，在处理以数值为基础的空间数据问题时，一般知识规则会显得能力不足；其次，专家知识和经验带有不确定性与模糊性，很难直接在计算机中通过模型或数学方法进行量化描述。所以，专家系统自动综合方法还不能完全解决地图自动综合。
（2）基于Agent的综合方法
Agent即智能体，具有主动性、通信性、移动性、自学习性、协调工作能力等特性，因其能够模仿人类的部分思维过程，因此在制图综合的应用中，可以作为模仿综合专家思维过程的一条途径[59]。
多名学者[60⇓⇓-63]分别基于Agent提出了CartCom模型（Cartographic generalisation with Communicating Agents）、GAEL模型（for Generali-sation based on Agent and ELasticity）和DIOGEN模型以及线要素化简模型。国内相关研究中，钱海忠等[64]提出了ABTM模型（Agent Based TIN Model, ABTM），一种建筑物自动合并新算法；舒方国[65]采用Agent技术实现了等高线与河流的协同综合。然而在综合过程中，计算机自主运用知识进行智能辅助决策的作用没有有效发挥，因此，使用Agent技术距离期待的制图综合智能化要求还有不小的距离。
（3）基于机器学习的综合方法
地图自动综合发展的一个重要瓶颈就是制图者经验知识很难形式化[66]。随着机器学习技术的发展，很多学者开始将机器学习的方法引入到地图自动综合中。包括神经网络、朴素贝叶斯、决策树、SVM（支持向量机）等方法（表4）。深度学习作为机器学习深层次发展，具有更深的层次、更复杂的结构和更强的学习能力[67]。其目的在于建立并模拟人脑进行分析学习的神经网络。基于深度学习的智能化地图综合研究主要集中在地图综合知识获取和地图综合算子研究，处于智能化地图综合研究的起步阶段，因此将一些相对成熟的深度学习模型（卷积神经网络CNN、图卷积神经网络GNN、循环神经网络RNN、生成对抗网络GAN）列入神经网络的研究中一起讨论。
表4 基于机器学习的自动综合方法

Tab. 4 Automatic generalization method based on machine learning

方法 优点 缺点 应用
神经网络 在约束条件下，能表现出更好地合理性和对约束条件的适应能力 对成组等高线的综合、地物选取数量和位移的计算有一定局限性；过程缺乏透明性 利用GCNN对建筑物分类[68]、采用人工神经网络获取自动制图综合知识[69]、利用SOM神经网络实现识别道路结构和居民地选取[70-71]、结合BP神经网络实现对街道选取[72]、借助U-net全卷积神经网络对建筑物进行综合[73]、利用CNN卷积神经网络对立交桥进行识别[74]、利用CNN与U-net从道路网中提取公路路口[75]、利用GCN识别道路网空间分布模式[76]等
朴素贝叶斯 逻辑简单，易于实现；效率高；性能稳定，健壮性较好 分类决策存在一定的错误率；对输入数据的表达形式很敏感 对树状河系主、支流识别分级[77]等
决策树 构建成本较低；可移植性强；具备升级和完善能力 训练数据时容易出现较复杂结构，需进行大量的过拟合 利用C4.5决策树算法评价建筑物排列质量[78]、采用C5.0决策树算法进一步指导同类居民地的自动综合[79]
支持向量机 无需人为操作和干预，不需要选择特定的综合算法，化简效率高；分类效果较好 解决多分类问题存在困难；对确实数据敏感，对参数和核函数的选择敏感 提出一种新的线化简方法[80]
（4）基于智能优化算法的综合方法
在地图综合过程中常需要进行寻优处理，智能化的方法被广泛应用于自动综合中。其中常用方法包括遗传算法（Genetic Algorithm, GA）、案例类比及案例归纳推理、模拟退火、Rough集理论、人工蜂群算法等。
遗传算法是通过模拟自然进化过程搜索最优解的方法。基于遗传算法的自动综合研究包括提出解决随尺度变换而产生的要素压盖问题[81]、研究地图标记配置以及要素选取等问题[82]等。该方法稳定性强、算法灵活、具有可扩展性，结果接近最优解，但仍存在效率相对较低、且容易出现过早收敛等问题。
案例推理是将定量分析和定性分析相结合的方法，具有动态知识库和增量学习的特点[83]。基于案例推理法的自动综合相关研究包括基于案例的建筑物要素分类及选取办法[84-85]、基于案例推理的居民地选取方法[86]、提出智能化专题制图的案例[87]、利用本体组织案例进行知识推理的道路网选取方法[88]等。基于案例推理的自动综合研究具有解决专家系统获取知识困难的瓶颈，成长性、兼容性强的优点，但仍存在容易出现噪声和冲突、部分结果需要人工参与决策等问题，相关应用还有待进一步研究。
随着计算机技术的不断发展，其他思路的人工智能算法也不断地被引入自动综合中。如基于模拟退火算法的类地图可视化设计[89]、Rough集理论[90-91]等。但受人工智能算法本身的限制，目前借助人工智能方法实现真正的智能化综合，仍然任重道远[92]，但可以肯定的是，在未来，人工智能方法在自动综合的解决方案中会扮演越来越重要的角色。

3.2 基于渐进式综合的多尺度变换

郭庆胜[93]提出渐进式综合概念，主要思想是将地图综合理解为图形的连续抽象变化，让其在视觉上循序变化。即把大跨度的地图综合问题转换为小跨度的图形简化问题。
渐进式地图的基础算法主要包括：空间目标的渐进式图形简化、空间目标的渐进式选取或删除、空间目标的降维或典型化、空间目标聚合等[94]，如表5所示。
表5 渐进式综合方法

Tab. 5 Progressive generalization method

思想 应用
渐进式曲线化简 考虑多方面约束条件的从局部到整体的综合方法 道路网示意性地图的渐进式综合方法[95]、基于弯曲海岸线的渐进式化简方法[96]、基于三角网的建筑物渐进式化简方法[97]、新的渐进式多边形曲线化简算法[98]等
渐进式选取或删除 针对重要程度相同的目标，采用渐进式选取或删除方法控制 利用渐进式方法对街道进行选取[71,99]等
空间目标降维和典型化 当空间目标抽象到一定程度时，其几何维度会发生变化，或用典型的空间模式来描述该目标群 建筑物群渐进式典型化方法、直线排列建筑物群的渐进式典型化方法[100-101]；基于Mesh网格化简的渐进式典型化方法[102]等
空间目标聚合 一个包含多个空间目标的复杂面目标逐渐减少其复杂程度，最后聚合成一个简单的面 郭庆胜等[103]提出的图斑合并的渐进式方法

3.3 基于LOD的多尺度变换

细节层次模型（LOD）是对于地理要素，使用不同细节层次方法得到的一组模型，经常用于计算机图形的实时三维显示。在GIS中，由于往往同时具备几个不同尺度的数据，且每个尺度的数据再现时又可以呈现出更多不同的尺度，因此产生了使用LOD技术的概念。
从变换方式不同的角度来看，LOD尺度变换可以分为几何特征级、目标级和复合型。其中，几何特征级LOD尺度变换主要面向单个要素，目标级LOD尺度变换则面向完整的地理目标对象。从LOD模型在多尺度表达中的见面对象与方法不同的角度来看，可以分为离散LOD模型、连续LOD模型和多分辨率模型[104]。
依据LOD变换的思想，建立了不规则多边形的凸壳层次化剖分和建筑物多边形的矩形层次化剖分模型[105]，提出了一种地理信息语义表达以及相似性的度量模型[106]，提出基于LOD的数据表达模式[107]，利用LOD对三维地物模型进行多尺度表达[108]等。
总的来说，基于LOD模型的尺度变换与表达在实际应用中，尺度变化范围有限，一般适用于独立目标的形态从复杂到简单的表达，目标复合产生的大跨度尺度变换应用比较困难。

3.4 基于Morphing的多尺度变换

Morphing尺度变换是计算机图像学中几何形状的融合技术，将这种思想运用到空间数据的尺度变换与表达中，其基本思想是将输入的2个确定的形体通过融合内插得到新的几何形体，通过调节 2个输入形体的各自控制作用权重，得到不同的输出几何形体。在具体流程上，需先建立同名实体在不同尺度下的对应匹配关系，再生成中间尺度表达。
在Morphing尺度变换思想的基础上，提出了河网的Morphing多尺度变换方法[109]，面状居民地Morphing变换方法[110⇓-112]，线状要素Morphing变换方法[113⇓-115]，基于Morphing思想的SCM-HI模型[116]等。
Morphing尺度变换下输出的新尺度表达受两端原始尺度表达的控制，进而内插出中间表达，与传统地图综合技术只受一端控制的尺度变换相比，Morphing尺度变换效果要好一些。但Morphing的结果主要受到匹配精度的影响，并且Morphing的 2个跨越尺度不能太大，否则容易出现较明显的模糊线性。同时，2个表达需要有相似性，具有一定的局限性。
此外，相关的尺度变换方法还有很多，如傅里叶变换[117-118]、聚类[119]、分形插值法[120]及克里金法[121]等。

4 地图多尺度表达

在地理空间数据可视化中，主要对面向地图设计的多尺度表达方法进行讨论。地图作为地理空间数据最重要的多尺度可视化表达方式之一，可以帮助用户更好的理解并量化地理空间关系、揭示地理空间分布规律。随着科技的不断发展，电子地图的应用已占据主流，地图设计贯穿整个地图制图工作，包括地图内容选取、地图综合原则和显示规则确定、地图表示方法和符号设计、地图的模型设计以及地图图面设计和整饰等。不针对空间数据本身进行尺度变换而仅进行分辨率或者比例缩放的情况下依然可以实现部分地理空间数据的多尺度表达，即基于地图设计的多尺度表达方法。区别于地图自动综合以图形的形状改变为核心的多尺度表达，面向地图设计的多尺度表达更多的以地图设计为中心，在不同尺度上进行统一规则的表达模型的建立。
早期Frank等[122]提出，在不借助制图综合技术的情况下，对地图要素和符号进行显示上的改变来实现部分多尺度显示的要求。之后较为典型的有ScaleMaster[123]，一种辅助多尺度地图设计的工具，在此基础上不同学者开展了一系列相关研究与扩展，如Suba[124]的多尺度地图设计系统、Grobe等[125]提出的多尺度地图显示规则等。徐丰等[126]根据地图符号视觉参量设计了不确定的分级表达模型（图3）。Suba等[127-128]将道路同时表示为面状与线状要素，在尺度变换中使道路网结合面状要素的综合，保留更多的道路网络连接情况，使整体地图的显示质量更加符合用户需求。Dumont等[129]通过对16个现有地图的多比例尺地图范例进行分析，总结建筑物和道路的多尺度显示办法。俞童[130]及杨敏[131]分别基于兴趣点数据提出一种顾及用户兴趣的矢量地图多尺度表达方法和面向城市设施POI数据的多尺度可视化方法。随着电子地图的出现与发展，在电子地图模型设计和符号设计多尺度表达方面的相关研究逐渐增多，包括对电子地图多尺度表达概念的提出与模型设计[16]、导航电子地图的自适应多尺度表达的概念与模型设计[132]、基于地图视觉感受和用户实际需求的网络地图多尺度表达设计[133]、依据地图符号学理论建立世界电子地图多尺度表达分级体系[134]等。地图形式发展多样化，各类地图多尺度表达形式不一，如三维地图主要对全球尺度、国家尺度、城市宏观尺度的场景进行可视化研究[135]，旨从地图设计的角度提高地图的视觉信息提取率与有效性[136]，噪声地图则在不同地图等级下设立相应细节层次的符号尺寸和定位排列方式进行多尺度地图展示[137]。
图3 空间数据多尺度表达的可视化视觉变量[126]

Fig. 3 Visual variables of multi-scale representation of spatial data

可以发现，在面向地图设计的空间数据多尺度表达研究中，在已经建立的多尺度数据库上建立表达模型与方法，使地图在尺度变换过程中更加连续与流畅。面向地图设计的多尺度显示模型早期往往忽略自动综合的操作，且涉及的数据源较为单一，目前研究的内容已经从单纯的单一设计规则逐渐过渡到与自动综合等相关的算法建立融合，如贾奋励等[138]提出多尺度地图设计模型，主要包括对多尺度算子的设计、多尺度地图设计模型及可视化方法，结合地图表达相关评价体系来制定规则，建立相关的地理空间多尺度表达模型等。

5 评述与展望

5.1 评述

纵观已有研究，不同学者针对不同多尺度数据库建立、地理空间数据多尺度变换、面向地图设计的多尺度表达等方面对地理空间数据多尺度表达方法开展了大量理论和案例研究。这些研究对于揭示地理空间数据的多尺度管理、转换、表达等具有启发和指导意义。然而，由于地理空间数据多尺度表达方法本身的复杂性以及涉及学科和领域颇多，并且一直没有完整清晰的脉络，目前仍存在一些问题：
（1）多尺度数据库与多尺度空间索引
多尺度数据库的构建与尺度变换和尺度表达息息相关。多尺度的数据是人们空间认知中重要的信息导航，在多尺度表达中能够帮助人们进行大范围到局部信息内容的动态表达。多库多版本、一库多版本和一库一版本3种数据库能够帮助多尺度表达方法构建较好的数据基础和支撑。同时，层次化的多尺度空间索引也是主流的多尺度数据库构建结构。但目前多尺度数据库与多尺度空间索引方法还没有解决不同层次数据的集成与匹配能力，特别在数据更新方面，实时的对不同尺度数据进行一致性调整特别是级联更新的能力还不足。
（2）地理空间数据多尺度变换
目前可使用的地理空间数据的尺度变换方法和变换模式很多，但多数研究都是基于单一的变换模式，由于不同尺度变换各有优缺点，单一的变换模式不足以支撑目前所需，并且连续尺度变换还达不到理想效果。尺度变换缺乏完善的质量控制机制[93]，现有的尺度变换方法过多关注操作本身，而忽略了对综合对象的分析，导致自动尺度变换的结果存在很大的不确定性。尺度变换引起的信息量变化缺乏系统研究[139]，且在地理空间数据尺度变换方面还缺乏较为完善的理论技术体系。而自动综合作为地理空间数据多尺度表达的核心研究方向，从传统的研究方法到如今以各类人工智能算法为基础的智能化方法。站在多学科的角度来看，自动综合因其复杂性与不确定性，能够很好的和人工智能技术相结合，利用人工智能技术处理当今海量数据的自动综合早已成为主流研究方向。但当前智能化的自动综合相关成果大多只能用于辅助决策，还需要对综合知识的表现形式和自主学习进行深入研究。
（3）面向地图设计的多尺度表达
相比传统纸质地图，多尺度地图极大地扩展了地图的潜在用途。为满足用户对不同详细程度、不同时间跨度及不同空间格局的地图的需求，需在地图内容、样式、符号色彩等设计方面视情况增加或减少地图载负量。尽管目前面向地图设计的多尺度显示模型已与地图自动综合算法建立融合，但由于地图数据类型多源、种类丰富且使用灵活，多尺度显示的复杂性较高，因此，面向地图设计的多尺度表达需进一步探索。

5.2 展望

在当前的研究背景下，本文从以下4个方面对地理空间数据的多尺度表达进行展望：
（1）智能化自动综合方法
在自动综合方向上，由于自动综合的操作大多具有创造性，单纯数学方法难以直接解决。许多新的技术方法在处理大数据、自然语言、空间拓扑关系等领域都有了新的进展，自动综合的智能化研究方向将结合具体综合任务的需求，整合其他学科领域的知识与经验。在研究上除了具体算法改进，将更加的宏观与动态化，自动综合智能化过程模型会更加完善。同时，通用自动综合系统依然实现困难，人机交互仍是主流，但是结合人工智能的自动综合决策辅助系统将在前人基础上将得以完善，支持决策。
（2）连续多尺度表达模型
目前的多尺度表达模型在适用性方面，还很难适应空间数据的多数据源特征，仅针对一种或者几种空间数据，空间数据的尺度变换与表达方法将能够根据数据的空间结构等特征进行贴合特征的变换方法与表达方法的选择。同时，地理空间数据的多尺度表达的最终目的是在不同尺度的数据支撑下，动态的调整与显示用户所需要的内容。未来的多尺度表达模型将更接近连续比例尺表达这一目标。
（3）深度学习与制图综合
机器学习与制图综合的结合作为新的发展趋势，其中深度学习方法在地图制图领域的应用有很好的发展前景[140]。如今面对海量的地理空间数据，深度学习方法善于发掘多维数据中错综复杂的关系，并且利用深度学习方法可以完全实现由机器对大量尺度表达的案例进行训练，从一个新的角度为自动综合提供了新思路与技术。应用深度学习方法，制图综合的知识获取与表达研究将会继续得到进一步发展，通过在自动制图综合中不断调整与完善，结合GIS的实时多要素自动制图综合模型也会出现，以期在满足多个制图规则约束的条件下得到较好的表达效果。
（4）“新”时代多尺度表达
随着智能化、互联网、云技术等新兴技术的发展，时空大数据的时代已经到来，围绕时空大数据多尺度存储管理、智能综合、多尺度数据库自动生成、级联更新、分析挖掘及可视化等功能进行研究，将会给地理信息科学理论、技术与产业发展注入新活力。泛在制图作为时空大数据地图表达的主要方式，成为目前和未来一段时期地理信息产业发展的重要方向之一[6]，因此，建立与探索新型多粒度与多尺度数据模型、管理与分析、可视化及平台研制等技术，会有效推动我国空间信息技术以及未来智慧城市的发展与建设。孪生空间拥有多尺度特性，随着尺度增大，孪生空间结构与关系也更加复杂，因此建立不同尺度不同规模孪生空间之间的联系，寻找贯通各尺度孪生空间的关系仍有待进一步研究[141]。

References

Publishing order | Descend order by publishing year | Descend order by cited within
[1]
孙庆先, 李茂堂, 路京选, 等. 地理空间数据的尺度问题及其研究进展[J]. 地理与地理信息科学, 2007, 23(4):53-56,80.

[ Sun Q X, Li M T, Lu J X, et al. Scale issue and its research progress of geospatial data[J]. Geography and Geo-information Science, 2007, 23(4):53-56,80. ] DOI:10.3969/j.issn.1672-0504.2007.04.014

DOI

[2]
Robinson A C, Demšar U, Moore A B, et al. Geospatial big data and cartography: Research challenges and opportunities for making maps that matter[J]. International Journal of Cartography, 2017, 3(sup1):32-60. DOI:10.1080/23729333.2016.1278151

DOI

[3]
曾梦熊, 华一新, 张江水, 等. 多粒度时空对象动态行为表达模型与方法研究[J]. 地球信息科学学报, 2021, 23(1):104-112.

DOI

[ Zeng M X, Hua Y X, Zhang J S, et al. Research on dynamic behavior expression model and method of multi-granularity spatio-temporal objects[J]. Journal of Geo-information Science, 2021, 23(1):104-112. ] DOI:10.12082/dqxxkx.2021.200420

DOI

[4]
华一新, 张江水, 曹一冰. 基于时空域的全空间数字世界时空对象组织与管理研究[J]. 地球信息科学学报, 2021, 23(1):76-83.

DOI

[ Hua Y X, Zhang J S, Cao Y B. Research on organization and management of spatio-temporal objects in pan-spatial digital world based on spatio-temporal domain[J]. Journal of Geo-information Science, 2021, 23(1):76-83. ] DOI:10.12082/dqxxkx.2021.200417

DOI

[5]
曹一冰, 张江水, 华一新, 等. 全空间时空对象可视化工具的设计与实现[J]. 测绘科学技术学报, 2021, 38(2):173-180.

[ Cao Y B, Zhang J S, Hua Y X, et al. Design and implementation of the visualization tool for spatio-temporal objects in pan-spatial information system[J]. Journal of Geomatics Science and Technology, 2021, 38(2):173-180. ]

[6]
李志林, 刘万增, 徐柱, 等. 时空数据地图表达的基本问题与研究进展[J]. 测绘学报, 2021, 50(8):1033-1048.

[ Li Z L, Liu W Z, Xu Z, et al. Cartographic representation of spatio-temporal data: Fundamental issues and research progress[J]. Acta Geodaetica et Cartographica Sinica, 2021, 50(8):1033-1048. ] DOI:10.11947/j.AGCS.2021.20210072

DOI

[7]
高俊. 地理空间数据的可视化[J]. 测绘工程, 2000, 9(3):1-7.

[ Gao J. Visualization in geo-spatial data[J]. Engineering of Surveying and Mapping, 2000, 9(3):1-7. ] DOI:10.19349/j.cnki.issn1006-7949.2000.03.001

DOI

[8]
王志华, 杨晓梅, 周成虎. 面向遥感大数据的地学知识图谱构想[J]. 地球信息科学学报, 2021, 23(1):16-28.

DOI

[ Wang Z H, Yang X M, Zhou C H. Geographic knowledge graph for remote sensing big data[J]. Journal of Geo-information Science, 2021, 23(1):16-28. ] DOI:10.12082/dqxxkx. 2021.200632

DOI

[9]
刘俊楠, 刘海砚, 陈晓慧, 等. 面向多源地理空间数据的知识图谱构建[J]. 地球信息科学学报, 2020, 22(7):1476-1486.

DOI

[ Liu J N, Liu H Y, Chen X H, et al. The construction of knowledge graph towards multi-source geospatial data[J]. Journal of Geo-information Science, 2020, 22(7):1476-1486. ] DOI:10.12082/dqxxkx.2020.190565

DOI

[10]
彭楚骄, 李连营, 郭邦祁, 等. 使用知识图谱推荐专题地图可视化方法[J]. 测绘科学, 2022, 47(6):188-194.

[ Peng C J, Li L Y, Guo B Q, et al. Recommendation of thematic map visualization method using knowledge graph[J]. Science of Surveying and Mapping, 2022, 47(6):188-194. ] DOI:10.16251/j.cnki.1009-2307.2022.06.024

DOI

[11]
赵江洪, 王继伟, 王晏民, 等. 一种新的散乱点云数据多级空间索引[J]. 地球信息科学学报, 2015, 17(12):1450-1455.

DOI

[ Zhao J H, Wang J W, Wang Y M, et al. A new multi-level spatial index of scattered point cloud data[J]. Journal of Geo-information Science, 2015, 17(12):1450-1455. ] DOI:10.3724/SP.J.1047.2015.01450

DOI

[12]
汪文琪, 李宗春, 付永健, 等. 融合点、体素和对象特征的多基元点云分类[J]. 地球信息科学学报, 2022, 24(2):365-377.

DOI

[ Wang W Q, Li Z C, Fu Y J, et al. The multiple primitives classification of point cloud combining point, voxel and object features[J]. Journal of Geo-information Science, 2022, 24(2):365-377. ] DOI:10.12082/dqxxkx.2022.210313

DOI

[13]
张伟丽, 叶信岳, 李栋, 等. 网络关联、空间溢出效应与中国区域经济增长——基于腾讯位置大数据的研究[J]. 地理科学, 2019, 39(9):1371-1377.

DOI

[ Zhang W L, Ye X Y, Li D, et al. Network association, spillover effect and China's regional economic growth based on tencent's location big data[J]. Scientia Geographica Sinica, 2019, 39(9):1371-1377. ] DOI:10.13249/j.cnki.sgs.2019.09.002

DOI

[14]
艾廷华, 成建国. 对空间数据多尺度表达有关问题的思考[J]. 武汉大学学报·信息科学版, 2005, 30(5):377-382.

[ Ai T H, Cheng J G. Key issues of multi-scale representation of spatial data[J]. Geomatics and Information Science of Wuhan University, 2005, 30(5):377-382. ] DOI:10.3969/j.issn.1671-8860.2005.05.001

DOI

[15]
Cecconi A, Weibel R, Barrault M. Improving automated generalisation for on-demand web mapping by multiscale databases[M]//Advances in Spatial Data Handling. Berlin, Heidelberg: Springer Berlin Heidelberg, 2002:515-531. DOI:10.1007/978-3-642-56094-1_38

DOI

[16]
贾奋励. 电子地图多尺度表达的研究与实践[D]. 郑州: 解放军信息工程大学, 2010.

[ Jia F L. Research and practice of electric map multi-scale representation[D]. Zhengzhou: PLA Information Engineering University, 2010. ]

[17]
李霖, 吴凡. 空间数据多尺度表达模型及其可视化[M]. 北京: 科学出版社, 2005.

[ Li L, Wu F. Spatial multi-scale representation model and its visualization[M]. Beijing: Science Press, 2005. ]

[18]
黄勇奇, 赵追. 地理空间数据自动综合方法的研究现状与发展趋势[J]. 测绘科学, 2009, 34(1):17-20,59.

[ Huang Y Q, Zhao Z. Research status and development trend of automatic generalization methods for geographical spatial data[J]. Science of Surveying and Mapping, 2009, 34(1):17-20,59. ] DOI:10.3771/j.issn.1009-2307.2009.01.004

DOI

[19]
Timpf S, Frank A U. A multi-scale DAG for cartographic objects[C]. Proceedings of Autocarto 12. ACM/ASPRS, 1995:157-163.

[20]
邓红艳, 武芳, 翟仁健, 等. 一种用于空间数据多尺度表达的R树索引结构[J]. 计算机学报, 2009, 32(1):177-184.

[ Deng H Y, Wu F, Zhai R J, et al. R-tree index structure for multi-scale representation of spatial data[J]. Chinese Journal of Computers, 2009, 32(1):177-184. ]

DOI

[21]
Oosterom P V. The reactive-tree: A storage structure for a seamless, scaleless geographic database[C]. Autocarto-Conference.Vol.6.ASPRS American Society for Photogrammetry AND, 1991.

[22]
程昌秀. 矢量数据多尺度空间索引方法的研究[J]. 武汉大学学报·信息科学版, 2009, 34(5):597-601.

[ Cheng C X. A multi-scale spatial index method[J]. Geomatics and Information Science of Wuhan University, 2009, 34(5):597-601. ]

[23]
Pan Y Y, Gao H, Lin H, et al. Identification of bacteriophage virion proteins using multinomial Naïve Bayes with g-gap feature tree[J]. International Journal of Molecular Sciences, 2018, 19(6):1779. DOI:10.3390/ijms19061779

DOI

[24]
Van Oosterom P. Variable-scale topological data structures suitable for progressive data transfer: The GAP-face tree and GAP-edge forest[J]. Cartography and Geographic Information Science, 2005, 32(4):331-346.

DOI

[25]
Kwon J H, Yoon Y I. An access method for integrating multi-scale geometric data[M]//Advances in Databases and Information Systems. Berlin, Heidelberg: Springer Berlin Heidelberg, 2002:204-217. DOI:10.1007/3-540-45710-0_17

DOI

[26]
陆桑璐, 周晓方, 陈贵海, 等. 空间信息检索及其数据库概化技术[J]. 软件学报, 2002, 13(8):1534-1539.

[ Lu S L, Zhou X F, Chen G H, et al. Spatial information retrieval and database generalization[J]. Journal of Software, 2002, 13(8):1534-1539. ]

[27]
Meer P, Sher C A, Rosenfeld A. The chain pyramid: Hierarchical contour processing[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1990, 12(4):363-376. DOI:10.1109/34.50622

DOI

[28]
王家耀. 空间信息系统原理[M]. 北京: 科学出版社, 2001.

[ Wang J Y. Principle of spatial information system[M]. Beijing: Science Press, 2001. ]

[29]
Grünreich D. Development of computer-assisted generalization on the basis of cartographic model theory[M]// GIS and Generalization. Boca Raton: CRC Press, 2020:47-55.

[30]
武芳. 空间数据的多尺度表达与自动综合[M]. 北京: 解放军出版社, 2003.

[ Wu F. Multi-scale representation and automatic synthesis of spatial data[M]. Beijing: PLA Press, 2003. ]

[31]
Schuurman N C. Critical GIS: Theorizing an emerging science[D]. Vancouver: University of British Columbia, 2000.

[32]
Douglas D H, Peucker T K. Algorithms for the reduction of the number of points required to represent a digitized line or its caricature[J]. Cartographica: the International Journal for Geographic Information and Geovisualization, 1973, 10(2):112-122. DOI:10.3138/fm57-6770-u75u-7727

DOI

[33]
王殷行, 李白英, 徐泮林. 基于特普费尔公式的制图综合取舍比例探讨[J]. 山东科技大学学报(自然科学版), 2006, 25(1):40-42,46.

[ Wang Y X, Li B Y, Xu P L. Study on the proportion with synthetic acceptance or rejection on cartography based on F.fopfer formula[J]. Journal of Shandong University of Science and Technology (Natural Science), 2006, 25(1):40-42,46. ] DOI:10.16452/j.cnki.sdkjzk.2006.01.011

DOI

[34]
孙庆先, 方涛, 郭达志. 空间数据挖掘中的尺度转换研究[J]. 计算机工程与应用, 2005, 41(16):17-19.

[ Sun Q X, Fang T, Guo D Z. Scale transformation in spatial data mining[J]. Computer Engineering and Applications, 2005, 41(16):17-19. ] DOI:10.3321/j.issn:1002-8331.2005.16.006

DOI

[35]
Balboa J L G, López F J A. Frequency filtering of linear features by means of wavelets. A method and an example[J]. The Cartographic Journal, 2000, 37(1):39-49. DOI:10.1179/caj.2000.37.1.39

DOI

[36]
胡云锋, 徐芝英, 刘越, 等. 地理空间数据的尺度转换[J]. 地球科学进展, 2013, 28(3):297-304.

DOI

[ Hu Y F, Xu Z Y, Liu Y, et al. A review of the scaling issues of geospatial data[J]. Advances in Earth Science, 2013, 28(3):297-304. ] DOI:10.11867/j.issn.1001-8166.2013.03.0297

DOI

[37]
张立华, 唐露露, 贾帅东, 等. 多条海岸线协同化简的层次化三角网分区法[J]. 测绘学报, 2019, 48(4):520-531.

[ Zhang L H, Tang L L, Jia S D, et al. A collaborative simplification method for multiple coastlines based on the hierarchical triangulation network partition[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(4):520-531. ] DOI:10.11947/j.AGCS.2019.20180382

DOI

[38]
王荣, 闫浩文, 禄小敏. Douglas-Peucker算法全自动化的多尺度空间相似关系方法[J]. 地球信息科学学报, 2021, 23(10):1767-1777.

DOI

[ Wang R, Yan H W, Lu X M. Automation of the Douglas-Peucker algorithm based on spatial similarity relations[J]. Journal of Geo-information Science, 2021, 23(10):1767-1777. ] DOI:10.12082/dqxxkx.2021.210016

DOI

[39]
钱海忠, 何海威, 王骁, 等. 采用三元弯曲组划分的线要素化简方法[J]. 武汉大学学报·信息科学版, 2017, 42(8):1096-1103.

[ Qian H Z, He H W, Wang X, et al. Line feature simplification method based on bend group division[J]. Geomatics and Information Science of Wuhan University, 2017, 42(8):1096-1103. ] DOI:10.13203/j.whugis20150239

DOI

[40]
王桥, 吴纪桃. 制图综合方根规律模型的分形扩展[J]. 测绘学报, 1996, 25(2):104-109.

[ Wang Q, Wu J T. Fractal transformation of square root model in cartographic generalization[J]. Acta Geodaetica et Cartographica Sinica, 1996, 25(2):104-109. ]

[41]
Xia Z G, Clarke K C. Approaches to scaling of geo-spatial data[J]. Scale in remote sensing and GIS, 1997:309-360.

[42]
张华国, 黄韦艮. 基于分形的海岸线遥感信息空间尺度研究[J]. 遥感学报, 2006, 10(4):463-468.

[ Zhang H G, Huang W G. Study on spatial scale of shoreline remote sensing information based on fractal theory[J]. Journal of Remote Sensing, 2006, 10(4):463-468. ] DOI:10.3321/j.issn:1007-4619.2006.04.005

DOI

[43]
毋河海. 基于扩展分形的地图信息自动综合研究[J]. 地理科学进展, 2001, 20(S1):14-28.

[ Wu H H. Research on extended-fractal based automatic map generalization[J]. Progress in Geography, 2001, 20(S1):14-28. ] DOI:10.11820/dlkxjz.2001.s1.002

DOI

[44]
Jiang B, Liu X T, Jia T. Scaling of geographic space as a universal rule for map generalization[J]. Annals of the Association of American Geographers, 2013, 103(4):844-855. DOI:10.1080/00045608.2013.765773

DOI

[45]
Jiang B, Yin J J. Ht-index for quantifying the fractal or scaling structure of geographic features[J]. Annals of the Association of American Geographers, 2014, 104(3):530-540. DOI:10.1080/00045608.2013.834239

DOI

[46]
吴纪桃, 王桥. 小波分析在GIS线状数据图形简化中的应用研究[J]. 测绘学报, 2000, 29(1):71-75.

[ Wu J T, Wang Q. A study on automatic cartographic generalization using wavelet analysis in GIS[J]. Acta Geodaetica et Cartographic Sinica, 2000, 29(1):71-75. ]

[47]
刘春, 王家林, 刘大杰. 多尺度小波分析用于DEM网格数据综合[J]. 中国图象图形学报, 2004, 9(3):340-344.

[ Liu C, Wang J L, Liu D J. Generalization of DEM grid data based on multi band wavelet analysis[J]. Journal of Image and Graphics, 2004, 9(3):340-344. ]

[48]
王光霞, 杨培. 数学形态学在居民地街区合并中的应用[J]. 测绘学院学报, 2000, 17(3):201-203,206.

[ Wang G X, Yang P. Application of mathematic morphology in uniting blocks of residential area[J]. Journal of the PLA Institute of Surveying and Mapping, 2000, 17(3):201-203,206. ] DOI:10.3969/j.issn.1673-6338.2000.03.014

DOI

[49]
Su B, Li Z L, Lodwick G, et al. Algebraic models for the aggregation of area features based upon morphological operators[J]. International Journal of Geographical Information Science, 1997, 11(3):233-246. DOI:10.1080/136588197242374

DOI

[50]
艾廷华, 郭仁忠. 支持地图综合的面状目标约束Delaunay三角网剖分[J]. 武汉测绘科技大学学报, 2000, 25(1):35-41.

[ Ai T H, Guo R Z. A constrained Delaunay partitioning of areal objects to support map generalization[J]. Journal of Wuhan Technical University of Surveying and Mapping, 2000, 25(1):35-41. ] DOI:10.13203/j.whugis2000.01.007

DOI

[51]
郭沛沛, 李成名, 殷勇. 建筑物合并的Delaunay三角网分类过滤法[J]. 测绘学报, 2016, 45(8):1001-1007.

[ Guo P P, Li C M, Yin Y. Classification and filtering of constrained Delaunay triangulation for automated building aggregation[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(8):1001-1007. ] DOI:10.11947/j.AGCS.2016.20150587

DOI

[52]
王培, 赵军喜, 崔虎平, 等. 采用道路骨架线stroke的复杂道路匹配方法[J]. 测绘科学技术学报, 2019, 36(1):95-99.

[ Wang P, Zhao J X, Cui H P, et al. Method for complex road matching based on road skeleton line stroke[J]. Journal of Geomatics Science and Technology, 2019, 36(1):95-99. ] DOI:10.3969/j.issn.1673-6338.2019.01.018

DOI

[53]
翟仁健, 武芳, 邓红艳, 等. 基于遗传多目标优化的河流自动选取模型[J]. 中国矿业大学学报, 2006, 35(3):403-408.

[ Zhai R J, Wu F, Deng H Y, et al. Automated elimination of river based on multi-objective optimization using genetic algorithm[J]. Journal of China University of Mining & Technology, 2006, 35(3):403-408. ]

[54]
刘春, 丛爱岩. 基于 “知识规则” 的GIS水系要素制图综合推理[J]. 测绘通报, 1999(9):21-24.

[ Liu C, Cong A Y. Comprehensive reasoning of GIS water system elements mapping based on “knowledge rules”[J]. Bulletin of Surveying and Mapping, 1999(9):21-24. ] DOI:10.3969/j.issn.0494-0911.1999.09.007

DOI

[55]
尹向军, 印洁, 黄志洲, 等. 地理信息数据自动综合知识规则构建——以房屋要素为例[J]. 测绘通报, 2018(12):129-132,147.

[ Yin X J, Yin J, Huang Z Z, et al. Construction of automated generalisation knowledge rules for geographic information data: Taking building elements as an example[J]. Bulletin of Surveying and Mapping, 2018(12):129-132,147. ] DOI:10.13474/j.cnki.11-2246.2018.0398

DOI

[56]
张文星, 张晓春. 地图制图与专家系统[J]. 地图, 1990(4):48-50.

[ Zhang W X, Zhang X C. The expert system of map-making[J]. Map, 1990(4):48-50. ]

[57]
孙群. 专家系统以及它在地图制图领域中的应用[J]. 解放军测绘学院学报, 1992, 9(1):67-73.

[ Sun Q. Expert system and its application in cartography[J]. Journal of the PLA Institute of Surveying and Mapping, 1992, 9(1):67-73. ]

[58]
王家耀, 吴战家, 武芳. 制图综合专家系统工具研究[J]. 解放军测绘学院学报, 1992, 9(4):66-72.

[ Wang J Y, Wu Z J, Wu F. The research on tools of the cartographic generalization expert system[J]. Journal of the PLA Institute of Surveying and Mapping, 1992, 9(4):66-72. ]

[59]
钱海忠, 王家耀. 空间信息系统中的Agent技术[J]. 测绘科学, 2004, 29(1):10-12,16.

[ Qian H Z, Wang J Y. The agent technology used in geo-spatial information system[J]. Science of Surveying and Mapping, 2004, 29(1):10-12,16. ] DOI:10.3771/j.issn.1009-2307.2004.01.003

DOI

[60]
Duchêne C, Ruas A, Cambier C. The CartACom model: Transforming cartographic features into communicating agents for cartographic generalisation[J]. International Journal of Geographical Information Science, 2012, 26(9):1533-1562. DOI:10.1080/13658816.2011.639302

DOI

[61]
Gaffuri J. Field deformation in an agent-based generalisation model: The GAEL model[J]. GI-days, 2007:1-24.

[62]
Guilbert E. Feature‐Driven Generalization of Isobaths on Nautical Charts: A Multi‐Agent System Approach[J]. Transactions in GIS, 2016, 20(1):126-143.

DOI

[63]
Maudet A, Touya G, Duchêne C, et al. DIOGEN, a multi-level oriented model for cartographic generalization[J]. International Journal of Cartography, 2017, 3(1):121-133. DOI:10.1080/23729333.2017.1300997

DOI

[64]
钱海忠, 武芳, 谭笑, 等. 基于ABTM的城市建筑物合并算法[J]. 中国图象图形学报, 2005, 10(10):1224-1233.

[ Qian H Z, Wu F, Tan X, et al. The algorithm for merging city buildings based on ABTM[J]. Journal of Image and Graphics, 2005, 10(10):1224-1233. ] DOI:10.3969/j.issn.1006-8961.2005.10.004

DOI

[65]
舒方国. 基于多Agent的等高线与河流协同综合方法研究[D]. 南京: 南京师范大学, 2012.

[ Shu F G. Collaborative map generalization method of contours and rivers based on multi-agent[D]. Nanjing: Nanjing Normal University, 2012. ]

[66]
张新长, 何显锦, 孙颖, 等. 多尺度空间数据联动更新技术研究现状及展望[J]. 测绘学报, 2022, 51(7):1520-1535.

[ Zhang X C, He X J, Sun Y, et al. Advance and future development of the multi-scale spatial data linkage updating[J]. Acta Geodaetica et Cartographica Sinica, 2022, 51(7):1520-1535. ] DOI:10.11947/j.AGCS.2022.20220095

DOI

[67]
武芳, 杜佳威, 钱海忠, 等. 地图综合智能化研究的发展与思考[J/OL]. 武汉大学学报·信息科学版:1-15[2022-04-30].

[ Wu F, Du J W, Qian H Z, et al. Overview of the research progress and reflections in intelligent map generalization[J/OL]. Geomatics and Information Science of Wuhan University: 1-15[2022-04-30]. ]

[68]
Yan X F, Ai T H, Yang M, et al. A graph convolutional neural network for classification of building patterns using spatial vector data[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2019, 150:259-273. DOI:10.1016/j.isprsjprs.2019.02.010

DOI

[69]
王家耀, 田震. 海图水深综合的人工神经元网络方法[J]. 测绘学报, 1999, 28(4):335-339.

[ Wang J Y, Tian Z. The cartographic generalization of soundings on chart by artificial neural network techniques[J]. Acta Geodaetica et Cartographica Sinica, 1999, 28(4):335-339. ] DOI:10.3321/j.issn:1001-1595.1999.04.011

DOI

[70]
张圆, 李精忠, 帅赟. 使用自组织映射网络识别城市道路主要结构[J]. 测绘与空间地理信息, 2018, 41(10):27-29,34.

[ Zhang Y, Li J Z, Shuai Y. Identifying major structures of urban roads using self-organizing map networks[J]. Geomatics ＆ Spatial Information Technology, 2018, 41(10):27-29,34. ] DOI:10.3969/j.issn.1672-5867.2018.10.009

DOI

[71]
钟吉, 钱海忠, 王骁, 等. 顾及多特征的散列式居民地SOM聚类选取算法[J]. 测绘科学技术学报, 2020, 37(6):643-651.

[ Zhong J, Qian H Z, Wang X, et al. SOM clustering selection algorithm of hash-style settlements considering multiple characters[J]. Journal of Geomatics Science and Technology, 2020, 37(6):643-651. ]

[72]
蔡永香, 郭庆胜. 基于神经网络的街道渐进式选取[J]. 测绘信息与工程, 2008, 33(5):24-26.

[ Cai Y X, Guo Q S. Method for streets progressive selection based on neural network techniques[J]. Journal of Geomatics, 2008, 33(5):24-26. ]

[73]
Sester M, Feng Y, Thiemann F. Building generalization using deep learning[J]. The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2018, XLII-4:565-572. DOI:10.5194/isprs-archives-xlii-4-565-2018

DOI

[74]
何海威, 钱海忠, 谢丽敏, 等. 立交桥识别的CNN卷积神经网络法[J]. 测绘学报, 2018, 47(3):385-395.

[ He H W, Qian H Z, Xie L M, et al. Interchange recognition method based on CNN[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(3):385-395. ] DOI: 10.11947/j.AGCS.2018.20170265

DOI

[75]
Touya G, Lokhat I. Deep learning for enrichment of vector spatial databases: Application to highway interchange[J]. ACM Transactions on Spatial Algorithms and Systems, 2020, 6(3):21. DOI:10.1145/3382080

DOI

[76]
王米琪, 艾廷华, 晏雄锋, 等. 图卷积网络模型识别道路正交网格模式[J]. 武汉大学学报·信息科学版, 2020, 45(12):1960-1969.

[ Wang M Q, Ai T H, Yan X F, et al. Grid pattern recognition in road networks based on graph convolution network model[J]. Geomatics and Information Science of Wuhan University, 2020, 45(12):1960-1969. ] DOI:10.13203/j.whugis20200022

DOI

[77]
段佩祥, 钱海忠, 何海威, 等. 案例支撑下的朴素贝叶斯树状河系自动分级方法[J]. 测绘学报, 2019, 48(8):975-984.

[ Duan P X, Qian H Z, He H W, et al. Naive Bayes-based automatic classification method of tree-like river network supported by cases[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(8):975-984. ] DOI:10.11947/j.AGCS.2019.20180370

DOI

[78]
Cetinkaya S, Basaraner M. Characterisation of building alignments with new measures using C4.5 decision tree algorithm[J]. Geodetski Vestnik, 2014, 58(3):552-567.

DOI

[79]
何海威, 钱海忠, 刘闯, 等. 采用决策树算法进行居民地自动综合[J]. 测绘科学技术学报, 2016, 33(6):623-628.

[ He H W, Qian H Z, Liu C, et al. Auto generalization of settlement by using decision tree algorithm[J]. Journal of Geomatics Science and Technology, 2016, 33(6):623-628. ] DOI:10.3969/j.issn.1673-6338.2016.06.014

DOI

[80]
段佩祥, 钱海忠, 何海威, 等. 基于支持向量机的线化简方法[J]. 武汉大学学报·信息科学版, 2020, 45(5):744-752,783.

[ Duan P X, Qian H Z, He H W, et al. A line simplification method based on support vector machine[J]. Geomatics and Information Science of Wuhan University, 2020, 45(5):744-752,783. ] DOI:10.13203/j.whugis20180434

DOI

[81]
Wilson I D, Ware J M, Ware J A. Reducing graphic conflict in scale reduced maps using a genetic algorithm[C]// Workshop on progress in automated map generalisation, commission on map generalisation, Paris, France, 2003.

[82]
武芳, 邓红艳. 基于遗传算法的线要素自动化简模型[J]. 测绘学报, 2003, 32(4):349-355.

[ Wu F, Deng H Y. Using genetic algorithms for solving problems in automated line simplification[J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(4):349-355. ] DOI:10.3321/j.issn:1001-1595.2003.04.013

DOI

[83]
曹占吉. 一种集成的案例推理方法研究及其应用[D]. 大连: 大连理工大学, 2014.

[ Cao Z J. A study on hybrid case based reasoning method and its application[D]. Dalian: Dalian University of Technology, 2014. ]

[84]
Mustiere S. Cartographic generalization of roads in a local and adaptive approach: A knowledge acquistion problem[J]. International Journal of Geographical Information Science, 2005, 19(8/9):937-955. DOI:10.1080/13658810509161245

DOI

[85]
Steiniger S, Taillandier P, Weibel R. Utilising urban context recognition and machine learning to improve the generalisation of buildings[J]. International Journal of Geographical Information Science, 2010, 24(2):253-282.

DOI

[86]
谢丽敏, 钱海忠, 何海威, 等. 基于案例推理的居民地选取方法[J]. 测绘学报, 2017, 46(11):1910-1918.

[ Xie L M, Qian H Z, He H W, et al. A habitation selection method by using case-based reasoning[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(11):1910-1918. ] DOI:10.11947/j.AGCS.2017.20170061

DOI

[87]
李洪省, 王英杰, 余卓渊, 等. 基于案例推理的统计地图表示方法智能选取中的应用[J]. 地球信息科学学报, 2009, 11(6):819-825.

[ Li H S, Wang Y J, Yu Z Y, et al. Applying case-based reasoning techniques in selection of representation method of statistic map[J]. Journal of Geo-information Science, 2009, 11(6):819-825. ]

DOI

[88]
郭漩, 钱海忠, 王骁, 等. 道路网选取的案例与本体推理方法[J]. 测绘学报, 2021, 50(12):1717-1727.

[ Guo X, Qian H Z, Wang X, et al. A method of road network selection based on case and ontology reasoning[J]. Acta Geodaetica et Cartographica Sinica, 2021, 50(12):1717-1727. ] DOI:10.11947/j.AGCS.2021.20200360

DOI

[89]
Ai T H, Xin R, Yan X F, et al. Shape decision-making in map-like visualization design using the simulated annealing algorithm[J]. IEEE Access, 7:131577-131592. DOI:10.1109/ACCESS.2019.2939977

DOI

[90]
宋鹰, 何宗宜, 粟卫民. 基于Rough集的居民地属性知识约简与结构化选取[J]. 武汉大学学报·信息科学版, 2005, 30(4):329-332.

[ Song Y, He Z Y, Su W M. Attributes reduction and structured selection in automatic cartographical generalization based on rough set[J]. Geomatics and Information Science of Wuhan University, 2005, 30(4):329-332. ] DOI:10.3321/j.issn:1671-8860.2005.04.012

DOI

[91]
李雯静, 邱佳, 龙毅. 粗集方法在地图综合中的应用[J]. 测绘学报, 2012, 41(2):298-301,308.

[ Li W J, Qiu J, Long Y. Application of rough set theory in map generalization[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2):298-301,308. ]

[92]
Touya G, Zhang X, Lokhat I. Is deep learning the new agent for map generalization?[J]. International Journal of Cartography, 2019, 5(2/3):142-157. DOI:10.1080/23729333.2019.1613071

DOI

[93]
郭庆胜. 线状要素图形综合的渐进方法研究[J]. 武汉测绘科技大学学报, 1998, 23(1):52-56.

[ Guo Q S. Study on progressive approach to graphic generalization of linear feature[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1998, 23(1): 52-56. ]

[94]
郭庆胜, 黄远林, 郑春燕, 等. 空间推理与渐进式地图综合[M]. 武汉: 武汉大学出版社, 2007.

[ Guo Q S, Huang Y L, Zheng C Y, et al. Spatial reasoning and progressive map synthesis[M]. Wuhan: Wuhan University Press, 2007. ]

[95]
董卫华, 郭庆胜, 刘纪平, 等. 道路网示意性地图的渐进式综合研究[J]. 武汉大学学报·信息科学版, 2007, 32(9):829-832,837.

[ Dong W H, Guo Q S, Liu J P, et al. Progressive generalization research of schematic road network maps[J]. Geomatics and Information Science of Wuhan University, 2007, 32(9):829-832,837. ] DOI:10.3969/j.issn.1671-8860.2007.09.020

DOI

[96]
杜佳威. 海岸线自动化简方法研究[D]. 郑州: 战略支援部队信息工程大学, 2018.

[ Du J W. Research on automated coastline simplification methods[D]. Zhengzhou: Information Engineering University, 2018. ]

[97]
Li H S, Wang Y J, Guo Q S, et al. Progressive simplification and transmission of building polygons based on triangle meshes[C]//Proc SPIE 7840, Sixth International Symposium on Digital Earth:Models, Algorithms, and Virtual Reality, 2010, 7840:307-314. DOI:10.1117/12.872704

DOI

[98]
Buchin K, Konzack M, Reddingius W. Progressive simplification of polygonal curves[J]. Computational Geometry, 2020, 88:101620. DOI:10.1016/j.comgeo.2020.101620

DOI

[99]
田晶, 郭庆胜, 冯科, 等. 基于信息损失的街道渐进式选取方法[J]. 武汉大学学报·信息科学版, 2009, 34(3):362-365.

[ Tian J, Guo Q S, Feng K, et al. Progressive selection approach of streets based on information loss[J]. Geomatics and Information Science of Wuhan University, 2009, 34(3):362-365. ]

[100]
郭庆胜, 李洪省, 刘纪平. 基于加权网格简化的建筑物群渐进式典型化[J]. 武汉大学学报·信息科学版, 2005, 30 (4):293-296.

[ Guo Q S, Li H S, Liu J P. Buildings progressive typification based on weighted mesh simplifica tion[J]. Geomatics and Information Science of Wuhan University, 2005, 30(4):293-296. ] DOI:10.3321/j.issn:1671-8860.2005.04.003

DOI

[101]
郭庆胜, 李国贤, 王勇, 等. 直线排列建筑物群渐进式典型化方法[J]. 测绘学报, 2020, 49(10):1354-1364.

[ Guo Q S, Li G X, Wang Y, et al. The method of progressive typification for building groups with straight linear patterns[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(10):1354-1364. ] DOI:10.11947/j.AGCS.2020.20190495

DOI

[102]
Wang X, Burghardt D. A mesh-based typification method for building groups with grid patterns[J]. ISPRS International Journal of Geo-information, 2019, 8(4):168. DOI:10.3390/IJGI8040168

DOI

[103]
郭庆胜, 王晓妍, 刘纪平. 图斑群合并的渐进式方法研究[J]. 武汉大学学报·信息科学版, 2012, 37(2):220-223,232.

[ Guo Q S, Wang X Y, Liu J P. Progressive combination of polygon groups[J]. Geomatics and Information Science of Wuhan University, 2012, 37(2):220-223,232. ] DOI:10.13203/j.whugis2012.02.020

DOI

[104]
胡志蕊, 祝国瑞, 徐智勇. LOD技术与制图综合在多尺度地图适时显示中的应用研究[J]. 测绘科学, 2006, 31(5):78-79,47,6.

[ Hu Z R, Zhu G R, Xu Z Y. Research on the visualization of multi-scale cartographic with LOD technology and cartographic generalization[J]. Science of Surveying and Mapping, 2006, 31(5):78-79,47,6. ] DOI:10.3771/j.issn.1009-2307.2006.05.025

DOI

[105]
Ai T H, Li Z L, Liu Y L. Progressive transmission of vector data based on changes accumulation model[M]//Developments in Spatial Data Handling. Berlin/Heidelberg: Springer-Verlag, 2006:85-96. DOI:10.1007/3-540-26772-7_7

DOI

[106]
贾小斌, 艾廷华, 彭子凤, 等. 地理信息语义的LOD表达与相似性度量[J]. 武汉大学学报·信息科学版, 2016, 41(10):1299-1306.

[ Jia X B, Ai T H, Peng Z F, et al. The LOD representation and proximity measurement of semantic about geographic information[J]. Geomatics and Information Science of Wuhan University, 2016, 41(10):1299-1306. ] DOI:10.13203/j.whugis20140711

DOI

[107]
胡绍永. 基于LOD技术的空间数据多尺度表达[D]. 武汉: 武汉大学, 2004.

[ Hu S Y. Multi-scale representation of spatial data based on LOD technology[D]. Wuhan: Wuhan University, 2004. ]

[108]
史云飞, 刘克辉, 李向伟, 等. 一种含室内空间结构的建筑物3D LOD概念模型与生成方法[J]. 武汉大学学报·信息科学版, 2022, 47(4):561-569,596.

[ Shi Y F, Liu K H, Li X W, et al. A 3D LOD conceptual model of building with indoor spatial structure and its generating method[J]. Geomatics and Information Science of Wuhan University, 2022, 47(4):561-569,596. ] DOI:10.13203/j.whugis20200087

DOI

[109]
彭东亮, 邓敏, 赵彬彬. 河网多尺度Morphing的变换方法研究[J]. 遥感学报, 2012, 16(5):953-959,961.

[ Peng D L, Deng M, Zhao B B. Multi-scale transformation of river networks based on morphing technology[J]. Journal of Remote Sensing, 2012, 16(5):953-959,961. ] DOI:10.11834/jrs.20121272

DOI

[110]
Li J Z, Li X G, Xie T. Morphing of building footprints using a turning angle function[J]. ISPRS International Journal of Geo-information, 2017, 6(6):173. DOI:10.3390/ijgi6060173

DOI

[111]
万瑞康, 翟仁健, 李安平, 等. 一种改进的基于转角函数法的面状居民地Morphing变换方法[J]. 测绘科学技术学报, 2021, 38(1):97-103,110.

[ Wan R K, Zhai R J, Li A P, et al. An improved morphing method of planar building based on steering angle function[J]. Journal of Geomatics Science and Technology, 2021, 38(1):97-103,110. ]

[112]
谢天, 李精忠. 面状居民地Morphing变换的转向角函数法[J]. 测绘学报, 2015, 44(7):797-804.

[ Xie T, Li J Z. Steering angle function algorithm of morphing of residential area[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(7):797-804. ] DOI:10.11947/j.AGCS.2015.20140333

DOI

[113]
谢天, 李精忠, 陈凯. 顾及线状要素综合要求的Morphing 算法[J]. 武汉大学学报·信息科学版, 2018, 43(5):792-797.

[ Xie T, Li J Z, Chen K. Morphing algorithm for linear feature considering generalization requirements[J]. Geomatics and Information Science of Wuhan University, 2018, 43(5):792-797. ] DOI:10.13203/j.whugis20150513

DOI

[114]
Li J Z, Ai T H, Liu P C, et al. Continuous scale transformations of linear features using simulated annealing-based morphing[J]. ISPRS International Journal of Geo-information, 2017, 6(8):242.

DOI

[115]
巩现勇, 武芳, 李靖涵, 等. 线要素移位的Morphing变换方法[J]. 测绘科学技术学报, 2018, 35(3):291-297.

[ Gong X Y, Wu F, Li J H, et al. An extended morphing approach for linear feature displacement[J]. Journal of Geomatics Science and Technology, 2018, 35(3):291-297. ]

[116]
Gao A J, Li J Z, Chen K. A morphing approach for continuous generalization of linear map features[J]. PLoS One, 2020, 15(12):e0243328. DOI:10.1371/journal.pone.0243328

DOI

[117]
刘鹏程, 肖天元, 艾廷华, 等. 基于傅里叶能量度量的曲线多尺度表达[J]. 中国矿业大学学报, 2020, 49(3):587-594.

[ Liu P C, Xiao T Y, Ai T H, et al. Multi-scale representation of curves based on Fourier energy metric[J]. Journal of China University of Mining ＆ Technology, 2020, 49(3):587-594. ] DOI:10.13247/j.cnki.jcumt.001154

DOI

[118]
李精忠, 高阿骥, 陈凯, 等. 一种面向DEM多尺度表达的傅里叶能量谱模型[J/OL]. 武汉大学学报·信息科学版:1-10[2022-05-02].

[ Li J Z, Gao A Y, Chen K, et al. A fourier energy spectrum model for DEM multi-scale representation[J/OL]. Geomatics and Information Science of Wuhan University: 1-10[2022-05-02]. ]

[119]
段佩祥, 钱海忠, 何海威, 等. 一种基于动态多尺度聚类的湖泊选取方法[J]. 武汉大学学报·信息科学版, 2019, 44(10):1567-1574.

[ Duan P X, Qian H Z, He H W, et al. A lake selection method based on dynamic multi-scale clustering[J]. Geomatics and Information Science of Wuhan University, 2019, 44(10):1567-1574. ] DOI:10.13203/j.whugis20170316

DOI

[120]
李佳星, 赵书良, 安磊, 等. 基于广义分形插值理论的多尺度分类尺度下推算法[J]. 计算机应用研究, 2019, 36(7):1970-1974.

[ Li J X, Zhao S L, An L, et al. Scaling-down algorithm of multi-scale classification based on generalized fractal interpolation theory[J]. Application Research of Computers, 2019, 36(7):1970-1974. ] DOI:10.19734/j.issn.1001-3695.2018.01.0031

DOI

[121]
王璐, 胡月明, 赵英时, 等. 克里格法的土壤水分遥感尺度转换[J]. 地球信息科学学报, 2012, 14(4):465-473.

DOI

[ Wang L, Hu Y M, Zhao Y S, et al. Remote sensing scale transformation of soil moisture based on block kriging[J]. Journal of Geo-information Science, 2012, 14(4):465-473. ] DOI:10.3724/SP.J.1047.2012.00465

DOI

[122]
Frank A U, Timpf S. Multiple representations for cartographic objects in a multi-scale tree: An intelligent graphical zoom[J]. Computers & Graphics, 1994, 18(6):823-829. DOI:10.1016/0097-8493(94)90008-6

DOI

[123]
Touya G, Girres J F. ScaleMaster 2.0: A ScaleMaster extension to monitor automatic multi-scales generalizations[J]. Cartography and Geographic Information Science, 2013, 40(3):192-200.

DOI

[124]
Šuba R. Design and development of a system for vario-scale maps[J]. Architecture and the Built Environment, 2017(18):1-162.

[125]
Gröbe M, Burghardt D. Developing and Evaluating Multi-Scale Map Styles: Creating a Multi-Scale Legend[J]. Abstracts of the ICA, 2019, 1:NA-NA.

[126]
徐丰, 牛继强. 空间数据多尺度表达的不确定性可视化模型[J]. 信阳师范学院学报(自然科学版), 2016, 29(2):217-221.

[ Xu F, Niu J Q. Uncertainty visualization models for multi-scale representation of spatial data[J]. Journal of Xinyang Normal University (Natural Science Edition), 2016, 29(2):217-221. ] DOI:10.3969/j.issn.1003-0972.2016.02.015

DOI

[127]
Šuba R, Meijers M, Oosterom P. Continuous road network generalization throughout all scales[J]. International Journal of Geo-information, 2016, 5(8):145. DOI:10.3390/ijgi5080145

DOI

[128]
Šuba R, Meijers M, van Oosterom P. Large scale road network generalization for vario-scale map[C]// Proceedings of the 18th ICA Workshop on General-isation and Multiple Representation, Rio de Janeiro, Brazil, 2015:1-10.

[129]
Marion D, Guillaume T, Cécile D. Designing multi-scale maps: Lessons learned from existing practices[J]. International Journal of Cartography, 2020, 6(1):121-151.

DOI

[130]
俞童, 邓术军, 钱海忠, 等. 剖分网格下顾及用户兴趣的矢量地图多尺度表达方法[J]. 测绘学报, 2016, 45(S1):127-134.

[ Yu T, Deng S J, Qian H Z, et al. A method of vector map multi-scale representation considering user interest on subdivision grid[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(S1):127-134. ] DOI:10.11947/j.AGCS.2016.F016

DOI

[131]
杨敏, 艾廷华, 卢威, 等. 自发地理信息兴趣点数据在线综合与多尺度可视化方法[J]. 测绘学报, 2015, 44(2):228-234.

[ Yang M, Ai T H, Lu W, et al. A real-time generalization and multi-scale visualization method for POI data in volunteered geographic information[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(2):228-234. ] DOI:10.11947/j.AGCS.2015.20130564

DOI

[132]
杨必胜, 孙丽. 导航电子地图的自适应多尺度表达[J]. 武汉大学学报·信息科学版, 2008, 33(4):363-366.

[ Yang B S, Sun L. Adaptive multi-scale visualizations of road network for navigation[J]. Geomatics and Information Science of Wuhan University, 2008, 33(4):363-366. ]

[133]
蒋雪. 基于地图视觉感受的网络地图多尺度表达设计[J]. 测绘与空间地理信息, 2014, 37(2):43-45.

[ Jiang X. The multi-scale expression design for web map based on map visual perception[J]. Geomatics ＆ Spatial Information Technology, 2014, 37(2):43-45. ]

[134]
熊金华, 江南, 曹亚妮. 基于SuperMap世界电子地图多尺度表达的研究[J]. 测绘与空间地理信息, 2011, 34(4):156-158.

[ Xiong J H, Jiang N, Cao Y N. The research on multi-scale display of world electronic map based on SuperMap[J]. Geomatics ＆ Spatial Information Technology, 2011, 34(4):156-158. ]

[135]
蒯希, 贺彪, 罗恒, 等. 城市空间三维地图及其在智慧城市中的应用[J]. 测绘地理信息, 2021, 46(1):66-70.

[ Kuai X, He B, Luo H, et al. Three-dimensional map of urban space and its application to smart cities[J]. Journal of Geomatics, 2021, 46(1):66-70. ] DOI:10.14188/j.2095-6045.2020470

DOI

[136]
刘兵, 董卫华, 王彦文, 等. 视场角与观察角度对三维地图视觉信息加工的影响研究[J]. 地球信息科学学报, 2015, 17(12):1490-1496.

DOI

[ Liu B, Dong W H, Wang Y W, et al. The influence of FOV and viewing angle on the visual information processing of 3D maps[J]. Journal of Geo-information Science, 2015, 17(12):1490-1496. ] DOI:10.3724/SP.J.1047.2015.01490

DOI

[137]
付乐宜, 艾廷华, 黄丽娜, 等. 基于交通轨迹数据的三维动态噪声地图[J]. 地球信息科学学报, 2020, 22(9):1789-1798.

DOI

[ Fu L Y, Ai T H, Huang L N, et al. Three-dimensional dynamic noise map based on traffic trajectory data[J]. Journal of Geo-information Science, 2020, 22(9):1789-1798. ] DOI:10.12082/dqxxkx.2020.200140

DOI

[138]
贾奋励, 游雄, 刘芳. 多尺度表达的地图设计模型[J]. 测绘科学技术学报, 2011, 28(2):153-156.

[ Jia F L, You X, Liu F. Map design model for multi-scale representation[J]. Journal of Geomatics Science and Technology, 2011, 28(2):153-156. ] DOI:10.3969/j.issn.1673-6338.2011.02.019

DOI

[139]
李志林, 王继成, 谭诗腾, 等. 地理信息科学中尺度问题的30年研究现状[J]. 武汉大学学报·信息科学版, 2018, 43(12):2233-2242.

[ Li Z L, Wang J C, Tan S T, et al. Scale in Geo-information science: An overview of thirty-year development[J]. Geomatics and Information Science of Wuhan University, 2018, 43(12):2233-2242. ] DOI:10.13203/j.whugis20180303

DOI

[140]
艾廷华. 深度学习赋能地图制图的若干思考[J]. 测绘学报, 2021, 50(9):1170-1182.

[ Ai T H. Some thoughts on deep learning enabling cartography[J]. Acta Geodaetica et Cartographica Sinica, 2021, 50(9):1170-1182. ] DOI:10.11947/j.AGCS.2021.20210091

DOI

[141]
李双成, 张文彬, 陈立英, 等. 孪生空间及其应用——兼论地理研究空间的重构[J]. 地理学报, 2022, 77(3):507-517.

DOI

[ Li S C, Zhang W B, Chen L Y, et al. Digital twin space and its applications: Concurrent discussion on the space reconstruction of geographical research[J]. Acta Geographica Sinica, 2022, 77(3):507-517. ] DOI:10.11821/dlxb202203001

DOI

Options
Outlines

/

〈 〉