EN中文

Journal of Geo-information Science >

2023 , Vol. 25 >Issue 1: 115 - 130

DOI: https://doi.org/10.12082/dqxxkx.2023.220321

A Spatial-temporal Causal Convolution Model for Fine-grained Individual Air Quality Index (IAQI) Prediction

  • ZHANG Yumin , 1 ,
  • ZHAO Junjie 1 ,
  • MEI Qiang 2 ,
  • LIU Xiliang , 1, * ,
  • CHEN Zhuodong 3 ,
  • LI Jianqiang 1 ,
  • WANG Shaohua 4 ,
  • SHI Yuliang 1 ,
  • CHAI Jinchuan 5 ,
  • GAO Yuyao 1 ,
  • JING Xiaoqian 1 ,
  • YANG Niandi 1 ,
  • MA Xiaoyan 1
Expand
  • 1. College of Software, Beijing University of Technology, Beijing 100124, China
  • 2. Navigation College, Jimei University, Xiamen 361021, China
  • 3. China National Petroleum Corporation Auditing Service Center, Beijing 100028, China
  • 4. Key Laboratory of Digital Earth Science, Aerospace Information Research Institute, Chinese Academy of Sciences, Beijing 100094, China
  • 5. National Railway Track Test Center, China Academy of Railway Sciences Corporation Limited, Beijing 100015, China
*LIU Xiliang, E-mail:

Received date: 2022-05-18

  Revised date: 2022-06-15

  Online published: 2023-03-25

Supported by

National Key Research and Development Program of China(2020YFB2104400)

Fold

Abstract

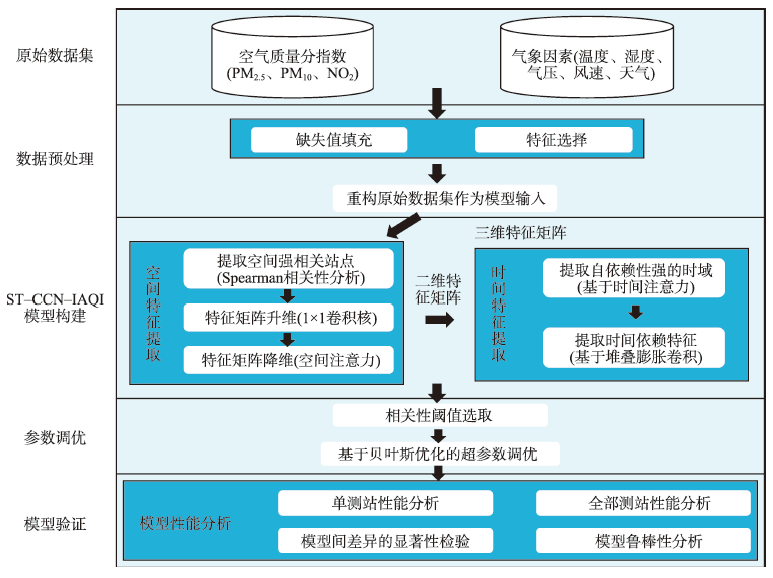
Accurate and fine-grained individual Air Quality Index (IAQI) prediction is the basis of Air Quality Index (AQI), which is of great significance for air quality control and human health. Traditional approaches such as time series modeling, Recurrent Neural Network (RNN) or Graph Convolutional Network (GCN) cannot effectively integrate spatial-temporal and meteorological factors and manage dynamic edge relationship among scattered monitoring stations. In this paper, a ST-CCN-IAQI model is proposed based on spatial-temporal causal convolution networks. Firstly, both the spatial effects of multi-source air pollutants and meteorological factors are considered via spatial attention mechanism. Secondly, time-dependent features in causal convolution network are extracted by stacked dilated convolution and time attention. Finally, multiple parameters in ST-CCN-IAQI are tuned by Bayesian optimization. In this paper, the Individual Air Quality Index (IAQI-PM2.5) data of Shanghai air monitoring station are used to carry out the experiment, and a series of baseline models (AR, MA, ARMA, ANN, SVR, GRU, LSTM, and ST-GCN) are employed to compare with ST-CCN-IAQI. Our results show that: (1) In the single station test, RMSE and MAE values of ST-CCN-IAQI are 9.873 and 7.469, respectively, which decreases by 24.95% and 16.87% on average, respectively; R2 is 0.917, about 5.69% higher than that of the baselines; (2) The prediction of IAQI-PM2.5, IAQI-PM10, and IAQI-NO2 of all stations proves that ST-CCN-IAQI has strong generalization ability and stability; (3) Shapley analysis shows IAQI-PM10, humidity, and IAQI-NO2 have a great impact on the prediction of IAQI-PM2.5. Friedman test under different data sampling conditions proves that ST-CCN-IAQI has significant performance improvement by comparisons with baselines. The ST-CCN-IAQI method provides a robust and feasible solution for accurate prediction of fine-grained IAQI.

Key words： individual air quality Index prediction; multi-source factors; temporal and spatial attention; causal convolution network; Bayesian optimization; shapley analysis; Friedman test; Shanghai

Cite this article

ZHANG Yumin , ZHAO Junjie , MEI Qiang , LIU Xiliang , CHEN Zhuodong , LI Jianqiang , WANG Shaohua , SHI Yuliang , CHAI Jinchuan , GAO Yuyao , JING Xiaoqian , YANG Niandi , MA Xiaoyan . A Spatial-temporal Causal Convolution Model for Fine-grained Individual Air Quality Index (IAQI) Prediction[J]. Journal of Geo-information Science, 2023 , 25(1) : 115 -130 . DOI: 10.12082/dqxxkx.2023.220321

1 引言

近年来，在中国工业化、城镇化快速发展的背景下，城市空气污染问题日益严重[1]。长期暴露在高浓度污染空气会显著增加多种患病风险，严重损害人体自身的呼吸系统、神经系统、心血管系统及生殖系统[2]。据统计，中国每年因空气污染物致死大约为100万人[3]，空气污染已成为美国近25年造成死亡的主要原因[4]。如何精细化确定空气污染程度对于日常出行具有重要参考意义[3,6]。
空气质量指数（Air Quality Index, AQI）对空气污染程度进行分级，包括优、良、轻度污染、中度污染以及重度污染[5]，可以依据AQI分级标准判断当前空气质量对自身健康的影响，并采纳合适的防范措施。AQI作为空气污染物污染程度定量表征，其取值通常是选取所有空气质量分指数（Individual Air Quality Index, IAQI）中的最大值。以PM2.5为例，IAQI-PM2.5的计算公式如式（1）所示① (① http://www.beijing-air.com/a/index.php/iaqi.html)。
I = I h i g h - I l o w C h i g h - C l o w ( C - C l o w ) + I l o w
式中： I表示PM2.5的空气质量分指数； C表示PM2.5浓度值； C h i g h、 C l o w分别PM2.5浓度的高位值和低位值； I h i g h、 I l o w分别为 C h i g h、 C l o w所对应的空气质量分指数。
根据文献综述，一个良好的IAQI预测模型需要考虑以下因素：
（1）根据监测站的实际监测情况，将多种影响因素纳入IAQI预测建模。这些因素包括气象因素（温度、风速、降水等）、多种空气污染物（PM2.5、PM10、NO2、CO等）。
（2）由于IAQI数据在空间和时间维度上是相互依赖的，通常具有较高的自相关性，因此需要捕获监测站之间的时空相关性和时空异质性[7-8]。
（3）为了获得更好的AQI估计结果，IAQI预测建模应融合先进的时空特征提取方法，且该模型对不同的空气污染物预测（PM2.5、PM10、SO3、NO2等）均具有较好的稳定性、鲁棒性和较高的预测精度。
当前IAQI预测建模方法主要包括传统模型和深度学习模型。
传统模型包括气象模型、时间序列模型和浅层神经网络。气象模型主要基于大气物理和化学过程对污染物形成与扩散过程进行建模[9⇓-11]，然而，气象模型严重依赖理论假设，难以表达大气过程的非线性和异质性[12]。时间序列模型包括自回归（Autoregressive, AR）、移动平均（Moving Average, MA）和自回归移动平均（Autoregressive Moving Average, ARMA）等模型，是处理IAQI序列数据的首选模型[13-14]。Barthwal利用ARMA对印度首都德里的日平均AQI进行了预测，取得了较好的效果[25]。然而，空气污染物扩散演化是动态非线性过程，线性统计模型[15]和时间序列模型不能反映其复杂性，预测偏差一般较大。支持向量回归机（Support Vector Regression, SVR）[16]和人工神经网络（Artificial Neural Network, ANN）[17-18]等浅层神经网络已应用于序列预测任务中并取得了一定的成果。Motesaddi等人利用ANN对SO2的IAQI值进行了预测。该模型能很好的学习输入输出之间复杂的非线性依赖关系，不仅具有良好的鲁棒性和自适应特性，且模型训练的时间复杂度较低[19]。与时间序列模型相比，浅层神经网络通常具有更好的性能[18⇓⇓-21]。然而，浅层学习在有限样本和计算单元的情况下对复杂函数的表示能力有限，使其泛化能力受到一定的制约。此外，这类模型在大规模监测站点网络中难以捕捉站点之间复杂的时空相关性，在实际应用中有较大局限性[9,12]。
近年来，深度学习在大气污染预测中得到了广泛的应用。目前，用于IAQI预测的深度学习模型大致可以分为三类:基于序列、基于图和基于卷积的深度模型。基于序列的模型包括循环神经网络（Recurrent Neural Network, RNN[22]）、门控循环单元（Gate Recurrent Unit, GRU[23⇓-25]）和长短期记忆（Long-short Term Memory, LSTM[26⇓⇓⇓-30]），这些模型在空气污染预测中表现出了巨大的优势[13,31-32]。然而，基于RNN的序列方法存在迭代传播耗时、梯度爆炸和梯度消失的问题[33]。基于图的模型被广泛运用于空气污染物空间特征提取，但由于图节点间连接的缺失，使得该模型难以稳定地捕获节点间的边缘关系[34-35]。基于卷积的模型，如来自图像处理领域的因果卷积网络（Causal Convolution Network, CCN），也被广泛应用于IAQI预测研究[12-13]。由于其体系结构中不包含复杂的递归结构，如门控机制，CCN在IAQI预测建模中更简单、更有效[9,35]。此外，CCN模型的内存需求可以通过堆叠膨胀卷积来解决，以扩大感受野大小[12]。
大量IAQI预测研究表明，时空依赖因素与大气环境因素对模型效果有重要影响。
空气监测站点间的时空依赖性直接影响IAQI预测效果。Jiao等[36]以预测站点为中心，选取距离最近的5个站点数据作为空间信息输入。Li等[26]以行政区划作为周边站点的空间范围。Feng等[37]通过气团轨迹分析得到研究区域的污染输入路径，在各个路径中人为选取一个站点作为空间信息输入。Pak等[38]通过提取不同位置多个监测站的时间序列的时空相关性进行IAQI预测，取得了更准确、更稳定的预测性能。
大气环境因素对空气污染物的扩散、传输的驱动作用也不可忽视[39]。空气质量指数与气象因素之间存在很强相关性，与气温呈负相关，与风、相对湿度、气压呈正相关[39-40]。徐艺武[41]以2015年北京市12个国控监测点的监测数据为基础，研究了PM2.5与主要空气污染物之间的关系，结果证明PM2.5与PM10、NO2浓度呈正相关性且极为显著。原因在于，空气污染物有着极为相似的污染物排放源，且彼此之间会相互反应、相互转化。
基于上述文献综述，本文提出一种基于时空因果卷积网络的细粒度IAQI预测模型ST-CCN-IAQI。在影响因素选择方面，考虑了空气污染物、气象因素以及监测站点间的时空依赖性，从中提取非线性因素；在细粒度预测方面，本文模型在时间维度上达到小时级别预测粒度，在空间维度上达到城市测站级精度；在建模方面，本文采用卷积神经网络和因果卷积网络提取空气污染物时空特征，并采用时空注意力机制优化模型特征提取，以期达到稳定、鲁棒的细粒度IAQI预测效果。

2 研究方法

2.1 技术路线

本文将多种空气质量分指数和气象因素纳入IAQI预测建模，挖掘序列间时空依赖关系，以提升IAQI预测精度。本文首先对获取到的空气质量分指数和气象因素进行数据预处理，经过缺失值填充和特征选择，将多测站数据融合重构为三维特征矩阵作为模型输入。其次，进行空间特征提取和时间特征提取。在空间特征提取模块中，本文使用斯皮尔曼相关性分析获取与目标站点强相关的站点，然后将强相关站点数据重构为三维矩阵，通过1×1卷积核和空间注意力模块对三维矩阵进行升维、降维处理，以优化模型对空间相关性特征的提取能力。空间注意力模块处理后的特征矩阵，端到端的作为时间特征提取模块的输入。在时间特征提取模块，利用时间注意力机制从特征矩阵中筛选自依赖性强的时域（时间间隔）作为堆叠膨胀卷积的数据窗口，并将特征矩阵作为堆叠膨胀卷积的数据输入。通过堆叠膨胀卷积，提取有效的时间依赖特征对未来时的IAQI值做出预测。本文优化了阈值的选择，并采用贝叶斯优化器选取最佳模型参数组合。最后，将ST-CCN-IAQI与一系列基线模型进行了单测站性能分析、全部测站性能分析。基于模型间差异显著性检验、模型鲁棒性分析验证了模型的泛化性。本文技术路线如图1所示。
图1 ST-CCN-IAQI的技术路线

Fig. 1 Technical route of ST-CCN-IAQI

2.2 研究区域与数据集介绍

本文选择上海市为研究区域，监测站点（图2中以黑色三角形表示）所在区域及分布如图2所示。本文选取站点2作为本文的目标站点（图2种以红色三角表示）。由于该站点处于市区中心且周边分布着较多空气监测站，对该站点进行预测能够较好的反映时空相关性对模型预测的影响，具有一定的代表性。
图2 研究区域及站点分布

注:该图基于自然资源部标准地图服务网站下载的审图号为沪S(2021)083号的标准地图制作，底图无修改。

Fig. 2 Study area and monitoring stations' distribution

本文采用上海市9个监测站2013年8月26日至9月28日的小时级空气质量分指数数据与气象数据[42]，将IAQI-PM2.5（空气质量指数的主要估算因子）作为本文的研究对象。原始数据预处理包括缺失值处理和特征选择。对于短时间跨度（1 h或2 h）的缺失值采用一阶、二阶拉格朗日插值法进行填充，对于长时间跨度（5 h及5 h以上）的缺失值，使用临近日期的同时段数据插补。其次，采用斯皮尔曼秩相关性系数方法识别并剔除原始数据集中与IAQI-PM2.5弱相关的特征。最终选择的特征包括IAQI-PM2.5、IAQI-PM10、IAQI-NO2值、温度（Temperature）、压强（Pressure）、湿度（Humidity）、风速（Wind speed）和天气类型（Weather）共八项，其中天气类型使用整数表示多种不同天气（雪=0，多云=1，晴=2，阴=3，雨=4，雾=5，尘=6）。各项数据说明如表1所示。
表1 数据集说明

Tab. 1 Dataset description

数据种类 特征名称 数据类型 单位
空气质量分指数 IAQI-PM2.5 数值 -
IAQI-PM10 数值 -
IAQI-NO2 数值 -
气象数据
 Temperature 数值 ℃
Pressure 数值 hpa
Humidity 数值 %
Wind speed 数值 km/h
Weather 数值 -

2.3 空间特征提取

本文利用斯皮尔曼秩关系数来衡量周边站点与目标站点的某种空气质量分指数（即研究对象）的相关程度，计算得到的相关性系数介于0~1之间。相关系数越趋近于1代表2个站点的相关性越强。计算公式如式(2)所示。
ρ ( Y * , Y k ) = 1 - 6 ∑ i = 1 S ( Y i - Y k i ) 2 S ( S 2 - 1 )
式中： ρ ( Y * , Y k )表示计算2个序列的斯皮尔曼相关性系数；其中 Y *代表目标站点的IAQI历史数据按数值降序排序后的序列 ; Y k代表周边第 k个站点的IAQI历史数据按数值降序排序后的序列； Y i代表 Y *中第 i项数据； Y k i代表 Y k中第 i项数据； S表示序列中样本数量，即全部站点数。如式(3)中 ρ _ l i s t是计算出的目标站点与所有站点之间的相关系数。
ρ _ l i s t = [ ρ ( Y * , Y 1 ) , ρ ( Y * , Y 2 ) , … , ρ ( Y * , Y k ) , … , ρ ( Y * , Y S ) ]
本文将相关系数与优化后的阈值 ρ t h进行比较，最终得到与目标站点相关系数大于 ρ t h的 M个站点集合如式(4)所示。
X = { X i | ρ ( Y * , Y i ) > ρ t h , i ∈ 1 , … , M }
式中： X i ∈ R T × L表示第i个与目标站点空间强相关站点的特征矩阵； X ∈ R M × T × L代表与目标站点空间强相关的三维特征矩阵，其中 M < = S， M代表与目标站点空间强相关的站点数量； S代表全部站点数量； T代表历史数据时间步长； L代表特征维度。
本文利用1×1卷积核实现特征矩阵升维，经过升维处理后三维矩阵变为 X ∈ R M n e w × T × L，其中 M n e w表示升维后的通道数量。
如图3所示，利用卷积神经网络中的1×1卷积核以增加输出通道数的方式对特征矩阵 A进行升维处理。中间的矩形框中包含了 M n e w个滤波器，滤波器的维度是 1 × 1 × M（ M是卷积核数），其中卷积核数与原有特征矩阵的通道数相同。在局部视角， 3个红色方形通过与 M n e w个滤波器的卷积操作，得到 M n e w个黄色方形，从全局来看，升维处理对原始特征矩阵的通道数的进行了扩充，新生成的特征矩阵为 X ∈ R M n e w × T × L。在升维过程中，特征矩阵与滤波器的卷积运算使不同通道的信息得以交互和融合，提升了模型对非线性特征的提取能力。
图3 利用1×1卷积核对特征矩阵进行升维

Fig. 3 Ascending dimension of the eigenmatrix via 1×1 convolution kernel

基于空间注意力机制的特征矩阵降维过程如图4所示。
图4 利用空间注意力模块对特征矩阵降维处理

Fig. 4 Dimension reduction of eigenmatrix via spatial attention

在第一阶段，计算目标站点的第 i项特征序列与多通道中第 i项特征序列之间的相关性系数，如式(5)所示。
S i m m i = S i m i l a r i t y ( f t a r g e t i , f m i ) = S p e a r m a n ( f t a r g e t i , f m i )
式中： S i m m i表示第 m个通道第 i项特征序列与目标序列的相关性系数； f t a r g e t i ∈ R T表示目标站点的第 i项特征序列； f m i ∈ R T表示第 m个通道的第 i项特征序列； S p e a r m a n ( )代表斯皮尔曼秩相关性系数计算方法。
之后依据相关性系数计算每个通道第 i项特征序列的权重分布。在第二阶段中，利用SoftMax的计算方法对第一阶段的相关性系数进行数值转换，将原始相关性系数整理成所有元素权重之和为1的概率分布，这种处理方法使模型更加关注于有助于提升其预测性能的特征序列。计算公式如（6）所示。
a m i = S o f t m a x ( S i m m i ) = e x p ( S i m m i ) ∑ j = 1 M n e w e x p ( S i m j i )
式中： a m i表示第 i个特征序列在第 m个通道中的注意力权值。
最后，将各通道的第 i项特征序列乘以对应的权重值再求和，使第 i项特征序列聚合为最终序列，由聚合后的各项特征序列构成最终特征矩阵。因此最终降维聚合后的特征序列 A i及特征矩阵 A应如式（7）所示。
A i = ∑ j = 1 M n e w a j i × f j i , A = ( A 1 , . . . , A i , . . . , A l )

2.4 时间特征提取

本文根据时间注意力机制，采用随机搜索，筛选时间自依赖性强的时间间隔作为堆叠膨胀卷积的输入窗口尺寸，以优化堆叠膨胀卷积对时间依赖性特征的提取。首先，设定滑动窗口尺寸为在4~24的范围内，以4为间隔采样，并从各监测站点历史数据中的上四分位数、中位数、下四分位数的附近分别抽取10%的数据用于训练堆叠膨胀卷积。其次，利用MSE、RMSE、MAE、R2等指标来评价模型，选择使模型预测性能最佳的滑动窗口。最后，本文基于全部站点在3个数据集上筛选出的最佳滑动窗口数值列表，从中选取出现频次最大的滑动窗口数值作为堆叠膨胀卷积的参数。经过调优，将堆叠膨胀卷积的滑动窗口设置为24。
本文将聚合后空间特征矩阵作为堆叠膨胀卷积的输入，利用堆叠膨胀卷积模型提取二维特征矩阵中的时间依赖特征。图5为堆叠膨胀卷积的架构图。
图5 基于堆叠膨胀卷积提取时间特征

Fig. 5 The architecture of stacked dilated convolution

堆叠膨胀卷积以特征映射的方式与前一层的局部感受野连接，局部感受野中每 K（卷积核大小）个数据为一组参与卷积运算，且引入了膨胀率 d，允许卷积核处理数据时跳过 d个数据进行处理，同时膨胀率随网络层数的增加呈指数型增长。如图5，卷积核在处理输入层中数据时，膨胀卷积参数设置为 d = 1 , K = 4。此时输入层以1为间隔进行采样，且每4个特征向量为一组，经过卷积核运算，再利用激活函数的非线性计算得到隐藏层1中的一个特征值。以此类推，处理隐藏层1中的数据时，参数设置为 d = 2 , K = 4，处理隐藏层2中的数据，参数设置为 d = 4 , K = 4。堆叠膨胀卷积这种独特的结构，使它无需很大的网络深度就可以获得较大的感受野，并获得长距离的历史数据。不仅降低了空间损失和信息损失，且使得特征提取更加全面，有利于提升模型整体的预测精度。堆叠膨胀卷积公式如式(8)所示。
( F * d X ) ( x t ) = ∑ k = 1 K f k x t - ( K - k ) d
式中： f k k = 1,2 , 3 , · · ·表示滤波器， x t t = 1,2 , 3 , · · ·代表某一时刻的特征向量； d为膨胀率，表示模型采样的节点间隔； K为卷积核大小，表示局部感受野中参与膨胀卷积运算的节点数。 堆 叠膨胀卷积的感受野大小为 ( K + 1 ) d + 1，通过增大卷积核大小 或膨胀率可以使模型 获 得宽阔的感受野。根据Bai等[43]和Zhang等[44]的研究，本文将卷积核数设置为4，网络层深度置为4，膨胀率设置为 d = 2 i，其中 i为网络层深度。在后续实验中本文将利用贝叶斯调优方法对堆叠膨胀卷积模型的部分参数进一步优化。

2.5 贝叶斯优化

贝叶斯优化调参方法具有迭代次数少，速度快等优势[45]，本文通过构建贝叶斯优化器对模型参数进行自动寻优，以高效、精确地捕获最佳参数组合。图6是贝叶斯优化的基本过程。
图6 贝叶斯优化基本过程

Fig. 6 Parameter tuning process via Bayesian optimization.

贝叶斯参数调优的最终目标是选出一组参数组合使得模型的损失函数获得全局最小值。如图6，横轴表示参数组合的搜索空间。蓝色点表示已知的实际观测值，即 ( x i , y i )。其中， x i代表一组参数值， y i代表模型训练后得到的损失函数值。黑色实线为估计得到的函数分布，紫色实线之间的区域为估计函数的置信区间。黑色虚线表示实际的模型损失函数，绿色实线表示采集函数。首先，贝叶斯优化器基于观测点，利用高斯混合模型的概率代理函数，得到损失函数 f ( x )的估计函数 f *。其次，优化器利用概率代理模型的输出结果( f *)计算出采集函数，并利用采集函数选择下一个观测点。采集函数衡量观测点（参数搜索空间中的样本点）对于拟合 f *与 f ( x )的影响程度。并选择影响最大的点来执行下一步的观测。如图6中，贝叶斯优化器计算得到了采集函数的最大值点 x，然后将 x代表的这组参数带入模型中去训练，得到实际损失值 y。最后将新的观测点 ( x , y )加入到已知的观测点中。通过一定的迭代次数，估计函数 f *会逐渐逼近实际损失函数 f ( x )，计算 f *的最小值点即为调优后的参数组合。

3 实验及结果分析

3.1 参数调优

3.1.1 相关性阈值选取

在前文的空间特征提取建模中，需要设定相关性阈值以确定纳入模型预测的监测站。本文采用统计学中的相关程度标准并结合相关性系数分布来选择阈值，相关程度标准为0.8~1为极强相关，0.6~0.8为强相关，0.4~0.6为中等相关，小于0.4为弱相关。通过斯皮尔曼秩相关性计算方法计算了目标站点（stn.2）与其他站点IAQI-PM2.5历史序列之间的相关性。站点间相关性系数如图7所示。
图7 站点间相关性系数

Fig. 7 Correlation coefficient between stations

观察图7可以发现，站点2和其他站点的相关性系数几乎全部在0.8~1.0的范围内，这表明站点2和其他站点间具有极其密切的关系。针对本文的研究区域，空间特征提取模块中的相关性阈值被设置为0.8，可避免强相关的空间信息遗漏。在后续研究中，本文统一将空间特征提取模块中阈值参数设置为0.8。

3.1.2 基于贝叶斯优化的参数调优

本文利用贝叶斯优化器调优了堆叠膨胀卷积中的hidden_size、levels、kernel_size、dropout 4项参数。其中hidden_size表示隐藏层中的节点数目，levels表示网络层深度，kernel_size是膨胀卷积内核，dropout是每次迭代随机移除的节点比率。
在贝叶斯优化过程中，本文将模型在验证集上的RMSE值作为优化器的损失函数。对于目标站点，由图8可知贝叶斯优化器在38次迭代后趋于收敛。考虑到模型运行时间较长，本文的贝叶斯优化器迭代次数选择50。
图8 迭代次数对模型损失值的影响

Fig. 8 The influence of the number of optimizer iterations on the model loss value

参数优化选取的范围分别设置为：dropout取值范围是0.5~0.9，步长为0.01；kernel_size取值范围是3~9，步长为1；levels取值范围是3~9，步长为1；hidden_size取值范围是48~64，步长为8[12]。图9展示了参数的贝叶斯优化过程。
图9 优化器迭代过程中的参数值变化

Fig. 9 The Bayesian optimization process

如图9所示，经过50次迭代，模型的最佳参数组合为： d r o p o u t = 0.59， h i d d e n _ s i z e = 56.0， k e r n e l _ s i z e = 9.0， l e v e l s = 3.0，这组最佳参数组合被运用于下文实验。

3.2 模型性能分析

3.2.1 单测站性能分析

本文将单个监测站点（stn.2）作为目标站点，采用一系列基线模型与ST-CCN-IAQI进行了对比分析。基线模型包括：自回归模型（AR）、滑动平均模型（MA）、自回归移动平均模型（ARMA）、人工神经网络（ANN）、支持向量机回归（SVR）、门控循环单元（GRU）、长短期记忆网络（LSTM）以及时空图卷积网络（Spatial-Temporal Graph Convolutional Network, ST-GCN）。对于基于平稳时间序列的AR模型，通过F检验选择合适的阶数P=3，采用自适应方法预测[46]。对于MA模型，首先确定模型的阶P=3，其次确定历史数据与当前数据的自相关性进行预测[47]。基于非平稳时间序列的ARMA模型经过平稳性检验、模型识别和检验确定模型，将ARMA模型的p、q阶数分别设置为5、6[13]。ANN模型设置包含有2个隐藏层，每个隐藏层各包含50个神经元，使用ReLU激活函数与Adam随机梯度优化模型参数[19]。SVR模型选择RBF核函数，设置惩罚项参数值C为1000[31]。GRU模型舍弃率设置为0.2、隐藏层为1，隐藏节点数为（16, 25）[23]。LSTM模型采用三层隐含层，节点数分别为30、50、70，学习率为1[26]。 ST-GCN是一种常用的时序图模型，ST-GCN三层通道分别为64、16和64，图卷积核大小K和时间卷积核大小Kt设置为3[34]。对于线性统计与时序模型，将IAQI-PM2.5历史序列作为模型输入。对于浅层学习和深度学习模型，采用和本文模型相同的特征序列作为输入。此外，上述基线模型的参数均采用文献中的通用性参数配置进行多次测试，使基线模型性能达到最佳。
本文采用RMSE、MAE、R2作为各种模型的评价指标，并使用5折交叉验证方法获得各模型性能。本文将模型输入数据分成5组，每个子集数据分别做一次验证集，其余的4组子集数据作为训练集。将训练得到的5个模型分别在验证集中评估结果，将RMSE、MAE、R2分别求和取平均得到模型最终预测值。实验结果如表2所示。
表2 各模型的性能比较（单一站点stn.2）

Tab. 2 Performance comparison of each model (single station stn.2)

模型 RMSE MAE R2
AR 12.366 8.397 0.888
MA 17.287 11.897 0.782
ARMA 12.504 8.477 0.885
ANN 13.032 9.030 0.876
SVR 12.821 8.554 0.880
GRU 12.883 8.829 0.878
LSTM 12.853 8.807 0.879
ST-GCN 12.621 8.713 0.884
ST-CCN 9.873 7.469 0.917
如表2，ST-CCN-IAQI在IAQI-PM2.5预测任务中，在RMSE、MAE和R2方面的表现均优于基线模型。整体上，ST-CCN-IAQI的RMSE和MAE值相比基线模型平均下降了24.95%和16.87%，R2值平均提升了5.69%。相比线性统计和时序模型，ST-CCN-IAQI的RMSE和MAE平均下降了28.03%和19.93%，R2平均提升了8.03%。对比浅层学习模型，其RMSE和MAE分别平均下降了23.55%和14.98%，R2值平均提升了4.44%。ST-CCN-IAQI相比深度学习模型也有较大的提升，RMSE和MAE分别平均降低了22.77%，14.96%，R2平均提升了4.17%。实验结果证明了本文的模型在细粒度预测IAQI方面提供了一个具有潜力的研究方向。为了方便直观地对比各模型，本文绘制了模型性能对比条形图，如图10所示。
图10 各模型性能对比(RMSE、MAE、R2)

Fig. 10 Performance comparison of each model(RMSE、MAE、R2)

观察图10(a)、图10(b)、图10(c)可以发现，尽管MA模型表现最差，但无论是在RMSE还是MAE上，传统AR模型和ARMA模型的结果几乎都优于其他所有复杂模型，如ANN、SVR、GRU、LSTM和ST-GCN。一种可能的解释是由于实验数据具有较强的周期性，基于线性和时间序列的模型可以更好地提取时间依赖性。ST-CCN-IAQI对于单站点IAQI-PM2.5的预测拟合效果如图11所示。
图11 ST-CCN-IAQI对单测站IAQI-PM2.5的预测效果图

Fig. 11 IAQI-PM2.5 prediction performance via ST-CCN-IAQI on target station

对于绝大部分时刻，模型预测值和真实值之间偏差较小；某些时刻（如图11中的140、360时刻）IAQI-PM2.5预测值偏差较大。从整体上看，该模型在IAQI-PM2.5的平稳时段和非平稳时段均有着稳定、精确的预测表现，证明了模型对于IAQI-PM2.5具有良好的预测性能。

3.2.2 全部测站性能分析

为了进一步探究模型对各类空气污染物IAQI预测的泛化能力，本文采用ST-CCN-IAQI预测上海市全部站点IAQI-PM2.5、IAQI-PM10和IAQI-NO2，以RMSE、MAE、R2作为模型评价指标，并使用5折交叉验证方法，实验结果如表3。
表3 全部站点3种IAQI预测精度比较

Tab. 3 Comparison of three IAQI prediction accuracy of all stations

站点号 IAQI-PM2.5 IAQI-PM10 IAQI-NO2
RMSE MAE R2 RMSE MAE R2 RMSE MAE R2
1 11.079 8.474 0.885 5.822 4.619 0.812 3.508 2.735 0.872
2 9.873 7.469 0.917 6.447 5.085 0.827 3.378 2.470 0.867
3 10.018 7.766 0.878 5.713 4.524 0.782 2.056 1.567 0.870
4 9.020 6.652 0.909 4.917 3.865 0.869 3.047 2.267 0.859
5 10.293 7.972 0.895 5.904 4.666 0.825 3.070 2.236 0.878
6 9.845 7.611 0.929 5.124 3.961 0.929 3.347 2.593 0.880
7 9.294 7.131 0.930 6.387 4.937 0.778 3.156 2.405 0.870
8 10.004 7.747 0.887 5.011 3.816 0.884 4.181 3.269 0.771
9 9.218 6.926 0.928 7.330 5.826 0.800 2.710 2.029 0.875
平均值 9.849 7.527 0.906 5.850 4.588 0.834 3.161 2.396 0.860
表3中，ST-CCN-IAQI对全部站点的IAQI-PM2.5预测中，RMSE、MAE的平均值为9.849和7.527，R2的均值为0.906，说明模型的预测精度较高。与IAQI-PM2.5的结果相比，对全部站点的IAQI-PM10预测中，RMSE和MAE平均值分别为5.85和4.588，R2平均值为0.834，对全部站点的IAQI-NO2预测中，RMSE和MAE平均值分别为3.161和2.396，R2平均值为0.86，表明模型对IAQI-PM10和IAQI-NO2也有较好的预测效果。实验结果证明了模型的预测误差与拟合优度的波动区间较小且具有较强的泛化能力。为了直观显示模型对各站点空气污染物预测性能差异，本文以IAQI-PM2.5为例绘制了不同站点的模型预测性能对比图，如图12所示。
图12 不同站点预测性能对比

Fig. 12 Comparison of prediction performance among different stations.

如图12，相对于分布密集区站点（图2中的2、6、7等站点），ST-CCN-IAQI模型对边缘站点（图2中的1、3、8等站点）IAQI-PM2.5的预测效果相对较差，此外，ST-CCN-IAQI对一些内部站点（图2中的站点5）的IAQI-PM2.5预测时，模型有较大的预测误差且拟合程度偏差。一个可能的解释在于站点5所处的环境条件更加复杂，容易受到各种外界突发因素（交通状况，工厂生产等）的干扰。

3.2.3 模型差异显著性检验

本文采用Friedman检验测试ST-CCN-IAQI在细粒度IAQI预测方面是否明显优于基线模型，对模型差异显著性进行检验。本文从数据集的上四分位点、中位数、下四分位点的位置分别抽取原始数据集的10%的数据（每个四分位点前后分别提取5%原始数据集），构造3个Friedman检验数据集：data_25%、data_50%、data_75%。本文基于构造好的3个检验数据集和9种测试模型进行Friedman检验。首先利用3个Friedman检验数据集分别训练 9种模型，对IAQI-PM2.5进行单步预测，得到不同模型的RMSE值。其次，计算九种模型在3个数据集上RMSE值的平均排序数，如表4所示。最后通过计算 χ F 2和 F F，检验零假设H0：ST-CCN-IAQI和基线模型之间RMSE无显著差异。式(9)、式(10)分别是2个统计量的计算方法。
χ F 2 = 12 N k ( k + 1 ) ∑ R j 2 - k ( k + 1 ) 2 4
F F = ( N - 1 ) χ F 2 N ( k - 1 ) - χ F 2
式中： N和 k分别表示独立数据集数与模型数量； R j表示第 j个模型在不同数据集上的性能指标平均排名。
表4 9种模型在3种数据集上RMSE指标排名

Tab. 4 RMSE index ranking of 9 models in 3 data sets

数据集 AR MA ARMA ANN SVR GRU LSTM ST-GCN ST-CNN
data_25% 12.35(2) 17.12(9) 12.57(3) 13.03(8) 12.81(5) 12.87(7) 12.84(6) 12.61(4) 9.85(1)
data_50% 12.47(2) 17.67(9) 12.63(3) 13.12(7) 12.92(5) 13.12(7) 13.04(6) 12.76(4) 9.96(1)
data_75% 12.15(2) 17.43(9) 12.45(3) 12.93(7) 12.85(6) 12.97(8) 12.77(5) 12.68(4) 9.62(1)
平均值 2 9 3 7.3 5.3 7.3 5.7 4 1

注：括号内的数值代表模型在该数据集上RMSE值的排名（RMSE按升序排序）。

如表4分别计算出了9种模型在3个Friedman检验数据集上的RMSE值的平均排序数。本文利用式(9)、式(10)计算出与模型RMSE指标相关的 χ F 2 = 23.62， F F = 125.06。由于本文采用了9种算法模型和3个数据集，因此 F F遵循(9-1=8)和 ((9-1)×(3-1)=16)的自由度。当置信水平 α = 0.05时， F ( 8,16 )的临界值为2.59。显然，与RMSE指标相关的统计量 F F值均大于临界值2.59，因此拒绝之前的零假设，证明了本文提出的ST-CCN-IAQI与本文引用的基线模型预测性能有着显著 差异。

3.2.4 模型鲁棒性分析

为了探究ST-CCN-IAQI模型预测能力的鲁棒性，本文利用ST-CCN-IAQI分别预测各站点24个时刻的IAQI-PM2.5值，且对每个时刻进行十次预测。全部站点的实验结果为 X ∈ R S × H × T，其中S表示监测站点数，H代表不同时刻，T表示测试次数，从S轴将聚合实验结果，将实验结果压缩至二维，即 X n e w ∈ R H × T。降维是为了便于显示不同时刻的平均预测区间和预测值整体的变化趋势。本文基于降维处理后的数据绘制了小提琴图，如图13所示。
图13 基于全部站点的24个时刻IAQI-PM2.5预测值小提琴图

Fig. 13 Violin figure of IAQI-PM2.5 prediction at 24 moments

如图13，以小提琴图展示了未来24 h IAQI-PM2.5的波动区间与演变趋势。小提琴图由核密度图和箱线图融合构成。对于每个小提琴子图，内部是箱线图，外部包围的是核密度图。核密度图直观的显示了IAQI预测值的数据分布。通过箱线图，可以查看对应时刻的IAQI预测值的基本分布信息，例如内外限、上四分位数、下四分位数以及中位数。从不同时刻对应的小提琴子图，可以直观的看出24 h的IAQI-PM2.5值在稳定的区间内波动。且预测值有很大概率分布于真实值附近，证明了模型对IAQI预测的稳定性和准确性。图中蓝色线条表示10次预测均值，红色线条表示真实值。可以看出在7:00—10:00时间段内预测均值与真实值的误差相对较大，但绝大部分时刻IAQI-PM2.5的预测均值与真实值比较拟合，证明模型鲁棒性较强。

3.3 输入特征的影响力分析

为了定量分析输入特征对模型预测效果的影响，本文使用Shapley分析从局部（单样本）和全局角度（全部样本）分析各项输入特征对模型预测的正、负向增益。Shapley分析属于模型事后解释的方法，其核心思想是将所有输入特征视为贡献者，计算输入特征对预测值的贡献。对于每个预测样本（包含多项输入特征），黑盒模型都产生一个预测值，Shapley分析为每个特征计算影响力权重。然后，从全局和局部2个层面对黑盒模型进行解释。如图14是基于单个样本的Shapley局部分析结果。
图14 单个样本输入特征对IAQI-PM2.5的预测影响(局部)

Fig. 14 Influence of input features on IAQI-PM2.5 prediction (from local perspective)

如图14，利用Shapley分析方法可视化了单个样本中输入特征对输出特征预测的影响力，横轴为影响力权重值，纵轴表示各项输入特征与其数值。图14中 f ( x )代表考虑所有输入特征后一次预测的值， E ( f ( x ) )代表多次预测的均值，红条显示了一个特定特征在多大程度上增加了预测值，蓝条显示了某特征在多大程度上降低了预测值。在局部视角，IAQI-PM10对于IAQI-PM2.5有最大程度正向增益，使预测值上升了30.95。大气压强和温度对IAQI-PM2.5有较大程度的负向增益，使预测值分别降低了7.25、4.80。其余几项特征对输出特征的影响权重相对较小。
为了捕获各项输入特征对输出特征的实际影响权重，本文采用Shapley分析方法对全部样本中各项输入特征进行了分析，实验结果如图15所示。
图15 全部样本输入特征对IAQI-PM2.5的预测影响(全局)

Fig.15 Influence of input features on IAQI-PM2.5 prediction (from global perspective)

如图15，展示了全部样本中输入特征对IAQI-PM2.5预测的影响权重，横轴表示某项特征对模型输出的影响力权重，左侧纵轴代表不同特征，右侧纵轴用不同颜色代表特征值的高低，图中由高至低代表输入特征影响力的重要性的降低。从图15可以看出，PM10、湿度、NO2对PM2.5预测具有较强的影响能力，温度、压强、风速、天气4项特征对PM2.5预测影响能力相对较弱。在影响力较强的三项特征中，随着PM10、NO2值的降低，PM2.5的预测值有很大可能性随之降低，可能的原因是PM2.5、PM10、NO2同为交通尾气排放、工厂生产的主要污染物，它们一定程度呈正相关[48]。当湿度值较大时，对PM2.5的预测有正向驱动作用；当湿度较小时，对PM2.5预测值有负向驱动作用。这是因为较大的空气湿度更有利于PM2.5在空气中悬浮、滞留；相反，较低的空气湿度更有利于PM2.5借助风力扩散输送[49]。

4 讨论

4.1 多源影响因子对于预测结果的影响

3.3小节采用Shapley分析量化了多源影响因子对于模型预测结果的影响程度，实验结果表明，空气污染物之间相互影响程度比较显著，部分气象因素对IAQI也有重要影响。实验结果与常理相符，因为空气污染物之间会发生物理、化学耦合反应，从而改变空气污染物浓度。气象因素如风向、风速、气温、气压等对大气污染物的输送、扩散、稀释有着重要作用。
当前实验结果表明，融合多源影响因子对模型预测有着正向驱动作用。受当前数据条件所限，本文仍缺乏考虑以下影响因子，如地形、地物、交通状况等。在城市中，高大建筑物会使运动着的大气产生涡流，在涡流区内大气污染物很难逸散，涡流区会完全处在污染之中，在丘陵或山谷盆地也会产生类似的情况。此外，城市地区的交通状况也会带来大量污染物排放，包括颗粒物（PM）、CO、CO2、NOx等。如何量化这些影响因子对于模型预测结果的影响程度，是本文未来进一步的研究方向。

4.2 ST-CCN-IAQI相比典型深度学习模型的优势

当前IAQI预测领域中热门的时间、空间特征提取模型分别为基于RNN的模型和基于图的模型。基于RNN的模型存在着梯度消失和梯度爆炸、迭代传播耗时、内存需求大等弊端。基于图的模型也存在许多不稳定因素，比如人为定义变量之间的关系、利用马尔可夫假设解释变量间的交互以及难以捕获稳定的节点间的边缘关系。本文提出的ST-CCN-IAQI模型很好的克服了上述模型存在的问题。卷积神经网络可以捕获稳定的空间分布特征。堆叠膨胀卷积能够在内存需求小且避免梯度问题的前提下捕获长时、有效的时间特征。其次，ST-CCN-IAQI基于空间注意力机制优化了卷积神经网络对于空气污染物的空间特征提取。利用时间注意力机制使堆叠膨胀卷积更加关注时间依赖性强的时间段。时空注意力机制的引入使ST-CCN-IAQI相比深度学习模型有更强的时空特征提取能力。此外，本文提出的ST-CCN-IAQI模型提供了一个开放的框架。相比基于RNN的模型、基于图的模型，ST-CCN-IAQI能方便的将多源影响因素、多种卷积结构纳入空气污染物的预测建模中。

5 结论

本文提出了基于时空因果卷积网络的IAQI预测模型ST-CCN-IAQI。本文将多源影响因素作为模型输入，利用基于空间注意力的卷积神经网络提取站点间空间相关性，采用融合时间依赖性的堆叠膨胀卷积提取时间依赖性。本文通过贝叶斯优化方法自动提取了最佳参数组合，采用上海市空气监测站空气质量分指数（IAQI-PM2.5）数据展开实验，并采用一系列基线模型（AR、MA、ARMA、ANN、SVR、GRU、LSTM和ST-GCN）与ST-CCN-IAQI效果进行对比。实验结果表明：
（1）对于单个站点，ST-CCN-IAQI在IAQI-PM2.5预测任务中，在RMSE、MAE和R2方面的表现均优于基线模型。整体上ST-CCN-IAQI的RMSE和MAE值分别为9.873、7.469，相比基线模型平均下降了24.95%和16.87%，R2值平均提升了5.69%；
（2）对于全部站点，在IAQI-PM2.5预测任务中，ST-CCN-IAQI模型平均RMSE和MAE分别为9.849和7.527，R2值为0.906。该模型对全部站点的平均预测精度接近单站点预测精度，且模型的预测误差与拟合优度波动范围稳定。在IAQI-PM10、IAQI-NO2的预测中，该模型的性能维持在稳定的波动区间中，且平均预测性能仍具有良好的水平。证明了ST-CCN-IAQI具有较强的泛化能力和稳定性；
（3）采用Friedman检验论证了ST-CCN-IAQI在细粒度IAQI预测方面明显优于基线模型，包括自回归模型（AR）、滑动平均模型（MA）、自回归移动平均模型（ARMA）、人工神经网络（ANN）、支持向量机回归（SVR）、门控循环单元（GRU）、长短期记忆网络（LSTM）以及时空图卷积网络（ST-GCN）；
（4）通过Shapley方法定量分析了多源因素影响，证明了IAQI-PM10、湿度、IAQI-NO2对IAQI-PM2.5的预测有重要作用，温度、压强、风速、天气四项特征对IAQI-PM2.5的预测作用相对较小。本文采用的Shapley分析是完全基于数据驱动的方法，区别于传统大气模型，适用于影响因子的量化评价。Shapley分析可有效结合大气科学模型进行深入研究，适用于大气污染影响因子量化评价。
本文针对细粒度IAQI的预测研究将会在很大程度上提升城市空气质量指数的研究水平，为大气污染预测提供了一种新的研究思路。当前研究仍然存在一些局限：首先，当样本数据集太小时，本文的时空因果模型表现不佳；其次，本文仅对目标站点IAQI进行了单步预测，未来将围绕上述问题展开进一步研究。

：衷心感谢审稿专家、编辑部以及中国科学院大气物理研究所邓兆泽老师对本文提出的宝贵修改意见。

References

Publishing order | Descend order by publishing year | Descend order by cited within
[1]
Yang J, Yang Y X, Sun D Q, et al. Influence of urban morphological characteristics on thermal environment[J]. Sustainable Cities and Society, 2021, 72:103045. DOI:10.1016/j.scs.2021.103045

DOI

[2]
林金煌, 陈文惠, 张岸. 2019年北京市 PM2.5人群暴露剂量特征分析[J]. 地球信息科学学报, 2020, 22(12):2348-2357.

DOI

[Lin J H, Chen W H, Zhang A. Analysis of PM2.5 population exposure doses characteristics in Beijing in 2019[J]. Journal of Geo-Information Science, 2020, 22(12):2348-2357. ] DOI:10.12082/dqxxkx.2020.190624

DOI

[3]
Hong C P, Zhang Q, Zhang Y, et al. Impacts of climate change on future air quality and human health in China[J]. PNAS, 2019, 116(35):17193-17200. DOI:10.1073/pnas.1812881116

DOI PMID

[4]
Goodkind A L, Tessum C W, Coggins J S, et al. Fine-scale damage estimates of particulate matter air pollution reveal opportunities for location-specific mitigation of emissions[J]. PNAS, 2019, 116(18):8775-8780. DOI:10.1073/pnas.1816102116

DOI PMID

[5]
师泽源, 赵俭辉, 张文昱, 等. 基于扩展场强模型的稀疏AQI空间插值新算法[J]. 武汉大学学报·信息科学版, 2017, 42(7):968-974.

[Shi Z Y, Zhao J H, Zhang W Y, et al. New spatial interpolation algorithm for sparse AQI based on extended field intensity model[J]. Geomatics and Information Science of Wuhan University, 2017, 42(7):968-974. ] DOI:10.13203/j.whugis20140980

DOI

[6]
Samal K K R, Panda A K, Babu K S, et al. An improved pollution forecasting model with meteorological impact using multiple imputation and fine-tuning approach[J]. Sustainable Cities and Society, 2021, 70:102923. DOI:10.1016/j.scs.2021.102923

DOI

[7]
程诗奋, 彭澎, 张恒才, 等. 异质稀疏分布时空数据插值、重构与预测方法探讨[J]. 武汉大学学报·信息科学版, 2020, 45(12):1919-1929.

[Cheng S F, Peng P, Zhang H C, et al. Review of interpolation, reconstruction and prediction methods for heterogeneous and sparsely distributed geospatial data[J]. Geomatics and Information Science of Wuhan University, 2020, 45(12):1919-1929. ] DOI:10.13203/j.whugis20200488

DOI

[8]
冯子钰, 施润和. 中国近地面PM2.5浓度与排放的时空分布及其关联分析[J]. 地球信息科学学报, 2021, 23(7):1221-1230.

DOI

[Feng Z Y, Shi R H. Spatio-temporal features and the association of ground-level PM2.5 concentration and its emission in China[J]. Journal of Geo-Information Science, 2021, 23(7):1221-1230. ] DOI:10.12082/dqxxkx.2021.200367

DOI

[9]
Yu B, Yin H T, Zhu Z X. Spatio-temporal graph convolutional networks: A deep learning framework for traffic forecasting[EB/OL]. 2017: arXiv: 1709.04875. https://arxiv.org/abs/1709.04875

[10]
钟雨桐, 韦晶, 郑月明, 等. 基于静风期污染物的PM2.5排放清单空间精细化方法[J]. 地球信息科学学报, 2021, 23(11):1971-1983.

DOI

[Zhong Y T, Wei J, Zheng Y M, et al. Spatial refinement method of the PM2.5 emission inventory based on the quiescent period pollutant[J]. Journal of Geo-Information Science, 2021, 23(11):1971-1983. ] DOI:10.12082/dqxxkx.2021.210290

DOI

[11]
Sharma A, Valdes A C F, Lee Y H. Impact of wildfires on meteorology and air quality (PM2.5and O3) over western United States during September 2017[J]. Atmosphere, 2022, 13(2):262. DOI:10.3390/atmos13020262

DOI

[12]
Zhao J J, Lin S F, Liu X L, et al. ST-CCN-PM2.5: Fine-grained PM2.5 concentration prediction via spatial-temporal causal convolution network[C]// ARIC '21: Proceedings of the 4th ACM SIGSPATIAL International Workshop on Advances in Resilient and Intelligent Cities. 2021:48-55. DOI:10.1145/3486626.3493433

DOI

[13]
Barthwal A, Acharya D. An IoT based sensing system for modeling and forecasting urban air quality[J]. Wireless Personal Communications, 2021, 116(4):3503-3526. DOI:10.1007/s11277-020-07862-6

DOI

[14]
Gu Y L, Li B H, Meng Q G. Hybrid interpretable predictive machine learning model for air pollution prediction[J]. Neurocomputing, 2022, 468:123-136. DOI:10.1016/j.neucom.2021.09.051

DOI

[15]
杜震洪, 吴森森, 王中一, 等. 基于地理神经网络加权回归的中国PM2.5浓度空间分布估算方法[J]. 地球信息科学学报, 2020, 22(1):122-135.

DOI

[Du Z H, Wu S S, Wang Z Y, et al. Estimating ground-level PM2.5 concentrations across China using geographically neural network weighted regression[J]. Journal of Geo-information Science, 2020, 22(1):122-135. ] DOI:10.12082/dqxxkx.2020.190533

DOI

[16]
李清泉, 高德荃, 杨必胜. 基于模糊支持向量机的城市道路交通状态分类[J]. 吉林大学学报(工学版), 2009, 39(S2):131-134.

[Li Q Q, Gao D Q, Yang B S. Urban Road traffic status classification based on fuzzy support vector machines[J]. Journal of Jilin University (Engineering and Technology Edition), 2009, 39(S2):131-134. ] DOI:10.1329/j.cnki.jdxbgxb2009.s2.049

DOI

[17]
Hung W T, Lu C H S, Alessandrini S, et al. Estimation of PM2.5 concentrations in New York State: Understanding the influence of vertical mixing on surface PM2.5 using machine learning[J]. Atmosphere, 2020, 11(12):1303. DOI: 10.3390/atmos11121303

DOI

[18]
Nidzgorska-Lencewicz J. Application of artificial neural networks in the prediction of PM10 levels in the winter months: A case study in the tricity agglomeration, Poland[J]. Atmosphere, 2018, 9(6):203. DOI:10.3390/atmos9060203

DOI

[19]
Motesaddi S, Nowrouz P, Alizadeh B, et al. Sulfur dioxide AQI modeling by artificial neural network in Tehran between 2007 and 2013[J]. Environmental Health Engineering and Management Journal, 2015, 2(4):173-178.

[20]
Bera B, Bhattacharjee S, Sengupta N, et al. PM2.5 concentration prediction during COVID-19 lockdown over Kolkata metropolitan city, India using MLR and ANN models[J]. Environmental Challenges, 2021, 4:100155. DOI:10.1016/j.envc.2021.100155

DOI

[21]
Zhou Y L, Chang F J, Chen H, et al. Exploring Copula-based Bayesian Model Averaging with multiple ANNs for PM2. 5 ensemble forecasts[J]. Journal of Cleaner Production, 2020, 263:121528. DOI:10.1016/j.jclepro.2020.121528

DOI

[22]
Hu J L, Yang B, Guo C J, et al. Stochastic origin-destination matrix forecasting using dual-stage graph convolutional, recurrent neural networks[C]// 2020 IEEE 36th International Conference on Data Engineering. IEEE, 2020:1417-1428. DOI:10.1109/ICDE48307.2020.00126

DOI

[23]
Wang J Y, Li X L, Wang T T, et al. A CA-GRU-based model for air quality prediction[J]. International Journal of Ad Hoc and Ubiquitous Computing, 2021, 38(1/2/3):184. DOI:10.1504/ijahuc.2021.119098

DOI

[24]
Yang G, Lee H, Lee G. A hybrid deep learning model to forecast particulate matter concentration levels in Seoul, south Korea[J]. Atmosphere, 2020, 11(4):348. DOI:10.3390/atmos11040348

DOI

[25]
Weerakody P B, Wong K W, Wang G J, et al. A review of irregular time series data handling with gated recurrent neural networks[J]. Neurocomputing, 2021, 441:161-178. DOI:10.1016/j.neucom.2021.02.046

DOI

[26]
Li X, Peng L, Yao X J, et al. Long short-term memory neural network for air pollutant concentration predictions: Method development and evaluation[J]. Environmental Pollution (Barking, Essex: 1987), 2017, 231(Pt 1):997-1004. DOI:10.1016/j.envpol.2017.08.114

DOI

[27]
Jiang X C, Luo Y W, Zhang B. Prediction of PM2.5 concentration based on the LSTM-TSLightGBM variable weight combination model[J]. Atmosphere, 2021, 12(9):1211. DOI:10.3390/atmos12091211

DOI

[28]
Dai H B, Huang G Q, Wang J J, et al. Prediction of air pollutant concentration based on one-dimensional multi-scale CNN-LSTM considering spatial-temporal characteristics: A case study of Xi'an, China[J]. Atmosphere, 2021, 12(12):1626. DOI:10.3390/atmos12121626

DOI

[29]
Park D O, Yoo G W, Park S, et al. Assessment and calibration of a low-cost PM2.5 sensor using machine learning (HybridLSTM neural network): Feasibility study to build an air quality monitoring system[J]. Atmosphere, 2021, 12(10):1306. DOI:10.3390/atmos12101306

DOI

[30]
Shi L K, Zhang H Z, Xu X, et al. A balanced social LSTM for PM2.5 concentration prediction based on local spatiotemporal correlation[J]. Chemosphere, 2022, 291:133124. DOI:10.1016/j.chemosphere.2021.133124

DOI

[31]
Liu B C, Binaykia A, Chang P C, et al. Urban air quality forecasting based on multi-dimensional collaborative Support Vector Regression (SVR): A case study of Beijing-Tianjin-Shijiazhuang[J]. PLoS One, 2017, 12(7):e0179763. DOI:10.1371/journal.pone.0179763

DOI

[32]
Yan R, Liao J Q, Yang J, et al. Multi-hour and multi-site air quality index forecasting in Beijing using CNN, LSTM, CNN-LSTM, and spatiotemporal clustering[J]. Expert Systems With Applications, 2021, 169:114513. DOI:10.1016/j.eswa.2020.114513

DOI

[33]
Seo Y, Defferrard M, Vandergheynst P, et al. Structured sequence modeling with graph convolutional recurrent networks[M]// Neural Information Processing. Cham: Springer International Publishing, 2018:362-373. DOI:10.1007/978-3-030-04167-0_33

DOI

[34]
Zhao L, Song Y, Zhang C, et al. T-GCN: A temporal graph convolutional network for traffic prediction[J]. IEEE Transactions on Intelligent Transportation Systems, 2019:21,3848-3858. DOI:10.1109/TITS.2019.2935152

DOI

[35]
Wu Z H, Pan S R, Long G D, et al. Graph WaveNet for deep spatial-temporal graph modeling[EB/OL]. 2019: arXiv: 1906.00121. https://arxiv.org/abs/1906.00121

[36]
Jiao Y, Wang Z F, Zhang Y. Prediction of air quality index based on LSTM[C]// 2019 IEEE 8th Joint International Information Technology and Artificial Intelligence Conference. IEEE, 2019:17-20. DOI:10.1109/ITAIC.2019.8785602

DOI

[37]
Feng X, Li Q, Zhu Y J, et al. Artificial neural networks forecasting of PM2.5 pollution using air mass trajectory based geographic model and wavelet transformation[J]. Atmospheric Environment, 2015, 107:118-128. DOI:10.1016/j.atmosenv.2015.02.030

DOI

[38]
Pak U, Ma J, Ryu U, et al. Deep learning-based PM2.5 prediction considering the spatiotemporal correlations: A case study of Beijing, China[J]. The Science of the Total Environment, 2020, 699:133561. DOI:10.1016/j.scitotenv.2019.07.367

DOI

[39]
高旺旺, 冯建中, 白林燕, 等. 海南岛气溶胶时空变化及来源追溯[J]. 地球信息科学学报, 2020, 22(7):1532-1543.

DOI

[Gao W W, Feng J Z, Bai L Y, et al. Spatiotemporal dynamics and tracing of aerosol over Hainan Island[J]. Journal of Geo-Information Science, 2020, 22(7):1532-1543. ] DOI:10.13203/j.whugis20200488

DOI

[40]
Zhang L B, Liu Y Q, Zhao F J. Important meteorological variables for statistical long-term air quality prediction in Eastern China[J]. Theoretical and Applied Climatology, 2018, 134(1/2):25-36. DOI:10.1007/s00704-017-2245-z

DOI

[41]
徐艺武. 北京市PM2.55污染的时空分布与主要空气污染物的关系[J]. 科技创新与应用, 2016(33):143.

[Xu Y W. Relationship between the temporal and spatial distribution of PM2.5 pollution and major air pollutants in Beijing[J]. Technology Innovation and Application, 2016(33): 143. ] DOI:CNKI:SUN:CXYY.0.2016-33-123

DOI

[42]
Zheng Y, Liu F, Hsieh H P. U-air: When urban air quality inference meets big data[C]// Proceedings of the 19th ACM SIGKDD international conference on Knowledge discovery and data mining, 2013:1436-1444. DOI:10.1145/2487575.2488188

DOI

[43]
Bai S J, Kolter J Z, Koltun V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling[J]. arXiv preprint arXiv, 2018,1803.01271. DOI:10.48550/arXiv.1803.01271

DOI

[44]
Zhang L, Na J M, Zhu J, et al. Spatiotemporal causal convolutional network for forecasting hourly PM2.5 concentrations in Beijing, China[J]. Computers & Geosciences, 2021, 155:104869. DOI:10.1016/j.cageo.2021.104869

DOI

[45]
Mihaljević B, Bielza C, Larrañaga P. Bayesian networks for interpretable machine learning and optimization[J]. Neurocomputing, 2021, 456:648-665. DOI:10.1016/j.neucom.2021.01.138

DOI

[46]
Marcellino M, Stock J H, Watson M W. A comparison of direct and iterated multistep AR methods for forecasting macroeconomic time series[J]. Journal of Econometrics, 2006, 135(1/2):499-526. DOI:10.1016/j.jeconom.2005.07.020

DOI

[47]
Lento C. Forecasting security returns with simple moving averages[J]. International Business & Economics Research Journal (IBER), 2011, 7(11):11-22. DOI:10.19030/iber.v7i11.3304

DOI

[48]
Xie Y Y, Zhao B, Zhang L, et al. Spatiotemporal variations of PM2.5 and PM10 concentrations between 31 Chinese Cities and their relationships with SO2, NO2, CO and O3[J]. Particuology, 2015, 20:141-149. DOI:10.1016/j.partic.2015.01.003

DOI

[49]
宋明, 韩素芹, 张敏, 等. 天津大气能见度与相对湿度和PM10及 PM2.5的关系[J]. 气象与环境学报, 2013, 29(2):34-41.

[Song M, Han S Q, Zhang M, et al. Relationship between visibility and relative humidity, PM10, PM2.5 in Tianjin[J]. Journal of Meteorology and Environment, 2013, 29(2):34-41. ] DOI:10.3969/j.issn.1673-503X.2013.02.006

DOI

Options
Outlines

/

〈 〉