EN中文

Journal of Geo-information Science >

2023 , Vol. 25 >Issue 1: 142 - 152

DOI: https://doi.org/10.12082/dqxxkx.2023.220520

A Thinning Algorithm of Multibeam Sounding Data Considering Slope and Elevation

  • QI Linjun , 1 ,
  • ZHAI Renjian , 1, * ,
  • LI Anping 1, 2
Expand
  • 1. Information Engineering University, Geospatial Information Institute, Zhengzhou 450001, China
  • 2. 78098 Troops, Chengdu 610000, China
*ZHAI Renjian, E-mail:

Received date: 2022-07-11

  Revised date: 2022-10-09

  Online published: 2023-03-25

Supported by

National Security Major Basic Research Project(613317)

Fold

Abstract

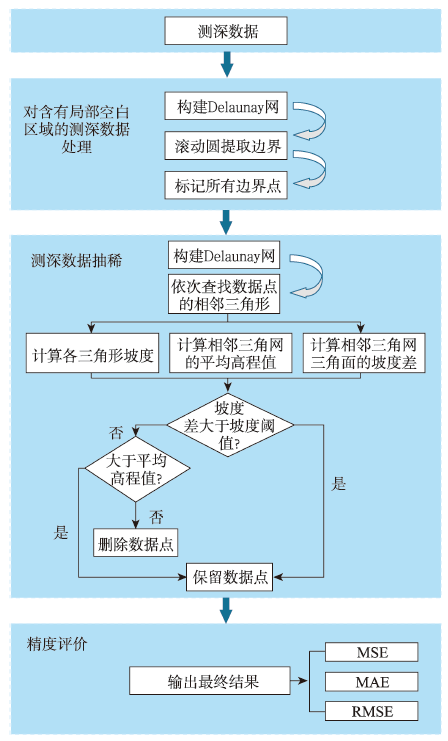
The submarine topographic data are important data source for marine scientific research and engineering construction. The bathymetric information, as the basic information of submarine topographic data, reflects the undulating changes of submarine topography. Therefore, how to effectively process bathymetric data has become a key research content of marine mapping. In order to solve the problem of data redundancy of massive multibeam bathymetry data, a multibeam bathymetry data thinning algorithm taking into account the slope and elevation is proposed, which can balance the accuracy of data thinning and the retaining of topographic feature points. Considering that the multibeam bathymetry data contain local blank areas such as cavities and concave boundaries, the Alpha Shape algorithm is first used to extract boundary points from the multibeam bathymetry data, so as to avoid the problem of losing terrain feature points due to thinning of the local bathymetry data blank areas. Then, a combination of slope and elevation thinning algorithms was used to delete redundant points and retain terrain feature points, and the boundary points of the thinned multibeam bathymetric data (containing local blank areas) are combined to obtain final thinning results. The accuracy is evaluated by using the checkpoint method. In the study area, the comparison experiments are carried out using the slope-based thinning, terrain complexity-based thinning, and system based thinning algorithms as references. The results show that: (1) The isobath derived from our proposed algorithm in the area containing local blank areas is closer to the isobath variation of the original bathymetric data compared to three reference thinning algorithms, and can more precisely express the fine features at the concave boundaries, hollows, and other areas and effectively maintain the morphological integrity of the seafloor topography; (2) The accuracy of the proposed algorithm is improved in different degrees compared with the reference thinning algorithms. Especially, as the thinning rate decreases, the Mean Square Error (MSE) of the proposed algorithm is decreased by 16%, 27%, 14%, and 10%, 36%, 2%, respectively in two kinds of terrain, and the Root Mean Square Error (RMSE) is decreased by 7%, 12%, 7% and 5%, 17%, 3% for two types of terrain, respectively, which demonstrates the effectiveness and generalizability of the proposed algorithm for thinning of multibeam bathymetric data in different types of terrains, improving the accuracy of bathymetric data thinning effectively, and meeting the needs of subsequent bathymetric data construction of high-precision seafloor topography.

Key words： multibeam sounding data; Delaunay triangulation network; thinning algorithm; topographic features; data processing

Cite this article

QI Linjun , ZHAI Renjian , LI Anping . A Thinning Algorithm of Multibeam Sounding Data Considering Slope and Elevation[J]. Journal of Geo-information Science, 2023 , 25(1) : 142 -152 . DOI: 10.12082/dqxxkx.2023.220520

1 引言

海洋测绘技术日渐成熟，为获取大面积、高精度的海洋基础地理信息提供了技术支撑。海底地形测量是海洋测绘的一项基础性任务[1]，多采用船基海底地形测量、水深测量和反演技术等测量方法。水深测量中的多波束测深具有高密度、高分辨率、全覆盖等特点，已广泛应用于海洋工程建设、海洋生态治理等领域。
多波束测深系统的单个条带能包含多达几百甚至上千个高密度数据点，在数十至数百平方千米的工作范围内，获得的多波束测深数据通常会产生TB级的数据量[2]，条带内的高密度水深数据存在冗余信息和数据重叠，庞大数据量为存储和实际应用带来诸多不便。因此，需要对修正后的海量多波束测深数据进行抽稀简化，抽稀后的测深数据集应满足精准表达海底地形特征的需求，满足海图生产和高精度海底地形构建的需要。
目前，国内外现有点云数据抽稀根据地形特征因素的保留与否，可分为随机采样[3]和考虑地形特征因素的抽稀算法。随机采样抽稀主要方法包括：① 基于格网的抽稀[4]，将所有水深点划分为若干个规则格网，每个格网中保留一个水深点；② 基于系统的抽稀[5]，是在所有水深点中选取某个点作为起始点，按照采样间隔随机抽取一点保留。非选择性抽稀算法的优点是处理速度快，但冗余信息和非冗余信息受到同等削弱，不能有效保留地形特征点[6]。
考虑地形特征因素的抽稀算法主要方法有以下6种：① 基于高程抽稀。Pamela[7]提出的DDR抽稀算法依靠搜索半径及高差阈值2个参数控制抽稀的程度和精度；徐景中等[8]提出的点云离散度抽稀算法借助数据点高程差异的量化大小表示地形起伏的高低，通过点的离散度判断该点对局部区域地形起伏的贡献程度，利用高程和距离阈值确定区域内数据点的保留与否[3]；② 基于TIN抽稀，构建不规则三角网后，采用法向量夹角[9]、坡度[5]和高差[10⇓⇓-13]等参数对点云数据进行抽稀；Yin等[14]在不规则三角网内嵌入等深线约束，利用改进的多对角交换算法调整三角网结构来保留特征点；③ 基于边界抽稀[15-16]，利用网格法判别数据的空间边界范围后，再基于凸壳内缩法对空间范围内的数据提取边界； ④ 顾及地形复杂度抽稀[17]，通过提取数据的各单一地形因子计算其贡献值，得到融合各因子的地形复杂度，再依据量化的地形复杂值设置不同的地形和相应的抽稀策略。⑤ 基于OptD法抽稀。Blaszczak等[18]提出设置优化标准f （例如抽稀后的点数， DEM平均误差等标准），通过对实验区域所划分的测量条带进行Douglas-Peucker[19]算法分析，不断调整公差和测量带宽度，直到满足优化标准；⑥ 基于TBDRed[20⇓-22]法抽稀，将测深数据集划分为更小的子集，通过利用神经网络进行聚类，在聚类后给定的子集中选择一个或多个最小深度的点。综上所述的抽稀方法，其优点在于考虑了海底地形特征点的保留，但仍存在一些问题，如基于高程抽稀的算法需不断搜索一定范围内的点，数据处理的速度不高[5]；基于TIN的抽稀阈值一般采用单一的地形因子，如坡度、高差进行抽稀，但单一的地形指标是一种简单的抽稀判断依据，在坡度较小的区域易出现错误[17]；边界抽稀算法采用网格提取边界，涉及大量的空间运算，处理海量水深数据时效率较低；顾及地形复杂度抽稀算法将海底地形按照量化的地形复杂值分为3类，但在局部水深信息空白区域易出现错误的地形分类，导致地形特征点丢失；基于TBDRed法的所有参数值都依赖于数据范围和测试区域的深度，适用于浅水区域，在更深海域时效率较低。
由于海底地形复杂多变，外业测量中的多波束测深数据含有数据空白（陆地岛屿）、边界内凹等区域。为了提高多波束测深数据抽稀的准确性，本文提出一种顾及坡度和高程的多波束抽稀算法，首先利用Alpha Shape算法提取水深数据中空洞、凹边界等局部空白区域边界点，确保海底地形的整体形态完整性，遵循了地形完善性准则[23]；将坡度和高程值相结合，利用对高程值的二次判断辅助提取地形特征点，提高测深数据抽稀的准确性且兼顾海底地形特征的表达，精确反映海底地形的变化情况。

2 研究方法

本文提出了一种适用于多波束测深数据的抽稀方法，研究的技术路线如图1所示。当受陆地地形等因素导致多波束测深数据含有空洞、凹边界等局部空白区域时：①利用Alpha Shape算法对此类测深数据进行提取边界点的预处理；② 利用顾及坡度和高程的抽稀算法对测深数据抽稀；③对输出得到的结果进行精度评价。
图1 技术流程

Fig. 1 Technical flow chart

2.1 轮廓边界提取

海底地形数据是海洋学各类研究的基础数据，在海洋气象和化学等领域发挥着重要作用[24⇓-26]。许多海洋工程的应用需要详细的海底地形数据和水深测绘信息[27]，反映出海底地形的起伏变化，其中测深数据边界点是等深线几何轮廓形状最基础的保证，但在抽稀过程中易丢失，导致抽稀后海底地形形态不完整。因此，本文在抽稀过程中先提取测深数据中空洞、内凹等局部空白区域轮廓点，明确了陆地岛屿区域，确保海底地形特征的完整性，为工程应用、海洋科学研究等提供更详细的海底地形信息。
Edelsbrunner[28]提出的Alpha Shape算法是一种简单、有效的点云轮廓提取算法，其基本原理是将半径为a的圆绕任意形状的点集滚动，不断调整滚动圆半径a的取值，当滚动圆只在边界点上滚动，其滚动的痕迹则为点集的边界线。Alpha Shape算法能够保留无序点集的形状细节，常用于提取LiDAR数据的建筑物轮廓线[29]。因测深数据和LiDAR数据存在较多相似之处， Alpha Shape算法同样适用于点云密度相对均匀的多波束测深数据，可以有效提取多波束测深数据的内部空洞、凹边界等轮廓，避免出现测深数据中空洞、凹边界等局部空白区域因抽稀导致地形特征点丢失的问题。
本文参照文献[30]的Alpha Shape算法对含有空洞、凹边界的多波束测深数据提取边界点。 ① 确定滚动圆半径a，将给定的三维测深点集S投影至二维平面；② 构建点集S的二维Delaunay三角网，具体步骤如下：
（1）对点集S构建Delaunay三角网；
（2）计算三角形中某条边的长度，若大于2×a，无法找到过该边的2个圆，不作处理继续计算，若小于2×a，则进行步骤（3）；
（3）遍历三角形，对三角形的每条边进行判断：过某条边的两点p、q且半径为a的2个圆，其中一个圆不包含点集中的其他点（图2(a)），则标记为边界点，反之删除该三角形（图2(b)）；
图2 Alpha Shape算法提取边界示意图[30]

Fig. 2 Schematic of the Alpha Shape algorithm for extracting boundaries

（4）将步骤（2）—（3）中符合要求的测深点构成点集的边界，标记所有边界点（图2(c)）。

2.2 测深数据抽稀

基于TIN的抽稀算法是对离散的原始多波束测深数据构建TIN，不规则三角网充分考虑了每个点对其周围邻域的贡献度，依据不同的单一参数对测深数据抽稀。顾及坡度和高程的多波束测深数据抽稀是在构建TIN的基础上，将坡度和高程特征用于测深点取舍判断。坡度和高程值分别反映了局部区域的倾斜程度和地形变化，是判断海底地形特征的重要因素。坡度是以三角形的3个顶点坐标 x 1 , y 1 , z 1 、 x 2 , y 2 , z 2 、 x 3 , y 3 , z 3确定的拟合平面为基础，式（1）为拟合平面的一般表达式，其中 A 、 B 、 C 、 D为待定系数，将其变换得到式（2）关于x和y的函数 z， f u 、 f v表示X和Y方向上的高程变化率，计算得到三角形的坡度。
A x + B y + C z + D = 0
z = - A C x - B C y - D C
f u = - A C f v = - B C s l o p e = a r c t a n f u 2 + f v 2
本文对坡度抽稀[5]算法加以改进，考虑到测深数据特点和《海道测量规范》[31]未明确海底地形的量化分类指标，不再设定地形类别，通过设置坡度阈值和高程阈值保留地形特征点，避免了在坡度较小区域出现地形特征点丢失的情况。对顾及坡度和高程的测深数据抽稀进行分析，可分为以下2种情况：① 坡度差值较大的非平坦区域。坡差较大的区域通常为斜坡或局部凹凸，表明地形起伏较大，通过设置坡度阈值易保留地形特征点；② 坡度差值较小的区域。若相邻三角形间的坡差较小，则分为坡度小的平坦区域和陡坡处的平缓地带，为避免区域地形特征点的丢失，通过结合高程值进行二次判断，保留符合要求的地形特征点。
具体抽稀算法步骤如下：
（1）对所有离散测深点，生成不规则三角网；
（2）遍历测深点，依次读入每一个点作为中心点，通过三角网拓扑关系找到该中心点（如图3中H点）的相邻三角形；
图3 中心点H的相邻三角形

Fig. 3 Adjacent triangle to centre point H

（3）计算中心点相邻三角形中各三角形的坡度；
（4）求得中心点所在相邻三角网的平均高程；
（5）求取中心点相邻三角形中最大和最小坡度的差值，即坡度差；
（6）设置坡度阈值，若坡度差大于坡度阈值，保留该中心点，反之则进行下一步判断；
（7）判断该中心点高程值和其相邻三角形中平均高程值的大小，若大于平均高程值，保留该点，否则删除；
（8）遍历所有的数据点，重复步骤(2)—（7）。
当多波束测深数据存在空洞、凹边界等区域时，首先采用Alpha Shape算法提取边界点，然后将边界点与抽稀后的测深点合并，得到最终结果。

2.3 精度评价

测深数据抽稀是在海量数据和精度之间达到最优平衡，并没有改变测深点原有的高程值。因此，多波束测深数据抽稀前后的数据精度采用检查点法进行评价，即从原始多波束测深数据中抽取一定比例的测深点作为检查点，其余点作为训练点集。利用抽稀后的训练点集内插生成DEM，获得检查点的高程值。通过计算检查点实际高程值和内插高程值的接近程度和偏离程度反映地形特征点保留的准确性，其常用指标有均方误差（Mean Square Error, MSE）、平均绝对误差（Mean Absolute Error, MAE）和均方根误差（Root Mean Square Error, RMSE），依据上述3种精度评价指标验证抽稀算法的精度。
M S E = ∑ i = 1 n Z k - P k 2 n
M A E = ∑ i = 1 n Z k - P k n
R M S E = ∑ i = 1 n Z k - P k 2 n
式中： Z k表示第 k个检查点的真实水深值； P k表示第 k个训练点集抽稀后内插出的高程值， n为检查点个数。

3 实验与分析

3.1 实验区域

为验证本文算法对多波束测深数据抽稀的有效性，选取多个海域的原始多波束测深数据进行分析，如图4所示。测区A的水下地形较平坦，其水深值在0.1~31 m间，平均水深约为14 m，测深数据点的平均密度约1.4 个/m2。测区B的水下整体地形较复杂且波动起伏较大，从南到北呈现“U”形走向，在南侧海域地势较高且含有多个突变起伏，海域中部水深值较大呈下凹状，向北侧延伸逐渐趋向平坦，其总体水深值在20~70 m间，平均水深约为 38 m，测深数据点的平均密度约24.5 个/m2。
图4 测区位置示意

Fig. 4 Location map of the survey area

3.2 边界提取

如上述图4（a）所示，测区A的中部区域是呈东北-西南走向的陆地岛屿，因受到岛屿地形要素影响，多波束测深系统在该陆地岛屿的水下区域出现数据空白区，即测区A的多波束测深数据含有空洞、凹边界等复杂区域。为提高测深数据抽稀的准确性且更加精确地显示局部信息，利用Alpha Shape算法对含有空洞等复杂区域的多波束测深数据进行处理。如图5所示，图中圆圈是半径为a的滚动圆，红色线段是滚动圆绕测深数据点集提取的边界线，线段中的各点是需要保留的边界点。其中半径a的取值一般与测深数据的平均点间距相关[32-33]，在实验过程中依据边界点的提取效果和抽稀要求确定最佳值，本文经过多次实验给定a ≈0.56。根据图中提取的局部边界线可以看出，空洞区域的轮廓和凹边界处的突变点能够被识别标记，表明了Alpha Shape算法识别提取空洞等复杂区域边界点的效果较好，确保了测深区域内海底地形形态的完整性。
图5 测区A的局部边界提取

注:凹边界、空洞为局部水深点空白区域。

Fig. 5 Local boundary extraction for survey area A

为验证测深数据边界点的提取能够有效保留海底地形的细节信息，在相同抽稀率下，分别将提取边界点、未提取边界点的本文算法与坡度抽稀[5]算法、顾及地形复杂度抽稀[17]算法、系统抽稀算法进行比较。如图6所示，图6（b）—图6（f）是各抽稀算法得到的等深线，通过与图6（a）原始数据等深线进行比对，可以明显看出图6（c）—图6（f）在空洞区域等深线处的细小弯曲部分表达不够细致，图6（c）、（d）和图6（f）在间隙较小的等深线处产生不合理收缩（图6红色圆圈标注区域）。相较而言，本文算法（图6（b））在空洞区域等深线的形态轮廓更贴近原始数据等深线的曲折变化，在细小等深线的弯曲突起处也能够清晰地表达，由此可知本文算法提取边界点利于海底地形特征的表达和保留更加丰富的地形信息。
图6 测区A的局部等深线

Fig. 6 Local isobaths in survey area A

3.3 精度评价结果及比较

将本文抽稀算法与基于坡度抽稀[5]算法、顾及地形复杂度抽稀[17]算法、系统抽稀算法进行对比实验，比较在不同抽稀率下上述4种抽稀算法结果的数据精度。
多波束测深数据抽稀精度因受多波束测深系统性能和工作设置、测深数据差异（水深值、测深点个数和测深点密度）等因素影响，不同海区、不同设备数据源和不同深度的误差指标大小存在差异。从表1可以看出，当测区A的多波束测深数据在相同抽稀率的情况下，本文抽稀算法的3种误差均小于基于坡度、顾及地形复杂度抽稀算法和系统抽稀算法的抽稀误差，可反映出本文算法对含有空洞等区域的多波束测深数据的抽稀精度优于对比的抽稀算法。由表2可知，当测区B保持较高抽稀率时，本文算法和顾及地形复杂度抽稀算法精度较高，坡度抽稀算法和系统抽稀算法精度较低。其中随着测区数据抽稀率的降低，本文抽稀算法的误差变化幅度较小，基于坡度抽稀、顾及地形复杂度抽稀算法和系统抽稀算法的误差则出现较大幅度增长，表明本文抽稀算法中地形特征表达的准确性受抽稀率的变化影响较小，其抽稀结果较稳定且精度较高。
表1 测区A抽稀方法评估

Tab. 1 Survey area A thinning method assessment

数据源 抽稀率/% 抽稀方法 MSE MAE RMSE




测区A		 92 本文算法 8.879 1.727 2.979
坡度抽稀法 9.261 1.794 3.043
顾及地形复杂度抽稀法 10.829 1.969 3.290
系统抽稀法 9.280 1.817 3.046
68 本文算法 9.395 1.738 3.065
坡度抽稀法 10.940 1.957 3.307
顾及地形复杂度抽稀法 11.971 2.122 3.460
系统抽稀法 10.775 1.972 3.282
表2 测区B抽稀方法评估

Tab. 2 Survey area B thinning method assessment

数据源 抽稀率/% 抽稀方法 MSE MAE RMSE




测区B		 85 本文算法 0.165 0.130 0.407
坡度抽稀法 0.173 0.128 0.416
顾及地形复杂度抽稀法 0.150 0.126 0.387
系统抽稀法 0.170 0.131 0.412
50 本文算法 0.235 0.172 0.483
坡度抽稀法 0.260 0.168 0.510
顾及地形复杂度抽稀法 0.321 0.209 0.567
系统抽稀法 0.242 0.175 0.498
对测区A、B的原始数据DDM和各抽稀方法插值DDM的水深值进行量化评价，选用最小值、最大值和标准差作为衡量指标，其中标准差反映了水深值的变化与起伏程度，值越大则地形起伏程度越大，量化结果如表3所示。当2组测深数据在抽稀程度较大时，与原始数据DDM进行比较，可知本文算法的最小、最大值和标准差更接近原始数据DDM，表明本文算法内插DDM的地形起伏变化能保持较高的精确性，从侧面反映了提取地形特征点的准确性。
表3 水深值量化评价

Tab. 3 Quantitative Evaluation of Water Depth Values

数据源 类型 最小值/m 最大值/m 标准差


测区A		 原始数据 -30.71 -0.10 6.86
本文算法 -28.91 -0.24 6.22
坡度抽稀法 -27.12 -0.24 6.08
顾及地形复杂度抽稀法 -26.69 -0.35 6.02
系统抽稀法 -28.10 -0.34 6.12


测区B		 原始数据 -69.44 -20.60 13.41
本文算法 -69.41 -20.38 13.41
坡度抽稀法 -69.59 -17.24 13.41
顾及地形复杂度抽稀法 -69.34 -21.63 13.35
系统抽稀法 -69.40 -16.91 13.42
测区B各抽稀法内插DDM与原始DDM的量化值进行比较，可知本文算法的最小值和最大值更为贴近原始DDM，而四种抽稀方法的标准差值较小，因此将从视觉感受效果进行分析（图7），图7（a）是测区B原始多波束测深数据的三维地形，图7（b）—（e）是测深数据在同一抽稀率下不同抽稀算法结果的三维地形。通过与图7（a）地形对比，可以看出基于坡度抽稀算法、顾及地形复杂度抽稀算法和系统抽稀算法的微地形特征信息丢失较多（如图7（c）—图7（e）红色圆圈标注区域），相较而言，本文抽稀算法的地形特征信息损失较少，能够较好地表达地形细节特征。结合表3和图7可知，本文抽稀方法能有效识别和保留地形特征点，兼顾抽稀的精度和地形特征的表达，整体抽稀效果较好。
图7 抽稀结果地形图

Fig. 7 Topographical map of the results of the thinning

4 结论与讨论

4.1 结论

针对海量多波束测深数据冗余，且现有抽稀算法在空洞、坡度较小等区域难以同时兼顾抽稀精度和地形特征表达的问题，本文提出了一种顾及坡度和高程的多波束测深数据抽稀算法，并选取不同海域的多波束测深数据进行实验和精度分析。 ① 对含有空洞、凹边界等局部空白区域的测区A利用Alpha Shape算法提取边界点，保留局部空白区域的形态轮廓，避免出现因抽稀导致地形特征点丢失、精度下降的问题；② 将坡度和高程参数相结合对不同地形的多波束测深数据进行抽稀，避免了在坡度较小区域出现地形特征点丢失的情况。通过与基于坡度抽稀、顾及地形复杂度抽稀算法、系统抽稀算法进行比较，对比分析4种抽稀算法的实验效果，结果表明：
（1）本文利用Alpha Shape算法对含有空洞、凹边界等局部空白区域的多波束测深数据提取边界点，较未提取边界点的本文算法、基于坡度抽稀算法、顾及地形复杂度抽稀算法和系统抽稀算法可以精细地刻画出空洞区域等深线的细小曲折，更贴近原始测深数据等深线形态，更好地反映等深线的弯曲变化，有效保持海底地形的形态完整性。
（2）本文选取不同地形的测深数据抽稀，在对地形较平坦的测区A和地形起伏较大的测区B不同程度抽稀时，本文算法的精度较基于坡度抽稀算法、顾及地形复杂度抽稀算法和系统抽稀算法有不同程度的提高，体现出本文算法对不同地形多波束测深数据进行抽稀的有效性和通用性。尤其随着测区A、B抽稀率的降低，本文算法较上述3种抽稀算法在MSE分别提升了16%、27%、14%和10%、36%、2%， RMSE分别提升了7%、12%、7%和5%、17%、3%，可量化地反映出本文抽稀算法结果能够保留海底地形的基本特征，有效提高了测深数据的准确性且能够较好地保留地形细节特征，满足后续构建高精度海底地形的需要。

4.2 讨论

本文对多波束测深数据抽稀研究还存在一些不足：① 抽稀算法中半径a和坡度阈值都是影响抽稀精度的关键因素，可以进一步优化a和坡度阈值参数；② 针对测区B不同抽稀率时，本文算法的MAE精度提升不明显的情况可进一步研究。

References

Publishing order | Descend order by publishing year | Descend order by cited within
[1]
赵建虎, 欧阳永忠, 王爱学. 海底地形测量技术现状及发展趋势[J]. 测绘学报, 2017, 46(10):1786-1794.

[Zhao J H, Ouyang Y Z, Wang A X. Status and development tendency for seafloor terrain measurement technology[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10):1786-1794. ] DOI:10.11947/j.AGCS.2017.20170276

DOI

[2]
曹鸿博, 张立华, 朱穆华, 等. 海量多波束数据抽稀方法的比对分析[J]. 海洋测绘, 2010, 30(5):81-83.

[Cao H B, Zhang L H, Zhu M H, et al. Comparison and analysis of thinning methods for mass data acquired by multibeam sounders[J]. Hydrographic Surveying and Charting, 2010, 30(5):81-83. ] DOI:10.3969/j.issn.1671-3044.2010.05.023

DOI

[3]
钱金菊, 张昌赛, 王柯, 等. 机载LiDAR点云数据抽稀算法研究述评[J]. 测绘通报, 2017(S1):33-35,58.

[Qian J J, Zhang C S, Wang K, et al. Research review on thinning algorithm of airborne LiDAR point cloud data[J]. Bulletin of Surveying and Mapping, 2017(S1):33-35,58. ] DOI:10.13474/j.cnki.11-2246.2017.0610

DOI

[4]
Gao J L. Two-dimensional and three-dimensional surface image processing algorithms and their application[D]. Newark: New Jersey Institute of Technology, 2001.

[5]
缪志修, 齐华, 王国昌, 等. 基于机载LiDAR数据构建的DEM抽稀算法研究[J]. 铁道勘察, 2010, 36(4):35-40.

[Miao Z X, Qi H, Wang G C, et al. Discussion on thinning algorithm for construction of DEM based on airborne LiDAR data[J]. Railway Investigation and Surveying, 2010, 36(4):35-40. ] DOI:10.19630/j.cnki.tdkc.2010.04.011

DOI

[6]
Wang R J, Li C P. Comparison and analysis of thinning methods for multi-beam sounding data[J]. The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2020, XLII-3/W10:807-813. DOI:10.5194/isprs-archives-xlii-3-w10-807-2020

DOI

[7]
Pamela S. A data density reduction algorithm for post-processed airborne LIDAR bathymetric survey data[D]. Gainesville: University of Florida, 2000.

[8]
徐景中, 万幼川, 张圣望. LIDAR地面点云的简化方法研究[J]. 测绘信息与工程, 2008, 33(1):32-34.

[Xu J Z, Wan Y C, Zhang S W. On simplification method for lidar ground points cloud[J]. Journal of Geomatics, 2008, 33(1):32-34. ] DOI:10.3969/j.issn.1007-3817.2008.01.014

DOI

[9]
刘春, 吴杭彬. 基于平面不规则三角网的DEM数据压缩与质量分析[J]. 中国图象图形学报, 2007, 12(5):836-840.

[Liu C, Wu H B. Data compress of DEM based on plane triangulation irregular network[J]. Journal of Image and Graphics, 2007, 12(5):836-840. ] DOI:10.3969/j.issn.1006-8961.2007.05.011

DOI

[10]
冯宇瀚, 殷晓冬, 王少帅, 等. 基于三角网构建海底DEM的抽稀算法[J]. 海洋测绘, 2012, 32(6):33-35,39.

[Feng Y H, Yin X D, Wang S S, et al. A method for data thinning based on the topology of triangulation irregular net to construct submarine DEM[J]. Hydrographic Surveying and Charting, 2012, 32(6):33-35,39. ] DOI:10.3969/j.issn.1671-3044.2012.06.010

DOI

[11]
曹文涛, 何伟. 利用TIN和高程梯度进行高程点抽稀[J]. 测绘通报, 2017(5):110-112.

[Cao W T, He W. Sparsing elevational points using TIN and elevational gradients[J]. Bulletin of Surveying and Mapping, 2017(5):110-112. ] DOI:10.13474/j.cnki.11-2246.2017.0166

DOI

[12]
马丹, 樊妙, 闫循鹏, 等. 一种改进的基于TIN的多波束测深数据抽稀算法[J]. 海洋技术学报, 2019, 38(5):49-54.

[Ma D, Fan M, Yan X P, et al. An improved TIN-based multi-beam bathymetric data thinning algorithm[J]. Journal of Ocean Technology, 2019, 38(5):49-54. ] DOI:10.3969/j.issn.1003-2029.2019.05.009

DOI

[13]
杨明军, 苏春梅, 康冰锋, 等. 平原地区机载激光雷达数据的抽稀算法分析[J]. 测绘通报, 2019(1):101-107.

[Yang M J, Su C M, Kang B F, et al. Study and application on thinning algorithm of airborne LiDAR data in plain area[J]. Bulletin of Surveying and Mapping, 2019(1):101-107. ] DOI:10.13474/j.cnki.11-2246.2019.0021

DOI

[14]
Yin X D, Xu W M, Liu T Y, et al. Multi-beam sounding data thinning method based on characteristic spots and isobath constraint[C]// Proc SPIE 12173, International Conference on Optics and Machine Vision (ICOMV 2022), 2022, 12173:149-153. DOI:10.1117/12.2634387

DOI

[15]
程星会, 王明军, 翁敏, 等. 一种支持海量水深数据抽稀的边界提取方法[J]. 测绘地理信息, 2018, 43(4):108-110,115.

[Cheng X H, Wang M J, Weng M, et al. A boundary extraction method for massive water depth data thinning[J]. Journal of Geomatics, 2018, 43(4):108-110,115. ] DOI:10.14188/j.2095-6045.2016413

DOI

[16]
陶桐桐, 王明军, 杨龙, 等. 基于边界搜索的海量水深数据抽稀方法[J]. 测绘地理信息, 2018, 43(6):62-65.

[Tao T T, Wang M J, Yang L, et al. A diluting method of water depth data based on boundary searching[J]. Journal of Geomatics, 2018, 43(6):62-65. ] DOI:10.14188/j.2095-6045.2016248

DOI

[17]
文佳昕, 李靖涵, 行瑞星, 等. 顾及地形复杂度的多波束测深数据抽稀算法[J]. 测绘科学技术学报, 2018, 35(4):435-440.

[Wen J X, Li J H, Xing R X, et al. A thinning algorithm of multibeam sounding data considering the complexity of seabed terrain[J]. Journal of Geomatics Science and Technology, 2018, 35(4):435-440. ] DOI:10.3969/j.issn.1673-6338.2018.04019

DOI

[18]
Błaszczak-Bąk W, Sobieraj-Żłobińska A, Kowalik M. The OptD-multi method in LiDAR processing[J]. Measurement Science and Technology, 2017, 28(7):075009. DOI:10.1088/1361-6501/aa7444

DOI

[19]
Douglas D H, Peucker T K. Algorithms for the reduction of the number of points required to represent a digitized line or its characteristics[J]. Cartographica: the International Journal for Geographic Information and Geovisualization, 1973, 10(2):112-122. DOI:10.3138/fm57-6770-u75u-7727

DOI

[20]
Stateczny A, Wlodarczyk-Sielicka M. Self-organizing artificial neural networks into hydrographic big data reduction process[M]// Rough Sets and Intelligent Systems Paradigms. Cham: Springer International Publishing, 2014:335-342. DOI:10.1007/978-3-319-08729-0_34

DOI

[21]
Wlodarczyk-Sielicka M, Stateczny A, Lubczonek J. The reduction method of bathymetric datasets that preserves true geodata[J]. Remote Sensing, 2019, 11(13):1610. DOI:10.3390/rs11131610

DOI

[22]
Wlodarczyk-Sielicka M, Blaszczak-Bak W. Processing of bathymetric data: The fusion of new reduction methods for spatial big data[J]. Sensors(Basel, Switzerland), 2020, 20(21):E6207. DOI:10.3390/s20216207

DOI

[23]
夏伟, 黄谟涛, 刘雁春, 等. 多波束测深数据抽稀准则研究[J]. 测绘科学, 2010, 35(S1):17-19.

[Xia W, Huang M T, Liu Y C, et al. Research on the rule of multibeam echo sounding system data thinning[J]. Science of Surveying and Mapping, 2010, 35(S1):17-19. ] DOI:10.16251/j.cnki.1009-2307.2010.s1.011

DOI

[24]
Coleman R. Satellite altimetry and Earth sciences: A handbook of techniques and applications[J]. Eos, Transactions American Geophysical Union, 2001, 82(34):376. DOI:10.1029/01eo00233

DOI

[25]
李振洪, 李鹏, 丁咚, 等. 全球高分辨率数字高程模型研究进展与展望[J]. 武汉大学学报·信息科学版, 2018, 43(12):1927-1942.

[Li Z H, Li P, Ding D, et al. Research progress of global high resolution digital elevation models[J]. Geomatics and Information Science of Wuhan University, 2018, 43(12):1927-1942. ] DOI:10.13203/j.whugis20180295

DOI

[26]
Yue L W, Shen H F, Zhang L P, et al. High-quality seamless DEM generation blending SRTM-1, ASTER GDEM v2 and ICESat/GLAS observations[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2017, 123:20-34. DOI:10.1016/j.isprsjprs.2016.11.002

DOI

[27]
Brock J C, Purkis S J. The emerging role of lidar remote sensing in coastal research and resource management[J]. Journal of Coastal Research, 2009, 10053:1-5. DOI:10.2112/si53-001.1

DOI

[28]
Edelsbrunner H, Kirkpatrick D, Seidel R. On the shape of a set of points in the plane[J]. IEEE Transactions on Information Theory, 1983, 29(4):551-559. DOI:10.1109/TIT.1983.1056714

DOI

[29]
沈蔚, 李京, 陈云浩, 等. 基于LIDAR数据的建筑轮廓线提取及规则化算法研究[J]. 遥感学报, 2008, 12(5):692-698.

[Shen W, Li J, Chen Y H, et al. Algorithms study of building boundary extraction and normalization based on LIDAR data[J]. Journal of Remote Sensing, 2008, 12(5):692-698. ]

[30]
Widyaningrum E, Peters R Y, Lindenbergh R C. Building outline extraction from ALS point clouds using medial axis transform descriptors[J]. Pattern Recognition, 2020, 106:107447. DOI:10.1016/j.patcog.2020.107447

DOI

[31]
国家质量技术监督局. 海道测量规范: GB 12327-1998[S]. 北京: 中国标准出版社, 2004.

[State Bureau of Quality and Technical Supervision of the People's Republic of China. Specifications for hydrographic survey: GB 12327-1998[S]. Beijing: Standards Press of China, 2004. ]

[32]
廖中平, 陈立, 白慧鹏, 等. 自适应α-shapes平面点云边界提取方法[J]. 长沙理工大学学报(自然科学版), 2019, 16(2):15-21.

[Liao Z P, Chen L, Bai H P, et al. Adaptive Alpha-shapes plane point cloud boundary extraction method[J]. Journal of Changsha University of Science & Technology(Natural Science), 2019, 16(2):15-21. ]

[33]
李世林, 李红军. 自适应步长的Alpha?shape表面重建算法[J]. 数据采集与处理, 2019, 34(3):491-499.

[Li S L, Li H J. Surface reconstruction algorithm using self?adaptive step Alpha?shape[J]. Journal of Data Acquisition and Processing, 2019, 34(3):491-499. ] DOI:10.16337/j.1004-9037.2019.03.012

DOI

Options
Outlines

/

〈 〉