EN中文

Journal of Geo-information Science >

2023 , Vol. 25 >Issue 1: 49 - 62

DOI: https://doi.org/10.12082/dqxxkx.2023.220151

Application of Peridynamic Theory in Regional Land Subsidence Modeling

  • ZHANG Ke , 1, 2 ,
  • GONG Huili 1, 2, 3 ,
  • LI Xiaojuan , 1, 2, 3, * ,
  • ZHU Lin 1, 2, 3 ,
  • WANG Che 1, 2 ,
  • CHEN Beibei 1, 2, 3 ,
  • HE Jijun 1, 2 ,
  • GUO Lin 1, 2, 3 ,
  • LYU Mingyuan 1, 2 ,
  • YAN Qianmeng 1, 2 ,
  • Li Jiangtao 1, 2
Expand
  • 1. College of Resource Environment and Tourism, Capital Normal University, Beijing 100048, China
  • 2. Key Laboratory of Mechanism, Prevention and Mitigation of Land Subsidence, Ministry of Education of the People's Republic of China, Capital Normal University, Beijing 100048, China
  • 3. Hebei Cangzhou Groundwater and Land Subsidence National Observation and Research Station, Cangzhou 061000, China
*LI Xiaojuan, E-mail:

Received date: 2022-04-05

  Revised date: 2022-06-10

  Online published: 2023-03-25

Supported by

National Natural Science Foundation of China(41930109)

Beijing Outstanding Young Scientist Program(BJJWZYJH01201910028032)

Fold

Abstract

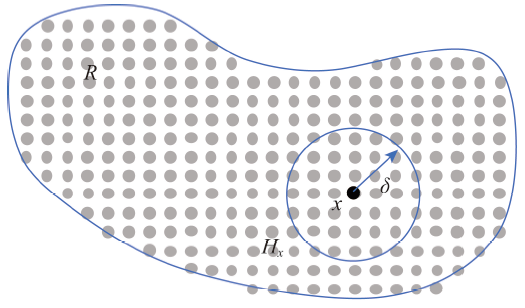
Land subsidence is an important factor that influences the sustainable development of a region. Due to the complexity of land subsidence, the uncertainty and risk caused by land subsidence disasters are increasing. Therefore, new methods need to be developed to quantify the nonlinear land subsidence processes, identify emerging risk, and improve urban resilience. In this paper, the necessity of introducing peridynamic to land subsidence modeling is discussed by analyzing the progress and shortcomings of current land subsidence modeling. For natural discontinuous structures such as fractures and faults, current deterministic models based on differential equations are insufficient to describe land subsidence. Therefore, the peridynamic theory which is suitable for discontinuous and nonlinear characteristics is introduced. The peridynamic theory (PD) describes the mechanical behavior of matter by solving integral equations and has advantages in analyzing discontinuous and multi-scale problems. The applicability of peridynamic in land subsidence is analyzed from the aspects of material properties and modeling methods, respectively. By establishing a peridynamic model of land subsidence, discontinuous disasters such as ground crack and ground collapse can be included, so as to realize the multi-field and multi-scale recognition of land subsidence under a unified framework. In the light of the “Higher-bigger-deeper” urban construction, combined with the CAS-ESM, the simulation of future evolution of ground subsidence and ground fractures can be carried out. However, there are still problems to be solved in the interdisciplinary research, such as the reasonable generalization of material properties, material structure, and the balance between operation accuracy and operation cost. Then, based on theoretical principles, the modeling method, solving process, and optimization method of peridynamic land subsidence model are given. Besides the establishment, solution and optimization of the model, a variety of spatial monitoring methods and data are also needed, e.g., subsidence data monitored by InSAR technology, the underground structure and density information obtained by Seismic Frequency Resonance Technology (SFRT), bedrock and stratified scale data, groundwater level data, building information data, and road network data. In this paper, a peridynamic land subsidence model with a range of 4km*6km and a depth of 0.2 km is established in Liyuan-Taihu -Zhangjiawan area in the eastern Beijing, and the evolution process of land subsidence is simulated by using the monthly average rate of groundwater level decline from 2007 to 2010 as the boundary condition. The mean absolute error between the simulated and the measured values is 18mm, which verifies the effectiveness of this interdisciplinary research. The peridynamic theory has superiority in the field of materials and the study of fatigue, damage, fracture, and so on. Our study provides new ideas and new methods for regional land subsidence modeling. Furthermore, with the support of big data, cloud computing platforms, and Geo-AI, new opportunities are emerging for preventing, controlling, slowing down, and avoiding land subsidence hazards.

Key words： peridynamic; land subsidence; ground fissure; integral modeling; InSAR technology; seismic frequency resonance technology

Cite this article

ZHANG Ke , GONG Huili , LI Xiaojuan , ZHU Lin , WANG Che , CHEN Beibei , HE Jijun , GUO Lin , LYU Mingyuan , YAN Qianmeng , Li Jiangtao . Application of Peridynamic Theory in Regional Land Subsidence Modeling[J]. Journal of Geo-information Science, 2023 , 25(1) : 49 -62 . DOI: 10.12082/dqxxkx.2023.220151

1 引言

地面沉降是一种由自然和人类活动引发的地下松散岩层固结压缩，造成一定区域内地面高程下降的地质灾害。随着全球变暖、海平面升高、水资源短缺、人口增加和城市化进程加快，全球地面沉降问题愈加突出，主要表现在沉降范围扩大，复杂性、危险性与不确定性的增加。据联合国教科文组织的一项研究，到2040年，地面沉降可能影响全球19%的人口[1]。2019年，我国地面沉降严重区域（年沉降量>50 mm）的面积约为1.14万km2 [2]。华北平原由于长期高强度开采地下水，已形成全球最大的地下水降落漏斗和全球最大的地面沉降区，地面沉降已经成为区域可持续发展的重要影响因素。在气候变化、南水北调与控采回灌新水情、京津冀一体化新发展、区域地上地下轨道交通新工程等因素的综合作用下，地面沉降的时空演化过程在差异性、非线性、突变性、风险致灾性等方面都呈现新的特征。为此，在统一框架下构建地面沉降-地裂缝一体化模型，是开展新情势下区域地面沉降机理研究与演化预测的重要基础，可为地裂缝、地面塌陷等灾害的早期识别预警提供支持。

2 现阶段地面沉降建模与近场动力学应用的进展分析

2.1 现阶段地面沉降建模的主要方法与不足

地面沉降建模方法主要有随机性模型、Geo-AI人工智能模型及确定性模型等[3]。基于统计的随机性模型是根据地面沉降影响因素的多样性，利用概率统计分析方法发现多因素间的关系，从而建立相应的随机模型，如回归模型、时序模型、灰色模型等[4⇓-6]。然而，地面沉降作为一个非线性的复杂系统问题，成因众多且各因素间关系复杂。随机统计模型作为物理解释的经验模型，在前期观测数据不足时建立的模型存在一定的片面性。人工智能模型基于学习的方法，采用机器学习、深度学习等技术实现地面沉降影响因素的定量分析、沉降模拟预测等[7⇓-9]。作为在地面沉降领域近年兴起的方法，其在地面沉降领域发挥的作用有待进一步深入。
确定性模型包括水流模型、土体变形模型及两者的部分耦合、完全耦合模型等，用于开展地面沉降的模拟预测研究[10⇓-12]。在太沙基固结理论、比奥固结理论基础上建立的确定性模型，不仅可以考察地面沉降的水土应力应变关系，还可以将地裂缝引入模型开展研究[13]。应用有限元（Finite Element Method，FEM）、有限差分（Finite Difference Method，FDM）、离散元（Discrete Element Method，DEM）等偏微分方程数值求解方法，实现地裂缝从形成到扩展过程的模拟[14-15]。由于此类理论的控制方程以导数微分的形式出现，式（1）为太沙基固结理论基本公式。
C v ∂ 2 u ∂ z 2 = ∂ u ∂ t
式中： u为超静孔压； C v为固结系数；z为埋深；t为时间；在面对地裂缝等不连续结构时，存在导数无定义的情况。在数值求解的过程中，需要基于连续性假设、引入外部准则等对裂缝补充定义描述。同一模型中连续与不连续结构使用不同的处理方式，这使得建模不能在统一框架下实现[16]，对开展地面沉降-地裂缝-地面塌陷一体化综合模拟带来一定的限制。然而，地裂缝、节理和断层作为天然地质体中的不连续结构，会对地质体的稳定性产生影响[17]。以积分模型为核心的近场动力学理论的出现，为这一问题的解决提供了新的思路。

2.2 近场动力学在相关领域中的研究进展

近场动力学（Peridynamic，PD）是一种基于非局部作用思想建立模型、并通过求解空间积分方程描述物质力学行为的方法。PD对于连续到非连续、微观到宏观的力学行为具有统一表述，数值上天然具有无网格属性和不连续求解功能[18]，在分析不连续、多尺度等问题时展现出适用性与可靠性[19]。其在建模时无需获得关于建模对象内部不连续结构的先验知识，在无初始裂缝的情况下允许新裂缝的萌生与发展。目前应用近场动力学开展地面沉降模拟的相关研究较少，通过讨论其在岩石水力压裂[20]、滑坡[21]、饱水岩土材料[22]等领域的应用，可以帮助认识近场动力学在地面沉降建模研究中的适用性。
Turner[23]将孔隙压力引入近场动力学方程，建立了可用于模拟水力压裂过程中的泄露影响、饱水岩石的固结、开采地质储层流体引起地面沉降的近场动力学流固耦合非局部模型。Ouchi等[24]通过模拟孔隙压力对多孔介质变形的作用，提出了模拟非均质孔隙弹性介质中流体驱动裂缝扩展的近场动力学模型；开展饱水岩石的一维固结模拟实验，验证了孔隙弹性模型的有效性。张钰彬等[25-26]扩展了态型近场动力学理论，用于模拟流固耦合及水力压裂，研究了固体的变形及开裂行为。Ni等[27]模拟了饱和多孔介质中水力压裂的裂缝扩展过程，采用比奥固结理论，运用有限元方法描述流体运动及孔隙压力变化，引入态型理论描述固体形变及裂缝发展。Shou等[28]在近场动力学理论的框架内导出了裂隙多孔岩石的水-力耦合方程，建立了一维、二维条件下近场动力学导水率与经典导水率之间的关系，并将比奥固结理论引入非常规态型近场动力学方程，实验验证了方程数值解与解析解的一致性。Sun等[29]也采用类似思路，建立了饱和多孔介质受水力裂缝扩展的近场动力学-有限元耦合方程。
从材料力学的角度分析，地面沉降的发生发展演化及地裂缝、地面塌陷的产生，是岩土材料受力而发生疲劳、损伤甚至失效的过程。上述研究的建模对象均为岩土材料，部分研究讨论了比奥固结理论等引入近场动力学的研究思路，这些特点与地面沉降研究均有相似之处，为开展近场动力学在地面沉降建模中的应用奠定了良好基础。

3 近场动力学理论原理及与地面沉降研究结合的关键问题

3.1 近场动力学理论原理

近场动力学基本理论由Silling[30]在2000年提出，称为键型理论；2007年Silling[31]将键型理论扩展为态型理论，对近场动力学进行了完善。近场动力学应用于非连续应力场-形变场的模拟与预测，其研究一方面集中于发展完善理论模型和计算体系，另一方面关注将方法应用到不同类型的不连续力学问题分析，包括宏观尺度的大变形、静/动力破坏、失稳、穿透问题和细微观尺度破坏问题等[32-33]。
对于某时刻t内，占据空间区域R的物质体，近场动力学控制方程如式（2）：
ρ u ¨ x , t = ∫ H x f u x ' , t - u x , t , x ' - x d H + b ( x , t )
式中：等式左边两项乘积表示物质体所受合外力； ρ为材料密度； u代表物质点的位移矩阵； H x表示以物质点 x为中心且邻域半径 δ划定的近场范围；t为时间； b为施加在物质点 x上的体积力； f为物质点 x与物质点 x '之间的“力密度函数”，也即表示两物质点间相互作用力，模型具体如图1所示。
图1 近场动力学模型[19]

注:R为物质体所占的空间区域,Hx为以物质点x为中心、以δ为邻域半径划定的近场范围

Fig. 1 Peridynamic model

近场动力学的键型理论对各向同性材料的泊松比限制为1/4，适用于弹性、脆性材料，不支持不可压缩材料及塑性材料。为了消除键型对材料属性的限制，基于物质点状态的概念，改进得到了更为通用的公式，即常规/非常规态型近场动力学理论。态型理论可以适用于泊松比不固定为1/4的包括流体、固体在内的其他材料，二者主要区别如表1所示。
表1 近场动力学键型理论与态型理论对比

Tab. 1 Comparison of bond-based PD and state-based PD

键型理论 态型理论
适用材料
泊松比		 弹性、脆性材料
各向同性材料的泊松比限制为1/4		 可用于流体、固体等其他材料
泊松比不固定为1/4
计算代价 计算代价较小 计算代价高




变形构型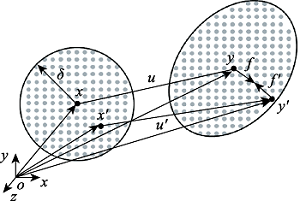
物质点 x和 x '变形前（左）与变形后（右）
两点间作用力大小相等、方向相反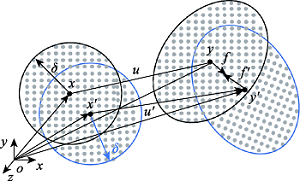
物质点 x和 x '变形前（左）与变形后（右）
两点间作用力大小不等、方向相反

注：在以δ为半径的邻域内，变形前的物质点对由 x与 x '表示，变形后的物质点对由 y与 y '表示， u与 u '分别表示两点发生的位移， f与 f '表示两点间作用力。

近场动力学方程解的构造涉及时间、空间积分，受到“材料区域R的边界B上的约束条件和载荷条件”以及“位移场、速度场和初始条件”的影响。求解上述近场动力学控制方程首先通过明确初边值条件，得到区域内每个点发生运动时受到的力，根据牛顿第二定律中加速度与力之间的关系，得到每个点的加速度、速度也即运动状态，最后可得每个点发生的位移。

3.2 近场动力学与地面沉降结合的研究方向

近场动力学与地面沉降研究的结合可实现沉降-地裂缝-地面塌陷一体的发生发展演化全过程模拟预测；利用遥感GIS方法构建多种初始、边界条件，可从多方面开展研究，具体而言：
（1）分析涵盖地裂缝的地面沉降成因机理。地面沉降不同演化模式的影响因素存在差异，依据控制变量思想结合InSAR历年沉降监测结果，一体化分析地下水-地面沉降-地裂缝与城市建设、区域水循环间的互馈关系。
（2）预测涵盖地裂缝的地面沉降未来演化。在全球已发生的地面沉降灾害中，人类引起的地面沉降占全球沉降事件的77%，而地下水开采占这类地面沉降的60%[34]。同时，大气降水对地下水变化有直接的影响。地下水位作为模型重要边界条件，开展地面沉降演化预测研究首先需确定未来地下水位动态变化特征。2021年6月，我国研制成功首个地球系统数值模拟大科学装置CAS-ESM（Chinese Academy of Sciences-Earth System Model），其集成耦合了包含大气、海洋、海冰、陆面、植被生态、气溶胶和大气化学、海洋生化、陆地生化在内的8个分系统[35]，能够模拟预测包括大气圈在内的多个圈层的演变，为区域地下水模拟预测提供了更加科学的基础数据，也为开展地面沉降预测研究提供依据。

3.3 地面沉降研究区概化与模型参数选取关键问题

近场动力学可以反映由应急水源地高强度开采、地下空间开发利用等引起的应力场不连续特征，有助于更好地模拟不均匀沉降、地裂缝，深入对地面沉降机理的认识。模拟预测的精度依赖于建模精度，对于近场动力学地面沉降模型而言，建模精度取决于对地下空间结构、组分特征的合理概化。由于地面沉降的研究范围较大，地下结构、岩土材料构成存在差异，直接用某地获得的结构信息与材料参数代替其他地方或整个区域的特征是不合适的，应当在资料收集的基础上结合一定的概化方法，既保证实验精度又平衡建模复杂度。
物质点尺寸、近场范围、临界伸长率、积分时间步长、总时间步数等近场动力学离散参数会对结果的收敛性、精度、运算效率造成影响。因此，在进行模型的数值离散求解过程中，需要设计既可以降低计算成本又能扩大建模规模的离散方法，在获得合理演算结果的同时保持必要的运算精度。

4 近场动力学地面沉降模型的构建

4.1 近场动力学地面沉降模型的建立与求解

依据近场动力学积分方程的特点，在确定研究对象空间初始条件、边界条件、空间结构及空间参数的基础上，综合考虑“渗流场-形变场-应力场”多场变分辨率、建模多尺度与多影响因素，一体化构建包含初始地裂缝（建模时预置）或不含初始地裂缝的近场动力学区域地面沉降积分模型，考察随各类边界条件的施加模型内部初始地裂缝的发展与新地裂缝的萌生，技术路线如图2。
图2 基于近场动力学的区域地面沉降建模流程

Fig. 2 Flow chart of regional land subsidence modeling based on peridynamic

近场动力学地面沉降模型的求解过程可利用Python、FORTRAN等语言编程实现，算法流程如图3。需要注意的是，由于理论特性，在本文模型中各类参数均为无量纲数值，其物理含义单位按需自定但应保持尺度一致。
图3 基于近场动力学的区域地面沉降模型求解算法流程

Fig. 3 Solution algorithm flow of regional land subsidence model based on peridynamic

结合前述近场动力学建模方程与地面沉降建模方法可知：
（1）参数初始化包括研究区空间范围形状、考察研究区是否有初始地裂缝、岩土材料属性（杨氏模量、泊松比、质量密度）等的确定。
（2）积分时间步长依据实际的模拟时间跨度确定，通常为1，等价为模型的时间分辨率；模拟预测的时间跨度由总时间步数表征。
（3）与现阶段模拟方法多将研究区划为格网不同，模型离散要求将研究区分为众多物质点。依据研究实际确定x、y、z 3个方向需要划分的物质点总数、物质点间距及单个物质点体积（均视研究实际而定），并确定近场范围（通常为3倍物质点间距）及临界伸长率（依据材料性质而定）2类近场动力学参数。单个质点为模型的最小单元，其代表的研究区范围即为模型的空间分辨率。当划分物质点间距小、数量多时，模型拥有较高的空间分辨率，可用于开展研究区精细建模。但物质点数量的增加会导致计算成本的增长，因此在划定最小单元尺寸（确定模型空间分辨率）时需结合研究实际及算力综合考虑。
（4）虽然态型理论更具有一般性，许多学者对于泊松比不为1/4的材料，出于对计算复杂度的考虑，仍选择了键型理论建模。2类理论虽有些许差别，但其建立与求解的流程基本一致。
（5）模型初始条件指在模拟开始前（时域积分前）各物质点的速度、位移等运动状态。边界条件对应式（2）中的 b ( x , t )，也即是地下水、动静载荷等条件。其中，地下水边界条件通过获得地下水位变化相关数据，将其转化为附加应力随时间的变化施加在模型上表征；动静载荷边界条件也将其变化转化为对地下空间的作用力带入模型运算。
（6）在遍历模型内全部物质点并运行全部时间步后，输出最终各物质点的速度、位移等信息，即得到模拟的地面沉降速率、沉降量、预置地裂缝的演化结果及新生地裂缝的萌生发展结果等。

4.2 近场动力学地面沉降模型的优化

近场动力学地面沉降模型的优化包括模拟结果与运算效率两部分内容。模拟结果的优化离不开实测数据（真值）的支持。本文模型的模拟精度受地下结构刻画、初始、边界条件确立等多方面影响。因此，在近场动力学地面沉降模型的建立、求解与优化的各个阶段，均需要多种空间监测方法与数据的参与，包括InSAR技术监测的沉降数据、三维地震频谱谐振勘探技术（Seismic Frequency Resonance Technology，SFRT）获得的地下结构与密度信息、基岩标与分层标数据、地下水位数据、建筑信息数据与路网数据等。各类方法参与模型优化的具体路线如图4所示。
图4 多种空间监测方法联合的模型优化

Fig. 4 Model optimization combined with multiple spatial monitoring methods

明确研究区地下空间的结构组分是开展近场动力学地面沉降模拟的基础。由于地面沉降的研究区范围通常较大，其结构组分特征存在空间差异性。SFRT作为有效探查地下空间结构的技术，可以更好的反应地下结构与地层密度信息；通过进一步结合野外台站的监测数据（基岩标、分层标、钻孔等），优化对地下空间的概化。边界条件会对模拟结果造成显著影响，近场动力学地面沉降模型的边界条件主要包括地下水开采、建筑静载荷及交通动载荷等。依据历年各层含水层水位变化数据、静载荷数据（如Landsat-TM/ETM遥感影像数据、航空摄影测量解译的建筑信息数据等）、动载荷数据（如OpenStreetMap（OSM）路网数据），采用函数拟合、机器学习等方法构建符合时序发展变化的各类边界条件，实现边界条件的优化。
InSAR技术监测的沉降数据是模型优化不可缺少的部分。参考机器学习等对数据集的划分方式，可依据沉降演化的不同阶段将沉降数据集分为“训练集”、“验证集”、“测试集”等，通过设计阈值等开展对模拟结果的校准优化与精度评价。其中，“训练集”中的历年沉降值、沉降速率等数据作为边界条件参与模型运算；“验证集”可用于结果验证与评价，“测试集”可用于讨论模型预测沉降未来演化的能力。运算效率的优化则与现阶段求解微分形式的地面沉降模型常用数值技术（有限元法FEM、有限差分FDM、离散元DEM等）结合，在保证精度前提下实现高效建模求解[36⇓-38]，结合思路之一如 图5所示（根据文献[39]改绘）。
图5 有限元法与近场动力学耦合模式示意图（改绘自文献[39]）

Fig. 5 Schematic diagram of coupling model between FEM and PD (modified according to reference[39])

5 近场动力学地面沉降模型的初步实验与讨论

5.1 模型构建与数据介绍

我国地面沉降的类型、成因众多，在北京地区，地下水超量开采为最主要诱因。为验证近场动力学地面沉降模型的实用性和有效性，本节基于《地面沉降及地下水位变化对地铁工程的影响研究》[40]及文献[41]中北京东八里庄-大郊亭沉降区的研究资料（图6），选择含有3组可压缩层组、3组含水层组且无基岩存在的梨园-台湖镇-张家湾镇区域为实验区，建立了实验区4 km×6 km范围、0.2 km深度的（图6红框标识区域）近场动力学地面沉降模型，对2007—2010年地面沉降过程进行模拟。图6中第二、第三可压缩层及第二、第三含水层组均为二部分，在建模时忽略第二含水层组中的部分第二可压缩层、第三可压缩层中的部分第三含水层组，并在模型底部增加虚拟边界层以提高模拟精度。图7为模型离散为众多物质点后的示意图。
图6 实验区示意图（改绘自文献[40]）

Fig. 6 Schematic diagram of experimental area (modified according to reference[40])

图7 实验区三维模型示意图（离散后）

Fig. 7 Sketch of three-dimensional cuboid model (after discretization)

本次实验需要的参数（表2）共有材料属性（表3）、近场动力学参数（表4）与边界条件[40-41]3类。值得注意的是，物质点间距、单个物质点体积及各方向物质点个数均依据研究对象实际情况确定。依据所定数值不同，同一个物质点可代表不同空间尺度与空间分辨率的地质体，模型具备多尺度变分辨率特性。
表2 近场动力学地面沉降模型所需数据基本信息

Tab. 2 Basic information of data required for the peridynamic land subsidence model

数据名称 本文数据来源
实验区概化数据 《地面沉降及地下水位变化对地铁工程的影响研究》[40]、文献[41]
边界条件数据（地下水位）
验证数据（沉降监测值）
模型各层材料属性 钻孔数据（https://zk.cgsi.cn）、文献[42]
模型离散参数 结合研究实际自定
表3 近场动力学地面沉降模型中各层材料属性

Tab. 3 Material properties of layers in the peridynamic land subsidence model

杨氏模量(N/m2) 泊松比 质量密度(kg/m3)
第一压缩层组 5.0×106 0.30 1800
第一含水层组 1.5×108 0.25 1600
第二压缩层组 8.0×106 0.30 1800
第二含水层组 1.5×108 0.25 1600
第三压缩层组 2.0×107 0.30 1900
第三含水层组 1.5×108 0.25 1600
虚拟边界层 14.0×109 0.26 2500
表4 近场动力学地面沉降模型求解的离散参数

Tab. 4 Discrete parameters of the peridynamic land subsidence model

参数名称 参数值
物质点间距∆ 0.1 km
单个物质点体积∆V 1×10-3 km3
X方向物质点总数/个 60
Y方向物质点总数/个 21（含有1虚拟边界层）
Z方向物质点总数/个 40
邻域范围δ 3.015 ∆
临界伸长率 1（不考虑损伤）、0.044 72（考虑损伤）
时间步长∆t 1月
总时间步数T 50月

5.2 模型实验与讨论分析

模型内各物质点初始速度、位移均为0；虚拟边界层设有固定位移0。根据建模区含水层组分布特征及地下水位监测数据，将建模区地下水分为四层。第一层地下水对应第一含水层组，第二层、第三层地下水对应第二含水层组，第四层地下水对应第三含水层组。在2007—2010年第一层地下水水位回升约为1.5 m；第二层地下水水位下降约为 1 m；第三层地下水水位下降约为3 m；第四层地下水水位下降约为4 m。因此，认为2007—2010年地下水位共下降约8 m，年均下降速率约为2 m/year，月均下降速率约为0.17 m/month，并将月均下降速率作为边界条件。依据孔隙水压力及有效应力原则转换为垂向有效应力的增加代入模型运算，模拟结果如图8、图9所示。
图8 近场动力学地面沉降模拟结果

Fig. 8 Simulation results of peridynamic land subsidence model

图9 模拟沉降量与实测沉降量对比

Fig. 9 Comparison between simulated subsidence and measured subsidence

随着运行时间不断增加，模型中物质点逐渐向下位移。模型以1个月为时间步长，认为每12时间步表征一年。图8显示了模型内所有物质点在不同年份的点位移情况，图中颜色越红表示点位移越大。通过统计垂向（y方向）上点位移情况，得到2007—2010年逐年的模拟沉降量（图9）。本文选择平均绝对误差MAE（Mean Absolute Error）作为衡量模拟结果偏离实测结果程度的指标，计算可得MAE为18 mm。地面沉降对地下水开采的响应存在滞后效应[43]，由于在模拟开始时未考虑2007年之前地下水位对地面沉降的影响，模型内物质点以初始位移0（未发生沉降）的状态开始运动，使得2007年模拟值小于实测值28 mm。不同于真实地下水位的波动变化趋势，由于设定模型边界条件为地下水位以月均速率匀速下降、且未考虑第一层地下水位回升造成的影响，模型的垂向有效应力增量以线性施加，导致模拟沉降量呈线性变化趋势并在2010年的模拟值大于实测值34 mm。
本次实验初步验证了近场动力学在地面沉降建模研究中的适用性。在效率方面，由于所选实验区范围较小，所建立的模型中共含有50 400个物质点，运行全部50时间步共用时70 s，耗时较短。然而，本次实验未开展模型的优化工作。下一步应当基于MAE等误差分析结果、结合4.2节中的优化思路，通过设计InSAR监测结果与模拟值间的误差阈值，调整模型的空间结构、初始条件及边界条件等，进一步提高模拟精度。
实验结果表明，在研究区合理概化及建模相关参数明确的前提下，北京地区近场动力学地面沉降模拟结果精度受地下水位边界条件控制，仅以地下水位变化均值为边界条件存在一定的局限性。应在综合考虑超采、控采回灌、南水进京等情形下，结合统计分析、机器学习等方法准确刻画地下水位变化趋势，并据此开展模拟预测研究以保证实验结果的准确性。同时，由于近场动力学理论将模型离散为大量物质点，随边界条件施加部分点可能会出现“穿越”现象（如：位于模型上部的物质点持续向下运动，穿过模型到达模型底部）。对地面沉降的近场动力学模拟而言，应当在模拟时将模型层与层之间物质点的“穿越”纳入考量。通过在层间设计一定的排斥力或分析边界条件在层间的传递关系，将模型内部的相互作用纳入模型运算，使模拟结果更为合理。

6 结语

针对现阶段地面沉降模拟的确定性模型不能在统一框架下实现连续、非连续结构（地面沉降、地裂缝）建模的限制，本文提出利用近场动力学理论开展地面沉降的建模研究。文章讨论了应用近场动力学开展地面沉降模拟的优势与可行性；分析了研究方向与关键问题；提出了建模求解优化的一般方法；并对2007—2010年北京东部梨园-台湖镇-张家湾镇区域的地面沉降过程进行模拟，初步验证了近场动力学地面沉降模型的实用性和有效性。
近场动力学作为一种以积分建模为核心、无需预知裂缝的位置、走向、深度等信息即可允许其萌生发展的理论，其特点契合地面沉降的研究主体即地下空间的组成结构特征。近年来对岩石水力压裂、滑坡、饱水岩土材料等研究的出现、与有限元法等结合的计算求解方法的提出，使近场动力学理论引入地面沉降研究成为可能。开展其在地面沉降领域的应用研究，可实现地面沉降-地裂缝-地面塌陷的地上、地下一体化综合分析，为区域地面沉降研究提供新思路。随着高精度InSAR技术的不断发展、三维地震频谱谐振勘探技术在地面沉降研究中的应用[44]、地球系统数值模拟大科学装置对未来气候的模拟预测，近场动力学地面沉降模型的实用性、模拟预测能力及对地裂缝、地面塌陷等的识别和预警能力将得到有效提高，从而为防控、减缓、治理地面沉降及其伴生灾害奠定基础，保障城市空间安全。

References

Publishing order | Descend order by publishing year | Descend order by cited within
[1]
Herrera-García G, Ezquerro P, Tomás R, et al. Mapping the global threat of land subsidence[J]. Science, 2021, 371(6524):34-36. DOI:10.1126/science.abb8549

DOI PMID

[2]
李文鹏, 王龙凤, 郭海朋, 等. 中国地面沉降防治成效与对策建议[J]. 中国水利, 2021(7):32-35.

[Li W P, Wang L F, Guo H P, et al. Effectiveness and countermeasures of land subsidence control in China[J]. China Water Resources, 2021(7):32-35. ] DOI:10.3969/j.issn.1000-1123.2021.07.015

DOI

[3]
岳建平, 方露. 城市地面沉降监控理论与技术[M]. 北京: 科学出版社, 2012.

[Yue J P, Fang L. Urban land subsidence monitoring theory and technology[M]. Beijing: Science Press, 2012. ]

[4]
Deng Z, Ke Y H, Gong H L, et al. Land subsidence prediction in Beijing based on PS-InSAR technique and improved Grey-Markov model[J]. GIScience & Remote Sensing, 2017, 54(6):797-818. DOI:10.1080/15481603.2017.1331511

DOI

[5]
Lyu M Y, Ke Y H, Guo L, et al. Change in regional land subsidence in Beijing after south-to-north water diversion project observed using satellite radar interferometry[J]. GIScience & Remote Sensing, 2020, 57(1):140-156. DOI:10.1080/15481603.2019.1676973

DOI

[6]
Ikuemonisan F E, Ozebo V C, Olatinsu O B. Geostatistical evaluation of spatial variability of land subsidence rates in Lagos, Nigeria[J]. Geodesy and Geodynamics, 2020, 11(5):316-327. DOI:10.1016/j.geog.2020.04.001

DOI

[7]
Zhou C F, Gong H L, Chen B B, et al. Quantifying the contribution of multiple factors to land subsidence in the Beijing Plain, China with machine learning technology[J]. Geomorphology, 2019, 335:48-61. DOI:10.1016/j.geomorph.2019.03.017

DOI

[8]
Chen R P, Zhang P, Wu H N, et al. Prediction of shield tunneling-induced ground settlement using machine learning techniques[J]. Frontiers of Structural and Civil Engineering, 2019, 13(6):1363-1378. DOI:10.1007/s11709-019-0561-3

DOI

[9]
Li H J, Zhu L, Gong H L, et al. Land subsidence modelling using a long short-term memory algorithm based on time-series datasets[J]. Proceedings of the International Association of Hydrological Sciences, 2020, 382:505-510. DOI:10.5194/piahs-382-505-2020

DOI

[10]
罗跃, 叶淑君, 吴吉春. 三维区域地面沉降数值模拟[J]. 岩土力学, 2018, 39(3):1063-1070.

[Luo Y, Ye S J, Wu J C. Numerical model for simulating 3D regional land subsidence[J]. Rock and Soil Mechanics, 2018, 39(3):1063-1070. ] DOI:10.16285/j.rsm.2016.0599

DOI

[11]
Giao P H, Hue V T, Han N D, et al. Land subsidence prediction for a new urban mass rapid transit line in Hanoi[J]. Underground Space, 2020, 5(2):93-104. DOI:10.1016/j.undsp.2018.11.002

DOI

[12]
罗勇, 田芳, 秦欢欢, 等. 地下水人工回灌和停采对地面沉降控制的影响分析[J]. 水资源与水工程学报, 2020, 31(1):52-57.

[Luo Y, Tian F, Qin H H, et al. Effects of groundwater artificial recharge and the termination of groundwater exploitation on land subsidence control[J]. Journal of Water Resources and Water Engineering, 2020, 31(1):52-57. ] DOI:10.11705/j.issn.1672-643X.2020.01.08

DOI

[13]
万佳威, 李滨, 谭成轩, 等. 中国地裂缝的发育特征及成因机制研究——以汾渭盆地、河北平原、苏锡常平原为例[J]. 地质论评, 2019, 65(6):1383-1396.

[Wan J W, Li B, Tan C X, et al. Characteristics and mechanism of earth fissures in China: a case study of Fenhe river—Weihe River Basin, Hebei plain and Suzhou-Wuxi-Changzhou plain[J]. Geological Review, 2019, 65(6):1383-1396. ] DOI:10.16509/j.georeview.2019.06.006

DOI

[14]
王艺伟, 叶淑君, 于军, 等. 中国“采水型”地裂缝特征和成因分析[J]. 高校地质学报, 2016, 22(4):741-752.

[Wang Y W, Ye S J, Yu J, et al. Features and mechanisms of earth fissures induced groundwater withdrawal in China[J]. Geological Journal of China Universities, 2016, 22(4):741-752. ] DOI:10.16108/j.issn1006-7493.2015259

DOI

[15]
刘方翠. 北京市平原区典型地裂缝发育特征及成因机制研究[D]. 北京: 中国地质大学(北京), 2017.

[Liu F C. Study on the characteristics and genetic mechanism of typical ground fissures in Beijing plain[D]. Beijing: China University of Geosciences, 2017. ]

[16]
乔丕忠, 张勇, 张恒, 等. 近场动力学研究进展[J]. 力学季刊, 2017, 38(1):1-13.

[Qiao P Z, Zhang Y, Zhang H, et al. A review on advances in peridynamics[J]. Chinese Quarterly of Mechanics, 2017, 38(1):1-13. ] DOI:10.15959/j.cnki.0254-0053.2017.01.001

DOI

[17]
Zhou X P, Wang Y T. State-of-the-art review on the progressive failure characteristics of geomaterials in peridynamic theory[J]. Journal of Engineering Mechanics, 2021, 147(1):03120001. DOI:10.1061/(ASCE)EM.1943-7889.0001876

DOI

[18]
黄丹, 章青, 乔丕忠, 等. 近场动力学方法及其应用[J]. 力学进展, 2010, 40(4):448-459.

[Huang D, Zhang Q, Qiao P Z, et al. A review on peridynamics(PD) method and its applications[J]. Advances in Mechanics, 2010, 40(4):448-459. ] DOI:10.6052/1000-0992-2010-4-j2010-002

DOI

[19]
埃尔多安·马德西, 英额尔坎·奥特库斯著, 余音, 胡祎乐译. 近场动力学理论及其应用[M]. 上海: 上海交通大学出版社, 2019.

[Erdogan M, Erkan O, Yu Y, et al. Peridynamic theory and its application[M]. Shanghai: Shanghai Jiao Tong University Press, 2019. ]

[20]
Hattori G, Trevelyan J, Augarde C E, et al. Numerical simulation of fracking in shale rocks: Current state and future approaches[J]. Archives of Computational Methods in Engineering, 2017, 24(2):281-317. DOI:10.1007/s11831-016-9169-0

DOI PMID

[21]
廖洋, 刘立胜, 刘齐文, 等. 近场动力学方法在边坡稳定性分析中的应用[J]. 安全与环境工程, 2018, 25(1):45-50.

[Liao Y, Liu L S, Liu Q W, et al. Application of peridynamic method to slope stability analysis[J]. Safety and Environmental Engineering, 2018, 25(1):45-50. ] DOI:10.13 578/j.cnki.issn.1671-1556.2018.01.008

DOI

[22]
Lai X, Ren B, Fan H F, et al. Peridynamics simulations of geomaterial fragmentation by impulse loads[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2015, 39(12):1304-1330. DOI:10.1002/nag.2356

DOI

[23]
Turner D Z. A non-local model for fluid-structure interaction with applications in hydraulic fracturing[J]. International Journal for Computational Methods in Engineering Science and Mechanics, 2013, 14(5):391-400. DOI:10. 1080/15502287.2013.784382

DOI

[24]
Ouchi H, Katiyar A, York J, et al. A fully coupled porous flow and geomechanics model for fluid driven cracks: Aperidynamics approach[J]. Computational Mechanics, 2015, 55(3):561-576. DOI:10.1007/s00466-015-1123-8

DOI

[25]
张钰彬, 黄丹. 页岩水力压裂过程的态型近场动力学模拟研究[J]. 岩土力学, 2019, 40(7):2873-2881.

[Zhang Y B, Huang D. State-based peridynamic study on the hydraulic fracture of shale[J]. Rock and Soil Mechanics, 2019, 40(7):2873-2881. ]

[26]
Zhang Y B, Huang D, Cai Z, et al. An extended ordinary state-based peridynamic approach for modelling hydraulic fracturing[J]. Engineering Fracture Mechanics, 2020, 234:107086. DOI:10.1016/j.engfracmech.2020.107086

DOI

[27]
Ni T, Pesavento F, Zaccariotto M, et al. Hybrid FEM and peridynamic simulation of hydraulic fracture propagation in saturated porous media[J]. Computer Methods in Applied Mechanics and Engineering, 2020, 366:113101. DOI:10.1016/j.cma.2020.113101

DOI

[28]
Shou Y D, Zhou X P. A coupled hydro-mechanical non-ordinary state-based peridynamics for the fissured porous rocks[J]. Engineering Analysis with Boundary Elements, 2021, 123:133-146. DOI:10.1016/j.enganabound.2020.12.001

DOI

[29]
Sun W, Fish J. Coupling of non-ordinary state-based peridynamics and finite element method for fracture propagation in saturated porous media[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2021, 45(9):1260-1281. DOI:10.1002/nag.3200

DOI

[30]
Silling S A. Reformulation of elasticity theory for discontinuities and long-range forces[J]. Journal of the Mechanics and Physics of Solids, 2000, 48(1):175-209. DOI:10.1016/S0022-5096(99)00029-0

DOI

[31]
Silling S A, Epton M, Weckner O, et al. Peridynamic states and constitutive modeling[J]. Journal of Elasticity, 2007, 88(2):151-184. DOI:10.1007/s10659-007-9125-1

DOI

[32]
Madenci E, Oterkus E. Peridynamic theory and its applications[M]. New York: Springer, 2014.

[33]
Zhang Y, Qiao P Z. An axisymmetric ordinary state-based peridynamic model for linear elastic solids[J]. Computer Methods in Applied Mechanics and Engineering, 2018, 341:517-550. DOI:10.1016/j.cma.2018.07.009

DOI

[34]
Bagheri-Gavkosh M, Hosseini S M, Ataie-Ashtiani B, et al. Land subsidence: a global challenge[J]. Science of the Total Environment, 2021, 778:146193. DOI:10.1016/j.scitotenv.2021.146193

DOI

[35]
王天一, 姜金荣, 迟学斌, 等. 地球系统模式CAS-ESM 2.0性能评估与分析[J]. 计算机系统应用, 2021, 30(6):9-17.

[Wang T Y, Jiang J R, Chi X B, et al. Performance evaluation and analysis of CAS-ESM 2.0[J]. Computer Systems & Applications, 2021, 30(6):9-17.] DOI:10.15888/j.cnki.csa.007960

DOI

[36]
Macek R W, Silling S A. Peridynamics via finite element analysis[J]. Finite Elements in Analysis and Design, 2007, 43(15):1169-1178. DOI:10.1016/j.finel.2007.08.012

DOI

[37]
Giannakeas I N, Papathanasiou T K, Fallah A S, et al. Coupling XFEM and peridynamics for brittle fracture simulation—part I: Feasibility and effectiveness[J]. Computational Mechanics, 2020, 66(1):103-122. DOI:10.1007/s00466-020-01843-z

DOI

[38]
Yang Y, Liu Y J. Modeling of cracks in two-dimensional elastic bodies by coupling the boundary element method with peridynamics[J]. International Journal of Solids and Structures, 2021, 217/218:74-89. DOI:10.1016/j.ijsolstr.2021.02.002

DOI

[39]
Kilic B, Madenci E. Coupling of peridynamic theory and the finite element method[J]. Journal of Mechanics of Materials and Structures, 2010, 5(5):707-733. DOI:10.2140/jomms.2010.5.707

DOI

[40]
北京市轨道交通建设管理有限公司, 北京市勘察设计研究院有限公司,北京市测绘设计研究院. 地面沉降及地下水位变化对地铁工程的影响研究[M]北京: 北京市科学技术委员会, 2014.

[Beijing MTR Construction Administration Corporation, BGI Engineering Consultants Ltd. and Beijing Institute of Surveying and Mapping. Study on the influence of ground subsidence and groundwater level change on subway engineering[M]. Beijing: Beijing Municipal Science & Technology, 2014. ]

[41]
罗文林, 韩煊, 杜修力, 等. 北京东部区域地下水位变化特征及其对地面沉降的影响研究[J]. 工业建筑, 2016, 46(11):127-131.

[Luo W L, Han X, Du X L, et al. Groundwater level variation and its impact on land subsidence in the eastern area of Beijing[J]. Industrial Construction, 2016, 46(11):127-131. ] DOI:10.13204/j.gyjz201611023

DOI

[42]
杜钊锋. 北京典型区域不均匀地面沉降成因机制分析[D]. 北京: 首都师范大学, 2013.

[Du Z F. Analysis of the mechanism of uneven land subsidence in typical areas of Beijing[D]. Beijing: Capital Normal University, 2013. ]

[43]
Cao Y, Wei Y N, Fan W, et al. Experimental study of land subsidence in response to groundwater withdrawal and recharge in Changping District of Beijing[J]. PLoS ONE, 2020, 15(5):e0232828. DOI:10.1371/journal.pone.0232828

DOI

[44]
Guo L, Gong H L, Li J W, et al. Understanding uneven land subsidence in Beijing, China, using a novel combination of geophysical prospecting and InSAR[J]. Geophysical Research Letters, 2020, 47(16): e2020GL088676. DOI:10.1029/2020GL088676

DOI

Options
Outlines

/

〈 〉