EN中文

Journal of Geo-information Science >

2023 , Vol. 25 >Issue 2: 311 - 323

DOI: https://doi.org/10.12082/dqxxkx.2023.220397

Prediction of Passenger Demand for Online Car-hailing based on Spatio-temporal Multi-graph Convolution Network

  • HUANG Xin , 1, 2 ,
  • MAO Zhengyuan , 1, 2, *
Expand
  • 1. Academy of Digital China, Fuzhou University, Fuzhou 350108, China
  • 2. Key Laboratory of Spatial Data Mining and Information Sharing of Ministry of Education, Fuzhou University, Fuzhou 350108, China
* MAO Zhengyuan, E-mail:

Received date: 2022-06-09

  Revised date: 2022-09-07

  Online published: 2023-04-19

Supported by

National Natural Science Foundation of China(41801324)

National Natural Science Foundation of China(41701491)

General Project of Nat ural Science Foundation of Fujian Province(2019J01244)

General Project of Nat ural Science Foundation of Fujian Province(2019J01791)

Fold

Abstract

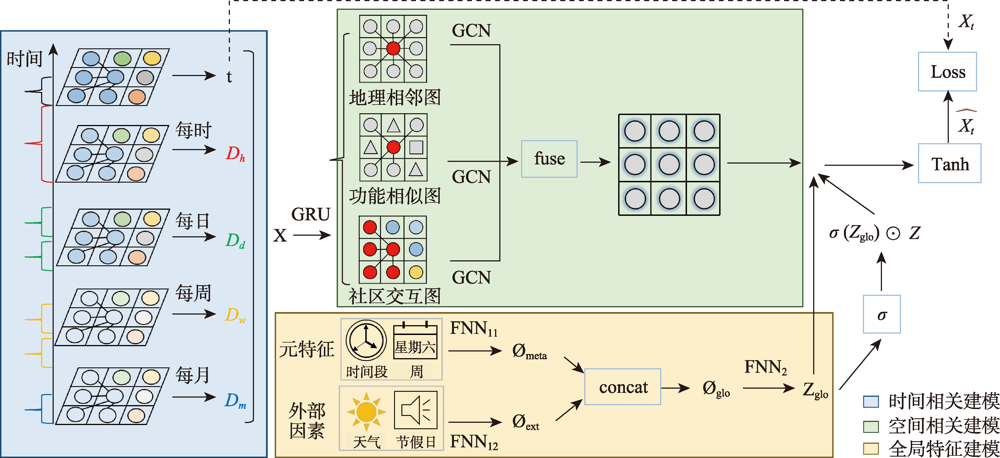
With the popularization of smartphones, online car-hailing has become a common travel alternative and plays an important role in meeting public travel demand. Therefore, online car-hailing operation platforms have been a major component of Intelligent Transportation Systems in which passenger demand prediction is one of the core problems to be solved. However, models proposed in the existing literature usually ignore the long-term temporal correlation and multiple spatial correlations. This paper presented a Spatio-Temporal Multi-Graph Convolutional Network Fused With Global Features (GST-MGCN) to address the limitations of existing research achievements, taking full account of the unique spatiotemporal correlations of the travel demand of online car-hailing passengers. Following the Closeness, Period, and Trend (CPT) paradigm, the model fitted temporal dependencies with time series information. By identifying multiple spatial semantic correlations, the corresponding relational graph structure was constructed, and a multi-graph convolutional model was built in which the global features fusion module employed gated fusion and sum fusion methods to capture sudden and gradual changes of passenger demand, respectively. Taking the Haikou city dataset as an example, our experimental results show that the values of the three indicators, MAE, RMSE, and MAPE of the GST-MGCN model proposed in this paper were 2.269, 3.917, and 21.447, respectively, which were lower than those derived from other similar mainstream models. This study demonstrated that the proposed model GST-MGCN can effectively mine the spatio-temporal pattern of online car hailing passenger travel demand, extract the impact of global features, and accurately predict it.

Key words： online car-hailing demand forecast; graph convolutional neural network; external factor fusion; spatio-temporal data; global features; deep learning; urban computing

Cite this article

HUANG Xin , MAO Zhengyuan . Prediction of Passenger Demand for Online Car-hailing based on Spatio-temporal Multi-graph Convolution Network[J]. Journal of Geo-information Science, 2023 , 25(2) : 311 -323 . DOI: 10.12082/dqxxkx.2023.220397

1 引言

随着我国城市化进程的持续推进，小汽车保有量逐年增长，交通拥堵在大中城市越来越严重，成为亟待解决的问题。交通拥堵问题本质上是出行需求与供给的矛盾冲突，增加供给是解决该矛盾的基本前提，如何实现供需匹配是需要解决的关键问题。随着移动互联网的高速发展，特别是智能手机的普及，近年来网约车行业快速壮大，成为替代传统出行方式的新选择。网约车的运营方式在一定程度上能克服传统出租车供需信息不对称的问题，但随着用户规模的增长，如何保持网约车供需时空平衡难度增加，网约车需求精准预测成为需要解决的新问题。
智能交通系统（Intelligent Transport System，ITS）[1]正在大力发展，网约车需求预测是其中的重要组成部分，出行需求的精准预测可提高路网的通行能力和效率，降低出行成本，对于提升智能交通系统效能、缓解城市交通拥堵具有重要意义。传统机器学习模型是早期用于解决网约车相关问题的预测方法。2004年，Wu等[2]将支持向量回归应用于行程时间预测，结果证明该方法具有较强的泛化能力，但预测效果过于依赖所选择或构建特征的质量。近年来，深度学习兴起并在诸多领域中取得巨大的成功，基于深度学习的方法成为网约车需求预测问题解决方案的主流。Zhang等[3]提出了基于卷积神经网络（Convolutional Neural Networks，CNN）的深度时空预测模型，通过对多个不同时间尺度的历史交通流特征建模，同时考虑外部变量（气象因素等）的影响，在几个公开的交通流数据集上均取得良好的预测效果，该方法的不足是只能对时空数据中的空间依赖性建模，不能显式地针对时序依赖关系建模。
为了耦合时空依赖关系建模，Guo等[4]引入了3D卷积计算[5]以同时提取时空维度特征，更好地实现了人群流量预测。而Yao等[6]则基于循环神经网络（Recurrent Neural Network，RNN）提出了深度多视角时空预测模型，该模型通过CNN提取局部空间特征，再利用长短期记忆网络（Long Short-Term Memory，LSTM）提取时序特征，有效地提升了模型的预测性能。
上述方法在空间维度上使用传统的CNN，只能捕获格网结构数据上各位置的局部空间相关性，无法考虑更大空间范围的信息。近年来，适用于图结构数据特征提取与学习的图卷积网络逐渐兴起，图神经网络（Graph Neural Network，GNN）+RNN很快成为交通流预测领域最流行的方法。宋龙泽等[7]提出了一种时空图卷积结构，全面建模影响空载时间的时空相关性因素。冯宁等[8]提出了一种新颖的多组件时空图卷积网络，通过3个组件分别建模流量数据的近期、日周期、周周期特性，每个组件同时利用空间维图卷积和时间维卷积有效捕获交通数据的时空相关性。Zhao等[9]、Yu等[10]以及Cui等[11]采用图卷积网络从道路网络拓扑结构中学习空间关联，分别结合门控循环单元（Gated Recurrent Unit，GRU），门控卷积（Gated Convolutional Neural Network，GCNN）和LSTM学习时间关联实现了交通流时空预测。
上述模型仅从结点间的位置关系视角考虑其空间相关性，忽略了结点交通流在其他视角下存在的关联性。针对现有模型存在的不足，Chai等[12]提出了一种多图卷积神经网络模型预测站点级自行车流量。该研究构建了多个图反映异构的站间关系，获取区域间的不同依赖关系，并利用图卷积网络预测未来的站点级自行车流量，预测效果较现有同类方法有提升，但仍然缺乏对复杂外部因素影响特点的充分考虑。
本研究针对上述方法存在的不足提出了一种新的解决方案，该方案充分利用时间上下文信息，遵循CPT范式[13]模拟多种类型的时间依赖关系，并利用门控循环单元进行编码。通过识别几种空间语义相关性并构建对应的关系图结构，使用多图卷积拟合空间依赖性。此外，通过引入一种外部嵌入机制提取全局特征（天气条件等）对流量预测的影响，模型既能捕捉到乘客需求的稳定趋势（渐变），又能捕捉其突变。以海口市数据集为样本进行实验，验证方案的有效性。

2 基于时空多图卷积网络的算法框架

2.1 问题定义

根据不同的粒度和语义，区域可以有多种定义。本文采用了交通领域的经典处理方法[14]，将整个城市沿着经纬度均匀等分成N个网格 ( N = a × b )，每个网格代表一个区域。收集信息所需的时间段定义为时间间隔。以τ为时间间隔将历史时间划分为T个时间段。根据区域和时间的划分，有以下变量的定义。
定义1(需求强度)：将研究区域划分为网格，汇总特定时间间隔内每个网格的出行次数，需求强度则定义为汇总的结果。例如，第t个时间间隔内第m个区域的需求强度用 d t m表示。
定义2(区域图)：使用图 G = ( V 、 A 、 X )将所有区域合并成数据结构。在图中，V为节点集，每个节点表示一个网格区域。V=[1,…, i,…, N]，i表示研究区内按从左至右、从上至下顺序的第i个区域。A为邻接矩阵，其元素值表示节点是否连接（即节点间是否存在边），对应区域之间的异质空间相关性。X为节点的特征矩阵， X ∈ R N × P，R为实数集，N为区域数，P为历史时间序列的长度。 X m = [ d t - P     m , …   ,   d t - 1 m ]表示对第m个区域所有历史时间间隔的需求强度， X t = [ d t       1 , …   ,   d t N ]表示第t个时间间隔内所有区域的需求强度。
采用上述定义中的术语，乘客需求预测问题可表述为：给定之前P个时间间隔上的区域图G，本研究的目的是预测下一个时间间隔内所有区域的乘客需求强度。

2.2 模型概述

融合全局特征的时空多图卷积神经网络模型（以下简称GST-MGCN）是本文所设计的解决方案中的核心内容，它由3个部分组成（图1）。
图1 GST-MGCN模型框架

Fig. 1 The GST-MGCN model framework

（1）时间相关处理子块：为了充分利用时间上下文信息，从单个区域的历史观测中提取关键帧，拼接成一个特征向量，对所有区域进行相同处理，拼接生成的特征矩阵作为GRU层的输入。
（2）空间相关处理子块：基于GRU层的输出，构造3个图编码异质空间相关性，利用图卷积（Graph Convolutional Network，GCN）层表征每个图的空间关系。从拓扑结构级考虑相邻关系、从节点特征级考虑功能相似度，综合2个角度考虑社区交互度，并对这3个图进行融合。
（3）全局特征处理子块：在外部组件中，本文将全局特征分为元特征和外部因素分别输入不同的全连接层，获得不同的潜在表示。同时还设计了一个融合模块，用于融合多个不同特征的潜在表示，该模块基于门控融合和总和融合2种融合方法分别用于捕捉其中的突变和渐变。本节以下依次介绍每个模块实现的细节。

2.3 时间相关性建模

城市区域中乘客需求的分布一般表现出明显的时间相关性[15]。图2为利用海口市网约车订单数据绘制得到的乘客出行需求随时间变化的关系图。图2（a）系选取海口市某天的订单数据得到，观察该图可知乘客需求受到临近历史需求的影响， 图2（b）选取了海口市某三周的订单数据，该图显示网约车乘客需求具有明显的周期性，包括日、周周期。图2（c）选取了海口市所有周二的订单数据，该图表明乘客需求还具有一定的趋势性。对于特定的预测周期有许多历史观测值，但预测中输入变量的长度是有限的。
图2 海口市网约车乘客需求随时间变化的关系

Fig. 2 Time characteristics of passenger demand for online car-hailing in Haikou

本文遵循CPT范式利用时间临近性、周期性和趋势性从历史观测值中提取关键帧来编码时间相关性，考虑一种类型的临近、2种类型的周期和一种类型的趋势，分别选择相应的每时、每日、每周、和每月的时间步作为关键时间步，分别构建关键时间步长的流矩阵列表，以构造如下4个输入：
（1）每小时临近组件 D h：包括过去几小时的同期需求强度，用于描述临近历史需求的影响。
D h = D t - L h   ,   D t - L h + 1   ,   …   ,   D t - 2   ,   D t - 1
（2）每日周期组件 D d：由过去几天同期的需求强度组成，反映日周期性。
D d = D t - L d * P d ,   D t - L d - 1 * P d ,   … ,   D t - 2 * P d ,   D t - P d
（3）每周周期组件 D w：由过去几周同期的需求强度组成，反映周周期性。
D w = D t - L w * P w ,   D t - L w - 1 * P w ,   … ,   D t - 2 * P w   ,   D t - P w
（4）每月趋势组件 D m：由过去几月同期的需求强度组成，反映长时间的趋势性。
D m = D t - L m * P m ,   D t - L m - 1 * P m ,   …   ,   D t - 2 * P m   ,   D t - P m
式中： L h、 L d、 L w、和 L m分别为每时、每日、每周和每月列表的输入长度，通过小网格搜索法分别设置为18、3、2、1。 P d和 P w是每日和每周周期跨度； P m是月趋势跨度。图3显示了一个关键帧提取的例子。
图3 关键帧提取的例子(t = 0:00, q = 15 min)

Fig. 3 An example of keyframe extraction (t = 0:00, q = 15 min)

（5）时间相关性：将4个片段 D h、 D d、 D w和 D m拼接成一个特征向量 X m，以编码长期的时间相关性。
D h   ,   D d   ,   D w   ,   D m = D t - L m * P m   ,   …   ,   D t - P m   ,   D t - L w * P w ,   …   ,   D t - P w   ,   D t - L d * P d   ,   …   ,   D t - P d   ,   D t - L h   ,   …   ,   D t - 1
X m = D h   ,   D d   ,   D w   ,   D m
针对每个区域提取上述特征向量，然后叠加所有特征向量得到特征矩阵X。再将这个特征矩阵发送到GRU层，提取各区域的时间特征。

2.4 空间相关性建模

不同区域的乘客需求在空间相关性分析中表现出异质性。本文为研究区域构建了3种关系图，以对其不同区域之间复杂的空间关系进行建模。为了能够从这些地理相邻区域、功能相似区域和社区交互区域感知整个城市出行需求模式的变化，通过以下3种关系图编码不同区域之间的空间关系。
（1）地理相邻图（Geographically Adjacent Graph，GAG）：根据地理学第一定律[16]，所有的事物都与其他事物相关，但是距离相近的事物，比远处的事物更相关。因此，本研究首先考虑了距离相近的事物之间的空间关系，即邻近关系。通过连接2个地理上相邻的区域来构建该图，以便信息可以通过边缘流动，地理相邻图定义为 G g a = V   ,   A g a   ,   X， A g a为其邻接矩阵，区域i与区域j之间的边 A g a i , j定义如式（7）所示。
A g a i , j =   1                   区 域 i 与 区 域 j 相 邻   0                   其 他
（2）功能相似图（Functional similarity graph，FSG）：研究发现，即使相隔很远，具有相似功能的区域在出行需求模式上具有高度相似性。同时，已经有研究证明，兴趣点（Point of Interest，POI）的分布可以衡量城市区域的功能性[17]。因此，采用POI相似性来量化不同区域之间的功能相似性，思路如下：对给定区域i分配一个14维POI特征向量 p i，对应14类实体，向量中的特定值表示属于每个实体类别的密度。其中，实体密度参照自然语言处理领域的词频逆向文件频率（Term Frequency-Inverse Document Frequency，TF-IDF）设计，为总数较少的POI类别分配较高的权重（式（8））。
P i [ t ] = m i t m i × l o g M M t
式中: m i t是区域i内t类POI的数量； m i是区域i内POI的总数； M t是POI数据集中t类POI的数量；M是POI数据集中POI的总数； P i t是区域i内t类POI的密度。
本文利用余弦函数计算任意2个区域之间的POI相似度，并根据POI相似度的值来决定这2个区域之间是否有一条边。相似度的阈值设置为0.8。功能相似图定义为 G f s = V   ,   A f s   ,   X， A f s为其邻接矩阵，区域i与区域j之间的边 A f s i , j定义如 式（9）所示。
A f s i , j =   1             c o s ( P i ,   P j ) > 0.8   0           其 他
式中： P i、 P j为区域i和区域j的POI特征向量； cos（*）为余弦函数的计算函数。
（3）社区交互图（Community Interaction Graph，CIG）：在进行时空预测时，历史订单数据可以提供大量的信息来构建图。例如，如果在区域i和区域j之间存在很多订单数据。那么2个区域i和j在出行需求模式方面往往会相互影响[18]。考虑到这个想法，本文构建了一个社区交互图，根据历史订单数据以表明2个区域是否经常相互交互。通过应用鲁汶算法，将研究区域划分为几个社区。鲁汶算法通过模块度（Q）来衡量一个社区的紧密程度，计算方法如式（10）、式（11）所示。
Q = 1 2 m ∑ i , j A i j - k i k j 2 m δ c i ,   c j
δ u   ,   v =   1                   u = = v   0                 其 他
式中：m表示图中所有边权值的和； A i j表示区域i和区域j之间的边权值； k i表示连接到区域i的边的权值的和；ci表示节点i所属的社区。求解过程中 式（10）与式（11）被反复执行，直到图的模块度不再改变或计算达到迭代的最大值，即可得到每个区域所属的社区。
社区内部的区域联系更加密切，本文将这些位于同一个社区的区域定义为“交互”，社区交互图定义为 G c i = V   ,   A c i   ,   X， A c i为其邻接矩阵，区域i与区域j之间的边 A c i i , j定义如式（12）所示。
A c i i , j =     1                         区 域 i   ϵ   社 区 1   ︙                                       ︙     n                         区 域 i   ϵ   社 区 n
在构建了上述3张图后，应用GCN来提取空间相关性。从地理相邻图、功能相似图和社区 交互图中捕获每个区域的空间特征，如式（13）—式（15）所示。
G g a = V   ,   A g a   ,   X   G C N _   G g a = V   ,   A g a ,   Z g a
G f s = V   ,   A f s   ,   X   G C N _   G f   s = V   ,   A f s ,   Z f s
G c i = V   ,   A c i   ,   X   G C N _   G c i = V   ,   A c i ,   Z c i
式中: Z g a、 Z f s、 Z c i表示3个图中提取的特征矩阵。本文将进一步融合3个图的空间特征，如 式（16）—式（18）所示。
Z = Z g a   ,   Z f s   ,   Z c i
A i , j = A g a i , j   o r   A f s i , j   o r   A c i i , j
G g a   =   V ,   A g a   ,   Z g a G f s   =   V   ,   A f s   ,   Z f s → f u s e G = V ,   A ,   Z G c i   =   V   ,   A c i   ,   Z c i
式中：Z和A表示融合图中的新特征矩阵和邻接矩阵。

2.5 全局特征建模

全局特征由元特征和外部因素组成。全局特征信息对于预测一个地区的乘客需求至关重要，不同的因素可能以不同的方式改变流量[19]。其中，高峰时间和天气条件在流量预测中起着主要作用[20]。本文提出的模型框架可以灵活地结合其他功能，同时考虑到数据的可获取性，为预测模型考虑以下几个全局特征信息：① 元特征：周特征、分时段特征；② 外部因素：天气、节假日。
图4（a）与图4（b）分别显示了网约车需求量的周特征及分时段特征，该种特征显示需求量的变化是渐进式、有规律可循的。图4（a）显示了网约车需求量和对应的周特征有较为密切的关系。图4（b）表明，一周中同一周几属性分时段的变化趋势大致相同。图4（c）与图4（d）分别显示了外部因素对乘客需求的影响。外部因素如天气、节假日会调节人群流量，影响人们对出行方式的选择。对乘客需求的影响就像开关一样，如果发生，乘客需求将会发生巨大的变化。由图4（c）可见，当天气开始下雨时，网约车需求急剧和显著地减少。图4（d）显示国庆节假期前一周开始，网约车需求开始减少。假期期间，网约车需求急剧和显著地减少。
图4 全局特征对乘客需求的影响

Fig. 4 The impact of global features on passenger demand

基于这些认识，本文堆叠了两层全连接神经网络（FNN）分别对外部因素 I e x t和元特征 I m e t a进行建模，第一层可以看做是每个因素的嵌入层，将它们输入不同的嵌入层，以获得不同的潜在表示 ∅ e x t和 ∅ m e t a。第二层用来确保与空间相关性建模部分的输出矩阵Z具有相同的形式，先将 ∅ e x t和 ∅ m e t a进行简单连接得到 ∅ g l o，再添加全连接层重塑获得 Z g l o。
本文利用2种不同的融合方法来处理这2种类型的情况。由于网约车需求存在元特征如周特征和分时段特征这类渐进式变化的特点，先采用总和融合法，即 Z + Z g l o。由于存在天气和节假日这类使网约车需求发生瞬时变化的外部因素，本文还采用基于门控机制的融合，即 σ ( Z g l o ) ⊙   Z，其中σ为近似的门控激活函数sigmoid。当 Z g l o捕获到某些特殊的外部信息时，由于sigmoid函数的特性，与 Z g l o相比， σ ( Z g l o ) ⊙   Z会发生巨大的变化，在大多数情况下，该项的值应该接近零。基于上述2种融合方法，最终输出计算如式（19）所示。
X t ^ = f o Z + Z g l o + σ ( Z g l o ) ⊙   Z
式中： f o是激活函数tanh。

3 实验配置

3.1 数据集与数据处理

本文使用的网约车历史订单数据来源于滴滴出行“盖亚”数据开放计划（Data source: Didi Chuxing GAIA Initiative）的出行数据集，目前能够获取的是2017年5月1日至10月31日海口市每天的订单数据。网约车乘客需求的热力分布如图5所示，密度从低到高对应的颜色变化为从绿到红。由图可知，网约车需求量整体上集中于秀英区、美兰区、龙华区及琼山区。本研究选择这4个区所在的经纬度范围，以1200 m×1200 m的网格大小为标准，将研究区划分为8×8的网格（图6）。本文综合考虑预测性能与数据量大小[21]，以τ=15 min为时间间隔，根据历史订单数据计算出各个时间段、各个区域出行次数。其中网格大小的划分以及时间间隔长短的选择标准为：保证大部分区域和时间段都有样本的情况下使区域和时间粒度尽可能小，其中训练集、验证集、测试集按照7:2:1的比例划分。
图5 网约车乘客需求热力图

Fig. 5 Heat map of online car-hailing passenger demand

图6 研究区栅格示意图

Fig. 6 Schematic diagram of the grid of the study area

本文还收集了源自高德地图的POI数据集来匹配研究区域，该数据集由国家信息中心合作企业北京国信宏数科技有限责任公司提供，时间跨度为截止到2018年9月30日的全量数据。本文用POI数据量化研究区域之间的功能相似性。

3.2 评价指标

为精确地评价GST-MGCN模型的预测精度，本文引入3种精度评价指标，分别是：平均绝对误差（MAE）、均方根误差（RMSE）、平均绝对百分误差（MAPE）。其中，RMSE、MAE、MAPE越小，说明预测误差越小，即预测效果越好。评价指标如式（20）、式（21）、式（22）：
M A E = 1 N ∑ i = 1 N y i - y i ^
R M S E = 1 N ∑ i = 1 N y i - y i ^ 2
M A P E = 1 N ∑ i = 1 N y i - y i ^ y i
式中：N是样本总数， y i和 y i ^是第i个需求强度的真实值和预测值。由于MAPE受非常小的值影响很大，本文只计算需求强度高于或等于10的样本的MAPE。

3.3 模型设置

GST-MGCN模型的实现步骤与参数设置如下：
实现步骤：① 在时间相关建模部分，堆叠2层GRU，每层GRU都包含24种隐藏状态。将第2.3节中定义的 L h、 L d、 L w、和 L m通过小网格搜索法分别设置为18、3、2、1。② 在空间相关建模部分，构建3个2层的GCN模型，上层隐藏单元的数量设置为20，下层设置为32。③ 全局特征建模模块使用两个不同的全连接层，1层包含60个ReLU神经元，1层为线性输出层。
参数设置：基于深度学习库构建和训练GST-MGCN模型，GST-MGCN使用Adam优化器优化参数，学习率设置为0.01，批量大小设置为72。本文使用L2损失训练模型，还通过监测最佳分数对验证集使用早期停止（其轮数设为10），以便在训练过程中选择最佳的泛化网络。

4 实验结果与分析

4.1 GST-MGCN与基准模型的比较实验

为证明模型的有效性和准确性,本文将GST-MGCN模型与下述8种现有预测方法进行对比。
（1）XGBoost：一种强大的提升树方法，广泛应用于各种回归任务中，因其高学习效率已应用于许多交通预测任务。Kankanamge等[22]利用XGBoost回归模型，预测出租车出行时间。
（2）GRU：GST-MGCN的一个变体，区别是该模型仅考虑时间相关性。其门控循环单元在序列建模中具有良好的预测性能，在乘客需求预测中有许多成功的应用。
（3）LSTM：时间序列建模中常用的神经网络，Fu等[23]曾将该模型用于短时交通流量预测，实验表明，采用基于循环神经网络的深度学习方法实现的LSTM，优于自回归移动平均模型。
（4）GCN：GST-MGCN的一个变体，区别是该模型仅考虑空间相关性。
（5）卷积长短期记忆网络（Convolutional Long Short-Term Memory，ConvLSTM）：Lu等[24]提出一种基于图像的网约车需求预测模型，它通过提取交通信息中的时空相关特征生成图像，预测短期网约车需求。该模型扩展了LSTM，使其具有卷积结构，从而能有效利用网约车乘客需求数据的时间和空间信息，更好地捕获时空相关性。
（6）ST-MGCN：GST-MGCN的一个变体，区别是GST-MGCN考虑了全局特征。
（7）T-GCN：用于交通预测的高级时空图卷积神经网络。该模型使用GRU拟合时间相关性，使用GCN捕捉区域之间的空间依赖性，使用拓扑结构信息实现图卷积运算。Zhao等[9]曾利用该模型基于城市道路网预测交通流量。实验表明T-GCN模型可以捕获交通数据中的时空相关性，且预测效果良好。
（8）Graph WaveNet：系Wu等[25]提出的一种新的图神经网络，用于时空图建模。它通过将图卷积与扩展的因果卷积相结合，能有效捕获时空依赖性。
为保持评估的公平性，上述所有模型使用相同的数据集来进行训练、验证和测试。所有模型的输入数据相同，但根据不同模型所需的数据格式进行了相应的调整。本文将时间间隔设置为15分钟进行预测，并将GST-MGCN模型与前述8种基准方法进行了比较。
表1显示了在同一测试集上进行10次实验的平均结果。观察表1可知3种预测精度（MAE、RMSE、MAPE）在所有模型上基本呈现出一致性，且本文提出的GST-MGCN模型在3种测量条件下都取得了最佳的预测结果。
表1 不同方法在海口数据集上的预测结果

Tab. 1 Prediction results of different methods on the Haikou dataset

方法 MAE RMSE MAPE/%
XGBoost 6.146 8.565 32.255
GRU 4.823 5.289 28.780
LSTM 4.832 5.214 29.028
GCN 5.741 5.887 30.038
ConvLSTM 3.449 4.123 25.297
ST-MGCN 3.038 4.036 23.180
T-GCN 2.873 3.960 22.291
Graph WaveNet 2.635 3.985 23.612
GST-MGCN 2.269 3.917 21.447
从结果中可以看出以下趋势：传统的机器学习方法XGBoost由于不能捕获区域间的空间相关性，预测效果不理想。同时考虑乘客需求时空相关性的ConvLSTM及其相应模型比传统的神经网络方法GRU和LSTM具有更好的预测性能。GCN忽略了时间依赖性的影响，产生了较大的误差。基于图卷积的方法获得了比传统卷积更好的预测结果，其中ConvLSTM模型中采用的是传统卷积，而使用图卷积的T-GCN与Graph WaveNet模型能够捕获到图结构中蕴含的更丰富的空间相关性，因此其效果优于其他基于传统卷积的模型。此外，本文模型也比仅考虑不同区域之间的时空相关性的模型具有更好的预测性能，相较于GRU与GCN, GST-MGCN模型的预测结果误差MAE分别降低了2.554、3.472。GST-MGCN与忽视全局特征的ST-MGCN相比，MAE降低了0.769。证明了该框架同时考虑乘客需求时空相关性以及全局特征影响的有效性和优越性。

4.2 不同GST-MGCN模型变体的比较试验

为了进一步探索时空相关性模块以及全局特征模块在乘客需求预测中的有效性，本文通过在模型中改变不同的组件得到GST-MGCN相关的几个变体模型进行评估。

4.2.1 时间相关性变体

GST-MGCN将时间相关性编码为由4个时间序列片段组成的向量。此处变体仅选取考虑每小时临近分量和每日周期分量的2种相应模型： G S T - M G C N h：以每个区域过去6 h的历史旅客需求强度为输入数据集； G S T - M G C N d：仅以过去 24 d相同时间间隔的历史旅客需求强度作为输入数据集。模型结构均与GST-MGCN相同。由于每周周期和每月趋势对需求预测的影响是长期的，且相对较弱，因此没有选择只考虑这2种成分的模型。
表2表明仅考虑每小时临近分量的 G S T - M G C N h和仅考虑每日周期分量的 G S T - M G C N d两种模型性能均变得更差，证实了GST-MGCN模型同时考虑4个时间序列分量的优越性和必要性。其中 G S T - M G C N d模型与 G S T - M G C N h模型相比产生了更高的MAE、RMSE和MAPE，且在训练过程中产生了抖动现象（图7），造成这种现象的原因可能是每日周期的乘客需求更不稳定，历史观测的相关性相对较弱。
表2 时间相关性GST-MGCN模型变体在海口数据集上的预测结果

Tab. 2 Prediction results of the time-dependent GST-MGCN model variants on the Haikou dataset

方法 MAE RMSE MAPE/%
GST-MGCNh 3.823 4.289 24.780
GST-MGCNd 5.832 6.214 28.028
GST-MGCN 2.269 3.917 21.447
图7 GST-MGCN模型及其时间相关性模型变体在验证集上的不同轮数的性能比较

Fig. 7 Performance comparison of the GST-MGCN model and its temporal correlation model variants at different epochs on the validation set

4.2.2 空间相关性变体

在空间相关性方面，分别选择考虑2张图的相应模型作为候选模型： G S T - M G C N g a - f s：在空间相关性建模中只保留地理相邻图和功能相似图； G S T - M G C N g a - c i：只保留地理相邻图和社区交互图； G S T - M G C N f s - c i：只保留功能相似图和社区交互图。
在模型比较中可以看出，融合3个空间图的GST-MGCN优于其他只融合2个空间图的模型 （图8）。这表明地理相邻属性、功能相似属性和社区交互属性均在空间相关性建模中发挥作用，有效提高了模型的预测精度。观察表3可知，除了GST-MGCN外， G S T - M G C N g a - c i的整体表现最好。说明历史出行需求中反应的社区交互属性对未来的出行需求有明显的指示作用。 G S T - M G C N g a - f s表现出较差的精度，一个潜在的原因是POI数据被平均表示为点。实际上，不同尺寸的POI可能对出行需求有不同程度的影响（大商场通常比小商店对出行需求的影响更大）。
图8 GST-MGCN模型及其空间相关性模型变体在验证集上的不同轮数的性能比较

Fig. 8 Performance comparison of the GST-MGCN model and its spatial correlation model variants at different epochs on the validation set

表3 空间相关性GST-MGCN模型变体在海口数据集上的预测结果

Tab. 3 Prediction results of spatially correlated GST-MGCN model variants on the Haikou dataset

方法 MAE RMSE MAPE/%
GST-MGCNga-fs 2.941 4.788 24.038
GST-MGCNga-ci 2.469 4.036 23.180
GST-MGCNfs-ci 2.489 4.423 23.297
GST-MGCN 2.269 3.917 21.447

4.2.3 全局特征变体

在全局特征建模方面，分别选择只考虑一种融合机制的模型作为候选模型： G S T - M G C N s u m：所有全局特征均使用SUM融合机制；GST-MGCNgat：所有全局特征均使用GATING融合机制。
观察表4发现：本文提出的集成两种融合机制的方法，克服了单一融合机制的预测方法存在的局限性，实现了预测精度的提升，表明GST-MGCN考虑到不同全局特征对乘客需求的影响方式不同，采用不同的融合机制，有效地提升了模型的性能。 图9进一步显示了随着训练轮次增加，GST-MGCN模型及其全局特征模型变体的验证误差。可以看出， G S T - M G C N g a t整体性能最差，其原因可能是门控融合机制由于其激活函数的特性，在大多数情况下不会发生变化，不能很好地捕获元特征这类渐进式因素的变化趋势。
表4 全局特征GST-MGCN模型变体在海口数据集上的预测结果

Tab. 4 Prediction results of global feature GST-MGCN model variants on the Haikou dataset

方法 MAE RMSE MAPE/%
GST-MGCNsum 2.573 3.960 22.291
GST-MGCNgat 3.335 4.985 25.612
GST-MGCN 2.269 3.917 21.447
图9 GST-MGCN模型及其全局特征模型变体在验证集上的不同轮数的性能比较

Fig. 9 Performance comparison of the GST-MGCN model and its global feature model variants at different epochs on the validation set

从上述表2—表4中，可以进一步看到，与最佳变体模型相比，GST-MGCN预测结果误差MAE降低了0.2，结合图7—图9，可以进一步说明整合各种相关性（空间、时间相关性）和全局特征（节假日和天气等），可以获得更好的性能。

4.3 GST-MGCN模型与同领域其他研究的比较实验

本文选取了同领域其他研究在海口市数据集上的预测结果（表5）。观察表5可知，在MAE、RMSE与MAPE指标上，本文模型预测精度最高。相对于WT_FCBF_LSTM与The improved GRU Model，GST-MGCN模型性能均有明显提升，说明同时考虑乘客需求时空相关性可以提高预测精度。GST-MGCN预测精度略优于同时考虑时空特征及其他特点的Stacking ensemble，说明GST-MGCN能更有效地捕捉网约车订单数据时空趋势和全局特征因素所造成的需求变化。
表5 同领域其他研究在海口数据集上的预测结果

Tab. 5 Prediction results of other research in the same field on the Haikou dataset

预测方法 MAE RMSE MAPE/%
WT_FCBF_LSTM（综合)[26] 26.056
The improved GRU Model [27] 454.080 329.230 31
Stacking ensemble Learning（10 min）[21] 2.994 3.929
GST-MGCN 2.269 3.917 21.447

4.4 GST-MGCN模型的可移植性实验

本文设置2组可移植性实验验证GST-MGCN模型的泛化能力。分别选择图10、图11所示范围作为实验区域。选取2017年5月1日至10月31日海口市每天的订单数据作为数据集，其中训练集、验证集、测试集按照7:2:1的比例划分。预测结果误差如表6所示。据表6可知，2个实验区域预测结果均与GST-MGCN模型基本持平，说明GST-MGCN模型具有一定泛化能力，能够一定程度上克服网约车订单数据空间上的异质性特征获得满意的预测结果。
图10 实验区域1栅格示意图

Fig. 10 Schematic diagram of the grid of the experimental area 1

图11 实验区域2栅格示意图

Fig. 11 Schematic diagram of the grid of the experimental area 2

表6 不同实验区域在海口数据集上的预测结果

Tab. 6 Prediction results of different experimental regions on the Haikou dataset

实验区域 MAE RMSE MAPE/%
实验区域1 2.361 3.942 22.189
实验区域2 2.482 4.131 22.931
原始研究区 2.269 3.917 21.447

5 结论与讨论

5.1 结论

网约车乘客需求预测因其在交通管理和公共安全方面的重要性，在深度学习研究领域受到越来越多的关注，由于区域间具有复杂的时空依赖性，并且乘客需求受到多种全局特征的影响，这项任务具有挑战性。为了解决这一关键问题，本文提出了一种新的融合全局特征的时空多图卷积神经网络模型（GST-MGCN）。相对于同类模型，该模型具有下列特点：① 在模型构建的过程中综合利用了地理相邻属性、功能相似属性和社区交互属性；② 可捕获包括临近、周期（每日、每周等）和趋势（每月）在内的多类型时间属性；③ 预测过程中充分利用外部嵌入组件提取各种全局特征（天气和时间段特征等）并与局部特征融合。
基于海口市2017年5月1日至10月31日订单数据集的实验表明：本文提出的GST-MGCN性能明显优于其它主流的网络模型，反映预测结果误差的MAE指标相对于GRU、GCN与ST-MGCN，分别降低了2.554、3.472与0.769。将GST-MGCN模型应用于海口市2个不同的实验区域，也得到了满意的预测结果，表明GST-MGCN模型具有良好的泛化性能。

5.2 讨论

本文提出的GST-MGCN模型在海口市数据集上得到了满意的预测结果，但是否适用于其他数据集，仍有待验证。如何通过融合路网信息获得与道路结构一致的子区提升模型的预测能力是后续研究的目标；在时间相关性建模中引入注意力机制能否提高预测性能是值得进一步探索的方向。进一步挖掘数据的时空相关性以及外部因素（交通拥堵指数等）对模型的影响是需要重点关注的内容。

References

Publishing order | Descend order by publishing year | Descend order by cited within
[1]
Zhang J P, Wang F Y, Wang K F, et al. Data-driven intelligent transportation systems: A survey[J]. IEEE Transactions on Intelligent Transportation Systems, 2011, 12(4):1624-1639. DOI:10.1109/TITS.2011.2158001

DOI

[2]
Wu C H, Ho J M, Lee D T. Travel-time prediction with support vector regression[J]. IEEE Transactions on Intelligent Transportation Systems, 2004, 5(4):276-281. DOI:10.1109/TITS.2004.837813

DOI

[3]
Zhang J B, Zheng Y, Qi D K, et al. DNN-based prediction model for spatio-temporal data[C]// Proceedings of the 24th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. Burlingame, California. New York: ACM, 2016:1-4. DOI:10.1145/2996913.2997016

DOI

[4]
Guo S N, Lin Y F, Li S J, et al. Deep spatial-temporal 3D convolutional neural networks for traffic data forecasting[J]. IEEE Transactions on Intelligent Transportation Systems, 2019, 20(10):3913-3926. DOI:10.1109/TITS.2019.2906365

DOI

[5]
Ji S W, Xu W, Yang M, et al. 3D convolutional neural networks for human action recognition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(1):221-231. DOI:10.1109/TPAMI.2012.59

DOI PMID

[6]
Yao H X, Wu F, Ke J T, et al. Deep multi-view spatial-temporal network for taxi demand prediction[J]. Proceedings of the AAAI Conference on Artificial Intelligence, 2018, 32(1):2588-2595. DOI:10.1609/aaai.v32i1.11836

DOI

[7]
宋龙泽, 万怀宇, 郭晟楠, 等. 面向出租车空载时间预测的多任务时空图卷积网络[J]. 计算机科学, 2021, 48(7):112-117.

DOI

[ Song L Z, Wan H Y, Guo S N, et al. Multi-task spatial-temporal graph convolutional network for taxi idle time prediction[J]. Computer Science, 2021, 48(7):112-117. ] DOI:10.11896/jsjkx.201000089

DOI

[8]
冯宁, 郭晟楠, 宋超, 等. 面向交通流量预测的多组件时空图卷积网络[J]. 软件学报, 2019, 30(3):759-769.

[ Feng N, Guo S N, Song C, et al. Multi-component spatial-temporal graph convolution networks for traffic flow forecasting[J]. Journal of Software, 2019, 30(3):759-769. ] DOI:10.1 3328/j.cnki.jos.005697

DOI

[9]
Zhao l, Song y j, Zhang c, et al. T-GCN: A temporal graph convolutional network for traffic prediction[J]. IEEE Transactions on Intelligent Transportation Systems, 2020, 21(9):3848-3858. DOI:10.1109/TITS.2019.2935152

DOI

[10]
Yu B, Yin H T, Zhu Z X. Spatio-temporal graph convolutional networks: A deep learning framework for traffic forecasting[C]// Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence. California: International Joint Conferences on Artificial Intelligence Organization, 2018:3634-3640. DOI:10.24963/ijcai.2018/505

DOI

[11]
Cui Z Y, Henrickson K, Ke R M, et al. Traffic graph convolutional recurrent neural network: A deep learning framework for network-scale traffic learning and forecasting[J]. IEEE Transactions on Intelligent Transportation Systems, 2020, 21(11):4883-4894. DOI:10.1109/tits.2019.2950416

DOI

[12]
Chai D, Wang L Y, Yang Q. Bike flow prediction with multi-graph convolutional networks[C]// Proceedings of the 26th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. Seattle, Washington. New York: ACM, 2018:397-400. DOI:10.1 145/3274895.3274896

DOI

[13]
Zhang J B, Zheng Y, Qi D K. Deep spatio-temporal residual networks for citywide crowd flows prediction[C]// Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence. New York: ACM, 2017:1655-1661.

[14]
Hamilton W L, Ying R, Leskovec J. Inductive representation learning on large graphs[C]// Proceedings of the 31st International Conference on Neural Information Processing Systems. New York: ACM, 2017:1025-1035.

[15]
Lv M Q, Hong Z X, Chen L, et al. Temporal multi-graph convolutional network for traffic flow prediction[J]. IEEE Transactions on Intelligent Transportation Systems, 2021, 22(6):3337-3348. DOI:10.1109/TITS.2020.2983763

DOI

[16]
Tobler W R. A computer movie simulating urban growth in the Detroit region[J]. Economic Geography, 1970, 46:234. DOI:10.2307/143141

DOI

[17]
Zhang T Q, Sun L S, Yao L Y, et al. Impact analysis of land use on traffic congestion using real-time traffic and POI[J]. Journal of Advanced Transportation, 2017, 2017:7164790. DOI:10.1155/2017/7164790

DOI

[18]
Tang J J, Liang J, Liu F, et al. Multi-community passenger demand prediction at region level based on spatio-temporal graph convolutional network[J]. Transportation Research Part C: Emerging Technologies, 2021, 124:102951. DOI:10.1016/j.trc.2020.102951

DOI

[19]
Sun J K, Zhang J B, Li Q F, et al. Predicting citywide crowd flows in irregular regions using multi-view graph convolutional networks[J]. IEEE Transactions on Knowledge and Data Engineering, 2022, 34(5):2348-2359. DOI:10.1109/TKDE.2020.3008774

DOI

[20]
Jia H W, Luo H Y, Wang H, et al. ADST: Forecasting metro flow using attention-based deep spatial-temporal networks with multi-task learning[J]. Sensors, 2020, 20(16):4574. DOI:10.3390/s20164574

DOI

[21]
Jin Y M, Ye X F, Ye Q M, et al. Demand forecasting of online car-Hailing with stacking ensemble learning approach and large-scale datasets[J]. IEEE Access, 8:199513-199522. DOI:10.1109/ACCESS.2020.3034355

DOI

[22]
Kankanamge K D, Witharanage Y R, Withanage C S, et al. Taxi trip travel time prediction with isolated XGBoost regression[C]// Moratuwa Engineering Research Conference (MERCon). IEEE,:2019:54-59. DOI:10.1109/MERCon.2019.8818915

DOI

[23]
Fu R, Zhang Z, Li L. Using LSTM and GRU neural network methods for traffic flow prediction[C]// 2016 31st Youth Academic Annual Conference of Chinese Association of Automation (YAC). IEEE,:324- 328. DOI:10.1109/YAC.2016.7804912

DOI

[24]
Lu X J, Ma C X, Qiao Y H. Short-term demand forecasting for online car-Hailing using ConvLSTM networks[J]. Physica A: Statistical Mechanics and Its Applications, 2021, 570:125838. DOI:10.1016/j.physa.2021.125838

DOI

[25]
Wu Z H, Pan S R, Long G D, et al. Graph wavenet for deep spatial-temporal graph modeling[C]// Proceedings of the 28th International Joint Conference on Artificial Intelligence. New York: ACM, 2019:1907-1913.

[26]
李雪峰. 混合需求条件下城市网约车需求预测及派单方法研究[D]. 南京: 东南大学, 2021.

[ Li X F. The forecasting of passenger demand and the order dispatch method under hybrid ride-Hailing service modes[D]. Nanjing: Southeast University, 2021. ]

[27]
Qi Q R, Cheng R J, Ge H X. Short-term travel demand prediction of online ride-Hailing based on multi-factor GRU model[J]. Sustainability, 2022, 14(7):4083. DOI:10.3390/su14074083

DOI

Options
Outlines

/

〈 〉