EN中文

Journal of Geo-information Science >

2023 , Vol. 25 >Issue 6: 1202 - 1214

DOI: https://doi.org/10.12082/dqxxkx.2023.220761

Reasoning of Spatial Distribution Pattern of Building Cluster based on Geographic Knowledge Graph

  • TANG Zengyang ,
  • AI Tinghua , * ,
  • XU Haijiang
Expand
  • College of Resources and Environmental Sciences, Wuhan University, Wuhan 430072, China
*AI Tinghua, E-mail:

Received date: 2022-10-08

  Revised date: 2022-12-07

  Online published: 2023-06-02

Supported by

National Natural Science Foundation of China(42071450)

Fold

Abstract

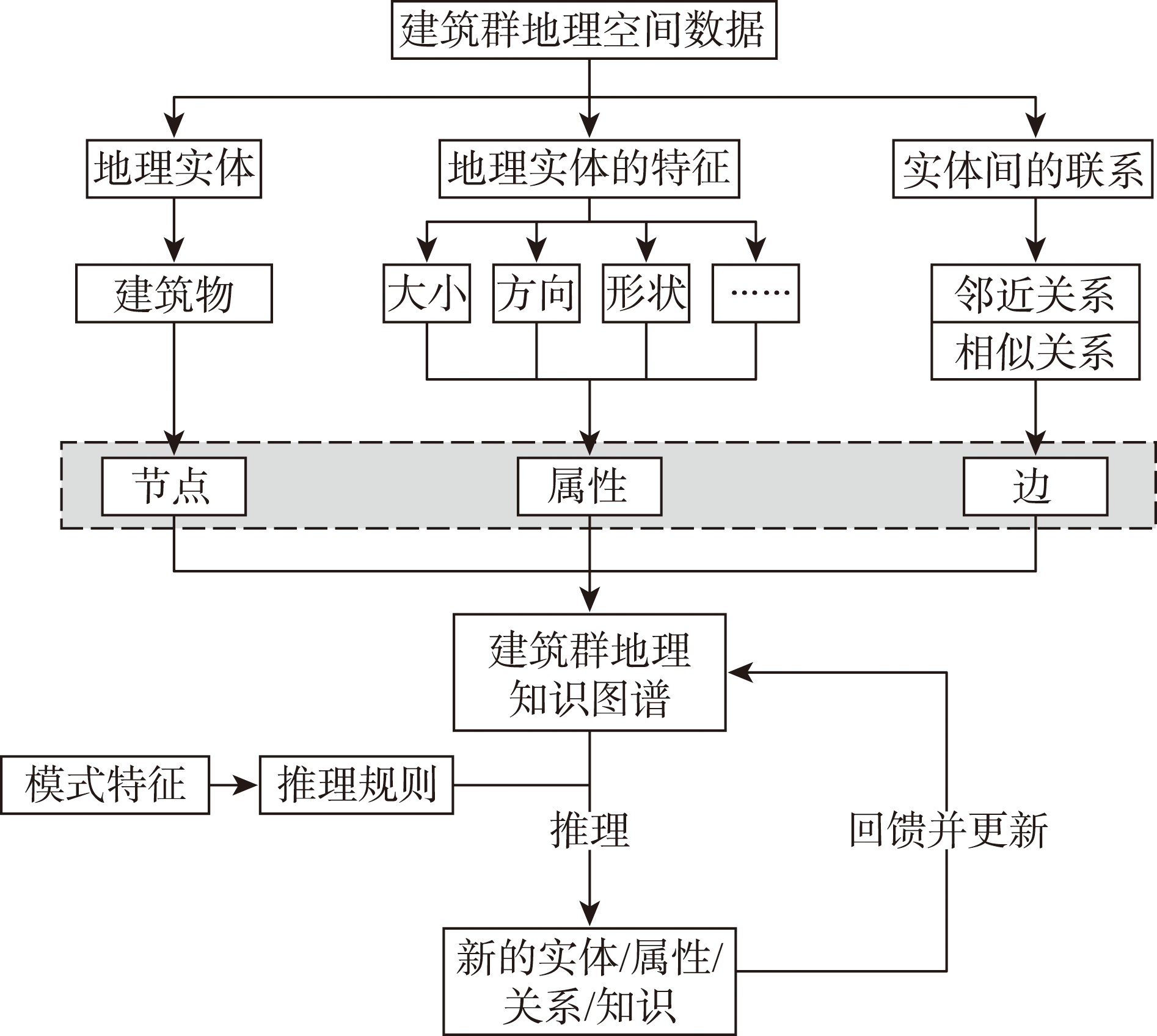
The graph structure-based knowledge graph plays important roles not only in the description and reasoning of semantic network, but also in the structured abstraction and spatial reasoning of spatial entities. The relational information of spatial entities is recorded in edges in the knowledge graph. Through the edge-based knowledge graph computational reasoning such as path detection, sub graph alignment, pattern discovery, etc., it can play an important role in spatial scene cognition. Geographic knowledge graph is a knowledge system that formally describes geographic concepts, entities, and their interrelationships. It has both the connotation and characteristics of general knowledge and the specific spatiotemporal characteristics of geographic knowledge. It can connect semantic models with spatiotemporal models to describe semantic relations, spatial relations, and temporal relations, and has great application potential in the expression, understanding, acquisition, and reasoning of geographic knowledge. The existing research work of geographic knowledge graph is mostly focused on semantics, and the extraction and expression of semantic relations are very rich and comprehensive, which can support further functions such as semantic search and association analysis of geographic knowledge. However, the knowledge expression of geographic knowledge graph in spatiotemporal model is relatively lacking, and the existing spatial relationship is limited between elements, rarely involving the further distribution situation and spatial pattern in spatial cognition. Thus, the geographic knowledge graph needs to be strengthened in terms of spatial semantic knowledge. Based on the principle of knowledge graph construction, this paper takes the construction of geographic knowledge graph of buildings as an example to realize the grid-pattern recognition of buildings. Firstly, the buildings are abstracted into entities and expressed as nodes of the graph, and the spatial neighborhood relations between buildings is extracted based on geometric proximity analysis, so as to build the geographic knowledge graph of the building group. On this basis, combined with the domain knowledge of building pattern recognition, it further infers and constructs other spatial semantic relations, and improves the geographic knowledge graph. Then the grid-pattern of the buildings complex scene is expressed as the rules of the knowledge graph, which is based on NoSQL language for reasoning. The results show that this method can effectively extract the linear pattern of buildings and further deduce the grid-pattern, which demonstrates the important role of geographic knowledge graph in spatial reasoning and its good adaptability in domain problem research, and provides ideas for the application of geographic knowledge graph in the field of spatial cognition.

Key words： knowledge graph; spatial reasoning; building cluster pattern recognition; grid-pattern; geographic knowledge; geographic entity; spatial relationship; spatial cognition

Cite this article

TANG Zengyang , AI Tinghua , XU Haijiang . Reasoning of Spatial Distribution Pattern of Building Cluster based on Geographic Knowledge Graph[J]. Journal of Geo-information Science, 2023 , 25(6) : 1202 -1214 . DOI: 10.12082/dqxxkx.2023.220761

1 引言

基于图结构存储表达的知识图谱在语义网络[1]的描述与推理方面获得了广泛发展，显著提升了智能问答、信息推送、自然语言处理等AI应用领域的智能化水平。语义概念、规则及知识的推理在图结构下可充分估计多因素的上下文影响，为不确定性知识的衍生提供了支持。问答系统中传统的形式语义、框架语义等语义表达形式存在描述不全面、难以消除歧义等局限[2]；常规推荐系统一直面临着交互数据稀疏等问题，导致推荐结果不准确[3]。知识图谱的基本组成单位是三元组：<实体，关系，实体>或<实体，属性，属性值>，其本质是具有属性的实体之间通过关系连接而形成的一个语义信息图数据库。知识图谱本体化的知识表示方法将概念与属性抽象出来并建立本体，语义与本体核心紧密相关，形式化、结构化地表达概念与关系，通过概念、关系的组合进而表示大量的复杂知识，同时以其精确性和共享性确保消除歧义[4-5]，这些特征在知识图谱的领域应用中发挥着重要赋能作用。
知识图谱对于空间实体的结构化抽象与空间推理也具有重要意义，空间实体、联系可看作是与定位有关的特殊语义网络表达，实体概念具有显式的定位性和空间关联，通过图谱的路径探测、子图对齐、模式发现实现基于知识图谱的空间推理。人类活动产生的信息数据绝大部分与地理空间位置有关[6]，而地理空间的表达通常是基于形象化符号的地图，空间格局与结构关系依比例缩小可视化，能够真实模拟实景特征。然而针对空间推理思维，往往是基于抽象的结构体系，通过概括实体主要特征、归纳实体间重要联系，进而演绎出派生信息。常规的具象化地图表达，对于空间推理并不是最好的表达，需要作抽象概括的预处理。受语义网络知识图谱表达的启示，如果把空间表达中的地理实体单元抽象成节点、实体联系抽象成边，基于图的数据结构用知识图谱描述空间场景，则会有利于知识表达与空间推理。
地理知识的时空特征与知识图谱结合即形成地理知识图谱，地理知识图谱是一种对地理概念、实体及其相互关系进行形式化描述的知识系统[7]，是集地理概念、语义关系、人地交互信息于一体的知识表达，以描述地理过程变化为核心，目标是解决人地关系。在地理知识图谱中可表达多样化的关系，现实物理空间中的空间关系、语言空间中的语义关系、时间演化形成的过程与时态关系等都可以在地理知识图谱中表达。如表1所示，一方面地理场景被空间化，实体间的关系可以涉及方位、拓扑、时态等空间时间维度；另一方面，大量语义信息同空间位置关联起来，实体间的关系也可以表示语义信息：功能关系如地铁线路间的换乘、管理关系如总部与分部、依附关系如水电站与河流。随着语义网络技术的发展，GeoNames Ontology、Linked Geo Data等地理语义网络已经逐渐出现，拥有大量的地理实体和丰富的空间关系，能提供系统、全面、深层次的结构化地理信息。当前，地理知识图谱在构建上已有较多工作。在知识抽取方面，一些地理实体与实体关系从语义网络中被抽取出来，如张春菊等[8]利用网络爬虫与地名识别技术解析网页文本，进而获取地理命名实体的文本集合，Blessing[9]和 Loglisci[10]分别抽取建立了河流与水系的汇入关系和地理实体之间的拓扑、方位关系。同时结合地图、影像等基础地理空间数据，蒋秉川等[11]提出了基于多源异构地理信息数据的地理知识构建技术体系，刘俊楠等[12]在地理知识图谱中将地理实体与百科信息链接，覆盖率较高，扩充了地理实体的概念描述信息。在知识表示方面，张雪英等[13]提出了包含“地理概念-地理实体-地理关系”3个层次的地理知识表达模型，可以用于描述不同粒度地理知识语义单元的基本组成及其逻辑关系。在关系推理方面，现有地理知识图谱的相关工作较少，段鹏飞[14] 构建了基于空间投影和关系路径的地理知识图谱表示学习算法，用于推理知识图谱中的关系，但其推理预测的可解释性较差。综上所述，在语义上，现有地理知识图谱对语义关系的抽取、表达比较丰富，可以支持进一步的语义搜索、关联分析等；与语义相比，地理知识图谱在空间上的抽取、表达较弱，如现有的拓扑关系、方位关系均为要素与要素之间的空间关系，很少涉及到空间模型中进一步的分布态势、空间格局等，在空间语义方面有待增强。若结合GIS界的主要研究视角，关注基础地理信息数据的空间位置、场所及其可量测特征，在图谱之上聚焦空间关系加以推理进一步的空间特征，便可增强地理实体在空间知识方面的语义表达。
表1 空间关系与语义关系

Tab. 1 Spatial relation and semantic relation

地理知识图谱中的关系分类 关系示例
空间关系 Intersects，Disjoint，Contains，Within，……，
over-，up-，in-，out-，……
语义关系 河流的汇入关系，资产的权属关系，
管理结构的层级关系，人的社会关系，……
本着以上动机，本研究以地理实体为节点，以基本邻近关系和其他语义关系为边构建图结构，得到空间位置相关的地理知识图谱，强调空间实体的承载作用，描述空间事物或现象的分布、属性、状态以及空间事件与空间行为，进而表达空间事物或现象的时态演化和相互作用规律。地理知识图谱一方面可以将人工智能领域在知识图谱推理中的最新模型方法引入，基于知识图谱发展空间推理方法，为解决GIS领域这一长期存在的瓶颈做出贡献。另一方面知识图谱的抽象化表达也为空间表达提供了一种新的范式，自然语言、地图语言长期以来作为地理空间表达的第一、第二语言，知识图谱可望成为一种全新的表达语言，在地理知识表达与空间推理上为GIS研究开辟新的途径。伴随着地理信息服务向地理知识服务转型升级的趋势[15]，地理知识图谱逐步成为地理信息科学领域中的研究重点。如何利用地理知识图谱探测地理实体间的空间关系与语义关系, 实现地理知识的快速获取、推理、融合，是地理信息科学的重要任务。
本研究在地理知识图谱上，本着可操作性目标，以建筑物格网模式识别为案例，在neo4j支持下构建建筑群地理知识图谱，结合建筑物模式识别的领域知识，通过cypher语言实现建筑物模式推理规则，试图验证地理知识图谱在空间推理上的作用和在领域问题研究中的良好适应性，为地理知识图谱在空间认知、空间推理领域的应用提供了思路。

2 面向建筑物格网模式的地理知识图谱表达方法

在不同的应用领域，可以依据领域知识构建相应的知识图谱。在以抽象化结构体系为基础的空间推理上，地理知识图谱有着巨大优势，其应用领域包括但不限于位置邻域内的搜索、自然语言词汇中的空间查询、大气洋流等空间现象的时空演化规律[16]等。在特定领域建立起个体知识图谱，多个个体知识图谱共同建立起群体知识图谱[17]。通过知识图谱更新知识的核心过程——“知识推理-知识融合-知识反馈”，将不同知识源的知识进行整合[18]，消除歧义，即可得到大规模高质量的知识图谱。在建筑物模式识别领域内，如图1所示，本文以建筑物认知的主要视觉变量为基础，结合约束Delaunay三角网的空间结构，实现实体、属性与空间邻近关系的抽取，组成地理知识图谱的最基础框架，完成建筑群的抽象化、知识化表达。然后将建筑物模式规则转化为知识图谱的推理规则，从而识别建筑物中基础的直线模式，并进一步推理识别格网模式。
图1 面向建筑物格网模式的地理知识图谱体系

Fig. 1 Geographic knowledge graph system for building grid pattern

（1）直线模式
直线型的建筑物模式定义为一组邻近且形状相似的建筑物在一条直线上排列。单个建筑物实体在直线模式中最多只能有2个邻近对象，在直线模式中保持其特征的最小基元则为处于同一直线上的具有邻近关系的三点——三元直线模式。
给定3个建筑物实体A、B、C，邻接边分别为 E A B与 E B C，当它们满足式（1）时，组成三元直线模式。
S i m i A B e x i s t s S i m i B C e x i s t s A n g l e E A B E B C < = A n g l e t h r e s h o l d M a x L e n E A B , L e n E B C M i n L e n E A B , L e n E B C < = L e n t h r e s h o l d
式中： S i m i A B表示建筑物A与B之间的相似关系，相似关系的详细定义见表3， S i m i B C同理； A n g l e E A B E B C表示两邻接边 E A B与 E B C的夹角； L e n E A B表示邻接边 E A B的长度， L e n E B C同理； A n g l e t h r e s h o l d与 L e n t h r e s h o l d分别表示为邻接边夹角和长度比的阈值。当2个三元直线模式中存在2个相同建筑物实体ID时，则其需要聚合成更长的直线模式。
（2）格网模式
格网型建筑物模式在城市建筑场景里常见且易于识别，其中建筑物在空间分布上较为规则。从特征来看，格网模式可视作多组平行的直线模式，相邻直线模式之间大部分建筑物成员有邻近关系。从单体建筑来看，格网模式中的建筑物之间均有相似性。给定2组直线模式，格网模式定义见式（2）。
D i r L P A - D i r L P B ≤ D i r t h r e s h o l d D i r L P A b u i l d i n g - D i r L P B b u i l d i n g ≤ D i r t h r e s h o l d b u i l d i n g [ P a t t e r n ( L P A ) ⋂ P a t t e r n ( L P B ) ] [ P a t t e r n ( L P A ) ⋃ P a t t e r n ( L P B ) ] ≥ C l o s e R a t e t h r e s h o l d
式中： D i r L P A、 D i r L P B分别是直线模式 L P A和 L P B的总体方向； D i r L P A b u i l d i n g、 D i r L P B b u i l d i n g分别是直线模式 L P A和 L P B中建筑物的平均方向； P a t t e r n ( L P A )和 P a t t e r n ( L P B )分别是直线模式 L P A和 L P B中的所有元素； D i r t h r e s h o l d、 D i r t h r e s h o l d b u i l d i n g分别为2个直线模式之间总体方向差值和建筑物平均方向差值的阈值；第3个公式计算所得为相邻的平行直线模式之间具有邻近关系的建筑物比例； C l o s e R a t e t h r e s h o l d则为该比例的阈值。

2.1 格网型建筑物模式研究

建筑物模式识别的现有研究多使用聚类，且聚类指标通常结合多方面的几何度量。学者们定义了多样化的指标与约束条件，如基于Voronoi图分割的局部密度指标[19]；综合讨论位置、大小、方向的视觉距离指标[20]；基于城市形态学的道路、河流全局约束[21]等。尽管指标与约束条件多样化，但相互之间鲜有关系，没有定义基本的指标本体与进一步的关系类型，不同指标之间难以组合。在聚类方法上，三角网、最小生成树等几何结构由于在空间位置上的表达适应性强而应用广泛[22]，然而并未构建多样的关系类型，缺乏基于关系的规则推理，导致模式规则没有形式化结构化的表达。SOM[23]、深度学习[24]等智能算法也应用于建筑物模式识别并取得初步进展，但该类方法需要大量的先验知识，且难以理解其知识聚合的逻辑过程，使得此类方法应用有限。
综上所述，现有的建筑物模式研究存在的问题：① 在聚类指标与约束上，没有定义基本的指标本体与关系类型，各个复杂指标之间缺乏一套联系机制；② 聚类方法上，模式规则没有形式化结构化的表达。孤立的个别指标在聚类方面已到达瓶颈，若不建立一套系统将各个指标和约束条件统一起来，并采用系统化、结构化的规则形式，那么传统方法将难以突破。
模式作为各个实体之间相互联系共同体现出来的形态特征，其必定由不同的基础实体之间的联系组合而成。尽管建筑物模式聚类所用的方法多种多样，但多数方法均可用节点和边组成的图结构来描述。图结构让知识图谱的构建有良好的可分解性[25]。先将图结构“分解”定义为基本类型的节点与关系，然后在此基础上运用规则对关系进行“组合”实现推理运算，即可获得新的知识。因此，将知识图谱引入建筑物模式识别问题中，在抽象的建筑群图结构上，应用边的路径扩展，基于知识图谱的推理运算进行空间模式识别，就能快速挖掘建筑物模式，弥补传统建筑物模式识别方法上的不足。同样重要的是，地理知识图谱理论上能将各种图结构聚类方法统一起来，不同的图结构聚类方法均能在其中得到分解表达，从而形成更完整的知识图谱，充分发挥知识图谱的知识融合能力。

2.2 格网型建筑物模式的地理知识图谱表达

在建筑物模式识别领域中，格式塔认知理论强调简洁、完备、联想、视知觉、部分与整体、抽象等认知过程[26]，是一套完备的心理认知学理论，从心理认知上为建筑物模式分析提供了理论基础。在建筑物的特征描述方面，Bertin[27]提出的视觉变量能较为完备地描述建筑物要素的视觉特征，其中的位置、尺寸、形状、方向在建筑物模式分析中成为主要认知变量。在空间关系上，Delaunay三角网作为广泛应用的几何结构，能够构建起建筑物之间的空间邻近关系。在知识图谱推理中，可以将格式塔原则、视觉变量、Delaunay三角网视为领域专业化规则知识，领域知识与图结构的推理框架做结合，体现了地理知识图谱在领域研究问题中良好的适应性。
记建筑群的知识图谱为G=(E，R)，其中E={ E 1, E 2,…, E m}为所有实体的集合，R={ R 1, R 2,…, R m}为所有关系的集合，节点与关系均有唯一ID，面向建筑物模式识别，知识图谱中的表达要素见表2。其中关系类型的详细定义如下：
表2 知识图谱中的表达要素

Tab. 2 Expression elements in knowledge graph

类型 要素 属性/描述
实体 建筑物（single） 形状、面积、方向等
标签 直线模式（linearPattern） lineList：建筑物ID列表
relaList：关系ID列表
格网模式（gridPattern）
关系 邻近关系（nextTo） 两建筑物邻近
相似关系（similarTo） 两建筑物相似
协同格网关系（gridWith） 两直线模式协同构成格网模式
（1）邻近关系：如图2所示，以建筑群地理数据为基础构建约束Delaunay三角网，将单体建筑物抽象成实体，提取建筑物之间的邻近关系。建筑物 B i和 B j邻近在知识图谱中表示为对应实体 E i和 E j之间存在类型为nextTo的关系。
图2 建筑群地理知识图谱的构建过程

Fig. 2 The construction process of geographic knowledge graph of building cluster

（2）相似关系：相似的定义为2个建筑物在形状、面积、方向上均有相似性，相关参数定义见 表3。当建筑物实体 B i和 B j之间满足式（3）。
表3 相似关系定义

Tab. 3 The definition of similarity relationship

参量 指标描述 计算方式
S i m i l a r i t y s h p a e 建筑物的延展度接近程度 两建筑物延展度差值的绝对值，延展度：最小外接矩形的长宽比
S i m i l a r i t y a r e a 建筑物的大小接近程度 两建筑物中较大面积值除以较小面积值
S i m i l a r i t y d i r e c t i o n 建筑物的最小外接矩形长边方向(Smallest bounding rectangle orientation)之间的接近程度 两建筑物最小外接矩形长边方向的差值
S i m i B i B j = { S i m i l a r i t y s h p a e ≤ α s , S i m i l a r i t y a r e a ≤ α a , S i m i l a r i t y d i r e c t i o n ≤ α d }
式中： α s、 α a、 α d分别为形状、面积、方向上的相似性阈值）时，它们之间有相似关系，在知识图谱中表示为对应实体 E i和 E j之间存在类型为similarTo 的关系。
（3）协同格网关系：直线模式 L P i和 L P j协同构成格网模式可表示为对应实体 E i和 E j之间存在类型为gridWith的关系。

2.3 建筑物模式的推理识别

建筑物模式识别的规则推理需要快速高效的查询作保证，本次实验采用neo4j作为知识图谱的数据库，基于其提供的cypher查询语言，结合建筑物模式识别规则进行推理识别，表4对推理规则中的要素进行了定义。
表4 直线模式和格网模式的推理规则要素

Tab. 4 The reasoning rules of linear pattern and grid pattern

推理规则要素 描述
shapeSimi(x,y) x,y形状相似
areaSimi(x,y) x,y大小相似
directionSimi_B(x,y) x,y建筑物方向相似
similar(x,y) x,y相似
near(x,y) x,y邻近
interval(x,y,z) x,y,z近似等距分布
sameLine(x,y,z) x,y,z在一条直线上
tmpThree(x,y,z) x,y,z组成三元直线模式
linerPattern(A) A中元素构成直线模式
directionSimi_Lp(A,B) A,B直线方向相似
close(A,B) A,B中大部分元素具有邻近关系
gridPattern(A,B) A,B协同形成格网模式
（1）直线模式的推理规则
根据直线模式的定义，直线模式的识别规则可分为2步： ① 识别出所有的三元直线模式； ② 合并至少有2个相同节点以上的三元直线模式为最终的直线模式，直到两两直线模式中至多只有一个相同建筑物，最终建立直线模式标签类型的节点，并存储对应的建筑物节点ID。依据表4，直线模式的推理规则描述如下，在知识图谱中的识别过程表达如图3所示。
图3 直线模式识别过程的知识图谱表达示意图

Fig. 3 The schematic diagram of knowledge graph expression in linear pattern recognition process

① shapeSimi(a,b)∧areaSimi (a,b)∧directionSimi_B(a,b) ⇒ similar(a,b);
similar(a,b)∧similar(b,c)∧near(a,b)∧near(b,c)∧interval(a,b,c)∧sameLine (a,b,c)
⇒ tmpThree (a,b,c);
② tmpThree (a,b,c)∧tmpThree (b,c,d) ⇒ linerPattern(A), a,b,c,d∈A;
（2）格网模式的推理规则
格网模式的提取规则分为2步： ① 识别出所有的直线模式，并计算各个直线模式的总体方向和其中建筑物的平均方向； ② 计算相邻的平行直线模式之间的具有邻近关系的建筑物占比，如果比例大于60%则在这2个直线模式之间添加协同格网关系。依据表4，格网模式的推理规则描述如下，在知识图谱中的识别过程表达为图4。
linerPattern(A)∧linerPattern(B)∧directionSimi_B(A,B)∧directionSimi_Lp(A,B)∧close(A,B) ⇒ gridPattern(A,B)
图4 格网模式识别过程的知识图谱表达示意图

Fig. 4 The schematic diagram of knowledge graph expression in grid pattern recognition process

3 实验与分析

3.1 实验数据

本次实验采用OpenStreetMap(OSM)的某城市部分建筑群作为实验数据，如图5所示，共5 108个建筑物。该区域街区特征划分明显，且形态、方向、大小各异的建筑物均有分布。所有建筑物的特征统计分析见图6，其中大部分建筑物的边数不超过9，面积不超过500 m 2，说明实验区域大部分区域的建筑物形状简单，其形状特征较好度量，如分布相对稀疏且建筑物形状简单的图5的a区域；同时也有紧密分布且建筑物形态较为复杂的区域，如图5的b区域，能够很好检验各主要认知要素在建筑物模式识别中的影响，可见实验区域具有较好的典型性、代表性。
图5 实验数据

Fig. 5 experimental data

图6 建筑物的形态大小特征统计

Fig. 6 Statistics of shape and size characteristics of buildings

实验以OSM的建筑群数据为基础，在适当数据预处理之后，将建筑物抽象为地理实体节点，并计算、抽取建筑物的大小、方向等属性数据，然后基于约束Delaunay三角网构建空间邻接关系。在此基础上，开始进行相似性、三元直线排列的空间推理，丰富知识图谱，并进一步完成直线模式、格网模式的推理识别。

3.2 实验结果

本文以约束Delaunay三角网为基础，在neo4j中构建起知识图谱，结合领域知识利用cypher查询语言表达直线模式、格网模式识别的推理规则。经过多次实验，设置实验参数如下： α s=2, α a=2, α d=15, A n g l e t h r e s h o l d=165, L e n t h r e s h o l d=2, D i r t h r e s h o l d = 10 , D i r t h r e s h o l d b u i l d i n g = 15 , C l o s e R a t e t h r e s h o l d = 60 %，进行格网模式的识别，共识别出1 580个三元直线，聚合后得到446个直线模式结果， C l o s e R a t e满足阈值的gridWith协同格网关系172组，结果见图7（直线模式）和图8（格网模式）。
图7 直线模式识别结果

Fig. 7 linear pattern recognition result

图8 格网模式识别结果

Fig. 8 grid pattern recognition result

格网模式的识别建立在直线模式识别成功的基础之上，2种模式的相关阈值由各自模式特征决定；而在同一模式下，区域的不同会有细微差别，相关阈值需要进行微调。具体阈值参数对结果的影响将在此节后面详细讨论。视觉认知十分依赖人类的主观性，本文通过与人眼视觉识别结果进行对比验证本文方法识别结果的可靠性，人眼视觉识别结果为4名地图学专业硕（博）士生的人工视觉识别结果，记为 R p；利用知识图谱的推理识别结果记为 R t；另外，与人眼视觉识别一致的结果记为 R a，不一致的记为 R d，漏识别的记为 R m，统计结果见 表5。实验结果表明，在直线与格网模式的识别结果中，识别准确率分别达到了89.2%和86.0%，且在与全部人眼视觉结果对比后，召回准确率分别达到87.3%和82.2%，说明本文利用知识图谱，能有效推理识别建筑物的直线与格网模式。
表5 模式识别结果统计

Tab. 5 Statistics of pattern recognition results

模式 R p R t R a R d R m A c c = R a / ( R a + R d ) r e c a l l = R a / ( R a + R m )
linearPattern 456 446 398 48 58 89.2% 87.3%
gridPattern 180 172 148 24 32 86.0% 82.2%
为验证本研究方法模式识别结果的合理性，将本文方法与文献[28]中综合多个算法的识别方法进行比较。在直线模式的提取上，现有方法因最小支撑树MST的单连通性，剪枝时会导致少部分直线信息丢失，导致在直线模式向格网模式的进一步推理识别上，现有方法的识别结果会偏少，不能令人满意。同时，在进行特定建筑物模式识别时，MST难以通过树各条边的权重大小按顺序剪枝得到，难以针对特定的模式形态进行识别。而本文方法在能较好识别直线模式的基础上，亦能进一步得到良好的格网模式识别结果。

3.3 实验参数讨论

本文中建筑物模式识别规则参考格式塔原则，视觉变量涉及位置、形状、尺寸、方向，不同的参量其阈值变化对识别结果的影响不同：
（1）相似关系
相似关系的定义涉及形状、尺寸、方向，主要描述的是单体建筑物之间的关系。如图9（a）、图9（b）所示，随着 α s， α a， α d的增大，形状、面积或方向相差较大的建筑物可能会被识别成为直线模式的一部分，而随着 α s， α a， α d的减小，直线模式中建筑物的形状、面积或方向的差异变小。可以发现，相关参量在其对应视觉变量上有着较好的影响力，这说明实验的参数定义比较符合认知。
图9 修改不同参数后的识别结果

Fig. 9 Recognition results after modifying different parameters

（2）直线排列空间模式
直线模式的识别过程以三元直线为基础，然后在三元的基础上聚合。在三元直线的识别中， L e n t h r e s h o l d与 A n g l e t h r e s h o l d的影响明显： L e n t h r e s h o l d主要影响建筑物之间的间距，当 L e n t h r e s h o l d较大时， 图9（c）右图的情况会被识别成三元直线模式，与视觉认知不符； A n g l e t h r e s h o l d在165~180时，识别结果较好，当 A n g l e t h r e s h o l d变小时，识别结果出现曲折，如图9（d）右图，同时在三元直线聚合成直线模式的过程中，若 A n g l e t h r e s h o l d较小，会出现识别的直线模式为图9（e）的情况，与视觉认知不符。
（3）格网排列空间模式
在直线模式识别较好的情况下，格网模式在建筑物方向和直线模式方向上其 D i r t h r e s h o l d b u i l d i n g、 D i r t h r e s h o l d的影响方式与 α d相同；而 C l o s e R a t e t h r e s h o l d越接近100%，相邻的2个直线模式建筑物邻近程度越高；在多个直线模式组合成格网模式时，相邻的gridWith关系的CloseRate值越接近（图9（f）），识别结果越趋近规则的格网模式。

3.4 其他建筑物模式

在地理知识图谱中识别出基础的直线型、格网型模式后，可延伸到更加复杂一些的“复合”建筑物模式，如“C”字型、“工”字型的建筑物模式。此类模式相较基础的直线型、格网型模式更不规则（图10），适宜通过典型模板构建相应的子图，然后将子图匹配分解为节点匹配与边匹配，进而在图谱中进行匹配识别，通过计算识别结果与模板的相似度检验识别的准确率。今后将会就此进行进一步的开展。
图10 “C”字型建筑物模式的识别流程

Fig. 10 Recognition process of "C" type building pattern

4 结论与展望

本文针对空间推理思维，论述了知识图谱在图结构聚类中的可行性。受语义网络知识图谱表达的启示，将空间实体单元抽象成节点、实体联系抽象成边，基于图的数据结构用知识图谱描述空间场景，构建地理知识图谱。并引入约束Delaunay三角网等领域知识，构建了建筑群场景下的地理知识图谱，基于空间关系推理实现了格网型模式的建筑物识别案例。实验证明，本文方法能够有效识别建筑物群中的格网模式，识别准确率达到了86.0%，与人工识别结果对比后，召回准确率达到82.2%，符合视觉认知，证明了知识图谱在领域专业化问题中的良好适应性。本文方法中直线模式识别结果受建筑物之间相似性的影响较大，而格网模式识别结果受直线模式之间邻近性的影响较大。本文方法中相似性暂只考虑了形状、面积与方向三个特征的相似，若增加其它特征或者采用其他指标来度量形状、方向等特征，则识别结果可能发生变化，需要重新调整参数。
面对信息数据爆炸式的增长，如何从中海量信息中归纳概括出知识是研究重点。地理知识图谱不仅拥有以概念、实体以及相互关系来抽象化表达、形式化描述知识的系统，更兼具地理上的地学特征与时空特征，让地理学知识在表达、获取及管理上建立了一套完整的联系机制，可成为地理空间的一种全新表达语言。利用知识图谱的抽象化表达系统，不仅能让地理学知识转换成可被计算机识别和处理的内容，使得机器也能学习这些知识，让地理学知识在人工智能领域的研究更进一步；同时也能充分发挥通过空间推理获取知识的巨大优势，加速“知识推理-知识融合-知识反馈”的更新过程，形成大规模、高质量的地理知识图谱，为人们能快速获取、推理与应用地理知识提供重要基础，这也是地理信息服务向地理问答系统等地理知识服务转型升级的关键。
在知识图谱的推理方法中，除了本文使用的基于规则的推理方法外，还有基于图结构的推理方法、基于表示学习的推理方法和基于神经网络的推理方法等。面对如今“数据海量”的背景，上述推理方法在地理知识图谱中都有着巨大的研究空间，地理实体在空间知识方面的语义增强仍需要人们的探索。

References

Publishing order | Descend order by publishing year | Descend order by cited within
[1]
Collins A M, et al. Retrieval time from semantic memory[J]. Journal of Verbal Learning and Verbal Behavior, 1969, 8(2):240-247. DOI:10.1016/S0022-5371(69)80069-1

DOI

[2]
王飞, 陈立, 易绵竹, 等. 新技术驱动的自然语言处理进展[J]. 武汉大学学报(工学版), 2018, 51(8):669-678.

[ Wang F, Chen L, Yi M Z, et al. Advances in natural language processing under new technology-driven[J]. Engineering Journal of Wuhan University, 2018, 51(8):669-678. ] DOI:10.14188/j.1671-8844.2018-08-002

DOI

[3]
秦川, 祝恒书, 庄福振, 等. 基于知识图谱的推荐系统研究综述[J]. 中国科学:信息科学, 2020, 50(7):937-956.

[ Qin C, Zhu H S, Zhuang F Z, et al. A survey on knowledge graph-based recommender systems[J]. Scientia Sinica(Informationis), 2020, 50(7):937-956. ]

[4]
漆桂林, 高桓, 吴天星. 知识图谱研究进展[J]. 情报工程, 2017, 3(1):4-25.

[ Qi G L, Gao H, Wu T X. The research advances of knowledge graph[J]. Technology Intelligence Engineering, 2017, 3(1):4-25. ] DOI:10.3772/j.issn.2095-915x.2017.01.002

DOI

[5]
刘峤, 李杨, 段宏, 等. 知识图谱构建技术综述[J]. 计算机研究与发展, 2016, 53(3):582-600.

[ Liu Q, Li Y, Duan H, et al. Knowledge graph construction techniques[J]. Journal of Computer Research and Development, 2016, 53(3):582-600. ]

[6]
Hahmann S, Burghardt D. How much information is geospatially referenced? Networks and cognition[J]. International Journal of Geographical Information Science, 2013, 27(6):1171-1189. DOI:10.1080/13658816.2012.743664

DOI

[7]
陆锋, 余丽, 仇培元. 论地理知识图谱[J]. 地球信息科学学报, 2017, 19(6):723-734.

DOI

[ Lu F, Yu L, Qiu P Y. On geographic knowledge graph[J]. Journal of Geo-Information Science, 2017, 19(6):723-734. ] DOI:10.3969/j.issn.1560-8999.2017.06.001

DOI

[8]
张春菊, 张雪英, 朱少楠, 等. 基于网络爬虫的地名数据库维护方法[J]. 地球信息科学学报, 2011, 13(4):492-499.

DOI

[ Zhang C J, Zhang X Y, Zhu S N, et al. Method of toponym database updating based on web crawler[J]. Journal of Geo-Information Science, 2011, 13(4):492-499. ] DOI:10.3724/SP.J.1047.2011.00492

DOI

[9]
Blessing A, Schütze H. Fine-grained geographical relation extraction from Wikipedia[C]. Proceedings of the 7th International Conference on Language Resources and Evaluation (LREC 2010), 2010:2949-2952.

[10]
Loglisci C, Ienco D, Roche M, et al. Toward geographic information harvesting: Extraction of spatial relational facts from web documents[C]// 2012 IEEE 12th International Conference on Data Mining Workshops. IEEE:789-796. DOI:10.1109/ICDMW.2012.20

DOI

[11]
蒋秉川, 万刚, 许剑, 等. 多源异构数据的大规模地理知识图谱构建[J]. 测绘学报, 2018, 47(8):1051-1061.

[ Jiang B C, Wan G, Xu J, et al. Geographic knowledge graph building extracted from multi-sourced heterogeneous data[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(8):1051-1061. ]

[12]
刘俊楠, 刘海砚, 陈晓慧, 等. 面向多源地理空间数据的知识图谱构建[J]. 地球信息科学学报, 2020, 22(7):1476-1486.

DOI

[ Liu J N, Liu H Y, Chen X H, et al. The construction of knowledge graph towards multi-source geospatial data[J]. Journal of Geo-Information Science, 2020, 22(7):1476-1486. ] DOI:10.12082/dqxxkx.2020.190565

DOI

[13]
张雪英, 张春菊, 吴明光, 等. 顾及时空特征的地理知识图谱构建方法[J]. 中国科学:信息科学, 2020, 50(7):1019-1032.

[ Zhang X Y, Zhang C J, Wu M G, et al. Spatiotemporal features based geographical knowledge graph construction[J]. Scientia Sinica (Informationis), 2020, 50(7):1019-1032. ]

[14]
段鹏飞, 王远, 熊盛武, 等. 基于空间投影和关系路径的地理知识图谱表示学习[J]. 中文信息学报, 2018, 32(3):26-33.

[ Duan P F, Wang Y, Xiong S W, et al. Space projection and relation path based representation learning for construction of geography knowledge graph[J]. Journal of Chinese Information Processing, 2018, 32(3):26-33. ] DOI:10.3969/j.issn.1003-0077.2018.03.004

[15]
陈军, 刘万增, 武昊, 等. 基础地理知识服务的基本问题与研究方向[J]. 武汉大学学报·信息科学版, 2019, 44(1):38-47.

[ Chen J, Liu W Z, Wu H, et al. Basic issues and research agenda of geospatial knowledge service[J]. Geomatics and Information Science of Wuhan University, 2019, 44(1):38-47. ] DOI:10.13203/j.whugis20180441

DOI

[16]
Woolley A W, Chabris C F, Pentland A, et al. Evidence for a collective intelligence factor in the performance of human groups[J]. Science, 2010, 330(6004):686-688. DOI:10.1126/science.1193147

DOI PMID

[17]
Zhang W, Mei H. A constructive model for collective intelligence[J]. National Science Review, 2020, 7(8):1273-1277. DOI:10.1093/nsr/nwaa092

DOI PMID

[18]
林珲, 游兰, 胡传博, 等. 时空大数据时代的地理知识工程展望[J]. 武汉大学学报·信息科学版, 2018, 43(12):2205-2211.

[ Lin H, You L, Hu C B, et al. Prospect of geo-knowledge engineering in the era of spatio-temporal big data[J]. Geomatics and Information Science of Wuhan University, 2018, 43(12):2205-2211. ] DOI:10.13203/j.whugis20180318

DOI

[19]
Anders K H, Sester M, Fritsch D, et al. Analysis of settlement structures by graph-based clustering[J]. Semantische Modellierung Smati, 1999:41-49.

[20]
艾廷华, 郭仁忠. 基于格式塔识别原则挖掘空间分布模式[J]. 测绘学报, 2007, 36(3):302-308.

[ Ai T H, Guo R Z. Polygon cluster pattern mining based on gestalt principles[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(3):302-308. ]

[21]
Li Z, Yan H, Ai T, et al. Automated building generalization based on urban morphology and Gestalt theory[J]. International Journal of Geographical Information Science, 2004, 18(5):513-534. DOI:10.1080/13658810410001702021

DOI

[22]
Cetinkaya S, Basaraner M, Burghardt D. Proximity-based grouping of buildings in urban blocks: A comparison of four algorithms[J]. Geocarto International, 2015, 30(6):618-632. DOI:10.1080/10106049.2014.925002

DOI

[23]
程博艳, 刘强, 李小文. 一种建筑物群智能聚类法[J]. 测绘学报, 2013, 42(2):290-294,303.

[ Cheng B Y, Liu Q, Li X W. Intelligent building grouping using a self-organizing map[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(2):290-294,303. ]

[24]
王米琪, 艾廷华, 晏雄锋, 等. 图卷积网络模型识别道路正交网格模式[J]. 武汉大学学报·信息科学版, 2020, 45(12):1960-1969.

[ Wang M Q, Ai T H, Yan X F, et al. Grid pattern recognition in road networks based on graph convolution network model[J]. Geomatics and Information Science of Wuhan University, 2020, 45(12):1960-1969. ] DOI:10.13203/j.whugis20200022

DOI

[25]
蒋逸, 张伟, 王佩, 等. 基于互联网群体智能的知识图谱构造方法[J]. 软件学报, 2022, 33(7):2646-2666.

[ Jiang Y, Zhang W, Wang P, et al. Knowledge graph construction method via Internet-based collective intelligence[J]. Journal of Software, 2022, 33(7):2646-2666. ] DOI:10.13328/j.cnki.jos.006313

DOI

[26]
Hartmann G W. Gestalt psychology: A survey of facts and principles[M]. New York: The Ronald press company, 1935

[27]
Bertin J. diagrams, networks, maps[M]. Madison, Wis.: University of Wisconsin Press, 1983

[28]
Zhang X, Ai T H, Stoter J, et al. Building pattern recognition in topographic data: Examples on collinear and curvilinear alignments[J]. GeoInformatica, 2013, 17(1):1-33. DOI:10.1007/s10707-011-0146-3

DOI

Options
Outlines

/

〈 〉