EN中文

Journal of Geo-information Science >

2023 , Vol. 25 >Issue 7: 1297 - 1311

DOI: https://doi.org/10.12082/dqxxkx.2023.220795

Physics-informed Machine Learning and Its Research Prospects in GeoAI

  • ZHANG Tong , 1, * ,
  • LIU Renyu 1 ,
  • WANG Peixiao 1 ,
  • GAO Chulin 1 ,
  • LIU Jie 1 ,
  • WANG Wangshu 2
Expand
  • 1. State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing Science, Wuhan University, Wuhan 430079, China
  • 2. Department of Geodesy and Geoinformation, TU Wien, Vienna A-1040, Austria
*ZHANG Tong, E-mail:

Received date: 2022-10-17

  Revised date: 2022-11-04

  Online published: 2023-06-30

Supported by

National Key R&D Program of China (International Scientific & Technological Cooperation Program)(2019YFE0106500)

National Natural Science Foundation of China under Grant(41871308)

Fold

Abstract

Scientists still cannot fully understand and explain many complex physical phenomena and dynamic systems, which cannot be described by deterministic mathematic equations and be analyzed and predicted through compact physical mechanistic models. With the ever-increasing of observational data, data-driven machine learning methods can effectively describe many complex non-linear phenomena. Nevertheless, pure data-driven models still have shortcomings in representation, interpretation, generalization capabilities, and sample efficiency. Conventional machine learning methods are confronted with challenges brought by spatiotemporal heterogeneity and sample sparsity. Recently, Physics-Informed Machine Learning (PIML) can effectively leverage observation data to describe and analyze dynamical systems when physical principles are uncertain. PIML has gain wide attention and been extensively applied in physics, computer science, biology, medical science, and geosciences. In recent years, artificial intelligence and machine learning technologies have been widely applied in geography, especially in GIScience and remote sensing, attracting wide research interests of geographers. This line of research is termed GeoAI and has become a cutting-edge research frontier in geography. PIML methods integrate the ideas of model-driven and data-driven methods, introducing new research paradigms for GeoAI and improving the description and prediction of complex geographical phenomena. This survey first summarizes recent progress in this domain from the perspectives of the representation of physical priors and the integration of physical priors in machine learning methods. Physical prior refers to existing independent knowledge that is already available before building machine learning models. This survey reviews the representation of physical priors from the aspects of augmented data and customized features, physical laws and constraints, governing equations as well as geometric properties. We also review how physical priors are integrated into various machine learning models, including constraint modeling, auxiliary task design as well as model training and inference. Based on the PIML survey framework, we explore the relationships between spatiotemporal priors and other physical priors, before briefly reviewing and summarizing typical case studies of spatiotemporal prior-informed GeoAI research. We also discuss the research agenda and future prospects of spatiotemporal prior representation and the spatiotemporal prior-informed GeoAI in the context of geo-machine learning and GeoAI frontiers. In light of fast progress of PIML, we contend that GeoAI studies that are well informed by spatiotemporal priors can gradually establish a generic geographical representation, analysis, prediction, and interpretation framework, which not only helps handle many classical problems in GIScience but also addresses future profound challenges of human being by encouraging geographers to explore more research opportunities when collaborating with researchers from other disciplines.

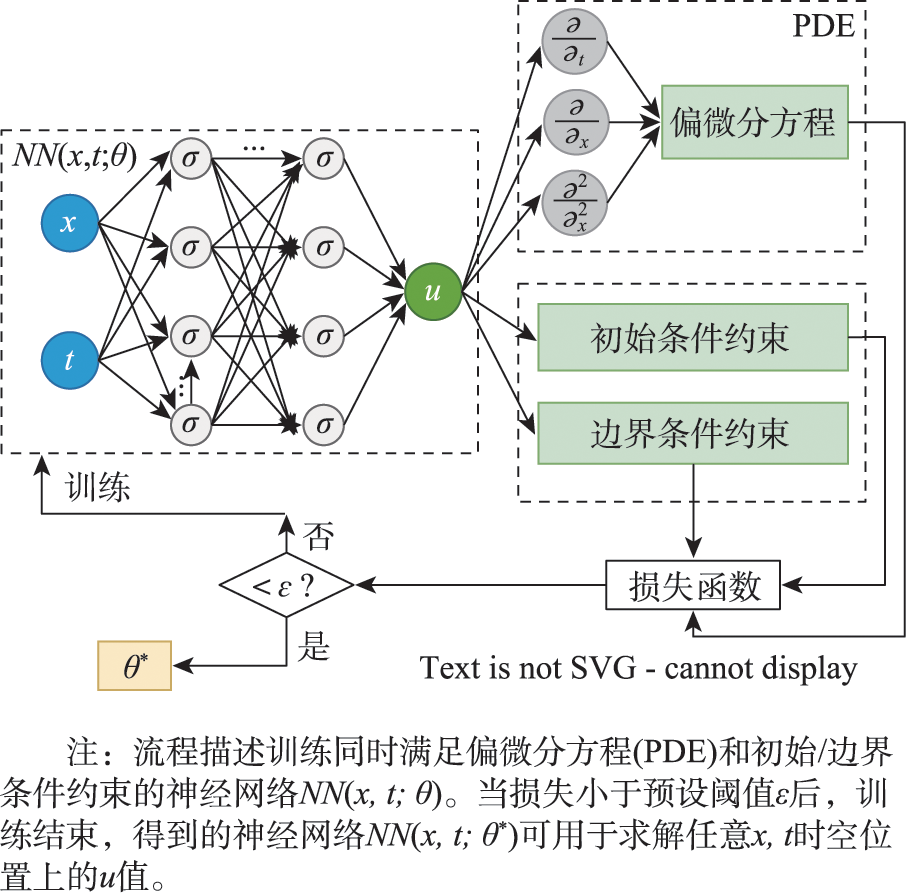
Key words： PIML; physical priors; machine learning; deep learning; spatiotemporal priors; spatio-temporal representation; Geospatial Intelligence; Geographic Information Science

Cite this article

ZHANG Tong , LIU Renyu , WANG Peixiao , GAO Chulin , LIU Jie , WANG Wangshu . Physics-informed Machine Learning and Its Research Prospects in GeoAI[J]. Journal of Geo-information Science, 2023 , 25(7) : 1297 -1311 . DOI: 10.12082/dqxxkx.2023.220795

1 引言

在许多自然科学领域，传统研究一般遵循物理学的机理模型（Mechanistic Models），通过构建精确的数学方程表达已知明确的物理过程和机制，确定性地表示各种物理变量之间的数学关系。然而许多复杂的物理现象和动态系统尚未为科学家所完全理解和解释，因此不能构建确定的数学方程来描述。此外对于一些方程部分或全部已知的问题，高精细时空分辨率条件下计算十分复杂（如短临气象预报），也不能在实际大规模应用中直接采用这些方程来进行分析和预测[1]。
机器学习特别是深度学习不仅在商业应用领域取得成功（图像、音频、翻译、推荐等），也逐步应用于科学计算和研究领域。但是常规深度学习方法在科学研究特别是地学领域的应用遇到一定的困难。首先深度学习算法通常需要大量高质量训练样本，然而地学领域的观测样本在时空分布上比较稀疏、采集质量不佳。其次完全数据驱动的方法不能保证拟合的模型能生成符合物理规律的结果。由于地学现象普遍的时空异质性问题，训练好的模型在训练环境之外的数据上泛化能力通常较差[2-3]。在动态系统中，数据分布可能会持续发生变化，给深度学习模型的泛化能力提出了很高要求。机器学习特别是深度学习方法的黑盒子特性，还存在解释性较差、可信度不足的缺点。
在物理机理模型已经明确的应用中，可直接使用确定的物理模型来进行分析和预测。在训练样本较为充裕和可靠的情况下，直接采用机器学习模型也能较好地解决应用问题。然而在物理原理不甚明确而观测数据数量不足、质量不佳的情况下，则可以尝试在机器学习建模中集成物理先验知识的方法，可取得优于纯物理或纯机器学习方法的结果[4]。这种方法一般被统称为感知物理先验的 (Physics-Informed Machine Learning，以下简称PIML)或者物理导引的机器学习(Physics-Guided Machine Learning)[4⇓-6]。一方面，动态系统中实体的运动模式和交互关系遵循基本的物理规律，物理先验可以作为严格的理论约束和归纳偏好(inductive bias)，可辅助提升机器学习模型的可解释性和结果的可信度，使得分析和预测结果更遵循物理原理，显著提升机器学习模型的时空表征能力、泛化能力和鲁棒性。另一方面PIML方法的训练速度和计算效率也能得到显著加强，提高了有限观测数据样本的利用效率，对于复杂和高时空分辨率的地学问题高效求解有很高的应用价值。
本文分别从物理先验的表达形式（第2节）和如何在机器学习中集成物理先验（第3节）2个方面概述了PIML领域的进展。然后结合地学机器学习和地理空间智能的发展和前沿问题，探讨了时空先验表征以及感知时空先验地理空间智能的未来研究规划和应用前景（第4节）。第五部分提出总结和展望。图1表示了本文各内容之间的关系。PIML建模方法是在物理机理部分已知的情况下开展，可集成传统机理模型和现代数据驱动机器学习方法的优点。我们认为各种先验知识可以统一在物理先验的整体框架下，同时地学先验如果不涉及时空维度信息，则不属于时空先验。由于时空先验不仅局限在地学领域，因此感知时空先验的机器学习也超越了地理空间智能和感知地学先验的机器学习范畴。感知地学先验的机器学习方法在时空表征、集成方法和应用等方面与感知时空先验的机器学习方法有共同之处，因此表现为一定的重叠。地理空间智能建模中许多方法也可以利用时空先验知识，因此也与感知时空先验的机器学习方法有所重叠，目前这一方向的研究还比较初级，未来将逐步扩展并采用更多集成时空先验的机器学习方法。
图1 感知各种先验的机器学习方法与地理空间智能的关系

Fig. 1 Relationships between various prior-informed machine learning methods and GeoAI

2 各种类型的物理先验

物理先验是在机器学习建模之前已经存在、独立于机器学习方法的知识。本文从增广的数据和定制特征、物理定律和约束规则、以偏微分方程为代表的支配方程(Governing Equation)、几何特性和归纳偏好等方面总结物理先验知识的表达形式及其如何被有效地用于机器学习建模和训练中。

2.1 增广数据和定制特征作为物理先验

对于数据样本稀缺的应用场景，可采用数据增广(Data Augmentation)方式将物理先验植入到数据中，也可以在领域先验知识的支持下设计专门的特征或者特征集，让机器学习模型获取更好的表征和泛化能力。增广的数据可通过开展更多的科学实验获取，但是成本较高。也可以用传统的物理仿真方法，依托特定的物理方程生成。但是由于很多物理动态现象和过程的原理方程还不够精确，这种方法不一定能生成符合实际物理规律的训练数据。因此越来越多的数据增广任务采用机器学习的生成方法，即通过少量已标记数据的内在概率分布来生成类似分布的新数据。生成对抗网络(Generative Adversarial Network, GAN)[7]是最常用的增广数据生成模型。GAN框架可以很方便地利用各种物理先验来生成仿真数据，如在生成器的损失函数中加入非精确或统计约束来模拟湍流等动态系统[8]。另一种常见的生成模型是变分自编码模型(Variational Autoencoder, VAE)[9]。VAE模型可加入各种约束生成符合特定特性的数据，如顾及形态约束的材料仿真[10]。标准化流（Normalizing Flows）是近年来兴起的一种深度生成模型[11-12]，通过构造的可逆变换函数可对复杂分布的数据样本进行精确高效的密度估计，对于数据生成和增广也有较好的应用潜力。
特征工程本身就是机器学习的核心问题。虽然深度学习具有自动学习特征表征的优势，但是如果事先能根据先验知识构建合理的特征或特征集，直接用于模型训练或者用于数据仿真都可以较好地为深度学习模型引入归纳性偏好，提高模型的表征和泛化能力。如在实时流体仿真中，可以构建符合Navier-Stokes 方程规定物理特性的特征向量，提高流体粒子行为的仿真能力和效率[13]。Bergman[14]通过生成和使用逆转对称不变特征证明对称性对于神经网络的优势。从这些案例可以看出，设计符合物理先验的特征需要紧密联系相关应用问题的专业知识，同时要熟知所使用机器学习模型对特征的拟合能力。

2.2 经典物理定律、算术方程和逻辑约束作为物理 先验

在描述物理动态系统和过程时，可将经典物理定律、公理作为先验集成到深度学习建模中。这些经典物理定律和公理通常可以用比较简洁的算术方程表达，如经典牛顿力学、运动学、电磁学定律方程等。这些方程已经作为先验集成到深度学习模型中，用于各种物理动态系统的建模和预测。在机器学习模型中集成这种类型的物理先验通常是通过损失函数中增加正则项，惩罚与经典物理定律不符合的参数组合，从而鼓励模型遵循基本的物理规律[15]，如基于重力模型的一般形式，利用神经网络或图自编码扩展其非线性表征能力，进行出行流量建模[16]或边预测[17]。引入经典的物理定律和公理可以让深度学习模型同时从数据和物理原理中学习知识，减少训练样本需要量，提高现有样本的利用率。
除经典物理定律和公理外，PIML还可以充分借鉴专业领域知识，特别是用简单算法方程和逻辑约束表达的经验知识。常见逻辑约束包括变量取值的范围、阈值不等式约束、经验规律或者单调约束等。这些知识虽然没有经典物理定律和公理得到广泛验证和认可，但同样是特定应用问题的长期知识的积累。可以用损失函数正则约束将先验集成到深度学习的框架中来。如Muralidhar等[18]在损失函数中加入近似范围和单调约束，有效地应对了水氧溶解预测中数据稀缺和噪声较多的问题。这些算术方程和逻辑约束还可以结合到深度神经网络的架构设计中。Wang等[19]在损失函数中加入多个预测结果尽可能相等的约束，有效解决了多视图交通预测的结果对齐问题。

2.3 以微分方程为代表的支配方程作为物理先验

各种形式的支配方程描述了各种物理动态系统的状态以及相关物理变量之间的关系，如经典的拉格朗日力学、Hamiltonian 力学、欧拉空气动力学、Navier-Stokes流体力学方程等。偏微分方程是较为常见的支配方程类型。对于时空连续变量u(x, t)，可以用一个通用的偏微分方程形式表达其在时间上的演化过程：
∂ u ∂ t = f t , x , u , ∂ u ∂ x i , ∂ 2 u ∂ x i ∂ x j , … , [ t , x ∈ Ω ] × [ 0 , T ]
式中：u∈ Rd是遵循以上偏微分方程的观测物理量；x ∈ Ω是位于有界区域 Ω内的二维位置坐标，t ∈ [0, T]为时间。f是支配u在时空上变化的物理函数。依据这个偏微分方程，一个物理动态系统可表达为时间导数和空间导数的非线性函数关系。
虽然神经网络很早就被用于求解偏微分方程[20]，但是浅层神经网络的非线性逼近和表达能力有限。Raissi等[21-22]较早提出在深度神经网络中集成以偏微分方程形式表达的物理先验，以粘性Burgers方程为例验证了深度学习在给定初始和边界条件下如何求解正向问题，并命名为感知物理的深度学习(Physics-Informed Deep Learning)，这一研究引发了近年来PIML研究热潮。偏微分方程提供了紧凑的先验表达模型，在其约束下，深度神经网络可充分利用观测样本数据高效求取近似解，不仅可以发现新的时空模式，还避免了数值求解方法的离散化过程，结果更加稳定。在初始条件和边界条件已知时，这些先验信息也可以用于辅助设计深度神经网络的架构[23-24]。
深度学习方法可有效地提升偏微分方程前向问题的计算能力。但是大多数物理动态过程中，支配方程的精确形式不一定确定，如参数值不确定、部分参数项未知等。这种不确定导致求解过程是随机的，此时可以用随机偏微分方程（Stochastic PDE）表示这种不确定状态下的物理先验[25]。

2.4 几何特性作为物理先验

不同的物理系统带有自身特有的几何特性，如各种不变性(invariance)和等变性(equivariance)。假设Φ f(x) = f(x-d)是对函数f的某种变换，在不变性条件下：
y [ Φ f ( x ) ] = y [ f ( x ) ]
在等变性条件下，上式可写为：
y [ Φ f ( x ) ] = Φ y [ f ( x ) ]
这些特性长期以来被作为先验以显性或隐性的形式引入到机器学习建模中，改善了模型的鲁棒性和泛化能力。许多经典深度学习模型在结构上已经实现了部分不变性，如循环神经网络的时间不变性、卷积神经网络的旋转和尺度不变性等。其他不变性则需要根据应用问题的不同，扩展已有的深度神经网络框架，如使用各向异性的卷积神经网络保持三维物体形状变形的不变性[26]、流体动力学建模中通过增加高阶乘网络层实现旋转不变性[27]、通过构建对称保持函数建立深度势能模型提升分子模拟的表达能力[28]等。
等变性卷积神经网络已有不少研究[29-30]，如支持预定义的任意连续变换[31]。相对于不变性，等变性保持了特征的相对位置和方向，因此能更加准确地描述物理动态系统的时空变化模式。如通过空间transformer网络的等变性改善大气流体模型的预测精度和稳定性[32-33]、集成U-net和空间Transformer保持时空动态特征的等变性实现物理一致的高精度天气预报[34]等。
目前此方面研究还停留在对相对简单和具备明确物理含义的几何特性建模上，由于对许多复杂动态系统不变性的理解还不够透彻，还不能很好地在深度神经网络中精确地描述复杂系统的这些几何特性[4]。如果几何特性只是部分确定，可将其作为软约束，建立灵活的不确定或近似几何特性建模方法[35]。可以在建模之前对几何特性进行测试，从而确定需要采用的几何特性先验[36]。在几何特性未知的情况下，可从数据中发现具体的不变性和等变性[37]。相关研究集中在对卷积神经网络的定制和扩展[38-39]。随着图神经网络方法的日益流行，也出现了面向图神经网络的几何特性先验建模方法，如等变性图神经网络可以按照方法分为不可约表征、常规表征和标量化3种方法[40]。以上进展基本上是局限于特定的物理系统或针对专门的研究问题而特殊设计，目前还缺乏较为普适、支持几何特性保持的深度神经网络设计原则和建模技术。大部分研究都是面向特定具体问题的专门设计，在理论层面上对复杂动态系统的各种几何特性的总结归纳还比较欠缺。

3 感知物理先验的机器学习的各种建模方法

本文主要从模型约束（3.1）、辅助任务设计（3.2）和模型训练推理（3.3）角度总结如何在机器学习特别是深度学习模型中有效地集成各种第二部分归纳的各种物理先验。

3.1 物理先验作为机器学习模型的各种约束

各种形式的物理先验可以作为约束条件灵活地集成到现有的深度学习网络，主要包括损失函数中加入的各种软约束和扩展深度神经网络架构和功能引入硬约束2种形式。这两种方法也是当前PIML建模最常见的方式。

3.1.1 定制损失函数引入物理先验软约束

最常见的软约束方法是在原有损失函数基础上，加入包含物理先验的至少一个正则项，起到惩罚违反物理先验或引入数据先验模式的作用。如图2所示，为时空连续变量u(x, t)，训练一个深度神经网络NN(x, t; θ)，其中θ为网络的参数。σ是非线性激活函数。该网络的损失函数包括基于观测真实值的监督误差损失和基于特定偏微分方程的先验约束损失：
L o s s = ∑ L ( N N ( x i , t i ) , u i ) + w ∑ L P D E | ( x j , t j )
式中： ∑ L ( N N ( x i , t i ) , u i )表示模型输出值和真值的差异； ∑ L P D E | ( x j , t j )表示基于特定偏微分方程以及相应的边界/初始条件计算的非监督损失，后者作为损失函数的一项物理先验正则项对损失函数加入软约束。
图2 物理先验作为软约束的深度神经网络[4]

Fig. 2 Deep neural networks with physical priors as soft constraints

这种定制方式较为灵活，可根据需要添加各种正则项，但是损失函数各项权重的超参数选择带来了新的问题，影响了模型的泛化能力[41]。大部分物理先验正则约束是鼓励算法在学习过程中尽量遵守先验方程规定的物理规律或数据先验统计模式，如以图神经网络更新函数形式表达的扩散和波动方程[15]、湖水温度、密度和水深之间的关系方程约束多层神经网络训练[42]、改善生成对抗网络的协方差结构约束[5]等。Basir和Senocak[43]针对软约束问题，提出了基于增强拉格朗日的优化方法约束求解，改善了多维偏微分方程前向和逆问题的求解精度。以损失函数的正则项形式体现的软约束提供了一种弱监督信息，但是并不能保证学习结果一定符合这些软约束条件，本质上是在原有损失和物理先验损失之间的一种平衡。

3.1.2 定制深度神经网络架构实现显式约束

为了保证模型求解必须遵守特定的物理原理、规律或经验约束，可在原有深度神经网络基础上定义专门的网络层、算子等强迫模型遵守显式定义的约束条件。相比损失函数定制的“软”约束，这些新扩展定义的网络组件实现的是“硬”约束，要求模型必须遵守物理一致性和其他特定特性，因此训练得到的模型对于新数据场景下具备较好的泛化能力，也提高了可解释性。
具体扩展定制的方法包括在网络架构中引入定义的专门物理变量[44]、固化网络参数为特定的物理变量值[45]、定制专门的网络层保持某些物理和几何特性[27,46]、引入专门的算子描述动态系统[47]、使用专门的数值积分方法提升网络对动态系统学习的稳定性和鲁棒性[48]。其中定制专门的网络层并在其中使用专门定义的各种卷积或算子是最为流行的方法，如拉格朗日流体仿真中的连续卷积相比离散卷积更精确地描述了动态流体粒子在时空中的移动特征[49]。
由于手工定制深度神经网络耗时耗力，也有研究采用自动架构搜索[50]寻找符合物理先验的最优深度神经网络框架[51-52]。将已有的传统物理模型与机器学习模型采用松耦合的混合模块化建模也是一个较为便捷的PIML方法[53-54]，具备机器学习推理速度快和物理先验保证泛化能力的优点。但是松耦合模型由于不是建立在端到端的统一学习框架下，部署和参数学习较为复杂。将动态系统分解为近似物理模型和数据驱动模型表达的部分，即机器学习模型用于解释物理模型的残差，在改善可解释性和提高泛化能力上也有一定的优势[55]。

3.2 物理先验指导辅助任务设计

在深度学习网络设计中，可在原有主任务网络分支基础上增加物理先验支持的辅助任务分支，两个分支之间通过共享所有参数或设置分支之间参数约束方式将物理先验引入主任务训练和推理过程。辅助任务与主任务共享主干网络框架，通过联合学习的方式提升学习效率、泛化能力和预测精度（图3）。与多任务学习不同，辅助任务主要是服务于机器学习的主任务而不是作为并列的学习任务，在测试时可以不增加计算量。设计辅助任务可从保持物理一致性、构建与主任务关联的子任务等角度开展，如预测分子能量主任务外设计预测原子间作用力[56]。在求解积分-微分方程（integro-differential equations）的前向和逆问题中，可定义辅助任务表达支配方程的积分并用辅助输出的自动微分取代积分运算，从而避开积分离散化限制[78]。辅助任务与主任务可以直接采用多任务学习联合损失的方式进行建模和训练，如利用多任务学习框架学习多个偏微分方程的共享表征提高求解的泛化能力[58]。
图3 物理先验指导下的辅助任务学习

Fig. 3 Auxiliary task learning guided by physical priors

近年来也有研究开始采用元深度学习框架，通过元学习的快速适应能力来改善模型对新任务的泛化性能。元学习是构建在任务级别，即以任务作为样本的高层次学习框架[59]，通过学习通用的元知识，让各种不同任务都能获得较好的泛化性能。此时物理先验可集成到元知识的学习过程。Seo等[60]认为在时空动态系统中如果观测数据稀缺，偏微分方程泛化能力则表现不佳，因此提出了采用模型无关的元学习方法学习空间模块，通过仿真数据获取的知识提升元测试任务的适应能力。

3.3 物理先验在机器学习模型训练和推理中的作用

物理先验除了在以上机器学习建模时发挥作用外，在模型训练和测试推理也能发挥提高泛化能力、提高训练数据利用率、加快训练效率、增加可解释性等优势。首先物理先验可以指导研究人员选取合理的数据预处理方法，如Qi和Majda[61]使用不同的经验分割函数来缩放训练数据输出的正负样本，从而更准确描述流体场的数据统计结构。其次，机器学习模型初始化可借助物理先验加快训练速度。特别是通过预训练等方式为深度神经网络设置较为合理的初始化参数，通过微调等方式快速将物理先验知识迁移到新问题域中，有利于改善未知数据分布条件下的泛化能力[62]。在实验或观测数据缺乏或者获取昂贵的情况下，可以利用仿真数据进行模型的预训练。为了应对现实应用问题与仿真环境的差异，研究者采用迁移学习或域适应技术来帮助物理先验更好地适用于真实物理系统[63-64]。
物理先验还可以支持模型训练，如基于物理先验的混合优化训练策略[65]、求解偏微分方程中引入物理先验帮助约束边界条件并聚焦到较高梯度区域[66]、利用高斯平滑模型提高二阶导数计算效率从而改善深度神经网络的训练效率[67]、优于经典梯度方法的半逆雅克比优化算法[68]等。机器学习得到的结果可基于物理先验进行校验和审核，排除或标记不符合物理先验或违反物理一致性的结果[69]。仿真数据和知识图谱是常见用于结果校验的物理先验形式[5,70-71]。

4 PIML在地理空间智能的研究前景

4.1 感知地学先验的机器学习方法及其应用

地理信息科学（GIScience）与地学领域面临很多相似的挑战。因此我们首先对感知地学先验的机器学习方法进行简要综述。地学应用机器学习已有很长历史[72]，从对地观测数据处理、数据同化、数值建模到异常监测和时空预测等方面，机器学习方法已经得到了广泛认可和应用[72⇓-74]。地学过程通常包含非定型目标的建模、复杂的时空相关、多尺度交互、高维结构、突出的时空异质性等特点，相比其他领域更加关注罕见事件[75]。地学数据采集和处理存在质量不佳、样本偏小、真实值数据缺乏等问题[75-76]。从地学专业角度的模型可解释性也是需要关注的问题[75]。因此直接照搬目前计算机领域机器学习模型不一定能很好地解决地学难题。
地学领域可以根据所研究的动态系统的特点，集成各种专业的时空先验知识。显式地在PIML建模中考虑时空关联等先验的研究还不多。这一方面的进展多出现在气候和天气领域。在各种大气和海洋系统中，跨尺度的时空相干(spatio-temporal coherence)结构广泛存在，也是组成气候和天气模式的基础[77]。在意识到时空相干结构的存在后，就可以定制各种机器学习方法，使之能够显式地描述和提取特定的时空模式[41,78]。在局部时空关联建模方面，可以构建各种神经网络模型表征不同地学现象的局部时空关联用于支持预测任务或数据生成，如场景生成网络表征流体的局部时空关联[79]、时空分离的先验感知模块化元学习方法[60]和可描述复杂动态系统局部时空关联的时空神经网络等[80]。除了局部时空关联外，长程时空关联有时也对动态系统的演化发挥重要的作用[81]。在扩展和改进现有机器学习方法，融入地学先验知识的地学建模方面还有很大的探索空间。
虽然地学学者已经广泛意识到PIML方法的优势和必要性，但是大部分已有研究是以在现有机器学习方法特别是深度神经网络基础上做少量的改进，在模型的定制和扩展中灵活而高效地融合地学先验知识的研究还比较少见。物理学较多采用简练而普适的数学公式作为先验，但是面对不同的地学过程和问题，人们的了解水平也有很大差异，有些已经建立了较为完整的数学模型（如大气流体动力方程），然而大部分地学现象和过程并没有彻底为科学家所理解，无法构建精确的数学描述，因此目前许多PIML建模方法不能直接应用于地学领域。因此如何在已有地学模型基础上更好地发挥数据驱动方法的优势成为地学领域面临的共同问题。一方面传统地学领域接纳机器学习方法的相对滞后，缺少对机器学习方法进行深层次的定制和改进，另一方面机器学习领域的研究较少顾及地学应用，大部分方法没有根据地学问题和数据特点研发。因此在未来研究中还需要2个领域研究人员的紧密合作和交流，为地学研究方法的转型提供更好的技术支持[75]。

4.2 PIML在地理空间智能的应用进展

4.2.1 地理空间智能的研究进展

人工智能和机器学习起源以来，一直在地理学的地图制图、空间分析、时空建模等领域得到了大量应用[82⇓⇓-85]。近年来，随着深度学习技术的飞速发展，其在GIScience领域也得到了广泛深入的应用。大部分研究依托已有的深度学习算法，基于时空大数据，在时空模式发现、空间插值、时空预测、智能推荐、地图制图、时空统计[86-87]等领域取得了一定的成果。将人工智能和机器学习技术引入到地理学尤其是GIScience和遥感领域，已经受到地理学者的广泛重视，并利用美国地理学者协会、美国计算机协会SIGSPATIAL等举行了多次有关学术研讨，已经成为一个热门的研究方向，可称为地理空间智能（GeoAI）[85,88⇓-90]。
研究人员已经意识到地理和GIScience研究和应用具有学科特有的挑战和难题。与其他学科相比，地理时空智能研究在多源数据融合、时空异质性泛化、可解释和可信、计算效率和样本集构建方面存在更多的困难[89]。人工智能和机器学习方法应该充分顾及这些挑战和特点，在方法设计和实现中显性考虑到地理时空模式、规律和应用需要[90-91]。部分研究已经开展了空间显式的人工智能建模方法(Spatially-explicit modeling)，本质上是在机器学习建模中顾及了地理空间先验，因此能显著改善模型的性能[92⇓-94]。未来研究可能涉及构建高质量基准数据集、改善模型的泛化能力、提高模型的可解释性、探索智能化的地理时空推理方法等[88⇓-90]。

4.2.2 地理时空先验

图4描述了物理先验、地学先验、时空先验和地理时空先验之间的关系。我们把所有的先验知识统一在物理先验框架下。虽然地学先验有很大一部分属于时空先验，时空先验却不仅限于地学领域，在医学影像、交通工程、高能物理等许多非地学领域许多应用特别是涉及动态系统的建模和预测时，也会定义和使用时空先验。如果地学先验如果不涉及时空维信息，则不属于时空先验。由于地理学整体属于地学范畴，地理时空先验同时属于地学先验和时空先验。地理时空先验的核心是包含地理学第一、第二和第三定律等在内的地理学核心概念，也涉及时空模式、时空统计和区位/方向/时间表征等先验知识。可以看出，地理时空先验由于缺乏确定的数学方程描述，大部分属于弱先验，这也给感知先验机器学习建模带来困难和挑战。
图4 各种先验之间的关系以及地理时空先验的典型类型

Fig. 4 Relationships between different categories of priors and typical spatio-temporal priors

相比物理、计算机等领域而言，感知地理时空先验的机器学习研究还比较少。地理学和GIScience学者需要密切注意PIML领域的进展，可在地理空间智能的框架下开展集成时空先验的机器学习研究。时空先验可以帮助设计合理的深度神经网络架构，如利用时序近邻、周期和趋势等设计深度时空残差网络预测交通流[95]，建立空间邻域、功能近似和交通连接等多视图的图卷积神经网络模型预测出租出行需求等[96]，基于注意力机制引入城市结构先验进行人类活动轨迹仿真[97]。在计算机视觉领域，利用地理先验也可以显著提高各种检测、识别、分类和分割等任务的精度和泛化能力[98⇓-100]。研究人员也开展了一些集成地理时空先验的遥感解译研究，如利用多时相遥感影像建立自监督学习的正样本集以及建立图像定位的前置任务(pre-text task)[101]，顾及地物位置的自监督密集表征发现提取时空不变特征用于精细遥感图像语义分割[102]等。

4.2.3 感知时空先验的地理空间智能方法

表1总结了各种感知地理时空先验的机器学习方法类型，分析了其优缺点，并给出了相关研究案例。除了第3节归纳的PIML方法类型，地理学的时空异质概念还需要强调如何充分顾及各种地理现象分布和过程演化的时空异质特点。如Klemmer等[103]在普通图神经网络框架下引入学习空间自相关的辅助任务，并作为损失函数的一部分，从而显式地顾及了各种地理数据中的空间自相关信息，显著改善了空间回归任务的精度。在网络结构定制方面，由于对算法设计和实现的要求较高，多数研究还是由计算机学者做出，如Zhang等[95]分别设计了不同的残差网络分支描述交通流在时间维度上的近邻、周期和趋势等模式，Geng等[96]建立了多视图的门控循环神经网络描述近邻、功能相似和联通等非欧关联，从而支持精确的出租出行需求预测。由于技术难度限制，网络架构定制和辅助任务设计等类型的研究还很少出现在地理学和GIScience领域。
表1 感知时空先验的机器学习方法分类和案例

Tab. 1 Types and case studies of spatio-temporal prior-informed machine learning

集成方法类型 优点 缺点 参考文献
损失函数定制 设计和实现方便、可以增加多个正则项表达各种先验 作为软约束不能保证时空先验的严格实现 [103]、[104]
网络架构定制 严格满足具体先验、设计灵活、扩展性好 技术难度高，需要对深度学习和研究问题有很深的理解 [95]、[96]
描述几何特性 引入合理的几何特性作为归纳偏好，可以显著改善泛化能力和训练效率 现有不变性、等变性定义过于粗略，特定动态系统的缺乏精细化几何特性定义 [34]
描述动态系统 精细化描述局部和远程时空相干和关联，灵活表征复杂动态系统 缺少明确的支配方程，时空先验的定义和集成实现技术难度大 [80]、[104]
辅助任务设计 可在元学习等框架下设计辅助任务，更充分地利用任务间关联集成先验知识 辅助任务的合理设计难度较高；如果相关性不强，辅助任务有可能影响主任务 [60]、[103]
描述时空异质 通过位置、方向的表征体现时空异质更好地描述地理动态系统 时空异质模式复杂，非地学领域研究较少，可参考借鉴的方法比较缺乏 [103]、[105-107]
在如何定制机器学习模型更好地描述几何特性方面，地学学者已经开始探索研究，如Chattopadhyay等[34]通过引入空间transformer保持自编码模型的等变几何特性，改善了气象数据预测性能。对于动态系统的时空预测，计算机领域则较多地集成了微分方程先验来更好地描述复杂的时空依赖关系并引导深度神经网络的学习过程，研究证明可以改善长期预测或复杂动态系统的时空预测精度[80,104]。但是相比于物理学领域集成经典物理定律或偏微分方程的神经网络方法，地理和GIScience内部的时空先验很少以确定而紧凑的数学公式形态出现，也不是科学和工程各领域广泛认可的定理，表现为弱地理先验，因此更加依赖数据驱动的机器学习模型，需要创新建立感知时空先验的表征方法，在传统地理概念的支持下，从时空数据中提取和归纳复杂的时空模式与规律。
与常规PIML不同，地理学内的相关研究需要重点关注区位（location）的表征学习[105]，即通过机器学习模型对位置坐标和区位关联等信息进行编码表征，从而更好地描述时空异质性。近期的成果有多尺度自编码非监督区位的二维和三维表征 模型[106-107]、集成空间关联辅助任务和空间坐标表征的图神经网络[103]。但是除了对区位和坐标的表征外，其他地理概念如方向和时间先验知识的表征学习的研究还比较少。受到计算机领域知识图谱机器学习发展的影响，地理知识图谱作为表达各种时空先验的工具，也已经被用于地理问题自动 回答[108-109]和选址[110]等应用中。目前区位表征方法可以一定程度上引入依赖于不同区位的时空异质先验信息，但是目前研究刚起步，还需要GIScience学者重新思考传统的地理概念，设计顾及时空异质的时空先验表征模型。
通过表1的总结和分析，总体上时空先验的形式化表征还未形成广泛使用的框架，研究人员还是根据自己的个人经验，结合机器学习方法进行一定的建模和分析，因此未来还有较为广阔的研究空间。为了深入集成时空和地理先验，地理和GIScience学者需要积极学习机器学习建模和实现技术，深入理解所研究问题和可利用地理时空先验的特点，才能研发出具备良好时空表征能力、可迁移、可解释、高精度、泛化能力强的地理空间智能模型。

4.3 感知时空先验的地理空间智能：挑战与研究规划

在地理学和GIScience内部，地理空间智能研究受到地理学基础理论方法的制约，目前还难以建立较为严密的数学体系，地理学的基本概念（如区位、领域、尺度等）和基础定律大多数是模糊的文字表述。这给时空先验的精确定义和建模带来了严重的困扰。
虽然地理空间智能已经取得了很大进展，但是相对于物理、地学、生物、医药等领域，在感知地理时空先验知识的机器学习方法创新和改进方面还较为滞后，尚未开展系统深入的研究探索工作。在应对各种地理应用问题和数据时，感知时空先验的地理空间智能方法还面临着许多理论和技术挑战，包括但不仅限于以下几个方面：
（1） 缺乏时空关联和时空依赖先验的统一描述和形式化的数学建模方法。虽然在各种自然和人文地理现象中广泛存在时空关联和依赖，但是由于这些关联和依赖关系的复杂性，现有的空间统计方法不足以充分描述非线性复杂关联，GIScience研究人员在描述各种复杂非线性地理过程的时候很少建立和依托确定的通用数学方程，难以将这些关联和依赖关系用数学语言系统而统一地描述成为地理时空先验，同时在建立机器学习模型的时候难以有效利用各种约束和归纳偏好，影响了模型的性能和泛化能力；
（2） 时空异质性的普遍存在导致地理先验的归纳较为困难。相比物理等其他领域，地理现象的时空异质现象较为普遍，因此很难归纳建立普适的先验方程或定律。目前地理空间智能方法专门针对时空异质性的显性建模还比较少，部分原因也是因为时空先验的提取和表征还比较困难；
（3） 地理过程和现象普遍存在的多尺度交互十分复杂，地理空间的划分方法（即经典的可变面元问题，Openshaw也会对机器学习的建模、训练和推理带来显著的影响，导致其结果不可靠和不稳定[83]。时空先验对建模分析结果的影响很不稳定。 GIScience领域对机器学习模型的鲁棒性和稳定性的评价还很缺乏，因此需要定义可靠的时空先验来提升模型的鲁棒性。
为了应对这些挑战，GIScience领域需要从理论、方法和应用方面加强研究：
（1） 理论研究：重新梳理各种地理和GIScience经典时空概念[111]，形式化定义各种地理时空先验，建立跨多尺度和不同空间划分的时空先验的异质性表达和更新方法，建立统一的时空归纳偏好框架，指导时空显式机器学习的建模和应用。研究地理问题的几何时空特性，即各种不变性和等变性，参考表征学习理论，建立支持地理空间智能方法的先验表征理论框架。参考神经网络结构搜索和自动机器学习理论，建立地理先验启发的时空深度学习框架自动构建和优化模型；
（2） 方法研究：在目前PIML方法基础上，深入探索地理数据的仿真和增广方法、从物理和地学领域引入时空动态系统的支配方程建模与PIML方法、研究适应低质量、稀缺时空观测数据的深度学习建模和训练技术、融合已有地理信息技术（如时空插值、空间统计等）的机器学习方法[112]、顾及时空先验的可解释时空显式深度学习方法等；
（3） 应用研究：分别针对自然地理和社会人文领域，与领域专家协作，选取经典和前沿问题，探索感知时空先验的机器学习方法的应用价值和潜在意义，为理论和方法研究提供实证支持。为了更好地开展方法的对比和验证，有必要效仿计算机科学领域，选取特定的应用问题，建立基准数据集，让研究人员在相同的实验环境下对比各自的研究方法，鼓励研究者开放源代码和数据，创办针对特定挑战的竞赛等，从而促进地理空间智能研究的健康发展。

5 总结与展望

本文回顾了近年来PIML研究进展，总结了该方法在地学的应用及在地理空间智能的应用研究前景和挑战。传统上机理建模方法和数据驱动方法建模思想截然不同，前者强调普适和解释，后者强调对复杂非线性现象的归纳和预测能力。随着人们逐步认识到纯机器学习模型在表征能力、可解释、泛化能力、样本利用效率方面的不足，PIML方法得到迅速发展。模型驱动和数据驱动的研究方法很早就用于地理学中[113]，地理学者同也长期受益于这些方法的启发。未来PIML方法融合了模型驱动和数据驱动思想，也必将为地理和GIScience的研究带来新的范式与思想，促进各种复杂地理现象的精细描述和预测。地理和GIScience相对物理学、计算机科学和其他地学研究，更多的是实证分析，总体上缺乏严密的理论和形式化的数学建模方法，因此建立感知时空先验的地理空间智能理论框架可以方便地向相关领域学习建模方法和研究范式，也是促进GIScience真正为科学界所认可的一个重要研究任务。PIML领域作为一个新兴研究方向，还没有建立理论原则来指导如何根据应用问题、观测数据和机器学习框架的具体情况，将物理先验有效地与机器学习集成。在这一方面，GIScience的研究者可以探索在不同应用场景下时空先验发挥的作用，逐步构建感知时空先验机器学习的建模和评估准则，为推进PIML发展做出自己的贡献。GIScience领域的学者已经开始逐步将各种经典的地理思想引入到机器学习的建模中。感知时空先验的机器学习也离不开计算机科学、地学、数学、统计学、交通以及各种社会科学的研究人员的共同参与，发挥多学科交叉协作的优势，共同促进 GIScience的健康发展。这些协作形式包括互相参加各领域的学术会议、召开联合研讨会、协同开展科学研究和联合发表学术论文等。此外许多地理应用还涉及人文社会的诸多问题，如贫困、平等、人口等，在建立数据驱动的机器模型时，除了要考虑时空先验知识，还需要考虑这些问题自身的道德、法律和社会公益等软约束，这方面的研究还比较稀缺。最后 GIScience学者还应该利用机器学习的强大建模能力，结合专业知识先验，探索解决人类未来面临的共同挑战，面向社会经济、安全、交通、气候变化、能源、公共卫生等实际应用，建立跨多时空尺度的通用地理空间智能表征、分析、预测和解释方法，提升地理和GIScience在学术界的影响力。

References

Publishing order | Descend order by publishing year | Descend order by cited within
[1]
Willard J, Jia X, Xu S, et al. Integrating physics-based modeling with machine learning: A survey[J/OL]. 2020, arXiv: 2003. 04919v4.

[2]
Karpatne A, Atluri G, Faghmous J H, et al. Theory-guided data science: A new paradigm for scientific discovery from data[J]. IEEE Transactions on Knowledge and Data Engineering, 2017, 29(10):2318-2331. DOI:10.1109/TKDE.2017.2720168

DOI

[3]
Willard J, Jia X, Xu S, et al. Integrating scientific knowledge with machine learning for engineering and environmental systems[J]. ACM Computing Surveys, 2022(in press).

[4]
Karniadakis G E, Kevrekidis I G, Lu L, et al. Physics-informed machine learning[J]. Nature Reviews Physics, 2021, 3:422-440. DOI:10.1038/S42254-021-00314-5

DOI

[5]
von Rueden L, Mayer S, Bechkh K, et al. Informed machine learning: a taxonomy and survey of integrating prior knowledge into learning systems[J]. IEEE Transactions on Knowledge and Data Engineering, 2022(in press). DOI:10.1109/TKDE.2021.3079836

DOI

[6]
李野, 陈松灿. 基于物理信息的神经网络:最新进展与展望[J]. 计算机科学, 2022, 49(4):254-262.

DOI

[Li Y, Chen S C. Physics-informed neural networks: Recent advances and prospects[J]. Computer Science, 2022, 49(4):254-262.] DOI:10.11896/jsjkx.210500158

DOI

[7]
Goodfellow I, Pouget-Abadie J, Mirza M, et al. Generative adversarial nets[C]. Proceedings of the 28th Annual Conference on Advances in Neural Information Processing Systems, 2014.

[8]
Wu J L, Kashinath K, Albert A, et al. Enforcing statistical constraints in generative adversarial networks for modeling chaotic dynamical systems[J]. Journal of Computational Physics, 2020, 406:109209. DOI:10.1016/j.jcp.2019.109209

DOI

[9]
Kingma D P, Welling M. Auto-encoding variational Bayes[EB/OL]. 2013: arXiv: 1312.6114. https://arxiv.org/abs/1312.6114

[10]
Cang R J, Li H C, Yao H, et al. Improving direct physical properties prediction of heterogeneous materials from imaging data via convolutional neural network and a morphology-aware generative model[J]. Computational Materials Science, 2018, 150:212-221. DOI:10.1016/j.commatsci.2018.03.074

DOI

[11]
Rezende D J, Mohamed S. Variational inference with normalizing flows[EB/OL]. 2015: arXiv: 1505.05770. https://arxiv.org/abs/1505.05770

[12]
Kobyzev I, Prince S J D, Brubaker M A. Normalizing flows: An introduction and review of current methods[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2021, 43(11):3964-3979. DOI:10.1109/TPAMI.2020.2992934

DOI

[13]
Ladický L, Jeong S, Solenthaler B, et al. Data-driven fluid simulations using regression forests[J]. ACM Transactions on Graphics, 2015, 34(6):199. DOI:10.1145/2816795.2818129

DOI

[14]
Bergman D L. Symmetry constrained machine learning[M]// Advances in Intelligent Systems and Computing. Cham: Springer International Publishing, 2019:501-512. DOI:10.1007/978-3-030-29513-4_37

DOI

[15]
Seo S, Liu Y. Differentiable physics-informed graph networks[EB/OL]. 2019: arXiv: 1902.02950. https://arxiv.org/abs/1902.02950

[16]
Simini F, Barlacchi G, Luca M, et al. A Deep Gravity model for mobility flows generation[J]. Nature Communications, 2021, 12:6576. DOI:10.1038/s41467-021-26752-4

DOI PMID

[17]
Salha G, Limnios S, Hennequin R, et al. Gravity-inspired graph autoencoders for directed link prediction[C]// Proceedings of the 28th ACM International Conference on Information and Knowledge Management. Beijing, China. New York: ACM, 2019:589-598. DOI:10.1145/3357384.3358023

DOI

[18]
Muralidhar N, Islam M R, Marwah M, et al. Incorporating prior domain knowledge into deep neural networks[C]// 2018 IEEE International Conference on Big Data (Big Data). IEEE:36-45. DOI:10.1109/BigData.2018.8621955

DOI

[19]
Wang P X, Zhang T, Zheng Y M, et al. A multi-view bidirectional spatiotemporal graph network for urban traffic flow imputation[J]. International Journal of Geographical Information Science, 2022, 36(6):1231-1257. DOI:10.1080/13658816.2022.2032081

DOI

[20]
Lagaris I E, Likas A, Fotiadis D I. Artificial neural networks for solving ordinary and partial differential equations[J]. IEEE Transactions on Neural Networks, 1998, 9(5):987-1000. DOI:10.1109/72.712178

DOI PMID

[21]
Raissi M, Perdikaris P, Karniadakis G E. Physics informed deep learning (part I): Data-driven solutions of nonlinear partial differential equations[EB/OL]. 2017: arXiv: 1711.10561. https://arxiv.org/abs/1711.10561

[22]
Raissi M, Perdikaris P, Karniadakis G E. Physics informed deep learning (part II): Data-driven discovery of nonlinear partial differential equations[EB/OL]. 2017: arXiv: 1711.10566. https://arxiv.org/abs/1711.10566

[23]
Lagari P L, Tsoukalas L H, Safarkhani S, et al. Systematic construction of neural forms for solving partial differential equations inside rectangular domains, subject to initial, boundary and interface conditions[J]. International Journal on Artificial Intelligence Tools, 2020, 29(5):2050009. DOI:10.1142/s0218213020500098

DOI

[24]
Dong S C, Ni N X. A method for representing periodic functions and enforcing exactly periodic boundary conditions with deep neural networks[J]. Journal of Computational Physics, 2021, 435:110242. DOI:10.1016/j.jcp.2021.110242

DOI

[25]
Yang L, Zhang D K, Karniadakis G E. Physics-informed generative adversarial networks for stochastic differential equations[J]. SIAM Journal on Scientific Computing, 2020, 42(1):A292-A317. DOI:10.1137/18m1225409

DOI

[26]
Boscaini D, Masci J, Rodolà E, et al. Learning shape correspondence with anisotropic convolutional neural networks[EB/OL]. 2016: arXiv: 1605.06437. https://arxiv.org/abs/1605.06437

[27]
Ling J L, Kurzawski A, Templeton J. Reynolds averaged turbulence modelling using deep neural networks with embedded invariance[J]. Journal of Fluid Mechanics, 2016, 807:155-166. DOI:10.1017/jfm.2016.615

DOI

[28]
Zhang L F, Han J Q, Wang H, et al. End-to-end symmetry preserving inter-atomic potential energy model for finite and extended systems[C]// Proceedings of the 32nd International Conference on Neural Information Processing Systems. New York: ACM, 2018:4441-4451.

[29]
Cohen T S, Welling M. Group equivariant convolutional networks[EB/OL]. 2016: arXiv: 1602.07576. https://arxiv.org/abs/1602.07576

[30]
Marcos D, Volpi M, Komodakis N, et al. Rotation equivariant vector field networks[C]// 2017 IEEE International Conference on Computer Vision. IEEE,: 5058-5067. DOI:10.1109/ICCV.2017.540

DOI

[31]
Tai K S, Bailis P, Valiant G. Equivariant transformer networks[C]. International Conference on Machine Learning, 2019.

[32]
Chattopadhyay A, Mustafa M, Hassanzadeh P, et al. Deep spatial transformers for autoregressive data-driven forecasting of geophysical turbulence[C]// Proceedings of the 10th International Conference on Climate Informatics. virtual, United Kingdom. New York: ACM, 2020:106-112. DOI:10.1145/3429309.3429325

DOI

[33]
Chattopadhyay A, Nabizadeh E, Hassanzadeh P. Analog forecasting of extreme-causing weather patterns using deep learning[J]. Journal of Advances in Modeling Earth Systems, 2020, 12(2): e2019MS001958. DOI:10.1029/2019ms001958

DOI

[34]
Chattopadhyay A, Mustafa M, Hassanzadeh P, et al. Towards physically consistent data-driven weather forecasting: Integrating data assimilation with equivariance-preserving deep spatial transformers[EB/OL]. 2021: arXiv: 2103.09360. https://arxiv.org/abs/2103.09360

[35]
Finzi M, Benton G, Wilson A G. Residual pathway priors for soft equivariance constraints[EB/OL]. 2021:arXiv: 2112.01388. https://arxiv.org/abs/2112.01388

[36]
Christie L G, Aston J A D. Testing for geometric invariance and equivariance[EB/OL]. 2022: arXiv: 2205.15 280. https://arxiv.org/abs/2205.15280.

[37]
Benton G, Finzi M, Izmailov P, et al. Learning invariances in neural networks[C]// Proceedings of the 34th International Conference on Neural Information Processing Systems. New York: ACM, 2020:17605-17616.

[38]
Chidester B, Do M N, Ma J. Rotation equivariance and invariance in convolutional neural networks[EB/OL]. 2018: arXiv: 1805.12301. https://arxiv.org/abs/1805.12301

[39]
Esteves C, Allen-Blanchette C, Makadia A, et al. Learning SO(3) equivariant representations with spherical CNNs[M]// Computer Vision - ECCV 2018. Cham: Springer International Publishing, 2018:54-70. DOI:10.1007/978-3-030-01261-8_4

DOI

[40]
Han J Q, Rong Y, Xu T Y, et al. Geometrically equivariant graph neural networks: A survey[EB/OL]. 2022: arXiv: 2202. 07230. https://arxiv.org/abs/2202.07230.

[41]
Kashinath K, Mustafa M, Albert A, et al. Physics-informed machine learning: Case studies for weather and climate modelling[J]. Philosophical Transactions Series A, Mathematical, Physical, and Engineering Sciences, 2021, 379(2194):20200093. DOI:10.1098/rsta.2020.0093

DOI

[42]
Daw A, Karpatne A, Watkins W, et al. Physics-guided neural networks (PGNN): An application in lake temperature modeling[EB/OL]. 2017: arXiv: 1710.11431. https://arxiv.org/abs/1710.11431.

[43]
Basir S, Senocak I. Physics and equality constrained artificial neural networks: Application to forward and inverse problems with multi-fidelity data fusion[J]. Journal of Computational Physics, 2022, 463:111301. DOI:10.1016/j.jcp.2022.111301

DOI

[44]
Muralidhar N, Bu J, Cao Z, et al. PhyNet: physics guided neural networks for particle drag force prediction in assembly[M]// Proceedings of the 2020 SIAM International Conference on Data Mining. Philadelphia, PA: Society for Industrial and Applied Mathematics, 2020:559-567. DOI:10.1137/1.9781611976236.63

DOI

[45]
Sun J, Niu Z, Innanen K A, et al. A theory-guided deep-learning formulation and optimization of seismic waveform inversion[J]. Geophysics, 2020, 85(2):87-99. DOI:10.1190/geo2019-0138.1

DOI

[46]
Wang R, Walters R, Yu R. Incorporating symmetry into deep dynamics models for improved generalization[EB/OL]. 2020: arXiv: 2002. 03061. https://arxiv.org/abs/2002.03061.

[47]
Zhong Y D, Dey B, Chakraborty A. Symplectic ODE-net: Learning Hamiltonian dynamics with control[EB/OL]. 2019: arXiv: 1909.12077. https://arxiv.org/abs/1909.12077.

[48]
Chen Z D, Zhang J Y, Arjovsky M, et al. Symplectic recurrent neural networks[EB/OL]. 2019: arXiv: 1909.13334. https://arxiv.org/abs/1909.13334

[49]
Ummenhofer B, Prantl L, Thuerey N, et al. Lagrangian fluid simulation with continuous convolutions[C]. International Conference on Learning Representations, 2019.

[50]
Elsken T, Metzen J H, Hutter F. Neural architecture search[M]// Automated Machine Learning. Cham: Springer International Publishing, 2019:63-77. DOI:10.1007/978-3-030-05318-5_3

DOI

[51]
Ba Y H, Zhao G Y, Kadambi A. Blending diverse physical priors with neural networks[EB/OL]. 2019: arXiv: 1910.00201. https://arxiv.org/abs/1910.00201.

[52]
Kasim M F, Watson-Parris D, Deaconu L, et al. Building high accuracy emulators for scientific simulations with deep neural architecture search[EB/OL]. 2020: arXiv: 2001. 08055. https://arxiv.org/abs/2001.08055.

[53]
Long Y, She X, Mukhopadhyay S. HybridNet: integrating model-based and data-driven learning to predict evolution of dynamical systems[C]. Proceedings of the 2nd Conference on Robot Learning, 2018.

[54]
de Avila Belbute-Peres F, Economon T D, Kolter J Z. Combining differentiable PDE solvers and graph neural networks for fluid flow prediction[C]// Proceedings of the 37th International Conference on Machine Learning. New York: ACM, 2020:2402-2411.

[55]
Yin Y, Le Guen V, Dona J, et al. Augmenting physical models with deep networks for complex dynamics forecasting[J]. Journal of Statistical Mechanics: Theory and Experiment, 2021, 2021(12): 124012. DOI:10.1088/1742-5468/ac3ae5

DOI

[56]
Schütt K T, Kindermans P J, Sauceda H E, et al. SchNet: A continuous-filter convolutional neural network for modeling quantum interactions[EB/OL]. 2017: arXiv: 1706.08566. https://arxiv.org/abs/1706.08566.

[57]
Yuan L, Ni Y Q, Deng X Y, et al. A-PINN: Auxiliary physics informed neural networks for forward and inverse problems of nonlinear integro-differential equations[J]. Journal of Computational Physics, 2022, 462:111260. DOI:10.1016/j.jcp.2022.111260

DOI

[58]
Thanasutives P, Numao M, Fukui K I. Adversarial multi-task learning enhanced physics-informed neural networks for solving partial differential equations[C]// 2021 International Joint Conference on Neural Networks (IJCNN). IEEE,: 1-9. DOI:10.1109/IJCNN52387.2021.9533606

DOI

[59]
Finn C, Abbeel P, Levine S. Model-agnostic meta-learning for fast adaptation of deep networks[EB/OL]. 2017: arXiv: 1703.03400. https://arxiv.org/abs/1703.03400.

[60]
Seo S, Meng C Z, Rambhatla S, et al. Physics-aware spatiotemporal modules with auxiliary tasks for meta-learning[EB/OL]. 2020: arXiv: 2006. 08831. https://arxiv.org/abs/2006.08831.

[61]
Qi D, Majda A J. Using machine learning to predict extreme events in complex systems[J]. Frontiers in Cardiovascular Medicine, 2020, 117(1):52-59. DOI:10.1073/pnas.1917285117

DOI

[62]
Read J S, Jia X W, Willard J, et al. Process-guided deep learning predictions of lake water temperature[J]. Water Resources Research, 2019, 55(11):9173-9190. DOI:10.1029/2019wr024922

DOI

[63]
Desai, Mattheakis M, Joy H, et al. One-shot transfer learning of physics-informed neural networks[EB/OL]. 2021: arXiv: 2110. 11286. https://arxiv.org/abs/2110.11286.

[64]
Jia X W, Willard J, Karpatne A, et al. Physics-guided machine learning for scientific discovery: An application in simulating lake temperature profiles[J]. ACM/IMS Transactions on Data Science, 2021, 2(3):20. DOI:10.1145/3447814

DOI

[65]
Holl P, Koltun V, Thuerey N. Scale-invariant learning by physics inversion[EB/OL]. 2021: arXiv:2109. 15048.

[66]
Basir S, Senocak I. Mitigating learning complexity in physics and equality constrained artificial neural networks[EB/OL]. 2022:arXiv:2206. 09321. https://arxiv.org/abs/2206.09321.

[67]
He D, Shi W L, Li S D, et al. Learning physics-informed neural networks without stacked back-propagation[EB/OL]. 2022: arXiv: 2202. 09340. https://arxiv.org/abs/2202.09340.

[68]
Schnell P, Holl P, Thuerey N. Half-inverse gradients for physical deep learning[EB/OL]. 2022: arXiv: 2203. 10131. https://arxiv.org/abs/2203.10131.

[69]
King R, Hennigh O, Mohan A, et al. From deep to physics-informed learning of turbulence: Diagnostics[EB/OL]. 2018: arXiv:1810.07785. https://arxiv.org/abs/1810.07785.

[70]
Du Y L, Liu Z J, Basevi H, et al. Learning to exploit stability for 3D scene parsing[C]// Proceedings of the 32nd International Conference on Neural Information Processing Systems. New York: ACM, 2018:1733-1743.

[71]
von Rueden L, Wirtz T, Hueger F, et al. Street-map based validation of semantic segmentation in autonomous driving[C]// 2020 25th International Conference on Pattern Recognition (ICPR). IEEE,: 10203-10210. DOI:10.1109/ICPR48806.2021.9413292

DOI

[72]
Dramsch J S. 70 years of machine learning in geoscience in review[J]. Advances in Geophysics, 2020, 61:1-55. DOI:10.1016/bs.agph.2020.08.002

DOI

[73]
Boukabara S A, Krasnopolsky V, Penny S G, et al. Outlook for exploiting artificial intelligence in the earth and environmental sciences[J]. Bulletin of the American Meteorological Society, 2021, 102(5):E1016-E1032. DOI:10.1175/bams-d-20-0031.1

DOI

[74]
Bergen K J, Johnson P A, de Hoop M V, et al. Machine learning for data-driven discovery in solid Earth geoscience[J]. Science, 2019, 363(6433): eaau0323. DOI:10.1126/science.aau0323

DOI

[75]
Karpatne A, Ebert-Uphoff I, Ravela S, et al. Machine learning for the geosciences: Challenges and opportunities[J]. IEEE Transactions on Knowledge and Data Engineering, 2019, 31(8):1544-1554. DOI:10.1109/TKDE.2018.2861006

DOI

[76]
Reichstein M, Camps-Valls G, Stevens B, et al. Deep learning and process understanding for data-driven Earth system science[J]. Nature, 2019, 566(7743):195-204. DOI:10.1038/s41586-019-0912-1

DOI

[77]
Haller G. Lagrangian coherent structures[J]. Annual Review of Fluid Mechanics, 2015, 47:137-162. DOI:10.1146/annurev-fluid-010313-141322

DOI

[78]
Xie Y, Franz E, Chu M Y, et al. tempoGAN[J]. ACM Transactions on Graphics, 2018, 37(4):1-15. DOI:10.1145/3197517.3201304

DOI

[79]
Jiang C, Esmaeilzadeh S, Azizzadenesheli K, et al. MESHFREEFLOWNET: A physics-constrained deep continuous space-time super-resolution framework[C]// SC20:International Conference for High Performance Computing, Networking, Storage and Analysis. IEEE,: 1-15. DOI:10.1109/SC41405.2020.00013

DOI

[80]
Huang Y, Li J, Shi M, et al. ST-PCNN: Spatio-temporal physics-coupled neural networks for dynamics forecasting[EB/OL]. 2021: arXiv: 2108. 05940. https://arxiv.org/abs/2108.05940.

[81]
Grigsby J, Wang Z, Qi Y J. Long-range transformers for dynamic spatiotemporal forecasting[EB/OL]. 2021: arXiv: 2109. 12218. https://arxiv.org/abs/2109.12218.

[82]
Smith T R. Artificial intelligence and its applicability to geographical problem solving[J]. The Professional Geographer, 1984, 36(2):147-158. DOI:10.1111/j.0033-0124.1984.00147.x

DOI

[83]
Openshaw S. The modifiable areal unit problem[M]. Norwich: Geobooks, 1984.

[84]
Mather P M, Openshaw S, Openshaw C. Artificial intelligence in geography[J]. The Geographical Journal, 1998, 164(3):353. DOI:10.2307/3060633

DOI

[85]
Lavallin A, Downs J A. Machine learning in geography: past, present, and future[J]. Geography Compass, 2021, 15(5):e12563. DOI:10.1111/gec3.12563

DOI

[86]
艾廷华. 深度学习赋能地图制图的若干思考[J]. 测绘学报, 2021, 50(9):1170-1182.

DOI

[ Ai T H. Some thoughts on deep learning enabling cartography[J]. Acta Geodaetica et Cartographica Sinica, 2021, 50(9):1170-1182.]

DOI

[87]
Kopczewska K. Spatial machine learning: New opportunities for regional science[J]. The Annals of Regional Science, 2022, 68(3):713-755. DOI:10.1007/s00168-021-01101-x

DOI

[88]
Janowicz K, Gao S, McKenzie G, et al. GeoAI: Spatially explicit artificial intelligence techniques for geographic knowledge discovery and beyond[J]. International Journal of Geographical Information Science, 2020, 34(4):625-636. DOI:10.1080/13658816.2019.1684500

DOI

[89]
张永生, 张振超, 童晓冲, 等. 地理空间智能研究进展和面临的若干挑战[J]. 测绘学报, 2021, 50(9):1137-1146.

DOI

[ Zhang Y S, Zhang Z C, Tong X C, et al. Progress and challenges of geospatial artificial intelligence[J]. Acta Geodaetica et Cartographica Sinica, 2021, 50(9):1137-1146.]

DOI

[90]
高松. 地理空间人工智能的近期研究总结与思考[J]. 武汉大学学报·信息科学版, 2020, 45(12):1865-1874.

[Gao S. A review of recent researches and reflections on geospatial artificial intelligence[J]. Geomatics and Information Science of Wuhan University, 2020, 45(12):1865-1874.] DOI:10.13203/j.whugis20200597

DOI

[91]
刘瑜, 郭浩, 李海峰, 等. 从地理规律到地理空间人工智能[J]. 测绘学报, 2022, 51(6):1062-1069.

DOI

[ Liu Y, Guo H, Li H F, et al. A note on GeoAI from the perspective of geographical laws[J]. Acta Geodaetica et Cartographica Sinica, 2022, 51(6):1062-1069.]

DOI

[92]
Cheng S F, Lu F, Peng P, et al. Multi-task and multi-view learning based on particle swarm optimization for short-term traffic forecasting[J]. Knowledge-Based Systems, 2019, 180:116-132. DOI:10.1016/j.knosys.2019.05.023

DOI

[93]
Yan B, Janowicz K, Mai G C, et al. A spatially explicit reinforcement learning model for geographic knowledge graph summarization[J]. Transactions in GIS, 2019, 23(3):620-640. DOI:10.1111/tgis.12547

DOI

[94]
Liu P Y, Biljecki F. A review of spatially-explicit GeoAI applications in Urban Geography[J]. International Journal of Applied Earth Observation and Geoinformation, 2022, 112:102936. DOI:10.1016/j.jag.2022.102936

DOI

[95]
Zhang J B, Zheng Y, Qi D K. Deep spatio-temporal residual networks for citywide crowd flows prediction[C]// Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence. New York: ACM, 2017:1655-1661.

[96]
Geng X, Li Y G, Wang L Y, et al. Spatiotemporal multi-graph convolution network for ride-Hailing demand forecasting[J]. Proceedings of the AAAI Conference on Artificial Intelligence, 2019, 33(1):3656-3663. DOI:10.1609/aaai.v33i01.33013656

DOI

[97]
Feng J, Yang Z Y, Xu F L, et al. Learning to simulate human mobility[C]// Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. Virtual Event, CA, USA. New York: ACM, 2020:3426-3433. DOI:10.1145/3394486.3412862

DOI

[98]
Yan B, Janowicz K, Mai G, et al. xnet+ sc: classifying places based on images by incorporating spatial contexts[C]. Proceedings of the 10th International Conference on Geographic Information Science, 2018.

[99]
Aodha O M, Cole E, Perona P. Presence-only geographical priors for fine-grained image classification[C]// 2019 IEEE/CVF International Conference on Computer Vision (ICCV). IEEE,: 9595-9605. DOI:10.1109/ICCV.2019.00969

DOI

[100]
Chu G, Potetz B, Wang W J, et al. Geo-aware networks for fine-grained recognition[C]// 2019 IEEE/CVF International Conference on Computer Vision Workshop (ICCVW). IEEE,:247-254. DOI:10.1109/ICCVW.2019.00033

DOI

[101]
Ayush K, Uzkent B, Meng C L, et al. Geography-aware self-supervised learning[C]// 2021 IEEE/CVF International Conference on Computer Vision (ICCV). IEEE,: 10161-10170. DOI:10.1109/ICCV48922.2021.01002

DOI

[102]
Muhtar D, Zhang X L, Xiao P F. Index your position: A novel self-supervised learning method for remote sensing images semantic segmentation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60:1-11. DOI:10.1109/TGRS.2022.3177770

DOI

[103]
Klemmer K, Safir N, Neill D B. Positional encoder graph neural networks for geographic data[EB/OL]. 2021: arXiv: 2111. 10144. https://arxiv.org/abs/2111.10144

[104]
de Bezenac E, Pajot A, Gallinari P. Deep learning for physical processes: Incorporating prior scientific knowledge[EB/OL]. 2017: arXiv: 1711.07970. https://arxiv.org/abs/1711.07970.

[105]
Mai G C, Janowicz K, Hu Y J, et al. A review of location encoding for GeoAI: Methods and applications[J]. International Journal of Geographical Information Science, 2022, 36(4):639-673. DOI:10.1080/13658816.2021.2004602

DOI

[106]
Mai G C, Janowicz K, Yan B, et al. Multi-scale representation learning for spatial feature distributions using grid cells[EB/OL]. 2020: arXiv: 2003. 00824. https://arxiv.org/abs/2003.00824

[107]
Mai G C, Xuan Y, Zuo W Y, et al. Sphere2Vec: Multi-scale representation learning over a spherical surface for geospatial predictions[EB/OL]. 2022: arXiv: 2201. 10489. https://arxiv.org/abs/2201.10489

[108]
Wang X, He X N, Cao Y X, et al. KGAT: Knowledge graph attention network for recommendation[C]// Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. Anchorage, AK, USA. New York: ACM, 2019:950-958. DOI:10.1145/3292500.3330989

DOI

[109]
Mai G C, Janowicz K, Cai L, et al. SEKGE: A locationaware knowledge graph embedding model for geographic question answering and spatial semantic lifting[J]. Transactions in GIS, 2020, 24(3):623-655. DOI:10.1111/tgis.12629

DOI

[110]
Liu Y, Ding J T, Li Y. Knowledge-driven site selection via urban knowledge graph[EB/OL]. 2021: arXiv: 2111. 00787. https://arxiv.org/abs/2111.00787

[111]
Kuhn W. Core concepts of spatial information for transdisciplinary research[J]. International Journal of Geographical Information Science, 2012, 26(12):2267-2276. DOI:10.1080/13658816.2012.722637

DOI

[112]
Wikle C K, Zammit-Mangion A. Statistical deep learning for spatial and spatio-temporal data[EB/OL]. 2022: arXiv: 2206. 02218. https://arxiv.org/abs/2206.02218

[113]
O’Sullivan D, Manson S M. Do physicists have geography envy? and what can geographers learn from it?[J]. Annals of the Association of American Geographers, 2015, 105(4):704-722. DOI:10.1080/00045608.2015.1039105

DOI

Options
Outlines

/

〈 〉