EN中文

Journal of Geo-information Science >

2023 , Vol. 25 >Issue 7: 1500 - 1513

DOI: https://doi.org/10.12082/dqxxkx.2023.220768

Travel Time Estimation Method based on Dual Graph Convolutional Networks via Joint Modeling of Road Segments and Intersections

  • JIN Guangyin , 1 ,
  • SHA Hengyu 1 ,
  • ZHANG Jinlei , 2, * ,
  • HUANG Jincai 1
Expand
  • 1. School of Systems Engineering, National University of Defense Technology, Changsha 410005, China
  • 2. School of Systems Science, Beijing Jiaotong University, Beijing 100089, China
*ZHANG Jinlei, E-mail:

Received date: 2022-10-10

  Revised date: 2023-01-05

  Online published: 2023-06-30

Supported by

National Natural Science Foundation of China(62073333)

National Natural Science Foundation of China(72201029)

National Natural Science Foundation of China(72288101)

Fold

Abstract

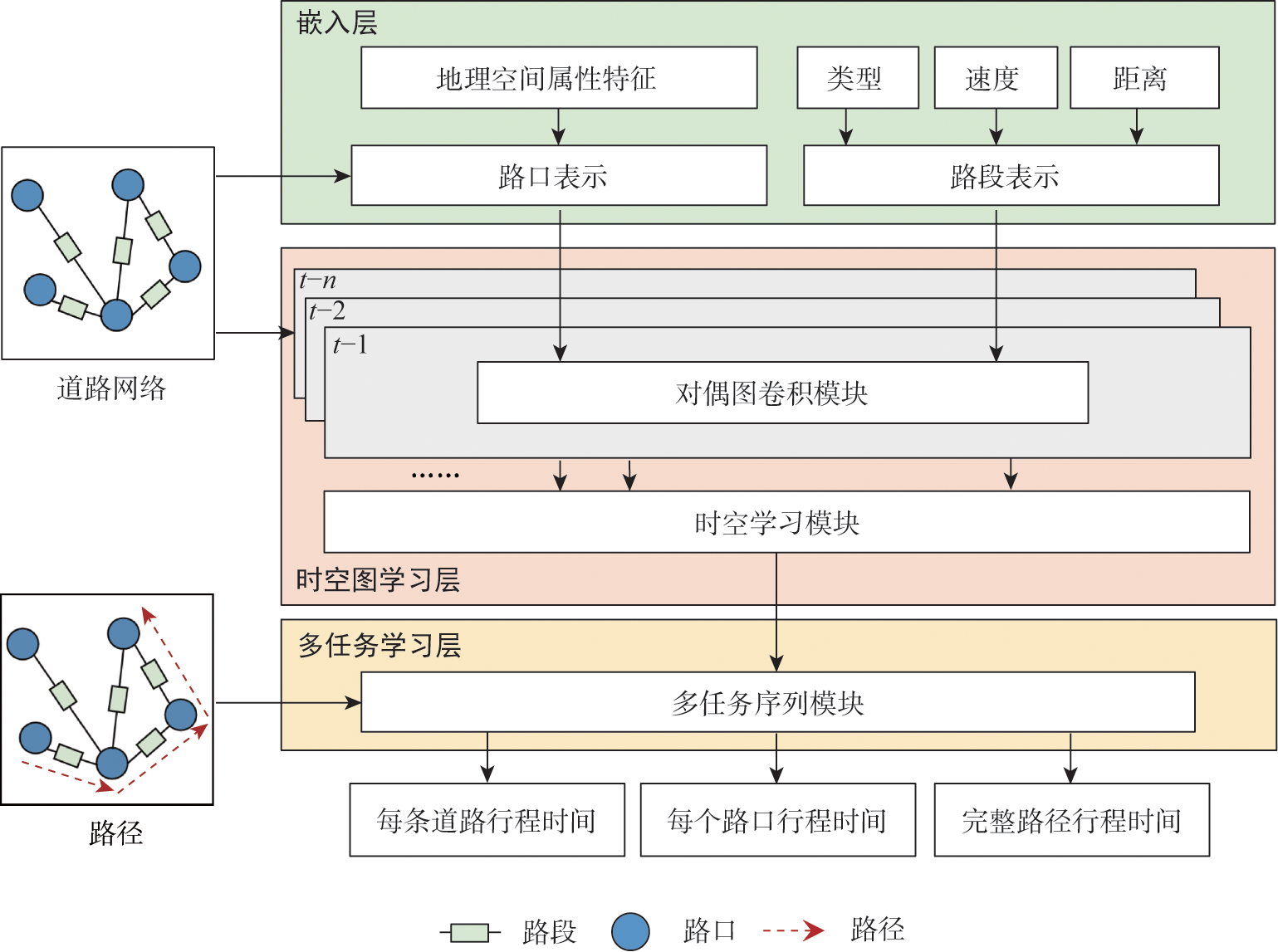
Estimating travel time for a given route plays an important role in many urban transportation systems, such as navigation and route planning. However, most of the existing works focus on modeling road segments or intersections individually, which cannot accurately estimate travel time, because intersections and road segments, as the basic elements of paths, not only contain diverse spatial attributes and temporal dynamics, but also have strong coupling correlation between them. To address the above problems, this paper proposes a novel end-to-end deep learning framework, Dual Graph Convolutional Network for Travel Time Estimation (DGCN-TTE), to jointly model intersections and road segments. Specifically, we adopt a dual graph convolution method to capture the complex relationship between intersections and road segments, in which a node-wise graph is constructed to characterize the correlation between intersections, and an edge-wise graph is constructed to characterize the interaction features between road segments. To capture the joint relationship of spatial and temporal features, we also introduce a spatiotemporal learning module that integrates multi-scale spatial relationships from multiple neighborhood scales while capturing temporal dependencies. This paper evaluates the proposed DGCN-TTE model through experiments on three real-world trajectory datasets, the results show that the proposed model significantly outperforms existing methods, and the evaluation metrics can achieve more than 10% improvement compared with the suboptimal method.

Key words： travel time estimation; graph convolutional network; spatiotemporal modeling; road modeling; intelligent transportation; deep learning; neural network

Cite this article

JIN Guangyin , SHA Hengyu , ZHANG Jinlei , HUANG Jincai . Travel Time Estimation Method based on Dual Graph Convolutional Networks via Joint Modeling of Road Segments and Intersections[J]. Journal of Geo-information Science, 2023 , 25(7) : 1500 -1513 . DOI: 10.12082/dqxxkx.2023.220768

1 引言

行程时间估计任务的目标是预测给定路径的行程时间，是路线规划、导航和拼车中的一个重要问题。谷歌、高德等众多在线地图服务商在其应用程序中提供该功能，帮助用户提前进行智能行程规划。如何准确预估行程时间是这些服务商提升应用使用体验的关键。
由于存在于交通网络上的路径序列是由依次交替的路段和交叉路口组成，因此表征交叉路口和路段的潜在特征对于道路网络上的行程时间的估计非常重要。具体而言，通常引入交通信号灯或者其他交通标志来引导交通行为的交叉路口对行车速度有显著影响。根据Tirachini等[1]的研究，发生在交叉路口的延误占出租车总行程时间的10%以上，说明交叉路口的影响不容忽视。同时，路段上的交通状态例如速度等也与行程时间估计的准确性密切相关。
早期的行程时间估计相关的工作主要采用了一些传统的数学建模方法和统计机器学习方法实现[2⇓⇓⇓⇓⇓⇓⇓-10]。例如Jenelius等[3]提出了一种统计方法来预测每个路段的行程时间，并将它们汇总以估计路径的行程时间；Yuan等[11]从历史出租车轨迹中建立了一个时间相关的地标图，其中地标是从前k 个经常穿过的路段中选择的，然后他们采用聚类方法来估计两个地标之间的行程时间分布；Wu等[5]使用支持向量回归来预测路段的行程时间；Wang等[10]基于具有相似来源和目的地的路径具有相似行程时间的假设提出了TEMP，通过查找附近的历史轨迹来估计路径的行程时间；Huang等[12]基于集成回归树模型GBDT对出租车的行程时间进行预测。但是这些方法难以有效地学习行程路径相关的交通路网复杂的时空模式，因此导致预测结果较差。为了更好地学习交通网络上时空动态特征，以提升行程时间估计的准确度，一些基于深度学习的方法近几年被提出应用于该领域。相比基于数学建模和统计机器学习的传统方法，基于深度学习的行程时间估计方法能够更好地学习路径相关的复杂时空特征，因此变得越来越重要[13⇓⇓-16]。例如， DeepTTE[15]是首个估计路径的行程时间的端到端的深度学习框架，它可以捕捉给定路径的空间和时间的关联特征；DeepIST[14]将每条路径视为一系列图像，并使用卷积神经网络捕获空间移动模式及其时间模式以进行行程时间估计。基于图结构的深度学习模型，图卷积神经网络近年来引起了大多数研究人员的兴趣，广泛应用于自然语言处理、计算机视觉等领域[17]。受到GNN进步的启发，有一些工作[18⇓⇓⇓⇓⇓-24]设计时空图卷积模型来编码交通预测中的时空信息。同样地，图卷积神经网络也被用于预测旅行时间[25⇓-27]。例如，ConSTGAT[26]采用图注意力机制来捕获空间和时间信息的联合关系，并应用卷积来挖掘路径的上下文信息；Fu等[25]设计了一个在线行程时间预测系统，该系统利用道路网络信息通过应用图注意力网络来学习路段之间的空间依赖性；Wang等[28]对交通路网上的交叉路口的特征进行深度图嵌入学习以估计经由不同路口的路径的行程时间。虽然这些基于深度学习的方法证明了它们相比于传统方法的优越性，然而它们都只通过对路段[25-26,29]或交叉路口[28]的单独建模来估计路径的行驶时间，而没有同时考虑路口和路段的特征以对这两者联合建模，因此难以在行程时间估计任务中获得更高的准确性。然而，如何对路口和路段进行联合建模是一个具有挑战性的问题。首先，路口和路段之间存在复杂的关系。具体来说，2个相邻的路口之间相互影响，并且相关性随着交通状况的变化而变化，例如当一个路口发生交通拥堵时则很可能将这种拥堵状态传播到邻接的路口。同时，与同一路口相连的路段也是紧密关联，之间的相互作用取决于上游或下游路段[23]。交通流是从上游路段流向下游路段，而路段的拥堵状态则是从下游到上游路段进行反向传播，因此邻接的上下游路段之间也存在很强的相关性。此外，交通网络上所附着的时空属性不仅与小范围的局部交通模式有关，还可能受到大范围区域内的全局交通模式的影响。
为了解决上述问题，本文提出了一种创新的基于图卷积神经网络(GCN)的端到端的学习框架DGCN-TTE来估计行程时间。首先，为了学习交叉路口和路段的复杂关系，该模型提出了一种对偶图卷积架构，不仅考虑了不同路口之间，不同路段之间的相关性，还探索了路口和路段之间的交互模式。模型中还设计了一个增强型GCN(R-GCN)模块来整合不同邻域范围内的空间信息，并且将门控循环神经网络(GRU)结构与其整合，在捕获道路网络动态属性的时间相关性的同时结合空间关系来实现时空依赖关联的学习。最后，模型采用多任务学习的方法同时估计完整路径、每个通行路段和路口的行程时间。

2 研究方法

2.1 基本定义和总体框架

本小节给出了本研究中所涉及的名词术语的基本定义，并描述了解决问题的总体框架。
轨迹：轨迹Y定义为一系列连续的长度为n的GPS 观测 Y = y 1 , y 2 , … , y n，每个都包括位置（即纬度 y i l 1和经度 y i l 2和时间戳 y i t）。
路网：可以定义为有向图G=(V, E)，其中V和E分别表示路网的节点集和边集。节点 v ∈ V表示路网中的一个交叉路口。边 e i , j ∈ E表示连接交叉路口 v i和 v j的路段。
路径：路径P是道路网络中的一系列路段和路口的序列，形如 P = e s t a r t , 1 , v 1 , e 1,2 , v 2 , … , e M - 1 , e n d。路径时通过路网匹配的方法从原始轨迹数据中得到的，其中 e s t a r t , 1代表路径起始的路段， e M - 1 , e n d代表的是路径结束的路段， e i , j代表的是2个路口 v i和 v j之间的路段。
任务描述：给定路径P和出发时间 t d，我们的目标是使用历史轨迹数据集D以及对应的网络G来估计行程时间 t θ，可以表示为:
t Θ ← F P , t d ∣ D , G
式中： Θ = P , v P , s P表示整条路径及其对应的交叉路口的集合 v P和路段的集合 s P。 F ( ∙ )是需要学习的用于行程时间估计的函数，即本文提出的神经网络架构。
本文提出的神经网络架构DGCN-TTE主要由3部分组成：嵌入层、时空图学习层和多任务学习层，总体的框架如图1所示。
图1 本文技术路线

Fig. 1 The overall framework of our proposed model DGCN-TTE

嵌入层：良好的路段和路口的初始表示向量（也称为嵌入）对于在框架的其他部分有效学习它们的复杂特征非常重要。一种可行的方式是使用独热编码表示，但它过于稀疏，无法很好地区分不同路段和路口的特征。为了解决这个问题，通过整合外部因素（例如，路段的类型和路口的地理空间属性）来初始化表示向量。特别是对于路口，还将其相邻路段的信息合并到路口表示向量中。
时空图学习层：为了解决路口和路段如何联合建模的挑战，首先设计了节点图和边图卷积来捕获它们的复杂关系。接下来，为了捕获不同尺度的空间特征，提出了R-GCN模型来整合来自多个空间信息尺度的特征，然后引入了时空学习方法来联合学习它们的时空特征。
多任务学习层：为了同时估计各个路段、路口和整条路径的行程时间，模型中采用了具有多任务损失函数的多任务序列模型，可以同时进行局部（即路口和路段）和全局（即路径）行程时间的估计。

2.2 嵌入层设计

由于路径的行程时间受许多重要因素（例如，行驶速度、道路类型和行驶距离）的影响，通过将这些因素纳入本文的模型来初始化路段的表示，如图2所示。具体来说，在时间t的路段的表示可以定义如下：
h → e t = t a n h W e ∙ s e t , d e , p e
式中： s e ( t )是在时间t的每条路段的实时速度； d e是路段的距离； p e是道路类型。 W e是一个可学习的参数矩阵。 是一个合并操作运算符。
图2 嵌入层的总体框架

Fig. 2 The overall framework of embedding layer

对于路口，由于它们与多个路段相连接，因此通过聚合连接路段的表示来初始化。同时，也有其特定的地理空间属性（例如十字路口的红绿灯）。因此，在时间t的路口的表示可以定义为：
z → v t = t a n h W 1 ∑   h i t + W 2 ∙ p v
式中：F(v)表示与路口节点v连接的路段集； p v表示路口是否有红绿灯； W 1和 W 2表示可学习的参数矩阵。

2.3 时空图学习层

DGCN-TTE模型的核心是时空图学习层，如图3所示。本节中介绍了该层中的3个重要部分，包括对偶图卷积方法、增强型GCN（R-GCN）和时空学习方法，它们可以实现对路口和路段的联合建模。
图3 时空图学习层的概要

Fig. 3 The overall framework of spatio-temporal graph learning layer

对偶图卷积：现有的方法[25-26]利用带有加权图的GCN来学习路段之间的交互，而连接路段的路口由固定标量（例如，加权和）表示，这忽略了路段与其相连的路口之间复杂的相互作用。为了学习它们的联合特征，设计了一种对偶图卷积方法来同时建模它们的复杂关系。
令 G = ( V , E , W )表示节点图，其中每个节点和边分别代表一个路口和路段。 G ' = V ' , E ' , Q是对应的边图，边图 G '的节点 V '是节点图边集合 E中的对应边， E '则是边图中新的边。 W和 Q是表征它们相互作用的加权邻接矩阵。节点图和边图的转化示例如图4所示，其中例如V1、V2是节点图中的节点， E12是节点图中连接V1、V2的边，由节点图转换成边图之后，原来的节点图中的边E12则变成了边图中的节点。
图4 节点图和边图的转换示意

Fig. 4 The schematic diagram of transformation between node-wise graph and edge-wise graph

在点图G中，任意2个相邻节点i和 j之间的边权重都不相同。直观地说，如果节点i和节点j分别有大量的出度和入度，那么代表节点i和节点j之间相关性的边权重很小。因此，将边权重 W计算为：
w i , j = R i j e - d e g + i + d e g - j - 2 2 σ 2 (i ≠ j)
式中： d e g + ( i )和 d e g - ( j )分别代表节点i和节点j的出度数和入度数。 σ是节点度数的标准差。 R i j表示图中节点i和节点j之间的相邻关系。具体来说，若2个节点i和j是互相邻接的则 R i j为 1，否则为 0。
在边图 G '中，边权重 q i , j定义为从路段i到路段j的流量的分数。显然，如果路段i到路段j的流量大于路段i到其他相邻路段的流量，则i到路段j之间的相关性很强。因此，将边权重 Q矩阵中的每个元素 q i , j计算为：
q i , j = R i j z i j ∑   z i k , i ≠ j
式中： z i j是从节点i到节点j的轨迹数。 N ( i )是节点i的一跳邻居的集合。
因此，k跳对偶图卷积可表述为：
Z l + 1 = θ n * G l Z l , M H l ( l = 0,1 , … , k - 1 )
H l + 1 = θ e * G l H l , M T Z l + 1 ( l = 0,1 , … , k - 1 )
式中： θ * G是带有参数 θ的图卷积运算； M ∈ R | V | × | E |是关联矩阵 对节点和边之间的连接关系进行编码，定义为： M i , ( i → j ) = M j , ( i → j ) = 1，否则为0。 Z ( l + 1 )和 H ( l + 1 )分别表示节点图和边图的输出。
增强型GCN(R-GCN)：图卷积可以聚合一跳邻居的信息[30]。通过堆叠多个图卷积层，可以扩大感受邻域的范围。然而随着网络层数的加深，节点的特征往往倾向于全局模式，而丢失了局部模式特征。因此需要整合多尺度信息以同时捕获全局和局部特征。为了解决这个问题，这里提出了一种增强型GCN(R-GCN)，如图5所示。
图5 R-GCN模型的架构

Fig. 5 The overall framework of R-GCN

为了从前几层的输出中捕获重要特征，本文改进了Luan等[31]采用滚雪球方法增量连接多尺度特征的方式，首次提出使用门控循环单元 (GRU)[32]进行特征的过滤和选择。与其他类型的RNN模型实现相比，GRU是一种简单但有效的结构，表示为：
c 0 = G R U r 0 , c - 1
r 1 = σ L r 0 W 0
r 2 = σ L r 0 , r 1 W 1
r l + 1 = σ L G R U r l - 1 , c l - 2 , r l W l ( l = 2,3 , … , n - 1 )
式中： L = D ˜ - 1 / 2 A ˜ D ˜ - 1 / 2 ; A ˜ = A + I ; D ˜ = d i a g ∑   A ˜ 1 j , … , ∑   A ˜ N j。 A是一个对称邻接矩阵； I是一个单位矩阵， A ˜是考虑自环连接的邻接矩阵； D ˜是邻接矩阵 A ˜的度矩阵，L是规范化的邻接矩阵； σ是一个非线性激活函数，在本文中使用函数Tanh。 r ( l )是第l跳处的路口或路段的隐藏表示。 c l是处理第l-1跳邻居后的隐藏状态，它的初始值 c ( - 1 ) = 0。再由GRU推导出隐藏状态的向量表示定义为：
u = σ W u 1 r t + U u 1 c t - 1 + b u 1
x = σ W x 1 r t + U x 1 c t - 1 + b x 1
c ' t = t a n h W h 1 r t + U h 1 x ⊙ c t - 1 + b h 1
c t = u ⊙ r t - 1 + 1 - u ⊙ c ' t
式中： ⊙代表逐元素乘法。 W u 1, U u 1, W x 1, U x 1, W h 1, U h 1是权重参数， b u 1, b x 1, b h 1是偏置参数。
时空学习方法：接下来使用 GRU 来捕获路口和路段特征的时序依赖性，如图4所示。使用了路口和路段的历史信息来学习它们的时序特征，公式可以表示为：
s i t = G R U h i t , s i ' t - 1 ∣ W Ω , U Ω , b Ω
x i t = G R U z i t , x i ' t - 1 ∣ W Ω ' . U Ω ' , b Ω '
s i ' t - 1 , x i ' t - 1 = f G , G ' , s i t - 1 , x i t - 1 , L
式中： f 代表对偶图卷积的函数； L代表对偶图卷积的层数； h i ( t )( z i ( t ))是在时间步t的第i个路口（路段）的表示； s i ( t ) ( x i ( t ) )是在时间步t经对偶图卷积操作处理后的第i个路口（路段）后的隐藏状态。 W Ω、 W Ω '、 U Ω和 U Ω '是权重矩阵，并且 b Ω， b Ω '是偏置参数，其中 Ω ∈ u , r , h。特别地，受Wang等[24]的启发，本文将对偶图卷积操作同时应用于GRU的输入和隐藏表示，以充分学习空间和时间信息。

2.4 多任务学习层

由于路径信息总是顺序依赖的，可以采用循环神经网络进一步学习路段和路口之间时序依赖关系，如图6所示。为简单起见使用q来表示s和x。因此公式可以表示为:
u = σ W u 2 q i t + U u 2 c i - 1 t + b u 2
r = σ W r 2 q i t + U r 2 c i - 1 t + b r 2
c i ' t = t a n h W h 2 q i t + U h 2 r ⊙ c i - 1 t + b h 2
c i t = u ⊙ c i - 1 t + 1 - u ⊙ c i ' t
式中： c i ( t )代表第i个路段或路口在时间步t的最终表示。
图6 多任务学习层的架构图

Fig. 6 The overall framework of multi-task learning layer

（1）预测：为了估计每个路段（路口）的行程时间，这里使用隐藏层规格为λ，输出层规格为1的2层全连接神经网络。定义 t l i t v j作为第i个路段（第j个路口）的行程时间。为了直接估计整条路径的行程时间，需要将多任务学习层中GRU得到的路段和路口的特征序列 c i转换成一个固定长度的向量。对于完整路径行程时间的估计表示为：
g P = ∑ i = 1 P   c i
式中： | P |是路径P中的路段和路口的总数。最后将 g P传递给几个大小相等的全连接层，并获得对整个路径行程时间的估计。
（2）损失函数：在训练阶段，使用平均绝对百分比误差（MAPE）作为目标函数来估计整个路径的行程时间，损失函数公式如下：
L P = ∑ i = 1 D   t i - t i ˆ t i ˆ + ϵ
式中： t i表示估计的行程时间； t i ˆ是第i条路径的行程时间的真实值。与Wang等[15]类似，添加了一个较小的参数 ϵ，以避免分母接近0时导致损失值爆炸。根据行程时间估计场景中的数据尺度，本文中将 ϵ设置为5。
对于局部路径行程时间估计，定义了相应的损失为所有局部路径的平均损失：
L l = ∑   ∑ j = 1 P + 1 2   t l j - t l j ˆ t l j ˆ + ϵ
式中： t l j ˆ表示第j个路段的行程时间的真实值。
对于路口行程时间的估计，定义了相应的损失为所有路口的平均损失：
L v = ∑   ∑ j = 1 P - 1 2   t v j - t v j ˆ t v j ˆ + ϵ
式中： t v j ˆ是第j个路口的行程时间的真实值。
本文模型经过训练以最小化3个损失项的加权组合，表示为：
L = α L P + β L l + 1 - α - β L v
式中： α和 β用于平衡 L P、 L l和 L v。由于本文提出的深度框架可以并行估计路段、路口和整条路径的行程时间，它有助于将其部署到实用的地图导航服务中。

3 实验及结果分析

本章在3个真实数据集上评估DGCN-TTE模型并进行了充分的实验。实验旨在回答以下问题： ①与3个数据集上的不同基线方法相比，DGCN-TTE模型表现如何? ② DGCN-TTE模型在不同的场景下（例如，高峰时间和非高峰时间）可以达到什么结果?③ DGCN-TTE模型的不同变体在消融研究中表现如何? 模型参数（例如，R-GCN层数）如何影响模型的性能?

3.1 实验设置

本文使用3个真实世界的数据集评估提出的模型，数据集基本情况如下所述。
成都数据集：包含2014年8月中国成都超过1.4万辆出租车的出租车轨迹，数据获取网址为 http://www.dcjingsai.com
波尔图数据集：它包含2013年7月至2014年6月在葡萄牙波尔图的442辆出租车的出租车轨迹，数据获取网址为 https://www.kaggle.com/crailtap/taxi-trajectory
北京数据集：它包含来自中国北京2020年12月15日上午8:00 至下午1:00 流行的移动应用程序Amap的34 696条匿名轨迹。使用这个数据集在高德地图的服务提供商的深度学习平台上评估我们提出的框架。
其中成都和波尔图的数据都是出租车轨迹数据，而北京数据还中除了出租车还包含了私家车的轨迹数据，且成都和北京数据中的轨迹相对密集，而波尔图数据中的轨迹比较稀疏。对于前2个公共数据集：① 从OpenStreetMap中获取成都和波尔图的路网信息，包括路段、路口及其连通性；② 对于每个数据集，使用现有的地图匹配方法[33]将每条轨迹投影到道路网络中，从而获得对应的路径； ③ 过滤与原始轨迹有显着偏差（ ± 10%）的不匹配路径[14]；④ 分别从波尔图和成都的数据集中提取了 310 507 和 1 788 723 条轨迹。由于计算资源的限制，本文中没有使用2个数据集中的所有匹配路径，而是选择了分布在市中心的路径，因为这些区域有存在相对大量的轨迹。对于北京数据集，经过高德数据平台的预处理，可以得到每条路径的路段和路口的序列。与其他2个数据集不同的是，该数据集中每个路口的行驶时间都可获得，这使得同时估计整个路径、路段和路口的行程时间成为可能。
表1显示了实验中使用的3个数据集的统计数据。由于地理空间和时间因素可能会影响旅行时间的预测性能，以验证本模型的普遍性，本文还根据郊区、高峰期和非高峰期3种场景选择成都数据集上的轨迹。特别是对于郊区场景，由于沿着郊区的路径遍历了一些轨迹，可以进一步验证数据稀疏性对模型性能的影响。同时，在市区定义了高峰和非高峰时间的场景。需要注意的是，本文将高峰时间定义为工作日的7:00 —9:00和17:00 —19:00 ，其他时间段被视为非高峰时间。表2展示了成都数据集在3种场景下的统计数据。
表1 实验数据集的基本信息

Tab. 1 Basic information of the experimental dataset

数据集 成都 波尔图 北京
轨迹数量/条 15 303 12 683 346 96
路段数量/条 873 544 714
路口数量/个 807 450 320
平均行程时间/s 246.54 248.49 343.3
平均移动距离/m 1435.34 1394.82 3929.7
表2 成都数据集在郊区、高峰和非高峰3个场景下的数值统计

Tab. 2 Numerical statistics of Chengdu dataset in suburban, peak and off-peak scenarios

场景 郊区 高峰时间 非高峰时间
轨迹数量/条 8 156 2 867 12 436
路段数量/条 639 873 873
路口数量/个 291 807 807
平均行程时间/s 242.42 249.81 243.57
平均移动距离/m 1 105.42 1 435.47 1 435.31
评估指标：和之前的相关工作一样[15,26]，这里选择了3个指标来评估所有方法，包括平均误差(MAE)、均方根误差(RMSE) 和平均绝对百分比误差(MAPE)。详细地说，MAE 和 RMSE 可以很好地反映估计结果与真实值之间的误差，其中RMSE对大误差更有用。 MAPE是衡量估计精度的相对误差。通过这些指标可以全面评估本文模型的性能。定义如下：
R M S E t ˆ i , t i = 1 D ∑ i = 1 D   t i - t ˆ i 2
M A E t ˆ i , t i = 1 D ∑ i = 1 D   t i - t ˆ i
M A P E t ˆ i , t i = 1 D ∑ i = 1 D   t i - t ˆ i t i
对于上述指标，较小的值代表更好的预测性能。在DGCN-TTE模型中，路口和路段的表示的维度大小设置为 20。R-GCN层数设置为3，对偶图卷积的跳数默设置为1。在时空学习模块中，使用前12个时间步以5 min为基本时间单元的路口和路段的历史信息来捕获它们的时空动态特征。多任务学习层中的全连接层数均设置为2，隐藏层数均设置为60。使用Adam优化器训练模型，学习率默认设置为0.001，训练批次大小设置为32，在TITAN XP GPU上运行模型，并在Python中使用Pytorch 1.5环境中实现，对于每个实验都重复进行5次取平均值。

3.2 对比模型

为了评估模型的有效性，这里选择了十种最先进的对比方法，总结如下：
（1） AVG：计算特定时间间隔内城市的平均路段速度。有了这样的历史平均速度，根据出发时间估计给定行驶路径的行驶时间。
（2） TEMP[10]：这是一种集体行程时间估计方法，使用具有相似起点和目的地的相邻历史轨迹。本文为每个要在实验中估计的轨迹分配5个相邻轨迹并取这些轨迹的平均行程时间为待估计轨迹的行程时间。
（3） GBDT[12]：使用梯度提升决策树进行回归来估计行程时间。与参考文献[15]类似，每个GPS点序列统一采样到128个。树模型的最大深度设置为8。
（4） MlpTTE：采用多层感知器来估计行程时间。在实验中，该模型的层数为5，激活函数是ReLU。MlpTTE中隐藏层的大小固定为64。
（5） RnnTTE：利用GRU作为循环神经网络将原始GPS序列处理为128维特征向量。然后将其传递给两个全连接层以获得行程时间的估计值。
（6） DeepTTE[15]：这是一个用于行程时间估计的端到端深度学习模型，基于查询路径上的连续采样GPS点捕获空间和时间依赖性。 Geo-Conv层和GRU层的隐藏大小分别设置为64和128。
（7） T-GCN[19]：这是一个时序GCN模型，它结合了GCN和GRU，同时表征交通预测的空间和时间依赖性。在实验中，使用它的核心架构来估计旅行时间，GCN模型的嵌入大小设置为 20，GRU 的隐藏大小设置为128。
8) DCRNN[20]：这是一个用于交通预测的时空图神经网络。利用GCN捕获空间依赖性，然后使用递归神经网络对时间依赖性进行建模。同样，利用其核心架构来估计行程时间，GCN嵌入大小和GRU隐藏大小的设置与T-GCN模型相同。
（9） ConSTGAT[26]：该模型采用图注意力机制来探索时空信息的联合关系，在行程时间估计中被证明是有效的。我们实现了它的核心架构，其中图注意力网络的嵌入大小设置为32。
（10） GCNAttTTE：与DGCN-TTE模型不同，该模型首先使用GCN对路段进行建模，然后采用注意力机制通过对连接路段的嵌入求和来学习路口的特征。在实验中，路段的嵌入大小设置为 20。

3.3 实验结果与分析

3.3.1 参数分析

为了验证模型中超参数选择的合理性，在不同的参数组合下进行了实验，包括R-GCN的层数（记为n）和对偶图卷积的跳数（记为k）。如图7(a)所示，可以发现在RMSE、MAE和MAPE方面，在2个城市的数据集上，在k=1的条件下，当n从1逐渐变为3 时，性能逐渐提高。但是，当n=4时性能会变差。这表明R-GCN 的层数越高并不表示性能越好。在图7(b) 中观察到，无论是哪个数据集，当R-GCN的层数为2时，其性能在k=2的条件下均达到最优。此外，该实验在每个数据集上比较了不同参数组合下的性能。表3的结果表明，DGCN-TTE模型在成都数据集上在n=3和k=1的条件下取得了最好的性能，而在波尔图数据集上在n=3和k=1或者n=2和k=2时都取得了较好性能。这表明R-GCN的层数和对偶图卷积的跳数都在获得更高的行程时间估计精度方面发挥着关键作用。因此R-GCN的层数越多，对偶图卷积的跳数越大并不意味着更好的性能，并且应根据相应的数据集选择最合适的参数数值。
图7 模型在不同参数组合下的性能变化

Fig. 7 The performance of the model under different parameter combinations

表3 DGCN-TTE及其变体在2个数据集上估计路径行程时间的性能

Tab. 3 Performance of DGCN-TTE under different combinations of k and n

参数组合 ( k , n ) 成都数据集 波尔图数据集
RMSE MAE MAPE RMSE MAE MAPE
(1,1) 154.11 88.34 0.297 5 55.52 42.03 0.166 3
(1,2) 141.60 78.39 0.265 3 54.12 41.03 0.160 8
(1,3) 140.30 77.60 0.258 5 50.95 40.06 0.155 8
(1,4) 143.78 80.55 0.268 9 53.76 40.83 0.159 6
(2,1) 151.67 86.23 0.286 5 54.84 41.62 0.163 1
(2,2) 140.52 77.78 0.259 6 51.17 38.83 0.154 4
(2.3) 141.22 78.92 0.261 2 52.59 40.20 0.157 9
(2,4) 146.75 83.32 0.275 6 54.12 41.24 0.160 8

注：表中加粗数字表示评估指标的最佳性能。

3.3.2 总体性能

本实验在3个数据集上将DGCN-TTE模型与其他基线方法进行比较。表4显示了估计路径行程时间的性能，其中最佳基线方法取得的性能用星号标记。从结果中，可以发现DGCN-TTE模型在所有3个指标方面都比其他方法取得了更好的性能。 具体来说，DGCN-TTE模型在成都数据集上的RMSE、MAE 和 MAPE 3个指标至少提升了5.39%、9.91%、9.14%，在波尔图数据集上的RMSE、MAE 和 MAPE 的改进率则至少为 6.90%、4.19%、4.83 %。部署在高德地图深度学习平台上，DGCN-TTE模型在北京数据集的 RMSE、MAE 和 MAPE 上分别获得了至少 10.51%、9.84%、6.25% 的改进，进一步证实了DGCN-TTE 是一种行程时间估计服务（例如导航服务）的实用解决方案。如此显著的改进可以从2个方面来解释。首先，对于一些基于图的方法，如T-GCN、DCRNN和ConSTGAT，它们只专注于对路段进行建模。然而，交叉路口作为连接多条连接路段的关键节点，在行程时间估计中也发挥着重要作用。因此，在不考虑路口的情况下设计模型无法获得更高的精度。其次对于像GCNAttTTE 这样的模型，它已经同时考虑了路口和路段，但它没有充分利用它们的联合关系，因此GCNAttTTE无法获得最佳性能。与它们不同的是，本文提出的DGCN-TTE模型不仅考虑了路口和路段特征，还捕获了它们的复杂关系，是方法中性能最好的。
表4 DGCN-TTE 和其他方法在3个数据集上估计路径行程时间的性能

Tab. 4 Performance of DGCN-TTE and other methods for estimating travel time on three datasets

算法 成都数据集 波尔图数据集 北京数据集
RMSE MAE MAPE RMSE MAE MAPE RMSE MAE MAPE
AVG 202.43 132.86 0.640 4 111.67 88.75 0.4509 338.43 264.55 0.736 7
TEMP 167.41 108.50 0.553 8 98.01 78.12 0.4127 342.08 272.46 1.642 5
GBDT 165.03 101.68 0.542 8 91.24 71.79 0.3914 372.87 262.49 0.685 4
MlpTTE 150.67 87.32 0.307 6 59.46 44.49 0.1783 124.92 79.75 0.253 2
RnnTTE 155.16 89.37 0.301 1 56.45 43.32 0.1702 127.80 86.59 0.292 4
DeepTTE 148.30* 86.40 0.298 4 57.32 43.54 0.1686 147.60 92.64 0.250 0
T-GCN 153.49 87.71 0.291 8 56.35 43.28 0.1678 129.56 85.66 0.275 8
DRCNN 151.59 86.14* 0.288 4 54.73* 41.81* 0.1673* 116.30 76.71 0.256 1
ConSTGAT 152.23 87.10 0.284 5* 56.67 43.22 0.1684 107.58* 69.90* 0.228 8*
GCNAttTTE 152.95 87.41 0.289 8 55.88 42.79 0.1654 112.88 73.82 0.237 2
DGCN-TTE 140.30 77.60 0.258 5 50.95 40.06 0.1558 96.27 63.02 0.214 5
提升比例/% 5.39 9.91 9.14 6.90 4.19 4.83 10.51 9.84 6.25

注：表中加粗数字表示评估指标的最佳性能。

由于DGCN-TTE模型可以同时估计路段、路口和整个路径的行程时间，本章还进行了实验，将该模型与其他基于图学习的方法在预测路段和路口的行程时间方面进行比较。需要注意的是，只有北京数据集有路口行程时间信息，并且对比的基线模型中除GCNAttTTE外的其他模型没有考虑路口。因此，实验中将模型与GCNAttTTE 进行比较，用于北京数据集的路口行程时间估计，其中路口的预测结果列在符号“/”之后。如表5所示，观察到对于路段行程时间，DGCN-TTE模型在3个数据集上获得了更好的预测性能。对于路口行程时间，DGCN-TTE模型与GCNAttTTE相比，RMSE提高了12.23%，MAE提高了20.55%，MAPE提高了20.53%，这是因为该模型捕获了路段和路口之间的交互关系，这有助于提高估计路段和路口行程时间的准确性。
表5 DGCN-TTE 和其他方法在3个数据集上估计路径行程时间的性能

Tab. 5 Performance of DGCN-TTE and other graph learning-based methods for estimating road segment travel time on three datasets

算法 成都数据集 波尔图数据集 北京数据集
RMSE MAE MAPE RMSE MAE MAPE RMSE MAE MAPE
T-GCN 57.84 24.85 0.553 7 22.48 13.03 0.552 1 47.06/- 23.87/- 0.588 6/-
DRCNN 57.82 24.76 0.551 3 20.59 11.68 0.460 5 49.14/- 26.23/- 0.630 6/-
ConSTGAT 58.17 24.55 0.550 3 21.76 12.23 0.486 5 47.26/- 21.64/- 0.507 4/-
GCNAttTTE 58.26 24.79 0.551 2 19.89 10.95 0.432 3 45.31/22.88 21.50/10.12 0.488 4/0.466 5
DGCN-TTE 55.91 22.88 0.512 2 15.81 8.06 0.301 6 41.34/20.60 18.87/8.04 0.441 4/0.370 7

注：表中加粗数字表示评估指标的最佳性能。

3.3.3 不同场景下的性能

由于地理空间和时间因素对行程时间估计有显著影响。具体来说，不同类型的地区有不同的交通状况。例如，市中心通常交通繁忙，而郊区则有少量机动车辆行驶。同时，交通状况随时间变化。例如，高峰时段比非高峰时段更容易发生交通拥堵。基于上述分析，进行了实验来评估模型在3种不同场景下估计路径的行程时间的性能，包括郊区、高峰时间和非高峰时间。表6展示了实验结果。可以观察到，虽然高峰时段可能会出现交通拥堵，但DGCN-TTE模型在RMSE、MAE 和 MAPE方面至少可以实现 7.36%、7.56%和6.86%的改进。 然而，在非高峰时段，该模型在RMSE、MAE 和 MAPE 方面至少实现了10.81%、13.24%和8.58%的改进。 同时在轨迹数量较少的郊区，DGCN-TTE模型在RMSE、MAE 和 MAPE的预测性能上也获得了至少2.27%、4.84%和8.46%的提升。 相对而言，DGCN-TTE模型在非高峰时段的场景下提升最大。但是无论在哪种情况下，它都明显优于其他方法。
表6 DGCN-TTE和其他方法在3种场景下估计路径行程时间的性能

Tab. 6 Performance of DGCN-TTE and other methods for estimating travel time in three scenarios

算法 郊区 高峰时段 非高峰时段
RMSE MAE MAPE RMSE MAE MAPE RMSE MAE MAPE
AVG 159.14 110.85 0.517 7 177.83 137.24 0.688 7 159.25 122.93 0.630 7
TEMP 148.26 101.43 0.458 9 156.97 112.18 0.512 0 150.12 115.24 0.493 6
GBDT 136.19 83.77 0.373 9 142.58 91.48 0.397 5 138.75 82.15 0.356 8
MlpTTE 125.49 78.48 0.293 8 131.78 87.64 0.311 5 127.11 79.67 0.311 9
RnnTTE 121.75 76.64 0.281 7 126.43 84.87 0.296 8 122.50 83.69 0.302 0
DeepTTE 114.47 72.55 0.287 9 129.45 87.67 0.312 1 123.36 83.97 0.296 8
T-GCN 121.58 76.38 0.277 5 132.05 89.74 0.303 9 121.21 83.17 0.290 5
DRCNN 120.34 75.40 0.274 8 131.22 89.10 0.297 6 120.76 82.78 0.285 3
ConSTGAT 118.89 72.12 0.264 8 128.79 88.06 0.293 0 118.64 81.89 0.282 1
GCNAttTTE 111.87 68.63 0.242 1 117.13 78.45 0.272 9 105.81 71.05 0.257 9
DGCN-TTE 159.14 110.85 0.517 7 177.83 137.24 0.688 7 159.25 122.93 0.630 7

注：表中加粗数字表示评估指标的最佳性能。

3.3.4 消融实验

为了验证DGCN-TTE中的时空学习方法如何有效地捕捉空间和时间属性的联合关系，在首先将R-GCN从GRU的隐藏状态中移除得到变体DGCN-TTE w/o R-GCN。从表7中可以发现在两个数据集上与 DGCN-TTE 相比，它无法获得良好的性能。通过与完整的DGCN-TTE模型比较，它在成都数据集上的RMSE、MAE和MAPE性能分别下降4.41%、5.4%和5.38%，这是因为空间信息未被纳入时间依赖关系中，这证明了模型中时空学习方法的有效性。接着构建了没有RNN的DGCN-TTE，它从DGCN-TTE模型中移除了时序学习部分，得到变体DGCN-TTE w/o RNN。结果如表7所示，从中可以发现去除时序学习部分后两个数据集的预测性能有明显下降。这是因为时序学习部分对于捕获路径沿线的交通历史信息至关重要，这表明单纯捕获空间特征无法获得更好的性能。基于上述分析，可以得出的结论是模型中的时空学习方法可以有效地学习时空属性的联合关系。
表7 DGCN-TTE及其变体在2个数据集上估计路径行程时间的性能

Tab. 7 Performance of DGCN-TTE and its variants in estimating travel time on two datasets

变体模型 成都数据集 波尔图数据集
RMSE MAE MAPE RMSE MAE MAPE
DGCN-TTE w/o R-GCN 146.78 82.03 0.273 2 51.64 40.82 0.158 8
DGCN-TTE w/o RNN 147.48 83.46 0.276 4 54.07 41.13 0.162 6
DGCN-TTE w/o Intersection 143.82 79.59 0.264 2 53.96 41.02 0.161 0
DGCN-TTE Simple GCN 144.56 80.21 0.270 9 53.87 40.95 0.162 2
DGCN-TTE 140.30 77.60 0.258 5 50.95 40.06 0.155 8

注：表中加粗数字表示评估指标的最佳性能。

该实验研究了路口建模如何影响性能。在DGCN-TTE w/o Intersection变体中，仅对路段进行建模以估计行程时间。如表7所示，可以观察到无论对于哪个数据集，性能都会变差。具体来说，在RMSE、MAE和 MAPE方面， DGCN-TTE w/o Intersection的性能在成都数据集上下降了2.45%、2.5%和2.16%，在波尔图数据集上下降了5.58%、2.34%和3.23%。原因是路口不仅包含自己的重要信息，而且与多个连接的路口具有很强的相关性。因此忽略路口特征的DGCN-TTE w/o Intersection无法获得良好的性能。最后实验展示了R-GCN在该DGCN-TTE模型中的影响。具体来说，该实验在DGCN-TTE Simple GCN变体中使用简单的GCN[30]代替了R-GCN，然后评估其性能。结果表明，模型与R-GCN结合使用可以在2个数据集上取得更好的性能，因此R-GCN在捕获多尺度时空信息方面具备更强的能力。

4 讨论

从以上的多组实验结果来看，本文提出的DGCN-TTE模型中的每个关键的组件都被证明是有效的，而且该模型在不同数据集，不同交通场景中的预测精度都优于现有的其他方法，这证明了DGCN-TTE模型是一种面向行程时间估计的有效方法。由于DGCN-TTE是一种神经网络模型，所以它在训练过程中具备一定的随机性，在所有超参数固定的情况下，每次训练结束的最终收敛的结果不会完全相同，但是会在一个平均水平上有微小的波动，但是通常预这种波动带来的预测指标造成的偏差幅度不超过1%。在模型超参数变化的情况下，例如参数实验中的对偶图卷积的跳数和R-GCN的层数的变化都可能对模型的最终预测结果带来较为明显的差异。还有一些与模型训练直接相关的固定参数，例如训练批次大小，学习率大小的调整都可能对最终结果产生影响。虽然本文的实验已经从多角度证明了DGCN-TTE模型的有效性，这项工作仍然存在一些局限性。首先，虽然本文提出的模型性能优越，但因为模型复杂度较高导致训练效率相对较低。其次，模型中未涉及一些可能对出行时间产生影响的时空事件，例如拥堵事件等。未来我们将开发一个更灵活、更轻量级并且能够集成多源相关时空信息的模型。

5 结论

本文面向路径的行程时间估计问题提出了一个名为DGCN-TTE的端到端的深度学习框架，为现实世界的地图服务系统和智慧交通系统中的相关需求提供了一个可行的解决方案。这篇论文的贡献总结如下：
（1） 本文的工作第一次尝试了对路口和路段的特征进行联合建模以对行程时间进行估计。为了实现这个目的，DGCN-TTE引入了一种对偶图卷积的方法来建模路口和路段的关系。该方法采用节点图来捕捉路口之间的相关性，并构建边图来刻画路段之间的交互特征。
（2） 在本文提出的DGCN-TTE框架中，还创新地设计了一种可以集成多尺度空间信息的增强型GCN模块，并且还通过引入了基于循环神经网络的序列学习方法来充分挖掘空间和时序尺度的关联特征。
（3） 最终，论文通过充分的实验证明了提出的深度学习框架DGCN-TTE的有效性。结果表明该模型显著优于现有的其他方法，在评估指标上相比于次优方法最多可以获得超过10%的提升。

References

Publishing order | Descend order by publishing year | Descend order by cited within
[1]
Tirachini A. Estimation of travel time and the benefits of upgrading the fare payment technology in urban bus services[J]. Transportation Research Part C: Emerging Technologies, 2013, 30:239-256. DOI:10.1016/j.trc.2011.11.007

DOI

[2]
Rice J, van Zwet E. A simple and effective method for predicting travel times on freeways[C]// ITSC 2001.2001 IEEE Intelligent Transportation Systems. Proceedings (Cat. No.01TH8585). IEEE, 2002: 227-232. DOI:10.1109/ITSC.2001.948660

DOI

[3]
Jenelius E, Koutsopoulos H N. Travel time estimation for urban road networks using low frequency probe vehicle data[J]. Transportation Research Part B: Methodological, 2013, 53:64-81. DOI:10.1016/j.trb.2013.03.008

DOI

[4]
Sevlian R, Rajagopal R. Travel time estimation using floating car data[EB/OL]. 2010: arXiv: 1012.4249. https://arxiv.org/abs/1012.4249

[5]
Wu C H, Wei C C, Su D C, et al. Travel time prediction with support vector regression[C]// Proceedings of the 2003 IEEE International Conference on Intelligent Transportation Systems. IEEE, 2003:1438-1442. DOI:10.1109/ITSC.2003.1252721

DOI

[6]
Yuan J, Zheng Y, Xie X, et al. T-drive: Enhancing driving directions with taxi drivers' intelligence[J]. IEEE Transactions on Knowledge and Data Engineering, 2013, 25(1):220-232. DOI:10.1109/TKDE.2011.200

DOI

[7]
Luo W M, Tan H Y, Chen L, et al. Finding time period-based most frequent path in big trajectory data[C]// Proceedings of the 2013 ACM SIGMOD International Conference on Management of Data. New York: ACM, 2013:713-724. DOI:10.1145/2463676.2465287

DOI

[8]
Rahmani M, Jenelius E, Koutsopoulos H N. Route travel time estimation using low-frequency floating car data[C]// 16th International IEEE Conference on Intelligent Transportation Systems (ITSC 2013). IEEE, 2014:2292-2297. DOI:10.1109/ITSC.2013.6728569

DOI

[9]
Wang Y L, Zheng Y, Xue Y X. Travel time estimation of a path using sparse trajectories[C]// Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining. New York: ACM, 2014:25-34. DOI:10.1145/2623330.2623656

DOI

[10]
Wang H J, Tang X F, Kuo Y H, et al. A simple baseline for travel time estimation using large-scale trip data[J]. ACM Transactions on Intelligent Systems and Technology, 2019, 10(2):1-22. DOI:10.1145/3293317

DOI

[11]
Yuan J, Zheng Y, Xie X, et al. T-drive: Enhancing driving directions with taxi drivers' intelligence[J]. IEEE Transactions on Knowledge and Data Engineering, 2013, 25(1):220-232. DOI:10.1109/TKDE.2011.200

DOI

[12]
Ke G L, Meng Q, Finley T, et al. LightGBM: A highly efficient gradient boosting decision tree[C]// Proceedings of the 31st International Conference on Neural Information Processing Systems. New York: ACM, 2017:3149-3157. DOI:10.5555/3294996.3295074

DOI

[13]
Zhang H Y, Wu H, Sun W W, et al. DeepTravel: A neural network based travel time estimation model with auxiliary supervision[EB/OL]. 2018: arXiv: 1802.02147. https://arxiv.org/abs/1802.02147

[14]
Fu T Y, Lee W C. DeepIST: Deep image-based spatio-temporal network for travel time estimation[C]// Proceedings of the 28th ACM International Conference on Information and Knowledge Management. New York: ACM, 2019:69-78. DOI:10.1145/3357384.3357870

DOI

[15]
Wang D, Zhang J B, Cao W, et al. When will You arrive? estimating travel time based on deep neural networks[J]. Proceedings of the AAAI Conference on Artificial Intelligence, 2018, 32(1). DOI:10.1609/aaai.v32i1.11877

DOI

[16]
Li X C, Cong G, Sun A X, et al. Learning travel time distributions with deep generative model[C]// WWW '19:The World Wide Web Conference. New York: ACM, 2019:1017-1027. DOI:10.1145/3308558.3313418

DOI

[17]
Wu Z H, Pan S R, Chen F W, et al. A comprehensive survey on graph neural networks[J]. IEEE Transactions on Neural Networks and Learning Systems, 2021, 32(1):4-24. DOI:10.1109/TNNLS.2020.2978386

DOI

[18]
Pan Z Y, Liang Y X, Wang W F, et al. Urban traffic prediction from spatio-temporal data using deep meta learning[C]// Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. New York: ACM, 2019:1720-1730. DOI:10.1145/3292500.3330884

DOI

[19]
Zhao L, Song Y J, Zhang C, et al. T-GCN: A temporal graph convolutional network for traffic prediction[J]. IEEE Transactions on Intelligent Transportation Systems, 2020, 21(9):3848-3858. DOI:10.1109/TITS.2019.2935152

DOI

[20]
Li Y G, Yu R, Shahabi C, et al. Diffusion convolutional recurrent neural network: Data-driven traffic forecasting[EB/OL]. 2017: arXiv: 1707.01926. https://arxiv.org/abs/1707.01926

[21]
Yu B, Yin H T, Zhu Z X. Spatio-temporal graph convolutional networks: A deep learning framework for traffic forecasting[EB/OL]. 2017: arXiv: 1709.04875. https://arxiv.org/abs/1709.04875

[22]
Guo S N, Lin Y F, Feng N, et al. Attention based spatial-temporal graph convolutional networks for traffic flow forecasting[J]. Proceedings of the AAAI Conference on Artificial Intelligence, 2019, 33(1):922-929. DOI:10.1609/aaai.v33i01.3301922

DOI

[23]
Chen W Q, Chen L, Xie Y, et al. Multi-range attentive bicomponent graph convolutional network for traffic forecasting[J]. Proceedings of the AAAI Conference on Artificial Intelligence, 2020, 34(4):3529-3536. DOI:10.1609/aaai.v34i04.5758

DOI

[24]
Wang X Y, Ma Y, Wang Y Q, et al. Traffic flow prediction via spatial temporal graph neural network[C]// Proceedings of The Web Conference 2020. New York: ACM, 2020:1082-1092. DOI:10.1145/3366423.3380186

DOI

[25]
Fu K, Meng F L, Ye J P, et al. CompactETA: A fast inference system for travel time prediction[C]// Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. New York: ACM, 2020:3337-3345. DOI:10.1145/3394486.3403386

DOI

[26]
Fang X M, Huang J Z, Wang F, et al. ConSTGAT: Contextual spatial-temporal graph attention network for travel time estimation at Baidu maps[C]// Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. New York: ACM, 2020:2697-2705. DOI:10.1145/3394486.3403320

DOI

[27]
Derrow-Pinion A, She J, Wong D, et al. ETA prediction with graph neural networks in google maps[C]// Proceedings of the 30th ACM International Conference on Information & Knowledge Management. New York: ACM, 2021:3767-3776. DOI:10.1145/3459637.3481916

DOI

[28]
Wang M X, Lee W C, Fu T Y, et al. Learning embeddings of intersections on road networks[C]// Proceedings of the 27th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. New York: ACM, 2019:309-318. DOI:10.1145/3347146.3359075

DOI

[29]
Wang Z, Fu K, Ye J P. Learning to estimate the travel time[C]// Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. New York: ACM, 2018:858-866. DOI:10.1145/3219819.3219900

DOI

[30]
Kipf T N, Welling M. Semi-supervised classification with graph convolutional networks[EB/OL]. 2016: arXiv: 160 9.02907. https://arxiv.org/abs/1609.02907

[31]
Luan S T, Zhao M D, Chang X W, et al. Break the ceiling: Stronger multi-scale deep graph convolutional networks[EB/OL]. 2019: arXiv: 1906.02174. https://arxiv.org/abs/1906.02174

[32]
Chung J, Gulcehre C, Cho K, et al. Empirical evaluation of gated recurrent neural networks on sequence modeling[EB/OL]. 2014: arXiv: 1412.3555. https://arxiv.org/abs/1412.3555

[33]
Yang C, Gidófalvi G. Fast map matching, an algorithm integrating hidden Markov model with precomputation[J]. International Journal of Geographical Information Science, 2018, 32(3):547-570. DOI:10.1080/13658816.2017.1400548

DOI

Options
Outlines

/

〈 〉