EN中文

Journal of Geo-information Science >

2023 , Vol. 25 >Issue 9: 1784 - 1797

DOI: https://doi.org/10.12082/dqxxkx.2023.230261

Urban Expansion Cellular Automata Simulation by Coupling Hierarchical Driving Mechanism of Cell and Patch Scales

  • WANG Yuying , 1 ,
  • WANG Haijun 1, 2 ,
  • ZHOU Xingang , 2, 3, 5, * ,
  • ZHANG Bin 4, 5, 6 ,
  • ZHOU Xiaoyan 1
Expand
  • 1. School of Resource and Environmental Science, Wuhan University, Wuhan 430079, China
  • 2. Key Laboratory of Spatial Intelligent Planning Technology, Ministry of Natural Resources, Shanghai 200092, China
  • 3. College of Architecture and Urban Planning, Tongji University, Shanghai 200092, China
  • 4. School of Public Administration, China University of Geosciences, Wuhan 430074, China
  • 5. Guangdong-Hong Kong-Macau Joint Laboratory for Smart Cities, Shenzhen 518000, China
  • 6. Key Laboratory of the Ministry of Natural Resources for Research on Rule of Law, Wuhan 430074, China
* ZHOU Xingang, E-mail:

Received date: 2023-05-12

  Revised date: 2023-07-08

  Online published: 2023-09-05

Supported by

National Key Research and Development Plan(2022YFC3800804)

National Natural Science Foundation of China(42171411)

Open Fund Project of Key Laboratory of the Ministry of Natural Resources for Research on Rule of Law(CUGFZ-2207)

Guangdong Science and Technology Strategic Innovation Fund (the Guangdong-Hong Kong-Macau Joint Laboratory Program(2020B1212030009)

Fold

Abstract

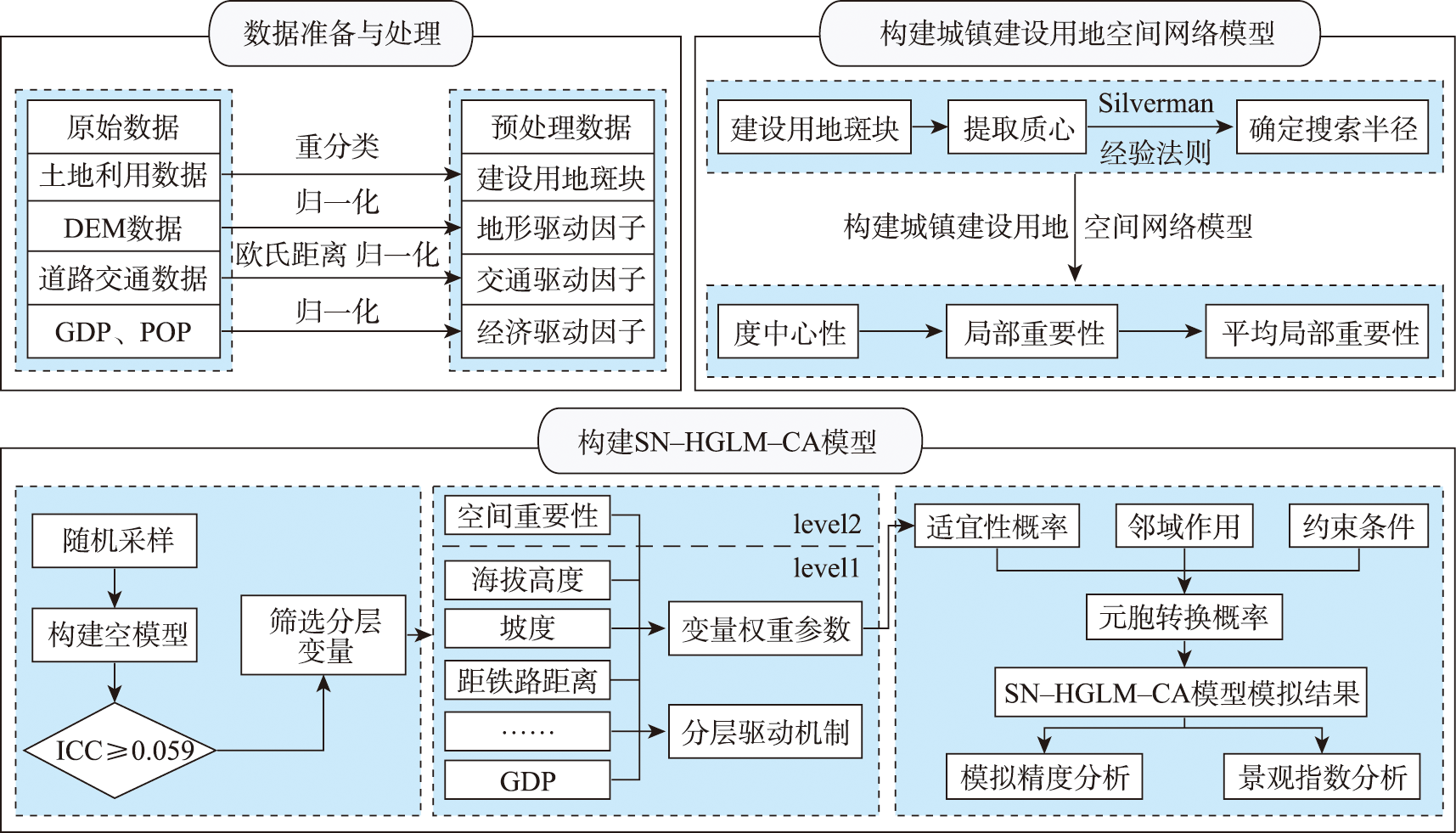
Requirements for the territorial spatial planning of the new era pose new challenges to the relationship between urban land expansion and agricultural and ecological spaces. Urban expansion is closely related to social and economic development as well as ecological environment protection. It is of great significance to study the urban expansion for promoting the urbanization process. The simulation of urban expansion can provide scientific support for formulating territorial spatial planning policies. The spatial characteristics of urban construction land patches are important factors affecting the expansion of urban land and are at different levels against the cell level. Therefore, hierarchically coupling the spatial characteristics of cells and patches can improve the simulation accuracy. Taking the Shanghai metropolitan area as an example, this paper constructs a cellular automata model (Spatial Network - Hierarchical Generalized Linear - Cellular Automata, SN-HGLM-CA) that takes into account both the spatial network structure of urban construction land and the hierarchical relationship of variables. Firstly, the spatial characteristics of patches are extracted through the spatial network model of urban construction land. The hierarchical relationship between variables is considered by using the HGLM to obtain the suitability probability of urban land expansion, and then embedded into the cellular automata model for urban land expansion simulation. This study draws the following research conclusions: ① The spatial network model based on urban construction land patches is of great significance for identifying the spatial importance characteristics of urban construction land and mining its expansion patterns; ② The HGLM model can reveal the hierarchical relationship between cells and patches during urban construction land expansion, which helps to improve the simulation accuracy of the cellular automata model; ③ The simulation of urban land expansion based on the SN-HGLM-CA model achieves good results in terms of simulation accuracy and landscape morphology, with the landscape similarity index exceeding 95%. In addition, compared to the SN-Logistic-CA model, the figure of merit value of our simulation increases by about 6.61%, which indicates that our simulation not only accurately reproduces the actual layout of urban construction land, but also improves the compactness of patch distribution. This paper explores the law of urban expansion from the spatial network structure characteristics of urban expansion, which can help urban planners to determine the reasonability of current trend considering the development status of urban expansion, and provide reference for the delineation of urban development boundaries.

Key words： urban construction land; network structure; urban land expansion; spatial heterogeneity; cellular automata model; hierarchical relationship; driving mechanism; Shanghai metropolitan area

Cite this article

WANG Yuying , WANG Haijun , ZHOU Xingang , ZHANG Bin , ZHOU Xiaoyan . Urban Expansion Cellular Automata Simulation by Coupling Hierarchical Driving Mechanism of Cell and Patch Scales[J]. Journal of Geo-information Science, 2023 , 25(9) : 1784 -1797 . DOI: 10.12082/dqxxkx.2023.230261

1 引言

土地资源是人类社会进行生产和生活的基础和载体[1]，城镇建设用地的无序蔓延、低效扩张会在一定程度上侵占农田、生态用地[2]，进而对社会经济的可持续发展带来不利影响[3]。城镇建设用地的扩展与社会经济发展和生态环境保护之间存在密切联系[4]，研究城镇建设用地的扩展模拟对推动城市化进程有显著意义，成为当前地理学研究的重要领域[5]。城镇建设用地扩展模型是分析城镇建设用地扩展规律和驱动机制的有效工具[6]，传统的城镇用地扩展模型根据其建模方式可以分为两大类：一类是以计量数学模型[7]和系统动力学模型[8]为代表的数理统计模型，利用数理统计方法表达动态的时间变化，是“自上而下”的分析方法。另一类是以元胞自动机（Cellular Automata, CA）[9-10]代表的基于元胞空间邻域关系的动态模型；在模拟复杂的城市系统时，此类模型可以较好的模拟城市系统演变自组织、突变等复杂现象[11]，是“自下而上”的建模方法。目前CA模型多与其他统计学方法或人工智能方法相耦合，如Markov模型[12]、逻辑回归模型[13]、人工神经网络[14]等，此外也出现一些先进的CA衍生模型，如FLUS[15]模型，使模拟结果更加准确。上述研究大多关注城镇建设用地扩展中元胞层面的转换规则，以提高模型的模拟精度，较少考虑城镇建设用地扩展中的分层驱动机制。土地利用系统具有等级特征，在城镇建设用地扩展过程中，各要素之间的相互作用和反馈往往发生在不同的组织层面和不同的尺度上[16]。因此，考虑城镇建设用地扩展中不同层面的分层驱动机制，有助于城镇用地扩展模拟的精度提升并加强其科学性。
现有对城镇建设用地扩展分层驱动机制的研究多从元胞和行政区划层面展开：元胞层面主要挖掘地形地貌、道路通达、空间化的社会经济[17-18]等多方面空间因子的驱动机制；城市群内各城市间的流动[19]、乡镇边界范围[20]等方面，较少考虑城镇建设用地元胞与斑块层面之间的层级关系。上述研究局限于行政区划范围进行分层驱动机制的分析，然而，斑块是土地利用在空间上的最小组成单位[21]，且城市内部各城镇建设用地斑块的空间结构并不相同，具有空间异质性特征[22]。传统以元胞尺度展开的城镇建设用地扩展模拟，以元胞为最小单元进行分析，而斑块位于元胞层级之上，故应考虑二者之间的分层驱动机制。因此，探究城镇建设用地元胞与斑块层面的分层驱动机制，对模拟城镇建设用地的扩展具有重要意义。
近些年对于土地利用斑块层面的研究广泛应用于地理学各个方面。在城镇建设用地扩展特征驱动机制方面，研究斑块几何分形特征的时空演变规律[23]；在城镇建设用地扩展模拟方面，现有研究利用矢量元胞自动机刻画不规则的城市空间表达，包括基于人口普查区块[24]、城市道路分割[25]、地籍调查定义[26]等的矢量元胞自动机构建。但上述研究忽略了城镇建设用地斑块之间的相互关系，欠缺对城镇建设用地自身空间网络结构的考虑，而通过分析城镇建设用地斑块的空间网络结构特征，能够捕捉城市扩展的空间维度、结构或模式[27]。空间网络模型现广泛应用于构建城市群复杂空间网络模型并识别出城市群的不同区域[28]等地理研究中，能够很好地揭示城市内部的城镇建设用地斑块的空间特征，体现了空间网络模型在解决地理问题上的优势。在城市化发展研究中，城镇建设用地的分布也具有特定的网络结构，因此，顾及城镇建设用地空间网络结构特征的城镇用地扩展模拟是科学合理的。
鉴于此，本文耦合空间网络模型和能够实现分层驱动机制的分层广义线性-元胞自动机（Hierarchical Generalized Linear-Cellular Automata, HGLM-CA）模型[29]，构建了空间网络-分层广义线性-元胞自动机（SN-HGLM-CA）模型，将元胞和斑块的空间特征分层级作用于城镇建设用地的变化模拟中。以上海市大都市圈为例，首先运用空间网络模型识别2000—2020年的城镇建设用地网络结构，进而构建空间网络-分层广义线性-元胞自动机模型（SN-HGLM-CA），模拟2015—2020年城镇建设用地扩展，可为上海大都市圈的国土空间规划提供理论依据，并对分层级耦合元胞与斑块空间特征的城镇模拟提供实践证明。

2 研究方法

本文首先基于城镇建设用地斑块构建空间网络模型，得到斑块的空间重要性特征，进而分层级耦合元胞和斑块的空间特征构建SN-HGLM-CA模型，以上海大都市圈为例进行城镇建设用地扩展模拟，通过对比SN-HGLM-CA模型和Logistic-CA、SN-Logistic-CA、ANN-CA、SN-ANN-CA模型的模拟精度和景观指数来验证模型的有效性，技术路线图如图1所示。
图1 技术路线

Fig. 1 Technical framework

2.1 构建城镇建设用地空间网络模型

首先以城镇建设用地斑块的几何质心，作为空间网络的点，再基于Silverman经验法则[30]计算搜索半径，将质心与落在其搜索半径范围内的其它质心相连，作为空间网络的边，构建网络。根据质心的连结数目、面积和与其它质心相连的距离属性，依次计算度中心性、局部重要性、平均局部重要性指标。
搜索半径( S e a r c h R a d i u s)计算公式如下：
S e a r c h R a d i u s = 0.9 × m i n ( S D , 1 l n 2 × D m )
式中： D m是空间网络中每个斑块质心到平均中心的距离的中值，平均中心是由所有质心的x、y坐标平均值构造的点； n是研究区内城镇建设用地斑块的数量； SD是标准距离，表示斑块质心相对于平均中心的分散程度。
度中心性指一个节点在网络中拥有的联结数目，对于一个包含g个城镇建设用地斑块的研究区，斑块i的度中心性 C D N i是i与其它g-1个斑块的直接联系总数，表示为如式（2）[31]。节点度中心性越大，反映该城镇建设用地斑块对周围地区的辐射能力越强。
C D N i = ∑ j = 1 g x i j
局部重要性[32]综合考虑了互相连接的2个城镇建设用地斑块的距离和面积属性，能够表征城镇建设用地网络内部斑块间的空间联系强弱。
S = A i A j D i s i , j 2
式中： A i与 A j分别表示斑块i和斑块j的面积； D i s i , j表示上述斑块节点之间的欧氏距离。
平均局部重要性[32]由节点的度中心性和相连的所有边的局部重要性计算得到，用于衡量斑块在全局中的空间重要性。
M S i = ∑ j = 1 D i S i , j D i
式中： D i表示城镇建设用地斑块i的度中心性； S i , j表示与斑块i相连的第j条边的局部重要性。

2.2 SN-HGLM-CA模型

HGLM模型在使用前需计算变量间组内相关系数（Intraclass Correlation Coefficient, ICC），判断实验数据是否适合进行分层研究。一般来说， ICC<0.059时为低度组内相关，组间因素造成的影响可忽略不计；0.059≤ICC<0.138时为中度组内相关，不同群组的样本存在一定差异； ICC≥0.138时为高度组内相关，组间差异不能忽视。本文采用HGLM模型将描述元胞特征的驱动因子置于较低层级（level 1），描述城镇建设用地斑块空间网络结构特征的土地空间重要性自变量置于较高层级（level 2），通过SN-HGLM模型计算得到驱动因子权重系数，公式如下：
level 1：
P S i j y i j = 1 = φ i j
l o g φ i j 1 - φ i j = η i j
η i j = β 0 j + ∑ n = 1 k β n j X n i j
level 2：
β 0 j = γ 00 + γ 0 W j + μ 0 j
β n j = γ n 0 + γ n W j + μ n j
式中： P S i j y i j = 1为元胞转变为城市用地的适宜性； η i j为描述元胞状态转变的向量； X n i j为元胞层（level 1）中位于斑块j的元胞i的第n个驱动因子； k为元胞层中驱动因子的个数； β 0 j为截距； β n j为 X n i j的回归系数； W m j为斑块层（level 2）中斑块j的空间重要性值； γ 00、 γ n 0分别为 β 0 j与 β n j的截距； γ 0 m、 γ n m为 W m j的回归系数； μ 0 j、 μ n j为残差项。
CA的基本架构一般包括五个部分，常被称为CA的五元组，即元胞与元胞空间、元胞状态、邻域、时间、转换规则，为进行模型精度的比较，暂不考虑随机效应的影响[33]，因此非城市元胞转换为城市元胞的概率可以表示为：
P i t = S i × N i t × Z i
式中：t表示模拟过程在第t次迭代中，t = 1,2,…； P i t为元胞i在第t次迭代时变为城市元胞的概率； S i为元胞i的适宜性概率，表征了空间驱动因素对元胞转换概率的影响，由HGLM模型对驱动因子的分析计算得到； N i t为元胞i在第t次迭代时接收到的邻域效应； Z i为约束条件对元胞i的影响。
在元胞自动机模型邻域大小的选择中， 3 × 3、 5 × 5、 7 × 7均是常用的邻域大小[34]，故本文使用最小的 3 × 3摩尔邻域进行研究。将水域设置为约束条件，并设定转换阈值，通过概率与阈值的比较，判断元胞状态是否发生改变。选取对应迭代个数的元胞概率为转换阈值 P t h r e d，判断元胞状态是否发生改变。元胞在下一时刻的状态 S i j t + 1为：
S i j t + 1 = 1 , P ≥ P t h r e d 0 , P < P t h r e d

2.3 模型评价方法

本文从空间对比分析和指标计算两方面对模拟结果进行对比分析。空间对比分析即在研究区全局范围内均匀选取特征明显的局部区域，进行模拟形态的对比；指标计算方面根据已有研究选取了下列8个具有代表性的指标，包括3个精度评价指标和5个景观指数指标。精度评价指标为：总体精度（Overall Accuracy, OA）、卡帕系数（Kappa）和品质因数（Figure of Merit，FoM），前2个指标从模式层次进行度量，FoM值从元胞层次进行度量[35]。以上精度评价指标的值均为0~1，且值越大代表模拟的精度越高。景观指数指标为：斑块个数（Number of Patches, NP）、平均周长面积比(Mean Perimeter-Area Ratio, PARA)、平均欧氏最近邻距离(Mean Euclidean Nearest-Neighbor Distance, ENN)、最大斑块指数（Largest patch index, LPI）和基于上述景观指数的组合，用于评估实际和模拟土地利用模式之间景观相似性的景观相似度指数 a I[36]。NP用于反映城镇建设用地斑块的破碎程度[37]， PARA即每个斑块周长与面积比值的平均值； ENN即为斑块质心之间的最近邻欧氏距离。LPI可表征主要城镇建设用地斑块的优势度。景观相似度 a I定义为上述景观指数的平均差异：
∆ I i = I i , s I i , o I i , o
a I = 1 - 1 n ∑ n i ∆ I i
式中： I i , s为模拟土地利用格局的第i个景观指数； I i , o为真实土地利用格局的第i个景观指数； ∆ I i为第i个景观指数的归一化差值；n代表景观指数的数量。

3 研究区概况与数据来源

3.1 研究区概况

上海大都市圈包括上海、无锡、常州、苏州、南通、宁波、湖州、嘉兴、舟山在内的9个城市（图2），涵盖了长江三角洲城市群的核心城市，经济发展迅速，城市化水平高。挖掘上海大都市圈的城镇建设用地分布规律和扩展模式，是助力该地区未来城市规划建设的重要举措。
图2 上海大都市圈城镇用地扩展

Fig. 2 Urban expansion in Shanghai metropolitan area

3.2 数据来源及处理

本文所使用行政区划矢量数据和土地利用栅格数据均来源于中国科学院资源环境科学数据中心（http://www.resdc.cn），分辨率为30 m×30 m，为提高模型计算效率，均重采样至60 m×60 m分辨率。土地利用数据包括2000、2005、2010、2015、2020年5期数据， 5期数据均用于城镇建设用地空间网络模型的时空演变特征分析，2015年和2020年2期数据重分类为建设用地、水域、其他用地3类，用于城镇建设用地的模拟。从地形地貌、道路交通、社会经济多个方面共选取12个2015年的驱动因子用于城镇建设用地的模拟，包括高程数据、道路数据、市县中心点数据、GDP公里格网数据、POP公里格网数据[17-18]，上述驱动因子数据统一进行归一化处理，使各变量取值区间位于0-1。详细信息如表1和图3所示。
表1 驱动因子数据信息

Tab. 1 Spatial variable factor data information

分类 驱动因子含义 数据来源 时间/年 原始数据值范围 数据预处理
地形地貌 海拔高度/m 中国科学院资源环境科学数据中心 2015 -76.96~1 548.99 归一化
坡度/° 2015 0~65.34 重采样、归一化
道路交通 距铁路距离/m Openstreetmap 2015 0~89 511.10 欧氏距离、归一化
距高速公路距离/m 2015 0~91 105.50 欧氏距离、归一化
距城市主干道距离/m 2015 0~92426.80 欧氏距离、归一化
距城市次干道距离/m 2015 0~70 250.10 欧氏距离、归一化
距城市支路距离/m 2015 0~41 121.00 欧氏距离、归一化
距高架快速路距离/m 2015 0~79 939.20 欧氏距离、归一化
距市中心距离/m 2015 0~125 522.00 欧氏距离、归一化
距区县中心距离/m 2015 0~77 802.20 欧氏距离、归一化
社会经济 公里格网GDP/万元/km2 中国科学院资源环境科学
数据中心		 2015 780.81~2 069 174.62 重采样、归一化
公里格网POP/人/km2 2015 151.80 ~ 41 863.10 重采样、归一化
图3 驱动因子示意

Fig. 3 Schematic diagram of spatial variable factors

为了检查并排除数据的多重共线性，采用SPSS软件对驱动因子数据进行方差膨胀因子(VIF)检验，一般认为当VIF>10时，模型存在多重共线性[38]，得到的结果如表2所示，VIF值均小于10，因此，本文选取的驱动因子之间不存在明显的多重共线性关系。
表2 驱动因子多重共线性检验

Tab. 2 Multicollinearity test list of driving factors

变量名称 VIF 变量名称 VIF
海拔高度 1.651 距城市支路距离 1.374
坡度 1.630 距高架快速路距离 2.311
距铁路距离 2.226 GDP 3.876
距高速公路距离 1.955 POP 3.809
距城市主干道距离 2.120 距市中心距离 1.908
距城市次干道距离 1.619 距区县中心距离 1.445

4 结果分析与讨论

4.1 城镇建设用地网络结构

通过构建城镇建设用地网络模型，得到其空间联系强度和空间重要性规律，提取上海大都市圈2000—2020年城镇建设用地的空间网络结构特征。

4.1.1 城镇建设用地空间联系强度

2000—2020年上海大都市圈内城镇建设用地面积保持稳定增加的现状，从2000年的2 404.56 km2增加至2020年的6 577.09 km2，共增加4 172.53 km2。本文构建的城镇建设用地网络模型中（表3），2000—2020年上海大都市圈的城镇建设用地斑块节点数逐渐减少，而搜索半径逐渐扩大；此外，网络模型的边数量由2000年的31 690条边减少至2020年的23 036条边，共减少8 654条边。由此说明上海大都市圈2000—2020年城镇建设用地面积扩张速度较快，且空间布局越发紧凑，破碎化的城镇建设用地斑块逐渐减少，整体呈现出相互连通、集聚发展的局势[39]。
表3 2000—2020年上海大都市圈城镇建设用地空间网络模型参数

Tab. 3 Parameters of urban land spatial network model in Shanghai metropolitan area from 2000 to 2020

年份 面积/km2 节点数/个 搜索半径/m 边数量/条
2000 2 404.56 861 22 720 31 690
2005 3 365.91 815 23 472 27 784
2010 5 343.97 746 25 693 26 382
2015 5 819.49 796 24 438 29 258
2020 6 577.09 700 25 531 23 036
由图4可见，2000—2020年上海大都市圈城镇建设用地的空间联系逐渐加强，具体表现在2个方面：① 空间联系强度的最大值在逐渐增大； ② 空间联系强度值在全局范围内出现大幅增长。其中，2000年空间联系较强的城镇建设用地斑块主要分布在上海浦西一带、常州东北部、无锡北部等地区。城市化加强了上述地区的空间联系强度和对周边地区的辐射，嘉兴北部、宁波北部、无锡东部、苏州中部、舟山南部等地区城镇建设用地的空间联系强度逐渐提升，至2020年上海大都市圈地区的城镇建设用地斑块紧凑度高，空间联系强度大。由此表明上海大都市圈的建设对于9个城市的协同发展有明显的促进作用，加强了城市之间的联系度，构建了城市之间的紧密传导机制，推进区域全面建设[40]。
图4 2000—2020年上海大都市圈城镇建设用地空间联系强度

Fig. 4 Spatial network structure of urban land in Shanghai metropolitan area from 2000 to 2020

4.1.2 城镇建设用地空间重要性

在城镇建设用地空间联系强度的基础上，综合考虑斑块的所有连接边的平均空间联系强度，衡量其空间重要性(图5）。上海大都市圈城镇建设用地的空间重要性在时间和空间上表现为两大特征：在时间尺度上，2000—2020年空间重要性逐步增长，具体表现为：空间重要性强的城镇建设用地斑块出现数量上的增加和面积上的扩展。此外，空间重要性强的斑块从2000年的零星、分散分布，至2020年出现了全局范围的集聚分布。在空间格局上，2000—2020年上海大都市圈中城镇建设用地空间重要性强的斑块主要分布在南通南部、常州东部、无锡北部、苏州北部、上海中部、嘉兴北部、宁波中部及湖州和舟山的部分地区，说明上海大都市圈的城市化日益发展为多中心的空间结构[41]。因此，应该不断提升核心城市的影响力范围和周边城市的联系强度，促进区域的整体发展[42]。城镇建设用地斑块的空间重要性刻画了不同斑块在全局范围内的重要性等级，将其置于城镇用地扩展模拟中，能够更好地顾及城镇建设用地的空间网络结构特征，进而提升模型的精度。
图5 2000—2020年上海大都市圈城镇建设用地空间重要性分布

Fig. 5 Spatial importance distribution of urban land in Shanghai metropolitan area 2000-2020

4.2 基于SN-HGLM-CA的城镇用地扩展模拟

4.2.1 分层驱动机制分析

构建SN-HGLM模型，计算得到的ICC= 0.525，为高度组内相关，组间差异不能忽视，因此采取分层分析。经过多次实验筛选解释变量与控制变量，最终确定驱动因子的层级结构为：坡度、距铁路距离、距高速公路距离、距城市主干道距离、距城市支路距离、距高架快速路距离为解释变量，其余空间因子变量为控制变量，不考虑空间重要性对其系数的影响。研究结果表明城镇建设用地斑块计算得到的空间重要性主要与地形和道路交通因子存在交互关系，与社会经济因子之间不存在明显的交互关系。此结果进一步说明了适宜的地形和完善的交通设施会有效促进城镇建设用地的分布，同时，建设用地也更容易用于交通设施的建设。得到变量参数识别结果如表4。
表4 SN-HGLM变量参数识别结果

Tab.4 Parameter identification of SN-HGLM

驱动因子 系数 P值 空间交互系数 空间交互P值
空间重要性 0.814 0.495 - -
坡度 -1.616 0.101 -7.942 0.032
距铁路距离 3.409 0.312 14.766 0.234
距高速距离 -0.734 0.835 8.048 0.515
距主干道距离 21.606 0.055 99.125 0.027
距支路距离 -0.501 0.903 22.805 0.108
距高架距离 3.910 0.312 -1.868 0.893
海拔高度 -1.472 0.000 - -
距次干道距离 -10.831 0.000 - -
距市中心距离 -1.352 0.000 - -
距区县中心距离 -5.620 0.000 - -
GDP -23.906 0.000 - -
POP 11.080 0.000 - -
结果显示，空间重要性与元胞状态转换为城镇建设用地的概率呈正相关，说明元胞所处的空间重要性越强，该元胞转换为城镇建设用地的概率越高。观察空间重要性对解释变量的分层驱动机制，空间重要性对距城市主干道距离的作用系数最大，说明空间重要性对距城市主干道距离的作用显著，其P值较小，说明距城市主干道距离和空间重要性对距城市主干道距离，对元胞转换为城镇建设用地的概率有显著影响。此外，空间重要性对坡度、距城市支路距离和据铁路距离的交互影响也较为显著。研究结果进一步证实了土地城镇化结构虽受经济、社会、政治、交通和自然等诸多因素的影响[43]，但交通基础设施在城镇建设用地的演变中起着至关重要的作用，被认为是一个重要的推动力这一论断[41]。因此，在进行城镇用地扩展研究中，建设用地斑块的空间异质性与其它因子之间的交互关系不容忽视，有必要在模拟中考虑各空间因子变量的分层驱动机制。

4.2.2 模拟结果分析和讨论

为检验SN-HGLM-CA模型的科学性，引入Logistic-CA、SN-Logistic-CA、ANN-CA和SN-ANN-CA模型对模拟结果进行对比分析。Logistic-CA模型由于其普及性和可扩展性被广泛用于模拟城市发展和土地利用变化。同时因其严格的统计学习理论基础和经验特征，成为城市CA的经典标定方法[44]。随着人工智能算法的快速发展，人工神经网络模型以其自组织、自学习、关联、记忆等功能有效简化了CA模型转换规则的获取，避免了主观因素，从而提高了仿真精度，因此ANN成为挖掘 CA 模型转换规则的一种有效的人工智能方法[45]。
对比5个模型的模拟精度（表5）可知，SN-HGLM-CA模型模拟精度优于SN-Logistic-CA模型，其中OA和Kappa值有小幅度提升，FoM值提升了约6.61%；与SN-ANN-CA模型的模拟结果对比，OA和Kappa值略低，FoM值略高。说明采用SN-HGLM-CA模型，考虑驱动因子的分层驱动机制，相较于线性回归的SN-Logistic-CA模型模拟精度更高，而人工智能算法的SN-ANN-CA模型在模拟上仍具有一定优势，整体精度更高。同时对比是否引入斑块层面空间网络结构的Logistic-CA和SN-Logistic-CA模型、以及ANN-CA和SN-ANN-CA模型发现，在这2种模型中引入斑块的空间特征对于精度的提升的不明显，这进一步证实了元胞和斑块层面的空间特征具有层级性，分层级耦合两者具有显著意义。
表5 2020年上海大都市圈城镇建设用地扩展模型精度对比

Tab. 5 Comparison of accuracy of urban land expansion models in Shanghai metropolitan area in 2020

Logistic-CA SN-Logistic-CA ANN-CA SN-ANN-CA SN-HGLM-CA
OA 0.983 4 0.983 4 0.984 1 0.984 3 0.984 0
Kappa 0.919 1 0.919 2 0.922 5 0.922 9 0.921 8
FoM 0.234 3 0.234 5 0.245 3 0.247 3 0.250 0
由于是否引入斑块空间特征的Logistic-CA和SN-Logistic-CA模型、以及ANN-CA和SN-ANN-CA模型的模拟精度差异并不明显，且本文旨在探究分层级耦合元胞和斑块尺度对于城镇建设用地扩展的优势，故在空间和景观指数的对比分析中，仅对比SN-Logistic-CA、SN-ANN-CA和SN-HGLM-CA模型。为直观地展示3个模型模拟结果在空间上的异同，同时在研究区范围内均匀选取了5个典型的局部区域，将3个模拟结果与2020年上海大都市圈的实际城镇用地扩展情况进行比较（图6）。观察区域a的模拟结果，对于集中连片的边缘式扩展，SN-Logistic-CA模型不能合理的控制扩展范围，出现了盲目扩展的情况，而SN-ANN-CA模型未能捕捉到边缘扩展的细节，SN-HGLM-CA模型能够较好的实现大区域的边缘式扩展模拟，与实际城镇建设用地的填充形态更为接近。观察区域b的模拟结果，SN-Logistic-CA和SN-ANN-CA模型不能有效捕捉到小面积斑块边缘的局部扩展，SN-HGLM-CA模型表现出更好的效果。观察区域c的模拟结果，对于整个斑块的外延式扩展模拟， SN-Logistic-CA和SN-ANN-CA模型容易出现过度扩展的情况，SN-HGLM-CA模型能够捕捉到更多细节信息。观察区域d的模拟结果，对于斑块内部的填充式扩展， SN-Logistic-CA和SN-ANN-CA模型模拟结果较为粗糙，笼统的将斑块内部全部填充， SN-HGLM-CA模型的模拟结果更加准确。观察区域e的模拟结果，对于城市飞地的模拟，相比于其它几种模型， SN-HGLM-CA模型对于相应区域扩展的元胞数量的预测有明显优势。
图6 模拟结果与实际的局部对比

Fig. 6 Local comparison between the simulated results and reality

在景观指数方面，本文共选取NP、PARA、ENN、LPI、 a I 5个指标进行对比（表6），对比模拟结果的城镇建设用地景观指数发现，3种模型得到的模拟结果与2020年实际的城镇建设用地相比，景观相似度均在95%以上，说明3种模型在模拟城镇建设用地斑块的景观特征时表现良好，其中SN-ANN-CA和SN-HGLM-CA的景观相似度高于SN-Logistic-CA，虽然SN-ANN-CA模型的景观相似度更高，但是ANN黑盒模型，不能揭示城镇建设用地扩展的驱动机制，而 SN-HGLM-CA模型能够解释驱动机制。景观指数的结果显示：① SN-HGLM-CA模型与SN-ANN-CA模型得到的城镇斑块数量小于SN-Logistic-CA模型，说明SN-HGLM-CA模型在景观破碎程度上的模拟效果与SN-ANN-CA模型一致，优于SN-Logistic-CA模型； ② PARA值均与真实值较为接近，其中SN-HGLM-CA模型的PARA值最小，说明其模拟的斑块形状更为紧凑，有助于城市规划建设的实施； ③ SN-HGLM-CA模型得到的ENN值与真实值最为接近，说明SN-HGLM-CA模型最大程度地还原了各斑块之间的分布结构； ④ LPI值均大于真实值，说明模拟得到的斑块布局更加紧凑。
表6 2020年上海大都市圈城镇建设用地模拟景观指数对比

Tab. 6 Comparison of landscape index of urban land expansion models in Shanghai metropolitan area in 2020

NP PARA ENN LPI a I/%
真实值 661 127.662 3 1 514.147 8 1.593 1 -
SN-Logistic-CA 686 130.249 7 1 384.005 2 1.652 7 95.46
SN-ANN-CA 675 122.478 7 1 420.680 5 1.621 6 96.46
SN-HGLM-CA 675 115.975 3 1 463.112 8 1.626 7 95.81
总体而言，本文构建的SN-HGLM-CA模型分层级耦合了元胞和斑块尺度的空间特征，相较于上述其它模型模拟精度更高。在景观形态上，得到的城镇斑块形状更加规整和紧凑，说明考虑驱动因素的层级关系，能够在一定程度上提高CA模型的模拟精度景观布局优势。因此，通过分析不同层级驱动因素与城镇用地扩展的相关关系，以及高层因素对低层因素的调节作用，便于解释城镇用地扩展机制，提高模型的模拟效果。

5 结论与展望

现阶段进行土地利用模拟时选取的空间变量因子数据大多涉及到自然地理环境、社会经济发展、人类活动各个方面，但已有研究较少关注城镇建设用地斑块的空间异质性特征对城镇用地扩展的影响。本文以上海大都市圈为例，构建SN-HGLM-CA模型顾及城镇建设用地斑块的空间异质性特征，并考虑驱动因子之间的层级关系，完成了城镇用地扩展的模拟，并与Logistic-CA、SN-Logistic-CA、ANN-CA、SN-ANN-CA模型对比模拟结果。本文将城镇建设用地斑块的空间异质性特征纳入驱动因素中，构建了基于分层回归方法的SN-HGLM-CA模型，实现了顾及斑块空间异质性的城镇用地扩展模拟。从城镇建设用地的空间网络结构特征中挖掘城镇扩展的规律，能够帮助政府决策者和规划者在城市规划中，在兼顾城镇建设用地发展现状的基础上分析现有趋势是否合理，是否需要对现有趋势加以改变，为城镇开发边界的划定提供参考依据，对于生态和农业空间保护具有重要意义。将城镇建设用地扩展模拟与景观指数评价结合起来，建立土地利用规划评价方法，为优化城镇建设用地扩展和布局提供科学支撑，具有一定的理论意义和实用价值。得出的主要结论如下：
（1）基于城镇建设用地斑块构建空间网络模型，能够识别研究区内斑块的空间重要性特征，挖掘城镇建设用地扩展的规律。
（2）分层回归模型相比于ANN模型能够揭示城镇建设用地扩展的驱动机制，同时相较于逻辑回归模型能够顾及变量间的层级性特征，有效剖析城镇建设用地扩展的分层驱动机制，在城镇建设用地扩展模拟中分层耦合了元胞和斑块的空间特征，在一定程度上提升了模型的可解释性和科学性。
（3）基于SN-HGLM-CA模型顾及城镇建设用地斑块空间异质性层级关系的城镇用地扩展模拟，在模拟精度和景观形态上均取得了良好效果，相较于SN-Logistic-CA模型，FoM值提高了约6.61%，但整体精度仍略低于SN-ANN-CA模型；在景观格局方面，斑块数量和景观形状指数均为最小，说明模拟得到的城镇斑块布局更加紧凑，且形状更加规整。因此，与Logistic-CA、SN-Logistic-CA、ANN-CA和SN-ANN-CA模型相比，所构建的SN-HGLM-CA模型能够获得最佳的模拟结果。
本文构建的SN-HGLM-CA模型，在分层级耦合元胞和斑块空间特征的城镇建设用地扩展模拟时虽然具有优良的效果，但仍存在以下议题需要进一步研究：① 土地斑块的空间分布结构具有高度复杂性和不规律性，可以进一步丰富提取其空间异质性特征的计算指标，如考虑使用道路距离代替欧氏距离； ② 该模型属于线性模型，虽然能够解析城镇用地扩展的驱动机制，但无法像学习模型那样捕捉城镇用地扩展的非线性特征，如何保留机制模型“简单”的优势，同时兼具学习模型非线性的特点，将成为下一步工作的重点。

References

Publishing order | Descend order by publishing year | Descend order by cited within
[1]
刘新智, 周韩梅. 土地资源配置如何影响城市经济效率——基于中国286个地级以上城市工业数据的实证检验[J]. 中国土地科学, 2022, 36(9):49-58.

[Liu X Z, Zhou H M. How does land resource allocation affect urban economic efficiency: An empirical test based on industrial data of 286 cities above prefecture level in China[J]. China Land Science, 2022, 36(9):49-58.] DOI:10.11994/zgtdkx.20220721.103159

DOI

[2]
陈理庭, 蔡海生, 张婷, 等. 基于Markov-FLUS模型的饶河流域土地利用多情景模拟分析[J]. 生态学报, 2022, 42(10):3947-3958.

[Chen L T, Cai H S, Zhang T, et al. Land use multi-scenario simulation analysis of Rao River Basin based on Markov-FLUS model[J]. Acta Ecologica Sinica, 2022, 42(10):3947-3958.] DOI:10.5846/stxb202106271705

[3]
郭远智, 李许红. 基于随机森林模型的黄河流域城市建设用地结构时空演化及其驱动机制研究[J]. 地理科学进展, 2023, 42(1):12-26.

DOI

[Guo Y Z, Li X H. Spatiotemporal changes of urban construction land structure and driving mechanism in the Yellow River Basin based on random forest model[J]. Progress in Geography, 2023, 42(1):12-26.]

DOI

[4]
刘小平. “土地利用模拟”专栏导言[J]. 地球信息科学学报, 2020, 22(3):516.

[Liu X P. Introduction to the column "land use simulation"[J]. Journal of Geo-information Science, 2020, 22(3):516.]

[5]
冯一凡, 李翅, 李宇, 等. 黄河下游滩区周边城镇空间扩展特征与驱动机制[J]. 地理研究, 2023, 42(4):955-976.

DOI

[Feng Y F, Li C, Li Y, et al. Characteristics of urban land expansion and its mechanism of cities and towns around the floodplain of the Lower Yellow River[J]. Geographical Research, 2023, 42(4):955-976.]

DOI

[6]
李丹, 胡国华, 黎夏, 等. 耦合地理模拟与优化的城镇开发边界划定[J]. 中国土地科学, 2020, 34(5):104-114.

[Li D, Hu G H, Li X, et al. Delineating Urban Development Boundaries (UDBs) by coupling geographical simulation and spatial optimization[J]. China Land Science, 2020, 34(5):104-114.] DOI:10.11994/zgtdkx.20200514.124053

DOI

[7]
卞子浩, 马小雪, 龚来存, 等. 不同非空间模拟方法下CLUE-S模型土地利用预测——以秦淮河流域为例[J]. 地理科学, 2017, 37(2):252-258.

DOI

[Bian Z H, Ma X X, Gong L C, et al. Land use prediction based on CLUE-S model under different non-spatial simulation methods: A case study of the Qinhuai River watershed[J]. Scientia Geographica Sinica, 2017, 37(2):252-258.] DOI:10.13249/j.cnki.sgs.2017.02.011

DOI

[8]
田贺, 梁迅, 黎夏. 基于SD模型的中国2010―2050年土地利用变化情景模拟[J]. 热带地理, 2017, 37(4):547-561.

DOI

[Tian H, Liang X, Li X, et al. Simulating multiple land use scenarios in China during 2010-2050 based on system dynamic model[J]. Tropical Geography, 2017, 37(4):547-561.] DOI:10.13284/j.cnki.rddl.002939

DOI

[9]
王海军, 夏畅, 张安琪, 等. 基于约束性CA的大都市郊区城镇增长的情景模拟与管控——以武汉市江夏区为例[J]. 地理科学进展, 2016, 35(7):793-805.

DOI

[Wang H J, Xia C, Zhang A Q, et al. Scenario simulation and control of metropolitan outskirts urban growth based on constrained CA: A case study of Jiangxia District of Wuhan City[J]. Progress in Geography, 2016, 35(7):793-805.]

[10]
Zhang B, Hu S G, Wang H J, et al. A size-adaptive strategy to characterize spatially heterogeneous neighborhood effects in cellular automata simulation of urban growth[J]. Landscape and Urban Planning, 2023, 229:104604. DOI:10.1016/j.landurbplan.2022.104604.

DOI

[11]
吴佩君, 刘小平, 黎夏, 等. 基于InVEST模型和元胞自动机的城市扩张对陆地生态系统碳储量影响评估——以广东省为例[J]. 地理与地理信息科学, 2016, 32(5):22-28,36,2.

[Wu P J, Liu X P, Li X, et al. Impact of urban expansion on carbon storage in terrestrial ecosystems based on InVEST model and CA: A case study of Guangdong Province, China[J]. Geography and Geo-Information Science, 2016, 32(5):22-28,36,2.] DOI:10.3969/j.issn.1672-0504.2016.05.004

DOI

[12]
罗紫薇, 胡希军, 韦宝婧. 基于多准则CA-Markov模型的城市景观格局演变与预测——以上杭县城区为例[J]. 经济地理, 2020, 40(10):58-66.

[Luo Z W, Hu X J, Wei B J, et al. Urban landscape pattern evolution and prediction based on multi-criteria CA-markov model:Take Shanghang County as an example[J]. Economic Geography, 2020, 40(10):58-66.] DOI:10.15957/j.cnki.jjdl.2020.10.007

DOI

[13]
Cao Y, Zhang X L, Fu Y, et al. Urban spatial growth modeling using logistic regression and cellular automata: A case study of Hangzhou[J]. Ecological indicators, 2020, 113:106200. DOI:10.1016/j.ecolind.2020.106200

DOI

[14]
刘荣增, 陆文涛, 杜力卿. 基于ANN-CA模型的郑州城市空间拓展研究[J]. 城市发展研究, 2019, 26(12):77-85,49.

[Liu R Z, Lu W T, Du L Q. Study on the space expansion of Zhengzhou based on the ANN-CA model[J]. Urban Development Studies, 2019, 26(12):77-85,49.]

[15]
Liu X P, Liang X, Li X, et al. A future land use simulation model (FLUS) for simulating multiple land use scenarios by coupling human and natural effects[J]. Landscape and Urban Planning, 2017, 168:94-116. DOI:10.1016/j.landurbplan.2017.09.019

DOI

[16]
Verburg P H, Overmars K P. Combining top-down and bottom-up dynamics in land use modeling: Exploring the future of abandoned farmlands in Europe with the Dyna-CLUE model[J]. Landscape Ecology, 2009, 24(9):1167-1181. DOI:10.1007/s10980-009-9355-7

DOI

[17]
Ke X L, Qi L Y, Zeng C. A partitioned and asynchronous cellular automata model for urban growth simulation[J]. International Journal of Geographical Information Science, 2016, 30(4):637-659. DOI:10.1080/13658816.2015.1084510

DOI

[18]
Feng Y L, Qi Y. Modeling patterns of land use in Chinese cities using an integrated cellular automata model[J]. ISPRS International Journal of Geo-Information, 2018, 7(10):403. DOI:10.3390/ijgi7100403

DOI

[19]
王海军, 武悦, 邓羽, 等. 基于城市流和层级性的城市群扩展模型构建[J]. 地理学报, 2021, 76(12):3012-3024.

DOI

[Wang H J, Wu Y, Deng Y, et al. Model construction of urban agglomeration expansion simulation considering urban flow and hierarchical characteristics[J]. Acta Geographica Sinica, 2021, 76(12):3012-3024.]

DOI

[20]
Shu B R, Zhu S H, Qu Y, et al. Modelling multi-regional urban growth with multilevel logistic cellular automata[J]. Comput Environ Urban Syst, 2020, 80:101457. DOI: 10.1016/j.compenvurbsys.2019.101457

DOI

[21]
郭旭东, 谢俊奇, 何挺. 基于斑块层次的土地利用变化对土地质量影响的初步分析——以河北省张北县为例[J]. 地理科学进展, 2006, 25(3):116-127,140.

[Guo X D, Xie J Q, He T. The effects of land use change on land quality at patch scale—a case study in Zhangbei County, Hebei Province[J]. Progress in Geography, 2006, 25(3):116-127,140.]

[22]
Luo J, Dennis Wei Y H. Modeling spatial variations of urban growth patterns in Chinese cities: The case of Nanjing[J]. Landscape and Urban Planning, 2009, 91(2):51-64. DOI:10.1016/j.landurbplan.2008.11.010

DOI

[23]
王海军, 张彬, 刘耀林, 等. 基于重心-GTWR模型的京津冀城市群城镇扩展格局与驱动力多维解析[J]. 地理学报, 2018, 73(6):1076-1092.

DOI

[Wang H J, Zhang B, Liu Y L, et al. Multi-dimensional analysis of urban expansion patterns and their driving forces based on the center of gravity-GTWR model: A case study of the Beijing-Tianjin-Hebei urban agglomeration[J]. Acta Geographica Sinica, 2018, 73(6):1076-1092.] DOI:10.11821/dlxb201806007

DOI

[24]
Norte Pinto N, Pais Antunes A. A cellular automata model based on irregular cells: Application to small urban areas[J]. Environment and Planning B: Planning and Design, 2010, 37(6):1095-1114. DOI:10.1068/b36033

DOI

[25]
Long Y, Shen Y, Jin X B. Mapping block-level urban areas for all Chinese cities[J]. Annals of the American Association of Geographers, 2016, 106(1):96-113. DOI:10.1080/00045608.2015.1095062

DOI

[26]
Benenson I, Omer I, Hatna E. Entity-based modeling of urban residential dynamics: The case of yaffo, tel aviv[J]. Environment and Planning B: Planning and Design, 2002, 29(4):491-512. DOI:10.1068/b1287

DOI

[27]
Taubenböck H, Wiesner M, Felbier A, et al. New dimensions of urban landscapes: The spatio-temporal evolution from a polynuclei area to a mega-region based on remote sensing data[J]. Applied Geography, 2014, 47:137-153. DOI:10.1016/j.apgeog.2013.12.002

DOI

[28]
Li S J, Guo H D, Sun Z C, et al. Patterns of typical Chinese urban agglomerations based on complex spatial network analysis[J]. Remote Sensing, 2023, 15(4):920. DOI: 10.3390/rs15040920

DOI

[29]
Lee Y, Nelder J A. Hierarchical generalized linear models[J]. Journal of the Royal Statistical Society: Series B (Methodological), 2018, 58(4):619-656.

DOI

[30]
Farokhi F. Deconvoluting kernel density estimation and regression for locally differentially private data[J]. Scientific Reports, 2020, 10:21361. DOI:10.1038/s41598-020-78323-0

DOI PMID

[31]
周俊, 凌昌隆. 长江中游城市群网络联系度与度中心性时序变化研究(2001—2016)[J]. 长江流域资源与环境,2021, 30(3):544-553.

[Zhou J, Ling C L. Study on temporal variations of network connectivity and degree centrality in the middle of the Yangtze River(2001-2016)[J]. Resources and Environment in the Yangtze Basin, 2021, 30(3):544-553.] DOI:10.11870/cjlyzyyhj202103003

DOI

[32]
刘涛, 陈忠, 陈晓荣. 复杂网络理论及其应用研究概述[J]. 系统工程, 2005, 23(6):1-7.

[Liu T, Chen Z, Chen X R. A brief review of complex networks and its application[J]. Systems Engineering, 2005(6):1-7.] DOI:10.3969/j.issn.1001-4098.2005.06.001

DOI

[33]
Wang H J, Guo J Q, Zhang B, et al. Simulating urban land growth by incorporating historical information into a cellular automata model[J]. Landscape and Urban Planning, 2021, 214:104168. DOI:10.1016/j.landurbplan.2021.104168

DOI

[34]
Zeng H R, Wang H J, Zhang B, et al. A methodology to quantify the neighborhood decay effect of urban cellular automata models[J]. International Journal of Geographical Information Science, 2023, 37(6):1236-1263. DOI:10.1080/13658816.2023.2186412

DOI

[35]
Pontius R G Jr, Boersma W, Castella J C, et al. Comparing the input, output, and validation maps for several models of land change[J]. The Annals of Regional Science, 2008, 42(1):11-37. DOI:10.1007/s00168-007-0138-2

DOI

[36]
Zhuang H M, Liu X P, Yan Y C, et al. Integrating a deep forest algorithm with vector-based cellular automata for urban land change simulation[J]. Transactions in GIS, 2022, 26(4):2056-2080. DOI:10.1111/tgis.12935

DOI

[37]
Wang H J, Zhang B, Xia C, et al. Using a maximum entropy model to optimize the stochastic component of urban cellular automata models[J]. International Journal of Geographical Information Science, 2020, 34(5):924-946. DOI: 10.1080/13658816.2019.1687898

DOI

[38]
李从欣, 张再生, 李国柱. 解决多重共线性的新思路:路径分析[J]. 统计与决策, 2013(1):28-30.

[Li C X, Zhang Z S, Li G Z. A new way to solve multicollinearity: Path analysis[J]. Statistics & Decision, 2013(1):28-30.] DOI:10.13546/j.cnki.tjyjc.2013.01.025

DOI

[39]
乔文怡, 黄贤金. 长三角城市群城镇用地扩展时空格局及驱动力解析[J]. 经济地理, 2021, 41(9):162-173.

[Qiao W Y, Huang X J. Patterns of urban land expansion and its driving forces in Yangtze River Delta urban agglomeration[J]. Economic Geography, 2021, 41(9):162-173.] DOI: 10.15957/j.cnki.jjdl.2021.09.017

DOI

[40]
熊健, 范宇, 张振广, 等. 区域协调与空间治理背景下的上海大都市圈空间协同规划编制创新探索[J]. 城市规划学刊, 2022(2):76-82.

[Xiong J, Fan Y, Zhang Z G, et al. Innovative collaborative spatial planning in Shanghai metropolitan area under the background of regional coordination and spatial governance[J]. Urban Planning Forum, 2022(2):76-82.] DOI:10.16361/j.upf.202202011

DOI

[41]
Meng M X, Shang Y P, Yang Y. Did highways cause the urban polycentric spatial structure in the Shanghai metropolitan area?[J]. Journal of Transport Geography, 2021, 92:103022. DOI:10.1016/j.jtrangeo.2021.103022

DOI

[42]
Xiao R, Lin M, Fei X F, et al. Exploring the interactive coercing relationship between urbanization and ecosystem service value in the Shanghai-Hangzhou Bay Metropolitan Region[J]. Journal of Cleaner Production, 2020, 253:119803. DOI:10.1016/j.jclepro.2019.119803

DOI

[43]
Duranton G, Puga D. Urban land use[M]//Handbook of Regional and Urban Economics. Amsterdam:Elsevier, 2015:467-560. DOI:10.1016/b978-0-444-59517-1.00008-8

DOI

[44]
Liao J F, Tang L N, Shao G F, et al. Incorporation of extended neighborhood mechanisms and its impact on urban land-use cellular automata simulations[J]. Environmental Modelling & Software, 2016, 75:163-175. DOI: 10.1016/j.envsoft.2015.10.014

DOI

[45]
Xu Q L, Wang Q, Liu J, et al. Simulation of land-use changes using the partitioned ANN-CA model and considering the influence of land-use change frequency[J]. ISPRS International Journal of Geo-information, 2021, 10(5):346. DOI:10.3390/ijgi10050346

DOI

Options
Outlines

/

〈 〉