EN中文

Journal of Geo-information Science >

2023 , Vol. 25 >Issue 12: 2329 - 2339

DOI: https://doi.org/10.12082/dqxxkx.2023.230236

A Method for Urban Rainstorm Cascading Disaster Scenario Converting Deduction by Integrating Multi-Source Spatial Data

  • LIU Zhaoge , 1, * ,
  • LI Xiangyang 2 ,
  • ZHU Xiaohan 3
Expand
  • 1. School of Public Affairs, Xiamen University, Xiamen 361005, China
  • 2. School of Management, Harbin Institute of Technology, Harbin 150001, China
  • 3. Administrative Committee of Wuhan East Lake High-tech Development Zone, Wuhan 430075, China
*LIU Zhaoge, E-mail:

Received date: 2023-04-28

  Revised date: 2023-06-16

  Online published: 2023-12-05

Supported by

Major Research Plan of the National Natural Science Foundation of China named Big data Driven Management and Decision-making Research(91746207)

General Program of the National Natural Science Foundation of China(71774043)

Humanities and Social Sciences Foundation of the Ministry of Education of China(22YJC630095)

Fold

Abstract

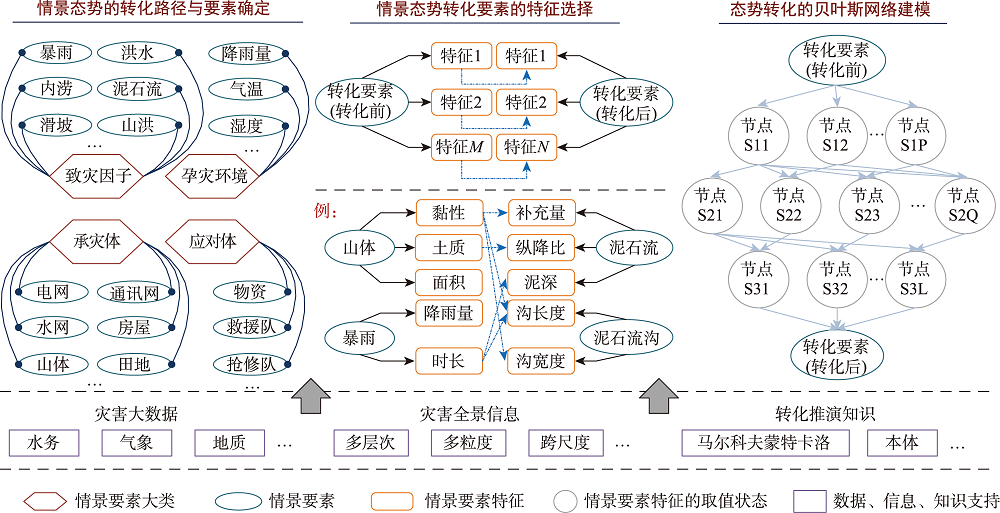
The converting evolution of cascading disaster scenario refers to that in the process of disaster scenario evolution, the disaster bearing bodies transform into new disaster hazards, forming a disaster chain. Rainstorm can easily cause serious secondary disasters such as waterlogging, debris flow and flood, and the combination of these secondary disasters will make the city more vulnerable. However, existing research on rainstorm cascading scenario deduction lacks the analysis of specific scenario evolution situations such as multi disaster combination, scenario element converting, and human-induced emergencies. Meanwhile, traditional research often relies on the probability inference based on existing scenario evolution networks, without providing a construction method for scenario evolution networks, making it difficult to adapt to the knowledge requirements of actual scenario situation converting deduction. To address the scenario converting evolution problems of urban rainstorm cascading disasters, this paper proposes a scenario converting deduction method for rainstorm cascading disaster response based on multi-source spatial data and probability analysis tools. First, based on local and non-local historical emergency cases, the scenario elements involved in the rainstorm cascading disaster scenarios and their potential converting paths are identified. Next, with the support of Baidu Encyclopedia and Wikipedia network knowledge resources, relevant scenario element features and their associations are extracted, and a Group Lasso machine learning method is adopted to achieve feature selection of involved scenario elements. Then, considering the multi-stage and complex scenario correlation in the process of cascading scenario evolution, a dynamic Bayesian network model for scenario converting deduction is constructed. Finally, a Markov chain Monte Carlo method is used to solve the Bayesian network and generate the converting probabilities. The proposed method is applied to the rainstorm response practice of Wuhan High-tech Zone. The use case results show that the proposed method can combine historical cases and network data to achieve rapid and effective generation of key scenario elements and their features, helping to improve the reliability of scenario converting deduction. At the same time, the proposed method supports the scenario converting deduction of small-scale disaster-bearing bodies such as geographic grids, which helps to provide more accurate rainstorm emergency decision-making support and provide good performance in visual analysis. The uncertainty analysis of the proposed method shows that the precision of original probabilities of key scenario element features and the size of generated geographic grids significantly affect the scenario converting deduction results. These findings provide important information for the local area and are expected to help the rainstorm disaster management of other jurisdictions.

Key words： urban rainstorms; cascading disaster; scenario deduction; scenario converting; spatial data; machine learning; historical cases; dynamic Bayesian network

Cite this article

LIU Zhaoge , LI Xiangyang , ZHU Xiaohan . A Method for Urban Rainstorm Cascading Disaster Scenario Converting Deduction by Integrating Multi-Source Spatial Data[J]. Journal of Geo-information Science, 2023 , 25(12) : 2329 -2339 . DOI: 10.12082/dqxxkx.2023.230236

1 引言

城市灾害应对因灾情不同而不同，即灾害情景应对存在一类情景依赖特性，如何有效认知灾害情景历来是灾害应急管理的基础问题[1]。城市级联灾害区别于一般灾害，多呈现多灾种组合、转化与人因诱发形态，造成后果的可能性更多而且难以把控、损失亦更大。近年来发生的暴雨灾害越来越 多地具有级联灾害的特征，典型的如2021年河南7·20暴雨引发内涝、滑坡和泥石流灾害，造成城市电网运行中断、地铁淹没、化工厂爆炸等严重、复杂多样的后果。级联灾害的情景推演是实现有效“情景-应对”模式的核心，以期能够准确、全面、深入地描述情景态势[2]。因此，本文重点关注暴雨级联灾害的情景态势推演问题。
在城市级联灾害情景态势演化过程中，存在另一种典型的级联灾害情景态势演化情形，即后序情景要素在变迁过程中发生类型改变，表现为承灾体在致灾因子作用下转化为新的致灾因子，形成灾害链。灾害情景要素转化是次生灾害产生的直接来源，是最能体现级联灾害特性的情景态势演化情形[3-4]。例如，在暴雨引发泥石流的过程中，山体由承灾体至致灾因子的转化；再如，在地震引发核泄漏的过程中，核电站由承灾体至致灾因子的转化。针对要素转化情况，情景态势转化推演是基于历史情景态势演化网络，根据前因情景要素与转化要素（转化前）因果关系、以及转化要素（转化前）与转化要素（转化后）因果关系，对情景要素转化的可能性大小进行判断，从而对衍生灾害情景态势进行预测[3]。级联灾害情景态势转化推演过程的实质是通过前因情景要素寻找转化要素及其变迁可能性的动态过程[5]。近年来，城市自然灾害情景态势推演由定性评估转向半定量或定量评估，利用历史灾情、自然地理、社会经济统计等数据进行建模，常用的建模方法有概率统计[6]、模糊数学[7]、基于信息扩散理论[8]、层次分析[9]、灰色系统[10]、人工神经网络[11]、加权综合评价[12]等。
上述研究在一定程度上推动了灾害情景态势推演的发展，但是研究中未对暴雨等级联灾害的情景态势转化推演与一般自然灾害的情景态势推演进行区分，缺少对多灾种组合、情景要素转化、人因诱发等具体情景演化情形的分析；同时，传统研究往往是在已有情景演化网络基础上的概率推断，并未提供情景演化网络的构建方法，难以适应实际情景态势转化推演的知识需求。另一方面，机器学习结合历史案例和网络数据能够较好地提供情景演化网络中的各项要素特征，在支持转化推演上具有可靠性，本文将以结合历史案例与机器学习方法确定暴雨情景态势演化网络的转化要素及其关键特征，为暴雨情景态势转化推演提供依据。此外，与传统研究相比，本文关注暴雨级联灾害背景下的情景态势转化推演过程，并将推演粒度进一步缩小，针对更细化的承灾体进行研究，以具体化灾害情景要素的描述特征，结果更加地精确；这也为分析暴雨情景态势的转化机理提供依据，可用于应急决策人员在事件发生或发生之前，迅速定位可能的衍生情景，为暴雨灾害预防和应对争取时间。

2 城市暴雨情景态势转化推演方法

本文主要针对暴雨灾害提出城市级联灾害的情景态势转化推演方法，包括情景态势的转化路径与转化要素确定、情景态势转化要素的特征选择以及情景态势转化的贝叶斯网络建模3个具体过程，其原理如图1所示。其中，情景要素转化是指承灾体要素（如城市中的山体）在特定致灾因子（如暴雨）作用下转化为新的致灾因子（如泥石流）的情况。此外，本文所提方法主要针对城市这一包含复杂情景要素的区域，其情景态势转化推演往往涉及多样化转化要素（包含致灾因子、承灾体、孕灾环境、应对体等）及关联特征。
图1 城市暴雨级联灾害的情景态势转化推演原理

Fig. 1 Scenario converting deduction theory of urban rainstorm cascading disasters

2.1 情景态势的转化路径与转化要素确定

情景态势转化推演应首选确定推演的对象，即需要推演的转化路径与转化要素是什么。转化路径确定情景态势转化推演的路线图，含有固定的情景要素，包括转化前的情景要素与转化后的情景要素。情景态势的转化演化具有地域差异性，明确本区域代表性的转化路径与转化要素既能节约推演成本，又能帮助决策者明确情景推演的关键点；另一方面，对潜在的、不甚显著的情景态势转化路径与转化要素，可根据历史案例结合数据分析生成。案例具有空间属性，即不同地域案例的指导意义是不同的，由此，将基于案例的转化路径确定分为基于本地案例的路径确定和基于异地案例的路径确定。
（1）基于本地案例的路径确定。应急管理人员在深入分析本地案例的基础上，结合本地应急管理工作的要求进行转化路径的确定。本地案例与现实情景在空间属性上具有统一性，由此确定的转化路径具有较高的借鉴价值。例如，本地有遭遇过暴雨引发泥石流的案例，应急管理人员经过研讨决定就该转化路径进行情景态势推演，由此启动了针对该类情景要素转化的推演决策。从管理实践角度出发，本地案例提供的转化路径再次出现的可能性较高，若应急准备工作未满足要求，将造成严重后果。在技术路线方面，本文主要关注承灾体要素（如山体）在特定致灾因子（如暴雨）作用下转化为新的致灾因子（如泥石流）的情况，根据本地历史案例记录确定承灾体要素转化前后的具体路径；若存在多个可能路径的情况，还可结合过程挖掘方法[13]进行路径网络模型构建。本文在进一步细化承灾体要素表达，将山体划分为若干地理网格，从而实现不同地理网格的转化推演，有助于更加精细化的应急决策。
（2）基于异地案例的路径确定。应急管理人员在深入分析异地案例的基础上，结合本地应急管理工作的要求进行转化路径的确定。部分异地案例与现实情景在空间属性上具有较高相似度，即便无法像本地案例具有完全统一的空间属性，仍需要以审慎的态度纳入本地的情景态势推演工作中。例如，本地管理人员在异地调研时发现其他区域发生过暴雨引发山体产生泥石流的情况，由此产生了极为严重的后果，可以考虑将这种情况纳入情景态势推演。在技术路线方面，可采用证据推理方法结合决策者经验确定异地经验在本地的适用度[14]，由此为本地转化路径的确定提供依据。

2.2 情景态势转化要素的特征选择

情景要素特征描述情景要素在各个时间节点的状态，情景要素的类型转化是当情景要素特征取值达到特定阈值时发生的。因此，转化推演的前提条件是明确情景要素特征间的复杂关联关系，这包括特征选择与特征关系建模两部分内容。本文通过网络知识挖掘，构造了情景要素特征关系的知识本体网络，再基于机器学习中的分组最小角回归模型[15]，根据选择的转化要素实现特征筛选。
根据选择的转化要素，设定关联模型及其展开模式分别如式（1）和式（2）所示。
y = X β + ε
y 1 y 2 . . . y N = x 11 x 12 . . . x 1 P x 21 x 22 . . . x 2 P . . . . . . . . . . . . x N 1 x N 2 . . . x N P β 1 β 2 . . . β P + ε 1 ε 2 . . . ε N
式中： X ∈ R N × P表示输入的特征取值矩阵（自变量），且所有特征取值均为实数； y ∈ R N表示输出的情景要素特征取值（因变量）； β ∈ R P代表各输入特征的权重系数； ε ∈ R N且 ε ~ N ( 0 , σ 2 I )为随机变量， I为单位向量；N为用于特征选择的案例或数据样本数， n ∈ { 1,2 , … , N }表示其中某个案例或样本；P为原始的输入特征数， p ∈ { 1,2 , … , P }表示其中某个特征。设定特征系数向量 β中的P个元素被划分为M个相互独立的组， G = { g m | m = 1,2 , … , M }， β = ⋃ g m， ∀ i ≠ j， g i ⋂ g j = ∅， d m表示组 g m包含的元素数， β m ∈ R d m表示叫做表示组 g m的子特征系数向量。在分组最小角回归中，特征选择的目标函数形式如下[13]。
β ^ = a r g m i n β ∈ R P 1 2 y - X β 2 2 + λ ∙ ∑ m = 1 M β m K m
式中： β m K m = β m T K m β m； λ ≥ 0；设 K m = n m I n m， I n m ∈ { 0,1 } n m × n m为单位矩阵。

2.3 情景态势转化的贝叶斯网络建模

经过转化要素确定与转化要素的特征选择之后，已经可以确定暴雨灾害情景要素转化过程中的各个变量，根据暴雨灾害案例将其划分为以下4类，这些变量构成了暴雨灾害转化的贝叶斯网络节点。
（1）时间戳t。在情景态势转化的不同时间节点，均应根据情景要素特征间关系，结合当时的特征取值确定输入变量、状态变量与输出变量。
（2）输入变量I。在建立贝叶斯模型时，将前述情景要素、情景要素特征及特征间关系输入，为驱动贝叶斯模型求解提供知识基础。
(3) 状态变量S。在级联灾害情景态势的转化推演中，状态变量是当前灾害情景态势的描述性信息，由全景模型结合知识本体获取，包括转化前情景要素c的特征取值，以及与要素转化相关的其他情景要素特征取值。
(4) 输出变量O。与状态变量相对应，特定时间节点的输出变量是指根据情景要素特征关系，结合状态变量确定的待生成/更新的情景信息，包括转化前情景要素c的特征值更新、其他相关要素特征值更新、以及与转化后情景要素s相关的情景要素特征取值。
在考虑时间变化时，应建立情景态势转化的动态贝叶斯网络（Dynamic Bayesian Network，DBN）[16]。设 G t * = < V t * , E t * >代表DBN，考虑的时间片段有 z>1个，其中的边为有向边，t*代表时间片段。其中， V t *和 E t *分别是时间片段t*的节点集合和有向边集合，则动态贝叶斯网络的迁移结构如下。
              E t * t r s = { ( a , b ) | a ∈ V t * - 1 , b ∈ V t * }         （ t ≤ t * ≤ t + z ）
情景态势的转化网络符合动态贝叶斯网络的一阶Markov假设，即各阶段贝叶斯网络分析的独立性。在此假设下，得到下式。
P ( G t * | G t * - 1 , G t * - 2 , … , G t ) = P ( G t * | G t * - 1 )
令动态贝叶斯网络 G = < V , E >，则有如下性质。
  V = V ( t , z ) = ∪ t * = t + 1 t + z V t *   E = E ( t , z ) = E t ∪ t * = t + 1 t + z E t * *
式中： E t * ⊂ V t * ⊗ V t *， E t * * = E t * ⋃ E t * t r s； ⊗表示集合的笛卡尔乘积。综合上述建模过程，级联灾害情景态势转化的贝叶斯网络如图2所示。其中，b(t)表示起始节点，时间片段为t； e(t+z)表示终止节点，时间片段为t+z； f1(t), f2(t), …, fn(t)表示转化过程中时间片段t涉及的情景要素特征。
图2 城市暴雨级联灾害情景态势转化的贝叶斯网络

Fig. 2 The Bayesian network of scenario converting of urban rainstorm cascading disasters

贝叶斯网络可以清晰地表明情景态势转化过程中情景要素特征取值状态之间的因果关系，这种因果关系具有很大的不确定性，转化方向也是不确定的，其方式主要有2种。设 F = { f 1 , f 2 , ⋯ ,   f n }为情景态势转化过程中涉及的情景要素特征集合，这些特征在时间片段t的取值状态集合为 F ( t ) = { f 1 ( t ) , f 2 ( t ) , ⋯ ,   f n ( t ) }，每个情景要素特征取值都有0和1两个状态，其中1代表情景要素特征取值达到设定状态，0代表情景要素特征取值未达到设定状态。将这些情景要素特征按前述规则划分为状态变量 F s ( t ) = { f s 1 ( t ) , f s 2 ( t ) , ⋯ ,   f s n ( t ) }与输出变量 F o ( t ) = { f o 1 ( t ) , f o 2 ( t ) , ⋯ ,   f o n ( t ) }， F ( t ) = F s ( t ) ⋃ F o ( t )， R F = F s ( t ) × F o ( t )为情景要素特征取值状态之间的关联关系，逻辑关系主要包括：“与”型和“或”型，具体描述符号如表1所示。
表1 情景要素特征取值关联关系的符号描述

Tab. 1 The description of symbols of the feature relationship among scenario elements

表示符号 关联关系说明
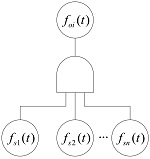“与”型：情景要素特征的输入变量 f s 1 ( t ) ,   f s 2 ( t ) ,   ⋯ ,   f s n ( t )在时间片段t均达到设定状态，输出变量 f o i ( t ) ∈ F o ( t )才能达到设定状态，即： { f s 1 ( t ) = 1         a n d     f s 2 ( t ) = 1       a n d . . .     a n d     f s n ( t ) = 1 } → f o i ( t ) = 1
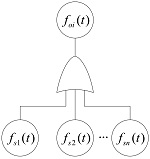“或”型：情景要素特征的输入变量 f s 1 ( t ) , f s 2 ( t ) , ⋯ , f s n ( t )在时间片段t至少有一个达到设定状态，输出变量 f o i ( t ) ∈ F o ( t )才能达到设定状态，即： { f s 1 ( t ) = 1         o r     f s 2 ( t ) = 1       o r . . .     o r     f s n ( t ) = 1 } → f o i ( t ) = 1

2.4 情景态势转化概率计算

假设 s ( i )为转化后情景要素s的特征 f i的取值状态，转化概率 p u即为 s ( i )发生的概率，用公式表示为 p u = p ( s ( i ) = t r u e )，而 s ( i )不是孤立存在的，其发生的概率取决于情景态势转化贝叶斯网络中各时刻的相关情景。假设相关的前因情景要素特征集为F，共有 n个相关情景要素特征，即 F = { f 1 , f 2 , ⋯ , f n }，这些情景要素的特征取值是随时间变化的，设定情景特征 f i在时刻 t的取值状态为 f i ( t )， F ( t )是情景要素特征集中各情景要素特征 f i ( t )在t时刻取值状态的集合。由于自然级联灾害发展的过程是不可逆的，且 t + 1时刻的情景状态仅依赖于 t时刻的情景状态，符合马尔可夫模型[17-18]，因此， s ( i )在 t + 1时刻的概率分布仅与F在 t时刻的状态有关，表示为：
p ( s ( i ) ( t + 1 ) | F ( 0 ) , F ( 1 ) , ⋯ , F ( t ) ) = p ( s ( i ) ( t + 1 ) | F ( t ) )
而 F ( t )属性状态又与 F ( t - 1 )属性状态相关，因此，转化概率计算是一个迭代的过程，针对建立的动态贝叶斯网络必须先定义先验概率和转移概率两部分：
（1）先验网络 B 0，表示自然灾害刚发生的初始状态 F ( 0 )的分布；
（2）转移网络 B →，表示每个时间t上的转移概率 p ( s ( i ) ( t + 1 ) | F ( t ) )。
事实上，自然级联灾害的演变过程有一定的时间范围，在有限的时间区间 [ 0 , ⋯ , T ]上， F i ( 0 )的父节点是先验网络 B 0，而 s ( i ) ( t + 1 )的父节点是时间片t的情景要素特征取值状态集，用类似的方法可求得这些变量的条件概率分布，进而确定等来计算情景 s ( i )的转化概率为：
p u = p ( s ( i ) ( t + 1 ) = t r u e ) = p ( F ( 0 ) ) ∏ t = 0 t p ( F ( t ) | F ( t - 1 ) )

3 用例分析

本文以2016年武汉暴雨灾害为用例，阐述本文所提情景态势转化推演方法的合理性。在推演开始前，在历史案例支持下梳理本地承灾体要素清单，确定了山体在暴雨作用下转化为泥石流这一典型的要素转化路径。用例分析使用的基础空间数据为：
（1）降雨资料，包括内涝期间的每小时降雨量观测值。
（2）地质数据。本文采用武汉市规划设计研究院提供的武汉高新区山体地质地图。
（3）地面高程数据，采用LocaSpace Viewer (LSV)下载的12 m精度DEM数据，涵盖高新区的 1 894个地理网格，为计算各地理网格山体高程差提供依据。
（4）地物遥感影像，通过谷歌地球截取武汉市东湖高新区的高清遥感影像图，影像级别为18级(分别率0.6 m)，提取其中的道路分布、湖泊、河流、绿地等数据，再结合武汉东湖高新区水务局提供的水系资料进行数据修正。地物数据用于根据情景推演情况确定灾害应对策略。
（5）情景要素特征数据，用于确定暴雨转化为泥石流过程中的关键情景要素特征及其特征关联关系，为构建贝叶斯网络提供依据。
用例分析使用数据的数据类型、数据量、数据来源等具体信息见表2。
表2 用例多源空间数据集

Tab. 2 Muti-source spatial datasets in use case

数据名称 数据描述 数据类型 数据量 数据来源
降雨数据 每小时降雨量观测值 数值 168条 武汉东湖高新区水务局
地质数据 山体边界 矢量 65条 武汉市规划设计研究院
山体面积、土质等地质属性 矢量 65条 武汉市规划设计研究院
地理数据 12 m数字高程模型(DEM) 栅格 518 km2 LocaSpaceViewer (LSV)
地物遥感影像 栅格 518 km2 谷歌地球
情景要素特征数据 暴雨转化为泥石流过程中的情景要素及其关联关系 文本 34 369条 百度百科
文本 14 118条 维基百科

注：表中数据的时间区间均为2016年武汉暴雨内涝期间，即2016-06-30—2016-07-06。

3.1 贝叶斯网络生成

根据转化路径，贝叶斯网络建模的核心情景要素为暴雨、山体和泥石流。情景态势转化推演开始阶段关注的情景要素为泥石流，即在2016年武汉暴雨情景下泥石流的发生位置与严重程度（主要指冲击力与流量）。因此，在进行情景要素的特征选择时，以泥石流的冲击力与流量为因变量，应用分组最小角回归方法训练数据样本。其中，数据样本的来源有百度百科和维基百科，来自百度百科的样本数为34 369条，来自维基百科的样本数为14 118条。经过训练，提炼与暴雨要素和山体要素相关自变量4个，分别为泥石流发生情况、泥石流流速、泥石流沟床纵降比、泥石流横截面泥深。再以上述4个变量为因变量，提炼与之相关的自变量，共生成固体物质补充量、山体高程差、山体面积和降雨量强度4个相关变量。其中，固体物质补充量、山体高程差和山体面积属于山体这一情景要素的特征，而降雨量强度属于暴雨情景要素的特征。再以上述变量为因变量，迭代上述过程，得到固体物质补充量的影响因素为山体土质以及降雨量强度；降雨量强度符合特定演化规律（如芝加哥雨型），即某时间片段的降雨量强度受上一时间片段的降雨量强度影响。
经过上述特征选择过程，可建立用例情景态势转化过程中的特征影响关系，构建相应的贝叶斯网络，如图3所示。其中，将各特征按统计数据各划分为2个取值状态，取值状态的分类规则如表3所示。
图3 用例情景态势转化的贝叶斯网络

Fig. 3 The Bayesian network of scenario converting evolution in use case

表3 情景要素特征取值状态分类规则

Tab. 3 The classification rules of feature values of scenario elements

情景要素 情景要素特征 特征取值状态 状态分类规则
暴雨 降雨量强度（f1） 降雨强 取值>100 mm
降雨弱 取值<100 mm
山体 固体物质补充量（f2） 补充量大 取值>104 m/km2
补充量小 取值<104 m/km2
山体高程差（f3） 坡度陡 取值>10 m(水平5 m)
坡度缓 取值<10 m(水平5 m)
山体面积（f4） 范围大 取值>10 km2
范围小 取值<10 km2
山体土质（f5） 酸性强 取值<5
酸性弱 取值>5
泥石流 泥石流发生情况（f6） 泥石流发生 取值=“1”
泥石流不发生 取值=“0”
流速（f7） 流速快 取值>5 m/s
流速慢 取值<5 m/s
沟床纵降比（f8） 纵降比大 取值>0.2
纵降比小 取值<0.2
横截面泥深（f9） 泥深高 取值>5 m
泥深低 取值<5 m
冲击力（f10） 冲击力强 取值>80 kPa
冲击力弱 取值<80 kPa
流量（f11） 流量大 取值>50 m3
流量小 取值<50 m3

3.2 贝叶斯网络求解

将上述贝叶斯网络划分为2个时间片段，分别为“暴雨影响山体”以及“山体形成泥石流”。根据马尔科夫链蒙特卡洛的方法，应用式（8），预测泥石流各特征的取值状态，求解上述贝叶斯网络。以固体物质补充量（f2）的取值状态预测为例，其概率计算如下（在用例中，降雨量强度被设定为“降雨强”，土质被设定为“酸性弱”）。此外，在未设定降雨量强度和土质状态的情况下，初始概率可根据历史统计数据获得。例如，根据高新区夏季历史暴雨情况绘制概率分布图[19]。
p ( f 2 = 1 ) = ∑ p ( f 2 = 1 | f 1 f 5 ) p ( f 1 f 5 )                                 = p ( f 2 = 1 | f 1 > 100 ,   f 5 < 5 ) p ( f 1 f 5 ) +                                         p ( f 2 = 1 | f 1 > 100 ,   f 5 > 5 )   p ( f 1 f 5 ) +                                         p ( f 2 = 1 | f 1 < 100 ,   f 5 < 5 ) p ( f 1 f 5 ) +                                         p ( f 2 = 1 | f 1 < 100 ,   f 5 > 5 ) p ( f 1 f 5 )                                 = 0.823 × 1 × 0 + 0.177 × 1 × 1 + 0.219 ×                                         0 × 0 + 0.781 × 0 × 1                                 = 0.177
p ( f 2 = 0 ) = ∑ p ( f 2 = 0 | f 1 f 5 ) p ( f 1 f 5 )                                   = p ( f 2 = 0 | f 1 > 100 ,   f 5 < 5 ) p ( f 1 f 5 ) +                                           p ( f 2 = 0 | f 1 > 100 ,   f 5 > 5 ) p ( f 1 f 5 ) +                                           p ( f 2 = 0 | f 1 < 100 , f 5 < 5 ) p ( f 1 f 5 ) +                                           p ( f 2 = 0 | f 1 < 100 , f 5 > 5 ) p ( f 1 f 5 )                                   = 0.177 × 1 × 0 + 0.823 × 1 × 1 + 0.781 ×                                           0 × 0 + 0.219 × 0 × 1                                   = 0.823
其他特征取值状态概率的计算类似，不再赘述。利用上述方法，可以根据山体的地质数据和暴雨情况生成情景态势转化概率，用以表征各山体的情景态势转化风险。

3.3 推演结果分析

通过改变暴雨重现期，可以观测不同降雨量强度下的情景转化概率，结果如图4所示。由图4可知，由暴雨引起泥石流的发生概率在研究区域范围内具有显著的空间分布差异，且在不同暴雨强度情景下，研究区域的泥石流发生概率随暴雨强度的增加而增加。具体而言，泥石流发生概率呈现出南高北低的特点，当暴雨强度为54 mm/h时，泥石流发生概率较低，最大发生概率为0.4。当暴雨强度增加到77 mm/h时，马鞍山南侧山体泥石流发生概率显著增大，最大发生概率达到0.65。当暴雨强度达到85 mm/h和96 mm/h时，泥石流发生概率进一步增大，最大发生概率分别为0.83、0.87，但影响范围仍主要集中于马鞍山中侧及南侧山体。当暴雨强度增大到96、123及136 mm/h，暴雨影响范围已涉及高新建成区北部所有山体，泥石流发生概率亦随之增大，最大发生概率分别为0.88、0.93和0.96。根据该区域的历史泥石流案例数据，东部、西部、南部、北部的泥石流发生数分别是12、6、19、2，计算结果与实际相符。同时，所得结果实现了更加细化的承灾体要素表达，能够直观反映各山体内部的转化概率分布，为应急决策提供了更加精细的信息支持。
图4 不同降雨量强度下山体转化泥石流的概率

注:本文研究区域为武汉东湖新技术开发区建成区;底图为路网、水系和山体分布图。

Fig. 4 The converting probabilities from mountains to debris flow under different rainfall intensity

3.4 推演结果不确定性分析

本文所提方法的推演精度预期受两方面因素影响：① 初始概率(本用例中包含降雨量强度和山体土质情况)，其影响后续概率计算与最终泥石流状态(包含泥石流冲击力和流量)概率；② 所选取地理网格的大小，其影响泥石流发生与状态分析的地理精度，从而影响相应的概率分析结果。在具体操作方面，从图4所示山体范围内随机选取10个样本点(地理网格)，改变初始概率与原始地理网格大小，观察其对最终概率分析结果的影响。其中，初始概率计算主要考虑降雨量强度估计的不确定性，以其作为代表进行分析；对最终结果的影响选取泥石流流量为指标。表4展示了改变初始概率和地理网格大小后的概率计算偏差情况。如表4所示，初始概率与地理网格的不确定性均对推演结果有显著影响，平均影响程度分别达到19%和17%。因此，在本方法的实际应用中，一方面应注意通过实时数据收集、历史案例统计等方式提升初始概率分析的准确性；另一方面，应尽可能提高地理网格的分析精度（本文用例中地理网格精度平均为70 m2），避免粗粒度计算对推演结果的负向影响。
表4 推演结果的不确定性分析

Tab. 4 Uncertainty analysis of the deduction results

样本序号 降雨量强度( f1 = 1)初始概率 地理网格大小
原始值 变更后 泥石流流量(f11 = 1)概率偏差 原始值/ m2 变更后 泥石流流量(f11 = 1)概率偏差
1 1 0.7 0.13 60 78 0.05
2 0 0.3 0.25 100 130 0.12
3 1 0.7 0.28 70 91 0.23
4 1 0.7 0.09 110 143 0.18
5 0 0.3 0.32 90 117 0.10
6 1 0.7 0.16 80 104 0.13
7 1 0.7 0.22 150 195 0.27
8 1 0.7 0.08 140 182 0.30
9 1 0.7 0.15 70 91 0.21
10 0 0.3 0.21 50 65 0.09
均值 - - 0.19 - - 0.17

4 结论与展望

考虑到城市级联灾害情景演化过程中的情景要素互转化，本文结合建模方法、动态贝叶斯网络和GIS空间分析技术提出一套城市暴雨级联灾害的情景态势转化推演框架。本文所述方法针对静态贝叶斯网络的不足，运用动态贝叶斯网络结合马尔科夫链蒙特卡洛方法计算情景态势的转化概率，分析情景态势的转化推演路径，为级联灾害预测、应对和决策提供支持；同时，该方法针对更小粒度的承灾体要素进行研究，实现了描述特征具体化，使得结果更加地精确；该方法利用分组最小角回归这一机器学习算法，基于历史案例和网络数据进行情景态势转化的特征提取和网络建模，在支持转化推演上具有可靠性。
本文以武汉东湖高新区建成区域为研究区域，对其2016年暴雨转化为泥石流的情景态势转化演化开展实证研究。计算结果显示：本文所述情景态势的转化推演方法能够较好地实现转化要素识别与路径预测，在可视化分析方面亦具有较好效果。具体而言，随着暴雨强度的增大，山体泥石流的发生概率不断增强，且泥石流发生概率呈现出南高北低的空间分布特点，模拟结果与历史相符，同时生成了不同地理网格的具体化要素转化概率情况。
进一步研究将关注3个方面的问题。① 探索洪水、内涝、泥石流等更多暴雨次生灾害组合发生的更复杂情景，集合多学科理论知识[20]，检验所提方法论的有效性，提炼有价值的结论，更好地服务于灾害“势”的预测； ② 受制于级联灾害案例和现实数据的可获得性，本文重点关注了特定要素转化路径（暴雨➝山体➝泥石流）的情景态势转化推演场景，对所提方法的有效性分析有赖进一步的数据支持。在未来研究中，应针对暴雨过程中的多样化承灾体要素及其转化路径，系统验证本文方法的有效性； ③ 拓展情景态势转化推演的应用场景，建立基于复杂情景演化的风险评估方法，为风险管理者提供更有针对性的决策支持。

References

Publishing order | Descend order by publishing year | Descend order by cited within
[1]
巴锐, 张宇栋, 刘奕, 等. 城市复杂灾害“三层四域”情景分析方法及应用[J]. 清华大学学报(自然科学版), 2022, 62(10):1579-1590.

[ Ba R, Zhang Y D, Liu Y, et al. “Three-layer and four-domain” scenario analysis method and its application to urban complex disasters[J]. Journal of Tsinghua University (Science and Technology), 2022, 62(10):1579-1590. ] DOI:10.16511/j.cnki.qhdxxb.2022.22.029

[2]
Qie Z J, Rong L L. A scenario modelling method for regional cascading disaster risk to support emergency decision making[J]. International Journal of Disaster Risk Reduction, 2022, 77:103102. DOI:10.1016/j.ijdrr.2022.103102

[3]
朱晓寒, 李向阳, 王诗莹. 自然灾害链情景态势组合推演方法[J]. 管理评论, 2016, 28(8):143-151.

[ Zhu X H, Li X Y, Wang S Y. Scenarios combination deduction method of natural disaster[J]. Management Review, 2016, 28(8):143-151. ] DOI:10.14120/j.cnki.cn11-5057/f.2016.08.018

[4]
郄子君, 荣莉莉. 面向灾害情景推演的区域模型构建方法研究[J]. 管理评论, 2020, 32(10):276-292.

[ Qie Z J, Rong L L. A construction method of hazard-affected region for disaster scenario evolution[J]. Management Review, 2020, 32(10):276-292. ] DOI:10.14120/j.cnki.cn11-5057/f.2020.10.022

[5]
饶文利, 罗年学. 台风风暴潮情景构建与时空推演[J]. 地球信息科学学报, 2020, 22(2):187-197.

DOI

[ Rao W L, Luo N X. Scenarios construction and spatial-temporal deduction of typhoon storm surge[J]. Journal of Geo-information Science, 2020, 22(2):187-197. ]

[6]
Korkmaz K A. Earthquake disaster risk assessment and evaluation for Turkey[J]. Environmental Geology, 2009, 57(2):307-320. DOI: 10.1007/s00254-008-1439-1

[7]
Liu M, Lo S M, Hu B Q, et al. On the use of fuzzy synthetic evaluation and optimal classification for computing fire risk ranking of buildings[J]. Neural Computing and Applications, 2009, 18(6):643-652. DOI:10.1007/s00521-009-0244-4

[8]
Liu X P, Zhang J Q, Cai W Y, et al. Information diffusion-based spatio-temporal risk analysis of grassland fire disaster in Northern China[J]. Knowledge-Based Systems, 2010, 23(1):53-60. DOI:10.1016/j.knosys.2009.07.002

[9]
Castellanos Abella E A, Van Westen C J. Generation of a landslide risk index map for Cuba using spatial multi-criteria evaluation[J]. Landslides, 2007, 4(4):311-325. DOI: 10.1007/s10346-007-0087-y

[10]
刘力丹, 朱权洁, 郑贵强, 等. 基于层次分析法和模糊综合评价法的洪涝灾害危险性评价[J]. 华北科技学院学报, 2022, 19(6):113-119.

[ Liu L D, Zhu Q J, Zheng G Q, et al. Risk assessment of flood hazard based on AHP and fuzzy comprehensive evaluation methods[J]. Journal of North China Institute of Science and Technology, 2022, 19(6):113-119. ] DOI:10.19956/j.cnki.ncist.2022.06.016

[11]
Wu J D, Li N, Yang H J, et al. Risk evaluation of heavy snow disasters using BP artificial neural network: The case of Xilingol in Inner Mongolia[J]. Stochastic Environmental Research and Risk Assessment, 2008, 22(6):719-725. DOI:10.1007/s00477-007-0181-7

[12]
Raaijmakers R, Krywkow J, van der Veen A. Flood risk perceptions and spatial multi-criteria analysis: An exploratory research for hazard mitigation[J]. Natural Hazards, 2008, 46(3):307-322. DOI: 10.1007/s11069-007-9189-z

[13]
刘聪, 李会玲, 曾庆田, 等. 跨组织业务流程模型挖掘与质量评估[J]. 计算机学报, 2023, 46(3):643-656.

[ Liu C, Li H L, Zeng Q T, et al. Discovery and evaluation of cross-organization business process models[J]. Chinese Journal of Computers, 2023, 46(3):643-656. ] DOI:10.11897/SP.J.1016.2023.00643

[14]
刘昭阁, 李向阳, 于峰. 案例驱动的社区应急疏散准备规划启动时机识别[J]. 系统工程理论与实践, 2021, 41(3):691-701.

DOI

[ Liu Z G, Li X Y, Yu F. Case-driven method for detecting the starting time of preparedness planning of community emergency evacuation[J]. Systems Engineering-Theory & Practice, 2021, 41(3):691-701. ] DOI:10.12011/SETP2019-2248

[15]
刘建伟, 崔立鹏, 罗雄麟. 结构稀疏模型[J]. 计算机学报, 2017, 40(6):1309-1337.

[ Liu J W, Cui L P, Luo X L. Structured sparse models[J]. Chinese Journal of Computers, 2017, 40(6):1309-1337. ] DOI:10.11897/SP.J.1016.2017.01309

[16]
Li L F, Wang J F, Leung H, et al. Assessment of catastrophic risk using Bayesian network constructed from domain knowledge and spatial data[J]. Risk Analysis, 2010, 30(7):1157-1175. DOI:10.1111/j.1539-6924.2010.01429.x

PMID

[17]
MiarNaeimi F, Azizyan G, Rashki M. Reliability sensitivity analysis method based on subset simulation hybrid techniques[J]. Applied Mathematical Modelling, 2019, 75:607-626. DOI:10.1016/j.apm.2019.05.038

[18]
Soliman A A, Abd-Ellah A H, Abou-Elheggag N A, et al. Modified Weibull model: A Bayes study using MCMC approach based on progressive censoring data[J]. Reliability Engineering & System Safety, 2012, 100:48-57. DOI:10.1016/j.ress.2011.12.013

[19]
于新文, 丁裕国. 中国东部地区暴雨的概率特征——基于泊松分布的统计模拟[J]. 自然灾害学报, 2006, 15(4):13-18.

[ Yu X W, Ding Y G. Probabilistic characteristics of rainstorm in eastern area of China: Poisson distribution-based statistical simulation[J]. Journal of Natural Disasters, 2006, 15(4):13-18. ] DOI:10.3969/j.issn.1004-4574.2006.04.003

[20]
程昌秀, 裴韬, 刘瑜, 等. 新时代自然灾害态势感知的实践与方法探索[J]. 地理学报, 2023, 78(3):548-557.

DOI

[ Cheng C X, Pei T, Liu Y, et al. The practice and method of natural disasters situational awareness in the new era[J]. Acta Geographica Sinica, 2023, 78(3):548-557. ] DOI:10.11821/dlxb202303003

Options
Outlines

/

〈 〉