EN中文

Journal of Geo-information Science >

2025 , Vol. 27 >Issue 5: 1163 - 1178

DOI: https://doi.org/10.12082/dqxxkx.2025.240698

3D Model Reconstruction of Airborne LiDAR Building Point Clouds Based on Squential Quadratic Programming and Elevation Step Correction

  • ZHANG Teng , 1 ,
  • WANG Jingxue , 2, * ,
  • XIE Xiao 3 ,
  • ZANG Dongdong 1
Expand
  • 1. School of Geomatics, Liaoning Technical University, Fuxin 123000, China
  • 2. School of Automation and Electronic Information, Xiangtan University, Xiangtan 411105, China
  • 3. Key Laboratory for Environment Computation & Sustainability of Liaoning Province, Institute of Applied Ecology, Chinese Academy of Sciences, Shenyang 110116, China
*WANG Jingxue，E-mail:

Received date: 2024-02-19

  Revised date: 2025-02-28

  Online published: 2025-04-23

Supported by

National Natural Science Foundation of China(41871379)

Fundamental Applied Research Foundation of Liaoning Province(2022JH2/101300273)

Fundamental Applied Research Foundation of Liaoning Province(2022JH2/101300257)

Sponsored by Beijing Nova Program(20230484351)

Huzhou Key Research and Development Program(2023ZD2046)

Fold

Abstract

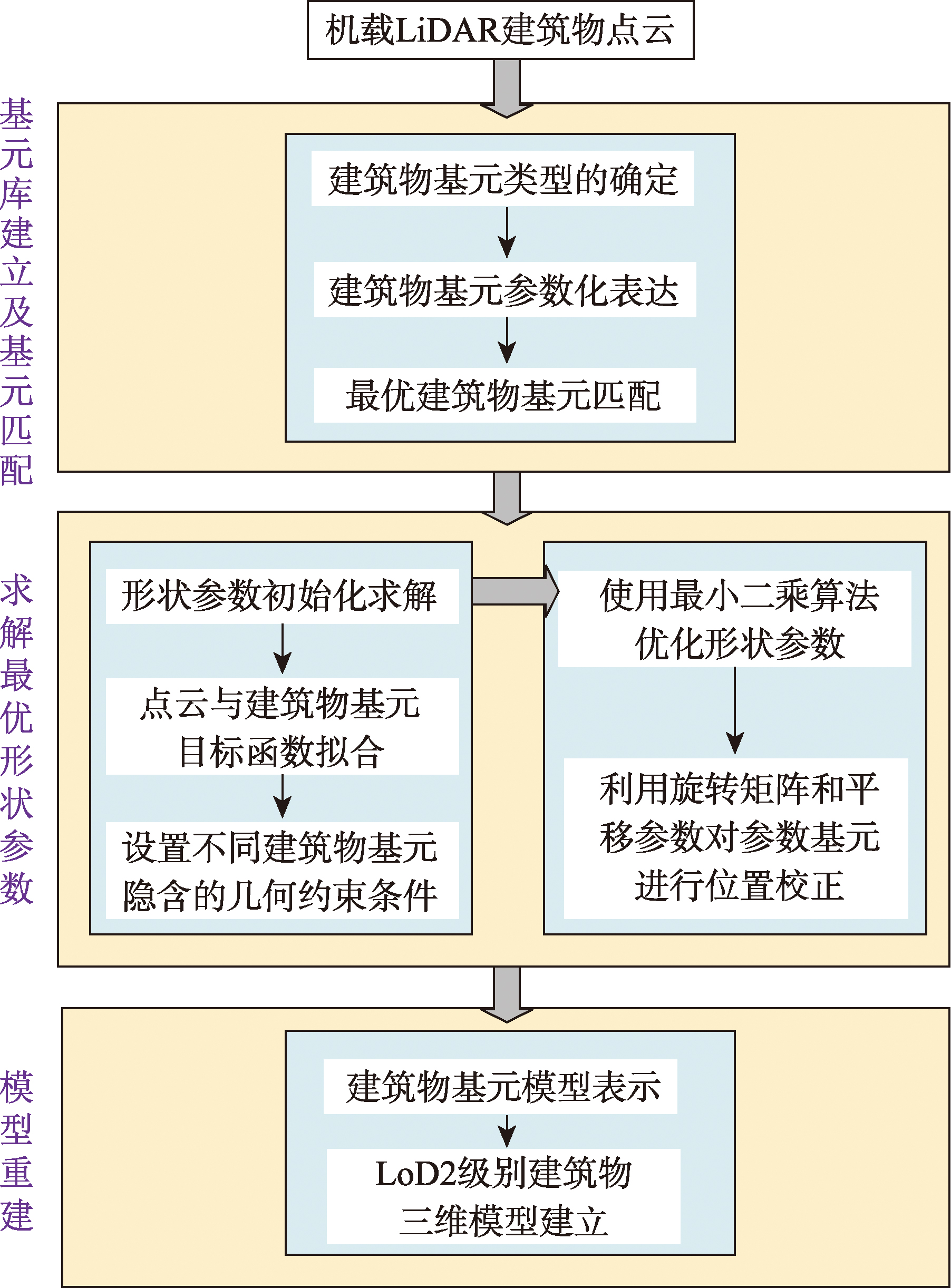
[Objectives] The 3D model reconstruction of buildings based on a model-driven approach using airborne LiDAR building point clouds relies on fitting the building point cloud to predefined geometric primitives. However, due to the uneven density and noise in the building point cloud, errors often arise in structural details during the primitive fitting process, leading to reduced reconstruction accuracy. To address this issue, this study proposes a 3D model reconstruction method for airborne LiDAR building point clouds based on sequential quadratic programming and elevation step correction. [Methods] First, a primitive library containing classical roof structures is established, including simple roofs, complex roofs, and steep roofs. An adjacency matrix is constructed by incorporating the adjacency relationships and ridge properties between roof patches. The best-matching primitives are then selected from the primitive library based on the adjacency matrix. Next, the shape parameters of the selected primitives are optimized using the sequential quadratic programming algorithm to achieve a globally optimal fitting state. The initial 3D model is then generated. To further enhance accuracy, the relative position of the building models and the roof point clouds in 3D space is refined through translation and rotation, reducing the relative distance deviation and improving the fitting precision. Finally, the City Geography Markup Language (CityGML) is used to store the reconstructed 3D building models, ensuring clear structure and correct topology, which facilitates the visual representation of reconstruction results. [Results] Ten sets of classical building point clouds from the 3D Building dataset were selected for the 3D model reconstruction experiment. The proposed method was compared with existing reconstruction approaches based on the same model-driven framework, and classical accuracy evaluation matrics were used for quantitative analysis. The average objective function value for the selected experimental data was 0.32 m, which is 0.03 m higher than the comparison method, indicating improved accuracy. The horizontal average deviation between the reconstructed building elements and the building point cloud was 0.10 m, while the vertical average deviation was 0.04 m. [Conclusions] In summary, the optimal shape parameters, obtained through the sequential quadratic programming algorithm, enable the construction of 3D building models with complete topology and regular shapes. Additionally, the elevation step correction, which utilizes the average point spacing of the roof point cloud as the step length, effectively enhances the reconstruction accuracy of 3D building models.

Key words： 3D model reconstruction; primitive library; building primitives; fitting accuracy; sequential quadratic programming; model-driven; airborne LiDAR building point cloud

Cite this article

ZHANG Teng , WANG Jingxue , XIE Xiao , ZANG Dongdong . 3D Model Reconstruction of Airborne LiDAR Building Point Clouds Based on Squential Quadratic Programming and Elevation Step Correction[J]. Journal of Geo-information Science, 2025 , 27(5) : 1163 -1178 . DOI: 10.12082/dqxxkx.2025.240698

1 引言

建筑物三维模型重建是摄影测量与遥感、计算机视觉、测绘地理信息等领域研究的热点问题[1]。机载激光探测与测量技术(Light Detection and Ranging, LiDAR)是可快速实时获取目标对象三维信息的重要技术手段[2]。随着三维数据采集技术的不断进步，机载LiDAR测量技术具有穿透性强，受天气影响小、数据精度高、作业更加高效等优点[3]，在3D城市建模、城市规划、制图分析等多领域，占有越来越重要的地位。基于点云的三维重建在建模精度和保证建筑物正确的拓扑关系方面都有很大的优势[4]，大量学者对点云处理和提升三维模型重建精度进行了深入研究与总结[5-7]，基于点云实现建筑物三维重建的主要两种途径为模型驱动和数据驱动[8-9]。
数据驱动方法不需事先识别建筑物类型，可直接根据点云建模，是一种自下而上的策略。通过结合随机样本一致性（Random Sample Consensus, RANSAC）[10]、聚类、区域增长[11-12]、以及基于成本函数[13]算法实现三维模型重建。 Dong等[14]将原始点云分割为多尺度的超体素，并采用混合区域生长方法进行处理，通过逐步合并具有相似特征的相邻体素来生成初始平面集，在全局能量优化框架下，进一步增强和细化屋顶面片的特征。如刘德强等[15]针对现有的建筑物点云分割数据效率低、抗噪性低等问题，以种子点的法向量和曲率以其邻域点到法平面的距离作为约束条件，提取符合平面模型的初始样本点集，然后采用RANSAC算法拟合平面点获取高精度的平面参数。洪绍轩等[16]利用Alpha-shapes算法与D-P算法进行轮廓线的粗略提取，利用最小二乘方法以及建筑物边界之间的向量、长度等特征确定建筑物关键点，通过寻找建筑物主方向，实现建筑物轮廓线规则化，解决Alpha-shapes算法提取的建筑物轮廓锯齿状的问题。Sampath等[17]对每个屋顶点进行特征点分析，得到每个点的法线并将屋顶点分为平面点和非平面点，使用K-means算法对所有平面点的法线进行聚类，然后估计聚类的数量，同时考虑几何的聚类相似性，通过构建屋顶的邻接矩阵来表示平面的连通性，最后基于平行和垂直线对的边界正则化实现建立几何正确的建筑模型。数据驱动通过充分挖掘机载LiDAR点云的原有数据特征，结合少量先验约束，完成对未定义屋顶结构建筑物点云的三维模型重建。理论上数据驱动方法适用于各种复杂和不规则的建筑物点云，有利于大规模城市场景下对建筑物的建模与分析。但由于机载LiDAR在树杂波、多径反射率、物体重叠率等多种野外条件的干扰下，采集到的点云数据缺乏拓扑完整性和几何严谨性，进而导致数据驱动策略下得到的建筑物三维模型存在畸变，与真实建筑物的屋顶结构不符。综上所述，数据驱动对点云数据质量要求较高、重建流程繁琐，前期处理结果对后期模型重建结构具有较大影响、易导致重建模型拓扑出现错误。
模型驱动需要预先确定建筑物类型，是一种自上而下的策略。基于模型驱动的建筑物重建的关键在于建立一个包含不同屋顶类型风格的建筑物基元库。Mass等[18]根据建筑物类型来确定需要求解的建筑物参数，通过建立不变矩与特征参数的函数关系从而求解参数，这种方法的基元库中只包含平面屋顶和人字型屋顶的建筑物，基元类型单一且不能涵盖大多数常见的复杂类型的建筑物屋顶，如双坡L型屋顶、双坡T型屋顶等。Verma等[19]对分割后的建筑物屋顶面点云构建拓扑图，通过对屋顶拓扑图搜索子图来识别可以组合成建筑物复杂屋顶结构的简单参数化屋顶形状，依据各参数选取合适的基元模板进行组合最终实现模型重建，但是该方法只包含三种简单形状的模板基元。Milde等[20]定义了五种简单的基元模板，将建筑物点云分割成平面块，并根据其邻接度对其进行标记，建立区域邻接图，通过形式语言和连接器对邻接图分析分解后的建筑物进行模型重建。Huang等[21]通过参数化表达的二维拓扑图方式定义11种屋顶基元类型，对点云进行栅格化处理，以生成二维栅格影像。在影像空间中进行基元的合并与融合，实现复杂屋顶的三维重建。Xiong等[22-23]以节点、边和最小环数为基础构建出屋顶拓扑图，并利用屋脊属性来识别选取相应的基元，采用了一种约束最小二乘拟合(Constrained Least Squares Fitting, CLSF)算法可以同时对所有屋顶参数调整，并对屋顶面片进行优化，最后获得拓扑关系正确的建筑物模型。张文元等[24]建立了八种建筑物基元模型，根据屋脊线属性构建拓扑图进行点云与对应基元类型的识别匹配，采用序列二次规划算法估计基元参数，最后构建几何语义一体化的CityGML LoD2模型。模型驱动方法对点云数据质量依赖性相对较低，且相较于数据驱动重建效率较高。但受限于基元库中基元类型有限，不能涵盖所有建筑物类型。此外，对于含有不规则结构的建筑物类型，存在参数求解困难的局限性，如弧形屋顶；当点云数据存在遮挡导致数据不完整时，还会影响模型拟合的精度以及参数求解的准确性。
综上所述，针对现有模型驱动重建结果精度低的问题，本文提出了联合序列二次规划及高程步长校正的机载LiDAR建筑物点云三维模型重建方法。建立一个含有多种屋顶类型的基元库，并采用文献[25]中的方法对屋顶点云进行特征线提取，依据提取到的屋脊线、轮廓线以及阶跃线等不同类型的特征线，用来构建屋顶点云的邻接矩阵用于匹配候选基元确定。将所有点到建筑物基元表面的最小距离平方的平均值作为目标函数，利用序列二次规划算法可以对各基元进行形状参数估计构建三维模型，并通过增加约束条件对模型参数优化，规范模型的几何结构。以对应屋顶点云平均点间距为步长校正建筑物点云与建筑物模型在空间上的相对位置，减小局部点云太密集或稀疏以及噪声对拟合结果的影响。同时，与文献[24]中建筑物三维模型重建方法进行对比，通过分析屋顶点云与基元屋顶表面的拟合精度，以凸显本文方法在提高建筑物三维重建精度方面的优势。

2 研究方法

本文提出联合序列二次规划及高程步长校正的机载LiDAR建筑物点云三维模型重建方法分为三部分：建立建筑物基元库，实现屋顶点云与对应建筑物基元识别；利用建筑物点云求解初始形状参数，通过目标函数以及对应屋顶结构设定的约束条件，使用序列二次规划算法优化形状参数；根据优化后形状参数进行建筑物基元参数化表示，构建LoD2级别建筑物三维模型。总体算法流程如图1所示。
图1 建筑物三维模型重建流程

Fig. 1 Flow chart of 3D model reconstruction of buildings

2.1 建筑物基元类型的确定

基于模型驱动的建筑物三维模型重建，关键在于建立一组类型多样、包容性强且具有代表性的建筑物基元。本文设计了包含经典屋顶结构的基元库，根据建筑物风格将所对应的建筑物基元屋顶分为3类，分别为简单的建筑物屋顶、复杂的建筑物屋顶和阶跃型屋顶。其中简单的建筑物屋顶包括水平屋顶、人字型屋顶、四坡型屋顶以及四角型屋顶；复杂的建筑物屋顶包括多面人字型屋顶、双坡L型屋顶、四坡L型屋顶、双坡T型屋顶；阶跃型屋顶包括具有高度显著变化的屋顶。并对基元库中的每一个建筑物基元进行了符合其屋顶结构特征的参数化表达。每类建筑物基元的对象如图2所示。
图2 建筑物基元库

Fig. 2 Primitive library of buildings

2.1.1 建筑物基元参数化表达

建筑物基元参数化表达需要根据不同建筑物的几何结构来表示，预定义多组描述不同基元类型的形状参数。由于基元库中的建筑物基元屋顶形状以及复杂程度不同，所以每种建筑物基元参数化表达所需要的形状参数个数也不同。其中可能用到的形状参数定义如下：形状参数包括X轴方向的建筑物长度Lx和宽度Wx，Y轴方向的建筑物长度Ly和宽度Wy，X轴方向的屋脊长度rx，Y轴方向的屋脊长度ry，建筑物高度h，屋顶高度he和墙体高度hw，共9个形状参数，θ=（Lx， Ly， Wx， Wy， rx，ry， h， he， hw），θ为形状参数集合。各基元屋顶几何结构的不同，需选用不同形状参数进行表达。首先需要确定其在局部坐标系下的原点坐标与坐标轴方向，对于没有屋脊线的建筑物基元以屋顶的几何中心或任一屋顶角点的水平面投影为坐标原点，X轴从左到右过原点与Lx平行，以原点为轴心，将X轴沿逆时针方向旋转90°设为Y轴方向，Z轴为与X、Y轴垂直的向上方向；对于有屋脊线的建筑物基元，若是只有一条屋脊线就以屋脊线的中点在水平面投影为坐标原点，X轴从左到右过原点与屋脊线rx平行，Y、Z轴设置方式同上；若是有两条相交的屋脊线则以屋脊线的交点在水平面的投影为坐标原点，X轴从左到右过原点与屋脊线rx平行，Y、Z轴设置方式同上。然后根据基元的形状参数可以确定其任意顶点在局部坐标系下的位置。如图3双坡L型屋顶，其顶点V1坐标可表示为：V1=(rx, Wy/2, 0)，人字型屋顶顶点V1坐标可表示为：V1=(-Lx/2, -Wy/2, 0)，水平屋顶的顶点V1坐标可表示为：V1=(0, Ly, 0)。
图3 3种类型建筑物基元局部坐标系原点的选取

Fig. 3 Selection of the origin of the local coordinate system of the three types of building primitives

2.1.2 最优建筑物基元匹配

基元库建立完成后，首要任务是实现屋顶点云与其对应的建筑物基元识别匹配，本文设计的屋顶点云与建筑物基元识别匹配流程如图4所示。首先，依据文献[24]中屋脊线的不同属性标记基元屋顶面片，分析面片间的邻接关系。以任一屋顶面片为起始面，依次编号，构造该顺序下的唯一邻接矩阵，以人字型屋顶为例（图5）；其次，提取屋顶点云的特征线建立该屋顶点云任意面片顺序下的所有邻接矩阵；最后，根据面片数量初步筛选建筑物基元，选取与屋顶点云面片数量相同的建筑物基元作为候选基元，将屋顶点云的邻接矩阵与各候选基元的唯一邻接矩阵对比，匹配到2个相同矩阵则匹配完成。
图4 屋顶点云与基元匹配的流程

Fig. 4 The process of matching roof point cloud with primitives

图5 人字型屋顶邻接矩阵构建

Fig. 5 Construction of herringbone roof adjacency matrix

建筑物基元独特的屋顶结构，导致屋顶面片之间不同类型屋脊的位置具有不同特征。根据屋顶面片的倾斜角度可分为水平屋顶、倾斜的凸屋顶和倾斜的凹屋顶，然后屋顶面片之间的屋脊根据其所处位置分为水平屋脊和倾斜屋脊。综上，可以将屋脊线的属性分为以下几类：由2个相邻屋顶面构成的方向向上的凸水平脊和方向向下的凹水平脊，位于2个相邻屋顶面形成凸角和凹角上的倾斜脊构成凸倾斜脊和凹倾斜脊，用不同颜色的线段表示不同的屋脊线属性。如图6所示，基元库中带有属性的屋脊线标记对基元库中4种经典的建筑物基元与屋顶点云进行识别，结果如表1所示。
图6 建筑物基元屋脊属性标记

Fig. 6 Marking of building primitives roof attribute

表1 点云与基元屋顶匹配结果

Tab. 1 The matching result of point cloud and roof primitive

屋顶类型 屋顶轮廓 邻接矩阵 参数基元模型
双坡L屋顶 0 1 0 4 1 0 2 0 0 2 0 1 4 0 1 0
四坡L屋顶 0 2 1 0 0 4 2 0 2 0 0 0 1 2 0 2 0 0 0 0 2 0 2 1 0 0 0 2 0 2 4 0 0 1 2 0
双坡T屋顶 0 1 0 0 4 1 0 1 0 0 0 1 0 4 0 0 0 4 0 1 4 0 0 1 0
人字型屋顶           0 1 1 0

注：表中屋顶轮廓中不同颜色屋脊线属性以及数字与图5中各屋脊线属性含义意义表示一致。序号①、②、③、④表示屋顶面中各面片索引。

2.2 屋顶点云在不同基元下邻接匹配误差分析

在完成基元库的建立后，需要实现对未知类型屋顶点云与对应建筑物基元的识别匹配。首先要通过点云屋顶面片数量对建筑物基元进行初步筛选缩小匹配范围。以四坡型屋顶点云为例，在基元库中双坡L型、四角型和四坡型基元的屋顶面片数量均为4个，但是只有四坡型基元与其拓扑结构一致。因此，矩阵匹配时在3个候选基元中只能与四坡型基元匹配成功。虽能缩小了候选基元范围，但在与候选基元进行矩阵匹配时容易出现多余基元匹配误差，如图7所示。
图7 四坡型屋顶点云邻接矩阵匹配误差

Fig. 7 Adjacency matrix matching error of four-slope roof point cloud

2.3 基于候选基元的建筑物三维模型重建

采用匹配后得到的候选基元对建筑物点云进行三维模型重建的整体流程如图8所示，根据建筑物基元屋顶结构进行形状参数初始化求解。设置建筑物点云与建筑物基元间的目标函数以及根据屋顶形状定义多个约束条件，然后使用最小二乘算法在各约束条件下进行形状参数求解。利用平移参数与旋转矩阵改变建筑物点云与建筑物基元之间的相对位置，最后对基元模型参数化表示建立LoD2级别的建筑物三维模型。
图8 基元库中各基元三维模型重建流程

Fig. 8 3D Model reconstruction process of each primitives in primitive library

2.3.1 形状参数初始化求解

建筑物基元形状参数的初始化求解是三维模型重建流程的首要步骤，初始形状参数决定屋顶顶点坐标的位置会直接影响由顶点拟合的屋顶面参数方程系数。然而，初始形状参数求解对建筑物点云的质量有一定要求，如点云的缺失以及噪声的存在都会影响参数求解的准确性也会降低算法的鲁棒性，进而影响点云与建筑物基元的拟合精度。
形状参数求解之前要确定局部坐标系，以点云分布方向作为局部坐标轴的方向，即与点云所处的笛卡尔坐标系方向相一致，从而与建筑物主方向相平行。不同建筑物基元的形状参数选取个数不同，水平屋顶的形状参数为Lx， Ly， h，双坡L型屋顶的形状参数为Lx， Ly， Wx， Wy， rx， ry， h， he， hw。不同建筑物基元形状参数选取如表2，形状参数求解公式和方法如表3所示。X与Y轴方向的建筑长度Lx， Ly，对应的初始值求解为X与Y坐标轴方向的最大值与最小值之差。X与Y轴方向的建筑物宽度Wx和Wy，初始求解为在坐标轴方向上取一定数量的x和y值较大值点作为边界候选点，计算候选点所处坐标轴方向y值与x值的最大值与最小值之差作为建筑物宽度Wx和Wy。由于脊线位于坐标轴上正上方，选取一定数量的z值较大的点，分别求这些点的x值的最大与最小值之差和y值的最大与最小值之差作为rx和ry。最后，对于建筑物高度h，屋顶高度he、和墙体高度hw的求解需要取Z轴方向上一定数量的z值最大和最小的坐标点取平均值二者相减作为h，同样的方法对屋顶点云求出屋顶高度he作为中间值，最后h与he相减得到墙体高度hw。
表2 不同建筑物基元形状参数选取

Tab. 2 Selection of shape parameters of different building primitives

建筑物基元类型 形状参数
人字型屋顶 Lx， Ly， rx， h， he， hw
多面人字型屋顶 Lx， Ly， Wx， Wy， rx， h， he， hw
四坡型屋顶 Lx， Wy， rx， h， he， hw
四角型屋顶 Lx， Ly， h， he， hw
四坡L型屋顶 Lx， Ly， Wx， Wy， rx， ry， h， he， hw
双坡T型屋顶 Lx， Ly， Wx， Wy， rx， ry， h， he， hw
阶跃型屋顶 Lx， Ly， Wx， Wy， h， he， hw
多面阶跃型屋顶 Lx， Ly， Wx， Wy， rx， h， he， hw
表3 基元形状参数初始值

Tab. 3 Initial value of the primitive shape parameters

形状参数 求解公式 形状参数描述
LX Lx=max(x)-max(x) X轴方向最大值与最小值之差
Ly Ly=max(y)-max(y) Y轴方向最大值与最小值之差
Wx Wx=maxy(x)-miny(x) 在Y轴方向，求x值最大值与最小值之差
Wy Wy=maxx(y)-minx(y) 在X轴方向，求y值最大值与最小值之差
rx rx=maxz(x) 取一定数量Z坐标较大点，求x值最大值与最小值之差
ry ry=maxz(y) 取一定数量Z坐标较大点，求y值最大值与最小值之差
h h=max(z)-min(z) Z轴方向最大值与最小值之差
he he=max(z)-mid(z) Z轴方向最大值与中间值之差
hw hw=mid(z)-min(z) Z轴方向中间值与最小值之差

2.3.2 点云与建筑物基元目标函数拟合

建筑物三维模型重建的过程，本质是在目标函数下求建筑物基元形状参数的最优解，即当所有点到建筑物基元屋顶拟合平面距离平方的平均值达到最小时，目标函数取得最优解。由于各基元屋顶结构各不相同，将其表面转换为三角网表示，通过计算每个点到与其对应的三角形所在平面的距离来计算建筑物点云到基元的距离，点到平面的距离公式如式（1）所示，拟合平面方程如式（2）。
D = a x i + b y i + c z i + d a 2 + b 2 + c 2
a x + b y + c z + d = 0
式中：(xi, yi, zi)为屋顶点云中第i个点的坐标； a、b、c、d为拟合平面方程系数。

2.3.3 不同建筑物基元隐含的几何约束条件

为了获得更精确的形状参数，利用建筑物基元隐含的先验几何知识对目标函数引入不同的约束条件。
首先通过屋顶顶点坐标值计算建筑物基元各边的长度用于面积的计算，用面积进行约束是对基元整体轮廓的约束。以图9双坡T型为例：
L y × W x + W y × L x - W x ≤ S
式中：S为对应屋顶点云在二维平面的投影面积，此处指双坡T型屋顶投影面积。
图9 双坡T型和四坡L型屋顶的约束策略

Fig. 9 Constraint strategies for double-slope T-shaped and four-slope L-shaped roofs

根据建筑物基元屋顶的几何结构可知屋顶长度大于宽度，对屋顶长和宽的约束定义约束条件如下：
L x ≥ W y L x ≥ W x L y ≥ W x L y ≥ W y
对于建筑物的高度通常等于墙体高度和屋顶高度之和，屋顶高度通常小于墙体高度，定义约束条件如下：
h ≥ h e + h w h w ≥ h e
综上，为了对双坡T型建筑物基元进行更加准确的形状参数求解，可对目标函数定义如下约束条件：
S - L y × W x + W y × L x - W x ≥ 0 L x - W y ≥ 0 L x - W x ≥ 0 L y - W x ≥ 0 L y - W y ≥ 0 h - h e - h w ≥ 0 h w - h e ≥ 0 h - h w ≥ 0
基元库中各建筑物基元屋顶形状结构不同，对应目标函数的约束条件也会有所不同，如图9的2种类型屋顶中具有屋脊线且屋顶长度大于屋脊的长度，可以分别增加以下约束条件，如式（7）、式（8）。
L x ≥ r x L y ≥ r y
L x - W x / 2 ≥ r x L y ≥ r y

2.3.4 约束条件对拟合结果的影响

各建筑物基元目标函数的约束条件会影响序列二次规划算法的收敛速度和形状参数的初值求解，以双坡T型屋顶为例，脊线由于缺少约束条件导致屋脊长度远大于屋顶长度或宽度，如图10(a)所示。若是增加约束条件，如式（9），则纠正后的基元模型的几何结构如图10(b)所示。建筑物点云与建筑物基元的拟合结果如图10(c)所示，屋顶的各个面片与点云均取得较好的拟合结果。
S - ( L y × W x ) - W y × ( L x - W x ) ≥ 0 W y - ( L x - W x / 2 ) ≥ 0
图10 有无约束条件对基元与点云拟合的影响

Fig. 10 The influence of constraints on the fitting of primitives and point cloud

2.3.5 使用最小二乘算法优化形状参数

采用最小二乘算法当中的序列二次规划(Sequential Quadratic Programming， SQP)算法[26]求解形状参数的过程，是一个非线性最小二乘求解问题，它可以优化具有约束条件的复杂问题。SPQ算法被广泛认为是求解约束非线性优化问题最有效的方法之一。除了定义约束条件还定义了建筑物基元参数的边界和初始估计值，这些边界合理的限制了参数的可能取值范围，而初始值则为优化算法提供了一个起点，序列二次规划算法会根据约束条件和边界限制对建筑物基元的各个参数进行多次迭代处理。当所有的点云到基元屋顶拟合平面的距离平方的平均值最小时说明此时点云与建筑物基元达到了最佳的拟合结果，同时也得到了最佳的形状参数值。

2.3.6 利用旋转矩阵和平移参数进行位置校正

建筑物基元与实际建筑物的各形状参数相同但是它们在各自坐标系下的位置不同，需通过平移、旋转与使它们对齐。平移参数为α=(tx， ty， tz)， 3个参数分别代表建筑物基元在坐标系下沿X轴、Y轴、Z轴方向的平移量。
平移参数由建筑物基元原点与点云原点的坐标差确定。平移到一致的位置后基元模型可能与其对应的建筑物点云存在位置上的相对偏差，利用旋转矩阵调整方向偏差。旋转矩阵的计算如式（10），旋转角度k由基元与点云在同一坐标轴方向的端点与原点构成的夹角确定，如在双坡L型屋顶中，基元原点与点云原点位置一致，仅需计算它们各自原点与X或Y轴端点相连向量的夹角k，如图11所示。旋转变换前后的拟合效果如表4所示，建筑物基元整体进行位置和方向变换后其对应的各顶点坐标可通过式（11）计算。
R k = c o s ( k ) - s i n ( k ) 0 s i n ( k ) c o s ( k ) 0 0 0 1
式中： V表示建筑物基元的某个顶点坐标； V '表示变换后的顶点坐标。
图11 旋转角度k的计算方法

Fig. 11 The calculation method of rotation angle k

表4 旋转变换对拟合结果的影响

Tab. 4 The influence of rotation transformation on the fitting results

屋顶类型 旋转变换前 旋转变换后
四坡L型屋顶
双坡T型屋顶

2.3.7 建筑物基元模型表示

经过SQP算法的多次迭代处理，得到了各建筑物基元的最佳参数。这些参数用于参数化表示建筑物基元模型实现了建筑物三维模型重建。为了更准确地描述建筑物模型，本文采用了城市地理标记语言(City Geography Markup Language, CityGML)中对城市实景三维的精细等级划分，构建LoD2级别的建筑物三维模型[27]。CityGML LoD2模型的核心在于其详细的三维表达，能够储存各类语义对象，包括对屋顶面(Roof Surface)、墙体面(Wall Surface)和屋底面(Ground Surface)的全面显示。这些细节不仅使模型在视觉上更加真实，而且能够高效地重建并显示建筑物的三维几何形状，通过这种方式能够快速生成语义内容丰富的建筑物模型。

3 实验与分析

3.1 实验数据

本文选择Building3D数据集提供的屋顶点云进行实验。该数据集为一个城市规模的数据集，多用于基于航空LiDAR点云建筑物模型重建实验。从中选择10栋具有代表性的建筑物进行模型重建实验，其中包括四坡L型屋顶、双坡T型屋顶、阶跃型屋顶等复杂屋顶结构，所用数据集如表5所示。
表5 测试数据集

Tab. 5 Test data set

屋顶类型 水平屋顶 人字型屋顶 多面人字型屋顶 四坡型屋顶 四角型屋顶
建筑物点云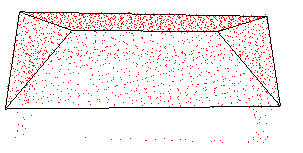
屋顶类型 双坡L型屋顶 四坡L型屋顶 双坡T型屋顶 阶跃型屋顶 多面阶跃型屋顶
建筑物点云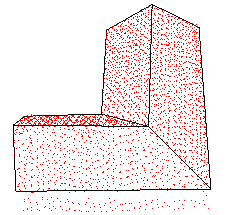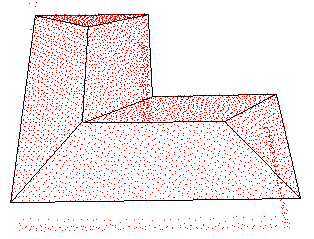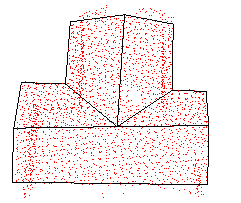

3.2 建筑物三维模型重建

对基元库中各建筑物基元屋顶设置符合其几何结构特征的约束条件，使各形状参数在全局范围内得到正确的估计，以基元库中4种经典复杂的建筑物基元为例，如表6所示，其中双坡L型屋顶、四坡L型屋顶、阶跃型屋顶的约束条件为式（12）、式（13）、式（14）。
表6 建筑物点云与对应基元模型拟合效果

Tab. 6 The fitting effect of the building point cloud and corresponding primitive model

屋顶类型 点云数据 设置约束条件前 设置约束条件后
双坡L型屋顶
四坡L型屋顶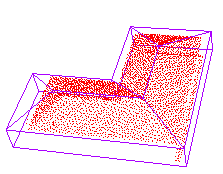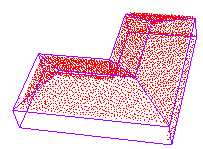
双坡T型屋顶
阶跃型屋顶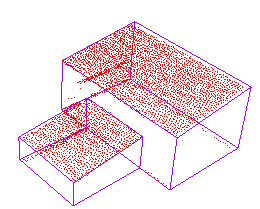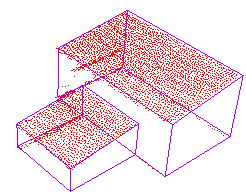
L x - W x ≥ 0 L x - r x ≥ 0 L y - W y ≥ 0 L y - r y ≥ 0 S - L x × W y - ( L y - W y ) × W x ≥ 0 h w - h e ≥ 0 h - h e - h w ≥ 0
L x - W x ≥ 0 L x - r x ≥ 0 L x - r x - W x / 2 ≥ 0 L y - W y ≥ 0 L y - r y ≥ 0 L y - r y - W y / 2 ≥ 0 S - L x × W y - ( L y - W y ) × W x ≥ 0 h w - h e ≥ 0 h - h e - h w ≥ 0
L x - L y ≥ 0 L x - W x ≥ 0 L y - W y ≥ 0 h w - h e ≥ 0 h - h w - h e ≥ 0 S - L y × W x - W y × ( L x - W x )
利用几何约束优化形状参数构建建筑物三维模型后，将其换成为CityGML LoD2标准的模型。从表7中可以看出，City GML能够准确记录建筑物屋顶及立面结构，保证重建模型结构的完整性以及各屋顶基元的拓扑一致性。
表7 建筑物模型重建结果

Tab. 7 Results of building model reconstruction

屋顶类型 水平屋顶 人字型屋顶 多面人字型屋顶 四坡型屋顶 四角型屋顶
模型重建结果
屋顶类型 双坡L型屋顶 四坡L型屋顶 双坡T型屋顶 阶跃型屋顶 多面阶跃型屋顶
模型重建结果

3.3 建筑物基元与点云拟合精度分析

对比表6中的拟合结果可以看出建筑物基元的初始状态与建筑物点云的拟合有很大的差异，如双坡L型屋顶的长和宽大于建筑物点云边界的长和宽，双坡T型屋顶的宽度小于建筑物点云的边界宽度。经过多次迭代约束后，建筑物基元与对应的建筑物点云间拟合状态差异逐渐减小，当屋顶点云中所有点到建筑物基元屋顶表面的最小距离平方的平均值最小时，此时点云与建筑物基元达到了最优的拟合效果。但受到建筑物点云分布不均且各点在高程方向上异常点与平面相距较远，局部点云在屋顶几何结构细节上存在太密集或稀疏以及噪声的影响，导致建筑物基元屋顶面片与建筑物点云在拟合时产生误差，从而影响拟合精度。为解决上述问题，采用平均点间距为步长，逐步多次上下调整建筑物基元屋顶的位置来校正拟合状态。同时，为充分体现本文方法能够有效提高拟合精度，选取10组数据，将本文方法与文献[24]方法进行对比，屋顶点云中所有点到建筑物基元屋顶拟合平面最小距离平方的平均值计算结果如表8所示。
表8 各建筑物三维重建精度统计

Tab. 8 Statistics of building 3D reconstruction accuracy

屋顶类型 建筑物点云 邻接矩阵匹配 目标函数平均值/m
文献[24]方法 本文方法
水平屋顶 0 0.002 0.002
人字型屋顶 0 1 1 0 0.570 0.540
多面人字型屋顶 0 1 0 1 0 1 0 1 0 0.440 0.410
四角型屋顶 0 2 0 2 2 0 2 0 0 2 0 2 2 0 2 0 0.700 0.670
四坡型屋顶
 0 2 0 2 2 0 2 1 0 2 0 2 2 1 2 0 0.200 0.180
双坡L型屋顶 0 1 0 4 1 0 2 0 0 2 0 1 4 0 1 0 0.430 0.400
四坡L型屋顶 0 2 1 0 0 4 2 0 2 0 0 0 1 2 0 2 0 0 0 0 2 0 2 1 0 0 0 2 0 2 4 0 0 1 2 0 0.380 0.340
双坡T型屋顶 0 1 0 0 4 1 0 1 0 0 0 1 0 4 0 0 0 4 0 1 4 0 0 1 0 0.070 0.060
阶跃型屋顶 0 5 5 0 0.230 0.210
多面阶跃型屋顶 0 1 0 0 1 0 1 5 0 1 0 5 0 5 5 0 0.410 0.390
基于模型驱动的建筑物三维重建预定义多组建筑物基元，需构建清晰准确的屋顶几何结构。但屋顶结构复杂多样，其局部细节处点云可能存在密度不均，受噪声影响异常点存在，从而影响拟合精度。本文通过高程步长校正的方法改进基元与对应屋顶点云的拟合状态，以减小局部点云对整体拟合精度。通过对比实验结果可以看出本文方法在处理上述问题中有着显著的优势。
为更好地凸显本文方法的准确性，选用4组数据对比设置约束条件前后基元模型特征线与参考数据的拟合程度，如表9所示。通过对比可以发现本文方法不仅提高了基元模型拟合精度，还有效保留并规范其几何结构。
表9 屋脊线准确性分析

Tab. 9 Accurate analysis of the ridge line

屋顶类型 参考数据 设置约束条件前 设置约束条件后
四坡型屋顶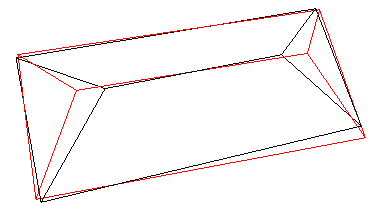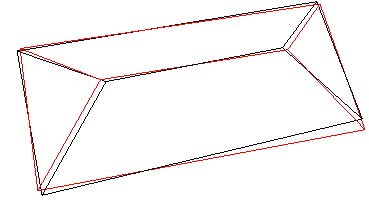
多面人字型屋顶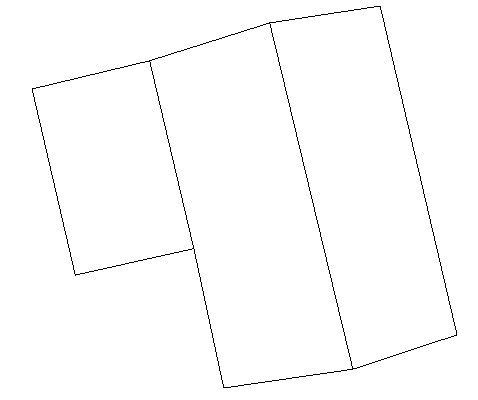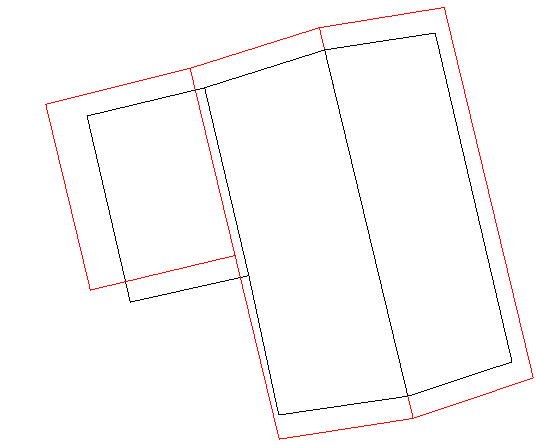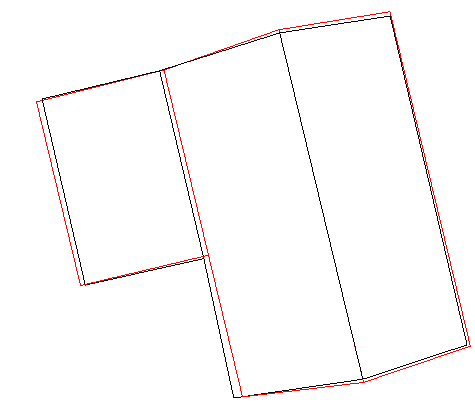
双坡L型屋顶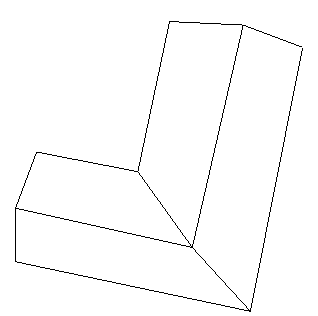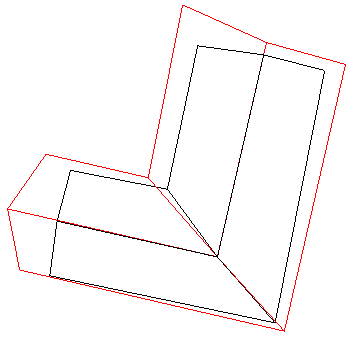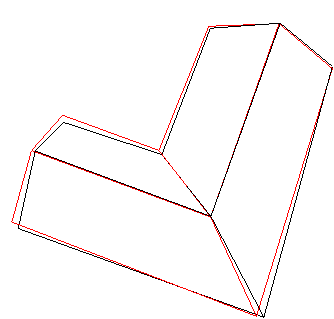
四坡L型屋顶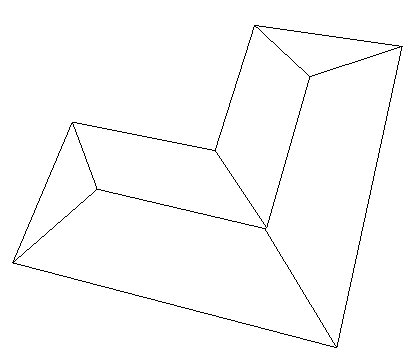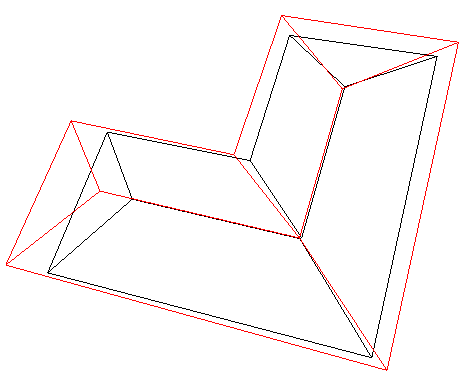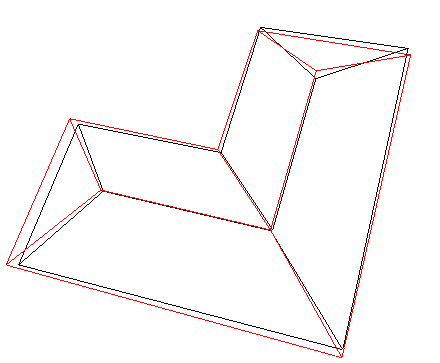

注：表中黑色线框为屋顶参考特征线，红色线框为建筑物基元模型特征线。

虽然在整体上已经取得了较好的拟合效果，但建筑物基元的各顶点与实际建筑物点云顶点在空间位置上仍存在一定的细小偏差。通过两点间距离式（15）和求高差绝对值式（16）分别来计算各方向偏差量，计算结果如表10所示。建筑物基元与建筑物点云在水平方向平均偏差为0.10 m，竖直方向的平均偏差为0.04 m，进一步说明本文方法可以准确获得各类建筑物对应的形状参数。
△ d = x 1 - x 2 2 + y 1 - y 2 2
△ h = z 1 - z 2
表10 建筑物三维模型重建偏差量

Tab. 10 Deviation of building 3D model reconstruction

屋顶类型 水平偏差/m 竖直偏差/m
水平屋顶 0.06 0.01
人字型屋顶 0.04 0.05
多面人字型屋顶 0.03 0.06
四角型屋顶 0.28 0.04
四坡型屋顶 0.04 0.02
双坡L型屋顶 0.04 0.08
四坡L型屋顶 0.17 0.06
双坡T型屋顶 0.06 0.03
阶跃型屋顶 0.05 0.01
多面阶跃型屋顶 0.25 0.02

4 结论

为解决建筑物屋顶点云在局部结构细节上可能存在的点云密度分布不均，受噪声影响异常点与拟合平面相距较远，导致模型重建拟合精度较低的问题，本文提出一种联合序列二次规划及高程步长校正的机载LiDAR建筑物点云三维模型重建方法。通过选用Building3D数据集中多组经典屋顶结构建筑物点云验证表明：
（1）本文通过增加对阶跃型基元阶跃线属性标注，扩大了建筑物基元屋顶拓扑图构建邻接矩阵的范围，进而解决了建筑物点云与阶跃型基元识别匹配的问题；
（2）使用最小二乘算法中的SPQ算法可以对多种形状建筑物基元进行参数求解，无需手动调节，提高了求解最佳参数的自动化程度，可灵活调节形状参数的规范建筑物模型屋顶的几何结构；
（3）建筑物基元与屋顶点云拟合后，以平均点间距为步长调节基元屋顶面与点云在高程上的相对位置，减小由点云密度不均匀和噪声影响导致的结构细节上存在的拟合误差。通过实验对比，屋顶点云中点到建筑物基元屋顶面的目标函数平均值由0.35 m提升到0.32 m，建筑物基元与建筑物点云的水平平均偏差为0.10 m，竖直平均偏差为0.04 m，提高了建筑物三维模型重建的精度。
本文方法可以实现几何结构规范的建筑物三维模型重建，在提高三维模型重建精度方面也有了很大的提升，但仍存在以下局限性。一方面，基元库中所包含的经典屋顶结构建筑物基元难以覆盖所有屋顶结构，如圆形屋顶，具有弧度的常见复杂屋顶等；另一方面，对原始点云数据的质量有较高要求，对于存在大范围缺失的建筑物点云数据，求解初始形状参数可能会不理想。未来将进一步扩充基元库中的建筑物基元类型，通过分解并组合基元的方式实现对复杂建筑物屋顶进行三维模型重建，同时根据基元屋顶的复杂程度设置可以描述其特征的形状参数，灵活结合基元的轮廓线与屋脊线的关系设置约束条件，在全局范围内求得最佳的参数值。
■本文图文责任编辑：蒋树芳 黄光玉

利益冲突： Conflicts of Interest 所有作者声明不存在利益冲突。

All authors disclose no relevant conflcts of interest.

References

Publishing order | Descend order by publishing year | Descend order by cited within
[1]
程亮, 龚健雅, 韩文泉. LiDAR与影像集成的真实感建筑物三维重建研究进展[J]. 测绘科学, 2009, 34(1):21-24.

[ Cheng L, Gong J Y, Han W Q. A review on realistic building 3D reconstruction using LiDAR and imagery[J]. Science of Surveying and Mapping, 2009, 34(1):21-24. ] DOI:10.3771/j.issn.1009-2307.2009.01.005

[2]
Wang H T, Zhang W M, Chen Y M, et al. Semantic decomposition and reconstruction of compound buildings with symmetric roofs from LiDAR data and aerial imagery[J]. Remote Sensing, 2015, 7(10):13945-13974. DOI:10.3390/rs71013945

[3]
钟国文. 机载LiDAR在地质灾害应急测绘中的应用研究[J]. 测绘与空间地理信息, 2023, 46(4):197-200.

[ Zhong G W. Application of airborne LiDAR in geological disaster emergency surveying and mapping[J]. Geomatics & Spatial Information Technology, 2023, 46(4):197-200. ] DOI:10.3969/j.issn.1672-5867.2023.04.054

[4]
文学东, 陈为民, 谢洪, 等. 一种融合多源特征的建筑物三维模型重建方法[J]. 武汉大学学报(信息科学版), 2019, 44(5):731-736,764.

[ Wen X D, Chen W M, Xie H, et al. A method for building model reconstruction based on multi-source feature fusion[J]. Geomatics and Information Science of Wuhan University, 2019, 44(5):731-736,764. ] DOI:10.13203/j.whugis20180320

[5]
杨必胜, 梁福逊, 黄荣刚. 三维激光扫描点云数据处理研究进展、挑战与趋势[J]. 测绘学报, 2017, 46(10):1509-1516.

DOI

[ Yang B S, Liang F X, Huang R G. Progress, challenges and perspectives of 3D LiDAR point cloud processing[J]. Acta Geoddactica et Cartographica Sinica, 2017, 46(10):1509-1516. ] DOI:10.11947/j.AGCS.2017.20170351

[6]
杜建丽, 陈动, 张振鑫, 等. 建筑点云几何模型重建方法研究进展[J]. 遥感学报, 2019, 23(3):374-391.

[ Du J L, Chen D, Zhang Z X, et al. Research progress of building reconstruction via airborne point clouds[J]. Journal of Remote Sensing, 2019, 23(3):374-391. ]

[7]
Xu Y S, Stilla U. Toward building and civil infrastructure reconstruction from point clouds: A review on data and key techniques[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2021, 14:2857-2885. DOI:10.1109/JSTARS.2021.3060568

[8]
Tarsha-Kurdi F, Landes T, Grussenmeyer P, et al. Model-driven and Data-driven approaches using LIDAR data: analysis and comparison[C]// ISPRS Workshop, Photogrammetric Image Analysis (PIA07). 2007:87-92.

[9]
Zang Y F, Mi W H, Xiao X W, et al. Compound 3D building modeling with structure-aware partition and primitive assembly from airborne laser scanning point clouds[J]. International Journal of Digital Earth, 2024, 17(1):2375112. DOI:10.1080/17538947.2024.2375112

[10]
Schnabel R, Wahl R, Klein R. Efficient RANSAC for point-cloud shape detection[J]. Computer Graphics Forum, 2007, 26(2):214-226. DOI:10.1111/j.1467-8659.2007.01016.x.

[11]
Vosselman G, Gorte B G H, Sithole G, et al. Recognising structure in laser scanner point clouds[J]. International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, 2004, 46(8):33-38.

[12]
Lari Z, Habib A. An adaptive approach for the segmentation and extraction of planar and linear/cylindrical features from laser scanning data[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2014, 93:192-212. DOI:10.1016/j.isprsjprs.2013.12.001

[13]
Nan L L, Wonka P. PolyFit: Polygonal surface reconstruction from point clouds[C]// 2017 IEEE International Conference on Computer Vision (ICCV). IEEE, 2017:2372-2380. DOI:10.1109/ICCV.2017.258

[14]
Dong Z, Yang B S, Hu P B, et al. An efficient global energy optimization approach for robust 3D plane segmentation of point clouds[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2018, 137:112-133. DOI:10.1016/j.isprsjprs.2018.01.013

[15]
刘德强, 曾力, 吴光星, 等. 区域增长与RANSAC模型结合的机载点云平面分割方法[J]. 建筑技术, 2024, 55(8):1020-1024.

[ Liu D Q, Zeng L, Wu G X, et al. Segmentation method of airborne point cloud plane based on regional growth and ransac model[J]. Architecture Technology, 2024, 55(8):1020-1024. ] DOI:10.13731/j.jzjs.2024.08.1020

[16]
洪绍轩, 袁枫, 王竞雪, 等. 机载LiDAR点云建筑物边界线规则化算法研究[J]. 测绘科学, 2020, 45(7):100-105,125.

[ Hong S X, Yuan F, Wang J X, et al. Research on buildings boundary regularization algorithm for aerial LiDAR point clouds[J]. Science of Surveying and Mapping, 2020, 45(7):100-105,125. ] DOI:10.16251/j.cnki.1009-2307.2020.07.015

[17]
Sampath A, Shan J. Segmentation and reconstruction of polyhedral building roofs from aerial lidar point clouds[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(3):1554-1567. DOI:10.1109/TGRS.2009.2030180

[18]
Maas H G, Vosselman G. Two algorithms for extracting building models from raw laser altimetry data[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 1999, 54(2/3):153-163. DOI:10.1016/S0924-2716(99)00004-0

[19]
Verma V, Kumar R, Hsu S. 3D building detection and modeling from aerial LIDAR data[C]// 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR'06). IEEE, 2006, 22:2213-2220. DOI:10.1109/CVPR.2006.12

[20]
Milde J, Zhang Y, Brenner C, et al. Building reconstruction using a stuctural description based on a formal grammar[J]. International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, 2008, 37: 47.

[21]
Huang H, Brenner C, Sester M. A generative statistical approach to automatic 3D building roof reconstruction from laser scanning data[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2013, 79:29-43. DOI:10.1016/j.isprsjprs.2013.02.004

[22]
Xiong B, Jancosek M, Elberink S Oude, et al. Flexible building primitives for 3D building modeling[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2015, 101:275-290. DOI:10.1016/j.isprsjprs.2015.01.002

[23]
Xiong B, Elberink S Oude, Vosselman G. A graph edit dictionary for correcting errors in roof topology graphs reconstructed from point clouds[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2014, 93:227-242. DOI:10.1016/j.isprsjprs.2014.01.007

[24]
张文元, 陈江媛, 谈国新. 基于3D基元拟合的复杂屋顶点云三维重建[J]. 地球信息科学学报, 2023, 25(8):1531-1545.

DOI

[ Zhang W Y, Chen J Y, Tan G X. Complex roof structure reconstruction by 3D primitive fitting from point clouds[J]. Journal of Earth Geo-information Science, 2023, 25(8):1531-1545. ] DOI:10.12082/dqxxkx.2023.220927

[25]
Yu J Z, Wang J X, Zang D D, et al. A feature line extraction method for building roof point clouds considering the grid center of gravity distribution[J]. Remote Sensing, 2024, 16(16):2969. DOI:10.3390/rs16162969

[26]
Boggs P T, Tolle J W. Sequential quadratic programming[J]. Acta Numerica, 1995, 4:1-51. DOI:10.1017/s0962492900002518

[27]
Gröger G, Plümer L. CityGML-Interoperable semantic 3D city models[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2012, 71:12-33. DOI:10.1016/j.isprsjprs.2012.04.004

Options
Outlines

/

〈 〉