EN中文

地球信息科学学报 >

2022 , Vol. 24 >Issue 9: 1742 - 1754

DOI: https://doi.org/10.12082/dqxxkx.2022.220329

地球信息科学理论与方法

基于地形数据的长距离越野路径快速规划方法研究

  • 冯世盛 ,
  • 徐青 , * ,
  • 朱新铭 ,
  • 邹霓霄 ,
  • 李帅
展开
  • 信息工程大学, 郑州 450001
* 徐 青（1982— ）,男,江苏宜兴人,教授,博士,主要从事与地图制图学与地理信息工程专业研究。E-mail:

冯世盛（1996— ）,男,山西晋中人,硕士生,主要从事越野路径规划研究。E-mail:

收稿日期: 2022-05-20

  修回日期: 2022-06-23

  网络出版日期: 2022-11-25

收起

Fast Method for Long-Distance Off-Road Path Planning based on Terrain Data

  • FENG Shisheng ,
  • XU Qing , * ,
  • ZHU Xinming ,
  • ZHOU Nixiao ,
  • LI Shuai
Expand
  • Information Engineering University, Geospatial Information Institute, Zhengzhou 450001, China
* XU Qing, E-mail:

Received date: 2022-05-20

  Revised date: 2022-06-23

  Online published: 2022-11-25

Fold

摘要

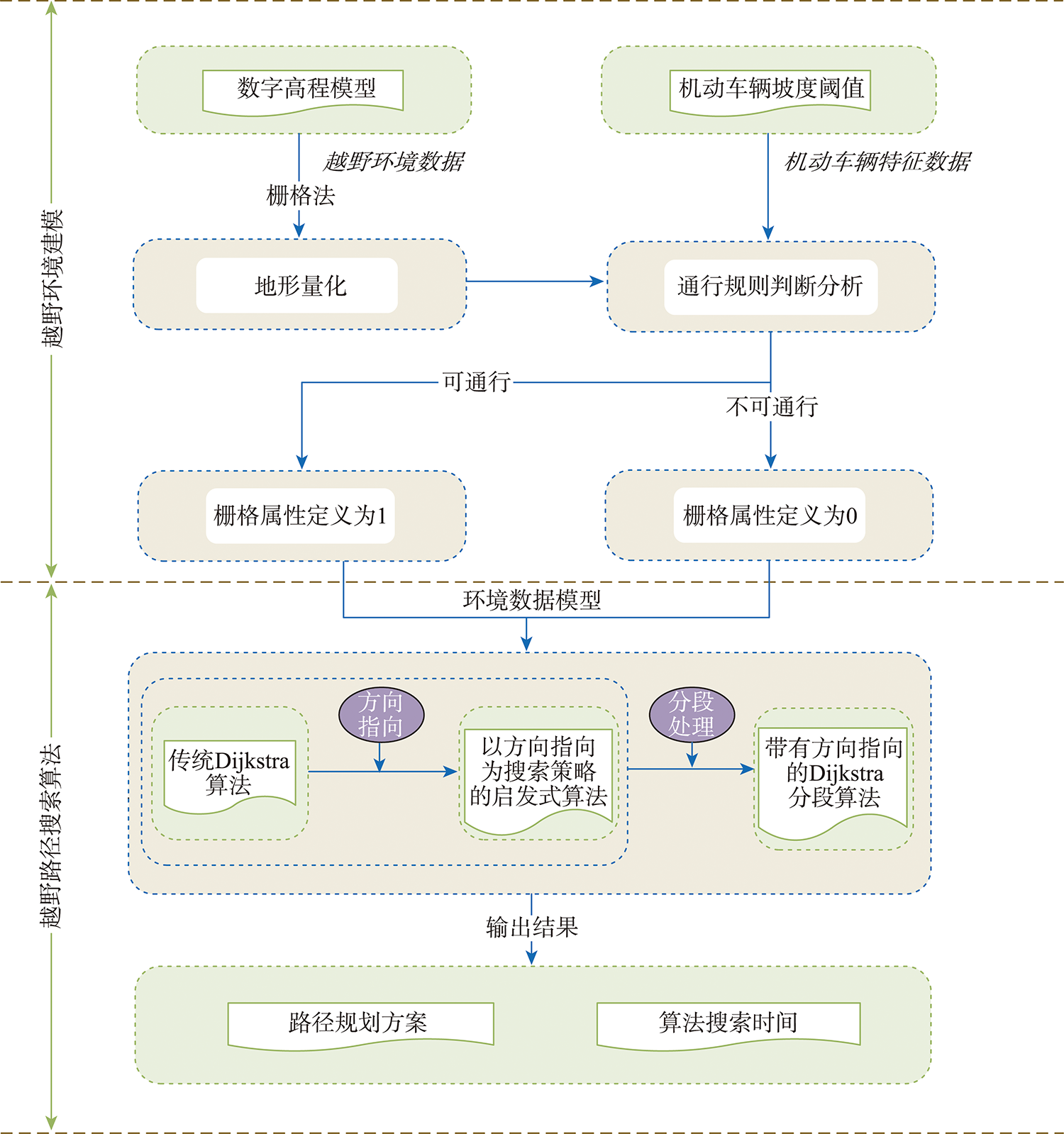
越野环境下机动车辆的快速路径规划在野外搜救、应急抢险及军事作战等领域均具有重要意义,在以上场景中,随着空间维数的增加,传统路径搜索算法计算复杂性急剧增长,可能无法在既定时间内求解可靠路径。为解决上述不足,本文结合越野路径规划不受路网通行限制以及两点之间直线最短的特点,提出以方向指向作为搜索策略的启发式算法,该算法搜索效率大幅提升,却难以保证求解质量。为进一步提高求解质量,提出了带有方向指向的Dijkstra分段算法,该算法在较低精度环境模型下通过Dijkstra算法找到最优路径,并将该路径进行分段,各分段以方向指向作为搜索策略进行路径搜索,从而在长距离越野路径规划中快速规划通行方案。为验证该算法的有效性,本文利用山西省某市的数字高程模型数据进行实验,引入了窗口移动法对地形进行先期的坡度计算和通行性分析,构建越野环境模型,调用路径搜索算法进行规划。实验结果表明,本文所提算法相比Dijkstra算法计算效率得到了大幅提升,且规划路径的长度接近于最优解。

关键词： 越野环境; 路径规划; 长距离; 环境建模; 路径搜索算法; 算法设计; 算法效率

本文引用格式

冯世盛 , 徐青 , 朱新铭 , 邹霓霄 , 李帅 . 基于地形数据的长距离越野路径快速规划方法研究[J]. 地球信息科学学报, 2022 , 24(9) : 1742 -1754 . DOI: 10.12082/dqxxkx.2022.220329

Abstract

The fast path planning of motor vehicles in the off-road environment is of great significance in the fields of field search and rescue, emergency rescue, and military operations. In the above scenarios, with the increase of spatial dimension, the computational complexity of traditional path search algorithms increases exponentially, and may not be able to be calculated within a given time. To solve the above deficiencies, this paper proposes a heuristic algorithm with directional pointing as a search strategy, combining the characteristics of off-road path planning that is not restricted by road network traffic and the shortest straight line between two points. In order to further improve the solution quality, a Dijkstra segmentation algorithm with directional pointing is proposed. This algorithm finds the optimal path through Dijkstra algorithm in a low-precision environment model and divides the path into segments. Each segment is oriented in a direction. Route search is performed as a search strategy to quickly plan passage schemes in long-distance off-road route planning. In order to verify the effectiveness of the algorithm, this paper uses the digital elevation model data of a city in Shanxi Province to conduct experiments and introduces the window movement method to perform preliminary slope calculation and trafficability analysis of the terrain, build an off-road environment model, and call the path search algorithm to carry out path planning. The experimental results show that the computational efficiency of the algorithm proposed in this paper has been greatly improved compared to the Dijkstra algorithm, and the length of the planned path is close to the optimal solution.

Key words： off-road environment; path planning; long distance; environmental modeling; path search algorithm; algorithm design; algorithm efficiency

1 引言

路径规划是融合运筹学、计算机科学以及地理信息科学等多个学科进行研究的热点领域,可以简单描述为在一定约束条件下,寻找一条从起始点到目标点连续且无碰撞的最优路径[1]。如今,随着数字化地图日渐完善,结构化道路信息愈加丰富且准确,基于路网信息的路径规划技术已经深入到各行各业,在实际中得到了广泛应用。但是该技术存在着一定的缺陷,即严重依赖交通路网数据,在村镇和山地等不具备良好路网数据的复杂越野环境中实用性差甚至无法使用[2]。决策人员需要通过地形数据建模,结合路径搜索算法,为越野环境路径规划提供合理的建议[3]。该工作可减少出发前的实地勘察,节省时间及人力成本,有效地提高通行方案的制订效率[4],对野外救援搜索、越野探索、应急抢险救灾以及军事作战行动均具有重要意义[5-6]。
近些年来,已有科研人员对越野路径规划问题展开了一系列探索性研究,其中优化路径搜索算法对越野路径安全高效地规划至关重要。根据越野环境信息的掌握程度,可以将路径规划分为全局路径规划和局部路径规划。全局路径规划是静态的,以不变的地图数据为输入;局部路径规划是动态的,以实时交通环境的数据为输入[7]。本文将关注全局路径规划问题。常见的全局越野路径规划算法主要有随机采样[8]、蚁群算法[9]、A*算法[10]、Dijkstra算法[11]等。Daniel[12]提出一种新的基于网格角度的路径规划算法,沿着网格边缘进行格元点扩展,最终达到规划最短距离路径的目的;林笃斌等[13]提出了基于DEM格网的优化A*路径搜索算法,作者考虑了DEM格网的路径可达性,根据地理空间分布特征选取A*算法的估价函数;吴天羿等[14]针对不同类型车辆的越野路径规划,分析地形坡度和地表属性综合影响下的路径规划,构造了改进A*算法的估价函数的估价函数,设计了考虑坡度和粗糙度约束的路径优化算法;Saranya[15]等研究车辆的路径规划,基于格网技术优化D*算法,以最短路径为目标,考虑地形坡度对估价函数的影响,通过仿真测试不同坡度对越野对象路径规划的影响。从上述研究可见当前在越野环境下的路径规划算法研究还相对薄弱,且主要集中在规避障碍算法研究,以通过改进基于路网信息的路径规划技术来满足越野环境下的路径规划研究,并没有较好的结合越野环境中的路径规划特点,主要还存在以下不足： ① 上述算法为越野路径规划研究提供了参考,但是改进后的算法大多采用简单的二维或三维仿真模型进行试验,例如构建的环境仿真模型单元分辨率为数公里,数据量和复杂程度都远远低于真实地形地图,导致搜索算法所规划的路径实用性较差,而越野机动车辆在越野环境中的实用性、安全性却尤为重要[16]。因此,为保证越野路径规划方案的实用性、安全性,越野路径搜索算法应基于高精度越野环境仿真模型进行研究;② 构建高精度越野环境仿真模型对长距离越野路径规划提出了新的挑战,主要体现在路径搜索算法的计算效率上。高精度越野环境仿真模型会占用大量的存储空间,随着目标点距离的增加,算法的搜索范围扩大,运算速度缓慢,甚至面临计算崩溃。例如,Ishigami等[17]使用Dijkstra算法进行路径搜索,选择8 m 2的越野环境为仿真模型进行测试,输出路径解的计算时间约47 min。由此可见Dijkstra算法计算效率与环境的规模大小密切相关,当起终点距离较远时,可能无法在既定时间内求解可靠路径。而越野环境的路径规划多应用于野外搜索、应急抢险等应急任务中,算法的计算效率尤为重要,因此路径规划算法需要尽可能地提高计算效率,以满足在越野环境中执行长距离路径规划任务。
综上分析,为克服长距离越野路径规划计算效率缓慢的局限性,本文在Dijkstra算法的基础上,结合越野路径规划的特点,提出了以方向指向作为搜索策略的启发式路径规划算法,该算法有效地提高了路径搜索的计算效率,但求解的长度成本难以保证。因此为进一步降低路径规划的长度成本,提出了带有方向指向的Dijkstra分段算法,该算法在较低精度模型下通过Dijkstra算法找到最短路径,随后将长距离路段进行分段,各分段以方向指向作为搜索策略进行路径搜索,从而在长距离越野路径规划中快速高效地规划通行方案。最后,利用山西省某市的DEM数据进行实验,引入窗口移动法对地形进行先期的坡度计算,结合机动车辆的坡度阈值进行通行性分析,并调用本文所提算法进行规划,验证算法的有效性。

2 研究方法

2.1 技术路线

本文越野路径规划研究技术路线如图1所示,路线主要分为越野环境建模与路径搜索算法2个部分。
图1 越野路径规划研究技术路线

Fig. 1 Off-road path planning research technology roadmap

（1）越野环境建模部分。首先准备相关数据,数据包括越野环境数据与机动车辆特征数据。本文机动车辆界定为履带式、轮式2种类型的越野车辆,其通行性的重要影响要素是坡度,因此本文以DEM数据来模拟复杂的地貌形态,以机动车辆的坡度阈值分析其环境通行性。在获取相关数据后,首先引入窗口移动法对地形进行先期的坡度计算,随后结合机动车辆的坡度阈值进行通行性分析,为路径搜索算法提供环境数据模型。
（2）路径搜索算法部分。在Dijkstra算法的基础上进行改进,融入方向指向为启发因子,提出以方向指向作为搜索策略的启发式算法。该算法搜索效率大幅提升,却难以保证求解质量,因此为进一步降低路径规划的长度成本,提出带有方向指向的Dijkstra分段算法,通过将长距离路段进行分段处理,有效地提高了算法的搜索效率。

2.2 越野环境建模

环境建模是实现越野环境下路径规划的首要前提,指通过对环境信息进行处理分析,构建相应的数学模型用于路径的搜索及优化。越野环境下的路径规划需考虑多种地理因素,例如气象、水文、地形、土壤质量、植被、道路、居民区等[18]。由于地表环境复杂,目前通常采用DEM模拟复杂的地貌形态,DEM实质上是一个由一系列数字填充的矩阵,表示相应位置的高度,方格的长度就是地图的精度。
越野路线搜索的前提是对越野机动范围进行通行性判断,本文利用地形坡度作为影响机动车辆通行性的重要参数,通过研究区的DEM数据计算研究区内的坡度值,并在此基础上根据越野车辆的可行坡度阈值划分地图通行区域。
本文首先采用窗口微分分析法（曲面拟合法）来计算坡度,根据网格中心单元和周围8个网格单元,形成一个3×3的窗口[19],DEM 3×3局部移动窗口如图2所示。其坡度 的计算公式为：
S l o p e = a r c t a n d z d x 2 + d z d y 2
式中： d z d x表示水平方向的变化率; d z d y是垂直方向的变化率,计算公式如下：
d z d x = z 3 - z 1 + 2 z 6 - z 4 + z 9 - z 7 / 8 g
d z d y = z 1 - z 7 + 2 z 4 - z 6 + z 7 - z 9 / 8 g
式中： z i表示栅格单元 i的高程值; g表示格网DEM数据的分辨率。
图2 DEM格网单元3×3局部移动窗口

Fig. 2 DEM grid cell 3×3 local moving window diagram

将研究区DEM数据利用上述方法求解对应的坡度值,并将其存储在栅格数据中,作为坡度图使用,如图3所示。随后结合越野车辆可行坡度阈值判断其地形通行性,若栅格像元坡度值在越野车辆坡度阈值内视为该栅格单元可通行,反之则不可通行,判断公式为：
S l o p e i ≤ V e h i c l e P a s s V a l u e → G r i d i ∈ ϑ P a s s S l o p e i > V e h i c l e P a s s V a l u e → G r i d i ∈ ϑ I m p a s s a b l e
式中： G r i d i指栅格像元 i; S l o p e i表示栅格像元 i的坡度; V e h i c l e P a s s V a l u e指车辆的坡度阈值; ϑ P a s s表示车辆可通行区域; ϑ I m p a s s a b l e表示车辆不可通行区域。通过该判断规则生成环境通行图,如图4所示,其中白色区域为可通行区域,黑色区域为不可通行区域。
图3 地形数据栅格化示意

注：右图中不同灰度表示不同地物。

Fig. 3 Schematic diagram of terrain data rasterization

图4 环境通行判断示意

注：左图不同颜色表示不同地物;右图白色区域为可通行区域,黑色区域为不可通行区域。

Fig. 4 Schematic diagram of environmental traffic judgment

2.3 算法设计思想

在路径搜索算法中,根据算法的求解质量可以将其分为精确算法和近似算法[20]。精确算法是采用全局遍历搜索保证找到最优解,但随着空间维数的增加,计算复杂性急剧增长,最终会面临维数灾难,该类算法显示出较差的可伸缩性,无法在越野环境中执行长距离路径规划任务。而近似算法是牺牲精度换取效率的方法,在可接受的精度及时间范围内获取接近精确值的近似值。为克服长距离越野路径规划计算效率缓慢的局限性,本文拟结合越野路径规划特点,寻求一种适合越野路径规划的搜索策略,实现在较短时间内得到问题的近似解。
越野环境路网信息缺失或不存在,使得目前较为成熟的基于路网信息的路径规划技术无法有效地应用在越野场景中,同时越野环境下的路径规划摆脱了路网的通行限制,可以依据地理数据进行通行性分析并用于路径规划。如图5所示,在理想化的无障碍平地区域且具有相同起点、终点的情况下,基于路网信息的路径规划与越野环境下的路径规划存在差异,二者规划效果见图5。由于两点之间距离最短,可见在该模拟中越野环境下的路径规划效果更优。
图5 路网/越野环境下路径规划对比

Fig. 5 Comparison of path planning under road network/off-road environment

综上分析,本文在Dijkstra算法的基础上展开设计：① 首先结合越野路径规划不受路网通行限制的特点、以及两点之间直线最短的理论知识,提出了以方向指向作为搜索策略的启发式算法。该算法以直线指向趋势为搜索策略,这种搜索策略可以快速求得路径解,但求解结果质量难以保证;② 为进一步降低路径规划的长度成本,提出了带有方向指向的Dijkstra分段算法,首先利用Dijkstra算法在低精度环境数据模型进行路径规划,之后将该路径进行分段,利用以方向指向作为搜索策略的启发式算法分别以每段分段路径的两端点为起终点重新进行路径规划,最后将各分段路径连通以得到最终路径,在提高算法运算效率的同时降低了路径规划的长度成本。下文分别对Dijkstra算法、以方向指向作为搜索策略的启发式算法、带有方向指向的Dijkstra分段算法进行介绍。

2.4 Dijkstra算法

Dijkstra算法是1959年由荷兰计算机科学家Edsger Wybe Dijkstra提出[21],是典型的全局遍历最短路径算法,用于计算起点到终点之间最短距离。其采用贪心算法的策略,以起始点为中心向外层扩展,直到扩展到终点为止,但由于Dijkstra算法遍历的节点过多,导致其计算效率低 。该算法的详细过程如算法1所示,其中 d i s t [ s , v i ]指起点 s到节点 v i的最短距离。
算法1 Dijkstra算法流程
输入：环境数字模型、起点 s、目标点 e
1.初始化像元,设立数组 S [ ] 、数组 V - S [ ]
2.将起点 s放入数组 S [ ],将 d i s t [ s , s ]初始化为0
3. for v i
If v i 与数组 S [ ]中节点相邻
将节点 v i其距起点s最短距离赋值于 d i s t [ s , v i ]
Else d i s t [ s , v i ] 为无穷大
4.将步骤3中 d i s t [ s , v i ] 值最小的点从数组 V - S 中取出
5.将所取出的点放入数组 S [ ]
6.循环步骤3-5,直至目标点 e放入数组 S [ ]
7.Return 起点 s到目标点 e的最短路径

2.5 以方向指向作为搜索策略的启发式算法

两点之间直线距离最短,若想构造一条理想最短路径,直线段是两点之间弧段中最短的一条。实际情况下两个节点之间存在直线段的可能性很小,但这条直线段却代表了最短路径的路线趋势。从概率上看,顺着直线段的方向的路段组成最短路径的可能性较大。
因此将方向指向作为搜索策略进行路径规划,该规划算法利用三点夹角取其最小的理论算出来的一条路径,基本思路是：利用当前点到终点的直线以及当前点各子点到终点的直线所形成的夹角,以此夹角表示其路线趋势,如图6所示为夹角示意图,图7为父子节点关系。随后将所求夹角进行比较取得其中的最小角作为路径的下一个选择点,直至路径延伸到目标点,其算法简化模型如图8所示,其中黑色部分表示障碍物,绿色部分为所规划路径,灰色部分为规划过程中所搜索过的像元,图中箭头表示子像元指向父像元。以方向指向作为搜索策略的启发式算法具体计算流程见算法2。
图6 当前点、子点、目标点夹角示意

Fig. 6 Schematic diagram of the angle between the current point, the sub point and the target point

图7 父子节点关系

Fig. 7 Parent-child relationship

图8 以方向指向作为搜索策略的启发式算法搜索简化模型

Fig. 8 Heuristic algorithm search simplified model with direction pointing as search strategy

算法2 以方向指向作为搜索策略的启发式算法流程
输入：环境数字模型、起点、目标点
1.初始化像元
2. If初始化标记为0,表示格元未被计算过
3. Else标记为1,表示为路径上的点或不可通行
4.创建容器m_openList,用于容纳路径节点
5.将起点加入m_openList中,作为当前节点
6.While（当前节点不是目标点）
7. 查看当前节点邻接可通行子节点的情况
8. If(有子节点已存在m_openList中)
9. 路径存在交叉,去掉该交叉部分
10. Else If(子节点存在可通行)
11. 计算邻接可通行子点的 F s h n值,计算见式(5)
12. 选择 F s h n值最小的邻接可通行子点
13. 添加到m_openList中,并将其作为路径的当前点
14. Else
15. 回退回上一级节点,并在剩余子节点中选最小 F s h n值,
16. 若回退到起始点则说明没找到路径
17. Return 寻路失败
18.Return m_openList
19.遍历路径上节点,获取路径信息
输出：由起点至目标点的路径

2.6 带有方向指向的Dijkstra分段算法

带有方向指向的Dijkstra分段算法将Dijkstra算法及以方向指向作为搜索策略的启发式算法相结合进行设计,改进算法的流程见图9。
图9 带有方向指向的Dijkstra分段算法流程

Fig. 9 Flowchart of Dijkstra's segmentation algorithm with directional pointing

带有方向指向的Dijkstra分段算法如下：
（1）计算起点、终点间的直线距离 D i s（式(5)）。
D i s = S t a r t P o i n t x - E n d P o i n t x 2 + S t a r t P o i n t y - E n d P o i n t y 2
式中： S t a r t P o i n t x 、 S t a r t P o i n t y分别为起点的 x 、 y坐标; E n d P o i n t x 、 E n d P o i n t y分别为目标点的 x 、 y坐标。
若该距离小于2 km,则直接运用以方向指向作为搜索策略的启发式算法进行路径搜索,该算法具体流程见算法3。
算法3 栅格单元合并算法
1. n u m = 1 / / n u m指栅格合并单元当前大小,初始为1
2. I f n u m < 64
3. f o r V i / / V i指有同一个顶点的4个栅格像元组合,且每个栅格像元仅属于一个Vi
4. i f V i所含4个栅格像元中3个或3个以上可通行
5. 将 V i 4个栅格像元合并且定义为可通行
6. e l s e 将 V i 4个栅格像元合并且定义为不可通行
7. n u m = n u m * 2
8. R e t u r n 栅格合并完成
（2）若距离Dis>2 km,则对栅格像元进行合并操作,合并为64×64的栅格大小,此时栅格单元长度为64×2 m,红框内64×64个初始的栅格像元合并为一个栅格像元,栅格单元合并算法见算法3。
（3）进行合并操作后,在该低精度栅格数据构建的环境模型下,利用Dijkstra算法在起点和终点之间进行路径规划,规划出一条较优路径。其中,Dijkstra算法的过程见算法4。
算法4 分段判断规则伪代码
1. i n t v _ n u m = r o u n d ( D i s / 10 k m ) // D i s计算见式(5)
2. I f v _ n u m < 2
3. P a r t = 2 // P a r t为分段数
4. E l s e I f
5. P a r t = v _ n u m + 1
（4）在规划出的较优路径上,依据算法4判断规则欲将路程分为几段进行规划,round()函数是四舍五入取整, P a r t为分段数,得到该数值后,将Dijkstra算法所规划的路径平均切分为若干段分段路径,如图10所示。
图10 路径分段示意

Fig. 10 Schematic diagram of path segmentation

（5）分别以每一段分段路径的两端点为起终点,采用以方向指向作为搜索策略的启发式算法重新进行路径规划,得到若干段较优分段路径。
（6）将步骤（5）中得到的各段较优分段路径连通以得到最终路径。

3 实验及结果

3.1 研究区域和数据集

本文选择地形特征明显的区域作为越野环境,山西省某市整体是黄土覆盖的山地、高原,自然条件复杂多样,过渡性质明显,适合模拟复杂的越野环境,因此选定山西省某市的DEM数据来构建越野环境,所选区域影像数据如图11(a)所示,红色框内为区域范围。在越野路径规划任务中,车辆被视为路径规划的粒子,因此所选取的DEM数据分辨率应当与车辆尺寸尽可能匹配,故本研究中使用的DEM数据分辨率为2 m,所选区域约有2亿个栅格数据,相当于实际面积约为800 km2,图11(b)为越野环境DEM栅格数据。
图11 越野环境区域数据

Fig. 11 Off-road environment area data

3.2 实验准备

本文为验证所提算法的可靠性、一致性、适用性及执行效率,在不同的路径规划应用场景下选择了不同的机动车辆进行了实验,实验使用在VS2017上编译的C++运行,分别运用Dijkstra算法、以方向指向作为搜索策略的启发式算法以及带有方向指向的Dijkstra分段算法进行比较。此外,为验证所提路径搜索算法在不同路径规划应用场景下的路径规划效果,本文选择不同距离且具有不同地形特征的路径规划任务,本文定义起终点直线距离10 km以上为长距离,10 km内又划分为短距离、较短距离、中距离、较长距离,所选规划的起终点详情见表1。
表1 路径规划实验的详细信息

Tab. 1 Details of the path planning experiment

实验编号 类别 起点经纬度 目标点经纬度 起终点直线距离/km 地形特点
1 短距离 （112.268 °E,39.373 °N） （112.287 °E,39.359 °N） 2.32 山区地段
2 较短距离 （112.303 °E,39.341 °N） （112.334 °E,39.324 °N） 3.33 平坦地段
3 中距离 （112.272 °E,39.369 °N） （112.314 °E,39.349 °N） 4.26 山区地段
4 较长距离 （112.266 °E,39.375 °N） （112.351 °E,39.361 °N） 7.67 山区、平地交错
5 长距离 （112.350 °E,39.388 °N） （112.349 °E,39.284 °N） 11.52 平坦地段
6 长距离 （112.276 °E,39.488 °N） （112.361 °E,39.298 °N） 22.33 山区、平地交错
由于不同车辆对应的可行坡度阈值不同,导致地图上规划的路线也不同,为验证算法不同机动车辆在相同应用场景下的规划效果,本文实验通过履带式、轮式2种类型的车辆进行实验和测试。根据越野车的实验数据和专家经验,履带式车辆的越野性能优于轮式车辆,对于越野车辆,轮式车辆的可行坡度阈值设定为25°,履带式车辆的可行坡度阈值设定为30°。通过2种类型的机动车辆的可行坡度阈值对越野环境通行性进行判断,判断过程见式(4),生成环境通行图,见图12所示,其中白色区域为可通行区域,黑色区域为不可通行区域,通过2种类型的车辆环境通行图比较也可以看出,可行坡度阈值高的机动车辆其通行性更优。
图12 越野环境通行图

Fig. 12 Off-road environmental traffic map

3.3 实验结果

实验从起点出发,分别运用Dijkstra算法、以方向指向作为搜索策略的启发式算法以及带有方向指向的Dijkstra分段算法,依据环境通行图确定到达终点的路径。表2列举了实验3中轮式车辆的规划路径,表3为不同场景下各算法的规划方案数据。从表2规划路径图可以看出,三类算法规划的路径走向基本一致,且规划的路径避开了不可通行区域,沿着山谷方向通行,可见在基于地形数据的情况下,规划的路径具有一定的可靠性、合理性。表3展示了2种类型的车辆在不同场景下各算法的规划方案数据,包括规划的路径长度及其路径搜索所用时间,由表中数据可知,本文所提算法在不同场景下的路径规划效率均取得了一定的提升。
表2 实验3中3种算法规划结果

Tab. 2 Planning results of three algorithms in experiment 3

算法 效果图
Dijkstra算法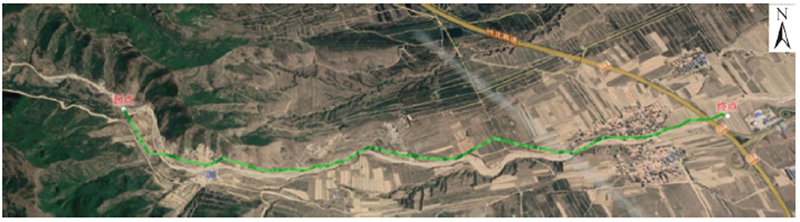
以方向指向作为搜索策略的启发式算法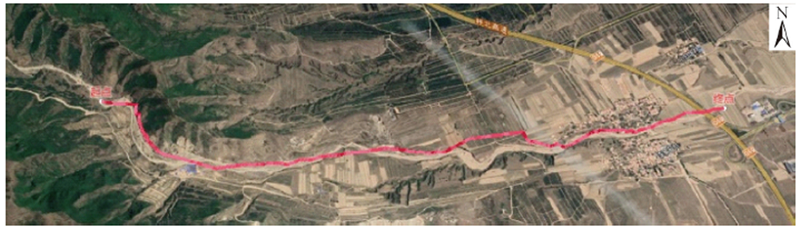
带有方向指向的Dijkstra分段算法
表3 3种算法在不同实验下的路径长度、搜索时间

Tab. 3 Path length and search time of three algorithms under different experiments

实验编号 车辆类型 Dijkstra算法 以方向指向作为搜索策略的启发式算法 带有方向指向的Dijkstra分段算法
路径长度/km 搜索时间/ s 路径长度/km 搜索时间/ s 路径长度/km 搜索时间/ s
1 轮式 2.63 82 2.78 1 2.68 1
履带式 2.63 24 2.79 1 2.81 1
2 轮式 3.53 2569 3.53 1 3.53 1
履带式 3.52 3971 3.52 2 3.52 1
3 轮式 4.77 881 5.10 342 5.08 75
履带式 4.77 2892 4.96 73 4.95 158
4 轮式 8.79 5740 9.28 2 9.20 2
履带式 8.78 6911 9.31 2 9.14 1
5 轮式 11.68 125 622 12.07 9 12.13 4
履带式 11.55 109 842 11.69 6 11.80 1
6 轮式 — >108 000 28.75 16 26.36 2
履带式 — >108 000 28.02 11 26.14 3

4 讨论与展望

将表3中数据进行可视化辅助分析及讨论,分析讨论如下：
（1）由图13可以看出随着规划距离的增长, Dijkstra算法的搜索时间急剧增长,最终面临着维数灾难,尤其是在地形特征为平坦的区域尤为明显,这意味着其无法在越野环境中执行长距离路径规划任务。
图13 Dijkstra算法规划数据可视化

Fig. 13 Dijkstra's algorithm planning data visualization diagram

（2）图14中3类算法的折线基本重合在一起,可见各类算法规划的路径长度相近。相比于规划长度最优的Dijkstra算法,实验中以方向指向作为搜索策略的启发式算法在规划长度方面平均相差了3.89%,带有方向指向的Dijkstra分段算法规划长度方面平均相差了3.38%。由上述分析可知,相比于Dijkstra算法,以方向指向作为搜索策略的启发式算法、带有方向指向的Dijkstra分段算法在规划长度上有一定增长,但相差不大,而带有方向指向的Dijkstra分段算法的平均规划长度又优于以方向指向作为搜索策略的启发式算法。
图14 3种算法规划路径长度比较

Fig. 14 Comparison diagram of three algorithm planning path lengths

（3）图15可以看出,与Dijkstra算法相比,以方向指向作为搜索策略的启发式算法计算效率在地形特征为山区的实验3中提升最少,仅提升了2.6倍,在地形特征为平坦且长距离的实验5中提升最多,提升了18 307倍;带有方向指向的Dijkstra分段算法计算效率在地形特征为山区的实验3中提升最少,仅提升了11.7倍,在地形特征为平坦且长距离的实验5中提升最多,提升了109 842倍。
图15 相比Dijkstra算法搜索效率比较

Fig. 15 Comparison chart of search efficiency compared to Dijkstra algorithm

从上述数据及图15可视化情况可知,本文所提算法相比Dijkstra算法计算效率均有不同程度的提升,提升倍数与实验案例规模相关,在小规模场景中计算效率提升了数十倍到数百倍,而在大规模场景中计算效率提升了数万倍,甚至数十万倍。由上述分析可知,以方向指向作为搜索策略的启发式算法、带有方向指向的Dijkstra分段算法相比Dijkstra算法在规划效率上得到了极大的提升,尤其在长距离、平坦等特点的路径规划场景下更为突出。
综上分析讨论可知,本文所提算法克服了在高精度越野环境模型下路径搜索缓慢的不足,极大地提高了越野路径的搜索效率,实现了在不同越野路径规划场景下的快速响应。但本文研究还存在一些缺陷,主要有以下不足：① 本文重在越野路径搜索算法方面的研究,在越野环境建模方面,通行性分析未综合考虑多因素共同影响,仅考虑了坡度,另外本文路径长度以所搜索路径节点之间二维距离累计表示,存在着一定的局限性;② 本文算法所规划的路径长度并未达到最优,稍偏离于最优解,且当栅格合并的精度过小时可能存在较大幅偏离最优解的风险,而栅格合并的精度较高时,相应的搜索时间也会增加。因此在不同的应用场景下,需要通过调节栅格合并大小参数,以此达到求解精度及求解时间的需求平衡。后续的研究将综合多因素共同影响构建环境模型,并在高效规划的基础上,进一步优化其规划效果。

5 结论

本文为克服长距离越野路径规划计算效率缓慢的局限性,提出了一种带有方向指向的Dijkstra分段算法,该算法进行了以下几点改进：① 融入方向指向为启发因子：两点之间直线距离最短,该直线段代表了最短路径的路线趋势,顺着直线段方向的路段组成最短路径的可能性较大,因此融入方向指向为启发因子,以提高算法搜索效率;② 路径分段处理：在低精度环境模型下将路径进行分段,各分段再分别进行路径搜索,从而将大规模问题分割为小规模问题,提高了计算效率。
最后利用山西省某市DEM数据构建越野环境模型,对本文方法进行了验证,实验结果表明： ①本文所提算法相比Dijkstra算法,在小规模场景中计算效率提升了数十倍到数百倍,而在大规模场景中计算效率提升了数万倍,甚至数十万倍,可见本文算法的路径搜索效率远超于Dijkstra算法,尤其在长距离规划任务场景下更为优越;②本文所提算法所搜索的路径长度逼近于Dijkstra算法规划的最优路径长度,相比于Dijkstra算法,以方向指向作为搜索策略的启发式算法规划长度平均相差3.89%,带有方向指向的Dijkstra分段算法规划长度平均相差3.38%。综上可见,本文提出的算法在执行效率上远优于Dijkstra算法,使得所提算法能够快速完成越野长途路径规划任务。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
刘爽. 基于地理信息系统的战术活动路径规划算法研究[D]. 哈尔滨: 哈尔滨工程大学, 2007.

[ Liu S. Research on the path programming Algorithm of Military Tactics Activities Based On Geography Information System[D]. Haerbin: Haerbin Engineering University, 2007. ] DOI: 10.7666/d.y1097883

DOI

[2]
赵德群, 段建英, 陈鹏宇, 等. 基于A*算法的三维地图最优路径规划[J]. 计算机系统应用, 2017, 26(7):146-152.

[ Zhao D Q, Duan J Y, Chen P Y. Optimal path planning for 3D map based on A* algorithm[J]. Computer Systems & Applications, 2017, 26(7):146-152.] DOI: 10.15888/j.cnki.csa.005859

DOI

[3]
晏福兴, 唐雪峰, 国林, 等. 鸭绿江老岭区域地质环境背景及重大灾害应急救援物资运输通行性分析[J]. 安全与环境工程, 2021, 28(5):131-136.

[ Yan F X, Tang X F, Guo L. Geological environment background of Laoling area of Yalu River and the trafficability analysis of emergency relief materials for major disasters[J]. Safety and Environmental Engineering, 2021, 28(5):131-136. ] DOI: 10.13578/j.cnki.issn.1671-1556.20200931

DOI

[4]
张德, 黄利民, 王强. 复杂环境下机动路线规划研究[J]. 测绘科学与工程, 2020, 40(3):38-44.

[ Zhang D, Huang L M, Wang Q. Study on maneuver route planning in complex environment[J]. Geomatics Science and Engineering, 2020, 40(3):38-44. ]

[5]
王登科. 部队机动的多需求路径规划[D]. 西安: 西安电子科技大学, 2020.

[ Wang D K. Multi requirement path planning for troop maneuver[D]. Xi'an: Xidian University, 2020. ]

[6]
Papadakis P. Terrain traversability analysis methods for unmanned ground vehicles: A survey[J]. Engineering Applications of Artificial Intelligence, 2013, 26(4):1373-1385. DOI: 10.1016/j.engappai.2013.01.006

DOI

[7]
Tang X R, Zhu Y K, Jiang X X. Improved A-star algorithm for robot path planning in static environment[C]. Journal of Physics: Conference Series. IOP Publishing, 2021, 1792(1):012067. DOI: 10.1088/1742-6596/1792/1/012067

DOI

[8]
Ji Y, Tanaka Y, Tamura Y, et al. Adaptive motion planning based on vehicle characteristics and regulations for off-road UGVs[J]. IEEE Transactions on Industrial Informatics, 2018, 15(1):599-611. DOI: 10.1109/TII.2018.2870662

DOI

[9]
吴天羿, 许继恒, 刘建永, 等. 多策略蚁群算法求解越野路径规划[J]. 解放军理工大学学报(自然科学版), 2014, 15(2):158-164.

[ Wu T Y, Xu J H, Liu J Y. Multi-strategy ant colony algorithm for cross-country path planning[J]. Journal of PLA University of Science and Technology (Natural Science Edition), 2014, 15(2):158-164. ]

[10]
Liu Q, Zhao L, Tan Z, et al. Global path planning for autonomous vehicles in off-road environment via an A-star algorithm[J]. International Journal of Vehicle Autonomous Systems, 2017, 13(4):330-339. DOI: 10.1504/IJVAS.2017.087148

DOI

[11]
田喜平, 苏志军, 李想, 等. 越野机动路线选择算法的改进[J]. 测绘与空间地理信息, 2013, 36(3):199-201,204.

[ Tian X P, Su Z J, Li X, et al. Algorithm improvement of cross-country route selection[J]. Geomatics & Spatial Information Technology, 2013, 36(3):199-201,204. ]

[12]
Daniel K, Nash A, Koenig S, et al. Theta*: Any-angle path planning on grids[J]. Journal of Artificial Intelligence Research, 2010, 39:533-579. DOI: 10.1613/jair.2994

DOI

[13]
林笃斌, 李欣. 基于DEM格网的改进型A*路径搜索算法[J]. 计算机工程与设计, 2011, 32(10):3414-3418.

[ Lin D B, Li X. Improved A* path-finding algorithm based on DEM-Grid[J]. Computer Engineering and Design, 2011, 32(10): 3414-3418. ] DOI: CNKI:SUN:SJSJ.0.2011-10-041

DOI

[14]
吴天羿, 许继恒, 刘建永, 等. 基于改进A*算法的越野路径规划研究[J]. 计算机应用研究, 2013, 30(6):1724-1726.

[ Wu T Y, Xu J H, Liu J Y. Research of cross-country path planning based on improved A* algorithm[J]. Application Research of Computers, 2013, 30(6):1724-1726. ] DOI: 10.3969/j.issn.1001-3695.2013.06.032

DOI

[15]
Saranya C, Unnikrishnan M, Ali S A, et al. Terrain based D∗ algorithm for path planning[J]. IFAC-PapersOnLine, 2016, 49(1):178-182. DOI: 10.1016/j.ifacol.2016.03.049

DOI

[16]
Gowdy J W, Stentz A, Hebert M. Hierarchical terrain representations for off-road navigation[C]. Mobile Robots V. International Society for Optics and Photonics, 1991, 1388: 131-140.

[17]
Ishigami G, Nagatani K, Yoshida K. Path planning and evaluation for planetary rovers based on dynamic mobility index[C]. 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems. IEEE, 2011:601-606.

[18]
黄鲁峰. 基于GIS的战场自然环境因子综合分析研究[D]. 郑州: 解放军信息工程大学, 2008.

[ Huang L F. A study of the comprehensive analysis of natural environmental factors in battlefield based on GIS[D]. Zhengzhou: The PLA Information Engineering University, 2008. ] DOI: CNKI:CDMD:2.2009.261542

DOI

[19]
袁仁进, 陈刚, 王冰冰. 地形坡度对越野机动时间影响分析[J]. 地理信息世界. 2017, 24(6):87-91.

[ Yuan R J, Chen G, Wang B B. Analysis of influence of terrain slope on off-road maneuvering time[J]. Geomatics World, 2017, 24(6): 87-91. ] DOI: 10.3969/j.issn.1672-1586.2017.06.018

DOI

[20]
范林林. 基于六角格网的越野路径规划技术方法研究[D]. 郑州: 解放军信息工程大学, 2017.

[ Fan L L. Research on cross-country path planning technology based on hexagonal grid[D]. Zhengzhou: The PLA Information Engineering University, 2017. ] DOI: CNKI:CDMD:2.1018.702497

DOI

[21]
Dijkstra E W. A note on two problems in connexion with graphs[J]. Numerische mathematik, 1959, 1(1):269-271. DOI: 10.1007/BF01386390

DOI

Options
文章导航

/

〈 〉