COVID-19疫情时空分析与建模研究进展
1
2021
... 2019年底新型冠状病毒肺炎(COVID-19)突发重大疫情暴发以来,全球开展了大量基于传染病模型的COVID-19疫情预测与防控措施的研究.截至2021年6月28日,使用“(COVID-19 OR SARS-COV-2) AND (model OR predict OR prediction OR forecast OR estimate OR simulate OR simulation OR evaluate)”作为检索式,在Web of Science中可以检索出44 774篇论文(注:含有部分临床诊断的建模论文,不属于本文的讨论范畴).这些研究在不同国家地区为不同COVID-19疫情阶段的实际防控提供了人类抵抗疾病肆虐的科学武器[1,2,3,4]. ...
COVID-19疫情时空分析与建模研究进展
1
2021
... 2019年底新型冠状病毒肺炎(COVID-19)突发重大疫情暴发以来,全球开展了大量基于传染病模型的COVID-19疫情预测与防控措施的研究.截至2021年6月28日,使用“(COVID-19 OR SARS-COV-2) AND (model OR predict OR prediction OR forecast OR estimate OR simulate OR simulation OR evaluate)”作为检索式,在Web of Science中可以检索出44 774篇论文(注:含有部分临床诊断的建模论文,不属于本文的讨论范畴).这些研究在不同国家地区为不同COVID-19疫情阶段的实际防控提供了人类抵抗疾病肆虐的科学武器[1,2,3,4]. ...
Wrong but useful: What COVID-19 epidemiologic models can and cannot tell us
1
2020
... 2019年底新型冠状病毒肺炎(COVID-19)突发重大疫情暴发以来,全球开展了大量基于传染病模型的COVID-19疫情预测与防控措施的研究.截至2021年6月28日,使用“(COVID-19 OR SARS-COV-2) AND (model OR predict OR prediction OR forecast OR estimate OR simulate OR simulation OR evaluate)”作为检索式,在Web of Science中可以检索出44 774篇论文(注:含有部分临床诊断的建模论文,不属于本文的讨论范畴).这些研究在不同国家地区为不同COVID-19疫情阶段的实际防控提供了人类抵抗疾病肆虐的科学武器[1,2,3,4]. ...
COVID-19: Challenges to GIS with Big Data
1
2020
... 2019年底新型冠状病毒肺炎(COVID-19)突发重大疫情暴发以来,全球开展了大量基于传染病模型的COVID-19疫情预测与防控措施的研究.截至2021年6月28日,使用“(COVID-19 OR SARS-COV-2) AND (model OR predict OR prediction OR forecast OR estimate OR simulate OR simulation OR evaluate)”作为检索式,在Web of Science中可以检索出44 774篇论文(注:含有部分临床诊断的建模论文,不属于本文的讨论范畴).这些研究在不同国家地区为不同COVID-19疫情阶段的实际防控提供了人类抵抗疾病肆虐的科学武器[1,2,3,4]. ...
Taking the pulse of COVID-19: A spatiotemporal perspective
1
2020
... 2019年底新型冠状病毒肺炎(COVID-19)突发重大疫情暴发以来,全球开展了大量基于传染病模型的COVID-19疫情预测与防控措施的研究.截至2021年6月28日,使用“(COVID-19 OR SARS-COV-2) AND (model OR predict OR prediction OR forecast OR estimate OR simulate OR simulation OR evaluate)”作为检索式,在Web of Science中可以检索出44 774篇论文(注:含有部分临床诊断的建模论文,不属于本文的讨论范畴).这些研究在不同国家地区为不同COVID-19疫情阶段的实际防控提供了人类抵抗疾病肆虐的科学武器[1,2,3,4]. ...
大数据时代的人类移动性研究
1
2014
... 由于宿主行为是传染病动态的决定性因素之一,疾病发展过程(尤其是呼吸道传播的疾病)会受到个体与群体的移动、活动与接触交互等复杂人群时空行为的严重影响,导致使用模型预知未来存在巨大挑战,尤其是较为长期的未来.因此,有效耦合人群时空行为对传染病模型具有重要意义.近十多年来,由于各种类型的人群移动大数据呈现出爆发式增长,其相关研究得到快速发展[5,6].相应地,此次COVID-19传染病模型研究中呈现出一个显著的特征,即大量研究在建模过程中耦合了人群时空行为,尤其是基于真实数据的人群移动特征[7,8].考虑到人群移动对传染病传播具有重要的影响,这属于传染病模型研究中的一项显著进展,也成为地理信息科学(GIS)与地理大数据在公共卫生领域的重要应用. ...
大数据时代的人类移动性研究
1
2014
... 由于宿主行为是传染病动态的决定性因素之一,疾病发展过程(尤其是呼吸道传播的疾病)会受到个体与群体的移动、活动与接触交互等复杂人群时空行为的严重影响,导致使用模型预知未来存在巨大挑战,尤其是较为长期的未来.因此,有效耦合人群时空行为对传染病模型具有重要意义.近十多年来,由于各种类型的人群移动大数据呈现出爆发式增长,其相关研究得到快速发展[5,6].相应地,此次COVID-19传染病模型研究中呈现出一个显著的特征,即大量研究在建模过程中耦合了人群时空行为,尤其是基于真实数据的人群移动特征[7,8].考虑到人群移动对传染病传播具有重要的影响,这属于传染病模型研究中的一项显著进展,也成为地理信息科学(GIS)与地理大数据在公共卫生领域的重要应用. ...
Progress in computational movement analysis - towards movement data science
1
2020
... 由于宿主行为是传染病动态的决定性因素之一,疾病发展过程(尤其是呼吸道传播的疾病)会受到个体与群体的移动、活动与接触交互等复杂人群时空行为的严重影响,导致使用模型预知未来存在巨大挑战,尤其是较为长期的未来.因此,有效耦合人群时空行为对传染病模型具有重要意义.近十多年来,由于各种类型的人群移动大数据呈现出爆发式增长,其相关研究得到快速发展[5,6].相应地,此次COVID-19传染病模型研究中呈现出一个显著的特征,即大量研究在建模过程中耦合了人群时空行为,尤其是基于真实数据的人群移动特征[7,8].考虑到人群移动对传染病传播具有重要的影响,这属于传染病模型研究中的一项显著进展,也成为地理信息科学(GIS)与地理大数据在公共卫生领域的重要应用. ...
Mobile phone data for informing public health actions across the COVID-19 pandemic life cycle
1
2020
... 由于宿主行为是传染病动态的决定性因素之一,疾病发展过程(尤其是呼吸道传播的疾病)会受到个体与群体的移动、活动与接触交互等复杂人群时空行为的严重影响,导致使用模型预知未来存在巨大挑战,尤其是较为长期的未来.因此,有效耦合人群时空行为对传染病模型具有重要意义.近十多年来,由于各种类型的人群移动大数据呈现出爆发式增长,其相关研究得到快速发展[5,6].相应地,此次COVID-19传染病模型研究中呈现出一个显著的特征,即大量研究在建模过程中耦合了人群时空行为,尤其是基于真实数据的人群移动特征[7,8].考虑到人群移动对传染病传播具有重要的影响,这属于传染病模型研究中的一项显著进展,也成为地理信息科学(GIS)与地理大数据在公共卫生领域的重要应用. ...
Multiscale dynamic human mobility flow dataset in the U.S. during the COVID-19 epidemic
2
2020
... 由于宿主行为是传染病动态的决定性因素之一,疾病发展过程(尤其是呼吸道传播的疾病)会受到个体与群体的移动、活动与接触交互等复杂人群时空行为的严重影响,导致使用模型预知未来存在巨大挑战,尤其是较为长期的未来.因此,有效耦合人群时空行为对传染病模型具有重要意义.近十多年来,由于各种类型的人群移动大数据呈现出爆发式增长,其相关研究得到快速发展[5,6].相应地,此次COVID-19传染病模型研究中呈现出一个显著的特征,即大量研究在建模过程中耦合了人群时空行为,尤其是基于真实数据的人群移动特征[7,8].考虑到人群移动对传染病传播具有重要的影响,这属于传染病模型研究中的一项显著进展,也成为地理信息科学(GIS)与地理大数据在公共卫生领域的重要应用. ...
... 自2020年1月起,由于COVID-19疫情的发生发展以及相应实施的限制人员流动、保持社交距离等非药物干预措施(Non-pharmaceutical Interventions, NPIs),全球范围内的人群流动性在不同阶段发生了不同程度的变化[22].基于多源人群移动数据,研究者从不同角度对人群移动性的变化进行了量化分析.例如,从整体的流动趋势上看,随着2020年上半年各类非药物干预措施的实施,欧洲地区各级地域统计单元的人口流入、人口流出以及区域内部的出行人次都明显减少[23].从个体的出行特征上看,2020年1—3月中国居民的出行时间、距离、交通方式、目的地类型偏好都发生了显著的变化[24].具体地,出行距离、活动范围、出行次数、目的地多样性均减少,居家时间则相应地变长[25].人群移动模式的变化不仅受到NPIs的外部影响[8,17],而且受到心理因素的内部影响.例如,相关研究表明,美国地区在实施限制政策之前,人群移动性就已经开始降低[11].结合社交媒体数据,研究者分析发现,这一自发的行为与人们对疫情的认知 有关[26,27].此外,有研究发现人群移动性的变化是不均衡的.例如,不同社会经济群体之间存在巨大且持久的差异,弱势群体移动性的变化远小于较富裕的群体[18].不同地区之间人群移动性变化也存在着差异,不平等程度高、人均收入较低的城市移动性收缩则更为强烈[28]. ...
The effect of human mobility and control measures on the COVID-19 epidemic in China
5
2020
... 一方面,针对疫情的跨地区输入性传播,通过对输入性人群进行统计建模,相关研究评估了各地区的输入性风险[9,10].例如,Xiong等[11]量化了美国各郡县的人群流入与COVID-19感染规模之间的动态正相关关系,并发现这种正相关关系在取消居家令的地区会出现逐步增强的效应.Mu等[12]使用回归模型得到结论:来自疫情中心城市的人口流入量的差异导致了城市之间COVID-19感染率的主要差异,离疫源地较近、城区人口较多的城市发病风险较高.另一方面,针对疫情本地传播,相关研究通过将研究区域内部各个单元之间的人群移动耦合于传染病传播模型中,进而揭示人群移动对疾病传播的复杂影响[13,14,15].例如,Badr等[16]发现人群流动性的降低与COVID-19病例增长率的减少有显著的正相关关系.Wang等[17]发现:在控制人群移动性的政策实施后7天内,人群流动与COVID-19传播之间的相关性会增强,但随后会减弱.Lai等[15]对中国各地日常出行网络进行建模和分析后得到:如能保持社交疏离政策,通过取消大型集会,关闭学校、工作场所这类措施以减少个体间接触率,则从2020年2月17日起取消湖北省的城际出行限制不会导致中国COVID-19病例的增加.Chang等[18]发现“超级传播者”以及弱势群体常到访的区域感染风险较高.此外,部分研究在区域内部人群移动强度的基础上进一步计算反映社会接触度的指标,如社交距离指数(Social Distancing Index, SDI)[19]、社交接触指数(Social Contact Index, SCI)[20,21]并研究其对疾病传播的作用.例如,Pan等[19]通过统计分析后得到:在SDI较高的地区,COVID-19感染率与SDI得分之间的相关性更强,Huang等[21]基于高时空精度的匿名地理位置数据构建了一个SCI,并使用该SCI指数构建了基于人群流动与接触的COVID-19传播模型,揭示了不同人群流动、人口密度、社交疏离措施对控制疫情反弹的效果. ...
... Related references of short-term epidemic prediction models coupled with human mobility
Tab. 1 | 分类 | 参考文献 | 模型 | 预测目标 | 预测的时间范围 | 研究区域 | 人群移动数据 | 评估指标 | 预测性能 |
| 人群移动一阶量 | [9] | 广义线性模型 | 每日COVID-19新增感染人数和累计感染人数 | 2020年2月1日—10日 | 中国的多个
省份 | 百度迁徙指数 | R2 | 预测截止至2020年2月10号(疫情初期)中国除武汉市外的累计病例数的R2为0.89 |
| [31] | 整合线性回归和自回归移动平均的预测模型 | 每日COVID-19输入性病例数 | 提前预测未来
12 d | 韩国的多个
省市 | 韩国电信的手机漫游数据 | 相关系数、均方根误差、平均绝对误差和平均相对误差 | 预测未来12 d后的新增输入病例人数时,该模型在第一个验证集(2020.03.28—04.30)的相关系数、均方根误差、平均绝对误差和平均相对误差分别为0.925、6.3、5.0和49.9%,在第二个验证集(2020.05.01-06.30)的相关系数、均方根误差、平均绝对误差和平均相对误差分别为0.798、4.1、2.8和22.3% |
| [32] | 多元线性回归
模型 | 每日COVID-19新增感染人数 | 2020年2月1日—2月15日(列举了分别预测1~5 d的精度) | 中国的4个城市(深圳、广州、珠海和中山市) | 百度迁徙数据 | 平均绝对误差、均方根误差和R2 | 以深圳市和广州市这两个人口流动较为频繁的城市为例,预测深圳市未来1天新增感染人数的平均绝对误差、均方根误差和R2分别为7、7.234和0.988,广州市的平均绝对误差、均方根误差和R2则分别为6.067、6.434和0.985 |
| [33] | 基于面板多元线性回归模型的行为模型和基于分布滞后模型的感染模型 | 每日COVID-19累计感染人数 | 提前预测未来1~10 d | 中国、美国、法国等80个国家的多种空间尺度(如,国家、省/州、市/县) | 谷歌社区移动性数据集、百度迁徙指数、SafeGraph社交距离指标、Facebook提供的网格间的人口移动次数 | 百分比误差的中位数(Median Percentage Error, MPE) | 以在粗粒度的空间尺度上预测未来1 d COVID-19的累计感染人数为例,全球的百分比误差中位数为0.9%,中国各省的百分比误差中位数为-0.2%,意大利各省的百分比误差中位数为0.89%,美国各州的百分比误差中位数为1.13% |
| [34] | 贝叶斯网络 | 每日COVID-19新增死亡人数 | 2020年3月30日—4月19日(列举了每周的预测精度) | 意大利、西班牙等11个国家 | 谷歌社区移动性数据集 | 平均误差以及平均相对误差 | 预测未来1周的死亡人数时,11个国家平均误差绝对值的均值为60,平均相对误差绝对值的均值则为2.5% |
| [35] | 融合弹性回归和主成分回归等多个模型的多层预测模型 | 每日COVID-19新增感染人数和累计感染人数 | 提前预测未来1、4和7 d的平均值 | 美国的多个县 | 谷歌社区移动性数据集 | 平均绝对误差、均方根误差和R2 | 预测未来1 d的新增感染人数时,R2、均方根误差和平均绝对误差分别为0.91、105和39;预测未来1 d的累计感染人数时,R2、均方根误差和平均绝对误差则分别为1.0、189和103 |
| 人群移动二阶量 | [30] | 基于图的神经
网络 | 每日COVID-19新增感染人数 | 提前预测未来2、7、14、21和28d | 美国的多个州 | 谷歌COVID-19聚合移动研究数据集 | 均方根误差和皮尔斯相关系数 | 预测未来第2 d时,均方根误差和皮尔森相关系数分别为313和0.298 |
| [36] | 时空图神经网络 | 每日COVID-19新增感染人数 | 提前预测未来1d | 美国的多个县 | 谷歌社区移动性数据集和谷歌COVID-19聚合移动研究数据集 | 均方根对数误差和皮尔斯相关系数 | 预测未来1 d时,均方根对数误差和皮尔森相关系数分别为0.0109和0.9980 |
| [37] | 时空注意力网络 | 每日COVID-19新增感染人数 | 提前预测未来5、15、20 d | 美国的多个州和多个县 | 通过重力模型计算的市/县和州之间的人群移动强度 | 平均绝对误差、均方误差和一致性相关系数 | 预测未来第5 d时,美国州级别的均方误差、平均绝对误差和一致性相关系数分别为237 412、220.5和0.84,美国县级别的均方误差、平均绝对误差和一致性相关系数分别为44177、79.8和0.66 |
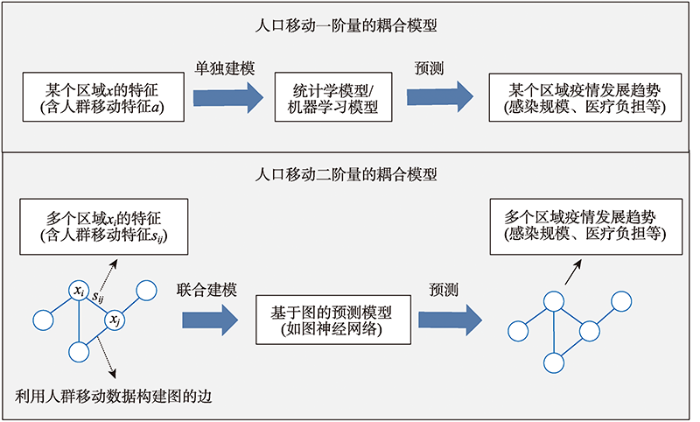
3.1 人群移动一阶量的耦合模型 人群移动一阶量的耦合模型通常基于人群移动对感染者数量等指标的影响分析,将人群移动数据作为区域的一种特征(例如,人口流入流出量、POI访问量以及外出的人口数量等)融入到建模过程中,进而实现对疫情更加有效的预测. ...
... COVID-19疫情短期预测模型中,一类研究主要采用统计模型.例如,Kraemer等[9]利用百度迁徙指数量化武汉到中国其他省份的流出人群规模,结合疾病传播特征,构建广义线性模型估计疫情早期中国不同省份的疫情规模与增长速度,预测结果的R2达到0.89,并明确在封城前武汉的人口流出仍然是中国其他区域疫情暴发的主要驱动力.Choi 等[31]使用韩国的手机漫游数据量化了全球各国到韩国各省市的人口流入,同时统计出全球COVID-19发病率与牛津COVID-19政府反应追踪指数计算得出的风险评分,将以上特征导入包含外生变量的整合移动平均自回归模型,用以预测韩国12 d后外来输入的COVID-19病例.韩国境外输入病例呈现出阶段性特征,在疫情早期主要来源地区为中国,2020年4月后其主要来源地区为欧洲,因此该模型耦合不同阶段的人群移动特征分别对韩国两个时间段的外来输入病例进行预测,预测结果的平均相对误差分别为49.9%和22.3%[31].Wang等[32]利用百度迁徙指数量化武汉与湖北省其他城市的人口流出规模,结合温湿度、空气质量等多源数据与疾病传播特征,构建固定效应的多元线性回归模型,对深圳、广州、珠海、中山四个城市疫情早期阶段的感染规模实现了比较准确的短期预测,提前 2 d预测的新增感染人数R2均可达到0.81以上,但模型预测效果随着政府管制措施的实行以及病例数量减少而有所降低.Ilin等[33]基于谷歌社区移动性数据集量化人们在不同类型地点停留时间的相对变化,基于百度迁徙指数量化中国城市之间的人口流量,结合SafeGraph基于移动设备离家平均距离得到的社交距离指标等人群移动特征与历史疫情数据,构建基于面板多元线性回归模型的行为模型与基于分布滞后模型的感染模型,分别对不同NPI下人类行为的变化和不同行为变化下COVID-19感染人数的变化进行建模,对全球多个区域不同空间尺度的COVID-19累计病例数进行预测.该模型短期预测的效果良好,以全球、美国多个州和多个县未来1 d的COVID-19累计感染人数预测为例,预测结果的百分比误差中位数(Median Percentage Error, MPE)分别为0.90%、1.13%和0.98%.但随着预测时间的增长,该模型在不同空间区域的预测误差也在不断增加,并且预测误差的变化趋势呈现了区域异质性. ...
... Related references of process simulation models coupled with human mobility
Tab. 2 | 分类 | 文献 | 研究区域 | 人群移动数据 | 模型模拟的干预措施 | 病例真实值 | 病例模拟值 | 模型效果 |
| 群体级别 | [47] | 意大利 | 人口流量调查 | 严格管控出行活动、加大疫情排查力度 | 74 386 | 约733 000 | 模拟的疾病发展曲线与实际情况吻符合程度较高 |
| [9] | 武汉 | 百度实时流动性数据 | - | 554 | 632 | 累计病例数的R2=0.99 |
| [45] | 中国375个城市 | 腾讯位置服务人口实时流动性数据 | 佩戴口罩、社交疏离、自我
隔离 | 13 562 | 约1.2万 | 预测的疾病报告率为14%,与实际武汉市疾病报告率15.8%非常接近 |
| [15] | 中国340个城市 | 百度迁徙人口流动数据 | 综合性非药物性干预 | 79 824 | 114 325 | 全国累计病例的R2=0.86,P值<0.001 |
| [21] | 中国 | 手机实时移动性和社交联系数据、腾讯移动设
备数据集 | 疫苗接种、社交疏离 | 未使用真实数据 | 未给出具体值 | 严格的干预措施可大幅降低传播能力 |
| [13] | 深圳市 | 手机移动信令数据 | 降低出行量、区域封锁 | 未使用真实数据 | R0=2.5时,峰值病例数减少了33% | 模拟的疾病发展曲线与实际情况吻合程度较高 |
| [14] | 美国康涅狄格州 | 城镇级人口流动数据,
智能手机热图,空中交
通流量 | 社交疏离 | 47 510 | 45 752~48 105 | 对康涅狄格州所有城镇模拟,实际统计的病例R2在0.907~0.924;按类别对城镇进行模拟,实际统计的病例R2为0.978~0.987 |
| [49] | 全球 | 航空与地面交通数据 | 降低本地传播率和国际旅行 | 未使用真实数据 | 未给出具体模拟值 | 严格的干预措施可大幅降低传播能力 |
| 个体级别 | [60] | 新加坡 | 交通数据 | 隔离感染者、关闭学校和工作场所 | 未使用真实数据 | R0=1.5时,7.4%的总人口感染;R0=2.0时,19.3%的总人口感染;R0=2.5时,32%的总人口感染 | 未给出具体评价指标 |
| [61] | 波士顿 | 手机位置数据 | 检测、密接追踪、居家隔离 | 未使用真实数据 | 无干预场景75%的人口被感染 | 未给出具体评价指标 |
| [62] | 纽约、西雅图 | 手机位置数据 | 无干预措施 | 每天每千人的死亡人数(未给出具体值) | 每天每千人的死亡人数(未给出具体值) | 模型结果与真实死亡人数的拟合效果较好,二者到达峰值的时间差略大于5 d |
| [63] | 澳大利亚 | 人口通勤数据 | 国际航空旅行限制、隔离感染者、居家隔离、增大社交距离、关闭学校 | 未使用真实数据 | 最佳干预场景下有8千~1万人被感染 | 未给出具体评价指标 |
| [64] | 深圳市 | 手机信令数据 | 密接追踪、及时检测、佩戴口罩、封城、逐步复工、隔离综合措施 | 418 | 416 | 每日新增发病数量的模拟值与实际报告值的RMSE=1.354;显性感染者数量在城市内各个行政区尺度上的R2=0.95 |
4.1 群体级别的耦合模型 群体级别的模型是一种长期以来广泛使用的传播动力学建模技术,其最基本的假设是研究单元内的每个个体具有相同的特征且彼此之间均匀接触,当作一个同质的群体来对待.其中,研究单元可以是同一个区域或者同一属性的人群/其他宿主等.根据感染和传播机制,模型通常由一组微分方程构建,通常是常微分方程.在COVID-19疫情中,人类感染新型冠状病毒SARS-COV-2之后存在潜隐期(Latent Period)与潜伏期(Incubation Period,对于显性感染者而言),因此,常用于COVID-19建模的基本仓室模型为SLIR与SEIR模型.以最基本的SEIR模型为例,针对给定研究单元,假设其总人口不变,其基于常微分方程的表达公式如下: ...
... 基于多个地理单元及其人群移动网络的种群模型,具有不同的空间尺度.将各个省/州看作多个地理单元,Gatto等[47]在意大利107个省际人群移动网络的基础上构建了种群SEIR模型,评估了遏制疫情传播措施的效果.将各个城市看作多个地理单元,Kraemer等[9]根据城市间的实时人群流动数据与病例旅行史,评估了输入病例在疫情传播中的作用.Li等[46]融入互联网人群迁徙数据,针对375个中国城市及其城际间人群流动构建了基于SEIR的种群模型,发现中国COVID-19疫情早期大量轻症和无症状的未记录感染者较大程度上促进了病毒传播.Lai等[15]基于互联网迁徙数据,针对340个中国城市及其城际间人群流动构建了基于SEIR的种群模型,评估了COVID-19疫情暴发以来中国实施的3类NPI的效果.该研究表明,中国采取的积极、强有力的综合性NPI在全国不同地区均取得了显著的防控效果,有效地阻断了病毒的传播,遏制了疫情的进一步扩散.Chinazzi等[48]使用COVID-19确诊病例校正了一个面向全球3200个种群的SEIR模型,进而评估了武汉出行限制措施对中国大陆及国际的疫情延缓效果.该模型中的种群集中于城市内大型交通枢纽的覆盖区域,种群之间的人群流动数据来自官方统计的航空和地面交通数据.Chen等[14]提出了一种专门针对中尺度空间单元的SEIR种群模型,不但基于huff-model量化了美国某州乡镇(town)之间的人群流动量,而且在模型中融入了居民对社交疏离的依从性(compliance)和遏制度(compliance)量化参数.将城市内部各个区域看作多个地理单元,Zhou等[13]基于手机移动定位数据,基于深圳市10个行政区构建了SEIR种群模型,并系统定量化评估了4类出行限制措施(即降低所有区域之间的出行量、封锁高风险地区、限制区域内部出行和限制感染者出行)的有效性.此外,Li等[49]在全球范围内选择了59个高风险位置(包括39个城市、10个郡县、4个省、3个地区、1个州、1个社区和1个国家)构建了基于SEIR的多尺度种群模型,融入气候驱动变量和人群移动导致的疫情空间扩散纳入各种干预方案.该研究发现,集中实施为期8周的“降低本地传播率和国际旅行”干预措施是高效且有效的,并建议对该策略从“全球干预中心”到次要高风险位置进行分层实施. ...
A simple model to assess Wuhan lock-down effect and region efforts during COVID-19 epidemic in China Mainland
1
... 一方面,针对疫情的跨地区输入性传播,通过对输入性人群进行统计建模,相关研究评估了各地区的输入性风险[9,10].例如,Xiong等[11]量化了美国各郡县的人群流入与COVID-19感染规模之间的动态正相关关系,并发现这种正相关关系在取消居家令的地区会出现逐步增强的效应.Mu等[12]使用回归模型得到结论:来自疫情中心城市的人口流入量的差异导致了城市之间COVID-19感染率的主要差异,离疫源地较近、城区人口较多的城市发病风险较高.另一方面,针对疫情本地传播,相关研究通过将研究区域内部各个单元之间的人群移动耦合于传染病传播模型中,进而揭示人群移动对疾病传播的复杂影响[13,14,15].例如,Badr等[16]发现人群流动性的降低与COVID-19病例增长率的减少有显著的正相关关系.Wang等[17]发现:在控制人群移动性的政策实施后7天内,人群流动与COVID-19传播之间的相关性会增强,但随后会减弱.Lai等[15]对中国各地日常出行网络进行建模和分析后得到:如能保持社交疏离政策,通过取消大型集会,关闭学校、工作场所这类措施以减少个体间接触率,则从2020年2月17日起取消湖北省的城际出行限制不会导致中国COVID-19病例的增加.Chang等[18]发现“超级传播者”以及弱势群体常到访的区域感染风险较高.此外,部分研究在区域内部人群移动强度的基础上进一步计算反映社会接触度的指标,如社交距离指数(Social Distancing Index, SDI)[19]、社交接触指数(Social Contact Index, SCI)[20,21]并研究其对疾病传播的作用.例如,Pan等[19]通过统计分析后得到:在SDI较高的地区,COVID-19感染率与SDI得分之间的相关性更强,Huang等[21]基于高时空精度的匿名地理位置数据构建了一个SCI,并使用该SCI指数构建了基于人群流动与接触的COVID-19传播模型,揭示了不同人群流动、人口密度、社交疏离措施对控制疫情反弹的效果. ...
Mobile device data reveal the dynamics in a positive relationship between human mobility and COVID-19 infections
2
2020
... 一方面,针对疫情的跨地区输入性传播,通过对输入性人群进行统计建模,相关研究评估了各地区的输入性风险[9,10].例如,Xiong等[11]量化了美国各郡县的人群流入与COVID-19感染规模之间的动态正相关关系,并发现这种正相关关系在取消居家令的地区会出现逐步增强的效应.Mu等[12]使用回归模型得到结论:来自疫情中心城市的人口流入量的差异导致了城市之间COVID-19感染率的主要差异,离疫源地较近、城区人口较多的城市发病风险较高.另一方面,针对疫情本地传播,相关研究通过将研究区域内部各个单元之间的人群移动耦合于传染病传播模型中,进而揭示人群移动对疾病传播的复杂影响[13,14,15].例如,Badr等[16]发现人群流动性的降低与COVID-19病例增长率的减少有显著的正相关关系.Wang等[17]发现:在控制人群移动性的政策实施后7天内,人群流动与COVID-19传播之间的相关性会增强,但随后会减弱.Lai等[15]对中国各地日常出行网络进行建模和分析后得到:如能保持社交疏离政策,通过取消大型集会,关闭学校、工作场所这类措施以减少个体间接触率,则从2020年2月17日起取消湖北省的城际出行限制不会导致中国COVID-19病例的增加.Chang等[18]发现“超级传播者”以及弱势群体常到访的区域感染风险较高.此外,部分研究在区域内部人群移动强度的基础上进一步计算反映社会接触度的指标,如社交距离指数(Social Distancing Index, SDI)[19]、社交接触指数(Social Contact Index, SCI)[20,21]并研究其对疾病传播的作用.例如,Pan等[19]通过统计分析后得到:在SDI较高的地区,COVID-19感染率与SDI得分之间的相关性更强,Huang等[21]基于高时空精度的匿名地理位置数据构建了一个SCI,并使用该SCI指数构建了基于人群流动与接触的COVID-19传播模型,揭示了不同人群流动、人口密度、社交疏离措施对控制疫情反弹的效果. ...
... 自2020年1月起,由于COVID-19疫情的发生发展以及相应实施的限制人员流动、保持社交距离等非药物干预措施(Non-pharmaceutical Interventions, NPIs),全球范围内的人群流动性在不同阶段发生了不同程度的变化[22].基于多源人群移动数据,研究者从不同角度对人群移动性的变化进行了量化分析.例如,从整体的流动趋势上看,随着2020年上半年各类非药物干预措施的实施,欧洲地区各级地域统计单元的人口流入、人口流出以及区域内部的出行人次都明显减少[23].从个体的出行特征上看,2020年1—3月中国居民的出行时间、距离、交通方式、目的地类型偏好都发生了显著的变化[24].具体地,出行距离、活动范围、出行次数、目的地多样性均减少,居家时间则相应地变长[25].人群移动模式的变化不仅受到NPIs的外部影响[8,17],而且受到心理因素的内部影响.例如,相关研究表明,美国地区在实施限制政策之前,人群移动性就已经开始降低[11].结合社交媒体数据,研究者分析发现,这一自发的行为与人们对疫情的认知 有关[26,27].此外,有研究发现人群移动性的变化是不均衡的.例如,不同社会经济群体之间存在巨大且持久的差异,弱势群体移动性的变化远小于较富裕的群体[18].不同地区之间人群移动性变化也存在着差异,不平等程度高、人均收入较低的城市移动性收缩则更为强烈[28]. ...
The interplay of spatial spread of COVID-19 and human mobility in the urban system of China during the Chinese New Year
1
2020
... 一方面,针对疫情的跨地区输入性传播,通过对输入性人群进行统计建模,相关研究评估了各地区的输入性风险[9,10].例如,Xiong等[11]量化了美国各郡县的人群流入与COVID-19感染规模之间的动态正相关关系,并发现这种正相关关系在取消居家令的地区会出现逐步增强的效应.Mu等[12]使用回归模型得到结论:来自疫情中心城市的人口流入量的差异导致了城市之间COVID-19感染率的主要差异,离疫源地较近、城区人口较多的城市发病风险较高.另一方面,针对疫情本地传播,相关研究通过将研究区域内部各个单元之间的人群移动耦合于传染病传播模型中,进而揭示人群移动对疾病传播的复杂影响[13,14,15].例如,Badr等[16]发现人群流动性的降低与COVID-19病例增长率的减少有显著的正相关关系.Wang等[17]发现:在控制人群移动性的政策实施后7天内,人群流动与COVID-19传播之间的相关性会增强,但随后会减弱.Lai等[15]对中国各地日常出行网络进行建模和分析后得到:如能保持社交疏离政策,通过取消大型集会,关闭学校、工作场所这类措施以减少个体间接触率,则从2020年2月17日起取消湖北省的城际出行限制不会导致中国COVID-19病例的增加.Chang等[18]发现“超级传播者”以及弱势群体常到访的区域感染风险较高.此外,部分研究在区域内部人群移动强度的基础上进一步计算反映社会接触度的指标,如社交距离指数(Social Distancing Index, SDI)[19]、社交接触指数(Social Contact Index, SCI)[20,21]并研究其对疾病传播的作用.例如,Pan等[19]通过统计分析后得到:在SDI较高的地区,COVID-19感染率与SDI得分之间的相关性更强,Huang等[21]基于高时空精度的匿名地理位置数据构建了一个SCI,并使用该SCI指数构建了基于人群流动与接触的COVID-19传播模型,揭示了不同人群流动、人口密度、社交疏离措施对控制疫情反弹的效果. ...
Effects of human mobility restrictions on the spread of COVID-19 in Shenzhen, China: A modelling study using mobile phone data
4
2020
... 一方面,针对疫情的跨地区输入性传播,通过对输入性人群进行统计建模,相关研究评估了各地区的输入性风险[9,10].例如,Xiong等[11]量化了美国各郡县的人群流入与COVID-19感染规模之间的动态正相关关系,并发现这种正相关关系在取消居家令的地区会出现逐步增强的效应.Mu等[12]使用回归模型得到结论:来自疫情中心城市的人口流入量的差异导致了城市之间COVID-19感染率的主要差异,离疫源地较近、城区人口较多的城市发病风险较高.另一方面,针对疫情本地传播,相关研究通过将研究区域内部各个单元之间的人群移动耦合于传染病传播模型中,进而揭示人群移动对疾病传播的复杂影响[13,14,15].例如,Badr等[16]发现人群流动性的降低与COVID-19病例增长率的减少有显著的正相关关系.Wang等[17]发现:在控制人群移动性的政策实施后7天内,人群流动与COVID-19传播之间的相关性会增强,但随后会减弱.Lai等[15]对中国各地日常出行网络进行建模和分析后得到:如能保持社交疏离政策,通过取消大型集会,关闭学校、工作场所这类措施以减少个体间接触率,则从2020年2月17日起取消湖北省的城际出行限制不会导致中国COVID-19病例的增加.Chang等[18]发现“超级传播者”以及弱势群体常到访的区域感染风险较高.此外,部分研究在区域内部人群移动强度的基础上进一步计算反映社会接触度的指标,如社交距离指数(Social Distancing Index, SDI)[19]、社交接触指数(Social Contact Index, SCI)[20,21]并研究其对疾病传播的作用.例如,Pan等[19]通过统计分析后得到:在SDI较高的地区,COVID-19感染率与SDI得分之间的相关性更强,Huang等[21]基于高时空精度的匿名地理位置数据构建了一个SCI,并使用该SCI指数构建了基于人群流动与接触的COVID-19传播模型,揭示了不同人群流动、人口密度、社交疏离措施对控制疫情反弹的效果. ...
... Related references of process simulation models coupled with human mobility
Tab. 2 | 分类 | 文献 | 研究区域 | 人群移动数据 | 模型模拟的干预措施 | 病例真实值 | 病例模拟值 | 模型效果 |
| 群体级别 | [47] | 意大利 | 人口流量调查 | 严格管控出行活动、加大疫情排查力度 | 74 386 | 约733 000 | 模拟的疾病发展曲线与实际情况吻符合程度较高 |
| [9] | 武汉 | 百度实时流动性数据 | - | 554 | 632 | 累计病例数的R2=0.99 |
| [45] | 中国375个城市 | 腾讯位置服务人口实时流动性数据 | 佩戴口罩、社交疏离、自我
隔离 | 13 562 | 约1.2万 | 预测的疾病报告率为14%,与实际武汉市疾病报告率15.8%非常接近 |
| [15] | 中国340个城市 | 百度迁徙人口流动数据 | 综合性非药物性干预 | 79 824 | 114 325 | 全国累计病例的R2=0.86,P值<0.001 |
| [21] | 中国 | 手机实时移动性和社交联系数据、腾讯移动设
备数据集 | 疫苗接种、社交疏离 | 未使用真实数据 | 未给出具体值 | 严格的干预措施可大幅降低传播能力 |
| [13] | 深圳市 | 手机移动信令数据 | 降低出行量、区域封锁 | 未使用真实数据 | R0=2.5时,峰值病例数减少了33% | 模拟的疾病发展曲线与实际情况吻合程度较高 |
| [14] | 美国康涅狄格州 | 城镇级人口流动数据,
智能手机热图,空中交
通流量 | 社交疏离 | 47 510 | 45 752~48 105 | 对康涅狄格州所有城镇模拟,实际统计的病例R2在0.907~0.924;按类别对城镇进行模拟,实际统计的病例R2为0.978~0.987 |
| [49] | 全球 | 航空与地面交通数据 | 降低本地传播率和国际旅行 | 未使用真实数据 | 未给出具体模拟值 | 严格的干预措施可大幅降低传播能力 |
| 个体级别 | [60] | 新加坡 | 交通数据 | 隔离感染者、关闭学校和工作场所 | 未使用真实数据 | R0=1.5时,7.4%的总人口感染;R0=2.0时,19.3%的总人口感染;R0=2.5时,32%的总人口感染 | 未给出具体评价指标 |
| [61] | 波士顿 | 手机位置数据 | 检测、密接追踪、居家隔离 | 未使用真实数据 | 无干预场景75%的人口被感染 | 未给出具体评价指标 |
| [62] | 纽约、西雅图 | 手机位置数据 | 无干预措施 | 每天每千人的死亡人数(未给出具体值) | 每天每千人的死亡人数(未给出具体值) | 模型结果与真实死亡人数的拟合效果较好,二者到达峰值的时间差略大于5 d |
| [63] | 澳大利亚 | 人口通勤数据 | 国际航空旅行限制、隔离感染者、居家隔离、增大社交距离、关闭学校 | 未使用真实数据 | 最佳干预场景下有8千~1万人被感染 | 未给出具体评价指标 |
| [64] | 深圳市 | 手机信令数据 | 密接追踪、及时检测、佩戴口罩、封城、逐步复工、隔离综合措施 | 418 | 416 | 每日新增发病数量的模拟值与实际报告值的RMSE=1.354;显性感染者数量在城市内各个行政区尺度上的R2=0.95 |
4.1 群体级别的耦合模型 群体级别的模型是一种长期以来广泛使用的传播动力学建模技术,其最基本的假设是研究单元内的每个个体具有相同的特征且彼此之间均匀接触,当作一个同质的群体来对待.其中,研究单元可以是同一个区域或者同一属性的人群/其他宿主等.根据感染和传播机制,模型通常由一组微分方程构建,通常是常微分方程.在COVID-19疫情中,人类感染新型冠状病毒SARS-COV-2之后存在潜隐期(Latent Period)与潜伏期(Incubation Period,对于显性感染者而言),因此,常用于COVID-19建模的基本仓室模型为SLIR与SEIR模型.以最基本的SEIR模型为例,针对给定研究单元,假设其总人口不变,其基于常微分方程的表达公式如下: ...
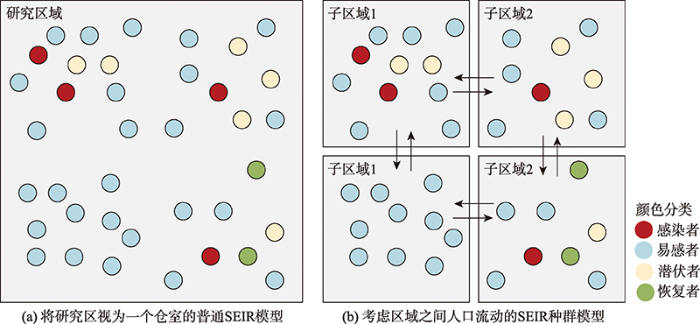
... 如图2所示,在群体级别的模型中,研究单元不但可以是单个地理单元(如国家、省份、城市),即将整个研究区视为同一种群[44,45];也可以是多个地理单元,即将不同地理单元的人群视为不同种群Meta-population),对每一个种群都构建微分方程组.由此,基于不同地理单元种群的模型可以天然地结合种群之间的人群移动,通过在每个种群的模型中添加由于人群移动造成的感染状态变化的数学表达,构建基于人群移动的种群模型,即一种典型的基于网络的种群模型(Network-based Meta-population Model)[13-14,46].由于国家、城市及城市内部不同尺度的人群移动在此次COVID-19疫情扩散中产生了显著影响,研究者面向不同研究目的、从不同角度构建了大量耦合人群移动的种群模型. ...
... 基于多个地理单元及其人群移动网络的种群模型,具有不同的空间尺度.将各个省/州看作多个地理单元,Gatto等[47]在意大利107个省际人群移动网络的基础上构建了种群SEIR模型,评估了遏制疫情传播措施的效果.将各个城市看作多个地理单元,Kraemer等[9]根据城市间的实时人群流动数据与病例旅行史,评估了输入病例在疫情传播中的作用.Li等[46]融入互联网人群迁徙数据,针对375个中国城市及其城际间人群流动构建了基于SEIR的种群模型,发现中国COVID-19疫情早期大量轻症和无症状的未记录感染者较大程度上促进了病毒传播.Lai等[15]基于互联网迁徙数据,针对340个中国城市及其城际间人群流动构建了基于SEIR的种群模型,评估了COVID-19疫情暴发以来中国实施的3类NPI的效果.该研究表明,中国采取的积极、强有力的综合性NPI在全国不同地区均取得了显著的防控效果,有效地阻断了病毒的传播,遏制了疫情的进一步扩散.Chinazzi等[48]使用COVID-19确诊病例校正了一个面向全球3200个种群的SEIR模型,进而评估了武汉出行限制措施对中国大陆及国际的疫情延缓效果.该模型中的种群集中于城市内大型交通枢纽的覆盖区域,种群之间的人群流动数据来自官方统计的航空和地面交通数据.Chen等[14]提出了一种专门针对中尺度空间单元的SEIR种群模型,不但基于huff-model量化了美国某州乡镇(town)之间的人群流动量,而且在模型中融入了居民对社交疏离的依从性(compliance)和遏制度(compliance)量化参数.将城市内部各个区域看作多个地理单元,Zhou等[13]基于手机移动定位数据,基于深圳市10个行政区构建了SEIR种群模型,并系统定量化评估了4类出行限制措施(即降低所有区域之间的出行量、封锁高风险地区、限制区域内部出行和限制感染者出行)的有效性.此外,Li等[49]在全球范围内选择了59个高风险位置(包括39个城市、10个郡县、4个省、3个地区、1个州、1个社区和1个国家)构建了基于SEIR的多尺度种群模型,融入气候驱动变量和人群移动导致的疫情空间扩散纳入各种干预方案.该研究发现,集中实施为期8周的“降低本地传播率和国际旅行”干预措施是高效且有效的,并建议对该策略从“全球干预中心”到次要高风险位置进行分层实施. ...
Compliance and containment in social distancing: Mathematical modeling of COVID-19 across townships
4
2021
... 一方面,针对疫情的跨地区输入性传播,通过对输入性人群进行统计建模,相关研究评估了各地区的输入性风险[9,10].例如,Xiong等[11]量化了美国各郡县的人群流入与COVID-19感染规模之间的动态正相关关系,并发现这种正相关关系在取消居家令的地区会出现逐步增强的效应.Mu等[12]使用回归模型得到结论:来自疫情中心城市的人口流入量的差异导致了城市之间COVID-19感染率的主要差异,离疫源地较近、城区人口较多的城市发病风险较高.另一方面,针对疫情本地传播,相关研究通过将研究区域内部各个单元之间的人群移动耦合于传染病传播模型中,进而揭示人群移动对疾病传播的复杂影响[13,14,15].例如,Badr等[16]发现人群流动性的降低与COVID-19病例增长率的减少有显著的正相关关系.Wang等[17]发现:在控制人群移动性的政策实施后7天内,人群流动与COVID-19传播之间的相关性会增强,但随后会减弱.Lai等[15]对中国各地日常出行网络进行建模和分析后得到:如能保持社交疏离政策,通过取消大型集会,关闭学校、工作场所这类措施以减少个体间接触率,则从2020年2月17日起取消湖北省的城际出行限制不会导致中国COVID-19病例的增加.Chang等[18]发现“超级传播者”以及弱势群体常到访的区域感染风险较高.此外,部分研究在区域内部人群移动强度的基础上进一步计算反映社会接触度的指标,如社交距离指数(Social Distancing Index, SDI)[19]、社交接触指数(Social Contact Index, SCI)[20,21]并研究其对疾病传播的作用.例如,Pan等[19]通过统计分析后得到:在SDI较高的地区,COVID-19感染率与SDI得分之间的相关性更强,Huang等[21]基于高时空精度的匿名地理位置数据构建了一个SCI,并使用该SCI指数构建了基于人群流动与接触的COVID-19传播模型,揭示了不同人群流动、人口密度、社交疏离措施对控制疫情反弹的效果. ...
... Related references of process simulation models coupled with human mobility
Tab. 2 | 分类 | 文献 | 研究区域 | 人群移动数据 | 模型模拟的干预措施 | 病例真实值 | 病例模拟值 | 模型效果 |
| 群体级别 | [47] | 意大利 | 人口流量调查 | 严格管控出行活动、加大疫情排查力度 | 74 386 | 约733 000 | 模拟的疾病发展曲线与实际情况吻符合程度较高 |
| [9] | 武汉 | 百度实时流动性数据 | - | 554 | 632 | 累计病例数的R2=0.99 |
| [45] | 中国375个城市 | 腾讯位置服务人口实时流动性数据 | 佩戴口罩、社交疏离、自我
隔离 | 13 562 | 约1.2万 | 预测的疾病报告率为14%,与实际武汉市疾病报告率15.8%非常接近 |
| [15] | 中国340个城市 | 百度迁徙人口流动数据 | 综合性非药物性干预 | 79 824 | 114 325 | 全国累计病例的R2=0.86,P值<0.001 |
| [21] | 中国 | 手机实时移动性和社交联系数据、腾讯移动设
备数据集 | 疫苗接种、社交疏离 | 未使用真实数据 | 未给出具体值 | 严格的干预措施可大幅降低传播能力 |
| [13] | 深圳市 | 手机移动信令数据 | 降低出行量、区域封锁 | 未使用真实数据 | R0=2.5时,峰值病例数减少了33% | 模拟的疾病发展曲线与实际情况吻合程度较高 |
| [14] | 美国康涅狄格州 | 城镇级人口流动数据,
智能手机热图,空中交
通流量 | 社交疏离 | 47 510 | 45 752~48 105 | 对康涅狄格州所有城镇模拟,实际统计的病例R2在0.907~0.924;按类别对城镇进行模拟,实际统计的病例R2为0.978~0.987 |
| [49] | 全球 | 航空与地面交通数据 | 降低本地传播率和国际旅行 | 未使用真实数据 | 未给出具体模拟值 | 严格的干预措施可大幅降低传播能力 |
| 个体级别 | [60] | 新加坡 | 交通数据 | 隔离感染者、关闭学校和工作场所 | 未使用真实数据 | R0=1.5时,7.4%的总人口感染;R0=2.0时,19.3%的总人口感染;R0=2.5时,32%的总人口感染 | 未给出具体评价指标 |
| [61] | 波士顿 | 手机位置数据 | 检测、密接追踪、居家隔离 | 未使用真实数据 | 无干预场景75%的人口被感染 | 未给出具体评价指标 |
| [62] | 纽约、西雅图 | 手机位置数据 | 无干预措施 | 每天每千人的死亡人数(未给出具体值) | 每天每千人的死亡人数(未给出具体值) | 模型结果与真实死亡人数的拟合效果较好,二者到达峰值的时间差略大于5 d |
| [63] | 澳大利亚 | 人口通勤数据 | 国际航空旅行限制、隔离感染者、居家隔离、增大社交距离、关闭学校 | 未使用真实数据 | 最佳干预场景下有8千~1万人被感染 | 未给出具体评价指标 |
| [64] | 深圳市 | 手机信令数据 | 密接追踪、及时检测、佩戴口罩、封城、逐步复工、隔离综合措施 | 418 | 416 | 每日新增发病数量的模拟值与实际报告值的RMSE=1.354;显性感染者数量在城市内各个行政区尺度上的R2=0.95 |
4.1 群体级别的耦合模型 群体级别的模型是一种长期以来广泛使用的传播动力学建模技术,其最基本的假设是研究单元内的每个个体具有相同的特征且彼此之间均匀接触,当作一个同质的群体来对待.其中,研究单元可以是同一个区域或者同一属性的人群/其他宿主等.根据感染和传播机制,模型通常由一组微分方程构建,通常是常微分方程.在COVID-19疫情中,人类感染新型冠状病毒SARS-COV-2之后存在潜隐期(Latent Period)与潜伏期(Incubation Period,对于显性感染者而言),因此,常用于COVID-19建模的基本仓室模型为SLIR与SEIR模型.以最基本的SEIR模型为例,针对给定研究单元,假设其总人口不变,其基于常微分方程的表达公式如下: ...
... 如图2所示,在群体级别的模型中,研究单元不但可以是单个地理单元(如国家、省份、城市),即将整个研究区视为同一种群[44,45];也可以是多个地理单元,即将不同地理单元的人群视为不同种群Meta-population),对每一个种群都构建微分方程组.由此,基于不同地理单元种群的模型可以天然地结合种群之间的人群移动,通过在每个种群的模型中添加由于人群移动造成的感染状态变化的数学表达,构建基于人群移动的种群模型,即一种典型的基于网络的种群模型(Network-based Meta-population Model)[13-14,46].由于国家、城市及城市内部不同尺度的人群移动在此次COVID-19疫情扩散中产生了显著影响,研究者面向不同研究目的、从不同角度构建了大量耦合人群移动的种群模型. ...
... 基于多个地理单元及其人群移动网络的种群模型,具有不同的空间尺度.将各个省/州看作多个地理单元,Gatto等[47]在意大利107个省际人群移动网络的基础上构建了种群SEIR模型,评估了遏制疫情传播措施的效果.将各个城市看作多个地理单元,Kraemer等[9]根据城市间的实时人群流动数据与病例旅行史,评估了输入病例在疫情传播中的作用.Li等[46]融入互联网人群迁徙数据,针对375个中国城市及其城际间人群流动构建了基于SEIR的种群模型,发现中国COVID-19疫情早期大量轻症和无症状的未记录感染者较大程度上促进了病毒传播.Lai等[15]基于互联网迁徙数据,针对340个中国城市及其城际间人群流动构建了基于SEIR的种群模型,评估了COVID-19疫情暴发以来中国实施的3类NPI的效果.该研究表明,中国采取的积极、强有力的综合性NPI在全国不同地区均取得了显著的防控效果,有效地阻断了病毒的传播,遏制了疫情的进一步扩散.Chinazzi等[48]使用COVID-19确诊病例校正了一个面向全球3200个种群的SEIR模型,进而评估了武汉出行限制措施对中国大陆及国际的疫情延缓效果.该模型中的种群集中于城市内大型交通枢纽的覆盖区域,种群之间的人群流动数据来自官方统计的航空和地面交通数据.Chen等[14]提出了一种专门针对中尺度空间单元的SEIR种群模型,不但基于huff-model量化了美国某州乡镇(town)之间的人群流动量,而且在模型中融入了居民对社交疏离的依从性(compliance)和遏制度(compliance)量化参数.将城市内部各个区域看作多个地理单元,Zhou等[13]基于手机移动定位数据,基于深圳市10个行政区构建了SEIR种群模型,并系统定量化评估了4类出行限制措施(即降低所有区域之间的出行量、封锁高风险地区、限制区域内部出行和限制感染者出行)的有效性.此外,Li等[49]在全球范围内选择了59个高风险位置(包括39个城市、10个郡县、4个省、3个地区、1个州、1个社区和1个国家)构建了基于SEIR的多尺度种群模型,融入气候驱动变量和人群移动导致的疫情空间扩散纳入各种干预方案.该研究发现,集中实施为期8周的“降低本地传播率和国际旅行”干预措施是高效且有效的,并建议对该策略从“全球干预中心”到次要高风险位置进行分层实施. ...
Effect of non-pharmaceutical interventions to contain COVID-19 in China
4
2020
... 一方面,针对疫情的跨地区输入性传播,通过对输入性人群进行统计建模,相关研究评估了各地区的输入性风险[9,10].例如,Xiong等[11]量化了美国各郡县的人群流入与COVID-19感染规模之间的动态正相关关系,并发现这种正相关关系在取消居家令的地区会出现逐步增强的效应.Mu等[12]使用回归模型得到结论:来自疫情中心城市的人口流入量的差异导致了城市之间COVID-19感染率的主要差异,离疫源地较近、城区人口较多的城市发病风险较高.另一方面,针对疫情本地传播,相关研究通过将研究区域内部各个单元之间的人群移动耦合于传染病传播模型中,进而揭示人群移动对疾病传播的复杂影响[13,14,15].例如,Badr等[16]发现人群流动性的降低与COVID-19病例增长率的减少有显著的正相关关系.Wang等[17]发现:在控制人群移动性的政策实施后7天内,人群流动与COVID-19传播之间的相关性会增强,但随后会减弱.Lai等[15]对中国各地日常出行网络进行建模和分析后得到:如能保持社交疏离政策,通过取消大型集会,关闭学校、工作场所这类措施以减少个体间接触率,则从2020年2月17日起取消湖北省的城际出行限制不会导致中国COVID-19病例的增加.Chang等[18]发现“超级传播者”以及弱势群体常到访的区域感染风险较高.此外,部分研究在区域内部人群移动强度的基础上进一步计算反映社会接触度的指标,如社交距离指数(Social Distancing Index, SDI)[19]、社交接触指数(Social Contact Index, SCI)[20,21]并研究其对疾病传播的作用.例如,Pan等[19]通过统计分析后得到:在SDI较高的地区,COVID-19感染率与SDI得分之间的相关性更强,Huang等[21]基于高时空精度的匿名地理位置数据构建了一个SCI,并使用该SCI指数构建了基于人群流动与接触的COVID-19传播模型,揭示了不同人群流动、人口密度、社交疏离措施对控制疫情反弹的效果. ...
... [15]对中国各地日常出行网络进行建模和分析后得到:如能保持社交疏离政策,通过取消大型集会,关闭学校、工作场所这类措施以减少个体间接触率,则从2020年2月17日起取消湖北省的城际出行限制不会导致中国COVID-19病例的增加.Chang等[18]发现“超级传播者”以及弱势群体常到访的区域感染风险较高.此外,部分研究在区域内部人群移动强度的基础上进一步计算反映社会接触度的指标,如社交距离指数(Social Distancing Index, SDI)[19]、社交接触指数(Social Contact Index, SCI)[20,21]并研究其对疾病传播的作用.例如,Pan等[19]通过统计分析后得到:在SDI较高的地区,COVID-19感染率与SDI得分之间的相关性更强,Huang等[21]基于高时空精度的匿名地理位置数据构建了一个SCI,并使用该SCI指数构建了基于人群流动与接触的COVID-19传播模型,揭示了不同人群流动、人口密度、社交疏离措施对控制疫情反弹的效果. ...
... Related references of process simulation models coupled with human mobility
Tab. 2 | 分类 | 文献 | 研究区域 | 人群移动数据 | 模型模拟的干预措施 | 病例真实值 | 病例模拟值 | 模型效果 |
| 群体级别 | [47] | 意大利 | 人口流量调查 | 严格管控出行活动、加大疫情排查力度 | 74 386 | 约733 000 | 模拟的疾病发展曲线与实际情况吻符合程度较高 |
| [9] | 武汉 | 百度实时流动性数据 | - | 554 | 632 | 累计病例数的R2=0.99 |
| [45] | 中国375个城市 | 腾讯位置服务人口实时流动性数据 | 佩戴口罩、社交疏离、自我
隔离 | 13 562 | 约1.2万 | 预测的疾病报告率为14%,与实际武汉市疾病报告率15.8%非常接近 |
| [15] | 中国340个城市 | 百度迁徙人口流动数据 | 综合性非药物性干预 | 79 824 | 114 325 | 全国累计病例的R2=0.86,P值<0.001 |
| [21] | 中国 | 手机实时移动性和社交联系数据、腾讯移动设
备数据集 | 疫苗接种、社交疏离 | 未使用真实数据 | 未给出具体值 | 严格的干预措施可大幅降低传播能力 |
| [13] | 深圳市 | 手机移动信令数据 | 降低出行量、区域封锁 | 未使用真实数据 | R0=2.5时,峰值病例数减少了33% | 模拟的疾病发展曲线与实际情况吻合程度较高 |
| [14] | 美国康涅狄格州 | 城镇级人口流动数据,
智能手机热图,空中交
通流量 | 社交疏离 | 47 510 | 45 752~48 105 | 对康涅狄格州所有城镇模拟,实际统计的病例R2在0.907~0.924;按类别对城镇进行模拟,实际统计的病例R2为0.978~0.987 |
| [49] | 全球 | 航空与地面交通数据 | 降低本地传播率和国际旅行 | 未使用真实数据 | 未给出具体模拟值 | 严格的干预措施可大幅降低传播能力 |
| 个体级别 | [60] | 新加坡 | 交通数据 | 隔离感染者、关闭学校和工作场所 | 未使用真实数据 | R0=1.5时,7.4%的总人口感染;R0=2.0时,19.3%的总人口感染;R0=2.5时,32%的总人口感染 | 未给出具体评价指标 |
| [61] | 波士顿 | 手机位置数据 | 检测、密接追踪、居家隔离 | 未使用真实数据 | 无干预场景75%的人口被感染 | 未给出具体评价指标 |
| [62] | 纽约、西雅图 | 手机位置数据 | 无干预措施 | 每天每千人的死亡人数(未给出具体值) | 每天每千人的死亡人数(未给出具体值) | 模型结果与真实死亡人数的拟合效果较好,二者到达峰值的时间差略大于5 d |
| [63] | 澳大利亚 | 人口通勤数据 | 国际航空旅行限制、隔离感染者、居家隔离、增大社交距离、关闭学校 | 未使用真实数据 | 最佳干预场景下有8千~1万人被感染 | 未给出具体评价指标 |
| [64] | 深圳市 | 手机信令数据 | 密接追踪、及时检测、佩戴口罩、封城、逐步复工、隔离综合措施 | 418 | 416 | 每日新增发病数量的模拟值与实际报告值的RMSE=1.354;显性感染者数量在城市内各个行政区尺度上的R2=0.95 |
4.1 群体级别的耦合模型 群体级别的模型是一种长期以来广泛使用的传播动力学建模技术,其最基本的假设是研究单元内的每个个体具有相同的特征且彼此之间均匀接触,当作一个同质的群体来对待.其中,研究单元可以是同一个区域或者同一属性的人群/其他宿主等.根据感染和传播机制,模型通常由一组微分方程构建,通常是常微分方程.在COVID-19疫情中,人类感染新型冠状病毒SARS-COV-2之后存在潜隐期(Latent Period)与潜伏期(Incubation Period,对于显性感染者而言),因此,常用于COVID-19建模的基本仓室模型为SLIR与SEIR模型.以最基本的SEIR模型为例,针对给定研究单元,假设其总人口不变,其基于常微分方程的表达公式如下: ...
... 基于多个地理单元及其人群移动网络的种群模型,具有不同的空间尺度.将各个省/州看作多个地理单元,Gatto等[47]在意大利107个省际人群移动网络的基础上构建了种群SEIR模型,评估了遏制疫情传播措施的效果.将各个城市看作多个地理单元,Kraemer等[9]根据城市间的实时人群流动数据与病例旅行史,评估了输入病例在疫情传播中的作用.Li等[46]融入互联网人群迁徙数据,针对375个中国城市及其城际间人群流动构建了基于SEIR的种群模型,发现中国COVID-19疫情早期大量轻症和无症状的未记录感染者较大程度上促进了病毒传播.Lai等[15]基于互联网迁徙数据,针对340个中国城市及其城际间人群流动构建了基于SEIR的种群模型,评估了COVID-19疫情暴发以来中国实施的3类NPI的效果.该研究表明,中国采取的积极、强有力的综合性NPI在全国不同地区均取得了显著的防控效果,有效地阻断了病毒的传播,遏制了疫情的进一步扩散.Chinazzi等[48]使用COVID-19确诊病例校正了一个面向全球3200个种群的SEIR模型,进而评估了武汉出行限制措施对中国大陆及国际的疫情延缓效果.该模型中的种群集中于城市内大型交通枢纽的覆盖区域,种群之间的人群流动数据来自官方统计的航空和地面交通数据.Chen等[14]提出了一种专门针对中尺度空间单元的SEIR种群模型,不但基于huff-model量化了美国某州乡镇(town)之间的人群流动量,而且在模型中融入了居民对社交疏离的依从性(compliance)和遏制度(compliance)量化参数.将城市内部各个区域看作多个地理单元,Zhou等[13]基于手机移动定位数据,基于深圳市10个行政区构建了SEIR种群模型,并系统定量化评估了4类出行限制措施(即降低所有区域之间的出行量、封锁高风险地区、限制区域内部出行和限制感染者出行)的有效性.此外,Li等[49]在全球范围内选择了59个高风险位置(包括39个城市、10个郡县、4个省、3个地区、1个州、1个社区和1个国家)构建了基于SEIR的多尺度种群模型,融入气候驱动变量和人群移动导致的疫情空间扩散纳入各种干预方案.该研究发现,集中实施为期8周的“降低本地传播率和国际旅行”干预措施是高效且有效的,并建议对该策略从“全球干预中心”到次要高风险位置进行分层实施. ...
Association between mobility patterns and COVID-19 transmission in the USA: A mathematical modelling study
1
2020
... 一方面,针对疫情的跨地区输入性传播,通过对输入性人群进行统计建模,相关研究评估了各地区的输入性风险[9,10].例如,Xiong等[11]量化了美国各郡县的人群流入与COVID-19感染规模之间的动态正相关关系,并发现这种正相关关系在取消居家令的地区会出现逐步增强的效应.Mu等[12]使用回归模型得到结论:来自疫情中心城市的人口流入量的差异导致了城市之间COVID-19感染率的主要差异,离疫源地较近、城区人口较多的城市发病风险较高.另一方面,针对疫情本地传播,相关研究通过将研究区域内部各个单元之间的人群移动耦合于传染病传播模型中,进而揭示人群移动对疾病传播的复杂影响[13,14,15].例如,Badr等[16]发现人群流动性的降低与COVID-19病例增长率的减少有显著的正相关关系.Wang等[17]发现:在控制人群移动性的政策实施后7天内,人群流动与COVID-19传播之间的相关性会增强,但随后会减弱.Lai等[15]对中国各地日常出行网络进行建模和分析后得到:如能保持社交疏离政策,通过取消大型集会,关闭学校、工作场所这类措施以减少个体间接触率,则从2020年2月17日起取消湖北省的城际出行限制不会导致中国COVID-19病例的增加.Chang等[18]发现“超级传播者”以及弱势群体常到访的区域感染风险较高.此外,部分研究在区域内部人群移动强度的基础上进一步计算反映社会接触度的指标,如社交距离指数(Social Distancing Index, SDI)[19]、社交接触指数(Social Contact Index, SCI)[20,21]并研究其对疾病传播的作用.例如,Pan等[19]通过统计分析后得到:在SDI较高的地区,COVID-19感染率与SDI得分之间的相关性更强,Huang等[21]基于高时空精度的匿名地理位置数据构建了一个SCI,并使用该SCI指数构建了基于人群流动与接触的COVID-19传播模型,揭示了不同人群流动、人口密度、社交疏离措施对控制疫情反弹的效果. ...
Examining the change of human mobility adherent to social restriction policies and its effect on COVID-19 cases in Australia
3
2020
... 一方面,针对疫情的跨地区输入性传播,通过对输入性人群进行统计建模,相关研究评估了各地区的输入性风险[9,10].例如,Xiong等[11]量化了美国各郡县的人群流入与COVID-19感染规模之间的动态正相关关系,并发现这种正相关关系在取消居家令的地区会出现逐步增强的效应.Mu等[12]使用回归模型得到结论:来自疫情中心城市的人口流入量的差异导致了城市之间COVID-19感染率的主要差异,离疫源地较近、城区人口较多的城市发病风险较高.另一方面,针对疫情本地传播,相关研究通过将研究区域内部各个单元之间的人群移动耦合于传染病传播模型中,进而揭示人群移动对疾病传播的复杂影响[13,14,15].例如,Badr等[16]发现人群流动性的降低与COVID-19病例增长率的减少有显著的正相关关系.Wang等[17]发现:在控制人群移动性的政策实施后7天内,人群流动与COVID-19传播之间的相关性会增强,但随后会减弱.Lai等[15]对中国各地日常出行网络进行建模和分析后得到:如能保持社交疏离政策,通过取消大型集会,关闭学校、工作场所这类措施以减少个体间接触率,则从2020年2月17日起取消湖北省的城际出行限制不会导致中国COVID-19病例的增加.Chang等[18]发现“超级传播者”以及弱势群体常到访的区域感染风险较高.此外,部分研究在区域内部人群移动强度的基础上进一步计算反映社会接触度的指标,如社交距离指数(Social Distancing Index, SDI)[19]、社交接触指数(Social Contact Index, SCI)[20,21]并研究其对疾病传播的作用.例如,Pan等[19]通过统计分析后得到:在SDI较高的地区,COVID-19感染率与SDI得分之间的相关性更强,Huang等[21]基于高时空精度的匿名地理位置数据构建了一个SCI,并使用该SCI指数构建了基于人群流动与接触的COVID-19传播模型,揭示了不同人群流动、人口密度、社交疏离措施对控制疫情反弹的效果. ...
... 自2020年1月起,由于COVID-19疫情的发生发展以及相应实施的限制人员流动、保持社交距离等非药物干预措施(Non-pharmaceutical Interventions, NPIs),全球范围内的人群流动性在不同阶段发生了不同程度的变化[22].基于多源人群移动数据,研究者从不同角度对人群移动性的变化进行了量化分析.例如,从整体的流动趋势上看,随着2020年上半年各类非药物干预措施的实施,欧洲地区各级地域统计单元的人口流入、人口流出以及区域内部的出行人次都明显减少[23].从个体的出行特征上看,2020年1—3月中国居民的出行时间、距离、交通方式、目的地类型偏好都发生了显著的变化[24].具体地,出行距离、活动范围、出行次数、目的地多样性均减少,居家时间则相应地变长[25].人群移动模式的变化不仅受到NPIs的外部影响[8,17],而且受到心理因素的内部影响.例如,相关研究表明,美国地区在实施限制政策之前,人群移动性就已经开始降低[11].结合社交媒体数据,研究者分析发现,这一自发的行为与人们对疫情的认知 有关[26,27].此外,有研究发现人群移动性的变化是不均衡的.例如,不同社会经济群体之间存在巨大且持久的差异,弱势群体移动性的变化远小于较富裕的群体[18].不同地区之间人群移动性变化也存在着差异,不平等程度高、人均收入较低的城市移动性收缩则更为强烈[28]. ...
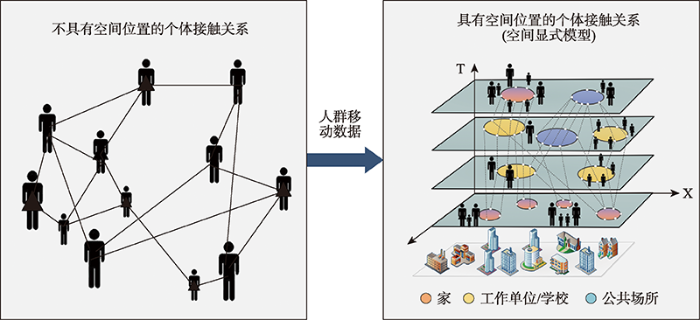
... COVID-19建模中所使用的人群移动数据大多以匿名的、聚合的形式被分析,数据来源丰富,包括电信运营商提供的手机位置数据、互联网企业(例如百度、腾讯、谷歌、Cuebiq、SafeGraph等)提供的位置数据、含有地理标记的社交媒体数据(如Twitter、新浪微博等)以及其他开源数据集.基于此,常规的流动性指标易于被提取,例如:出行时长、出行距离、目的地类型、区域间人流量等.相关研究也考虑了不同社会经济属性人群的流动性[18,20],不同类型微观场所人流量[17],不同地区的社交距离指 数[19].然而,COVID-19在人群中的传播从根本上取决于人际间不同接触模式的发生效率与时空分布[67],而聚合层面上的整体流动性特征并不能从机理层面表达家庭、写字楼、工厂、商场、学校、公共交通等各类场景下的复杂接触模式.因此,面向复杂社会接触模式的分析与建模至关重要,如何利用大数据或者大小数据相结合的更加智能的方式对其进行突破成为一项挑战.此外,人们对疫情的认知以及干预措施的实施均会对人群流动以及社会接触模式产生不可忽视的影响,如何基于真实数据对这种复杂的人群时空行为响应进行耦合建模,进而形成动态反馈,也成为需要进一步研究的内容.除此之外,不同类型节假日与大型活动下产生的特殊的人口流动与接触模式也值得被耦合建模分析.综上,虽然当前的传染病模型已经在多个方面对人群移动进行了耦合建模,但是由于人群时空行为的复杂性,导致该方向的研究仍然面临巨大挑战,亟需进一步发展. ...
Mobility network models of COVID-19 explain inequities and inform reopening
3
2021
... 一方面,针对疫情的跨地区输入性传播,通过对输入性人群进行统计建模,相关研究评估了各地区的输入性风险[9,10].例如,Xiong等[11]量化了美国各郡县的人群流入与COVID-19感染规模之间的动态正相关关系,并发现这种正相关关系在取消居家令的地区会出现逐步增强的效应.Mu等[12]使用回归模型得到结论:来自疫情中心城市的人口流入量的差异导致了城市之间COVID-19感染率的主要差异,离疫源地较近、城区人口较多的城市发病风险较高.另一方面,针对疫情本地传播,相关研究通过将研究区域内部各个单元之间的人群移动耦合于传染病传播模型中,进而揭示人群移动对疾病传播的复杂影响[13,14,15].例如,Badr等[16]发现人群流动性的降低与COVID-19病例增长率的减少有显著的正相关关系.Wang等[17]发现:在控制人群移动性的政策实施后7天内,人群流动与COVID-19传播之间的相关性会增强,但随后会减弱.Lai等[15]对中国各地日常出行网络进行建模和分析后得到:如能保持社交疏离政策,通过取消大型集会,关闭学校、工作场所这类措施以减少个体间接触率,则从2020年2月17日起取消湖北省的城际出行限制不会导致中国COVID-19病例的增加.Chang等[18]发现“超级传播者”以及弱势群体常到访的区域感染风险较高.此外,部分研究在区域内部人群移动强度的基础上进一步计算反映社会接触度的指标,如社交距离指数(Social Distancing Index, SDI)[19]、社交接触指数(Social Contact Index, SCI)[20,21]并研究其对疾病传播的作用.例如,Pan等[19]通过统计分析后得到:在SDI较高的地区,COVID-19感染率与SDI得分之间的相关性更强,Huang等[21]基于高时空精度的匿名地理位置数据构建了一个SCI,并使用该SCI指数构建了基于人群流动与接触的COVID-19传播模型,揭示了不同人群流动、人口密度、社交疏离措施对控制疫情反弹的效果. ...
... 自2020年1月起,由于COVID-19疫情的发生发展以及相应实施的限制人员流动、保持社交距离等非药物干预措施(Non-pharmaceutical Interventions, NPIs),全球范围内的人群流动性在不同阶段发生了不同程度的变化[22].基于多源人群移动数据,研究者从不同角度对人群移动性的变化进行了量化分析.例如,从整体的流动趋势上看,随着2020年上半年各类非药物干预措施的实施,欧洲地区各级地域统计单元的人口流入、人口流出以及区域内部的出行人次都明显减少[23].从个体的出行特征上看,2020年1—3月中国居民的出行时间、距离、交通方式、目的地类型偏好都发生了显著的变化[24].具体地,出行距离、活动范围、出行次数、目的地多样性均减少,居家时间则相应地变长[25].人群移动模式的变化不仅受到NPIs的外部影响[8,17],而且受到心理因素的内部影响.例如,相关研究表明,美国地区在实施限制政策之前,人群移动性就已经开始降低[11].结合社交媒体数据,研究者分析发现,这一自发的行为与人们对疫情的认知 有关[26,27].此外,有研究发现人群移动性的变化是不均衡的.例如,不同社会经济群体之间存在巨大且持久的差异,弱势群体移动性的变化远小于较富裕的群体[18].不同地区之间人群移动性变化也存在着差异,不平等程度高、人均收入较低的城市移动性收缩则更为强烈[28]. ...
... COVID-19建模中所使用的人群移动数据大多以匿名的、聚合的形式被分析,数据来源丰富,包括电信运营商提供的手机位置数据、互联网企业(例如百度、腾讯、谷歌、Cuebiq、SafeGraph等)提供的位置数据、含有地理标记的社交媒体数据(如Twitter、新浪微博等)以及其他开源数据集.基于此,常规的流动性指标易于被提取,例如:出行时长、出行距离、目的地类型、区域间人流量等.相关研究也考虑了不同社会经济属性人群的流动性[18,20],不同类型微观场所人流量[17],不同地区的社交距离指 数[19].然而,COVID-19在人群中的传播从根本上取决于人际间不同接触模式的发生效率与时空分布[67],而聚合层面上的整体流动性特征并不能从机理层面表达家庭、写字楼、工厂、商场、学校、公共交通等各类场景下的复杂接触模式.因此,面向复杂社会接触模式的分析与建模至关重要,如何利用大数据或者大小数据相结合的更加智能的方式对其进行突破成为一项挑战.此外,人们对疫情的认知以及干预措施的实施均会对人群流动以及社会接触模式产生不可忽视的影响,如何基于真实数据对这种复杂的人群时空行为响应进行耦合建模,进而形成动态反馈,也成为需要进一步研究的内容.除此之外,不同类型节假日与大型活动下产生的特殊的人口流动与接触模式也值得被耦合建模分析.综上,虽然当前的传染病模型已经在多个方面对人群移动进行了耦合建模,但是由于人群时空行为的复杂性,导致该方向的研究仍然面临巨大挑战,亟需进一步发展. ...
Quantifying human mobility behaviour changes during the COVID-19 outbreak in the United States
3
2020
... 一方面,针对疫情的跨地区输入性传播,通过对输入性人群进行统计建模,相关研究评估了各地区的输入性风险[9,10].例如,Xiong等[11]量化了美国各郡县的人群流入与COVID-19感染规模之间的动态正相关关系,并发现这种正相关关系在取消居家令的地区会出现逐步增强的效应.Mu等[12]使用回归模型得到结论:来自疫情中心城市的人口流入量的差异导致了城市之间COVID-19感染率的主要差异,离疫源地较近、城区人口较多的城市发病风险较高.另一方面,针对疫情本地传播,相关研究通过将研究区域内部各个单元之间的人群移动耦合于传染病传播模型中,进而揭示人群移动对疾病传播的复杂影响[13,14,15].例如,Badr等[16]发现人群流动性的降低与COVID-19病例增长率的减少有显著的正相关关系.Wang等[17]发现:在控制人群移动性的政策实施后7天内,人群流动与COVID-19传播之间的相关性会增强,但随后会减弱.Lai等[15]对中国各地日常出行网络进行建模和分析后得到:如能保持社交疏离政策,通过取消大型集会,关闭学校、工作场所这类措施以减少个体间接触率,则从2020年2月17日起取消湖北省的城际出行限制不会导致中国COVID-19病例的增加.Chang等[18]发现“超级传播者”以及弱势群体常到访的区域感染风险较高.此外,部分研究在区域内部人群移动强度的基础上进一步计算反映社会接触度的指标,如社交距离指数(Social Distancing Index, SDI)[19]、社交接触指数(Social Contact Index, SCI)[20,21]并研究其对疾病传播的作用.例如,Pan等[19]通过统计分析后得到:在SDI较高的地区,COVID-19感染率与SDI得分之间的相关性更强,Huang等[21]基于高时空精度的匿名地理位置数据构建了一个SCI,并使用该SCI指数构建了基于人群流动与接触的COVID-19传播模型,揭示了不同人群流动、人口密度、社交疏离措施对控制疫情反弹的效果. ...
... [19]通过统计分析后得到:在SDI较高的地区,COVID-19感染率与SDI得分之间的相关性更强,Huang等[21]基于高时空精度的匿名地理位置数据构建了一个SCI,并使用该SCI指数构建了基于人群流动与接触的COVID-19传播模型,揭示了不同人群流动、人口密度、社交疏离措施对控制疫情反弹的效果. ...
... COVID-19建模中所使用的人群移动数据大多以匿名的、聚合的形式被分析,数据来源丰富,包括电信运营商提供的手机位置数据、互联网企业(例如百度、腾讯、谷歌、Cuebiq、SafeGraph等)提供的位置数据、含有地理标记的社交媒体数据(如Twitter、新浪微博等)以及其他开源数据集.基于此,常规的流动性指标易于被提取,例如:出行时长、出行距离、目的地类型、区域间人流量等.相关研究也考虑了不同社会经济属性人群的流动性[18,20],不同类型微观场所人流量[17],不同地区的社交距离指 数[19].然而,COVID-19在人群中的传播从根本上取决于人际间不同接触模式的发生效率与时空分布[67],而聚合层面上的整体流动性特征并不能从机理层面表达家庭、写字楼、工厂、商场、学校、公共交通等各类场景下的复杂接触模式.因此,面向复杂社会接触模式的分析与建模至关重要,如何利用大数据或者大小数据相结合的更加智能的方式对其进行突破成为一项挑战.此外,人们对疫情的认知以及干预措施的实施均会对人群流动以及社会接触模式产生不可忽视的影响,如何基于真实数据对这种复杂的人群时空行为响应进行耦合建模,进而形成动态反馈,也成为需要进一步研究的内容.除此之外,不同类型节假日与大型活动下产生的特殊的人口流动与接触模式也值得被耦合建模分析.综上,虽然当前的传染病模型已经在多个方面对人群移动进行了耦合建模,但是由于人群时空行为的复杂性,导致该方向的研究仍然面临巨大挑战,亟需进一步发展. ...
Non-compulsory measures sufficiently reduced human mobility in Tokyo during the COVID-19 epidemic
2
2020
... 一方面,针对疫情的跨地区输入性传播,通过对输入性人群进行统计建模,相关研究评估了各地区的输入性风险[9,10].例如,Xiong等[11]量化了美国各郡县的人群流入与COVID-19感染规模之间的动态正相关关系,并发现这种正相关关系在取消居家令的地区会出现逐步增强的效应.Mu等[12]使用回归模型得到结论:来自疫情中心城市的人口流入量的差异导致了城市之间COVID-19感染率的主要差异,离疫源地较近、城区人口较多的城市发病风险较高.另一方面,针对疫情本地传播,相关研究通过将研究区域内部各个单元之间的人群移动耦合于传染病传播模型中,进而揭示人群移动对疾病传播的复杂影响[13,14,15].例如,Badr等[16]发现人群流动性的降低与COVID-19病例增长率的减少有显著的正相关关系.Wang等[17]发现:在控制人群移动性的政策实施后7天内,人群流动与COVID-19传播之间的相关性会增强,但随后会减弱.Lai等[15]对中国各地日常出行网络进行建模和分析后得到:如能保持社交疏离政策,通过取消大型集会,关闭学校、工作场所这类措施以减少个体间接触率,则从2020年2月17日起取消湖北省的城际出行限制不会导致中国COVID-19病例的增加.Chang等[18]发现“超级传播者”以及弱势群体常到访的区域感染风险较高.此外,部分研究在区域内部人群移动强度的基础上进一步计算反映社会接触度的指标,如社交距离指数(Social Distancing Index, SDI)[19]、社交接触指数(Social Contact Index, SCI)[20,21]并研究其对疾病传播的作用.例如,Pan等[19]通过统计分析后得到:在SDI较高的地区,COVID-19感染率与SDI得分之间的相关性更强,Huang等[21]基于高时空精度的匿名地理位置数据构建了一个SCI,并使用该SCI指数构建了基于人群流动与接触的COVID-19传播模型,揭示了不同人群流动、人口密度、社交疏离措施对控制疫情反弹的效果. ...
... COVID-19建模中所使用的人群移动数据大多以匿名的、聚合的形式被分析,数据来源丰富,包括电信运营商提供的手机位置数据、互联网企业(例如百度、腾讯、谷歌、Cuebiq、SafeGraph等)提供的位置数据、含有地理标记的社交媒体数据(如Twitter、新浪微博等)以及其他开源数据集.基于此,常规的流动性指标易于被提取,例如:出行时长、出行距离、目的地类型、区域间人流量等.相关研究也考虑了不同社会经济属性人群的流动性[18,20],不同类型微观场所人流量[17],不同地区的社交距离指 数[19].然而,COVID-19在人群中的传播从根本上取决于人际间不同接触模式的发生效率与时空分布[67],而聚合层面上的整体流动性特征并不能从机理层面表达家庭、写字楼、工厂、商场、学校、公共交通等各类场景下的复杂接触模式.因此,面向复杂社会接触模式的分析与建模至关重要,如何利用大数据或者大小数据相结合的更加智能的方式对其进行突破成为一项挑战.此外,人们对疫情的认知以及干预措施的实施均会对人群流动以及社会接触模式产生不可忽视的影响,如何基于真实数据对这种复杂的人群时空行为响应进行耦合建模,进而形成动态反馈,也成为需要进一步研究的内容.除此之外,不同类型节假日与大型活动下产生的特殊的人口流动与接触模式也值得被耦合建模分析.综上,虽然当前的传染病模型已经在多个方面对人群移动进行了耦合建模,但是由于人群时空行为的复杂性,导致该方向的研究仍然面临巨大挑战,亟需进一步发展. ...
Integrated vaccination and physical distancing interventions to prevent future COVID-19 waves
5
2021
... 一方面,针对疫情的跨地区输入性传播,通过对输入性人群进行统计建模,相关研究评估了各地区的输入性风险[9,10].例如,Xiong等[11]量化了美国各郡县的人群流入与COVID-19感染规模之间的动态正相关关系,并发现这种正相关关系在取消居家令的地区会出现逐步增强的效应.Mu等[12]使用回归模型得到结论:来自疫情中心城市的人口流入量的差异导致了城市之间COVID-19感染率的主要差异,离疫源地较近、城区人口较多的城市发病风险较高.另一方面,针对疫情本地传播,相关研究通过将研究区域内部各个单元之间的人群移动耦合于传染病传播模型中,进而揭示人群移动对疾病传播的复杂影响[13,14,15].例如,Badr等[16]发现人群流动性的降低与COVID-19病例增长率的减少有显著的正相关关系.Wang等[17]发现:在控制人群移动性的政策实施后7天内,人群流动与COVID-19传播之间的相关性会增强,但随后会减弱.Lai等[15]对中国各地日常出行网络进行建模和分析后得到:如能保持社交疏离政策,通过取消大型集会,关闭学校、工作场所这类措施以减少个体间接触率,则从2020年2月17日起取消湖北省的城际出行限制不会导致中国COVID-19病例的增加.Chang等[18]发现“超级传播者”以及弱势群体常到访的区域感染风险较高.此外,部分研究在区域内部人群移动强度的基础上进一步计算反映社会接触度的指标,如社交距离指数(Social Distancing Index, SDI)[19]、社交接触指数(Social Contact Index, SCI)[20,21]并研究其对疾病传播的作用.例如,Pan等[19]通过统计分析后得到:在SDI较高的地区,COVID-19感染率与SDI得分之间的相关性更强,Huang等[21]基于高时空精度的匿名地理位置数据构建了一个SCI,并使用该SCI指数构建了基于人群流动与接触的COVID-19传播模型,揭示了不同人群流动、人口密度、社交疏离措施对控制疫情反弹的效果. ...
... [21]基于高时空精度的匿名地理位置数据构建了一个SCI,并使用该SCI指数构建了基于人群流动与接触的COVID-19传播模型,揭示了不同人群流动、人口密度、社交疏离措施对控制疫情反弹的效果. ...
... Related references of process simulation models coupled with human mobility
Tab. 2 | 分类 | 文献 | 研究区域 | 人群移动数据 | 模型模拟的干预措施 | 病例真实值 | 病例模拟值 | 模型效果 |
| 群体级别 | [47] | 意大利 | 人口流量调查 | 严格管控出行活动、加大疫情排查力度 | 74 386 | 约733 000 | 模拟的疾病发展曲线与实际情况吻符合程度较高 |
| [9] | 武汉 | 百度实时流动性数据 | - | 554 | 632 | 累计病例数的R2=0.99 |
| [45] | 中国375个城市 | 腾讯位置服务人口实时流动性数据 | 佩戴口罩、社交疏离、自我
隔离 | 13 562 | 约1.2万 | 预测的疾病报告率为14%,与实际武汉市疾病报告率15.8%非常接近 |
| [15] | 中国340个城市 | 百度迁徙人口流动数据 | 综合性非药物性干预 | 79 824 | 114 325 | 全国累计病例的R2=0.86,P值<0.001 |
| [21] | 中国 | 手机实时移动性和社交联系数据、腾讯移动设
备数据集 | 疫苗接种、社交疏离 | 未使用真实数据 | 未给出具体值 | 严格的干预措施可大幅降低传播能力 |
| [13] | 深圳市 | 手机移动信令数据 | 降低出行量、区域封锁 | 未使用真实数据 | R0=2.5时,峰值病例数减少了33% | 模拟的疾病发展曲线与实际情况吻合程度较高 |
| [14] | 美国康涅狄格州 | 城镇级人口流动数据,
智能手机热图,空中交
通流量 | 社交疏离 | 47 510 | 45 752~48 105 | 对康涅狄格州所有城镇模拟,实际统计的病例R2在0.907~0.924;按类别对城镇进行模拟,实际统计的病例R2为0.978~0.987 |
| [49] | 全球 | 航空与地面交通数据 | 降低本地传播率和国际旅行 | 未使用真实数据 | 未给出具体模拟值 | 严格的干预措施可大幅降低传播能力 |
| 个体级别 | [60] | 新加坡 | 交通数据 | 隔离感染者、关闭学校和工作场所 | 未使用真实数据 | R0=1.5时,7.4%的总人口感染;R0=2.0时,19.3%的总人口感染;R0=2.5时,32%的总人口感染 | 未给出具体评价指标 |
| [61] | 波士顿 | 手机位置数据 | 检测、密接追踪、居家隔离 | 未使用真实数据 | 无干预场景75%的人口被感染 | 未给出具体评价指标 |
| [62] | 纽约、西雅图 | 手机位置数据 | 无干预措施 | 每天每千人的死亡人数(未给出具体值) | 每天每千人的死亡人数(未给出具体值) | 模型结果与真实死亡人数的拟合效果较好,二者到达峰值的时间差略大于5 d |
| [63] | 澳大利亚 | 人口通勤数据 | 国际航空旅行限制、隔离感染者、居家隔离、增大社交距离、关闭学校 | 未使用真实数据 | 最佳干预场景下有8千~1万人被感染 | 未给出具体评价指标 |
| [64] | 深圳市 | 手机信令数据 | 密接追踪、及时检测、佩戴口罩、封城、逐步复工、隔离综合措施 | 418 | 416 | 每日新增发病数量的模拟值与实际报告值的RMSE=1.354;显性感染者数量在城市内各个行政区尺度上的R2=0.95 |
4.1 群体级别的耦合模型 群体级别的模型是一种长期以来广泛使用的传播动力学建模技术,其最基本的假设是研究单元内的每个个体具有相同的特征且彼此之间均匀接触,当作一个同质的群体来对待.其中,研究单元可以是同一个区域或者同一属性的人群/其他宿主等.根据感染和传播机制,模型通常由一组微分方程构建,通常是常微分方程.在COVID-19疫情中,人类感染新型冠状病毒SARS-COV-2之后存在潜隐期(Latent Period)与潜伏期(Incubation Period,对于显性感染者而言),因此,常用于COVID-19建模的基本仓室模型为SLIR与SEIR模型.以最基本的SEIR模型为例,针对给定研究单元,假设其总人口不变,其基于常微分方程的表达公式如下: ...
... 此外,Huang等[21]利用腾讯提供的匿名移动定位数据度量了城市内部动态人口移动强度和社交接触强度,并基于此得到各城市动态的传播率参数,从而针对中国不同人口密度的城市构建了SEIRV模型(其中V代表已接种疫苗).研究结果表明,疫苗接种与社交疏离相结合可以在不依赖移动性降低的情况下遏制COVID-19再次暴发,而仅通过逐步疫苗接种措施则无法实现这一目标.该研究为人口密度各异的城市制定和实施疫情常态化时期的综合干预措施提供了科学依据[21]. ...
... [21]. ...
Mobility changes in response to COVID-19
1
2020
... 自2020年1月起,由于COVID-19疫情的发生发展以及相应实施的限制人员流动、保持社交距离等非药物干预措施(Non-pharmaceutical Interventions, NPIs),全球范围内的人群流动性在不同阶段发生了不同程度的变化[22].基于多源人群移动数据,研究者从不同角度对人群移动性的变化进行了量化分析.例如,从整体的流动趋势上看,随着2020年上半年各类非药物干预措施的实施,欧洲地区各级地域统计单元的人口流入、人口流出以及区域内部的出行人次都明显减少[23].从个体的出行特征上看,2020年1—3月中国居民的出行时间、距离、交通方式、目的地类型偏好都发生了显著的变化[24].具体地,出行距离、活动范围、出行次数、目的地多样性均减少,居家时间则相应地变长[25].人群移动模式的变化不仅受到NPIs的外部影响[8,17],而且受到心理因素的内部影响.例如,相关研究表明,美国地区在实施限制政策之前,人群移动性就已经开始降低[11].结合社交媒体数据,研究者分析发现,这一自发的行为与人们对疫情的认知 有关[26,27].此外,有研究发现人群移动性的变化是不均衡的.例如,不同社会经济群体之间存在巨大且持久的差异,弱势群体移动性的变化远小于较富裕的群体[18].不同地区之间人群移动性变化也存在着差异,不平等程度高、人均收入较低的城市移动性收缩则更为强烈[28]. ...
Measuring the impact of COVID-19 confinement measures on human mobility using mobile positioning data. A European regional analysis
1
2020
... 自2020年1月起,由于COVID-19疫情的发生发展以及相应实施的限制人员流动、保持社交距离等非药物干预措施(Non-pharmaceutical Interventions, NPIs),全球范围内的人群流动性在不同阶段发生了不同程度的变化[22].基于多源人群移动数据,研究者从不同角度对人群移动性的变化进行了量化分析.例如,从整体的流动趋势上看,随着2020年上半年各类非药物干预措施的实施,欧洲地区各级地域统计单元的人口流入、人口流出以及区域内部的出行人次都明显减少[23].从个体的出行特征上看,2020年1—3月中国居民的出行时间、距离、交通方式、目的地类型偏好都发生了显著的变化[24].具体地,出行距离、活动范围、出行次数、目的地多样性均减少,居家时间则相应地变长[25].人群移动模式的变化不仅受到NPIs的外部影响[8,17],而且受到心理因素的内部影响.例如,相关研究表明,美国地区在实施限制政策之前,人群移动性就已经开始降低[11].结合社交媒体数据,研究者分析发现,这一自发的行为与人们对疫情的认知 有关[26,27].此外,有研究发现人群移动性的变化是不均衡的.例如,不同社会经济群体之间存在巨大且持久的差异,弱势群体移动性的变化远小于较富裕的群体[18].不同地区之间人群移动性变化也存在着差异,不平等程度高、人均收入较低的城市移动性收缩则更为强烈[28]. ...
Understanding the impact of the COVID-19 pandemic on transportation-related behaviors with human mobility data
1
2020
... 自2020年1月起,由于COVID-19疫情的发生发展以及相应实施的限制人员流动、保持社交距离等非药物干预措施(Non-pharmaceutical Interventions, NPIs),全球范围内的人群流动性在不同阶段发生了不同程度的变化[22].基于多源人群移动数据,研究者从不同角度对人群移动性的变化进行了量化分析.例如,从整体的流动趋势上看,随着2020年上半年各类非药物干预措施的实施,欧洲地区各级地域统计单元的人口流入、人口流出以及区域内部的出行人次都明显减少[23].从个体的出行特征上看,2020年1—3月中国居民的出行时间、距离、交通方式、目的地类型偏好都发生了显著的变化[24].具体地,出行距离、活动范围、出行次数、目的地多样性均减少,居家时间则相应地变长[25].人群移动模式的变化不仅受到NPIs的外部影响[8,17],而且受到心理因素的内部影响.例如,相关研究表明,美国地区在实施限制政策之前,人群移动性就已经开始降低[11].结合社交媒体数据,研究者分析发现,这一自发的行为与人们对疫情的认知 有关[26,27].此外,有研究发现人群移动性的变化是不均衡的.例如,不同社会经济群体之间存在巨大且持久的差异,弱势群体移动性的变化远小于较富裕的群体[18].不同地区之间人群移动性变化也存在着差异,不平等程度高、人均收入较低的城市移动性收缩则更为强烈[28]. ...
Twitter reveals human mobility dynamics during the COVID-19 pandemic
1
2020
... 自2020年1月起,由于COVID-19疫情的发生发展以及相应实施的限制人员流动、保持社交距离等非药物干预措施(Non-pharmaceutical Interventions, NPIs),全球范围内的人群流动性在不同阶段发生了不同程度的变化[22].基于多源人群移动数据,研究者从不同角度对人群移动性的变化进行了量化分析.例如,从整体的流动趋势上看,随着2020年上半年各类非药物干预措施的实施,欧洲地区各级地域统计单元的人口流入、人口流出以及区域内部的出行人次都明显减少[23].从个体的出行特征上看,2020年1—3月中国居民的出行时间、距离、交通方式、目的地类型偏好都发生了显著的变化[24].具体地,出行距离、活动范围、出行次数、目的地多样性均减少,居家时间则相应地变长[25].人群移动模式的变化不仅受到NPIs的外部影响[8,17],而且受到心理因素的内部影响.例如,相关研究表明,美国地区在实施限制政策之前,人群移动性就已经开始降低[11].结合社交媒体数据,研究者分析发现,这一自发的行为与人们对疫情的认知 有关[26,27].此外,有研究发现人群移动性的变化是不均衡的.例如,不同社会经济群体之间存在巨大且持久的差异,弱势群体移动性的变化远小于较富裕的群体[18].不同地区之间人群移动性变化也存在着差异,不平等程度高、人均收入较低的城市移动性收缩则更为强烈[28]. ...
Spatial-temporal Analysis of COVID-19's Impact on Human Mobility: the Case of the United States
1
2020
... 自2020年1月起,由于COVID-19疫情的发生发展以及相应实施的限制人员流动、保持社交距离等非药物干预措施(Non-pharmaceutical Interventions, NPIs),全球范围内的人群流动性在不同阶段发生了不同程度的变化[22].基于多源人群移动数据,研究者从不同角度对人群移动性的变化进行了量化分析.例如,从整体的流动趋势上看,随着2020年上半年各类非药物干预措施的实施,欧洲地区各级地域统计单元的人口流入、人口流出以及区域内部的出行人次都明显减少[23].从个体的出行特征上看,2020年1—3月中国居民的出行时间、距离、交通方式、目的地类型偏好都发生了显著的变化[24].具体地,出行距离、活动范围、出行次数、目的地多样性均减少,居家时间则相应地变长[25].人群移动模式的变化不仅受到NPIs的外部影响[8,17],而且受到心理因素的内部影响.例如,相关研究表明,美国地区在实施限制政策之前,人群移动性就已经开始降低[11].结合社交媒体数据,研究者分析发现,这一自发的行为与人们对疫情的认知 有关[26,27].此外,有研究发现人群移动性的变化是不均衡的.例如,不同社会经济群体之间存在巨大且持久的差异,弱势群体移动性的变化远小于较富裕的群体[18].不同地区之间人群移动性变化也存在着差异,不平等程度高、人均收入较低的城市移动性收缩则更为强烈[28]. ...
Public awareness, emotional reactions and human mobility in response to the COVID-19 outbreak in China: A population-based ecological study
1
2020
... 自2020年1月起,由于COVID-19疫情的发生发展以及相应实施的限制人员流动、保持社交距离等非药物干预措施(Non-pharmaceutical Interventions, NPIs),全球范围内的人群流动性在不同阶段发生了不同程度的变化[22].基于多源人群移动数据,研究者从不同角度对人群移动性的变化进行了量化分析.例如,从整体的流动趋势上看,随着2020年上半年各类非药物干预措施的实施,欧洲地区各级地域统计单元的人口流入、人口流出以及区域内部的出行人次都明显减少[23].从个体的出行特征上看,2020年1—3月中国居民的出行时间、距离、交通方式、目的地类型偏好都发生了显著的变化[24].具体地,出行距离、活动范围、出行次数、目的地多样性均减少,居家时间则相应地变长[25].人群移动模式的变化不仅受到NPIs的外部影响[8,17],而且受到心理因素的内部影响.例如,相关研究表明,美国地区在实施限制政策之前,人群移动性就已经开始降低[11].结合社交媒体数据,研究者分析发现,这一自发的行为与人们对疫情的认知 有关[26,27].此外,有研究发现人群移动性的变化是不均衡的.例如,不同社会经济群体之间存在巨大且持久的差异,弱势群体移动性的变化远小于较富裕的群体[18].不同地区之间人群移动性变化也存在着差异,不平等程度高、人均收入较低的城市移动性收缩则更为强烈[28]. ...
Economic and social consequences of human mobility restrictions under COVID-19
1
2020
... 自2020年1月起,由于COVID-19疫情的发生发展以及相应实施的限制人员流动、保持社交距离等非药物干预措施(Non-pharmaceutical Interventions, NPIs),全球范围内的人群流动性在不同阶段发生了不同程度的变化[22].基于多源人群移动数据,研究者从不同角度对人群移动性的变化进行了量化分析.例如,从整体的流动趋势上看,随着2020年上半年各类非药物干预措施的实施,欧洲地区各级地域统计单元的人口流入、人口流出以及区域内部的出行人次都明显减少[23].从个体的出行特征上看,2020年1—3月中国居民的出行时间、距离、交通方式、目的地类型偏好都发生了显著的变化[24].具体地,出行距离、活动范围、出行次数、目的地多样性均减少,居家时间则相应地变长[25].人群移动模式的变化不仅受到NPIs的外部影响[8,17],而且受到心理因素的内部影响.例如,相关研究表明,美国地区在实施限制政策之前,人群移动性就已经开始降低[11].结合社交媒体数据,研究者分析发现,这一自发的行为与人们对疫情的认知 有关[26,27].此外,有研究发现人群移动性的变化是不均衡的.例如,不同社会经济群体之间存在巨大且持久的差异,弱势群体移动性的变化远小于较富裕的群体[18].不同地区之间人群移动性变化也存在着差异,不平等程度高、人均收入较低的城市移动性收缩则更为强烈[28]. ...
Enhancing fine-grained intra-urban dengue forecasting by integrating spatial interactions of human movements between urban regions
3
2020
... 疫情短期预测模型以预测感染规模、疾病负担等疫情短期发展趋势为目的,重点关注预测结果的准确性.COVID-19相关研究主要依据疫情历史数据以及气象、人口、交通等相关因素,构建统计或者机器学习模型,预测研究区域近期(通常为1天至1个月)的疾病发展趋势.如前所述,在疫情发展过程中,人群移动与疾病传播会形成复杂的交互影响,因此,对人群移动进行融合建模将有助于更好地预测疾病传播趋势[29,30]. ...
... 另一类研究则主要采用机器学习方法构建COVID-19疫情短期预测模型.例如,Bryant等[34]基于欧洲11个国家的零售和娱乐、杂货店和药房、交通场所、工作场所、住宅五类场所的人口流动性变化,结合疫情早期数据,通过贝叶斯网络模型进行模型训练,用以预测未来三周的累计感染人数、死亡人数以及基本再生数 ,并明确杂货店和药房的人群流动性对 的影响最大.Kuo等[35]利用区域的人口统计学特征(如,人口密度等)、环境特征(如,温湿度等)、基于谷歌的社区人群移动特征(人们在不同类型地点停留时间相对变化)、历史疫情感染规模等作为模型输入特征,构建融合弹性网络回归、主成分回归、K近邻模型、随机森林、广义线性模型等多模型的机器学习混合框架,对美国172个县未来1、4与7 d平均的COVID-19每日新增患者数量、累计患者数量进行预测,并评估实施隔离或开放政策的效用,指出大城市如能坚持一周以上的隔离措施则可明显降低感染率.此外,在其他传染病研究中,有研究提出可利用图嵌入技术将人群移动二阶量转换为人群移动一阶量,进而构建疫情预测模型[29]. ...
... 总体而言,将人口移动特征转化为区域的一个或多个属性进行建模,具有特征提取方便、模型构建灵活的特点.对于耦合了人群移动一阶量的模型,已有研究揭示其预测性能优于没有引入人群移动特征的预测模型[29].此次COVID-19疫情预测模型研究则较为广泛地耦合了人群移动一阶量,不仅实现了良好的短期预测,而且能帮助评估人群移动变化对疾病传播的影响,进而指导与之相关的干预措施部署. ...
Using mobility data to understand and forecast COVID19 Dynamics
3
... 疫情短期预测模型以预测感染规模、疾病负担等疫情短期发展趋势为目的,重点关注预测结果的准确性.COVID-19相关研究主要依据疫情历史数据以及气象、人口、交通等相关因素,构建统计或者机器学习模型,预测研究区域近期(通常为1天至1个月)的疾病发展趋势.如前所述,在疫情发展过程中,人群移动与疾病传播会形成复杂的交互影响,因此,对人群移动进行融合建模将有助于更好地预测疾病传播趋势[29,30]. ...
... Related references of short-term epidemic prediction models coupled with human mobility
Tab. 1 | 分类 | 参考文献 | 模型 | 预测目标 | 预测的时间范围 | 研究区域 | 人群移动数据 | 评估指标 | 预测性能 |
| 人群移动一阶量 | [9] | 广义线性模型 | 每日COVID-19新增感染人数和累计感染人数 | 2020年2月1日—10日 | 中国的多个
省份 | 百度迁徙指数 | R2 | 预测截止至2020年2月10号(疫情初期)中国除武汉市外的累计病例数的R2为0.89 |
| [31] | 整合线性回归和自回归移动平均的预测模型 | 每日COVID-19输入性病例数 | 提前预测未来
12 d | 韩国的多个
省市 | 韩国电信的手机漫游数据 | 相关系数、均方根误差、平均绝对误差和平均相对误差 | 预测未来12 d后的新增输入病例人数时,该模型在第一个验证集(2020.03.28—04.30)的相关系数、均方根误差、平均绝对误差和平均相对误差分别为0.925、6.3、5.0和49.9%,在第二个验证集(2020.05.01-06.30)的相关系数、均方根误差、平均绝对误差和平均相对误差分别为0.798、4.1、2.8和22.3% |
| [32] | 多元线性回归
模型 | 每日COVID-19新增感染人数 | 2020年2月1日—2月15日(列举了分别预测1~5 d的精度) | 中国的4个城市(深圳、广州、珠海和中山市) | 百度迁徙数据 | 平均绝对误差、均方根误差和R2 | 以深圳市和广州市这两个人口流动较为频繁的城市为例,预测深圳市未来1天新增感染人数的平均绝对误差、均方根误差和R2分别为7、7.234和0.988,广州市的平均绝对误差、均方根误差和R2则分别为6.067、6.434和0.985 |
| [33] | 基于面板多元线性回归模型的行为模型和基于分布滞后模型的感染模型 | 每日COVID-19累计感染人数 | 提前预测未来1~10 d | 中国、美国、法国等80个国家的多种空间尺度(如,国家、省/州、市/县) | 谷歌社区移动性数据集、百度迁徙指数、SafeGraph社交距离指标、Facebook提供的网格间的人口移动次数 | 百分比误差的中位数(Median Percentage Error, MPE) | 以在粗粒度的空间尺度上预测未来1 d COVID-19的累计感染人数为例,全球的百分比误差中位数为0.9%,中国各省的百分比误差中位数为-0.2%,意大利各省的百分比误差中位数为0.89%,美国各州的百分比误差中位数为1.13% |
| [34] | 贝叶斯网络 | 每日COVID-19新增死亡人数 | 2020年3月30日—4月19日(列举了每周的预测精度) | 意大利、西班牙等11个国家 | 谷歌社区移动性数据集 | 平均误差以及平均相对误差 | 预测未来1周的死亡人数时,11个国家平均误差绝对值的均值为60,平均相对误差绝对值的均值则为2.5% |
| [35] | 融合弹性回归和主成分回归等多个模型的多层预测模型 | 每日COVID-19新增感染人数和累计感染人数 | 提前预测未来1、4和7 d的平均值 | 美国的多个县 | 谷歌社区移动性数据集 | 平均绝对误差、均方根误差和R2 | 预测未来1 d的新增感染人数时,R2、均方根误差和平均绝对误差分别为0.91、105和39;预测未来1 d的累计感染人数时,R2、均方根误差和平均绝对误差则分别为1.0、189和103 |
| 人群移动二阶量 | [30] | 基于图的神经
网络 | 每日COVID-19新增感染人数 | 提前预测未来2、7、14、21和28d | 美国的多个州 | 谷歌COVID-19聚合移动研究数据集 | 均方根误差和皮尔斯相关系数 | 预测未来第2 d时,均方根误差和皮尔森相关系数分别为313和0.298 |
| [36] | 时空图神经网络 | 每日COVID-19新增感染人数 | 提前预测未来1d | 美国的多个县 | 谷歌社区移动性数据集和谷歌COVID-19聚合移动研究数据集 | 均方根对数误差和皮尔斯相关系数 | 预测未来1 d时,均方根对数误差和皮尔森相关系数分别为0.0109和0.9980 |
| [37] | 时空注意力网络 | 每日COVID-19新增感染人数 | 提前预测未来5、15、20 d | 美国的多个州和多个县 | 通过重力模型计算的市/县和州之间的人群移动强度 | 平均绝对误差、均方误差和一致性相关系数 | 预测未来第5 d时,美国州级别的均方误差、平均绝对误差和一致性相关系数分别为237 412、220.5和0.84,美国县级别的均方误差、平均绝对误差和一致性相关系数分别为44177、79.8和0.66 |
3.1 人群移动一阶量的耦合模型 人群移动一阶量的耦合模型通常基于人群移动对感染者数量等指标的影响分析,将人群移动数据作为区域的一种特征(例如,人口流入流出量、POI访问量以及外出的人口数量等)融入到建模过程中,进而实现对疫情更加有效的预测. ...
... 人群移动二阶量的耦合模型以人群移动的网络交互特征作为输入,考虑了不同区域之间的空间依赖关系,能够更高效地实现时空同时预测.当前COVID-19预测研究主要通过图神经网络(Graph Convolution Network, GCN)构建时空预测模型.例如,Wang等[30]利用谷歌提供的人群移动数据集以及COVID-19疫情监测数据构建了基于GCN的时空预测模型.该模型把每个州(state)当作图的一个节点,根据不同州之间的人群流动量来动态决定不同节点之间的连边.结果表明,从提前预测2、7、14、21、28 d的角度,该模型在大多数情况下取得了优于ARMA、LSTM和cola-GNN等其他基准方法的预测性能,但预测性能随预测时间长度的增加而下降.Kapoor等[36]基于谷歌的人群移动数据集、谷歌社区移动性报告以及纽约时报COVID-19数据集构建了时空图神经网络模型,用于预测美国县(county)级别的未来一天COVID-19新增病例数,同时还验证了引入人群移动性数据有助于改善深度学习模型的预测性能.Gao等[37]将区域的经纬度、人口规模和人口密度作为图中对应节点的静态特征,将区域的活跃确诊病例数、累计病例数、住院患者数以及重症患者数作为对应节点的动态特征,根据2个区域的人口规模与物理距离确定2个节点之间连边的人群交互权重,通过构建基于图注意力网络(Graph Attention Network, GAT)和门控循环单元(Gate Recurrent Unit, GRU)的时空注意力网络,对美国不同州和县的COVID-19感染病例数进行预测,在不同实验条件下该模型的预测性能均显著优于几个常用的疾病传播仓室模型与深度学习预测模型(GRU、cola-GNN和GNN[36])等基线模型[37]. ...
Forecasting imported COVID-19 cases in South Korea using mobile roaming data
3
2020
... Related references of short-term epidemic prediction models coupled with human mobility
Tab. 1 | 分类 | 参考文献 | 模型 | 预测目标 | 预测的时间范围 | 研究区域 | 人群移动数据 | 评估指标 | 预测性能 |
| 人群移动一阶量 | [9] | 广义线性模型 | 每日COVID-19新增感染人数和累计感染人数 | 2020年2月1日—10日 | 中国的多个
省份 | 百度迁徙指数 | R2 | 预测截止至2020年2月10号(疫情初期)中国除武汉市外的累计病例数的R2为0.89 |
| [31] | 整合线性回归和自回归移动平均的预测模型 | 每日COVID-19输入性病例数 | 提前预测未来
12 d | 韩国的多个
省市 | 韩国电信的手机漫游数据 | 相关系数、均方根误差、平均绝对误差和平均相对误差 | 预测未来12 d后的新增输入病例人数时,该模型在第一个验证集(2020.03.28—04.30)的相关系数、均方根误差、平均绝对误差和平均相对误差分别为0.925、6.3、5.0和49.9%,在第二个验证集(2020.05.01-06.30)的相关系数、均方根误差、平均绝对误差和平均相对误差分别为0.798、4.1、2.8和22.3% |
| [32] | 多元线性回归
模型 | 每日COVID-19新增感染人数 | 2020年2月1日—2月15日(列举了分别预测1~5 d的精度) | 中国的4个城市(深圳、广州、珠海和中山市) | 百度迁徙数据 | 平均绝对误差、均方根误差和R2 | 以深圳市和广州市这两个人口流动较为频繁的城市为例,预测深圳市未来1天新增感染人数的平均绝对误差、均方根误差和R2分别为7、7.234和0.988,广州市的平均绝对误差、均方根误差和R2则分别为6.067、6.434和0.985 |
| [33] | 基于面板多元线性回归模型的行为模型和基于分布滞后模型的感染模型 | 每日COVID-19累计感染人数 | 提前预测未来1~10 d | 中国、美国、法国等80个国家的多种空间尺度(如,国家、省/州、市/县) | 谷歌社区移动性数据集、百度迁徙指数、SafeGraph社交距离指标、Facebook提供的网格间的人口移动次数 | 百分比误差的中位数(Median Percentage Error, MPE) | 以在粗粒度的空间尺度上预测未来1 d COVID-19的累计感染人数为例,全球的百分比误差中位数为0.9%,中国各省的百分比误差中位数为-0.2%,意大利各省的百分比误差中位数为0.89%,美国各州的百分比误差中位数为1.13% |
| [34] | 贝叶斯网络 | 每日COVID-19新增死亡人数 | 2020年3月30日—4月19日(列举了每周的预测精度) | 意大利、西班牙等11个国家 | 谷歌社区移动性数据集 | 平均误差以及平均相对误差 | 预测未来1周的死亡人数时,11个国家平均误差绝对值的均值为60,平均相对误差绝对值的均值则为2.5% |
| [35] | 融合弹性回归和主成分回归等多个模型的多层预测模型 | 每日COVID-19新增感染人数和累计感染人数 | 提前预测未来1、4和7 d的平均值 | 美国的多个县 | 谷歌社区移动性数据集 | 平均绝对误差、均方根误差和R2 | 预测未来1 d的新增感染人数时,R2、均方根误差和平均绝对误差分别为0.91、105和39;预测未来1 d的累计感染人数时,R2、均方根误差和平均绝对误差则分别为1.0、189和103 |
| 人群移动二阶量 | [30] | 基于图的神经
网络 | 每日COVID-19新增感染人数 | 提前预测未来2、7、14、21和28d | 美国的多个州 | 谷歌COVID-19聚合移动研究数据集 | 均方根误差和皮尔斯相关系数 | 预测未来第2 d时,均方根误差和皮尔森相关系数分别为313和0.298 |
| [36] | 时空图神经网络 | 每日COVID-19新增感染人数 | 提前预测未来1d | 美国的多个县 | 谷歌社区移动性数据集和谷歌COVID-19聚合移动研究数据集 | 均方根对数误差和皮尔斯相关系数 | 预测未来1 d时,均方根对数误差和皮尔森相关系数分别为0.0109和0.9980 |
| [37] | 时空注意力网络 | 每日COVID-19新增感染人数 | 提前预测未来5、15、20 d | 美国的多个州和多个县 | 通过重力模型计算的市/县和州之间的人群移动强度 | 平均绝对误差、均方误差和一致性相关系数 | 预测未来第5 d时,美国州级别的均方误差、平均绝对误差和一致性相关系数分别为237 412、220.5和0.84,美国县级别的均方误差、平均绝对误差和一致性相关系数分别为44177、79.8和0.66 |
3.1 人群移动一阶量的耦合模型 人群移动一阶量的耦合模型通常基于人群移动对感染者数量等指标的影响分析,将人群移动数据作为区域的一种特征(例如,人口流入流出量、POI访问量以及外出的人口数量等)融入到建模过程中,进而实现对疫情更加有效的预测. ...
... COVID-19疫情短期预测模型中,一类研究主要采用统计模型.例如,Kraemer等[9]利用百度迁徙指数量化武汉到中国其他省份的流出人群规模,结合疾病传播特征,构建广义线性模型估计疫情早期中国不同省份的疫情规模与增长速度,预测结果的R2达到0.89,并明确在封城前武汉的人口流出仍然是中国其他区域疫情暴发的主要驱动力.Choi 等[31]使用韩国的手机漫游数据量化了全球各国到韩国各省市的人口流入,同时统计出全球COVID-19发病率与牛津COVID-19政府反应追踪指数计算得出的风险评分,将以上特征导入包含外生变量的整合移动平均自回归模型,用以预测韩国12 d后外来输入的COVID-19病例.韩国境外输入病例呈现出阶段性特征,在疫情早期主要来源地区为中国,2020年4月后其主要来源地区为欧洲,因此该模型耦合不同阶段的人群移动特征分别对韩国两个时间段的外来输入病例进行预测,预测结果的平均相对误差分别为49.9%和22.3%[31].Wang等[32]利用百度迁徙指数量化武汉与湖北省其他城市的人口流出规模,结合温湿度、空气质量等多源数据与疾病传播特征,构建固定效应的多元线性回归模型,对深圳、广州、珠海、中山四个城市疫情早期阶段的感染规模实现了比较准确的短期预测,提前 2 d预测的新增感染人数R2均可达到0.81以上,但模型预测效果随着政府管制措施的实行以及病例数量减少而有所降低.Ilin等[33]基于谷歌社区移动性数据集量化人们在不同类型地点停留时间的相对变化,基于百度迁徙指数量化中国城市之间的人口流量,结合SafeGraph基于移动设备离家平均距离得到的社交距离指标等人群移动特征与历史疫情数据,构建基于面板多元线性回归模型的行为模型与基于分布滞后模型的感染模型,分别对不同NPI下人类行为的变化和不同行为变化下COVID-19感染人数的变化进行建模,对全球多个区域不同空间尺度的COVID-19累计病例数进行预测.该模型短期预测的效果良好,以全球、美国多个州和多个县未来1 d的COVID-19累计感染人数预测为例,预测结果的百分比误差中位数(Median Percentage Error, MPE)分别为0.90%、1.13%和0.98%.但随着预测时间的增长,该模型在不同空间区域的预测误差也在不断增加,并且预测误差的变化趋势呈现了区域异质性. ...
... [31].Wang等[32]利用百度迁徙指数量化武汉与湖北省其他城市的人口流出规模,结合温湿度、空气质量等多源数据与疾病传播特征,构建固定效应的多元线性回归模型,对深圳、广州、珠海、中山四个城市疫情早期阶段的感染规模实现了比较准确的短期预测,提前 2 d预测的新增感染人数R2均可达到0.81以上,但模型预测效果随着政府管制措施的实行以及病例数量减少而有所降低.Ilin等[33]基于谷歌社区移动性数据集量化人们在不同类型地点停留时间的相对变化,基于百度迁徙指数量化中国城市之间的人口流量,结合SafeGraph基于移动设备离家平均距离得到的社交距离指标等人群移动特征与历史疫情数据,构建基于面板多元线性回归模型的行为模型与基于分布滞后模型的感染模型,分别对不同NPI下人类行为的变化和不同行为变化下COVID-19感染人数的变化进行建模,对全球多个区域不同空间尺度的COVID-19累计病例数进行预测.该模型短期预测的效果良好,以全球、美国多个州和多个县未来1 d的COVID-19累计感染人数预测为例,预测结果的百分比误差中位数(Median Percentage Error, MPE)分别为0.90%、1.13%和0.98%.但随着预测时间的增长,该模型在不同空间区域的预测误差也在不断增加,并且预测误差的变化趋势呈现了区域异质性. ...
A short-term prediction model at the early stage of the COVID-19 pandemic based on multisource urban data
2
2021
... Related references of short-term epidemic prediction models coupled with human mobility
Tab. 1 | 分类 | 参考文献 | 模型 | 预测目标 | 预测的时间范围 | 研究区域 | 人群移动数据 | 评估指标 | 预测性能 |
| 人群移动一阶量 | [9] | 广义线性模型 | 每日COVID-19新增感染人数和累计感染人数 | 2020年2月1日—10日 | 中国的多个
省份 | 百度迁徙指数 | R2 | 预测截止至2020年2月10号(疫情初期)中国除武汉市外的累计病例数的R2为0.89 |
| [31] | 整合线性回归和自回归移动平均的预测模型 | 每日COVID-19输入性病例数 | 提前预测未来
12 d | 韩国的多个
省市 | 韩国电信的手机漫游数据 | 相关系数、均方根误差、平均绝对误差和平均相对误差 | 预测未来12 d后的新增输入病例人数时,该模型在第一个验证集(2020.03.28—04.30)的相关系数、均方根误差、平均绝对误差和平均相对误差分别为0.925、6.3、5.0和49.9%,在第二个验证集(2020.05.01-06.30)的相关系数、均方根误差、平均绝对误差和平均相对误差分别为0.798、4.1、2.8和22.3% |
| [32] | 多元线性回归
模型 | 每日COVID-19新增感染人数 | 2020年2月1日—2月15日(列举了分别预测1~5 d的精度) | 中国的4个城市(深圳、广州、珠海和中山市) | 百度迁徙数据 | 平均绝对误差、均方根误差和R2 | 以深圳市和广州市这两个人口流动较为频繁的城市为例,预测深圳市未来1天新增感染人数的平均绝对误差、均方根误差和R2分别为7、7.234和0.988,广州市的平均绝对误差、均方根误差和R2则分别为6.067、6.434和0.985 |
| [33] | 基于面板多元线性回归模型的行为模型和基于分布滞后模型的感染模型 | 每日COVID-19累计感染人数 | 提前预测未来1~10 d | 中国、美国、法国等80个国家的多种空间尺度(如,国家、省/州、市/县) | 谷歌社区移动性数据集、百度迁徙指数、SafeGraph社交距离指标、Facebook提供的网格间的人口移动次数 | 百分比误差的中位数(Median Percentage Error, MPE) | 以在粗粒度的空间尺度上预测未来1 d COVID-19的累计感染人数为例,全球的百分比误差中位数为0.9%,中国各省的百分比误差中位数为-0.2%,意大利各省的百分比误差中位数为0.89%,美国各州的百分比误差中位数为1.13% |
| [34] | 贝叶斯网络 | 每日COVID-19新增死亡人数 | 2020年3月30日—4月19日(列举了每周的预测精度) | 意大利、西班牙等11个国家 | 谷歌社区移动性数据集 | 平均误差以及平均相对误差 | 预测未来1周的死亡人数时,11个国家平均误差绝对值的均值为60,平均相对误差绝对值的均值则为2.5% |
| [35] | 融合弹性回归和主成分回归等多个模型的多层预测模型 | 每日COVID-19新增感染人数和累计感染人数 | 提前预测未来1、4和7 d的平均值 | 美国的多个县 | 谷歌社区移动性数据集 | 平均绝对误差、均方根误差和R2 | 预测未来1 d的新增感染人数时,R2、均方根误差和平均绝对误差分别为0.91、105和39;预测未来1 d的累计感染人数时,R2、均方根误差和平均绝对误差则分别为1.0、189和103 |
| 人群移动二阶量 | [30] | 基于图的神经
网络 | 每日COVID-19新增感染人数 | 提前预测未来2、7、14、21和28d | 美国的多个州 | 谷歌COVID-19聚合移动研究数据集 | 均方根误差和皮尔斯相关系数 | 预测未来第2 d时,均方根误差和皮尔森相关系数分别为313和0.298 |
| [36] | 时空图神经网络 | 每日COVID-19新增感染人数 | 提前预测未来1d | 美国的多个县 | 谷歌社区移动性数据集和谷歌COVID-19聚合移动研究数据集 | 均方根对数误差和皮尔斯相关系数 | 预测未来1 d时,均方根对数误差和皮尔森相关系数分别为0.0109和0.9980 |
| [37] | 时空注意力网络 | 每日COVID-19新增感染人数 | 提前预测未来5、15、20 d | 美国的多个州和多个县 | 通过重力模型计算的市/县和州之间的人群移动强度 | 平均绝对误差、均方误差和一致性相关系数 | 预测未来第5 d时,美国州级别的均方误差、平均绝对误差和一致性相关系数分别为237 412、220.5和0.84,美国县级别的均方误差、平均绝对误差和一致性相关系数分别为44177、79.8和0.66 |
3.1 人群移动一阶量的耦合模型 人群移动一阶量的耦合模型通常基于人群移动对感染者数量等指标的影响分析,将人群移动数据作为区域的一种特征(例如,人口流入流出量、POI访问量以及外出的人口数量等)融入到建模过程中,进而实现对疫情更加有效的预测. ...
... COVID-19疫情短期预测模型中,一类研究主要采用统计模型.例如,Kraemer等[9]利用百度迁徙指数量化武汉到中国其他省份的流出人群规模,结合疾病传播特征,构建广义线性模型估计疫情早期中国不同省份的疫情规模与增长速度,预测结果的R2达到0.89,并明确在封城前武汉的人口流出仍然是中国其他区域疫情暴发的主要驱动力.Choi 等[31]使用韩国的手机漫游数据量化了全球各国到韩国各省市的人口流入,同时统计出全球COVID-19发病率与牛津COVID-19政府反应追踪指数计算得出的风险评分,将以上特征导入包含外生变量的整合移动平均自回归模型,用以预测韩国12 d后外来输入的COVID-19病例.韩国境外输入病例呈现出阶段性特征,在疫情早期主要来源地区为中国,2020年4月后其主要来源地区为欧洲,因此该模型耦合不同阶段的人群移动特征分别对韩国两个时间段的外来输入病例进行预测,预测结果的平均相对误差分别为49.9%和22.3%[31].Wang等[32]利用百度迁徙指数量化武汉与湖北省其他城市的人口流出规模,结合温湿度、空气质量等多源数据与疾病传播特征,构建固定效应的多元线性回归模型,对深圳、广州、珠海、中山四个城市疫情早期阶段的感染规模实现了比较准确的短期预测,提前 2 d预测的新增感染人数R2均可达到0.81以上,但模型预测效果随着政府管制措施的实行以及病例数量减少而有所降低.Ilin等[33]基于谷歌社区移动性数据集量化人们在不同类型地点停留时间的相对变化,基于百度迁徙指数量化中国城市之间的人口流量,结合SafeGraph基于移动设备离家平均距离得到的社交距离指标等人群移动特征与历史疫情数据,构建基于面板多元线性回归模型的行为模型与基于分布滞后模型的感染模型,分别对不同NPI下人类行为的变化和不同行为变化下COVID-19感染人数的变化进行建模,对全球多个区域不同空间尺度的COVID-19累计病例数进行预测.该模型短期预测的效果良好,以全球、美国多个州和多个县未来1 d的COVID-19累计感染人数预测为例,预测结果的百分比误差中位数(Median Percentage Error, MPE)分别为0.90%、1.13%和0.98%.但随着预测时间的增长,该模型在不同空间区域的预测误差也在不断增加,并且预测误差的变化趋势呈现了区域异质性. ...
Public mobility data enables COVID-19 forecasting and management at local and global scales
2
... Related references of short-term epidemic prediction models coupled with human mobility
Tab. 1 | 分类 | 参考文献 | 模型 | 预测目标 | 预测的时间范围 | 研究区域 | 人群移动数据 | 评估指标 | 预测性能 |
| 人群移动一阶量 | [9] | 广义线性模型 | 每日COVID-19新增感染人数和累计感染人数 | 2020年2月1日—10日 | 中国的多个
省份 | 百度迁徙指数 | R2 | 预测截止至2020年2月10号(疫情初期)中国除武汉市外的累计病例数的R2为0.89 |
| [31] | 整合线性回归和自回归移动平均的预测模型 | 每日COVID-19输入性病例数 | 提前预测未来
12 d | 韩国的多个
省市 | 韩国电信的手机漫游数据 | 相关系数、均方根误差、平均绝对误差和平均相对误差 | 预测未来12 d后的新增输入病例人数时,该模型在第一个验证集(2020.03.28—04.30)的相关系数、均方根误差、平均绝对误差和平均相对误差分别为0.925、6.3、5.0和49.9%,在第二个验证集(2020.05.01-06.30)的相关系数、均方根误差、平均绝对误差和平均相对误差分别为0.798、4.1、2.8和22.3% |
| [32] | 多元线性回归
模型 | 每日COVID-19新增感染人数 | 2020年2月1日—2月15日(列举了分别预测1~5 d的精度) | 中国的4个城市(深圳、广州、珠海和中山市) | 百度迁徙数据 | 平均绝对误差、均方根误差和R2 | 以深圳市和广州市这两个人口流动较为频繁的城市为例,预测深圳市未来1天新增感染人数的平均绝对误差、均方根误差和R2分别为7、7.234和0.988,广州市的平均绝对误差、均方根误差和R2则分别为6.067、6.434和0.985 |
| [33] | 基于面板多元线性回归模型的行为模型和基于分布滞后模型的感染模型 | 每日COVID-19累计感染人数 | 提前预测未来1~10 d | 中国、美国、法国等80个国家的多种空间尺度(如,国家、省/州、市/县) | 谷歌社区移动性数据集、百度迁徙指数、SafeGraph社交距离指标、Facebook提供的网格间的人口移动次数 | 百分比误差的中位数(Median Percentage Error, MPE) | 以在粗粒度的空间尺度上预测未来1 d COVID-19的累计感染人数为例,全球的百分比误差中位数为0.9%,中国各省的百分比误差中位数为-0.2%,意大利各省的百分比误差中位数为0.89%,美国各州的百分比误差中位数为1.13% |
| [34] | 贝叶斯网络 | 每日COVID-19新增死亡人数 | 2020年3月30日—4月19日(列举了每周的预测精度) | 意大利、西班牙等11个国家 | 谷歌社区移动性数据集 | 平均误差以及平均相对误差 | 预测未来1周的死亡人数时,11个国家平均误差绝对值的均值为60,平均相对误差绝对值的均值则为2.5% |
| [35] | 融合弹性回归和主成分回归等多个模型的多层预测模型 | 每日COVID-19新增感染人数和累计感染人数 | 提前预测未来1、4和7 d的平均值 | 美国的多个县 | 谷歌社区移动性数据集 | 平均绝对误差、均方根误差和R2 | 预测未来1 d的新增感染人数时,R2、均方根误差和平均绝对误差分别为0.91、105和39;预测未来1 d的累计感染人数时,R2、均方根误差和平均绝对误差则分别为1.0、189和103 |
| 人群移动二阶量 | [30] | 基于图的神经
网络 | 每日COVID-19新增感染人数 | 提前预测未来2、7、14、21和28d | 美国的多个州 | 谷歌COVID-19聚合移动研究数据集 | 均方根误差和皮尔斯相关系数 | 预测未来第2 d时,均方根误差和皮尔森相关系数分别为313和0.298 |
| [36] | 时空图神经网络 | 每日COVID-19新增感染人数 | 提前预测未来1d | 美国的多个县 | 谷歌社区移动性数据集和谷歌COVID-19聚合移动研究数据集 | 均方根对数误差和皮尔斯相关系数 | 预测未来1 d时,均方根对数误差和皮尔森相关系数分别为0.0109和0.9980 |
| [37] | 时空注意力网络 | 每日COVID-19新增感染人数 | 提前预测未来5、15、20 d | 美国的多个州和多个县 | 通过重力模型计算的市/县和州之间的人群移动强度 | 平均绝对误差、均方误差和一致性相关系数 | 预测未来第5 d时,美国州级别的均方误差、平均绝对误差和一致性相关系数分别为237 412、220.5和0.84,美国县级别的均方误差、平均绝对误差和一致性相关系数分别为44177、79.8和0.66 |
3.1 人群移动一阶量的耦合模型 人群移动一阶量的耦合模型通常基于人群移动对感染者数量等指标的影响分析,将人群移动数据作为区域的一种特征(例如,人口流入流出量、POI访问量以及外出的人口数量等)融入到建模过程中,进而实现对疫情更加有效的预测. ...
... COVID-19疫情短期预测模型中,一类研究主要采用统计模型.例如,Kraemer等[9]利用百度迁徙指数量化武汉到中国其他省份的流出人群规模,结合疾病传播特征,构建广义线性模型估计疫情早期中国不同省份的疫情规模与增长速度,预测结果的R2达到0.89,并明确在封城前武汉的人口流出仍然是中国其他区域疫情暴发的主要驱动力.Choi 等[31]使用韩国的手机漫游数据量化了全球各国到韩国各省市的人口流入,同时统计出全球COVID-19发病率与牛津COVID-19政府反应追踪指数计算得出的风险评分,将以上特征导入包含外生变量的整合移动平均自回归模型,用以预测韩国12 d后外来输入的COVID-19病例.韩国境外输入病例呈现出阶段性特征,在疫情早期主要来源地区为中国,2020年4月后其主要来源地区为欧洲,因此该模型耦合不同阶段的人群移动特征分别对韩国两个时间段的外来输入病例进行预测,预测结果的平均相对误差分别为49.9%和22.3%[31].Wang等[32]利用百度迁徙指数量化武汉与湖北省其他城市的人口流出规模,结合温湿度、空气质量等多源数据与疾病传播特征,构建固定效应的多元线性回归模型,对深圳、广州、珠海、中山四个城市疫情早期阶段的感染规模实现了比较准确的短期预测,提前 2 d预测的新增感染人数R2均可达到0.81以上,但模型预测效果随着政府管制措施的实行以及病例数量减少而有所降低.Ilin等[33]基于谷歌社区移动性数据集量化人们在不同类型地点停留时间的相对变化,基于百度迁徙指数量化中国城市之间的人口流量,结合SafeGraph基于移动设备离家平均距离得到的社交距离指标等人群移动特征与历史疫情数据,构建基于面板多元线性回归模型的行为模型与基于分布滞后模型的感染模型,分别对不同NPI下人类行为的变化和不同行为变化下COVID-19感染人数的变化进行建模,对全球多个区域不同空间尺度的COVID-19累计病例数进行预测.该模型短期预测的效果良好,以全球、美国多个州和多个县未来1 d的COVID-19累计感染人数预测为例,预测结果的百分比误差中位数(Median Percentage Error, MPE)分别为0.90%、1.13%和0.98%.但随着预测时间的增长,该模型在不同空间区域的预测误差也在不断增加,并且预测误差的变化趋势呈现了区域异质性. ...
Estimating the impact of mobility patterns on COVID-19 infection rates in 11 European countries
2
2020
... Related references of short-term epidemic prediction models coupled with human mobility
Tab. 1 | 分类 | 参考文献 | 模型 | 预测目标 | 预测的时间范围 | 研究区域 | 人群移动数据 | 评估指标 | 预测性能 |
| 人群移动一阶量 | [9] | 广义线性模型 | 每日COVID-19新增感染人数和累计感染人数 | 2020年2月1日—10日 | 中国的多个
省份 | 百度迁徙指数 | R2 | 预测截止至2020年2月10号(疫情初期)中国除武汉市外的累计病例数的R2为0.89 |
| [31] | 整合线性回归和自回归移动平均的预测模型 | 每日COVID-19输入性病例数 | 提前预测未来
12 d | 韩国的多个
省市 | 韩国电信的手机漫游数据 | 相关系数、均方根误差、平均绝对误差和平均相对误差 | 预测未来12 d后的新增输入病例人数时,该模型在第一个验证集(2020.03.28—04.30)的相关系数、均方根误差、平均绝对误差和平均相对误差分别为0.925、6.3、5.0和49.9%,在第二个验证集(2020.05.01-06.30)的相关系数、均方根误差、平均绝对误差和平均相对误差分别为0.798、4.1、2.8和22.3% |
| [32] | 多元线性回归
模型 | 每日COVID-19新增感染人数 | 2020年2月1日—2月15日(列举了分别预测1~5 d的精度) | 中国的4个城市(深圳、广州、珠海和中山市) | 百度迁徙数据 | 平均绝对误差、均方根误差和R2 | 以深圳市和广州市这两个人口流动较为频繁的城市为例,预测深圳市未来1天新增感染人数的平均绝对误差、均方根误差和R2分别为7、7.234和0.988,广州市的平均绝对误差、均方根误差和R2则分别为6.067、6.434和0.985 |
| [33] | 基于面板多元线性回归模型的行为模型和基于分布滞后模型的感染模型 | 每日COVID-19累计感染人数 | 提前预测未来1~10 d | 中国、美国、法国等80个国家的多种空间尺度(如,国家、省/州、市/县) | 谷歌社区移动性数据集、百度迁徙指数、SafeGraph社交距离指标、Facebook提供的网格间的人口移动次数 | 百分比误差的中位数(Median Percentage Error, MPE) | 以在粗粒度的空间尺度上预测未来1 d COVID-19的累计感染人数为例,全球的百分比误差中位数为0.9%,中国各省的百分比误差中位数为-0.2%,意大利各省的百分比误差中位数为0.89%,美国各州的百分比误差中位数为1.13% |
| [34] | 贝叶斯网络 | 每日COVID-19新增死亡人数 | 2020年3月30日—4月19日(列举了每周的预测精度) | 意大利、西班牙等11个国家 | 谷歌社区移动性数据集 | 平均误差以及平均相对误差 | 预测未来1周的死亡人数时,11个国家平均误差绝对值的均值为60,平均相对误差绝对值的均值则为2.5% |
| [35] | 融合弹性回归和主成分回归等多个模型的多层预测模型 | 每日COVID-19新增感染人数和累计感染人数 | 提前预测未来1、4和7 d的平均值 | 美国的多个县 | 谷歌社区移动性数据集 | 平均绝对误差、均方根误差和R2 | 预测未来1 d的新增感染人数时,R2、均方根误差和平均绝对误差分别为0.91、105和39;预测未来1 d的累计感染人数时,R2、均方根误差和平均绝对误差则分别为1.0、189和103 |
| 人群移动二阶量 | [30] | 基于图的神经
网络 | 每日COVID-19新增感染人数 | 提前预测未来2、7、14、21和28d | 美国的多个州 | 谷歌COVID-19聚合移动研究数据集 | 均方根误差和皮尔斯相关系数 | 预测未来第2 d时,均方根误差和皮尔森相关系数分别为313和0.298 |
| [36] | 时空图神经网络 | 每日COVID-19新增感染人数 | 提前预测未来1d | 美国的多个县 | 谷歌社区移动性数据集和谷歌COVID-19聚合移动研究数据集 | 均方根对数误差和皮尔斯相关系数 | 预测未来1 d时,均方根对数误差和皮尔森相关系数分别为0.0109和0.9980 |
| [37] | 时空注意力网络 | 每日COVID-19新增感染人数 | 提前预测未来5、15、20 d | 美国的多个州和多个县 | 通过重力模型计算的市/县和州之间的人群移动强度 | 平均绝对误差、均方误差和一致性相关系数 | 预测未来第5 d时,美国州级别的均方误差、平均绝对误差和一致性相关系数分别为237 412、220.5和0.84,美国县级别的均方误差、平均绝对误差和一致性相关系数分别为44177、79.8和0.66 |
3.1 人群移动一阶量的耦合模型 人群移动一阶量的耦合模型通常基于人群移动对感染者数量等指标的影响分析,将人群移动数据作为区域的一种特征(例如,人口流入流出量、POI访问量以及外出的人口数量等)融入到建模过程中,进而实现对疫情更加有效的预测. ...
... 另一类研究则主要采用机器学习方法构建COVID-19疫情短期预测模型.例如,Bryant等[34]基于欧洲11个国家的零售和娱乐、杂货店和药房、交通场所、工作场所、住宅五类场所的人口流动性变化,结合疫情早期数据,通过贝叶斯网络模型进行模型训练,用以预测未来三周的累计感染人数、死亡人数以及基本再生数 ,并明确杂货店和药房的人群流动性对 的影响最大.Kuo等[35]利用区域的人口统计学特征(如,人口密度等)、环境特征(如,温湿度等)、基于谷歌的社区人群移动特征(人们在不同类型地点停留时间相对变化)、历史疫情感染规模等作为模型输入特征,构建融合弹性网络回归、主成分回归、K近邻模型、随机森林、广义线性模型等多模型的机器学习混合框架,对美国172个县未来1、4与7 d平均的COVID-19每日新增患者数量、累计患者数量进行预测,并评估实施隔离或开放政策的效用,指出大城市如能坚持一周以上的隔离措施则可明显降低感染率.此外,在其他传染病研究中,有研究提出可利用图嵌入技术将人群移动二阶量转换为人群移动一阶量,进而构建疫情预测模型[29]. ...
Evaluating the impact of mobility on COVID-19 pandemic with machine learning hybrid predictions
2
2021
... Related references of short-term epidemic prediction models coupled with human mobility
Tab. 1 | 分类 | 参考文献 | 模型 | 预测目标 | 预测的时间范围 | 研究区域 | 人群移动数据 | 评估指标 | 预测性能 |
| 人群移动一阶量 | [9] | 广义线性模型 | 每日COVID-19新增感染人数和累计感染人数 | 2020年2月1日—10日 | 中国的多个
省份 | 百度迁徙指数 | R2 | 预测截止至2020年2月10号(疫情初期)中国除武汉市外的累计病例数的R2为0.89 |
| [31] | 整合线性回归和自回归移动平均的预测模型 | 每日COVID-19输入性病例数 | 提前预测未来
12 d | 韩国的多个
省市 | 韩国电信的手机漫游数据 | 相关系数、均方根误差、平均绝对误差和平均相对误差 | 预测未来12 d后的新增输入病例人数时,该模型在第一个验证集(2020.03.28—04.30)的相关系数、均方根误差、平均绝对误差和平均相对误差分别为0.925、6.3、5.0和49.9%,在第二个验证集(2020.05.01-06.30)的相关系数、均方根误差、平均绝对误差和平均相对误差分别为0.798、4.1、2.8和22.3% |
| [32] | 多元线性回归
模型 | 每日COVID-19新增感染人数 | 2020年2月1日—2月15日(列举了分别预测1~5 d的精度) | 中国的4个城市(深圳、广州、珠海和中山市) | 百度迁徙数据 | 平均绝对误差、均方根误差和R2 | 以深圳市和广州市这两个人口流动较为频繁的城市为例,预测深圳市未来1天新增感染人数的平均绝对误差、均方根误差和R2分别为7、7.234和0.988,广州市的平均绝对误差、均方根误差和R2则分别为6.067、6.434和0.985 |
| [33] | 基于面板多元线性回归模型的行为模型和基于分布滞后模型的感染模型 | 每日COVID-19累计感染人数 | 提前预测未来1~10 d | 中国、美国、法国等80个国家的多种空间尺度(如,国家、省/州、市/县) | 谷歌社区移动性数据集、百度迁徙指数、SafeGraph社交距离指标、Facebook提供的网格间的人口移动次数 | 百分比误差的中位数(Median Percentage Error, MPE) | 以在粗粒度的空间尺度上预测未来1 d COVID-19的累计感染人数为例,全球的百分比误差中位数为0.9%,中国各省的百分比误差中位数为-0.2%,意大利各省的百分比误差中位数为0.89%,美国各州的百分比误差中位数为1.13% |
| [34] | 贝叶斯网络 | 每日COVID-19新增死亡人数 | 2020年3月30日—4月19日(列举了每周的预测精度) | 意大利、西班牙等11个国家 | 谷歌社区移动性数据集 | 平均误差以及平均相对误差 | 预测未来1周的死亡人数时,11个国家平均误差绝对值的均值为60,平均相对误差绝对值的均值则为2.5% |
| [35] | 融合弹性回归和主成分回归等多个模型的多层预测模型 | 每日COVID-19新增感染人数和累计感染人数 | 提前预测未来1、4和7 d的平均值 | 美国的多个县 | 谷歌社区移动性数据集 | 平均绝对误差、均方根误差和R2 | 预测未来1 d的新增感染人数时,R2、均方根误差和平均绝对误差分别为0.91、105和39;预测未来1 d的累计感染人数时,R2、均方根误差和平均绝对误差则分别为1.0、189和103 |
| 人群移动二阶量 | [30] | 基于图的神经
网络 | 每日COVID-19新增感染人数 | 提前预测未来2、7、14、21和28d | 美国的多个州 | 谷歌COVID-19聚合移动研究数据集 | 均方根误差和皮尔斯相关系数 | 预测未来第2 d时,均方根误差和皮尔森相关系数分别为313和0.298 |
| [36] | 时空图神经网络 | 每日COVID-19新增感染人数 | 提前预测未来1d | 美国的多个县 | 谷歌社区移动性数据集和谷歌COVID-19聚合移动研究数据集 | 均方根对数误差和皮尔斯相关系数 | 预测未来1 d时,均方根对数误差和皮尔森相关系数分别为0.0109和0.9980 |
| [37] | 时空注意力网络 | 每日COVID-19新增感染人数 | 提前预测未来5、15、20 d | 美国的多个州和多个县 | 通过重力模型计算的市/县和州之间的人群移动强度 | 平均绝对误差、均方误差和一致性相关系数 | 预测未来第5 d时,美国州级别的均方误差、平均绝对误差和一致性相关系数分别为237 412、220.5和0.84,美国县级别的均方误差、平均绝对误差和一致性相关系数分别为44177、79.8和0.66 |
3.1 人群移动一阶量的耦合模型 人群移动一阶量的耦合模型通常基于人群移动对感染者数量等指标的影响分析,将人群移动数据作为区域的一种特征(例如,人口流入流出量、POI访问量以及外出的人口数量等)融入到建模过程中,进而实现对疫情更加有效的预测. ...
... 另一类研究则主要采用机器学习方法构建COVID-19疫情短期预测模型.例如,Bryant等[34]基于欧洲11个国家的零售和娱乐、杂货店和药房、交通场所、工作场所、住宅五类场所的人口流动性变化,结合疫情早期数据,通过贝叶斯网络模型进行模型训练,用以预测未来三周的累计感染人数、死亡人数以及基本再生数 ,并明确杂货店和药房的人群流动性对 的影响最大.Kuo等[35]利用区域的人口统计学特征(如,人口密度等)、环境特征(如,温湿度等)、基于谷歌的社区人群移动特征(人们在不同类型地点停留时间相对变化)、历史疫情感染规模等作为模型输入特征,构建融合弹性网络回归、主成分回归、K近邻模型、随机森林、广义线性模型等多模型的机器学习混合框架,对美国172个县未来1、4与7 d平均的COVID-19每日新增患者数量、累计患者数量进行预测,并评估实施隔离或开放政策的效用,指出大城市如能坚持一周以上的隔离措施则可明显降低感染率.此外,在其他传染病研究中,有研究提出可利用图嵌入技术将人群移动二阶量转换为人群移动一阶量,进而构建疫情预测模型[29]. ...
Examining COVID-19 Forecasting using spatio-temporal graph neural networks
3
2020
... Related references of short-term epidemic prediction models coupled with human mobility
Tab. 1 | 分类 | 参考文献 | 模型 | 预测目标 | 预测的时间范围 | 研究区域 | 人群移动数据 | 评估指标 | 预测性能 |
| 人群移动一阶量 | [9] | 广义线性模型 | 每日COVID-19新增感染人数和累计感染人数 | 2020年2月1日—10日 | 中国的多个
省份 | 百度迁徙指数 | R2 | 预测截止至2020年2月10号(疫情初期)中国除武汉市外的累计病例数的R2为0.89 |
| [31] | 整合线性回归和自回归移动平均的预测模型 | 每日COVID-19输入性病例数 | 提前预测未来
12 d | 韩国的多个
省市 | 韩国电信的手机漫游数据 | 相关系数、均方根误差、平均绝对误差和平均相对误差 | 预测未来12 d后的新增输入病例人数时,该模型在第一个验证集(2020.03.28—04.30)的相关系数、均方根误差、平均绝对误差和平均相对误差分别为0.925、6.3、5.0和49.9%,在第二个验证集(2020.05.01-06.30)的相关系数、均方根误差、平均绝对误差和平均相对误差分别为0.798、4.1、2.8和22.3% |
| [32] | 多元线性回归
模型 | 每日COVID-19新增感染人数 | 2020年2月1日—2月15日(列举了分别预测1~5 d的精度) | 中国的4个城市(深圳、广州、珠海和中山市) | 百度迁徙数据 | 平均绝对误差、均方根误差和R2 | 以深圳市和广州市这两个人口流动较为频繁的城市为例,预测深圳市未来1天新增感染人数的平均绝对误差、均方根误差和R2分别为7、7.234和0.988,广州市的平均绝对误差、均方根误差和R2则分别为6.067、6.434和0.985 |
| [33] | 基于面板多元线性回归模型的行为模型和基于分布滞后模型的感染模型 | 每日COVID-19累计感染人数 | 提前预测未来1~10 d | 中国、美国、法国等80个国家的多种空间尺度(如,国家、省/州、市/县) | 谷歌社区移动性数据集、百度迁徙指数、SafeGraph社交距离指标、Facebook提供的网格间的人口移动次数 | 百分比误差的中位数(Median Percentage Error, MPE) | 以在粗粒度的空间尺度上预测未来1 d COVID-19的累计感染人数为例,全球的百分比误差中位数为0.9%,中国各省的百分比误差中位数为-0.2%,意大利各省的百分比误差中位数为0.89%,美国各州的百分比误差中位数为1.13% |
| [34] | 贝叶斯网络 | 每日COVID-19新增死亡人数 | 2020年3月30日—4月19日(列举了每周的预测精度) | 意大利、西班牙等11个国家 | 谷歌社区移动性数据集 | 平均误差以及平均相对误差 | 预测未来1周的死亡人数时,11个国家平均误差绝对值的均值为60,平均相对误差绝对值的均值则为2.5% |
| [35] | 融合弹性回归和主成分回归等多个模型的多层预测模型 | 每日COVID-19新增感染人数和累计感染人数 | 提前预测未来1、4和7 d的平均值 | 美国的多个县 | 谷歌社区移动性数据集 | 平均绝对误差、均方根误差和R2 | 预测未来1 d的新增感染人数时,R2、均方根误差和平均绝对误差分别为0.91、105和39;预测未来1 d的累计感染人数时,R2、均方根误差和平均绝对误差则分别为1.0、189和103 |
| 人群移动二阶量 | [30] | 基于图的神经
网络 | 每日COVID-19新增感染人数 | 提前预测未来2、7、14、21和28d | 美国的多个州 | 谷歌COVID-19聚合移动研究数据集 | 均方根误差和皮尔斯相关系数 | 预测未来第2 d时,均方根误差和皮尔森相关系数分别为313和0.298 |
| [36] | 时空图神经网络 | 每日COVID-19新增感染人数 | 提前预测未来1d | 美国的多个县 | 谷歌社区移动性数据集和谷歌COVID-19聚合移动研究数据集 | 均方根对数误差和皮尔斯相关系数 | 预测未来1 d时,均方根对数误差和皮尔森相关系数分别为0.0109和0.9980 |
| [37] | 时空注意力网络 | 每日COVID-19新增感染人数 | 提前预测未来5、15、20 d | 美国的多个州和多个县 | 通过重力模型计算的市/县和州之间的人群移动强度 | 平均绝对误差、均方误差和一致性相关系数 | 预测未来第5 d时,美国州级别的均方误差、平均绝对误差和一致性相关系数分别为237 412、220.5和0.84,美国县级别的均方误差、平均绝对误差和一致性相关系数分别为44177、79.8和0.66 |
3.1 人群移动一阶量的耦合模型 人群移动一阶量的耦合模型通常基于人群移动对感染者数量等指标的影响分析,将人群移动数据作为区域的一种特征(例如,人口流入流出量、POI访问量以及外出的人口数量等)融入到建模过程中,进而实现对疫情更加有效的预测. ...
... 人群移动二阶量的耦合模型以人群移动的网络交互特征作为输入,考虑了不同区域之间的空间依赖关系,能够更高效地实现时空同时预测.当前COVID-19预测研究主要通过图神经网络(Graph Convolution Network, GCN)构建时空预测模型.例如,Wang等[30]利用谷歌提供的人群移动数据集以及COVID-19疫情监测数据构建了基于GCN的时空预测模型.该模型把每个州(state)当作图的一个节点,根据不同州之间的人群流动量来动态决定不同节点之间的连边.结果表明,从提前预测2、7、14、21、28 d的角度,该模型在大多数情况下取得了优于ARMA、LSTM和cola-GNN等其他基准方法的预测性能,但预测性能随预测时间长度的增加而下降.Kapoor等[36]基于谷歌的人群移动数据集、谷歌社区移动性报告以及纽约时报COVID-19数据集构建了时空图神经网络模型,用于预测美国县(county)级别的未来一天COVID-19新增病例数,同时还验证了引入人群移动性数据有助于改善深度学习模型的预测性能.Gao等[37]将区域的经纬度、人口规模和人口密度作为图中对应节点的静态特征,将区域的活跃确诊病例数、累计病例数、住院患者数以及重症患者数作为对应节点的动态特征,根据2个区域的人口规模与物理距离确定2个节点之间连边的人群交互权重,通过构建基于图注意力网络(Graph Attention Network, GAT)和门控循环单元(Gate Recurrent Unit, GRU)的时空注意力网络,对美国不同州和县的COVID-19感染病例数进行预测,在不同实验条件下该模型的预测性能均显著优于几个常用的疾病传播仓室模型与深度学习预测模型(GRU、cola-GNN和GNN[36])等基线模型[37]. ...
... [36])等基线模型[37]. ...
Stan: Spatio-temporal attention network for pandemic prediction using real world evidence
3
2008
... Related references of short-term epidemic prediction models coupled with human mobility
Tab. 1 | 分类 | 参考文献 | 模型 | 预测目标 | 预测的时间范围 | 研究区域 | 人群移动数据 | 评估指标 | 预测性能 |
| 人群移动一阶量 | [9] | 广义线性模型 | 每日COVID-19新增感染人数和累计感染人数 | 2020年2月1日—10日 | 中国的多个
省份 | 百度迁徙指数 | R2 | 预测截止至2020年2月10号(疫情初期)中国除武汉市外的累计病例数的R2为0.89 |
| [31] | 整合线性回归和自回归移动平均的预测模型 | 每日COVID-19输入性病例数 | 提前预测未来
12 d | 韩国的多个
省市 | 韩国电信的手机漫游数据 | 相关系数、均方根误差、平均绝对误差和平均相对误差 | 预测未来12 d后的新增输入病例人数时,该模型在第一个验证集(2020.03.28—04.30)的相关系数、均方根误差、平均绝对误差和平均相对误差分别为0.925、6.3、5.0和49.9%,在第二个验证集(2020.05.01-06.30)的相关系数、均方根误差、平均绝对误差和平均相对误差分别为0.798、4.1、2.8和22.3% |
| [32] | 多元线性回归
模型 | 每日COVID-19新增感染人数 | 2020年2月1日—2月15日(列举了分别预测1~5 d的精度) | 中国的4个城市(深圳、广州、珠海和中山市) | 百度迁徙数据 | 平均绝对误差、均方根误差和R2 | 以深圳市和广州市这两个人口流动较为频繁的城市为例,预测深圳市未来1天新增感染人数的平均绝对误差、均方根误差和R2分别为7、7.234和0.988,广州市的平均绝对误差、均方根误差和R2则分别为6.067、6.434和0.985 |
| [33] | 基于面板多元线性回归模型的行为模型和基于分布滞后模型的感染模型 | 每日COVID-19累计感染人数 | 提前预测未来1~10 d | 中国、美国、法国等80个国家的多种空间尺度(如,国家、省/州、市/县) | 谷歌社区移动性数据集、百度迁徙指数、SafeGraph社交距离指标、Facebook提供的网格间的人口移动次数 | 百分比误差的中位数(Median Percentage Error, MPE) | 以在粗粒度的空间尺度上预测未来1 d COVID-19的累计感染人数为例,全球的百分比误差中位数为0.9%,中国各省的百分比误差中位数为-0.2%,意大利各省的百分比误差中位数为0.89%,美国各州的百分比误差中位数为1.13% |
| [34] | 贝叶斯网络 | 每日COVID-19新增死亡人数 | 2020年3月30日—4月19日(列举了每周的预测精度) | 意大利、西班牙等11个国家 | 谷歌社区移动性数据集 | 平均误差以及平均相对误差 | 预测未来1周的死亡人数时,11个国家平均误差绝对值的均值为60,平均相对误差绝对值的均值则为2.5% |
| [35] | 融合弹性回归和主成分回归等多个模型的多层预测模型 | 每日COVID-19新增感染人数和累计感染人数 | 提前预测未来1、4和7 d的平均值 | 美国的多个县 | 谷歌社区移动性数据集 | 平均绝对误差、均方根误差和R2 | 预测未来1 d的新增感染人数时,R2、均方根误差和平均绝对误差分别为0.91、105和39;预测未来1 d的累计感染人数时,R2、均方根误差和平均绝对误差则分别为1.0、189和103 |
| 人群移动二阶量 | [30] | 基于图的神经
网络 | 每日COVID-19新增感染人数 | 提前预测未来2、7、14、21和28d | 美国的多个州 | 谷歌COVID-19聚合移动研究数据集 | 均方根误差和皮尔斯相关系数 | 预测未来第2 d时,均方根误差和皮尔森相关系数分别为313和0.298 |
| [36] | 时空图神经网络 | 每日COVID-19新增感染人数 | 提前预测未来1d | 美国的多个县 | 谷歌社区移动性数据集和谷歌COVID-19聚合移动研究数据集 | 均方根对数误差和皮尔斯相关系数 | 预测未来1 d时,均方根对数误差和皮尔森相关系数分别为0.0109和0.9980 |
| [37] | 时空注意力网络 | 每日COVID-19新增感染人数 | 提前预测未来5、15、20 d | 美国的多个州和多个县 | 通过重力模型计算的市/县和州之间的人群移动强度 | 平均绝对误差、均方误差和一致性相关系数 | 预测未来第5 d时,美国州级别的均方误差、平均绝对误差和一致性相关系数分别为237 412、220.5和0.84,美国县级别的均方误差、平均绝对误差和一致性相关系数分别为44177、79.8和0.66 |
3.1 人群移动一阶量的耦合模型 人群移动一阶量的耦合模型通常基于人群移动对感染者数量等指标的影响分析,将人群移动数据作为区域的一种特征(例如,人口流入流出量、POI访问量以及外出的人口数量等)融入到建模过程中,进而实现对疫情更加有效的预测. ...
... 人群移动二阶量的耦合模型以人群移动的网络交互特征作为输入,考虑了不同区域之间的空间依赖关系,能够更高效地实现时空同时预测.当前COVID-19预测研究主要通过图神经网络(Graph Convolution Network, GCN)构建时空预测模型.例如,Wang等[30]利用谷歌提供的人群移动数据集以及COVID-19疫情监测数据构建了基于GCN的时空预测模型.该模型把每个州(state)当作图的一个节点,根据不同州之间的人群流动量来动态决定不同节点之间的连边.结果表明,从提前预测2、7、14、21、28 d的角度,该模型在大多数情况下取得了优于ARMA、LSTM和cola-GNN等其他基准方法的预测性能,但预测性能随预测时间长度的增加而下降.Kapoor等[36]基于谷歌的人群移动数据集、谷歌社区移动性报告以及纽约时报COVID-19数据集构建了时空图神经网络模型,用于预测美国县(county)级别的未来一天COVID-19新增病例数,同时还验证了引入人群移动性数据有助于改善深度学习模型的预测性能.Gao等[37]将区域的经纬度、人口规模和人口密度作为图中对应节点的静态特征,将区域的活跃确诊病例数、累计病例数、住院患者数以及重症患者数作为对应节点的动态特征,根据2个区域的人口规模与物理距离确定2个节点之间连边的人群交互权重,通过构建基于图注意力网络(Graph Attention Network, GAT)和门控循环单元(Gate Recurrent Unit, GRU)的时空注意力网络,对美国不同州和县的COVID-19感染病例数进行预测,在不同实验条件下该模型的预测性能均显著优于几个常用的疾病传播仓室模型与深度学习预测模型(GRU、cola-GNN和GNN[36])等基线模型[37]. ...
... [37]. ...
A contribution to the mathematical theory of epidemics
1
1927
... 基于过程模拟的传染病模型能够从时间或时空维度推演疾病传播的全过程.这类模型以传播动力学模型(Transmission-dynamic Model)为核心,根据健康状态(例如,易感、潜伏、感染、恢复或者死亡等)将人群或者其他宿主对应到不同仓室(Compartment),然后基于疾病传播特征制定健康状态的转换规则,模拟不同仓室的动态发展,因此也常常被称作仓室模型(Compartment model).其典型代表是易感-感染-恢复(Susceptible-Infected-Recovered, SIR)与易感-感染-易感(Susceptible-Infected-Susceptible, SIS)模型[38,39].在此基础上,根据疾病发病机理、传播方式以及干预措施的不同,又发展了易感-感染-恢复-易感(Susceptible-Infected-Recovered-Susceptible, SIRS)模型、易感-潜伏-感染-恢复(Susceptible-Exposed-Infected-Recovered, SEIR)模型、带出生死亡或迁移的SIS模型以及具有年龄结构的模型等[40]. ...
Contributions to the mathematical theory of epidemics-II. The problem of endemicity
1
1991
... 基于过程模拟的传染病模型能够从时间或时空维度推演疾病传播的全过程.这类模型以传播动力学模型(Transmission-dynamic Model)为核心,根据健康状态(例如,易感、潜伏、感染、恢复或者死亡等)将人群或者其他宿主对应到不同仓室(Compartment),然后基于疾病传播特征制定健康状态的转换规则,模拟不同仓室的动态发展,因此也常常被称作仓室模型(Compartment model).其典型代表是易感-感染-恢复(Susceptible-Infected-Recovered, SIR)与易感-感染-易感(Susceptible-Infected-Susceptible, SIS)模型[38,39].在此基础上,根据疾病发病机理、传播方式以及干预措施的不同,又发展了易感-感染-恢复-易感(Susceptible-Infected-Recovered-Susceptible, SIRS)模型、易感-潜伏-感染-恢复(Susceptible-Exposed-Infected-Recovered, SEIR)模型、带出生死亡或迁移的SIS模型以及具有年龄结构的模型等[40]. ...
传播动力学模型回顾与展望
1
2018
... 基于过程模拟的传染病模型能够从时间或时空维度推演疾病传播的全过程.这类模型以传播动力学模型(Transmission-dynamic Model)为核心,根据健康状态(例如,易感、潜伏、感染、恢复或者死亡等)将人群或者其他宿主对应到不同仓室(Compartment),然后基于疾病传播特征制定健康状态的转换规则,模拟不同仓室的动态发展,因此也常常被称作仓室模型(Compartment model).其典型代表是易感-感染-恢复(Susceptible-Infected-Recovered, SIR)与易感-感染-易感(Susceptible-Infected-Susceptible, SIS)模型[38,39].在此基础上,根据疾病发病机理、传播方式以及干预措施的不同,又发展了易感-感染-恢复-易感(Susceptible-Infected-Recovered-Susceptible, SIRS)模型、易感-潜伏-感染-恢复(Susceptible-Exposed-Infected-Recovered, SEIR)模型、带出生死亡或迁移的SIS模型以及具有年龄结构的模型等[40]. ...
传播动力学模型回顾与展望
1
2018
... 基于过程模拟的传染病模型能够从时间或时空维度推演疾病传播的全过程.这类模型以传播动力学模型(Transmission-dynamic Model)为核心,根据健康状态(例如,易感、潜伏、感染、恢复或者死亡等)将人群或者其他宿主对应到不同仓室(Compartment),然后基于疾病传播特征制定健康状态的转换规则,模拟不同仓室的动态发展,因此也常常被称作仓室模型(Compartment model).其典型代表是易感-感染-恢复(Susceptible-Infected-Recovered, SIR)与易感-感染-易感(Susceptible-Infected-Susceptible, SIS)模型[38,39].在此基础上,根据疾病发病机理、传播方式以及干预措施的不同,又发展了易感-感染-恢复-易感(Susceptible-Infected-Recovered-Susceptible, SIRS)模型、易感-潜伏-感染-恢复(Susceptible-Exposed-Infected-Recovered, SEIR)模型、带出生死亡或迁移的SIS模型以及具有年龄结构的模型等[40]. ...
The effect of control strategies to reduce social mixing on outcomes of the COVID-19 epidemic in Wuhan, China: A modelling study
1
2020
... 式中:S、E、I和R分别代表易感人群数量、潜伏期人群数量、感染期人群数量与已恢复人群数量; N为研究单元人口总数,N=S+E+I+R;β、σ和γ分别为传播率(单位时间每个感染者所感染的易感者人数)、潜伏期患者出现症状的转化率(1/潜伏期)与感染者的恢复率(1/感染期).根据流行病学研究需求,单位时间t通常设置为天.自COVID-19暴发以来,研究人员根据SARS-COV-2传播特征及其对应的参数,从仓室类型与状态转换的不同角度对上述基础的SEIR模型进行了多种拓展[41,42,43]. ...
Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: A modelling study
1
2020
... 式中:S、E、I和R分别代表易感人群数量、潜伏期人群数量、感染期人群数量与已恢复人群数量; N为研究单元人口总数,N=S+E+I+R;β、σ和γ分别为传播率(单位时间每个感染者所感染的易感者人数)、潜伏期患者出现症状的转化率(1/潜伏期)与感染者的恢复率(1/感染期).根据流行病学研究需求,单位时间t通常设置为天.自COVID-19暴发以来,研究人员根据SARS-COV-2传播特征及其对应的参数,从仓室类型与状态转换的不同角度对上述基础的SEIR模型进行了多种拓展[41,42,43]. ...
Early dynamics of transmission and control of COVID-19: A mathematical modelling study
1
2020
... 式中:S、E、I和R分别代表易感人群数量、潜伏期人群数量、感染期人群数量与已恢复人群数量; N为研究单元人口总数,N=S+E+I+R;β、σ和γ分别为传播率(单位时间每个感染者所感染的易感者人数)、潜伏期患者出现症状的转化率(1/潜伏期)与感染者的恢复率(1/感染期).根据流行病学研究需求,单位时间t通常设置为天.自COVID-19暴发以来,研究人员根据SARS-COV-2传播特征及其对应的参数,从仓室类型与状态转换的不同角度对上述基础的SEIR模型进行了多种拓展[41,42,43]. ...
Modified SEIR and AI prediction of the epidemics trend of COVID-19 in China under public health interventions
1
2020
... 如图2所示,在群体级别的模型中,研究单元不但可以是单个地理单元(如国家、省份、城市),即将整个研究区视为同一种群[44,45];也可以是多个地理单元,即将不同地理单元的人群视为不同种群Meta-population),对每一个种群都构建微分方程组.由此,基于不同地理单元种群的模型可以天然地结合种群之间的人群移动,通过在每个种群的模型中添加由于人群移动造成的感染状态变化的数学表达,构建基于人群移动的种群模型,即一种典型的基于网络的种群模型(Network-based Meta-population Model)[13-14,46].由于国家、城市及城市内部不同尺度的人群移动在此次COVID-19疫情扩散中产生了显著影响,研究者面向不同研究目的、从不同角度构建了大量耦合人群移动的种群模型. ...
基于传染病动力学模型的宁波市新型冠状病毒肺炎防控措施效果评估
2
2020
... Related references of process simulation models coupled with human mobility
Tab. 2 | 分类 | 文献 | 研究区域 | 人群移动数据 | 模型模拟的干预措施 | 病例真实值 | 病例模拟值 | 模型效果 |
| 群体级别 | [47] | 意大利 | 人口流量调查 | 严格管控出行活动、加大疫情排查力度 | 74 386 | 约733 000 | 模拟的疾病发展曲线与实际情况吻符合程度较高 |
| [9] | 武汉 | 百度实时流动性数据 | - | 554 | 632 | 累计病例数的R2=0.99 |
| [45] | 中国375个城市 | 腾讯位置服务人口实时流动性数据 | 佩戴口罩、社交疏离、自我
隔离 | 13 562 | 约1.2万 | 预测的疾病报告率为14%,与实际武汉市疾病报告率15.8%非常接近 |
| [15] | 中国340个城市 | 百度迁徙人口流动数据 | 综合性非药物性干预 | 79 824 | 114 325 | 全国累计病例的R2=0.86,P值<0.001 |
| [21] | 中国 | 手机实时移动性和社交联系数据、腾讯移动设
备数据集 | 疫苗接种、社交疏离 | 未使用真实数据 | 未给出具体值 | 严格的干预措施可大幅降低传播能力 |
| [13] | 深圳市 | 手机移动信令数据 | 降低出行量、区域封锁 | 未使用真实数据 | R0=2.5时,峰值病例数减少了33% | 模拟的疾病发展曲线与实际情况吻合程度较高 |
| [14] | 美国康涅狄格州 | 城镇级人口流动数据,
智能手机热图,空中交
通流量 | 社交疏离 | 47 510 | 45 752~48 105 | 对康涅狄格州所有城镇模拟,实际统计的病例R2在0.907~0.924;按类别对城镇进行模拟,实际统计的病例R2为0.978~0.987 |
| [49] | 全球 | 航空与地面交通数据 | 降低本地传播率和国际旅行 | 未使用真实数据 | 未给出具体模拟值 | 严格的干预措施可大幅降低传播能力 |
| 个体级别 | [60] | 新加坡 | 交通数据 | 隔离感染者、关闭学校和工作场所 | 未使用真实数据 | R0=1.5时,7.4%的总人口感染;R0=2.0时,19.3%的总人口感染;R0=2.5时,32%的总人口感染 | 未给出具体评价指标 |
| [61] | 波士顿 | 手机位置数据 | 检测、密接追踪、居家隔离 | 未使用真实数据 | 无干预场景75%的人口被感染 | 未给出具体评价指标 |
| [62] | 纽约、西雅图 | 手机位置数据 | 无干预措施 | 每天每千人的死亡人数(未给出具体值) | 每天每千人的死亡人数(未给出具体值) | 模型结果与真实死亡人数的拟合效果较好,二者到达峰值的时间差略大于5 d |
| [63] | 澳大利亚 | 人口通勤数据 | 国际航空旅行限制、隔离感染者、居家隔离、增大社交距离、关闭学校 | 未使用真实数据 | 最佳干预场景下有8千~1万人被感染 | 未给出具体评价指标 |
| [64] | 深圳市 | 手机信令数据 | 密接追踪、及时检测、佩戴口罩、封城、逐步复工、隔离综合措施 | 418 | 416 | 每日新增发病数量的模拟值与实际报告值的RMSE=1.354;显性感染者数量在城市内各个行政区尺度上的R2=0.95 |
4.1 群体级别的耦合模型 群体级别的模型是一种长期以来广泛使用的传播动力学建模技术,其最基本的假设是研究单元内的每个个体具有相同的特征且彼此之间均匀接触,当作一个同质的群体来对待.其中,研究单元可以是同一个区域或者同一属性的人群/其他宿主等.根据感染和传播机制,模型通常由一组微分方程构建,通常是常微分方程.在COVID-19疫情中,人类感染新型冠状病毒SARS-COV-2之后存在潜隐期(Latent Period)与潜伏期(Incubation Period,对于显性感染者而言),因此,常用于COVID-19建模的基本仓室模型为SLIR与SEIR模型.以最基本的SEIR模型为例,针对给定研究单元,假设其总人口不变,其基于常微分方程的表达公式如下: ...
... 如图2所示,在群体级别的模型中,研究单元不但可以是单个地理单元(如国家、省份、城市),即将整个研究区视为同一种群[44,45];也可以是多个地理单元,即将不同地理单元的人群视为不同种群Meta-population),对每一个种群都构建微分方程组.由此,基于不同地理单元种群的模型可以天然地结合种群之间的人群移动,通过在每个种群的模型中添加由于人群移动造成的感染状态变化的数学表达,构建基于人群移动的种群模型,即一种典型的基于网络的种群模型(Network-based Meta-population Model)[13-14,46].由于国家、城市及城市内部不同尺度的人群移动在此次COVID-19疫情扩散中产生了显著影响,研究者面向不同研究目的、从不同角度构建了大量耦合人群移动的种群模型. ...
基于传染病动力学模型的宁波市新型冠状病毒肺炎防控措施效果评估
2
2020
... Related references of process simulation models coupled with human mobility
Tab. 2 | 分类 | 文献 | 研究区域 | 人群移动数据 | 模型模拟的干预措施 | 病例真实值 | 病例模拟值 | 模型效果 |
| 群体级别 | [47] | 意大利 | 人口流量调查 | 严格管控出行活动、加大疫情排查力度 | 74 386 | 约733 000 | 模拟的疾病发展曲线与实际情况吻符合程度较高 |
| [9] | 武汉 | 百度实时流动性数据 | - | 554 | 632 | 累计病例数的R2=0.99 |
| [45] | 中国375个城市 | 腾讯位置服务人口实时流动性数据 | 佩戴口罩、社交疏离、自我
隔离 | 13 562 | 约1.2万 | 预测的疾病报告率为14%,与实际武汉市疾病报告率15.8%非常接近 |
| [15] | 中国340个城市 | 百度迁徙人口流动数据 | 综合性非药物性干预 | 79 824 | 114 325 | 全国累计病例的R2=0.86,P值<0.001 |
| [21] | 中国 | 手机实时移动性和社交联系数据、腾讯移动设
备数据集 | 疫苗接种、社交疏离 | 未使用真实数据 | 未给出具体值 | 严格的干预措施可大幅降低传播能力 |
| [13] | 深圳市 | 手机移动信令数据 | 降低出行量、区域封锁 | 未使用真实数据 | R0=2.5时,峰值病例数减少了33% | 模拟的疾病发展曲线与实际情况吻合程度较高 |
| [14] | 美国康涅狄格州 | 城镇级人口流动数据,
智能手机热图,空中交
通流量 | 社交疏离 | 47 510 | 45 752~48 105 | 对康涅狄格州所有城镇模拟,实际统计的病例R2在0.907~0.924;按类别对城镇进行模拟,实际统计的病例R2为0.978~0.987 |
| [49] | 全球 | 航空与地面交通数据 | 降低本地传播率和国际旅行 | 未使用真实数据 | 未给出具体模拟值 | 严格的干预措施可大幅降低传播能力 |
| 个体级别 | [60] | 新加坡 | 交通数据 | 隔离感染者、关闭学校和工作场所 | 未使用真实数据 | R0=1.5时,7.4%的总人口感染;R0=2.0时,19.3%的总人口感染;R0=2.5时,32%的总人口感染 | 未给出具体评价指标 |
| [61] | 波士顿 | 手机位置数据 | 检测、密接追踪、居家隔离 | 未使用真实数据 | 无干预场景75%的人口被感染 | 未给出具体评价指标 |
| [62] | 纽约、西雅图 | 手机位置数据 | 无干预措施 | 每天每千人的死亡人数(未给出具体值) | 每天每千人的死亡人数(未给出具体值) | 模型结果与真实死亡人数的拟合效果较好,二者到达峰值的时间差略大于5 d |
| [63] | 澳大利亚 | 人口通勤数据 | 国际航空旅行限制、隔离感染者、居家隔离、增大社交距离、关闭学校 | 未使用真实数据 | 最佳干预场景下有8千~1万人被感染 | 未给出具体评价指标 |
| [64] | 深圳市 | 手机信令数据 | 密接追踪、及时检测、佩戴口罩、封城、逐步复工、隔离综合措施 | 418 | 416 | 每日新增发病数量的模拟值与实际报告值的RMSE=1.354;显性感染者数量在城市内各个行政区尺度上的R2=0.95 |
4.1 群体级别的耦合模型 群体级别的模型是一种长期以来广泛使用的传播动力学建模技术,其最基本的假设是研究单元内的每个个体具有相同的特征且彼此之间均匀接触,当作一个同质的群体来对待.其中,研究单元可以是同一个区域或者同一属性的人群/其他宿主等.根据感染和传播机制,模型通常由一组微分方程构建,通常是常微分方程.在COVID-19疫情中,人类感染新型冠状病毒SARS-COV-2之后存在潜隐期(Latent Period)与潜伏期(Incubation Period,对于显性感染者而言),因此,常用于COVID-19建模的基本仓室模型为SLIR与SEIR模型.以最基本的SEIR模型为例,针对给定研究单元,假设其总人口不变,其基于常微分方程的表达公式如下: ...
... 如图2所示,在群体级别的模型中,研究单元不但可以是单个地理单元(如国家、省份、城市),即将整个研究区视为同一种群[44,45];也可以是多个地理单元,即将不同地理单元的人群视为不同种群Meta-population),对每一个种群都构建微分方程组.由此,基于不同地理单元种群的模型可以天然地结合种群之间的人群移动,通过在每个种群的模型中添加由于人群移动造成的感染状态变化的数学表达,构建基于人群移动的种群模型,即一种典型的基于网络的种群模型(Network-based Meta-population Model)[13-14,46].由于国家、城市及城市内部不同尺度的人群移动在此次COVID-19疫情扩散中产生了显著影响,研究者面向不同研究目的、从不同角度构建了大量耦合人群移动的种群模型. ...
Substantial undocumented infection facilitates the rapid dissemination of novel coronavirus (SARS-CoV-2)
2
2020
... 如图2所示,在群体级别的模型中,研究单元不但可以是单个地理单元(如国家、省份、城市),即将整个研究区视为同一种群[44,45];也可以是多个地理单元,即将不同地理单元的人群视为不同种群Meta-population),对每一个种群都构建微分方程组.由此,基于不同地理单元种群的模型可以天然地结合种群之间的人群移动,通过在每个种群的模型中添加由于人群移动造成的感染状态变化的数学表达,构建基于人群移动的种群模型,即一种典型的基于网络的种群模型(Network-based Meta-population Model)[13-14,46].由于国家、城市及城市内部不同尺度的人群移动在此次COVID-19疫情扩散中产生了显著影响,研究者面向不同研究目的、从不同角度构建了大量耦合人群移动的种群模型. ...
... 基于多个地理单元及其人群移动网络的种群模型,具有不同的空间尺度.将各个省/州看作多个地理单元,Gatto等[47]在意大利107个省际人群移动网络的基础上构建了种群SEIR模型,评估了遏制疫情传播措施的效果.将各个城市看作多个地理单元,Kraemer等[9]根据城市间的实时人群流动数据与病例旅行史,评估了输入病例在疫情传播中的作用.Li等[46]融入互联网人群迁徙数据,针对375个中国城市及其城际间人群流动构建了基于SEIR的种群模型,发现中国COVID-19疫情早期大量轻症和无症状的未记录感染者较大程度上促进了病毒传播.Lai等[15]基于互联网迁徙数据,针对340个中国城市及其城际间人群流动构建了基于SEIR的种群模型,评估了COVID-19疫情暴发以来中国实施的3类NPI的效果.该研究表明,中国采取的积极、强有力的综合性NPI在全国不同地区均取得了显著的防控效果,有效地阻断了病毒的传播,遏制了疫情的进一步扩散.Chinazzi等[48]使用COVID-19确诊病例校正了一个面向全球3200个种群的SEIR模型,进而评估了武汉出行限制措施对中国大陆及国际的疫情延缓效果.该模型中的种群集中于城市内大型交通枢纽的覆盖区域,种群之间的人群流动数据来自官方统计的航空和地面交通数据.Chen等[14]提出了一种专门针对中尺度空间单元的SEIR种群模型,不但基于huff-model量化了美国某州乡镇(town)之间的人群流动量,而且在模型中融入了居民对社交疏离的依从性(compliance)和遏制度(compliance)量化参数.将城市内部各个区域看作多个地理单元,Zhou等[13]基于手机移动定位数据,基于深圳市10个行政区构建了SEIR种群模型,并系统定量化评估了4类出行限制措施(即降低所有区域之间的出行量、封锁高风险地区、限制区域内部出行和限制感染者出行)的有效性.此外,Li等[49]在全球范围内选择了59个高风险位置(包括39个城市、10个郡县、4个省、3个地区、1个州、1个社区和1个国家)构建了基于SEIR的多尺度种群模型,融入气候驱动变量和人群移动导致的疫情空间扩散纳入各种干预方案.该研究发现,集中实施为期8周的“降低本地传播率和国际旅行”干预措施是高效且有效的,并建议对该策略从“全球干预中心”到次要高风险位置进行分层实施. ...
Spread and dynamics of the COVID-19 epidemic in Italy: Effects of emergency containment measures
2
2020
... Related references of process simulation models coupled with human mobility
Tab. 2 | 分类 | 文献 | 研究区域 | 人群移动数据 | 模型模拟的干预措施 | 病例真实值 | 病例模拟值 | 模型效果 |
| 群体级别 | [47] | 意大利 | 人口流量调查 | 严格管控出行活动、加大疫情排查力度 | 74 386 | 约733 000 | 模拟的疾病发展曲线与实际情况吻符合程度较高 |
| [9] | 武汉 | 百度实时流动性数据 | - | 554 | 632 | 累计病例数的R2=0.99 |
| [45] | 中国375个城市 | 腾讯位置服务人口实时流动性数据 | 佩戴口罩、社交疏离、自我
隔离 | 13 562 | 约1.2万 | 预测的疾病报告率为14%,与实际武汉市疾病报告率15.8%非常接近 |
| [15] | 中国340个城市 | 百度迁徙人口流动数据 | 综合性非药物性干预 | 79 824 | 114 325 | 全国累计病例的R2=0.86,P值<0.001 |
| [21] | 中国 | 手机实时移动性和社交联系数据、腾讯移动设
备数据集 | 疫苗接种、社交疏离 | 未使用真实数据 | 未给出具体值 | 严格的干预措施可大幅降低传播能力 |
| [13] | 深圳市 | 手机移动信令数据 | 降低出行量、区域封锁 | 未使用真实数据 | R0=2.5时,峰值病例数减少了33% | 模拟的疾病发展曲线与实际情况吻合程度较高 |
| [14] | 美国康涅狄格州 | 城镇级人口流动数据,
智能手机热图,空中交
通流量 | 社交疏离 | 47 510 | 45 752~48 105 | 对康涅狄格州所有城镇模拟,实际统计的病例R2在0.907~0.924;按类别对城镇进行模拟,实际统计的病例R2为0.978~0.987 |
| [49] | 全球 | 航空与地面交通数据 | 降低本地传播率和国际旅行 | 未使用真实数据 | 未给出具体模拟值 | 严格的干预措施可大幅降低传播能力 |
| 个体级别 | [60] | 新加坡 | 交通数据 | 隔离感染者、关闭学校和工作场所 | 未使用真实数据 | R0=1.5时,7.4%的总人口感染;R0=2.0时,19.3%的总人口感染;R0=2.5时,32%的总人口感染 | 未给出具体评价指标 |
| [61] | 波士顿 | 手机位置数据 | 检测、密接追踪、居家隔离 | 未使用真实数据 | 无干预场景75%的人口被感染 | 未给出具体评价指标 |
| [62] | 纽约、西雅图 | 手机位置数据 | 无干预措施 | 每天每千人的死亡人数(未给出具体值) | 每天每千人的死亡人数(未给出具体值) | 模型结果与真实死亡人数的拟合效果较好,二者到达峰值的时间差略大于5 d |
| [63] | 澳大利亚 | 人口通勤数据 | 国际航空旅行限制、隔离感染者、居家隔离、增大社交距离、关闭学校 | 未使用真实数据 | 最佳干预场景下有8千~1万人被感染 | 未给出具体评价指标 |
| [64] | 深圳市 | 手机信令数据 | 密接追踪、及时检测、佩戴口罩、封城、逐步复工、隔离综合措施 | 418 | 416 | 每日新增发病数量的模拟值与实际报告值的RMSE=1.354;显性感染者数量在城市内各个行政区尺度上的R2=0.95 |
4.1 群体级别的耦合模型 群体级别的模型是一种长期以来广泛使用的传播动力学建模技术,其最基本的假设是研究单元内的每个个体具有相同的特征且彼此之间均匀接触,当作一个同质的群体来对待.其中,研究单元可以是同一个区域或者同一属性的人群/其他宿主等.根据感染和传播机制,模型通常由一组微分方程构建,通常是常微分方程.在COVID-19疫情中,人类感染新型冠状病毒SARS-COV-2之后存在潜隐期(Latent Period)与潜伏期(Incubation Period,对于显性感染者而言),因此,常用于COVID-19建模的基本仓室模型为SLIR与SEIR模型.以最基本的SEIR模型为例,针对给定研究单元,假设其总人口不变,其基于常微分方程的表达公式如下: ...
... 基于多个地理单元及其人群移动网络的种群模型,具有不同的空间尺度.将各个省/州看作多个地理单元,Gatto等[47]在意大利107个省际人群移动网络的基础上构建了种群SEIR模型,评估了遏制疫情传播措施的效果.将各个城市看作多个地理单元,Kraemer等[9]根据城市间的实时人群流动数据与病例旅行史,评估了输入病例在疫情传播中的作用.Li等[46]融入互联网人群迁徙数据,针对375个中国城市及其城际间人群流动构建了基于SEIR的种群模型,发现中国COVID-19疫情早期大量轻症和无症状的未记录感染者较大程度上促进了病毒传播.Lai等[15]基于互联网迁徙数据,针对340个中国城市及其城际间人群流动构建了基于SEIR的种群模型,评估了COVID-19疫情暴发以来中国实施的3类NPI的效果.该研究表明,中国采取的积极、强有力的综合性NPI在全国不同地区均取得了显著的防控效果,有效地阻断了病毒的传播,遏制了疫情的进一步扩散.Chinazzi等[48]使用COVID-19确诊病例校正了一个面向全球3200个种群的SEIR模型,进而评估了武汉出行限制措施对中国大陆及国际的疫情延缓效果.该模型中的种群集中于城市内大型交通枢纽的覆盖区域,种群之间的人群流动数据来自官方统计的航空和地面交通数据.Chen等[14]提出了一种专门针对中尺度空间单元的SEIR种群模型,不但基于huff-model量化了美国某州乡镇(town)之间的人群流动量,而且在模型中融入了居民对社交疏离的依从性(compliance)和遏制度(compliance)量化参数.将城市内部各个区域看作多个地理单元,Zhou等[13]基于手机移动定位数据,基于深圳市10个行政区构建了SEIR种群模型,并系统定量化评估了4类出行限制措施(即降低所有区域之间的出行量、封锁高风险地区、限制区域内部出行和限制感染者出行)的有效性.此外,Li等[49]在全球范围内选择了59个高风险位置(包括39个城市、10个郡县、4个省、3个地区、1个州、1个社区和1个国家)构建了基于SEIR的多尺度种群模型,融入气候驱动变量和人群移动导致的疫情空间扩散纳入各种干预方案.该研究发现,集中实施为期8周的“降低本地传播率和国际旅行”干预措施是高效且有效的,并建议对该策略从“全球干预中心”到次要高风险位置进行分层实施. ...
The effect of travel restrictions on the spread of the 2019 novel coronavirus (COVID-19) outbreak
1
2020
... 基于多个地理单元及其人群移动网络的种群模型,具有不同的空间尺度.将各个省/州看作多个地理单元,Gatto等[47]在意大利107个省际人群移动网络的基础上构建了种群SEIR模型,评估了遏制疫情传播措施的效果.将各个城市看作多个地理单元,Kraemer等[9]根据城市间的实时人群流动数据与病例旅行史,评估了输入病例在疫情传播中的作用.Li等[46]融入互联网人群迁徙数据,针对375个中国城市及其城际间人群流动构建了基于SEIR的种群模型,发现中国COVID-19疫情早期大量轻症和无症状的未记录感染者较大程度上促进了病毒传播.Lai等[15]基于互联网迁徙数据,针对340个中国城市及其城际间人群流动构建了基于SEIR的种群模型,评估了COVID-19疫情暴发以来中国实施的3类NPI的效果.该研究表明,中国采取的积极、强有力的综合性NPI在全国不同地区均取得了显著的防控效果,有效地阻断了病毒的传播,遏制了疫情的进一步扩散.Chinazzi等[48]使用COVID-19确诊病例校正了一个面向全球3200个种群的SEIR模型,进而评估了武汉出行限制措施对中国大陆及国际的疫情延缓效果.该模型中的种群集中于城市内大型交通枢纽的覆盖区域,种群之间的人群流动数据来自官方统计的航空和地面交通数据.Chen等[14]提出了一种专门针对中尺度空间单元的SEIR种群模型,不但基于huff-model量化了美国某州乡镇(town)之间的人群流动量,而且在模型中融入了居民对社交疏离的依从性(compliance)和遏制度(compliance)量化参数.将城市内部各个区域看作多个地理单元,Zhou等[13]基于手机移动定位数据,基于深圳市10个行政区构建了SEIR种群模型,并系统定量化评估了4类出行限制措施(即降低所有区域之间的出行量、封锁高风险地区、限制区域内部出行和限制感染者出行)的有效性.此外,Li等[49]在全球范围内选择了59个高风险位置(包括39个城市、10个郡县、4个省、3个地区、1个州、1个社区和1个国家)构建了基于SEIR的多尺度种群模型,融入气候驱动变量和人群移动导致的疫情空间扩散纳入各种干预方案.该研究发现,集中实施为期8周的“降低本地传播率和国际旅行”干预措施是高效且有效的,并建议对该策略从“全球干预中心”到次要高风险位置进行分层实施. ...
Global COVID-19 pandemic demands joint interventions for the suppression of future waves
2
2020
... Related references of process simulation models coupled with human mobility
Tab. 2 | 分类 | 文献 | 研究区域 | 人群移动数据 | 模型模拟的干预措施 | 病例真实值 | 病例模拟值 | 模型效果 |
| 群体级别 | [47] | 意大利 | 人口流量调查 | 严格管控出行活动、加大疫情排查力度 | 74 386 | 约733 000 | 模拟的疾病发展曲线与实际情况吻符合程度较高 |
| [9] | 武汉 | 百度实时流动性数据 | - | 554 | 632 | 累计病例数的R2=0.99 |
| [45] | 中国375个城市 | 腾讯位置服务人口实时流动性数据 | 佩戴口罩、社交疏离、自我
隔离 | 13 562 | 约1.2万 | 预测的疾病报告率为14%,与实际武汉市疾病报告率15.8%非常接近 |
| [15] | 中国340个城市 | 百度迁徙人口流动数据 | 综合性非药物性干预 | 79 824 | 114 325 | 全国累计病例的R2=0.86,P值<0.001 |
| [21] | 中国 | 手机实时移动性和社交联系数据、腾讯移动设
备数据集 | 疫苗接种、社交疏离 | 未使用真实数据 | 未给出具体值 | 严格的干预措施可大幅降低传播能力 |
| [13] | 深圳市 | 手机移动信令数据 | 降低出行量、区域封锁 | 未使用真实数据 | R0=2.5时,峰值病例数减少了33% | 模拟的疾病发展曲线与实际情况吻合程度较高 |
| [14] | 美国康涅狄格州 | 城镇级人口流动数据,
智能手机热图,空中交
通流量 | 社交疏离 | 47 510 | 45 752~48 105 | 对康涅狄格州所有城镇模拟,实际统计的病例R2在0.907~0.924;按类别对城镇进行模拟,实际统计的病例R2为0.978~0.987 |
| [49] | 全球 | 航空与地面交通数据 | 降低本地传播率和国际旅行 | 未使用真实数据 | 未给出具体模拟值 | 严格的干预措施可大幅降低传播能力 |
| 个体级别 | [60] | 新加坡 | 交通数据 | 隔离感染者、关闭学校和工作场所 | 未使用真实数据 | R0=1.5时,7.4%的总人口感染;R0=2.0时,19.3%的总人口感染;R0=2.5时,32%的总人口感染 | 未给出具体评价指标 |
| [61] | 波士顿 | 手机位置数据 | 检测、密接追踪、居家隔离 | 未使用真实数据 | 无干预场景75%的人口被感染 | 未给出具体评价指标 |
| [62] | 纽约、西雅图 | 手机位置数据 | 无干预措施 | 每天每千人的死亡人数(未给出具体值) | 每天每千人的死亡人数(未给出具体值) | 模型结果与真实死亡人数的拟合效果较好,二者到达峰值的时间差略大于5 d |
| [63] | 澳大利亚 | 人口通勤数据 | 国际航空旅行限制、隔离感染者、居家隔离、增大社交距离、关闭学校 | 未使用真实数据 | 最佳干预场景下有8千~1万人被感染 | 未给出具体评价指标 |
| [64] | 深圳市 | 手机信令数据 | 密接追踪、及时检测、佩戴口罩、封城、逐步复工、隔离综合措施 | 418 | 416 | 每日新增发病数量的模拟值与实际报告值的RMSE=1.354;显性感染者数量在城市内各个行政区尺度上的R2=0.95 |
4.1 群体级别的耦合模型 群体级别的模型是一种长期以来广泛使用的传播动力学建模技术,其最基本的假设是研究单元内的每个个体具有相同的特征且彼此之间均匀接触,当作一个同质的群体来对待.其中,研究单元可以是同一个区域或者同一属性的人群/其他宿主等.根据感染和传播机制,模型通常由一组微分方程构建,通常是常微分方程.在COVID-19疫情中,人类感染新型冠状病毒SARS-COV-2之后存在潜隐期(Latent Period)与潜伏期(Incubation Period,对于显性感染者而言),因此,常用于COVID-19建模的基本仓室模型为SLIR与SEIR模型.以最基本的SEIR模型为例,针对给定研究单元,假设其总人口不变,其基于常微分方程的表达公式如下: ...
... 基于多个地理单元及其人群移动网络的种群模型,具有不同的空间尺度.将各个省/州看作多个地理单元,Gatto等[47]在意大利107个省际人群移动网络的基础上构建了种群SEIR模型,评估了遏制疫情传播措施的效果.将各个城市看作多个地理单元,Kraemer等[9]根据城市间的实时人群流动数据与病例旅行史,评估了输入病例在疫情传播中的作用.Li等[46]融入互联网人群迁徙数据,针对375个中国城市及其城际间人群流动构建了基于SEIR的种群模型,发现中国COVID-19疫情早期大量轻症和无症状的未记录感染者较大程度上促进了病毒传播.Lai等[15]基于互联网迁徙数据,针对340个中国城市及其城际间人群流动构建了基于SEIR的种群模型,评估了COVID-19疫情暴发以来中国实施的3类NPI的效果.该研究表明,中国采取的积极、强有力的综合性NPI在全国不同地区均取得了显著的防控效果,有效地阻断了病毒的传播,遏制了疫情的进一步扩散.Chinazzi等[48]使用COVID-19确诊病例校正了一个面向全球3200个种群的SEIR模型,进而评估了武汉出行限制措施对中国大陆及国际的疫情延缓效果.该模型中的种群集中于城市内大型交通枢纽的覆盖区域,种群之间的人群流动数据来自官方统计的航空和地面交通数据.Chen等[14]提出了一种专门针对中尺度空间单元的SEIR种群模型,不但基于huff-model量化了美国某州乡镇(town)之间的人群流动量,而且在模型中融入了居民对社交疏离的依从性(compliance)和遏制度(compliance)量化参数.将城市内部各个区域看作多个地理单元,Zhou等[13]基于手机移动定位数据,基于深圳市10个行政区构建了SEIR种群模型,并系统定量化评估了4类出行限制措施(即降低所有区域之间的出行量、封锁高风险地区、限制区域内部出行和限制感染者出行)的有效性.此外,Li等[49]在全球范围内选择了59个高风险位置(包括39个城市、10个郡县、4个省、3个地区、1个州、1个社区和1个国家)构建了基于SEIR的多尺度种群模型,融入气候驱动变量和人群移动导致的疫情空间扩散纳入各种干预方案.该研究发现,集中实施为期8周的“降低本地传播率和国际旅行”干预措施是高效且有效的,并建议对该策略从“全球干预中心”到次要高风险位置进行分层实施. ...
A conceptual framework for an individual-based spatially explicit epidemiological model
1
2004
... 个体级别的模型提供一种微观尺度的、离散的传播动力学模拟系统[50,51,52].此类模型中,个体通常被设计成具有人口属性和接触模式的智能体(Agent),传染病通过智能体之间的接触进行传播.与种群内部个体均匀混合的群体模型不同,个体模型针对个体和特定接触环境进行自下而上建模,可以细致刻画个体异质性(如年龄、性别、种族、家庭结构、社会关系、职住特征等)和接触环境异质性(如环境中的接触模式、活动类型、活动场所等)[53]. ...
Strategies for containing an emerging influenza pandemic in Southeast Asia
2
2005
... 个体级别的模型提供一种微观尺度的、离散的传播动力学模拟系统[50,51,52].此类模型中,个体通常被设计成具有人口属性和接触模式的智能体(Agent),传染病通过智能体之间的接触进行传播.与种群内部个体均匀混合的群体模型不同,个体模型针对个体和特定接触环境进行自下而上建模,可以细致刻画个体异质性(如年龄、性别、种族、家庭结构、社会关系、职住特征等)和接触环境异质性(如环境中的接触模式、活动类型、活动场所等)[53]. ...
... 总体而言,相比于侧重对短期疫情规模进行精确预测的统计学习模型(如机器学习、回归模型),基于过程模拟的模型更关注推演疾病发展的中长期趋势,模拟评估不同干预措施的效果,并揭示疾病传播过程中一些隐蔽的特征.因此,基于过程模拟的模型不以准确预测未来感染规模为单一建模目的,而更是可以作为疫情中进行干预策略部署与调控决策的关键规划工具.对于个体模型,由于缺乏数据支撑,研究者长期以来主要利用人口普查、出行调查数据以及设定出行与接触规则等对个体移动和接触行为进行建模[51].得益于信息通讯技术的发展与人群时空活动大数据的涌现,个体模型逐步开始利用大规模手机定位等真实的轨迹大数据进行建模,向着时间、空间与人群3个维度的精细化方向不断发展[65,66],这一点在此次COVID-19建模研究中体现尤为明显.个体模型通过融合人类轨迹等多源时空大数据,利用计算机模拟技术对疾病传播过程中的个体、移动、接触、感染、场所、干预响应等诸多因素进行综合模拟与分析,是传染病模型面向真实世界建模的必然发展趋势,也得到研究者的愈加关注[67].然而,面对纷繁复杂的物理世界与人群行为,个体模型在耦合人群时空行为方面仍然面临巨大的挑战,还需利用多模态大数据,融合传播动力学、人工智能和复杂网络等多学科理论方法,深入开展个体属性与出行轨迹重构、个体移动接触网络构建等研究工作,为空间精准化、精细化的疫情预测与智能决策提供科学支持. ...
Spatiotemporal spread of the 2014 outbreak of Ebola virus disease in Liberia and the effectiveness of non-pharmaceutical interventions: A computational modelling analysis
1
2015
... 个体级别的模型提供一种微观尺度的、离散的传播动力学模拟系统[50,51,52].此类模型中,个体通常被设计成具有人口属性和接触模式的智能体(Agent),传染病通过智能体之间的接触进行传播.与种群内部个体均匀混合的群体模型不同,个体模型针对个体和特定接触环境进行自下而上建模,可以细致刻画个体异质性(如年龄、性别、种族、家庭结构、社会关系、职住特征等)和接触环境异质性(如环境中的接触模式、活动类型、活动场所等)[53]. ...
基于个体的传染病传播模型应用
1
2015
... 个体级别的模型提供一种微观尺度的、离散的传播动力学模拟系统[50,51,52].此类模型中,个体通常被设计成具有人口属性和接触模式的智能体(Agent),传染病通过智能体之间的接触进行传播.与种群内部个体均匀混合的群体模型不同,个体模型针对个体和特定接触环境进行自下而上建模,可以细致刻画个体异质性(如年龄、性别、种族、家庭结构、社会关系、职住特征等)和接触环境异质性(如环境中的接触模式、活动类型、活动场所等)[53]. ...
基于个体的传染病传播模型应用
1
2015
... 个体级别的模型提供一种微观尺度的、离散的传播动力学模拟系统[50,51,52].此类模型中,个体通常被设计成具有人口属性和接触模式的智能体(Agent),传染病通过智能体之间的接触进行传播.与种群内部个体均匀混合的群体模型不同,个体模型针对个体和特定接触环境进行自下而上建模,可以细致刻画个体异质性(如年龄、性别、种族、家庭结构、社会关系、职住特征等)和接触环境异质性(如环境中的接触模式、活动类型、活动场所等)[53]. ...
Susceptible-infected-recovered epidemics in dynamic contact networks
1
2007
... 受限于数据可获得性,个体模型在较长时期内难以基于真实数据刻画大规模个体的空间位置[54].随着信息通讯和移动定位技术的发展,带有空间位置属性的人群移动大数据(如用户GPS定位数据、手机定位数据、互联网签到数据等)日益丰富,个体模型进一步向耦合个体“移动-停留”等时空活动信息的空间显式(spatially explicit)模型发展(图3)[55].通过出行链构建或轨迹语义化,空间显式的个体模型可以进一步详细刻画个体在不同时段的活动位置和场所(如家、工作地、学校与休闲场所等),不但能够模拟疾病在时间和空间上的扩散过程,还支持基于个体与场所的精准防控策略制定,如追踪感染者同事/同学,以及在休闲娱乐等其他活动可能遇到的接触者,能够支撑各类型密接者追踪与隔离、各类型场所的封锁与开放、不同类型的出行限制、接种疫苗的空间优先级等各项“人群-时间-空间”精准干预措施的综合性建模. ...
Investigating physical encounters of individuals in urban metro systems with large-scale smart card data
1
2020
... 受限于数据可获得性,个体模型在较长时期内难以基于真实数据刻画大规模个体的空间位置[54].随着信息通讯和移动定位技术的发展,带有空间位置属性的人群移动大数据(如用户GPS定位数据、手机定位数据、互联网签到数据等)日益丰富,个体模型进一步向耦合个体“移动-停留”等时空活动信息的空间显式(spatially explicit)模型发展(图3)[55].通过出行链构建或轨迹语义化,空间显式的个体模型可以进一步详细刻画个体在不同时段的活动位置和场所(如家、工作地、学校与休闲场所等),不但能够模拟疾病在时间和空间上的扩散过程,还支持基于个体与场所的精准防控策略制定,如追踪感染者同事/同学,以及在休闲娱乐等其他活动可能遇到的接触者,能够支撑各类型密接者追踪与隔离、各类型场所的封锁与开放、不同类型的出行限制、接种疫苗的空间优先级等各项“人群-时间-空间”精准干预措施的综合性建模. ...
An agent-based model of the local spread of SARS-CoV-2: Modeling study
1
2021
... 面向COVID-19疫情,研究者们使用了多种耦合人群移动的个体化建模方法.部分研究结合人类移动的基本规律、人口普查与交通出行调查等传统调查数据,通过设定个体移动/活动与接触规则,构建基于个体智能体的疾病传播模型.例如,Alessio等使用智能体模型开源软件NetLogo,结合意大利、德国、瑞典、巴西4个国家的国家人口统计数据(National Population Statistics)研究了4个国家不同政治决策(包含检测、封城、戴口罩、保持身体距离等)对SARS-CoV-2传播的影响[56].该研究表明,采取限制人口流动措施的国家可以有效控制COVID-19的传播.Son等[57]利用抽样后的人口普查数据合成217万人口样本,基于构建的个体智能体模型分析了开学对韩国大邱市COVID-19疫情传播的影响,发现热点(即新天地教堂)与非热点(即大邱社区)具有不同的感染概率.Ferguson等[58]利用人口普查与通勤OD普查等数据,结合人口分布规则设定(例如,工作单位人数遵守幂律函数分布),构建了个体级别的COVID-19模型,模拟了英国与美国疫情发展情况,并评估了患者居家隔离、患者家人居家隔离、70岁以上人群社交疏离、整个人群社交疏离与关闭学校5种防控措施的效果,为英美两国的防疫策略制定提供了参考.Silva等[59]基于巴西人口密度、人口年龄分布等数据提出了一种新的智能体模型COVID-ABS,依据世界人权宣言(Universal Declaration of Human Rights)构建个体移动模式.基于该模型,研究者分析了7种不同的非药物干预方案(包含封城、隔离、口罩),指出就社会合作和实施难易程度而言,结合使用口罩和部分隔离对于抑制疫情更为有效. ...
Individual-based simulation model for COVID-19 transmission in Daegu, Korea
1
2020
... 面向COVID-19疫情,研究者们使用了多种耦合人群移动的个体化建模方法.部分研究结合人类移动的基本规律、人口普查与交通出行调查等传统调查数据,通过设定个体移动/活动与接触规则,构建基于个体智能体的疾病传播模型.例如,Alessio等使用智能体模型开源软件NetLogo,结合意大利、德国、瑞典、巴西4个国家的国家人口统计数据(National Population Statistics)研究了4个国家不同政治决策(包含检测、封城、戴口罩、保持身体距离等)对SARS-CoV-2传播的影响[56].该研究表明,采取限制人口流动措施的国家可以有效控制COVID-19的传播.Son等[57]利用抽样后的人口普查数据合成217万人口样本,基于构建的个体智能体模型分析了开学对韩国大邱市COVID-19疫情传播的影响,发现热点(即新天地教堂)与非热点(即大邱社区)具有不同的感染概率.Ferguson等[58]利用人口普查与通勤OD普查等数据,结合人口分布规则设定(例如,工作单位人数遵守幂律函数分布),构建了个体级别的COVID-19模型,模拟了英国与美国疫情发展情况,并评估了患者居家隔离、患者家人居家隔离、70岁以上人群社交疏离、整个人群社交疏离与关闭学校5种防控措施的效果,为英美两国的防疫策略制定提供了参考.Silva等[59]基于巴西人口密度、人口年龄分布等数据提出了一种新的智能体模型COVID-ABS,依据世界人权宣言(Universal Declaration of Human Rights)构建个体移动模式.基于该模型,研究者分析了7种不同的非药物干预方案(包含封城、隔离、口罩),指出就社会合作和实施难易程度而言,结合使用口罩和部分隔离对于抑制疫情更为有效. ...
Report 9: Impact of non-pharmaceutical interventions (NPIs) to reduce COVID-19 mortality and healthcare demand
1
... 面向COVID-19疫情,研究者们使用了多种耦合人群移动的个体化建模方法.部分研究结合人类移动的基本规律、人口普查与交通出行调查等传统调查数据,通过设定个体移动/活动与接触规则,构建基于个体智能体的疾病传播模型.例如,Alessio等使用智能体模型开源软件NetLogo,结合意大利、德国、瑞典、巴西4个国家的国家人口统计数据(National Population Statistics)研究了4个国家不同政治决策(包含检测、封城、戴口罩、保持身体距离等)对SARS-CoV-2传播的影响[56].该研究表明,采取限制人口流动措施的国家可以有效控制COVID-19的传播.Son等[57]利用抽样后的人口普查数据合成217万人口样本,基于构建的个体智能体模型分析了开学对韩国大邱市COVID-19疫情传播的影响,发现热点(即新天地教堂)与非热点(即大邱社区)具有不同的感染概率.Ferguson等[58]利用人口普查与通勤OD普查等数据,结合人口分布规则设定(例如,工作单位人数遵守幂律函数分布),构建了个体级别的COVID-19模型,模拟了英国与美国疫情发展情况,并评估了患者居家隔离、患者家人居家隔离、70岁以上人群社交疏离、整个人群社交疏离与关闭学校5种防控措施的效果,为英美两国的防疫策略制定提供了参考.Silva等[59]基于巴西人口密度、人口年龄分布等数据提出了一种新的智能体模型COVID-ABS,依据世界人权宣言(Universal Declaration of Human Rights)构建个体移动模式.基于该模型,研究者分析了7种不同的非药物干预方案(包含封城、隔离、口罩),指出就社会合作和实施难易程度而言,结合使用口罩和部分隔离对于抑制疫情更为有效. ...
COVID-ABS: An agent-based model of COVID-19 epidemic to simulate health and economic effects of social distancing interventions
1
2020
... 面向COVID-19疫情,研究者们使用了多种耦合人群移动的个体化建模方法.部分研究结合人类移动的基本规律、人口普查与交通出行调查等传统调查数据,通过设定个体移动/活动与接触规则,构建基于个体智能体的疾病传播模型.例如,Alessio等使用智能体模型开源软件NetLogo,结合意大利、德国、瑞典、巴西4个国家的国家人口统计数据(National Population Statistics)研究了4个国家不同政治决策(包含检测、封城、戴口罩、保持身体距离等)对SARS-CoV-2传播的影响[56].该研究表明,采取限制人口流动措施的国家可以有效控制COVID-19的传播.Son等[57]利用抽样后的人口普查数据合成217万人口样本,基于构建的个体智能体模型分析了开学对韩国大邱市COVID-19疫情传播的影响,发现热点(即新天地教堂)与非热点(即大邱社区)具有不同的感染概率.Ferguson等[58]利用人口普查与通勤OD普查等数据,结合人口分布规则设定(例如,工作单位人数遵守幂律函数分布),构建了个体级别的COVID-19模型,模拟了英国与美国疫情发展情况,并评估了患者居家隔离、患者家人居家隔离、70岁以上人群社交疏离、整个人群社交疏离与关闭学校5种防控措施的效果,为英美两国的防疫策略制定提供了参考.Silva等[59]基于巴西人口密度、人口年龄分布等数据提出了一种新的智能体模型COVID-ABS,依据世界人权宣言(Universal Declaration of Human Rights)构建个体移动模式.基于该模型,研究者分析了7种不同的非药物干预方案(包含封城、隔离、口罩),指出就社会合作和实施难易程度而言,结合使用口罩和部分隔离对于抑制疫情更为有效. ...
Interventions to mitigate early spread of SARS-CoV-2 in Singapore: a modelling study
2
2020
... Related references of process simulation models coupled with human mobility
Tab. 2 | 分类 | 文献 | 研究区域 | 人群移动数据 | 模型模拟的干预措施 | 病例真实值 | 病例模拟值 | 模型效果 |
| 群体级别 | [47] | 意大利 | 人口流量调查 | 严格管控出行活动、加大疫情排查力度 | 74 386 | 约733 000 | 模拟的疾病发展曲线与实际情况吻符合程度较高 |
| [9] | 武汉 | 百度实时流动性数据 | - | 554 | 632 | 累计病例数的R2=0.99 |
| [45] | 中国375个城市 | 腾讯位置服务人口实时流动性数据 | 佩戴口罩、社交疏离、自我
隔离 | 13 562 | 约1.2万 | 预测的疾病报告率为14%,与实际武汉市疾病报告率15.8%非常接近 |
| [15] | 中国340个城市 | 百度迁徙人口流动数据 | 综合性非药物性干预 | 79 824 | 114 325 | 全国累计病例的R2=0.86,P值<0.001 |
| [21] | 中国 | 手机实时移动性和社交联系数据、腾讯移动设
备数据集 | 疫苗接种、社交疏离 | 未使用真实数据 | 未给出具体值 | 严格的干预措施可大幅降低传播能力 |
| [13] | 深圳市 | 手机移动信令数据 | 降低出行量、区域封锁 | 未使用真实数据 | R0=2.5时,峰值病例数减少了33% | 模拟的疾病发展曲线与实际情况吻合程度较高 |
| [14] | 美国康涅狄格州 | 城镇级人口流动数据,
智能手机热图,空中交
通流量 | 社交疏离 | 47 510 | 45 752~48 105 | 对康涅狄格州所有城镇模拟,实际统计的病例R2在0.907~0.924;按类别对城镇进行模拟,实际统计的病例R2为0.978~0.987 |
| [49] | 全球 | 航空与地面交通数据 | 降低本地传播率和国际旅行 | 未使用真实数据 | 未给出具体模拟值 | 严格的干预措施可大幅降低传播能力 |
| 个体级别 | [60] | 新加坡 | 交通数据 | 隔离感染者、关闭学校和工作场所 | 未使用真实数据 | R0=1.5时,7.4%的总人口感染;R0=2.0时,19.3%的总人口感染;R0=2.5时,32%的总人口感染 | 未给出具体评价指标 |
| [61] | 波士顿 | 手机位置数据 | 检测、密接追踪、居家隔离 | 未使用真实数据 | 无干预场景75%的人口被感染 | 未给出具体评价指标 |
| [62] | 纽约、西雅图 | 手机位置数据 | 无干预措施 | 每天每千人的死亡人数(未给出具体值) | 每天每千人的死亡人数(未给出具体值) | 模型结果与真实死亡人数的拟合效果较好,二者到达峰值的时间差略大于5 d |
| [63] | 澳大利亚 | 人口通勤数据 | 国际航空旅行限制、隔离感染者、居家隔离、增大社交距离、关闭学校 | 未使用真实数据 | 最佳干预场景下有8千~1万人被感染 | 未给出具体评价指标 |
| [64] | 深圳市 | 手机信令数据 | 密接追踪、及时检测、佩戴口罩、封城、逐步复工、隔离综合措施 | 418 | 416 | 每日新增发病数量的模拟值与实际报告值的RMSE=1.354;显性感染者数量在城市内各个行政区尺度上的R2=0.95 |
4.1 群体级别的耦合模型 群体级别的模型是一种长期以来广泛使用的传播动力学建模技术,其最基本的假设是研究单元内的每个个体具有相同的特征且彼此之间均匀接触,当作一个同质的群体来对待.其中,研究单元可以是同一个区域或者同一属性的人群/其他宿主等.根据感染和传播机制,模型通常由一组微分方程构建,通常是常微分方程.在COVID-19疫情中,人类感染新型冠状病毒SARS-COV-2之后存在潜隐期(Latent Period)与潜伏期(Incubation Period,对于显性感染者而言),因此,常用于COVID-19建模的基本仓室模型为SLIR与SEIR模型.以最基本的SEIR模型为例,针对给定研究单元,假设其总人口不变,其基于常微分方程的表达公式如下: ...
... 得益于人群移动大数据的广泛研究与应用,部分COVID-19个体模型耦合了真实的人群轨迹、出行与活动模式数据.例如,Koo等[60]基于新加坡的公共交通刷卡数据,结合人口普查数据,构建了包含377万个体的智能体模型,并模拟了隔离病例、 关闭学校和工作场所4种防控场景的效果.Aleta等[61]使用波士顿大都市区6个月的大规模手机定位数据构建了包含8.5万个体的智能体模型.通过模拟不同场景下疫情二次暴发造成的医疗负担,发现严格社交疏离政策持续一段时期后,只要保持一定的检测率(50%的显性感染者)、密切接触者追踪率(40%)和居家隔离率(9%),即使重启社会也可将疫情控制在医疗负荷范围内.Aleta等[62]进一步基于纽约与西雅图2个城市的手机位置数据、人口普查数据构建智能体模型(纽约61.4万合成个体,西雅图14.2万合成个体),估计第一波COVID-19大流行期间2个城市的传播事件发生的地点、时间和数量.通过模拟发现,大多数感染者(80%)是由少数感染者(27%)传播的,大约10%的事件可被视为超级传播事件.Chang等[63]基于人口普查数据、上班族的通勤距离数据、各机场平均入境旅客人数,构建包含2400万个体的智能体模型用于评估国际航空旅行限制、病例隔离、家庭隔离、增大社交距离和关闭学校等干预措施效果,发现如果不执行高服从性的社交疏离政策,那么关闭学校则不会对遏制疫情带来决定性的效果.Yin等[64]基于大规模匿名手机定位、居民出行调查、居民社交调查、建筑物普查与人口普查等多源异构城市大数据,构建了面向超大城市人口1200万个体在建筑物粒度上的智能体模型,对深圳市第一波疫情期间实施的非药物干预措施的单项措施效果进行了量化评估[65],并系统化分析了深圳市COVID-19散发疫情在不同程度的密接追踪、口罩佩戴与及时检测3种NPI措施下再次暴发的概率,并推荐采用“密接II+80+40”策略(即追踪固定接触圈密接者+80%市民戴口罩+40%患者发病后及时检测)作为深圳市与中国其他大城市常态化防疫的最低防控水平,并为其他国家大型城市提供了不同防控需求下的防控策略参考. ...
Modelling the impact of testing, contact tracing and household quarantine on second waves of COVID-19
2
2020
... Related references of process simulation models coupled with human mobility
Tab. 2 | 分类 | 文献 | 研究区域 | 人群移动数据 | 模型模拟的干预措施 | 病例真实值 | 病例模拟值 | 模型效果 |
| 群体级别 | [47] | 意大利 | 人口流量调查 | 严格管控出行活动、加大疫情排查力度 | 74 386 | 约733 000 | 模拟的疾病发展曲线与实际情况吻符合程度较高 |
| [9] | 武汉 | 百度实时流动性数据 | - | 554 | 632 | 累计病例数的R2=0.99 |
| [45] | 中国375个城市 | 腾讯位置服务人口实时流动性数据 | 佩戴口罩、社交疏离、自我
隔离 | 13 562 | 约1.2万 | 预测的疾病报告率为14%,与实际武汉市疾病报告率15.8%非常接近 |
| [15] | 中国340个城市 | 百度迁徙人口流动数据 | 综合性非药物性干预 | 79 824 | 114 325 | 全国累计病例的R2=0.86,P值<0.001 |
| [21] | 中国 | 手机实时移动性和社交联系数据、腾讯移动设
备数据集 | 疫苗接种、社交疏离 | 未使用真实数据 | 未给出具体值 | 严格的干预措施可大幅降低传播能力 |
| [13] | 深圳市 | 手机移动信令数据 | 降低出行量、区域封锁 | 未使用真实数据 | R0=2.5时,峰值病例数减少了33% | 模拟的疾病发展曲线与实际情况吻合程度较高 |
| [14] | 美国康涅狄格州 | 城镇级人口流动数据,
智能手机热图,空中交
通流量 | 社交疏离 | 47 510 | 45 752~48 105 | 对康涅狄格州所有城镇模拟,实际统计的病例R2在0.907~0.924;按类别对城镇进行模拟,实际统计的病例R2为0.978~0.987 |
| [49] | 全球 | 航空与地面交通数据 | 降低本地传播率和国际旅行 | 未使用真实数据 | 未给出具体模拟值 | 严格的干预措施可大幅降低传播能力 |
| 个体级别 | [60] | 新加坡 | 交通数据 | 隔离感染者、关闭学校和工作场所 | 未使用真实数据 | R0=1.5时,7.4%的总人口感染;R0=2.0时,19.3%的总人口感染;R0=2.5时,32%的总人口感染 | 未给出具体评价指标 |
| [61] | 波士顿 | 手机位置数据 | 检测、密接追踪、居家隔离 | 未使用真实数据 | 无干预场景75%的人口被感染 | 未给出具体评价指标 |
| [62] | 纽约、西雅图 | 手机位置数据 | 无干预措施 | 每天每千人的死亡人数(未给出具体值) | 每天每千人的死亡人数(未给出具体值) | 模型结果与真实死亡人数的拟合效果较好,二者到达峰值的时间差略大于5 d |
| [63] | 澳大利亚 | 人口通勤数据 | 国际航空旅行限制、隔离感染者、居家隔离、增大社交距离、关闭学校 | 未使用真实数据 | 最佳干预场景下有8千~1万人被感染 | 未给出具体评价指标 |
| [64] | 深圳市 | 手机信令数据 | 密接追踪、及时检测、佩戴口罩、封城、逐步复工、隔离综合措施 | 418 | 416 | 每日新增发病数量的模拟值与实际报告值的RMSE=1.354;显性感染者数量在城市内各个行政区尺度上的R2=0.95 |
4.1 群体级别的耦合模型 群体级别的模型是一种长期以来广泛使用的传播动力学建模技术,其最基本的假设是研究单元内的每个个体具有相同的特征且彼此之间均匀接触,当作一个同质的群体来对待.其中,研究单元可以是同一个区域或者同一属性的人群/其他宿主等.根据感染和传播机制,模型通常由一组微分方程构建,通常是常微分方程.在COVID-19疫情中,人类感染新型冠状病毒SARS-COV-2之后存在潜隐期(Latent Period)与潜伏期(Incubation Period,对于显性感染者而言),因此,常用于COVID-19建模的基本仓室模型为SLIR与SEIR模型.以最基本的SEIR模型为例,针对给定研究单元,假设其总人口不变,其基于常微分方程的表达公式如下: ...
... 得益于人群移动大数据的广泛研究与应用,部分COVID-19个体模型耦合了真实的人群轨迹、出行与活动模式数据.例如,Koo等[60]基于新加坡的公共交通刷卡数据,结合人口普查数据,构建了包含377万个体的智能体模型,并模拟了隔离病例、 关闭学校和工作场所4种防控场景的效果.Aleta等[61]使用波士顿大都市区6个月的大规模手机定位数据构建了包含8.5万个体的智能体模型.通过模拟不同场景下疫情二次暴发造成的医疗负担,发现严格社交疏离政策持续一段时期后,只要保持一定的检测率(50%的显性感染者)、密切接触者追踪率(40%)和居家隔离率(9%),即使重启社会也可将疫情控制在医疗负荷范围内.Aleta等[62]进一步基于纽约与西雅图2个城市的手机位置数据、人口普查数据构建智能体模型(纽约61.4万合成个体,西雅图14.2万合成个体),估计第一波COVID-19大流行期间2个城市的传播事件发生的地点、时间和数量.通过模拟发现,大多数感染者(80%)是由少数感染者(27%)传播的,大约10%的事件可被视为超级传播事件.Chang等[63]基于人口普查数据、上班族的通勤距离数据、各机场平均入境旅客人数,构建包含2400万个体的智能体模型用于评估国际航空旅行限制、病例隔离、家庭隔离、增大社交距离和关闭学校等干预措施效果,发现如果不执行高服从性的社交疏离政策,那么关闭学校则不会对遏制疫情带来决定性的效果.Yin等[64]基于大规模匿名手机定位、居民出行调查、居民社交调查、建筑物普查与人口普查等多源异构城市大数据,构建了面向超大城市人口1200万个体在建筑物粒度上的智能体模型,对深圳市第一波疫情期间实施的非药物干预措施的单项措施效果进行了量化评估[65],并系统化分析了深圳市COVID-19散发疫情在不同程度的密接追踪、口罩佩戴与及时检测3种NPI措施下再次暴发的概率,并推荐采用“密接II+80+40”策略(即追踪固定接触圈密接者+80%市民戴口罩+40%患者发病后及时检测)作为深圳市与中国其他大城市常态化防疫的最低防控水平,并为其他国家大型城市提供了不同防控需求下的防控策略参考. ...
Quantifying the importance and location of SARS-CoV-2 transmission events in large metropolitan areas
2
... Related references of process simulation models coupled with human mobility
Tab. 2 | 分类 | 文献 | 研究区域 | 人群移动数据 | 模型模拟的干预措施 | 病例真实值 | 病例模拟值 | 模型效果 |
| 群体级别 | [47] | 意大利 | 人口流量调查 | 严格管控出行活动、加大疫情排查力度 | 74 386 | 约733 000 | 模拟的疾病发展曲线与实际情况吻符合程度较高 |
| [9] | 武汉 | 百度实时流动性数据 | - | 554 | 632 | 累计病例数的R2=0.99 |
| [45] | 中国375个城市 | 腾讯位置服务人口实时流动性数据 | 佩戴口罩、社交疏离、自我
隔离 | 13 562 | 约1.2万 | 预测的疾病报告率为14%,与实际武汉市疾病报告率15.8%非常接近 |
| [15] | 中国340个城市 | 百度迁徙人口流动数据 | 综合性非药物性干预 | 79 824 | 114 325 | 全国累计病例的R2=0.86,P值<0.001 |
| [21] | 中国 | 手机实时移动性和社交联系数据、腾讯移动设
备数据集 | 疫苗接种、社交疏离 | 未使用真实数据 | 未给出具体值 | 严格的干预措施可大幅降低传播能力 |
| [13] | 深圳市 | 手机移动信令数据 | 降低出行量、区域封锁 | 未使用真实数据 | R0=2.5时,峰值病例数减少了33% | 模拟的疾病发展曲线与实际情况吻合程度较高 |
| [14] | 美国康涅狄格州 | 城镇级人口流动数据,
智能手机热图,空中交
通流量 | 社交疏离 | 47 510 | 45 752~48 105 | 对康涅狄格州所有城镇模拟,实际统计的病例R2在0.907~0.924;按类别对城镇进行模拟,实际统计的病例R2为0.978~0.987 |
| [49] | 全球 | 航空与地面交通数据 | 降低本地传播率和国际旅行 | 未使用真实数据 | 未给出具体模拟值 | 严格的干预措施可大幅降低传播能力 |
| 个体级别 | [60] | 新加坡 | 交通数据 | 隔离感染者、关闭学校和工作场所 | 未使用真实数据 | R0=1.5时,7.4%的总人口感染;R0=2.0时,19.3%的总人口感染;R0=2.5时,32%的总人口感染 | 未给出具体评价指标 |
| [61] | 波士顿 | 手机位置数据 | 检测、密接追踪、居家隔离 | 未使用真实数据 | 无干预场景75%的人口被感染 | 未给出具体评价指标 |
| [62] | 纽约、西雅图 | 手机位置数据 | 无干预措施 | 每天每千人的死亡人数(未给出具体值) | 每天每千人的死亡人数(未给出具体值) | 模型结果与真实死亡人数的拟合效果较好,二者到达峰值的时间差略大于5 d |
| [63] | 澳大利亚 | 人口通勤数据 | 国际航空旅行限制、隔离感染者、居家隔离、增大社交距离、关闭学校 | 未使用真实数据 | 最佳干预场景下有8千~1万人被感染 | 未给出具体评价指标 |
| [64] | 深圳市 | 手机信令数据 | 密接追踪、及时检测、佩戴口罩、封城、逐步复工、隔离综合措施 | 418 | 416 | 每日新增发病数量的模拟值与实际报告值的RMSE=1.354;显性感染者数量在城市内各个行政区尺度上的R2=0.95 |
4.1 群体级别的耦合模型 群体级别的模型是一种长期以来广泛使用的传播动力学建模技术,其最基本的假设是研究单元内的每个个体具有相同的特征且彼此之间均匀接触,当作一个同质的群体来对待.其中,研究单元可以是同一个区域或者同一属性的人群/其他宿主等.根据感染和传播机制,模型通常由一组微分方程构建,通常是常微分方程.在COVID-19疫情中,人类感染新型冠状病毒SARS-COV-2之后存在潜隐期(Latent Period)与潜伏期(Incubation Period,对于显性感染者而言),因此,常用于COVID-19建模的基本仓室模型为SLIR与SEIR模型.以最基本的SEIR模型为例,针对给定研究单元,假设其总人口不变,其基于常微分方程的表达公式如下: ...
... 得益于人群移动大数据的广泛研究与应用,部分COVID-19个体模型耦合了真实的人群轨迹、出行与活动模式数据.例如,Koo等[60]基于新加坡的公共交通刷卡数据,结合人口普查数据,构建了包含377万个体的智能体模型,并模拟了隔离病例、 关闭学校和工作场所4种防控场景的效果.Aleta等[61]使用波士顿大都市区6个月的大规模手机定位数据构建了包含8.5万个体的智能体模型.通过模拟不同场景下疫情二次暴发造成的医疗负担,发现严格社交疏离政策持续一段时期后,只要保持一定的检测率(50%的显性感染者)、密切接触者追踪率(40%)和居家隔离率(9%),即使重启社会也可将疫情控制在医疗负荷范围内.Aleta等[62]进一步基于纽约与西雅图2个城市的手机位置数据、人口普查数据构建智能体模型(纽约61.4万合成个体,西雅图14.2万合成个体),估计第一波COVID-19大流行期间2个城市的传播事件发生的地点、时间和数量.通过模拟发现,大多数感染者(80%)是由少数感染者(27%)传播的,大约10%的事件可被视为超级传播事件.Chang等[63]基于人口普查数据、上班族的通勤距离数据、各机场平均入境旅客人数,构建包含2400万个体的智能体模型用于评估国际航空旅行限制、病例隔离、家庭隔离、增大社交距离和关闭学校等干预措施效果,发现如果不执行高服从性的社交疏离政策,那么关闭学校则不会对遏制疫情带来决定性的效果.Yin等[64]基于大规模匿名手机定位、居民出行调查、居民社交调查、建筑物普查与人口普查等多源异构城市大数据,构建了面向超大城市人口1200万个体在建筑物粒度上的智能体模型,对深圳市第一波疫情期间实施的非药物干预措施的单项措施效果进行了量化评估[65],并系统化分析了深圳市COVID-19散发疫情在不同程度的密接追踪、口罩佩戴与及时检测3种NPI措施下再次暴发的概率,并推荐采用“密接II+80+40”策略(即追踪固定接触圈密接者+80%市民戴口罩+40%患者发病后及时检测)作为深圳市与中国其他大城市常态化防疫的最低防控水平,并为其他国家大型城市提供了不同防控需求下的防控策略参考. ...
Modelling transmission and control of the COVID-19 pandemic in Australia
2
2020
... Related references of process simulation models coupled with human mobility
Tab. 2 | 分类 | 文献 | 研究区域 | 人群移动数据 | 模型模拟的干预措施 | 病例真实值 | 病例模拟值 | 模型效果 |
| 群体级别 | [47] | 意大利 | 人口流量调查 | 严格管控出行活动、加大疫情排查力度 | 74 386 | 约733 000 | 模拟的疾病发展曲线与实际情况吻符合程度较高 |
| [9] | 武汉 | 百度实时流动性数据 | - | 554 | 632 | 累计病例数的R2=0.99 |
| [45] | 中国375个城市 | 腾讯位置服务人口实时流动性数据 | 佩戴口罩、社交疏离、自我
隔离 | 13 562 | 约1.2万 | 预测的疾病报告率为14%,与实际武汉市疾病报告率15.8%非常接近 |
| [15] | 中国340个城市 | 百度迁徙人口流动数据 | 综合性非药物性干预 | 79 824 | 114 325 | 全国累计病例的R2=0.86,P值<0.001 |
| [21] | 中国 | 手机实时移动性和社交联系数据、腾讯移动设
备数据集 | 疫苗接种、社交疏离 | 未使用真实数据 | 未给出具体值 | 严格的干预措施可大幅降低传播能力 |
| [13] | 深圳市 | 手机移动信令数据 | 降低出行量、区域封锁 | 未使用真实数据 | R0=2.5时,峰值病例数减少了33% | 模拟的疾病发展曲线与实际情况吻合程度较高 |
| [14] | 美国康涅狄格州 | 城镇级人口流动数据,
智能手机热图,空中交
通流量 | 社交疏离 | 47 510 | 45 752~48 105 | 对康涅狄格州所有城镇模拟,实际统计的病例R2在0.907~0.924;按类别对城镇进行模拟,实际统计的病例R2为0.978~0.987 |
| [49] | 全球 | 航空与地面交通数据 | 降低本地传播率和国际旅行 | 未使用真实数据 | 未给出具体模拟值 | 严格的干预措施可大幅降低传播能力 |
| 个体级别 | [60] | 新加坡 | 交通数据 | 隔离感染者、关闭学校和工作场所 | 未使用真实数据 | R0=1.5时,7.4%的总人口感染;R0=2.0时,19.3%的总人口感染;R0=2.5时,32%的总人口感染 | 未给出具体评价指标 |
| [61] | 波士顿 | 手机位置数据 | 检测、密接追踪、居家隔离 | 未使用真实数据 | 无干预场景75%的人口被感染 | 未给出具体评价指标 |
| [62] | 纽约、西雅图 | 手机位置数据 | 无干预措施 | 每天每千人的死亡人数(未给出具体值) | 每天每千人的死亡人数(未给出具体值) | 模型结果与真实死亡人数的拟合效果较好,二者到达峰值的时间差略大于5 d |
| [63] | 澳大利亚 | 人口通勤数据 | 国际航空旅行限制、隔离感染者、居家隔离、增大社交距离、关闭学校 | 未使用真实数据 | 最佳干预场景下有8千~1万人被感染 | 未给出具体评价指标 |
| [64] | 深圳市 | 手机信令数据 | 密接追踪、及时检测、佩戴口罩、封城、逐步复工、隔离综合措施 | 418 | 416 | 每日新增发病数量的模拟值与实际报告值的RMSE=1.354;显性感染者数量在城市内各个行政区尺度上的R2=0.95 |
4.1 群体级别的耦合模型 群体级别的模型是一种长期以来广泛使用的传播动力学建模技术,其最基本的假设是研究单元内的每个个体具有相同的特征且彼此之间均匀接触,当作一个同质的群体来对待.其中,研究单元可以是同一个区域或者同一属性的人群/其他宿主等.根据感染和传播机制,模型通常由一组微分方程构建,通常是常微分方程.在COVID-19疫情中,人类感染新型冠状病毒SARS-COV-2之后存在潜隐期(Latent Period)与潜伏期(Incubation Period,对于显性感染者而言),因此,常用于COVID-19建模的基本仓室模型为SLIR与SEIR模型.以最基本的SEIR模型为例,针对给定研究单元,假设其总人口不变,其基于常微分方程的表达公式如下: ...
... 得益于人群移动大数据的广泛研究与应用,部分COVID-19个体模型耦合了真实的人群轨迹、出行与活动模式数据.例如,Koo等[60]基于新加坡的公共交通刷卡数据,结合人口普查数据,构建了包含377万个体的智能体模型,并模拟了隔离病例、 关闭学校和工作场所4种防控场景的效果.Aleta等[61]使用波士顿大都市区6个月的大规模手机定位数据构建了包含8.5万个体的智能体模型.通过模拟不同场景下疫情二次暴发造成的医疗负担,发现严格社交疏离政策持续一段时期后,只要保持一定的检测率(50%的显性感染者)、密切接触者追踪率(40%)和居家隔离率(9%),即使重启社会也可将疫情控制在医疗负荷范围内.Aleta等[62]进一步基于纽约与西雅图2个城市的手机位置数据、人口普查数据构建智能体模型(纽约61.4万合成个体,西雅图14.2万合成个体),估计第一波COVID-19大流行期间2个城市的传播事件发生的地点、时间和数量.通过模拟发现,大多数感染者(80%)是由少数感染者(27%)传播的,大约10%的事件可被视为超级传播事件.Chang等[63]基于人口普查数据、上班族的通勤距离数据、各机场平均入境旅客人数,构建包含2400万个体的智能体模型用于评估国际航空旅行限制、病例隔离、家庭隔离、增大社交距离和关闭学校等干预措施效果,发现如果不执行高服从性的社交疏离政策,那么关闭学校则不会对遏制疫情带来决定性的效果.Yin等[64]基于大规模匿名手机定位、居民出行调查、居民社交调查、建筑物普查与人口普查等多源异构城市大数据,构建了面向超大城市人口1200万个体在建筑物粒度上的智能体模型,对深圳市第一波疫情期间实施的非药物干预措施的单项措施效果进行了量化评估[65],并系统化分析了深圳市COVID-19散发疫情在不同程度的密接追踪、口罩佩戴与及时检测3种NPI措施下再次暴发的概率,并推荐采用“密接II+80+40”策略(即追踪固定接触圈密接者+80%市民戴口罩+40%患者发病后及时检测)作为深圳市与中国其他大城市常态化防疫的最低防控水平,并为其他国家大型城市提供了不同防控需求下的防控策略参考. ...
A data driven agent-based model that recommends non-pharmaceutical interventions to suppress Coronavirus disease 2019 resurgence in megacities
3
2021
... Related references of process simulation models coupled with human mobility
Tab. 2 | 分类 | 文献 | 研究区域 | 人群移动数据 | 模型模拟的干预措施 | 病例真实值 | 病例模拟值 | 模型效果 |
| 群体级别 | [47] | 意大利 | 人口流量调查 | 严格管控出行活动、加大疫情排查力度 | 74 386 | 约733 000 | 模拟的疾病发展曲线与实际情况吻符合程度较高 |
| [9] | 武汉 | 百度实时流动性数据 | - | 554 | 632 | 累计病例数的R2=0.99 |
| [45] | 中国375个城市 | 腾讯位置服务人口实时流动性数据 | 佩戴口罩、社交疏离、自我
隔离 | 13 562 | 约1.2万 | 预测的疾病报告率为14%,与实际武汉市疾病报告率15.8%非常接近 |
| [15] | 中国340个城市 | 百度迁徙人口流动数据 | 综合性非药物性干预 | 79 824 | 114 325 | 全国累计病例的R2=0.86,P值<0.001 |
| [21] | 中国 | 手机实时移动性和社交联系数据、腾讯移动设
备数据集 | 疫苗接种、社交疏离 | 未使用真实数据 | 未给出具体值 | 严格的干预措施可大幅降低传播能力 |
| [13] | 深圳市 | 手机移动信令数据 | 降低出行量、区域封锁 | 未使用真实数据 | R0=2.5时,峰值病例数减少了33% | 模拟的疾病发展曲线与实际情况吻合程度较高 |
| [14] | 美国康涅狄格州 | 城镇级人口流动数据,
智能手机热图,空中交
通流量 | 社交疏离 | 47 510 | 45 752~48 105 | 对康涅狄格州所有城镇模拟,实际统计的病例R2在0.907~0.924;按类别对城镇进行模拟,实际统计的病例R2为0.978~0.987 |
| [49] | 全球 | 航空与地面交通数据 | 降低本地传播率和国际旅行 | 未使用真实数据 | 未给出具体模拟值 | 严格的干预措施可大幅降低传播能力 |
| 个体级别 | [60] | 新加坡 | 交通数据 | 隔离感染者、关闭学校和工作场所 | 未使用真实数据 | R0=1.5时,7.4%的总人口感染;R0=2.0时,19.3%的总人口感染;R0=2.5时,32%的总人口感染 | 未给出具体评价指标 |
| [61] | 波士顿 | 手机位置数据 | 检测、密接追踪、居家隔离 | 未使用真实数据 | 无干预场景75%的人口被感染 | 未给出具体评价指标 |
| [62] | 纽约、西雅图 | 手机位置数据 | 无干预措施 | 每天每千人的死亡人数(未给出具体值) | 每天每千人的死亡人数(未给出具体值) | 模型结果与真实死亡人数的拟合效果较好,二者到达峰值的时间差略大于5 d |
| [63] | 澳大利亚 | 人口通勤数据 | 国际航空旅行限制、隔离感染者、居家隔离、增大社交距离、关闭学校 | 未使用真实数据 | 最佳干预场景下有8千~1万人被感染 | 未给出具体评价指标 |
| [64] | 深圳市 | 手机信令数据 | 密接追踪、及时检测、佩戴口罩、封城、逐步复工、隔离综合措施 | 418 | 416 | 每日新增发病数量的模拟值与实际报告值的RMSE=1.354;显性感染者数量在城市内各个行政区尺度上的R2=0.95 |
4.1 群体级别的耦合模型 群体级别的模型是一种长期以来广泛使用的传播动力学建模技术,其最基本的假设是研究单元内的每个个体具有相同的特征且彼此之间均匀接触,当作一个同质的群体来对待.其中,研究单元可以是同一个区域或者同一属性的人群/其他宿主等.根据感染和传播机制,模型通常由一组微分方程构建,通常是常微分方程.在COVID-19疫情中,人类感染新型冠状病毒SARS-COV-2之后存在潜隐期(Latent Period)与潜伏期(Incubation Period,对于显性感染者而言),因此,常用于COVID-19建模的基本仓室模型为SLIR与SEIR模型.以最基本的SEIR模型为例,针对给定研究单元,假设其总人口不变,其基于常微分方程的表达公式如下: ...
... 得益于人群移动大数据的广泛研究与应用,部分COVID-19个体模型耦合了真实的人群轨迹、出行与活动模式数据.例如,Koo等[60]基于新加坡的公共交通刷卡数据,结合人口普查数据,构建了包含377万个体的智能体模型,并模拟了隔离病例、 关闭学校和工作场所4种防控场景的效果.Aleta等[61]使用波士顿大都市区6个月的大规模手机定位数据构建了包含8.5万个体的智能体模型.通过模拟不同场景下疫情二次暴发造成的医疗负担,发现严格社交疏离政策持续一段时期后,只要保持一定的检测率(50%的显性感染者)、密切接触者追踪率(40%)和居家隔离率(9%),即使重启社会也可将疫情控制在医疗负荷范围内.Aleta等[62]进一步基于纽约与西雅图2个城市的手机位置数据、人口普查数据构建智能体模型(纽约61.4万合成个体,西雅图14.2万合成个体),估计第一波COVID-19大流行期间2个城市的传播事件发生的地点、时间和数量.通过模拟发现,大多数感染者(80%)是由少数感染者(27%)传播的,大约10%的事件可被视为超级传播事件.Chang等[63]基于人口普查数据、上班族的通勤距离数据、各机场平均入境旅客人数,构建包含2400万个体的智能体模型用于评估国际航空旅行限制、病例隔离、家庭隔离、增大社交距离和关闭学校等干预措施效果,发现如果不执行高服从性的社交疏离政策,那么关闭学校则不会对遏制疫情带来决定性的效果.Yin等[64]基于大规模匿名手机定位、居民出行调查、居民社交调查、建筑物普查与人口普查等多源异构城市大数据,构建了面向超大城市人口1200万个体在建筑物粒度上的智能体模型,对深圳市第一波疫情期间实施的非药物干预措施的单项措施效果进行了量化评估[65],并系统化分析了深圳市COVID-19散发疫情在不同程度的密接追踪、口罩佩戴与及时检测3种NPI措施下再次暴发的概率,并推荐采用“密接II+80+40”策略(即追踪固定接触圈密接者+80%市民戴口罩+40%患者发病后及时检测)作为深圳市与中国其他大城市常态化防疫的最低防控水平,并为其他国家大型城市提供了不同防控需求下的防控策略参考. ...
... COVID-19传染病模型覆盖了从全球宏观尺度到活动场所微观尺度的多空间粒度.全球和国家级别的宏观尺度建模能帮助及时把握疫情的整体发展趋势,城市与乡镇级别的中观尺度建模能够为局部区域的防控措施提供更加针对性的参考.然而,对于落实到执行层面的城市内部各个管理单元,也同样需要更加细粒度的微观尺度建模提供精准防控的依据.得益于时空大数据与人类移动大数据的发展,耦合人群移动的COVID-19建模中出现了数据驱动下的城市内部建筑物[64]以及活动场所[65]的微观尺度建模.这些微观尺度的模型能够支撑基于城市内部具体区域与活动场所的精准干预建模,进而提供更加具有空间针对性的防控措施建议,降低社会成本.例如,面对COVID-19散发疫情,微观尺度模型能够评估城市内部社区级别的风险扩散等级,缩小核酸检测与区域限制的范围.因此,对于城市管理部门,更加细粒度的空间模型具有直接的指导意义,成为未来传染病建模的一项重要内容. ...
深圳市快速抑制COVID-19疫情的非药物干预措施效果评估:基于智能体的建模研究
3
2021
... 得益于人群移动大数据的广泛研究与应用,部分COVID-19个体模型耦合了真实的人群轨迹、出行与活动模式数据.例如,Koo等[60]基于新加坡的公共交通刷卡数据,结合人口普查数据,构建了包含377万个体的智能体模型,并模拟了隔离病例、 关闭学校和工作场所4种防控场景的效果.Aleta等[61]使用波士顿大都市区6个月的大规模手机定位数据构建了包含8.5万个体的智能体模型.通过模拟不同场景下疫情二次暴发造成的医疗负担,发现严格社交疏离政策持续一段时期后,只要保持一定的检测率(50%的显性感染者)、密切接触者追踪率(40%)和居家隔离率(9%),即使重启社会也可将疫情控制在医疗负荷范围内.Aleta等[62]进一步基于纽约与西雅图2个城市的手机位置数据、人口普查数据构建智能体模型(纽约61.4万合成个体,西雅图14.2万合成个体),估计第一波COVID-19大流行期间2个城市的传播事件发生的地点、时间和数量.通过模拟发现,大多数感染者(80%)是由少数感染者(27%)传播的,大约10%的事件可被视为超级传播事件.Chang等[63]基于人口普查数据、上班族的通勤距离数据、各机场平均入境旅客人数,构建包含2400万个体的智能体模型用于评估国际航空旅行限制、病例隔离、家庭隔离、增大社交距离和关闭学校等干预措施效果,发现如果不执行高服从性的社交疏离政策,那么关闭学校则不会对遏制疫情带来决定性的效果.Yin等[64]基于大规模匿名手机定位、居民出行调查、居民社交调查、建筑物普查与人口普查等多源异构城市大数据,构建了面向超大城市人口1200万个体在建筑物粒度上的智能体模型,对深圳市第一波疫情期间实施的非药物干预措施的单项措施效果进行了量化评估[65],并系统化分析了深圳市COVID-19散发疫情在不同程度的密接追踪、口罩佩戴与及时检测3种NPI措施下再次暴发的概率,并推荐采用“密接II+80+40”策略(即追踪固定接触圈密接者+80%市民戴口罩+40%患者发病后及时检测)作为深圳市与中国其他大城市常态化防疫的最低防控水平,并为其他国家大型城市提供了不同防控需求下的防控策略参考. ...
... 总体而言,相比于侧重对短期疫情规模进行精确预测的统计学习模型(如机器学习、回归模型),基于过程模拟的模型更关注推演疾病发展的中长期趋势,模拟评估不同干预措施的效果,并揭示疾病传播过程中一些隐蔽的特征.因此,基于过程模拟的模型不以准确预测未来感染规模为单一建模目的,而更是可以作为疫情中进行干预策略部署与调控决策的关键规划工具.对于个体模型,由于缺乏数据支撑,研究者长期以来主要利用人口普查、出行调查数据以及设定出行与接触规则等对个体移动和接触行为进行建模[51].得益于信息通讯技术的发展与人群时空活动大数据的涌现,个体模型逐步开始利用大规模手机定位等真实的轨迹大数据进行建模,向着时间、空间与人群3个维度的精细化方向不断发展[65,66],这一点在此次COVID-19建模研究中体现尤为明显.个体模型通过融合人类轨迹等多源时空大数据,利用计算机模拟技术对疾病传播过程中的个体、移动、接触、感染、场所、干预响应等诸多因素进行综合模拟与分析,是传染病模型面向真实世界建模的必然发展趋势,也得到研究者的愈加关注[67].然而,面对纷繁复杂的物理世界与人群行为,个体模型在耦合人群时空行为方面仍然面临巨大的挑战,还需利用多模态大数据,融合传播动力学、人工智能和复杂网络等多学科理论方法,深入开展个体属性与出行轨迹重构、个体移动接触网络构建等研究工作,为空间精准化、精细化的疫情预测与智能决策提供科学支持. ...
... COVID-19传染病模型覆盖了从全球宏观尺度到活动场所微观尺度的多空间粒度.全球和国家级别的宏观尺度建模能帮助及时把握疫情的整体发展趋势,城市与乡镇级别的中观尺度建模能够为局部区域的防控措施提供更加针对性的参考.然而,对于落实到执行层面的城市内部各个管理单元,也同样需要更加细粒度的微观尺度建模提供精准防控的依据.得益于时空大数据与人类移动大数据的发展,耦合人群移动的COVID-19建模中出现了数据驱动下的城市内部建筑物[64]以及活动场所[65]的微观尺度建模.这些微观尺度的模型能够支撑基于城市内部具体区域与活动场所的精准干预建模,进而提供更加具有空间针对性的防控措施建议,降低社会成本.例如,面对COVID-19散发疫情,微观尺度模型能够评估城市内部社区级别的风险扩散等级,缩小核酸检测与区域限制的范围.因此,对于城市管理部门,更加细粒度的空间模型具有直接的指导意义,成为未来传染病建模的一项重要内容. ...
深圳市快速抑制COVID-19疫情的非药物干预措施效果评估:基于智能体的建模研究
3
2021
... 得益于人群移动大数据的广泛研究与应用,部分COVID-19个体模型耦合了真实的人群轨迹、出行与活动模式数据.例如,Koo等[60]基于新加坡的公共交通刷卡数据,结合人口普查数据,构建了包含377万个体的智能体模型,并模拟了隔离病例、 关闭学校和工作场所4种防控场景的效果.Aleta等[61]使用波士顿大都市区6个月的大规模手机定位数据构建了包含8.5万个体的智能体模型.通过模拟不同场景下疫情二次暴发造成的医疗负担,发现严格社交疏离政策持续一段时期后,只要保持一定的检测率(50%的显性感染者)、密切接触者追踪率(40%)和居家隔离率(9%),即使重启社会也可将疫情控制在医疗负荷范围内.Aleta等[62]进一步基于纽约与西雅图2个城市的手机位置数据、人口普查数据构建智能体模型(纽约61.4万合成个体,西雅图14.2万合成个体),估计第一波COVID-19大流行期间2个城市的传播事件发生的地点、时间和数量.通过模拟发现,大多数感染者(80%)是由少数感染者(27%)传播的,大约10%的事件可被视为超级传播事件.Chang等[63]基于人口普查数据、上班族的通勤距离数据、各机场平均入境旅客人数,构建包含2400万个体的智能体模型用于评估国际航空旅行限制、病例隔离、家庭隔离、增大社交距离和关闭学校等干预措施效果,发现如果不执行高服从性的社交疏离政策,那么关闭学校则不会对遏制疫情带来决定性的效果.Yin等[64]基于大规模匿名手机定位、居民出行调查、居民社交调查、建筑物普查与人口普查等多源异构城市大数据,构建了面向超大城市人口1200万个体在建筑物粒度上的智能体模型,对深圳市第一波疫情期间实施的非药物干预措施的单项措施效果进行了量化评估[65],并系统化分析了深圳市COVID-19散发疫情在不同程度的密接追踪、口罩佩戴与及时检测3种NPI措施下再次暴发的概率,并推荐采用“密接II+80+40”策略(即追踪固定接触圈密接者+80%市民戴口罩+40%患者发病后及时检测)作为深圳市与中国其他大城市常态化防疫的最低防控水平,并为其他国家大型城市提供了不同防控需求下的防控策略参考. ...
... 总体而言,相比于侧重对短期疫情规模进行精确预测的统计学习模型(如机器学习、回归模型),基于过程模拟的模型更关注推演疾病发展的中长期趋势,模拟评估不同干预措施的效果,并揭示疾病传播过程中一些隐蔽的特征.因此,基于过程模拟的模型不以准确预测未来感染规模为单一建模目的,而更是可以作为疫情中进行干预策略部署与调控决策的关键规划工具.对于个体模型,由于缺乏数据支撑,研究者长期以来主要利用人口普查、出行调查数据以及设定出行与接触规则等对个体移动和接触行为进行建模[51].得益于信息通讯技术的发展与人群时空活动大数据的涌现,个体模型逐步开始利用大规模手机定位等真实的轨迹大数据进行建模,向着时间、空间与人群3个维度的精细化方向不断发展[65,66],这一点在此次COVID-19建模研究中体现尤为明显.个体模型通过融合人类轨迹等多源时空大数据,利用计算机模拟技术对疾病传播过程中的个体、移动、接触、感染、场所、干预响应等诸多因素进行综合模拟与分析,是传染病模型面向真实世界建模的必然发展趋势,也得到研究者的愈加关注[67].然而,面对纷繁复杂的物理世界与人群行为,个体模型在耦合人群时空行为方面仍然面临巨大的挑战,还需利用多模态大数据,融合传播动力学、人工智能和复杂网络等多学科理论方法,深入开展个体属性与出行轨迹重构、个体移动接触网络构建等研究工作,为空间精准化、精细化的疫情预测与智能决策提供科学支持. ...
... COVID-19传染病模型覆盖了从全球宏观尺度到活动场所微观尺度的多空间粒度.全球和国家级别的宏观尺度建模能帮助及时把握疫情的整体发展趋势,城市与乡镇级别的中观尺度建模能够为局部区域的防控措施提供更加针对性的参考.然而,对于落实到执行层面的城市内部各个管理单元,也同样需要更加细粒度的微观尺度建模提供精准防控的依据.得益于时空大数据与人类移动大数据的发展,耦合人群移动的COVID-19建模中出现了数据驱动下的城市内部建筑物[64]以及活动场所[65]的微观尺度建模.这些微观尺度的模型能够支撑基于城市内部具体区域与活动场所的精准干预建模,进而提供更加具有空间针对性的防控措施建议,降低社会成本.例如,面对COVID-19散发疫情,微观尺度模型能够评估城市内部社区级别的风险扩散等级,缩小核酸检测与区域限制的范围.因此,对于城市管理部门,更加细粒度的空间模型具有直接的指导意义,成为未来传染病建模的一项重要内容. ...
Integration of spatialization and individualization: the future of epidemic modelling for communicable diseases
1
2020
... 总体而言,相比于侧重对短期疫情规模进行精确预测的统计学习模型(如机器学习、回归模型),基于过程模拟的模型更关注推演疾病发展的中长期趋势,模拟评估不同干预措施的效果,并揭示疾病传播过程中一些隐蔽的特征.因此,基于过程模拟的模型不以准确预测未来感染规模为单一建模目的,而更是可以作为疫情中进行干预策略部署与调控决策的关键规划工具.对于个体模型,由于缺乏数据支撑,研究者长期以来主要利用人口普查、出行调查数据以及设定出行与接触规则等对个体移动和接触行为进行建模[51].得益于信息通讯技术的发展与人群时空活动大数据的涌现,个体模型逐步开始利用大规模手机定位等真实的轨迹大数据进行建模,向着时间、空间与人群3个维度的精细化方向不断发展[65,66],这一点在此次COVID-19建模研究中体现尤为明显.个体模型通过融合人类轨迹等多源时空大数据,利用计算机模拟技术对疾病传播过程中的个体、移动、接触、感染、场所、干预响应等诸多因素进行综合模拟与分析,是传染病模型面向真实世界建模的必然发展趋势,也得到研究者的愈加关注[67].然而,面对纷繁复杂的物理世界与人群行为,个体模型在耦合人群时空行为方面仍然面临巨大的挑战,还需利用多模态大数据,融合传播动力学、人工智能和复杂网络等多学科理论方法,深入开展个体属性与出行轨迹重构、个体移动接触网络构建等研究工作,为空间精准化、精细化的疫情预测与智能决策提供科学支持. ...
Quantifying population contact patterns in the United States during the COVID-19 pandemic
2
2021
... 总体而言,相比于侧重对短期疫情规模进行精确预测的统计学习模型(如机器学习、回归模型),基于过程模拟的模型更关注推演疾病发展的中长期趋势,模拟评估不同干预措施的效果,并揭示疾病传播过程中一些隐蔽的特征.因此,基于过程模拟的模型不以准确预测未来感染规模为单一建模目的,而更是可以作为疫情中进行干预策略部署与调控决策的关键规划工具.对于个体模型,由于缺乏数据支撑,研究者长期以来主要利用人口普查、出行调查数据以及设定出行与接触规则等对个体移动和接触行为进行建模[51].得益于信息通讯技术的发展与人群时空活动大数据的涌现,个体模型逐步开始利用大规模手机定位等真实的轨迹大数据进行建模,向着时间、空间与人群3个维度的精细化方向不断发展[65,66],这一点在此次COVID-19建模研究中体现尤为明显.个体模型通过融合人类轨迹等多源时空大数据,利用计算机模拟技术对疾病传播过程中的个体、移动、接触、感染、场所、干预响应等诸多因素进行综合模拟与分析,是传染病模型面向真实世界建模的必然发展趋势,也得到研究者的愈加关注[67].然而,面对纷繁复杂的物理世界与人群行为,个体模型在耦合人群时空行为方面仍然面临巨大的挑战,还需利用多模态大数据,融合传播动力学、人工智能和复杂网络等多学科理论方法,深入开展个体属性与出行轨迹重构、个体移动接触网络构建等研究工作,为空间精准化、精细化的疫情预测与智能决策提供科学支持. ...
... COVID-19建模中所使用的人群移动数据大多以匿名的、聚合的形式被分析,数据来源丰富,包括电信运营商提供的手机位置数据、互联网企业(例如百度、腾讯、谷歌、Cuebiq、SafeGraph等)提供的位置数据、含有地理标记的社交媒体数据(如Twitter、新浪微博等)以及其他开源数据集.基于此,常规的流动性指标易于被提取,例如:出行时长、出行距离、目的地类型、区域间人流量等.相关研究也考虑了不同社会经济属性人群的流动性[18,20],不同类型微观场所人流量[17],不同地区的社交距离指 数[19].然而,COVID-19在人群中的传播从根本上取决于人际间不同接触模式的发生效率与时空分布[67],而聚合层面上的整体流动性特征并不能从机理层面表达家庭、写字楼、工厂、商场、学校、公共交通等各类场景下的复杂接触模式.因此,面向复杂社会接触模式的分析与建模至关重要,如何利用大数据或者大小数据相结合的更加智能的方式对其进行突破成为一项挑战.此外,人们对疫情的认知以及干预措施的实施均会对人群流动以及社会接触模式产生不可忽视的影响,如何基于真实数据对这种复杂的人群时空行为响应进行耦合建模,进而形成动态反馈,也成为需要进一步研究的内容.除此之外,不同类型节假日与大型活动下产生的特殊的人口流动与接触模式也值得被耦合建模分析.综上,虽然当前的传染病模型已经在多个方面对人群移动进行了耦合建模,但是由于人群时空行为的复杂性,导致该方向的研究仍然面临巨大挑战,亟需进一步发展. ...
Heterogeneity and network structure in the dynamics of diffusion: Comparing agent-based and differential equation models
1
2008
... 耦合了大规模真实人群时空行为的精细化模型具有诸多优势,但是其运算量巨大,对计算资源要求甚高[68,69].尽管使用高性能计算环境可以提供更多的计算资源,但是这依然无法改变精细化模型所需要的巨大的计算开销,严重影响其对突发重大疫情的应急响应能力.因此,提升精细化模型的计算效率至关重要.一方面,需要通过研究大规模并行计算方法以提高模型计算效率;另一方面,在沉重的时间和成本负担下,应考虑复杂模型、精细化模型的数学简化问题,研究模型效益与计算成本之间的基础性问题,提升精细化模型的日常可用性与应急响应能力. ...
Simulation of pandemics in real cities: Enhanced and accurate digital laboratories
1
2021
... 耦合了大规模真实人群时空行为的精细化模型具有诸多优势,但是其运算量巨大,对计算资源要求甚高[68,69].尽管使用高性能计算环境可以提供更多的计算资源,但是这依然无法改变精细化模型所需要的巨大的计算开销,严重影响其对突发重大疫情的应急响应能力.因此,提升精细化模型的计算效率至关重要.一方面,需要通过研究大规模并行计算方法以提高模型计算效率;另一方面,在沉重的时间和成本负担下,应考虑复杂模型、精细化模型的数学简化问题,研究模型效益与计算成本之间的基础性问题,提升精细化模型的日常可用性与应急响应能力. ...
Epidemic model guided machine learning for COVID-19 forecasts in the United States
1
... 得益于人工智能的快速发展,耦合人群移动的COVID-19建模中呈现出相关技术融合应用的趋势.一方面,随着疫情在全球范围内的发展,相关数据日益累积,机器学习/深度学习已经逐渐成为疫情短期预测的主要建模工具.另一方面,机器学习与自然语言处理技术也被应用于对过程模拟模型中部分关键参数的估计,例如病例发现率、实时传播效率与接触概率等[70,71,72],以此提升模型的实时性与有效性.由于人工智能技术在多模态人群动态感知、复杂情况的最优化求解等众多方面的发展,其与传染病时空建模的更多融合有待进一步探索. ...
Predicting COVID-19 in China using hybrid AI model
1
2020
... 得益于人工智能的快速发展,耦合人群移动的COVID-19建模中呈现出相关技术融合应用的趋势.一方面,随着疫情在全球范围内的发展,相关数据日益累积,机器学习/深度学习已经逐渐成为疫情短期预测的主要建模工具.另一方面,机器学习与自然语言处理技术也被应用于对过程模拟模型中部分关键参数的估计,例如病例发现率、实时传播效率与接触概率等[70,71,72],以此提升模型的实时性与有效性.由于人工智能技术在多模态人群动态感知、复杂情况的最优化求解等众多方面的发展,其与传染病时空建模的更多融合有待进一步探索. ...
An Epidemiological Neural network exploiting Dynamic Graph Structured Data applied to the COVID-19 outbreak
1
2021
... 得益于人工智能的快速发展,耦合人群移动的COVID-19建模中呈现出相关技术融合应用的趋势.一方面,随着疫情在全球范围内的发展,相关数据日益累积,机器学习/深度学习已经逐渐成为疫情短期预测的主要建模工具.另一方面,机器学习与自然语言处理技术也被应用于对过程模拟模型中部分关键参数的估计,例如病例发现率、实时传播效率与接触概率等[70,71,72],以此提升模型的实时性与有效性.由于人工智能技术在多模态人群动态感知、复杂情况的最优化求解等众多方面的发展,其与传染病时空建模的更多融合有待进一步探索. ...
1
2013
... 值得注意的是,类似于COVID-19这种普遍人群易感的呼吸道传播疾病,其时空扩散受到人群移动的显著影响,对其进行人群移动活动的耦合建模相对直观.然而,人类社会存在着发生、流行与传播规律各异的传染病.例如,传染源可能是有症状患者、病原携带者或受感染的动物,传播途径可能是空气、接触、水或食物、媒介节肢动物、土壤、母婴垂直传播等[73].面对不同的传染病,在对其疫情的短期预测、中长期推演以及精细尺度下的干预效果评估等方面,需要有针对性地对人类时空活动进行耦合建模.因此,在时空大数据支持下,耦合人类时空活动的传染病建模还需要在各种类型的疾病上进行探索. ...
1
2013
... 值得注意的是,类似于COVID-19这种普遍人群易感的呼吸道传播疾病,其时空扩散受到人群移动的显著影响,对其进行人群移动活动的耦合建模相对直观.然而,人类社会存在着发生、流行与传播规律各异的传染病.例如,传染源可能是有症状患者、病原携带者或受感染的动物,传播途径可能是空气、接触、水或食物、媒介节肢动物、土壤、母婴垂直传播等[73].面对不同的传染病,在对其疫情的短期预测、中长期推演以及精细尺度下的干预效果评估等方面,需要有针对性地对人类时空活动进行耦合建模.因此,在时空大数据支持下,耦合人类时空活动的传染病建模还需要在各种类型的疾病上进行探索. ...